2. 大连理工大学 工程抗震研究所, 辽宁 大连 116024;
3. 中石化石油工程设计有限公司, 山东 东营 257026
2. Institue of Earthquake Engineering, Dalian University of Technology, Dalian 116024, China;
3. Sinopec Petroleum Engineering Corporation, Dongying, Shandoug 257026, China
管线作为最安全和经济的输送方式,成为陆上和海上油气资源的开发过程中一个不可或缺的重要部分并得到了广泛的应用[1-5]。油气输送钢质管道受到外部复杂环境和内部输送介质的双重影响,极易发生腐蚀,管道内外表面产生金属损失缺陷,使管道抵抗外界荷载能力降低,引起管道在缺陷处产生内压破坏,造成输送物质泄露,资源浪费和环境污染。
为保证管道输送介质的正常运输,管道在使用过程中均为受压状态。内压荷载是控制管道的壁厚的主要影响因素[1],因此准确的评估失效压力对于管道正常使用非常必要。流变应力σflow是评估管道失效压力的重要参数,材料的流变应力σflow 是Hahn等[2]提出的经验值,表征材料的应力应变关系和加工硬化行为等综合特性。加工硬化对管材韧性的影响直接改变管道承载力性能[6-7],流变应力的取值不仅影响完整管道的爆破压力P0,也影响缺陷管道的失效压力Pf,该参数的取值决定了评估结果是否准确。
不同准则对于流变应力的定义并不相同,流变应力取值方法多依靠工程经验,而且所有准则中流变应力的表达式并未考虑钢材材料的影响,不同等级钢材的流变应力表达形式完全一致。这种取值方式并未考虑不同材料之间的差异性,对于不同等级钢材的管道失效压力评估是不合适。本文在考虑应变强化的基础上,得到流变应力的解析解,并依据实际管道爆破试验验证了该解析解的适用性。同时结合不同等级钢材特性,分析了不同规范定义的流变应力所适用的管道钢材的强度等级。
1 不同流变应力取值模型缺陷管道的失效压力Pf主要有2部分决定:完好管道失效压力P0和折减系数fR。其中P0是评价失效压力的基础,它主要受流变应力σflow、管道壁厚t以及管道外径D的影响。
不同规范对流变应力σflow有不同的定义。美国机械工程师协会(ASME)在20世纪90年代建立了腐蚀管道剩余强度评价标准ASME B31G[8],将流变应力定义为σflow=1.1σs,σs 为管道材料规定屈服强度(SMYS)。Kiefner等[9-11]针对ASME B31G评估标准的保守性,分别对流变应力、Folias膨胀系数以及腐蚀缺陷区域进行了修正,称为改进的B31G方法(MB31G)或者RSTRENG 0.85 dL方法,将流变应力定义为σflow=σs+69 MPa。21世纪初期BG与DNV结合各自研究成果,形成了DNV-RP-F101腐蚀管道标准[12],将流变应力由管道钢材料的极限抗拉强度σu代替。Stephens等[13]基于中高强度钢腐蚀管道的试验和有限元计算结果,发展了指数函数形式的腐蚀管道失效压力计算公式,称为PCROOC方法,PCORRC与DNV-RP-F101一致,将σflow定义为极限抗拉强度σu。2003年Choi等[14]通过非线性有限元分析回归得到适用于API 5 L X65钢腐蚀管道失效压力计算公式,将σflow定义为0.9σu。Kim等[15]基于腐蚀焊缝管道失效压力的有限元数值计算结果,提出适用于含轴向焊缝和环向焊缝腐蚀管道剩余强度的评估方法,即对于轴向焊缝腐蚀管道,将σflow定义为0.95σu;对于环向焊缝腐蚀管道,将σflow定义为0.9σu。Benjamin等[16-17]开展轴向腐蚀管道全尺寸试验研究和数值模拟,提出了评价缺陷管道失效压力的RPA方法,与RSTRENG 0.85 dL一致,将σflow定义为σflow=σs+69 MPa。
2 流变应力取值模型对比分析根据缺陷管道破坏机理,缺陷管道在内压作用下的失效主要由缺陷处管道的环向应力决定,当环向应力超过管道极限抗拉强度后,发生破坏。而管道环向应力主要受流变应力的影响。现有常用的规范中评估是失效压力的模型起源于NG-18准则,它为美国Battelle实验室开发的基于半经验公式的流变应力的失效准则。其中流变应力决定了完好或者腐蚀管道的环向应力,对于缺陷管道的环向应力σθ=σflowfR,而对于完好管道σθ=σflow。对于具有不同缺陷尺寸的相同属性的管道,其折减系数fR是变化的,而流变应力是不变的,因此流变应力是决定腐蚀管道失效压力的关键,也是对管道压力失效评估的关键。
流变应力决定了管道环向应力的大小,该参数的不同取值可导致管道失效压力预测结果的较大差别。在低强度等级管道、中等强度等级管道和高强度等级管道中分别选取X42、X60和X100 3种强度等级管道为例。以DNV-RP-F101规范方法为基础,对比不同腐蚀深度失效压力值。表 1为算例中3种不同等级的钢管材料参数。
| 表 1 不同等级钢管材料参数 Table 1 Material parameters of steel pipes of different grades |
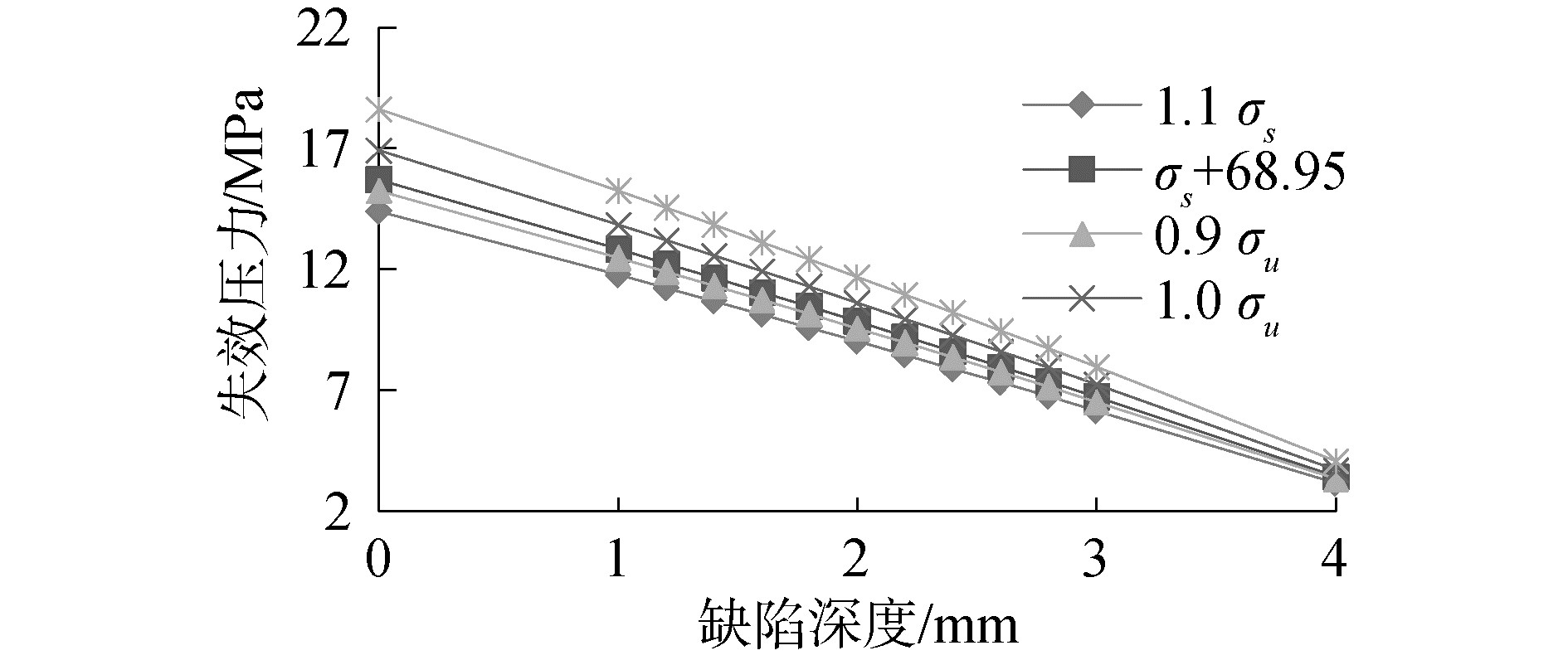
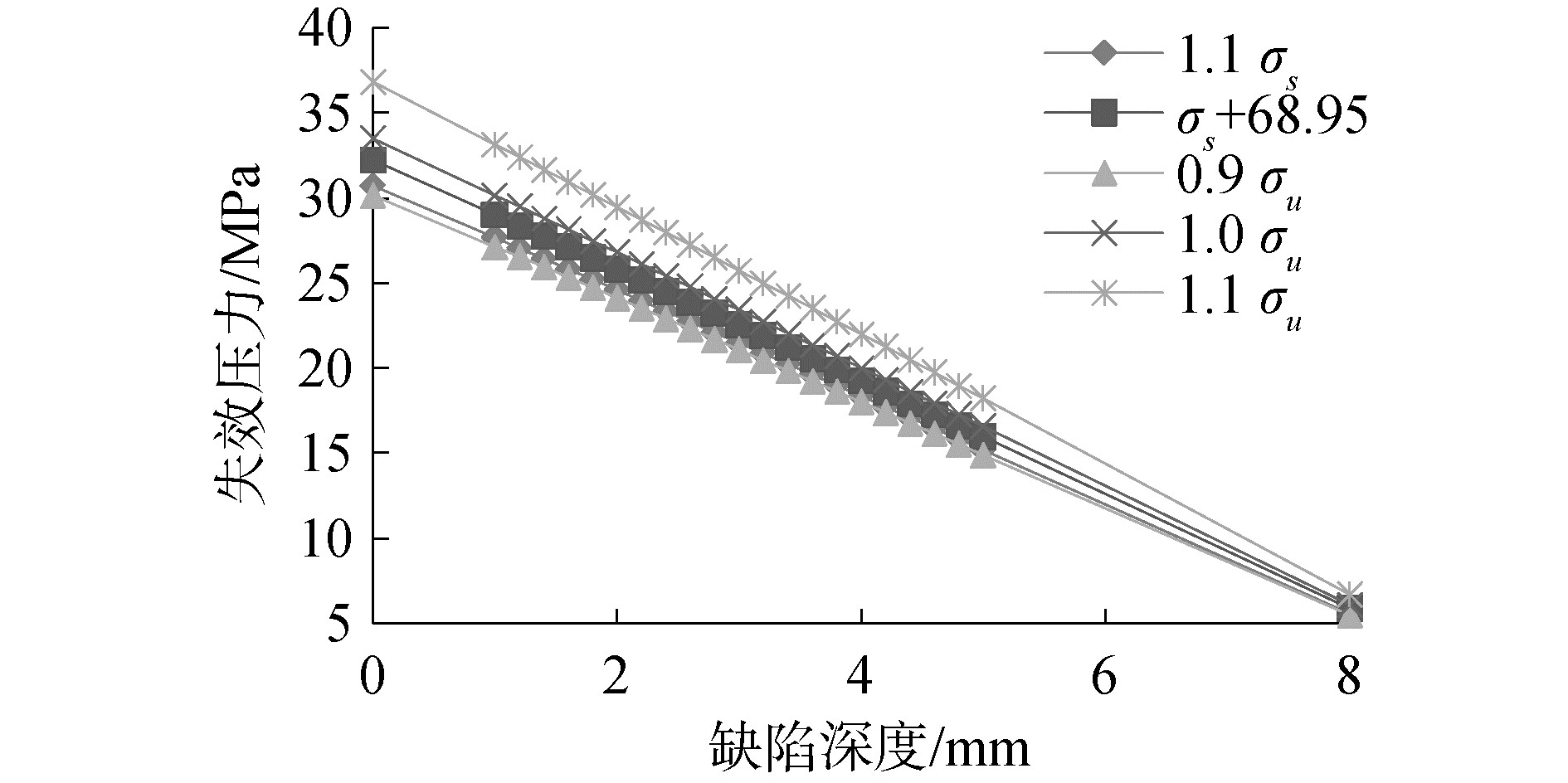
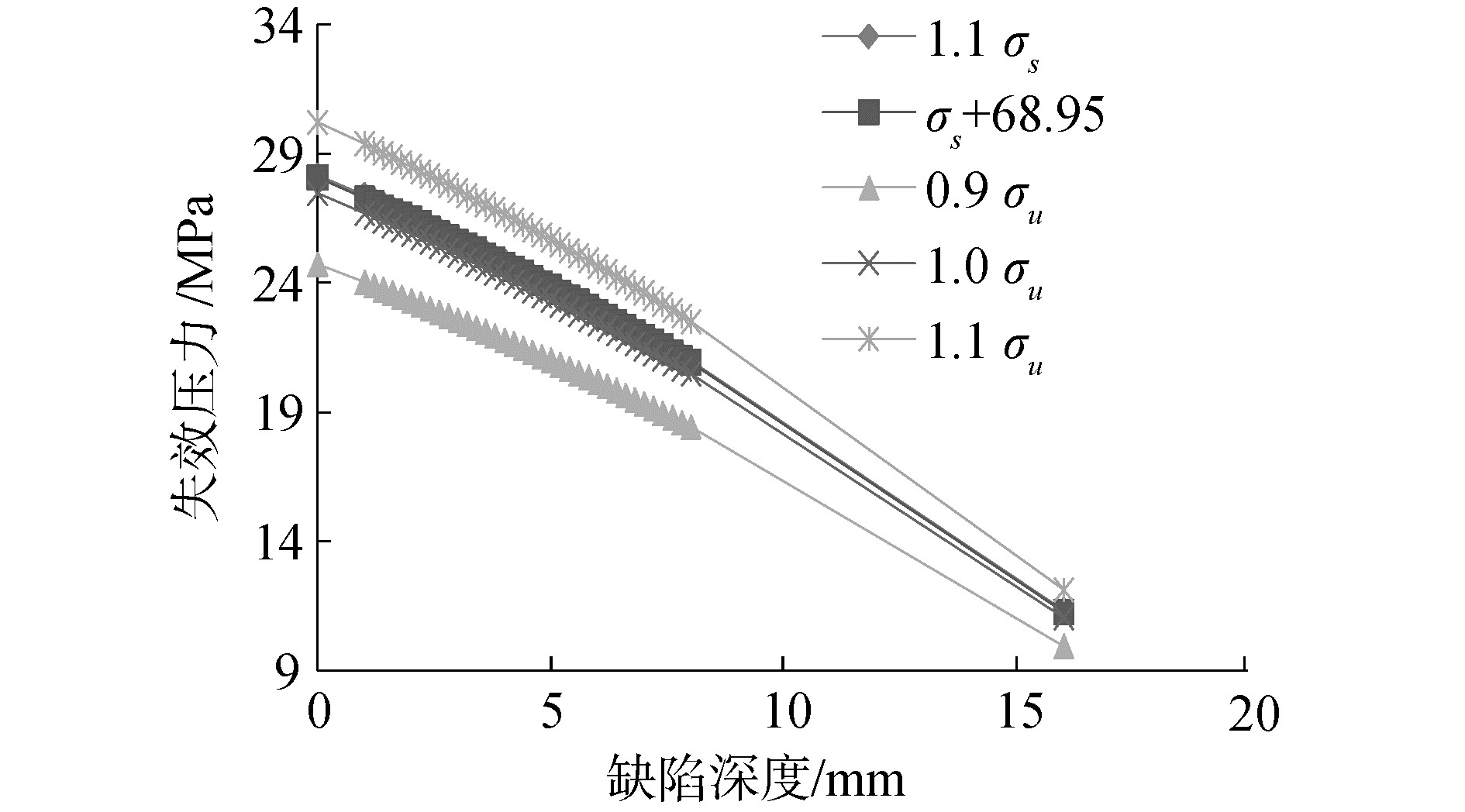
图 1~3为文献[18-20]中X42、X60和X100等级钢材采用不同流变应力取值方法失效压力随腐蚀深度变化趋势。对比看出,流变应力的取值方法的不同,造成管道失效压力评价结果的差异。对于X42算例最大差值4.24 MPa,相差29.44%;X60算例最大差值6.11 MPa,相差19.91%;X100算例最大差值5.5 MPa,相差22.22%。最大差值均出现在缺陷深度为0,即完好管道工况,当管道全部腐蚀时,失效压力为0 MPa,此时流变应力不同取值方法无差别。
|
Download:
|
| 图 1 流变应力对X42钢管失效压力的影响 Fig. 1 Effect of flow stress on failure pressure of X42 steel pipe | |
|
Download:
|
| 图 2 流变应力对X60钢管失效压力的影响 Fig. 2 Effect of flow stress on failure pressure of X60 steel pipe | |
|
Download:
|
| 图 3 流变应力对X100钢管失效压力的影响 Fig. 3 Effect of flow stress on failure pressure of X100 steel pipe | |
失效压力随着缺陷深度的增加而减小,而且下降幅度与流变应力呈正相关,流变应力越大下降幅度越大。当流变应力取较小值时,虽然起点失效压力较小,但是其下降幅度较小,因此随着缺陷深度的增加,流变应力的不同取值方式所计算得到的失效压力越来越接近。不同流变应力的取值方法在缺陷深度较小时对失效压力影响较大,随着缺陷深度的增加影响不断减小。
由不同钢管等级的流变应力取值对比图看出,不同等级钢材的不同流变应力取值方式对失效压力影响也不同。考虑到由于管材材料属性的差异,抗拉强度与屈服强度的比值(简称强屈比)随着钢材等级增加不断减小,X42强屈比为1.29,X60强屈比为1.199,X100强屈比为1.07。随着屈服强度的减小,屈服强度数值与抗拉强度数值越来越接近,造成不同强度等级钢材的不同取值方式的流变应力排列顺序额也各不相同。对于X42等级钢材,屈服强度σs与抗拉强度σu差距较大,1.1σs≤σs+68.95≤0.9σu≤1.0σu≤1.1σu;对于X60,1.1σs≤0.9σu≤σs+68.95≤1.0σu≤1.1σu,由于屈服强度σs与抗拉强度σu 差距较小,相比于X42,σs+68.95≥0.9σu;对于X100等级钢材,由于屈服强度σs与抗拉强度σu十分接近,0.9σu≤1.0σu≤σs+68.95≤1.1σs≤1.1σu。由此可见流变应力的不同取值方式不仅对失效压力影响较大,且对不同等级的管道影响模式并不一致,因此流变应力的取值应与钢材等级相关联。
3 考虑应变强化的流变应力计算模型根据缺陷管道破坏机理,缺陷管道在内压作用下的失效主要由缺陷处管道的环向应力决定,当环向应力超过管道极限抗拉强度后发生破坏。对于缺陷管道,腐蚀缺陷的尺寸、形状和管道属性决定了折减系数fR;流变应力σflow决定了完好管道的失效压力P0。因此流变应力σflow是确定腐蚀管道失效压力的要素,也是对管道压力失效评估的关键。
3.1 极限内压载荷的确定研究表明管道在内压影响下的失效行为为塑性大变形,可采用幂次强化模型对齐应变强化效应进行模拟[1],幕次强化模型可以表示为:
| $ {\sigma ^\prime } = K{({\varepsilon ^\prime })^n} $ | (1) |
式中:K为强化系数;n为强化指数;σ′为真实应力;ε′为真实应变。
对于管道类薄壁结构,径向应力可以忽略,由平衡方程可知:
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _1} = {\sigma _\theta } = \frac{{P\left( {{D^\prime } - 2{t^\prime }} \right)}}{{2{t^\prime }}}}\\ {{\sigma _2} = {\sigma _z} = \frac{{P\left( {{D^\prime } - 2{t^\prime }} \right)}}{{4{t^\prime }}}}\\ {{\sigma _3} = {\sigma _r} = P \approx 0} \end{array}} \right. $ | (2) |
式中:σ1、σ2和σ3分别为第一、第二和第三主应力;σθ、σz和σr分别为管道环向、轴向和径向应力;D′为外界荷载下管道发生变形后的外直径;t′为相应的变形后的管道壁厚。
根据von Mises形状改变比能屈服准则,该应力状态下,von Mises等效应力σe为:
| $ \begin{array}{l} {\sigma _e} = \sqrt {\frac{1}{2}\left[ {{{\left( {{\sigma _1} - {\sigma _2}} \right)}^2} + {{\left( {{\sigma _2} - {\sigma _3}} \right)}^2} + {{\left( {{\sigma _1} - {\sigma _3}} \right)}^2}} \right]} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {\sigma _\theta ^2 - {\sigma _\theta }{\sigma _z} + \sigma _z^2} = \frac{{\sqrt 3 }}{4}\frac{{P\left( {{D^\prime } - 2{t^\prime }} \right)}}{t} \end{array} $ | (3) |
对于管道在受压过程中发生的塑性变形,可认为管材体积不可压缩,所以环向应变εθ、轴向应变εz和径向应变εr之和为0,即εθ+εr+εz=0,轴向应变很小可以忽略不计εz≈0[1],因此εθ=-εr,von Mises有效应变εe为:
| $ {\varepsilon _e} = \sqrt {\frac{2}{3}[{\varepsilon _\theta }^2 + {\varepsilon _r}^2 + {\varepsilon _z}^2]} = \frac{2}{{\sqrt 3 }}{\varepsilon _\theta } $ | (4) |
管道的有限变形中,第一、第二和第三主应变ε1、ε2和ε3为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\varepsilon _1} = {\varepsilon _\theta } = \int {\rm{d}} \varepsilon = \int\limits_{D - 2t}^{{D^\prime } - 2{t^\prime }} {\frac{{{\rm{d}}l}}{l}} = \ln \frac{{{D^\prime } - 2{t^\prime }}}{{D - 2t}}}\\ {{\varepsilon _2} = {\varepsilon _z} = 0}\\ {{\varepsilon _3} = {\varepsilon _r} = \ln \left( {\frac{{{t^\prime }}}{t}} \right)} \end{array}} \right. $ | (5) |
式中:D为管道原始外直径;t为原始管道壁厚。
根据式(3)、(4)和(5),可以得到:
| $ \frac{{{t^\prime }}}{{{D^\prime } - 2{t^\prime }}} = \frac{t}{{D - 2t}}{{\rm{e}}^{ - \sqrt 3 {\varepsilon _e}}} $ | (6) |
所以爆破压力为:
| $ P = \frac{4}{{\sqrt 3 }}\frac{{{t^\prime }}}{{{D^\prime } - 2{t^\prime }}}{\sigma _e} = \frac{4}{{\sqrt 3 }}\frac{t}{{D - 2t}}{{\rm{e}}^{ - \sqrt 3 {\varepsilon _e}}}K{\varepsilon _e}^n $ | (7) |
当管道极限内压产生时,P达到极值,即
| $ {\varepsilon _e} = \frac{n}{{\sqrt 3 }} $ | (8) |
则管道的爆破失效压力解析解Plimit为:
| $ {P_{{\rm{limit }}}} = \frac{4}{{{{(\sqrt 3 )}^{n + 1}}}}\frac{t}{{D - 2t}}K{\left( {\frac{n}{e}} \right)^n} $ | (9) |
不同屈服准则下完好管道的失效压力可表示为:
| $ {P_{{\rm{limit }}}} = {\left( {\frac{C}{2}} \right)^{n + 1}}\frac{{4t}}{{D - 2t}}K{\left( {\frac{n}{e}} \right)^n} $ | (10) |
式中:C为不同屈服准则参数,采用Tresca准则C=1;采用von Mises准则
假设管道在变形时体积未发生变化,则可通过工程应力和工程应变得到真实应力和应变:
| $ {\varepsilon ^\prime } = \ln (1 + \varepsilon ),{\sigma ^\prime } = \sigma (1 + \varepsilon ) $ | (11) |
式中:ε′为真实应变;ε为工程应变;σ′为真实应力;σ为工程应力。
用工程应力和工程应变表达管道的本构模型为:
| $ \sigma = K\frac{{{{[\ln (1 + \varepsilon )]}^n}}}{{1 + \varepsilon }} $ | (12) |
在管材受拉过程中,对于塑性大变形失稳,定义为
| $ n = \ln (1 + {\varepsilon _u}) = {\varepsilon _u}^\prime $ | (13) |
式中εu′是极限强度的真实应变。
由此可知:
| $ K = {\sigma _u}{\left( {\frac{{\rm{e}}}{n}} \right)^n} $ | (14) |
将式(14)代入式(10),得到不同屈服准则的完好管道的失效压力为:
| $ {P_{{\rm{limit }}}} = {\left( {\frac{C}{2}} \right)^{n + 1}}\frac{{4t}}{{D - 2t}}{\sigma _u} $ | (15) |
完好管道内压破坏时的名义环向应力被定义为流变应力,由式(15)知管道破坏时的名义环向应力为:
| $ \begin{array}{*{20}{c}} {{\sigma _{{\rm{flow }}}} = {\sigma _\theta } = {P_{{\rm{limit }}}}\frac{{D - 2t}}{{2t}} = }\\ {{{\left( {\frac{C}{2}} \right)}^{n + 1}}\frac{{4t}}{{D - 2t}}{\sigma _u}\frac{{D - 2t}}{{2t}} = 2{{\left( {\frac{C}{2}} \right)}^{n + 1}}{\sigma _u}} \end{array} $ | (16) |
为得到完好管道的失效压力,需要知道管道强化指数参数。对于没有该参数实际数据的管道,可通过式(12)和式(13)得到管道强化指数:
| $ \begin{array}{*{20}{c}} {\frac{{{\sigma _s}}}{{{\sigma _u}}} = \frac{{{\sigma _s}^\prime }}{{1 + {\varepsilon _s}}}/\frac{{{\sigma _u}^\prime }}{{1 + {\varepsilon _u}}} = \frac{{{\sigma _s}^\prime }}{{{\sigma _u}^\prime }}\frac{{1 + {\varepsilon _u}}}{{1 + {\varepsilon _s}}} = }\\ {\frac{{K{{\left( {{\varepsilon _s}^\prime } \right)}^n}}}{{K{{\left( {{\varepsilon _u}^\prime } \right)}^n}}}\frac{{1 + {\varepsilon _u}}}{{1 + {\varepsilon _s}}} = \frac{1}{{1 + {\varepsilon _s}}}{{\left[ {\frac{{e\ln \left( {1 + {\varepsilon _s}} \right)}}{n}} \right]}^n}} \end{array} $ | (17) |
式中:σs′和σu′分别为真实屈服强度和抗拉强度,εs为屈服强度对应的工程应变,e= 2.718 28。结合式(17),通过屈服强度、抗拉强度和屈服应变可以得到管道钢材的强化指数。通常将0.2%塑性应变产生时对应的应力定义为屈服强度,则屈服应变为:εs=0.002+σs/E。
4 流变应力的数值验证本文搜集了22个管道全尺寸爆破试验,强度等级从X46到X120,包括了低等强度钢材、中等强度钢材和高等强度钢材。管道基本数据如表 2所示。Zhu等[21-22]结合Tresca和Mises 2种典型屈服理论,对管道失效压力进行分析,提出了完好管道的塑性失效模型。对于不同强度等级的钢材,主要区别在于屈强比,强度等级越高,屈强比数值越大。因此高强度等级钢材其屈服阶段到强化阶段的应力差别较小,该类型钢材内压失效不仅受到处于强化阶段第一主应力影响,还会受到处于屈服阶段的第二主应力的影响。根据研究结果,Zhu等[21-22]认为对于高应变钢材应采用Tresca屈服准则;对于低应变钢材应采用Mises屈服准则。由此可知,Mises准则适用于高强度等级钢材,Tresca准则适用于低等强度等级钢材。对于X80钢材,其屈强比为0.9,即屈服强度和抗拉强度相差不大。故对于X80以下等级钢材采用Tresca准则,令C=1;对于X80等级以上包括X80等级钢材,采用von Mises准则,令
| $ {P_0} = {O_{{\rm{flow}}}}\frac{{2t}}{{D - t}} $ | (18) |
| 表 2 完好管道爆破试验数据 Table 2 Blasting test data of intact pipeline |
流变应力分别选取1.1σs、σs+68.95、0.9σu、1.0σu、1.1σu 常用5种取值方式,以及本文提出的解析解,分别计算失效压力,并进行对比分析。不同流变应力的取值方法计算得到的失效压力与爆破实验结果的对比如表 3示。由对比可以看出,解析解的误差绝对值最小值、最大值和平均值均小于其他方法,且平均误差仅为4.01%远优于其他方法。由此可知解析解的准确性要优于其他方法。
| 表 3 不同计算方法误差对比 Table 3 Error comparison of different calculation methods |
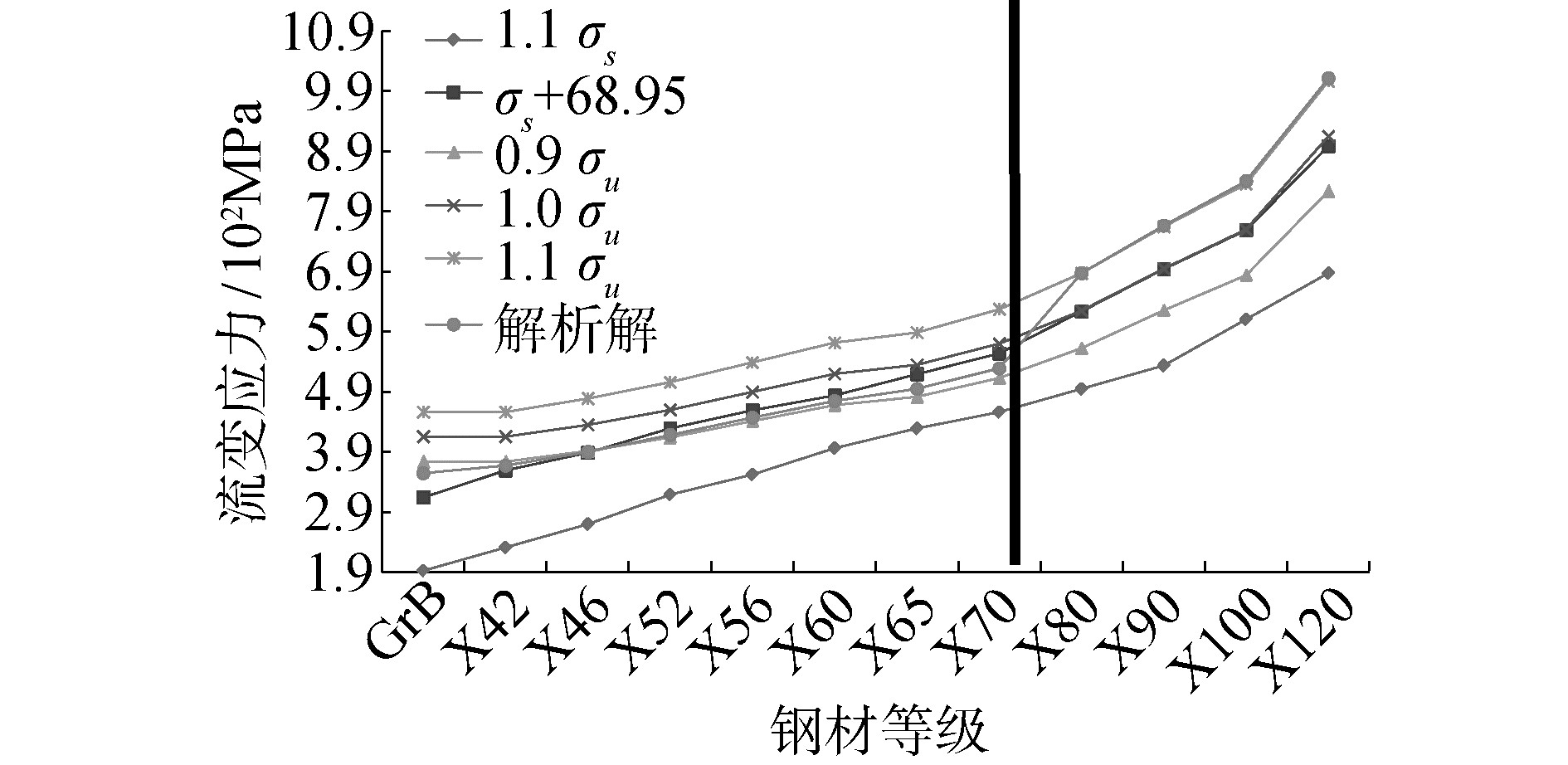
因为钢材自身的材料特性,不同等级钢材其屈强比并不相同,因此常用的流变应力5种取值方法1.1σs、σs+68.95、0.9σu、1.0σu和1.1σu 的适用性和差异性也并不相同。API Spec 5 L[26]管线钢管规范给出了不同等级钢管材拉伸试验结果,包括管材屈服强度和极限抗拉强度的变化范围。根据规范API 5 L规定的最小屈服应力和抗拉强度,由式(17)计算得到材料强化指数n。图6为不同流变应力取值方式对比,由图中可以看出所有的取值方法流变应力均随刚才强度等级的增加而增加,但是不同流变应力取值方式随着钢材等级的增加差异性发生变化。例如当钢材等级小于或等于X46时,流变应力取值0.9σu大于σs+68.95,因此流变应力按照σs+68.95方法取值更为保守;而当钢材等级大于等于X52时,流变应力取值σs+68.95大于0.9σu,因此流变应力按照0.9σu方法取值更为保守。又例如当钢材等级小于或等于X70时,即钢材为低中强度等级钢材时,流变应力取值1.0σu大于σs+68.95,因此流变应力按照σs+68.95方法取值更为保守;而当钢材等级大于等于X80时,即钢材为高强度等级钢材时,流变应力取值σs+68.95和1.0σu基本一样,此时两者的保守性一致,没有差异性。
图 4中圆点为解析解(式(16))的流变应力随管道等级变化规律,该种方法是在有限应变的基础上,考虑材料强化得到的解析解,相比其他方法更加准确。由图6中解析解与其他方法的对比可以看出,不同钢材等级的流变应力大致可以分为2段:
|
Download:
|
| 图 4 不同流变应力取值方式对比 Fig. 4 Comparison of different flow stress values | |
1) 当钢材等级小于等于X70时,钢材适用Tresca破坏准则,
2) 当钢材等级大于等于X80时,钢材适用Mises破坏准则,
由此可知,当钢材等级小于等于X70时,σs+68.95和0.9σu 取值方法与解析解更为接近,这2种取值方法更为适合该种等级钢材;当钢材等级大于等于X80时,1.1σu取值方法与解析解更为接近,这种取值方法更为适合该种等级钢材。而1.0σu的流变应力取值方法,正好处于低中强度等级钢材和高强度等级钢材取值之间,因此其失效压力预测误差最小值、最大值和平均值均处于所有方法的中间状态。但正是因为1.0σu的流变应力取值处于2种最优取值方法之间,当校核数据增多,钢材等级范围扩大时,特别是不能确定钢材适应哪种破坏准则时,采用1.0σu作为流变应力进行失效压力预测时,虽然不能做到与真实值极为接近,但是误差也不会非常大,此时1.0σu 流变应力取值方法就彰显了其自身的实用性。这也是DNV-RP-F101方法被证实其普遍性和实用性[12]的原因。
6 结论1) 管道的流变应力与强化指数和破坏准则相关,而管道的强化指数和破坏准则随着管道材料屈强比和管材等级变化而变化,因此不同强度等级的管道其流变应力取值系数
2) 常用的流变应力取值方法1.1σs、σs+68.95、0.9σu、1.0σu和1.1σu对所有等级的钢材均采用相同流变应力取值模型,并未考虑管道等级所造成的材料差异性,因此其适用范围较为狭窄,各个方法的差异性也随着管道等价的变化而变化。
3) 考虑到不同强度等级的管道所适合的破坏准则并不相同,当钢材等级小于等于X70时,σflow≈0.9σu,此时流变应力取值为0.9σu 时更为准确;当钢材等级大于等于X80时,σflow≈1.1σu,此时流变应力取值为1.1σu时更为准确。
| [1] |
张海琛, 佟丽莉, 王丽君, 等. 非粘结柔性立管轴对称载荷作用下的理论模型分析[J]. 应用科技, 2020, 47(3): 11-16. ZHANG Haichen, TONG Lili, WANG Lijun, et al. Theoretical model analysis of unbonded flexible riser under axisymmetric load[J]. Applied science and technology, 2020, 47(3): 11-16. (  0) 0)
|
| [2] |
王岳, 马瑞, 何磊. 船舶管件生产的CONWIP控制方案设计研究[J]. 应用科技, 2020, 47(1): 8-14. WANG Yue, MA Rui, HE Lei. Design of CONWIP control scheme for production of ship pipes[J]. Applied science and technology, 2020, 47(1): 8-14. (  0) 0)
|
| [3] |
余移山, 陆继东, 董美蓉, 等. T91金属管道表面特性对LIBS测量的影响[J]. 应用科技, 2020, 47(4): 82-87. YU Yishan, LU Jidong, DONG Meirong, et al. Study on the influence of surface characteristics of T91 metal pipeline on laser-induced breakdown spectroscopy measurement[J]. Applied science and technology, 2020, 47(4): 82-87. (  0) 0)
|
| [4] |
陈严飞. 海底腐蚀管道破坏机理和极限承载力研究[D]. 大连: 大连理工大学, 2009. CHEN Yanfei. Study on failure mechanism and ultimate load capacity of corroded submarine pipeline[D]. Dalian: Dalian University of Technology, 2009. (  0) 0)
|
| [5] |
HAHN G T, SARRATE M, ROSENFIELD A R. Criteria for crack extension in cylindrical pressure vessels[J]. International journal of fracture mechanics, 1969, 5(3): 187-210. (  0) 0)
|
| [6] |
刘志伟, 刘聪, 薛启超. 基于约束参数的断裂韧性转化研究[J/OL]. 应用科技: 1-6[2020-12-25]. http://kns.cnki.net/kcms/detail/23.1191.U.20201203.1049.002.html. LIU Zhiwei, LIU Cong, XUE Qichao. Transformation of fracture toughness based on constraint parameters[J/OL]. Applied Science and Technology: 1-6[2020-12-25]. http://kns.cnki.net/kcms/detail/23.1191.U.20201203.1049.002.html. (  0) 0)
|
| [7] |
刘志伟, 刘聪, 薛启超. 铁素体钢材韧脆转变温度数值分析[J/OL]. 应用科技: 1-7[2020-12-25]. http://kns.cnki.net/kcms/detail/23.1191.U.20201207.1530.006.html. LIU Zhiwei, LIU Cong, XUE Qichao. Numerical analysis of ductile brittle transition temperature of ferritic steel[J]. Applied Science and Technology: 1-7[2020-12-25]. http://kns.cnki.net/kcms/detail/23.1191.U.20201207.1530.006.html. (  0) 0)
|
| [8] |
AS ME. ASME B31G-1991, Manual for determining the remaining strength of corroded pipelines-a supplement to ASME B31 code for pressure piping[J]. New York: The American Society of Mechanical Engineers, 1991. (  0) 0)
|
| [9] |
KIEFNER J F, VIETH P H. A modified criterion for evaluating the remaining strength of corroded pipe, PR-3-805[J]. Columbus: Battelle Columbus, 1989. (  0) 0)
|
| [10] |
KIEFNER J F, VIETH P H, KIEFNER J F, et al. New method corrects criterion for evaluating corroded pipe[J]. Oil and gas journal, 1990, 88(32): 56-59. (  0) 0)
|
| [11] |
KIEFNER J F, VIETH P H. PC program speeds new criterion for evaluating corroded pipe[J]. Oil and gas journal, 1990, 88(34): 91-93. (  0) 0)
|
| [12] |
Det Norske Veritas. DNV-RP-F101, Recommend practice DNV-RP-F101 corroded pipelines[S]. Norway: Det Norske Veritas, 2004.
(  0) 0)
|
| [13] |
STEPHENS D R, LEIS B N. Development of an alternative criterion for residual strength of corrosion defects in moderate- to high-toughness pipe[C]//Proceedings of the 3rd International Pipeline Conference. Calgary, Alberta, Canada, 2000.
(  0) 0)
|
| [14] |
CHOI J B, GOO B K, KIM J C, et al. Development of limit load solutions for corroded gas pipelines[J]. International journal of pressure vessels and piping, 2003, 80(2): 121-128. DOI:10.1016/S0308-0161(03)00005-X (  0) 0)
|
| [15] |
KIM Y P, KIM W S, LEE Y K, et al. The evaluation of failure pressure for corrosion defects within girth or seam weld in transmission pipelines[C]//Proceedings of 2004 International Pipeline Conference. Calgary, Alberta, Canada, 2004.
(  0) 0)
|
| [16] |
BENJAMIN A C, ANDRADE E Q. Modified method for the assessment of the remaining strength of corroded pipelines[C]//Proceedings of the 1st Rio Pipeline Conference. Rio de Janeiro, Brazil, 2003.
(  0) 0)
|
| [17] |
ANDRADE E Q, BENJAMIN A C. Structural evaluation of corrosion defects in pipelines: comparison of FE analyses and assessment methods[C]//Proceedings of the Fourteenth International Offshore and Polar Engineering Conference. Toulon, France, 2004.
(  0) 0)
|
| [18] |
CRONIN D S, PICK R J. Experimental database for corroded pipe: evaluation of RSTRENG and B31G[C]//Proceedings of the 23rd International Pipeline Conference. Calgary, Alberta, Canada, 2000: 757-767.
(  0) 0)
|
| [19] |
FREIRE J L F, VIEIRA R D, CASTRO J T P, et al. Part 3: burst tests of pipeline with extensive longitudinal metal loss[J]. Experimental techniques, 2006, 30(6): 60-65. DOI:10.1111/j.1747-1567.2006.00109.x (  0) 0)
|
| [20] |
ADVANTICA. Project #153H: corrosion assessment guidance for high strength steels, No. L52294[R]. Houston, Texas, USA: PRCI, 2008.
(  0) 0)
|
| [21] |
ZHU X K, LEIS B N. Influence of yield-to-tensile strength ratio on failure assessment of corroded pipelines[J]. Journal of pressure vessel technology, 2005, 127(4): 436-442. DOI:10.1115/1.2042481 (  0) 0)
|
| [22] |
ZHU X K, LEIS B N. Theoretical and numerical predictions of burst pressure of pipelines[J]. Journal of pressure vessel technology, 2007, 129(4): 644-652. DOI:10.1115/1.2767352 (  0) 0)
|
| [23] |
LIESSEM A, GRDEF M K, KNAUF G, et al. In uence of thermal treatment on mechanical properties of UOE linepipe[C]//Proceedings of the Fourth International Conference of Pipeline Technology. Ostend, Belgium, 2004: 1263-1281.
(  0) 0)
|
| [24] |
BENJAMIN A C, FREIRE J L F, VIEIRA R D. Part 6: analysis of pipeline containing interacting corrosion defects[J]. Experimental techniques, 2007, 31(3): 74-82. DOI:10.1111/j.1747-1567.2007.00190.x (  0) 0)
|
| [25] |
PAPKA S D, STEVENS J H, MACIA M L, et al. Full-size testing and analysis of X120 linepipe[C]//Proceedings of the Thirteenth International Offshore and Polar Engineering Conference. Honolulu, Hawaii, USA, 2003.
(  0) 0)
|
| [26] |
American Petroleum Institute (API) Specification 5 L. Specification for line pipe[J]. Washington, DC, 2000. (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


