水面无人艇(umanned surface vehicle, USV)在大量的任务,如测深制图、环境监测和港口监视中证明它们对科学、商业和军事都具有重要价值应用[1]。在一个典型的预先计划的任务场景中水面无人艇被要求精确地沿着指定的路径。如在执行港口区域巡航时,其区域范围不大,同时具有多障碍物,因此要求每个过航点的容许误差足够小,水面无人艇速度能够随时改变且不影响跟踪精度,以确保区域跟踪完成度和安全避障。因此,在执行机构(舵机)响应速度确定的情况下,如何在路径跟踪精度和跟踪完成度进行取舍、如何尽可能地削减水面无人艇速度对路径精度的影响,成为当下路径跟踪方面研究的热点。
目前已有许多在工业上被广泛使用的移动机器人的路径跟踪控制方法,如胡萝卜跟踪法(CC)[3]在期望路径上引入虚拟目标点(virtual-target-point,VTP),通过追逐恒定距离的虚拟目标点最终到达期望目标点;向量场法(VF)[4]在期望路径周围建立矢量场,每个矢量均为引导机器人走向期望路径的最优方向;视线法(line-of-sight,LOS)[5]等。对于水面无人艇来说,目前的研究热点为视线法。虽然视线法已经在不同的水面无人艇上得到了不同程度的成功,但事实证明,大多数评估实验只在环境影响最小的理想环境中进行。在恶劣的天气条件下,研究人员依旧很难确定实际的视线法控制器的性能。董早鹏等[6]采用反步法提出了基于非对称模型的视线法改进。付悦文[7]在此基础上提出了基于无模型自适应视线法。陈霄等[8]提出了2种改进积分视线导引策略,并利用级联系统理论证明了当所有控制目标实现时,控制系统为全局k-指数稳定的。
视线法是基于一个沿着期望路径移动的虚拟目标,最初起源于导弹的跟踪。通过对运动目标的追逐,导弹最终会汇聚到路径上。作为一种基本方法,已被水面无人艇研究人员广泛应用于由直线和圆形路径组成的轨迹跟踪。本文针对水面无人艇纵向速度与横侧偏差的耦合及不同跟踪范围下平滑期望艏向曲线的问题提出基于自适应双曲正切视线法导引律,通过仿真试验比较基于自适应双曲正切视线法与传统视线法,分析基于自适应双曲正切视线法的优点。最后通过外场试验验证该算法在实际应用中的控制性能。
1 视线法制导律基于视线法设计路径跟随的制导系统,原理如图 1所示。

|
Download:
|
| 图 1 LOS制导律原理 Fig. 1 The LOS guidance based on lookahead distance | |
视线法制导律的目标在于减少横侧偏差δ,同时使得船体航向能够沿路径方向前进,即:
| $ {\mathop {{\rm{lim}}}\limits_{t \to \infty } \delta (t) = 0} $ | (1) |
| $ {\mathop {{\rm{lim}}}\limits_{t \to \infty } \left\| {\mathit{\boldsymbol{d}}(t)} \right\| = \mathop {{\rm{lim}}}\limits_{t \to \infty } \left\| {{\mathit{\boldsymbol{P}}_t} - {\mathit{\boldsymbol{P}}_{k + 1}}} \right\| = 0} $ | (2) |
由图 1得:
| $ {\delta (t) = - \Delta x{\rm{sin}}{\kern 1pt} {\kern 1pt} {\varphi _{pk}} + \Delta y{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _{pk}}} $ | (3) |
| $ \begin{array}{l} \dot \delta (t) = - \Delta \dot x{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _{pk}} - {{\dot \varphi }_{pk}}\Delta x{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _{pk}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta \dot y{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _{pk}} - {{\dot \varphi }_{pk}}\Delta y{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi _{pk}} \end{array} $ | (4) |
式中:Δx=xt-xk;Δy=yt-yk。
欠驱动水面无人艇三自由运动学和动力学模型为:
| $ \left\{ {\begin{array}{*{20}{l}} {\dot \eta = J(\psi )v}\\ {M\dot v + C(v)v + D(v) = Bf} \end{array}} \right. $ | (5) |
由式(5)和图 1所示几何关系得:
| $ \dot \delta (t) = U{\rm{sin}}(\varphi + \beta - {\varphi _{pk}}) $ | (6) |
式中:
由于期望路径是由多点组成,引入安全半径Rsafe判断水面无人艇是否进行下一个目标点的跟随,安全半径的距离一般设为船长的2~3倍。
| $ {R_{{\rm{safe}}}} = \left\{ {\begin{array}{*{20}{l}} {{P_{k + 1}},}&{{R_{{\rm{safe}}}} < \left\| {d(t)} \right\|}\\ {{P_{k + 2}},}&{{R_{{\rm{safe}}}} \ge \left\| {d(t)} \right\|} \end{array}} \right. $ | (7) |
视线法需要的参数较少,且为几何算法,能够高效地计算期望航向,同时期望航向的获取只与船舶的实时位置和给定的期望航线有关,因此被广泛的应用在水面无人艇的路径跟随中。但传统视线法忽略了航线范围和水面无人艇纵向速度u与横侧偏差δ的耦合关系,工程应用中水面无人艇在跟踪范围改变及变速情况下需要重新设置参数。为解决上述问题,本文基于包围圈视线法导引策略采用自适应观测技术以及针对包围圈引入tanh函数提出基于自适应双曲正切视线法导引策略。
2.1 基于双曲正切的视线法制导律期望路径与水面无人艇视线圆(r=R)的交点为虚拟目标点T,视线角φlos为当前虚拟目标点与水面无人艇的连线与期望路径之间夹角:
| $ {\varphi _{{\rm{los}}}} = {\rm{arctan}}\left( {\frac{\delta }{{\sqrt {{R^2} - {\delta ^2}} }}} \right) $ | (8) |
得期望艏向角为:
| $ {\varphi _d} = {\varphi _{{\rm{pk}}}} - {\varphi _{{\rm{los}}}} - \beta $ | (9) |
展开式(4),得:
| $ \begin{array}{*{20}{l}} {{\varphi _d} = {\rm{atan2}}({y_{k + 1}} - {y_k},{x_{k + 1}} - {x_k}) - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{arctan}}\left( {\frac{\delta }{{\sqrt {{R^2} - {\delta ^2}} }}} \right) - {\rm{arctan}}\frac{v}{u}} \end{array} $ | (10) |
式中:atan2为四象限反正切函数
从式(10)及图 3得,当δ≥R,上述传统视线法失效。为避免此情况发生,传统做法如下:

|
Download:
|
| 图 3 不同LOS制导律对比 Fig. 3 The compare of the different guidance methods | |
| $ \left\{ {\begin{array}{*{20}{l}} {R = R,}&{R > \delta }\\ {R = k\delta ,}&{R \le \delta } \end{array}} \right. $ | (11) |
式中:k为正的控制参数,取k>1。
文献[11]提出一种动态调节视线圆半径R的方法:
| $ R = \bar R/(|\delta + 1|) + k|\delta |) $ | (12) |
式中:R、k为正的控制参数,一般取R>10, k>1。
在水面无人艇执行变速任务时,若采用式(12)改进制导律,虽然能够保存制导律始终不出现奇异值,但由于水面无人艇时常变速导致控制精度不高,加之该改进的期望艏向曲线过渡段较短(见图 3),因此往往容易造成跟踪时的艏向震荡。
针对上述问题,引入tanh函数,tanh函数拥有平滑的曲线,稳定性较好,并且在能够抗饱和,相较sigmoid函数, tanh函数能够负输出,有:
| $ R = \left( {0.01 \times \frac{{{{\rm{e}}^\delta } - {{\rm{e}}^{ - \delta }}}}{{{{\rm{e}}^\delta } + {{\rm{e}}^{ - \delta }}}}| + k} \right)|\delta | + D $ | (13) |
式中:k、D为正向控制参数。
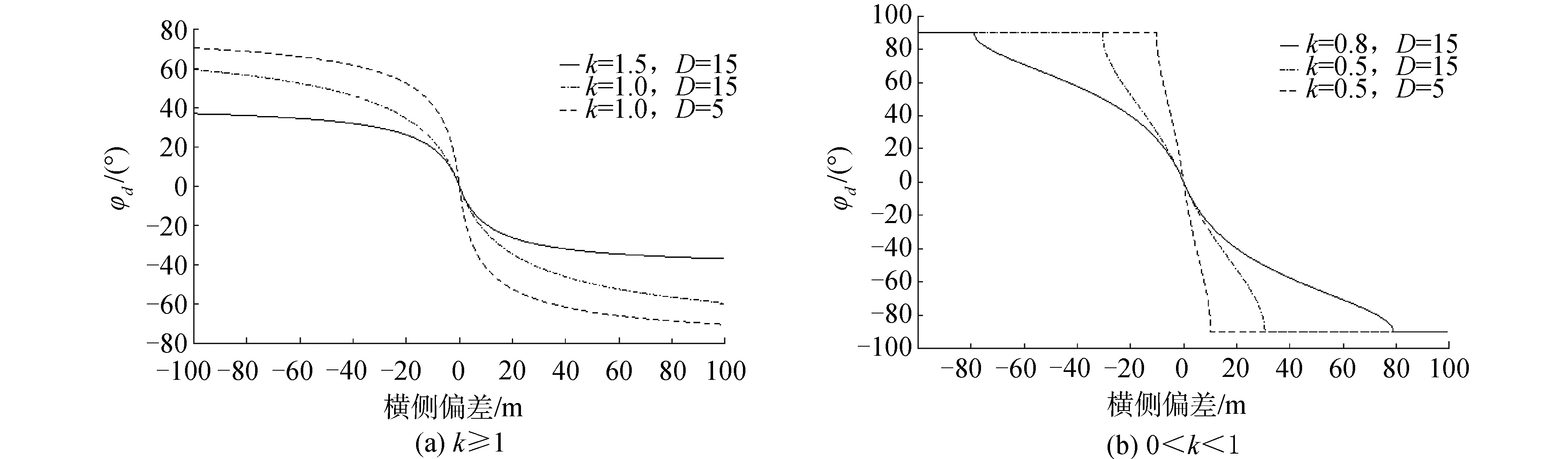
基于自适应双曲正切视线法参数k、D对期望艏向φd的影响如图 2。
|
Download:
|
| 图 2 ATLOS控制参数影响因子 Fig. 2 The exploration of the parameter space for ATLOS | |
3种不同视线法制导律的期望艏向φd曲线如图 3所示。
ALOS制导律即式(12)所给出的改进。分析图 2、3可知:
1) 参数k影响制导律形态,当k≤1,制导律类似传统视线法;当k≥1,制导律类似自适应视线法,但在平滑度上胜过自适应视线法。
2) 参数k与曲线的平缓度成正比,曲线随k的增大趋向平缓,反之亦然。
3) 参数D影响曲线的加速收敛的范围,加速收敛范围随D的增加而增大,反之亦然。
2.2 基于自适应双曲正切视线法导引策略本文的水面无人艇仿真系统的航向控制模型为:
| $ \left[ {\begin{array}{*{20}{c}} {\dot \varphi }\\ {\dot r} \end{array}} \right] = \mathit{\boldsymbol{A}}\left[ {\begin{array}{*{20}{l}} \varphi \\ r \end{array}} \right] + \mathit{\boldsymbol{B}}{\delta _r}(t) + \mathit{\boldsymbol{C}} $ | (14) |
其中:
| $ \begin{array}{l} \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 1&0\\ {\frac{{{N_r}u}}{{{I_{zz}} - {N_{\dot r}}}}}&0 \end{array}} \right],\mathit{\boldsymbol{B}} = {\left[ {\begin{array}{*{20}{c}} 0&{\frac{{{N_\delta }{u^2}}}{{{I_{zz}} - {N_{\dot r}}}}} \end{array}} \right]^{\rm{T}}},\mathit{\boldsymbol{C}} = \\ {\left[ {\begin{array}{*{20}{c}} {\frac{{{N_r}|r|r|r|}}{{{I_{zz}} - {N_{\dot r}}}}}&0 \end{array}} \right]^{\rm{T}}} \end{array} $ |
假设系统受到的随机干扰满足以下2个条件:
1) USV所受随机干扰的输入有界;
2) 随机干扰对USV水动力模型参数的影响有界。
则将式(10)化为状态方程,设状态向量x=[r, φ]T:
| $ \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{B}}{\delta _r}(t) + \mathit{\boldsymbol{h}}(\mathit{\boldsymbol{x}})\mathit{\boldsymbol{x}} $ | (15) |
式中:h(x)为外界干扰与系统强耦合项函数的叠加,并且h(x)小于某个阀值║h(x)║≤║T(x)║,有:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{h}}(\mathit{\boldsymbol{x}}) = \left[ {\begin{array}{*{20}{c}} 0&0\\ {{n_2} + \frac{{{N_r}|r|r|}}{{{I_{zz}} - {N_{\dot r}}}}}&{{n_1}} \end{array}} \right]}\\ {\mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {{d_1}}&{{d_2}}\\ 0&0 \end{array}} \right]} \end{array}} \right. $ | (16) |
式中:n1、n2为外界产生的干扰;d1、d2为固定值。
将模型(11)中的控制律δr(t)分解为PID控制器δr1(t)和在线补偿器δr2(t)进行控制,得:
| $ {\mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{B}}{\delta _{r1}}(t) + \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{\delta }}_{r2}}(t) + \mathit{\boldsymbol{h}}(x)} $ | (17) |
| $ {{\mathit{\boldsymbol{\delta }}_{r1}}(t) = {\mathit{\boldsymbol{K}}_p}\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{K}}_D}\mathit{\boldsymbol{\dot x}} + {\mathit{\boldsymbol{K}}_I}\int_0^t \mathit{\boldsymbol{x}} {\rm{d}}\tau } $ | (18) |
令
| $ \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{\tilde A}}x + \mathit{\boldsymbol{B}}{\delta _{r2}} + \mathit{\boldsymbol{h}}(\mathit{\boldsymbol{x}})\mathit{\boldsymbol{x}},(\mathit{\boldsymbol{\tilde A}} = \mathit{\boldsymbol{A}} + \mathit{\boldsymbol{Bk}}) $ | (19) |
引入虚拟控制量:
| $ {\delta _{r2}} = - {({\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}})^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{T}}(\mathit{\boldsymbol{x}})\mathit{\boldsymbol{x}} + \mathit{\boldsymbol{k}}(\mathit{\boldsymbol{\xi }})\mathit{\boldsymbol{\dot \xi }} $ | (20) |
其中:ξ=xd-x,xd为期望运动状态向量;x为实际输出运动状态向量。
为得到稳定的自适应控制参数k(ξ),构建Lyapunov函数:
| $ V = {\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{Px}} + {\mathit{\boldsymbol{\xi }}^{\rm{T}}}(x)\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{\xi }}(\mathit{\boldsymbol{x}}) $ | (21) |
代入式(17)、(18)得:
| $ \dot V < 2{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{PBk}}(\mathit{\boldsymbol{\xi }})\mathit{\boldsymbol{\dot \xi }}(\mathit{\boldsymbol{x}}) + 2{\mathit{\boldsymbol{\xi }}^{\rm{T}}}\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{\dot \xi }}(\mathit{\boldsymbol{x}}) $ | (22) |
设虚拟控制量k(ξ)=
| $ \dot V < - 2{\mathit{\boldsymbol{x}}^{\rm{T}}}\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\frac{{{\mathit{\boldsymbol{x}}_d}\mathit{\boldsymbol{x}}_d^{\rm{T}}}}{{{\mathit{\boldsymbol{x}}^{\rm{T}}}{\mathit{\boldsymbol{x}}_d}}}(\mathit{\boldsymbol{x}}) + 2\mathit{\boldsymbol{x}}_d^{\rm{T}}\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{\dot \xi }}(\mathit{\boldsymbol{x}}) \le 0 $ | (23) |
为便于分析参数,本文简化k(ξ)=
| $ \begin{array}{*{20}{c}} {\delta = \left( {{K_P} + \frac{{{d_1}}}{{b{u^2}}} + \frac{{{b_1}{u^2}({\xi _r}{\xi _{{{\dot \varphi }_e}}})}}{{\varphi _d^2 + r_d^2}}} \right){\varphi _e} + }\\ {\left( {{K_D} + \frac{{{d_2}}}{{b{u^2}}} + \frac{{b{u^2}({\xi _r}{{\dot \xi }_r})}}{{\varphi _d^2 + r_d^2}}} \right)r + {K_I}\int_0^t {{\varphi _e}} {\rm{d}}\tau } \end{array} $ | (24) |
式中:φe=φd-φ;ξr=rd-r;
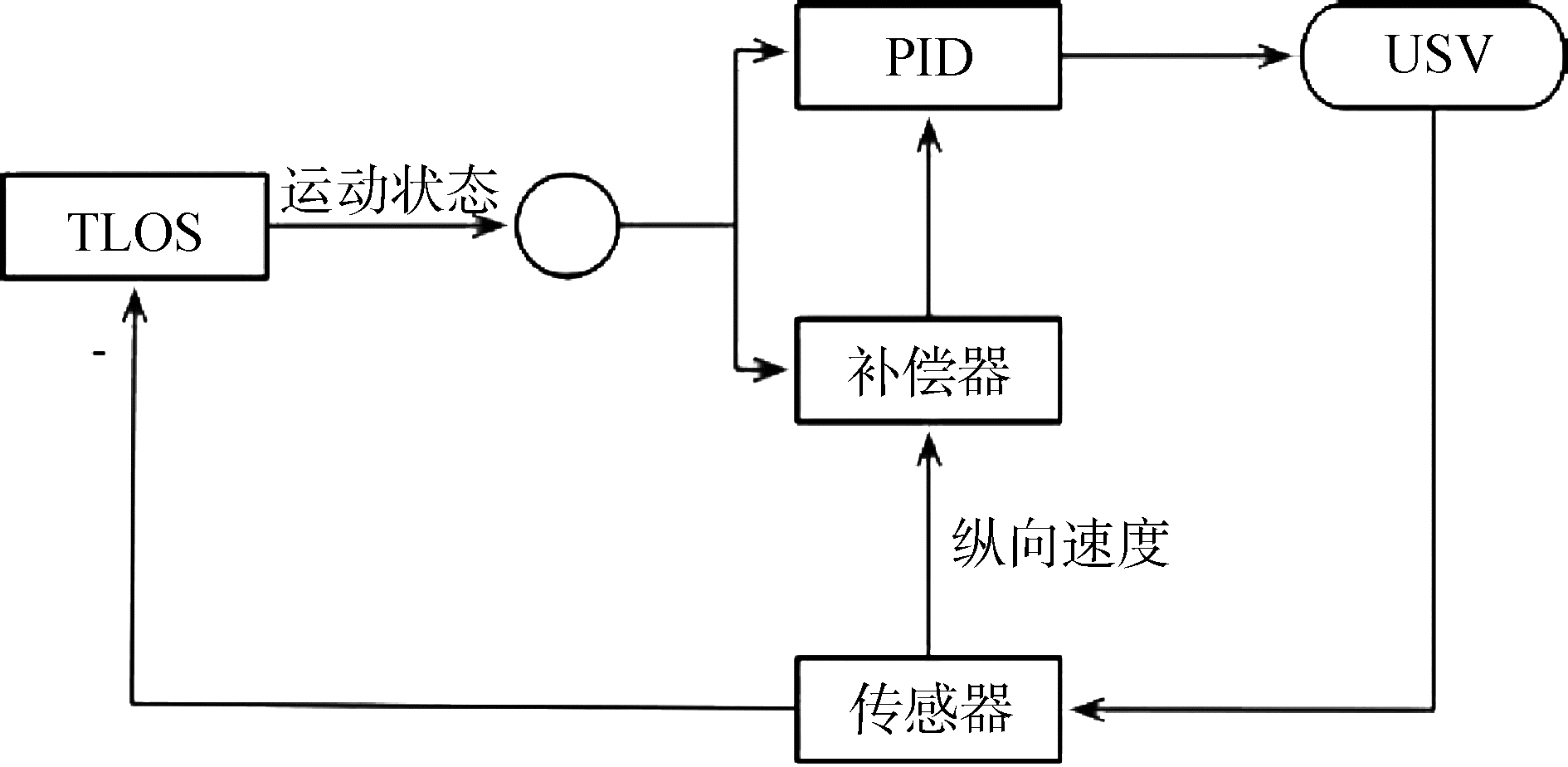
基于自适应双曲正切视线法导引策略框图如图 4所示。
|
Download:
|
| 图 4 ATLOS导引策略框图 Fig. 4 ATLOS guidance strategy diagram | |
本文结合C++和vega开发水面无人艇平面运动仿真平台。在这个干扰为慢运动学的仿真平台上,对比基于自适应双曲正切视线法和视线法,从仿真上分析两者差异。
速度控制为增量式PID控制器,参数选择:Kp=10.0,KI=0.0,KD=3.0,k=1.0
船体运动学、动力学模型建立方法见文献[13]。具体船体模型系数有:m=1 900.5,Iz=8 000,Mxx=184.57,Myy=15.338 4,Mrr=1 206,Yv=-0.475 1,Yr=0.071 6,Nv=-0.145 9,Nr=-0.055 7,Xvr=-0.002 5,Xvv=0.068 2,Xrr=0.003 9,Yvr=-0.29,Yvv=-0.4757,Yrr=-0.035,Nvv=0.014 8,Nrr=-0.04;其他未提及系数均为0。
LOS参数选择:R=20,k=2,Rsafe=40.0,KP=3.0,KI=0.0,KD=4.0
ATLOS参数选择:D=30,k=0.5,Rsafe=40.0,KP=3.0,KI=0.0,KD=4.0.
工况1:USV初始位置(x0, y0)=(0, 0),初始航向φ=0/π,初始速度u=0.0,安全半径Rsafe=40.0。无外界干扰d1=0,d2=0。期望路径与期望速度为表 1所示。
| 表 1 工况1参数 Table 1 Parameter of condition 1 |
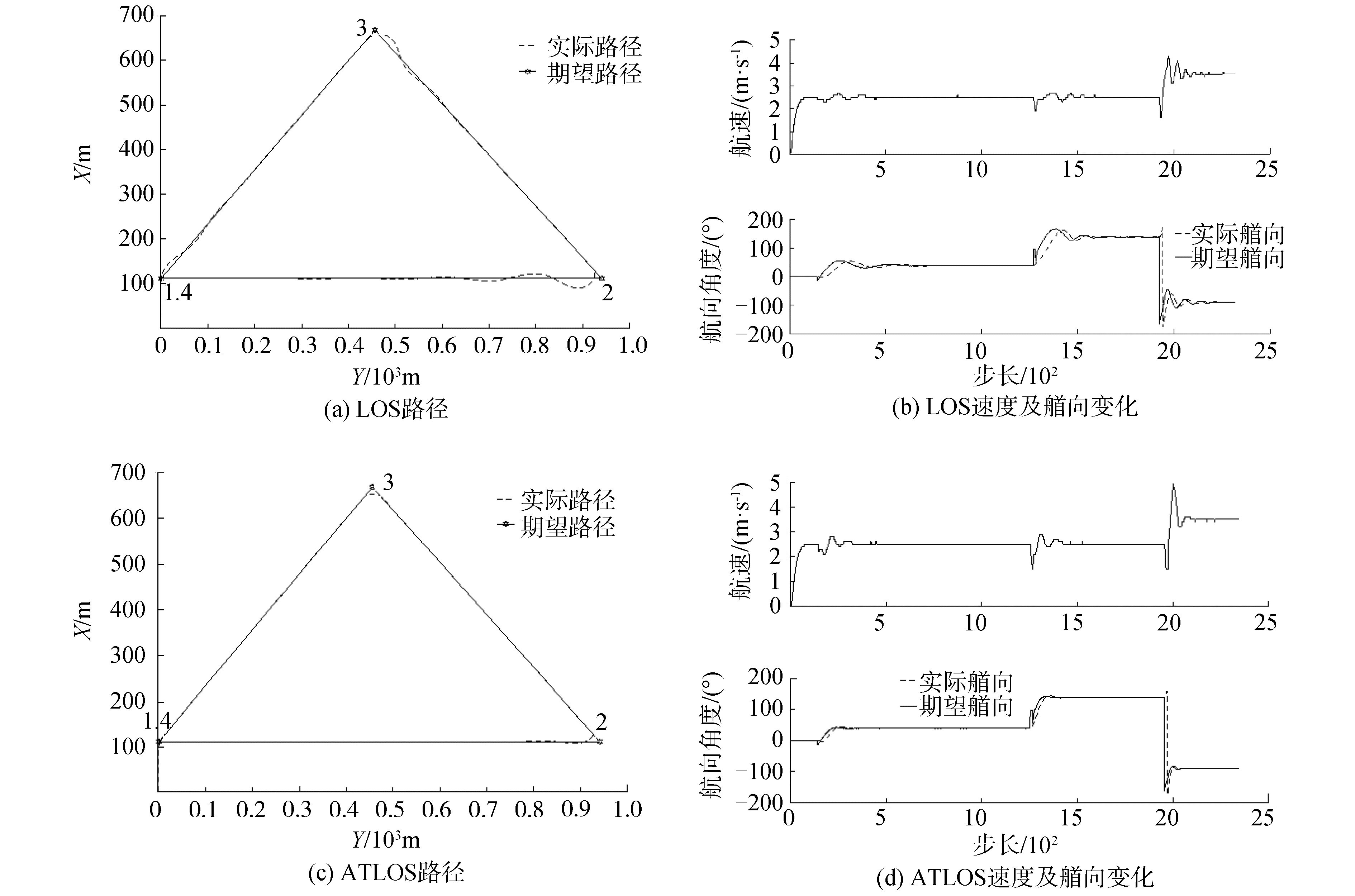
工况1仿真结果如图 5所示。在没有随机干扰的情况下,不论是视线法,还是基于自适应双曲正切视线法,导引策略都能够快速收敛。同时,在速度发生改变后的路径上基于自适应双曲正切视线法依旧保持良好的控制精度,视线法速度曲线震荡时间延长,且艏向跟踪精度变差。
|
Download:
|
| 图 5 工况1仿真结果 Fig. 5 Condition 1 simulation performance | |
工况2:水面无人艇初始位置(x0, y0)=(19.3, 7),初始航向φ=36.9/π,初始速度u=3.5,安全半径Rsafe=40.0。无外界干扰d1=0,d2=0。期望路径与期望速度如表 2所示。
| 表 2 工况2参数 Table 2 Parameter of condition 2 |
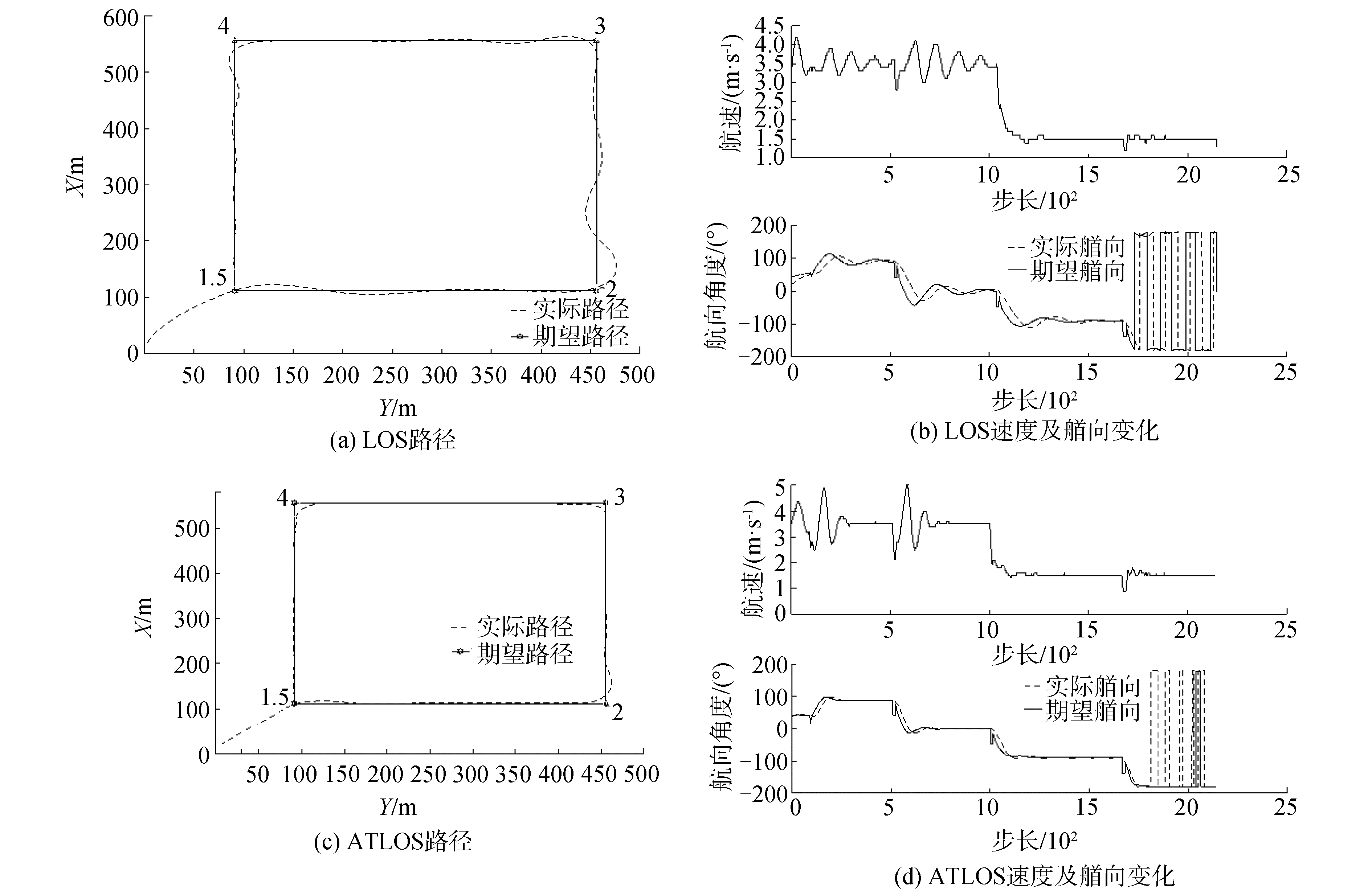
工况2仿真结果如图 6所示。在施加固定的外界干扰之后,视线法在速度为u=3.5的路段中,实际路径的超调及震荡明显增加,速度曲线没有收敛。基于自适应双曲正切视线法几乎不受影响。
|
Download:
|
| 图 6 工况2仿真结果 Fig. 6 Condition 2 simulation performance | |
对比图 5、图 6可知视线法的参数不具备自适应能力,即速度范围改变之后参数性能变差。但基于自适应的双曲正切视线法具备较好的自适应能力,同时基于自适应的双曲正切视线法导引的期望艏向变化幅度更加合理。基于自适应的双曲正切视线法的自适应参数考虑到了水面无人艇纵向速度与横侧偏差和模型的耦合,有效的修正了期望艏向曲线的变化幅度,同时增加了速度跟踪精度。其中图(6)艏向跟踪最后出现的跃变是由于期望艏向从180°~-180°的突变。
图 7所示为2工况的横侧偏差曲线,具体数值统计如下表 3所示。

|
Download:
|
| 图 7 工况1、2的横侧偏差 Fig. 7 Cross-track error of condition 1, 2 | |
| 表 3 横侧偏差数据统计 Table 3 Cross-track error statistics |
分析图 7及表 3可知,视线法和基于自适应的双曲正切视线法产生的超调均在可容许范围内,在给定一个恒定速度变化范围后,两者均能保持良好的控制精度。但在路径曲率和速度变化范围均发生改变的情况下,视线法控制系统震荡较大,收敛缓慢,基于自适应的双曲正切视线法系统基本不受影响。
2种策略比较总结如下:
1) 2种策略均能引导USV在期望路径航行;
2) 在变速情况下,基于自适应的双曲正切视线法导引的期望艏向更加合理;
3) 基于自适应的双曲正切视线法具备自适应能力,相对于视线法具有更好的鲁棒性。
3.2 外场试验为评估基于自适应的双曲正切视线法在环境干扰下的慢速性能,本文在哈尔滨太阳岛湿地公园进行了2次外场试验。试验用船为RobotX。由于外场试验有随机干扰,与仿真试验情况不同,为精确的检查基于自适应的双曲正切视线法的性能,更改控制参数k=1,D=22,KP=9,KI=0.08,KD=3.5,Nr=-0.043 9,
实体船与航行图如图 8所示。

|
Download:
|
| 图 8 RobotX外场试验图 Fig. 8 RobotX running in lake | |
工况1:水流平均流速在v=0.4 m/s,东北风4级。恒定纵向速度u=0.8 m/s,初始艏向φ=-74.4°。Rsafe=5。从经纬度(45.794 63°N,126.529 55°E)出发跟踪一条直线P1(45.794 44, 126.527 34),P2=(45.794 21, 126.526 75)。
工况2:水流平均流速在v=0.1 m/s。恒定纵向速度u=1.2 m/s,初始艏向φ=13.6°。Rsafe=10。从经纬度Pt0(45.794 83°N, 126.528 80°E)出发跟踪闭合曲线P1(45.795 10, 126.529 23), P2=(45.795 23, 126.531 21), P3=(45.796 68, 126.531 89), P4=(45.796 60, 126.531 13), P5=(45.795 10, 126.529 23)。
工况1试验结果如图 9所示。在期望速度恒定ud=0.8 m/s,水流速度平均在v=0.4 m/s,加上随机的环境干扰导致横漂角的影响较大。图中艏向变化曲线只截取了USV在进入期望路径之后航行时的数据。从图 9(a)可以看出ATLOS在随机环境干扰,横漂角影响较大的情况下,USV依旧能够很好的沿着期望路径航行。当USV在期望路径航行时,偏差在1.5 m之内,平均偏差为0.7 m。
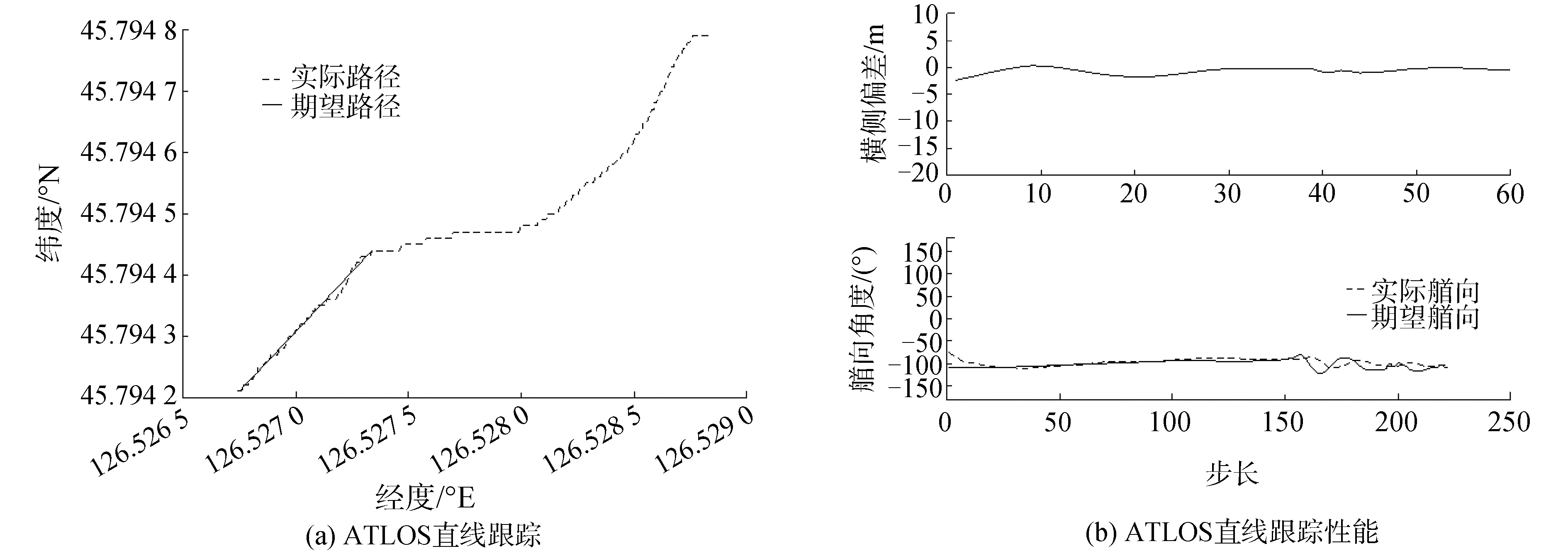
|
Download:
|
| 图 9 外场试验结果工况1 Fig. 9 Condition 1 the results of field experiment | |
工况2在600步左右,基于自适应的双曲正切视线法策略正在改变期望路径点,期望艏向出现62.2°的跃变,从而导致艏向跟踪缓慢引起,产生最大偏差7.9 m。当USV在期望路径航行时产生的平均偏差为1.0 m。如图 10所示。

|
Download:
|
| 图 10 外场试验结果工况2 Fig. 10 Condition 2 the results of field experiment | |
为评估基于自适应双曲正切视线法在环境干扰下的高速性能,本文在大连旅顺口区进行了一次外场试验。试验用船为天行一号,由于船型改变,修改参数k=1,D=30,KP=6.0,KI=0.22,KD=4.0,Nr=-0.062 1,
工况3,试验海况为三级海况,初始纵向速度u=0 m/s,初始艏向φ=-139.6°,期望纵向速度ud=12.5 m/s。Rsafe=100。从经纬度(38.791 677°N,121.123 300°E)出发跟踪两段直线P1(39.791 677, 121.123 300),P2=(38.791 677, 121.123 300),P3=(38.794 953, 121.116 379)。
可以从图 11看出,工况3在起步加速阶段由于干扰作用,横侧偏差产生了振荡,但是在50步左右之后,收敛趋向稳定。同时从艏向图可以进一步发现,即使艏向发生了振荡,横侧偏差仍保持平滑的收敛状态。本次试验产生最大偏差5.2 m,平均偏差在3.6 m。
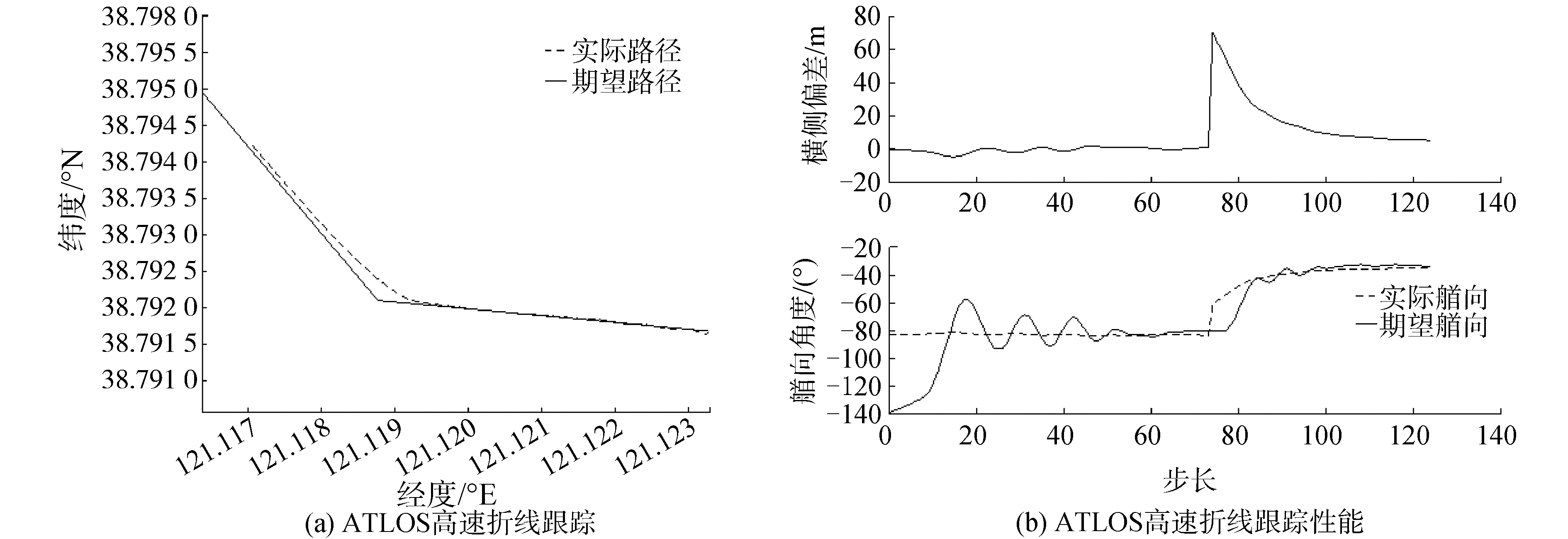
|
Download:
|
| 图 11 外场试验结果工况3 Fig. 11 Condition 3 the results of field experiment | |
3次试验与仿真模拟结果较吻合。可以看出ATLOS具有较好的稳定性和鲁棒性。通过该导引策略,USV在随机干扰下能够保持良好的控制精度。
4 结论1) 两者的收敛特性发现通过调整参数基于自适应双曲正切视线法和视线法均能在恒定速度和曲率变化范围内很好的收敛。
2) 在速度和曲率的范围会发生变化的情况下,基于自适应双曲正切视线法依旧能够保持良好的控制精度,视线法精度受损较大,其中速度震荡时间,横侧偏差超调明显变大。
3) 实验结果与模拟结果吻合较好,验证了ATLOS导引策略的稳定性和鲁棒性。
4) 在高速航行下仍具备较好的跟踪精度,说明ATLOS能够运用于较高速的航行情况。
下一步将研究不同路径跟踪范围下,避免期望艏向跃变产生较大横侧误差的方法以及在高速航行下的路径跟随问题。
| [1] |
MANLEY J E. Unmanned surface vehicles, 15 years of development[C]//OCEANS 2008. Quebec City, 2008: 1-4. https://www.infona.pl/resource/bwmeta1.element.ieee-art-000005152052
(  0) 0)
|
| [2] |
胡志强, 周焕银, 林扬, 等. 基于在线自优化PID算法的USV系统航向控制[J]. 机器人, 2013, 35(3): 263-268, 275. HU Zhiqiang, ZHOU Huanyin, LIN Yang, et al. The course control based on an on-line self-adjusted PID control algorithm for unmanned surface vehicles[J]. Robot, 2013, 35(3): 263-268, 275. (  0) 0)
|
| [3] |
SUJIT P B, SARIPALLI S, SOUSA J B. Unmanned aerial vehicle path following:a survey and analysis of algorithms for fixed-wing unmanned aerial vehicless[J]. IEEE control systems magazine, 2014, 34(1): 42-59. DOI:10.1109/MCS.2013.2287568 (  0) 0)
|
| [4] |
NELSON D R, BARBER D B, MCLAIN T W, et al. Vector field path following for miniature air vehicles[J]. IEEE transactions on robotics, 2007, 23(3): 519-529. DOI:10.1109/TRO.2007.898976 (  0) 0)
|
| [5] |
RYSDYK R. UAV path following for constant line-of-sight[C]//Proceedings of the 2nd AIAA "Unmanned Unlimited" Conference and Workshop & Exhibit. San Diego, 2003: 6626.
(  0) 0)
|
| [6] |
董早鹏, 万磊, 廖煜雷, 等. 基于非对称模型的欠驱动USV路径跟踪控制[J]. 中国造船, 2016, 57(1): 116-126. DONG Zaopeng, WAN Lei, LIAO Yulei, et al. Path following control of underactuated USV based on asymmetric model[J]. Shipbuilding of China, 2016, 57(1): 116-126. DOI:10.3969/j.issn.1000-4882.2016.01.013 (  0) 0)
|
| [7] |
付悦文.小型无人艇的无模型自适应跟踪方法研究[D].哈尔滨: 哈尔滨工程大学, 2017: 40-50. FU Yuewen. Study on tracking of small USV based on model-free adaptive control[D]. Harbin: Harbin Engineering University, 2017: 40-50. https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CMFD&dbname=CMFD201802&filename=1018074331.nh&v=MzE3MjZxZmIrWm9GeWpsVjc3SlZGMjZGck8vR3RMUHJwRWJQSVI4ZVgxTHV4WVM3RGgxVDNxVHJXTTFGckNVUjc= (  0) 0)
|
| [8] |
陈霄, 刘忠, 张建强, 等. 基于改进积分视线导引策略的欠驱动无人水面艇路径跟踪[J]. 北京航空航天大学学报, 2018, 44(3): 489-499. CHEN Xiao, LIU Zong, ZHANG Jianqiang, et al. Path following of underactuated USV based on modified integral line-of-sight guidance strategies[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(3): 489-499. (  0) 0)
|
| [9] |
田勇, 王丹, 彭周华, 等. 无人水面艇直线航迹跟踪控制器的设计与验证[J]. 大连海事大学学报, 2015, 41(4): 14-18. TIAN Yong, WANG Dan, PENG Zhouhua, et al. Design and validation of path tracking controller for USV along straight-lines[J]. Journal of Dalian Maritime University, 2015, 41(4): 14-18. (  0) 0)
|
| [10] |
LI Zhi, BACHMAYER R, VARDY A. Vector field path following control for unmanned surface vehicles[C]//OCEANS 2017-Aberdeen. Aberdeen, 2017.
(  0) 0)
|
| [11] |
NIELSEN M A. Neural networks and deep learning[M]. San Francisco, CA, USA: Determination Press, 2015.
(  0) 0)
|
| [12] |
GÉRON A. Hands-On Machine Learning with Scikit-Learn and TensorFlow:Concepts, Tools, and Techniques to Build Intelligent Systems[M]. O'Reilly Media, 2019.
(  0) 0)
|
| [13] |
廖煜雷.无人艇的非线性运动控制方法研究[D].哈尔滨: 哈尔滨工程大学, 2012. LIAO Yulei. Nonlinear motion control methors of unmamed surface vehicle[D]. Harbin: Harbin Engineering University, 2012. https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CDFD&dbname=CDFD1214&filename=1013004453.nh&v=MTU5MDZPNEd0WEpySkViUElSOGVYMUx1eFlTN0RoMVQzcVRyV00xRnJDVVI3cWZiK1pvRnlqbFY3M01WRjI2SGI= (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


