2. 海军大连舰艇学院, 辽宁大连 116018;
3. 中国科学院大气物理研究所LASG国家重点实验室, 北京 100029;
4. 中国海洋大学, 山东省海洋工程重点实验室, 山东 青岛 266100;
5. 中国人民解放军91001部队, 北京 100841
2. Dalian Naval Academy, Dalian 116018, China;
3. State Key Laboratory of Numerical Modeling for Atmospheric Sciences and Geophysical Fluid Dynamics(LASG), Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China;
4. Shandong Provincial Key Laboratory of Ocean Engineering, Ocean University of China, Qingdao 266100, China;
5. The Chinese PLA 91001 Troops, Beijing 100841, China
波浪能是指海洋表面波浪所具有的动能和势能,具有无污染、分布广、可再生、储量大等优点。波浪发电可为海水养殖场、海上灯船孤岛、海上气象浮标和石油平台等常规能源难以方便利用的场所提供电力[1-3],也可并入城市电网向工业和居民生活用电提供支撑,但由于受风向、风速和水深等因素影响,波浪能由离岸、近岸传播至沿岸时其能量变化规律有所不同,因此了解掌握波浪能的传播规律,对波力发电站选址等波浪能开发利用具有重要现实意义。目前,国内外对波浪能资源评估、单站能量采集等研究较多,如WAN等[4]利用西太平洋高度计数据研究了波浪能量资源评估方法,韩林生等[5]利用MIKE21 SW波浪模型结合实际观测对山东诸岛北部海域(中国建设中的波浪能试验场)波浪场进行模拟计算,分析了该海域波浪能资源分布情况,并评估了发电装置可进行试验测试的有效时间,万勇等[6]利用ERA-Interim再分析海浪场资料对山东半岛近岸海域波浪能的开发潜力进行计算评估,并对优势区域重点单站波浪能的集中度进行了分析。但目前对波浪能传播规律的研究还较少,如过去一直认为远海浪大因而波浪能资源较近岸更为丰富,但Folley[7]指出波浪由离岸传播至近岸时能量损失很小,近岸30 m水深的波浪能流密度大于距岸较远处50 m水深的能流密度,且浅水处的波浪能较深水处波浪能仅损失10%。谢媛媛等[8]使用SWAN模式分别模拟了沿岸流和离岸流作用下波浪向岸传播过程中波高沿途的变化,但未考虑能量变化情况。本文针对福建沿海地形构建了波浪能由离岸向近岸传播的简易模型,利用WW3模式采用定常风风场对波浪能的传播规律进行了探索分析,初步得到了不同传播方向波浪能损失和变化分布等情况。
1 WW3模式简介WW3模式是由美国国家海洋大气总局/美国国家环境预报中心(NOAA/NCEP)在原有模式基础上加以改进和发展的第3代海浪数值模式,现为美国国家环境预报中心(NCEP)业务化的全球和区域海浪预报模式[9]。模式充分考虑了风浪相互作用、非线性相互作用、耗散及底摩擦及波-波相互作用等物理过程,利用风场、水深等资料可对计算海域海浪进行较好地模拟,输出波高、周期和波长等31个海洋物理量,且对波高等模拟具有较高精度[10-11],因其采用半隐式有限差分格式,无条件稳定,因此对于浅水海域也具有较好模拟能力[12]。
2 波浪能计算方法波浪能包括水质点以一定速度运动所具有动能和离开平衡位置垂直位移所具有势能,是一种在风的作用下产生并以位能和动能形式由短周期波储存的机械能,其与风速、风的持续时间、传播距离、水深等因素等有关。波浪能的大小与波高的平方、波浪的运动周期以及迎波面的宽度成正比,大小常用波能功率密度来表示(波浪在传播方向上单位时间内通过单位波峰宽度上的能量,用P表示),其有多种计算方法[13], 本文计算方法[14]为:
深水中(d/λ≥1/2):
| $ P = 0.5H_{1/3}^2\overline T \left( {kW/m} \right) $ | (1) |
浅水中(d/λ<1/2):
| $ P = \frac{{rH_{1/3}^2}}{g}\sqrt {gd} \left( {kW/m} \right) $ | (2) |
式中:d为水深;λ为波长;H1/3为有效波高;T为平均周期;r 为海水密度。可见,波能功率密度与波高、周期、水深有关。深水时,波能功率密度仅与波高、周期有关;浅水时,波能功率密度仅与波高、水深有关。
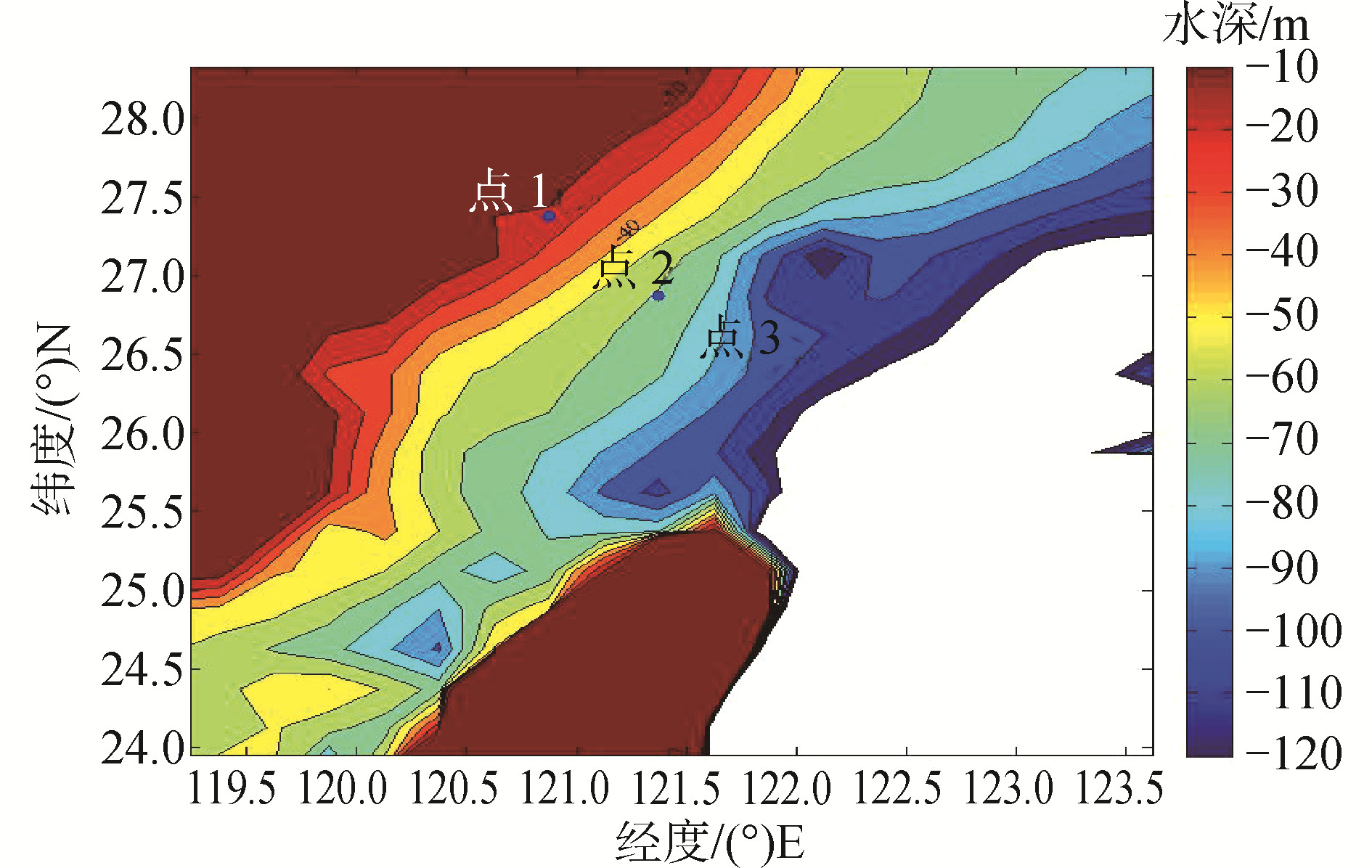
3 波浪能传播规律模拟分析 3.1 模型构建通常沿岸海域指的是常看到的岸边,这里波浪受风、大陆架及岸边阻力的影响破坏力较强,波力发电站需占用一定的陆地面积且有可能破坏沿海生态;近岸海域指的是离海岸线不太远的海岸,其波浪受涨潮和退潮的影响,水面存在较强涌浪,而水面下则存在流速较大的水流,在一些江河、海口出口这种现象更为突出;离岸海域指的是离海岸线较远的海域,这种海域的波浪均匀,波高和波幅较大。考虑到福建沿海的海岸线基本呈东北-西南走向,由岸至外海中水深由10~120 m逐渐增大,且等深线几乎与海岸线平行,又位于我国东南沿海海域,波浪能资源最为丰富,因此以其为基础建立波浪能传播模型。选取Point1(27.375°N,120.875°E,水深12.9 m),Point2(26.875°N,121.375°E,水深63 m),Point3(26.375°N,121.875°E,水深97.6 m),分别代表近岸(nearshore)、离岸(offshore)、深水(depth water)。如图 1所示,海岸线与近岸水深线基本平行,三站连线近似与海岸线垂直,亦即近似与等水深线垂直。
|
Download:
|
| 图 1 不同水深站点分布 Fig. 1 Distribution of stations with different water depths | |
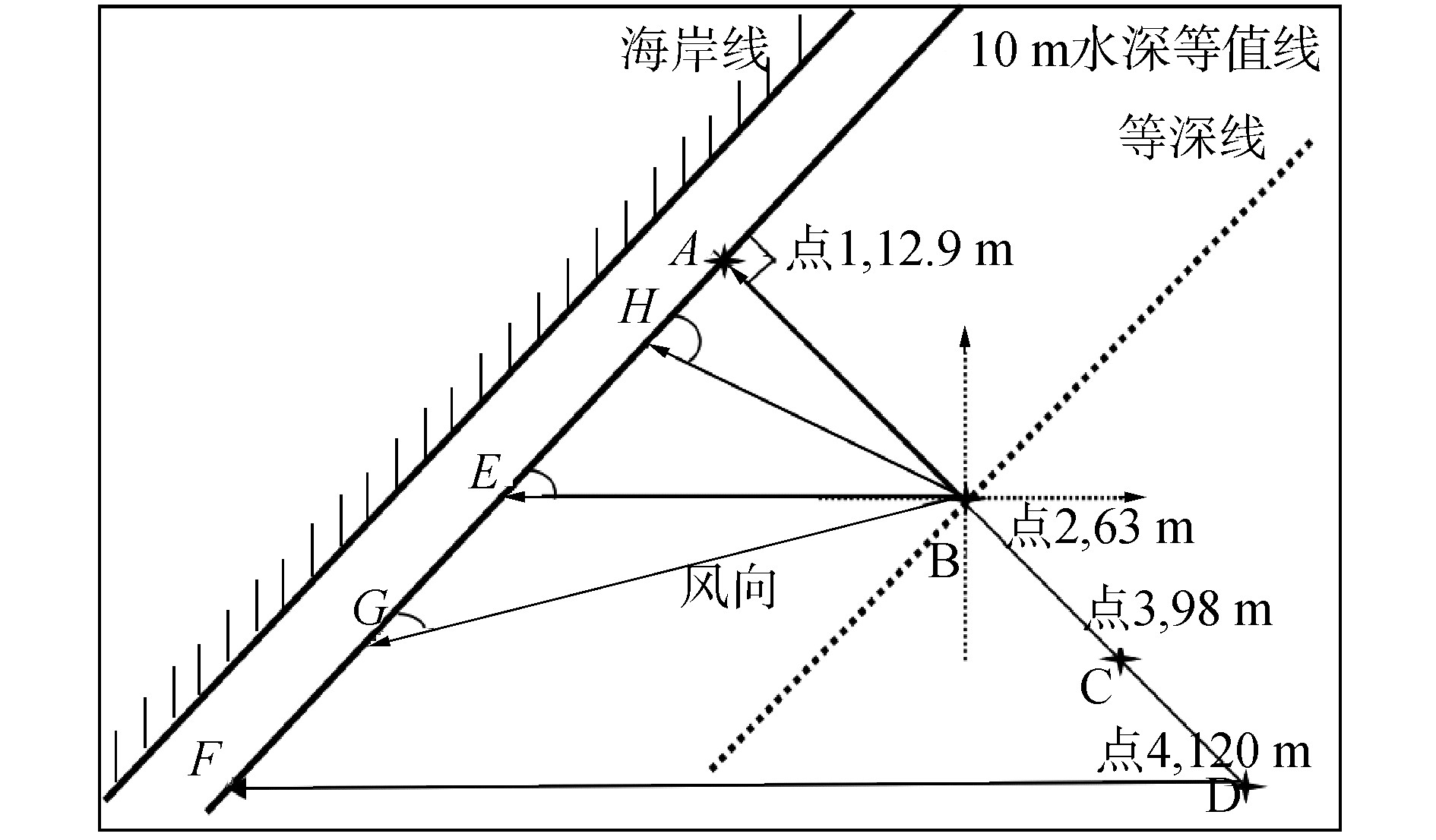
采用WW3模式进行模拟分析,取福建沿海真实水深,考虑不同方向定常风使波浪成长之后以研究其波浪能的变化规律,其中水深数据采用美国NOAA的ETOPO5地形数据,分辨率为5′×5′,将其插值为2′×2′,模拟范围为119.125°E~123.125°E,24.125°N~28.125°N,将图 1绘制为对应简图如图 2。
|
Download:
|
| 图 2 波浪能传播模型示意 Fig. 2 Schematic diagram of wave energy propagation model | |
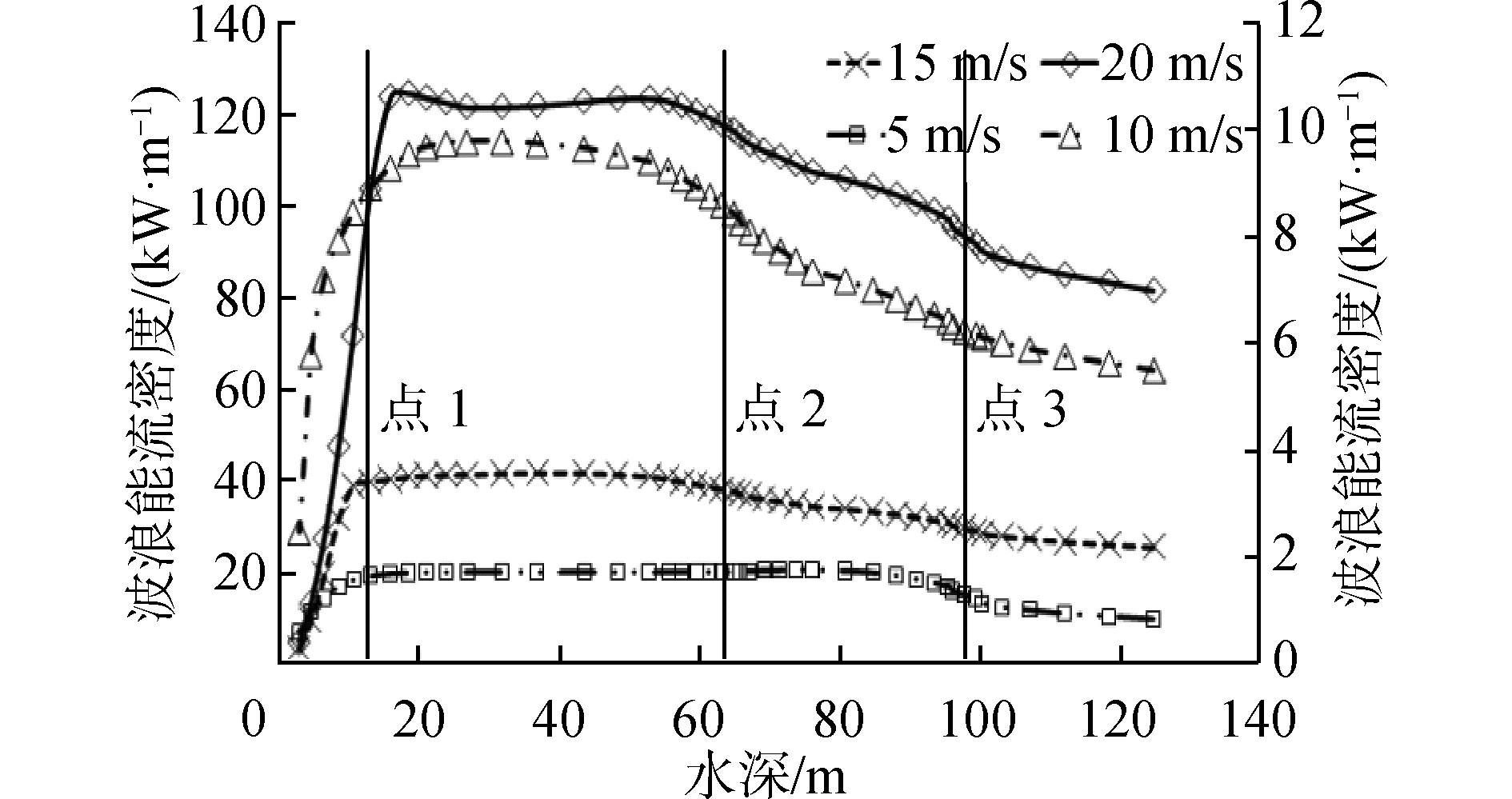
定义对于定常风当海域每个模式网格的波高都不在变化时,称其达到波浪充分成长状态。以不同的定常风速垂直于水深等值线持续由点3吹向点1(东南风)直至其波浪达到充分成长状态而不再变化,取图 2中AD线段上所有模式网格点的能量变化如图 3,其中15、20 m/s对应左侧坐标轴,5、10 m/s对应右侧坐标轴。可以看出,随着风速的增加,波浪能流密度迅速增加。虽然风速不同,但是波浪能最大值均集中在水深为20~60 m。水深小于20 m时,随着水深增加,波浪能迅速成长,至60 m水深其变化较为平稳,当超过60 m水深时,随着水深增加波浪能开始逐渐减小。
|
Download:
|
| 图 3 不同风速下能流密度随水深的变化 Fig. 3 The change of energy flux density with water depth under different wind speed | |
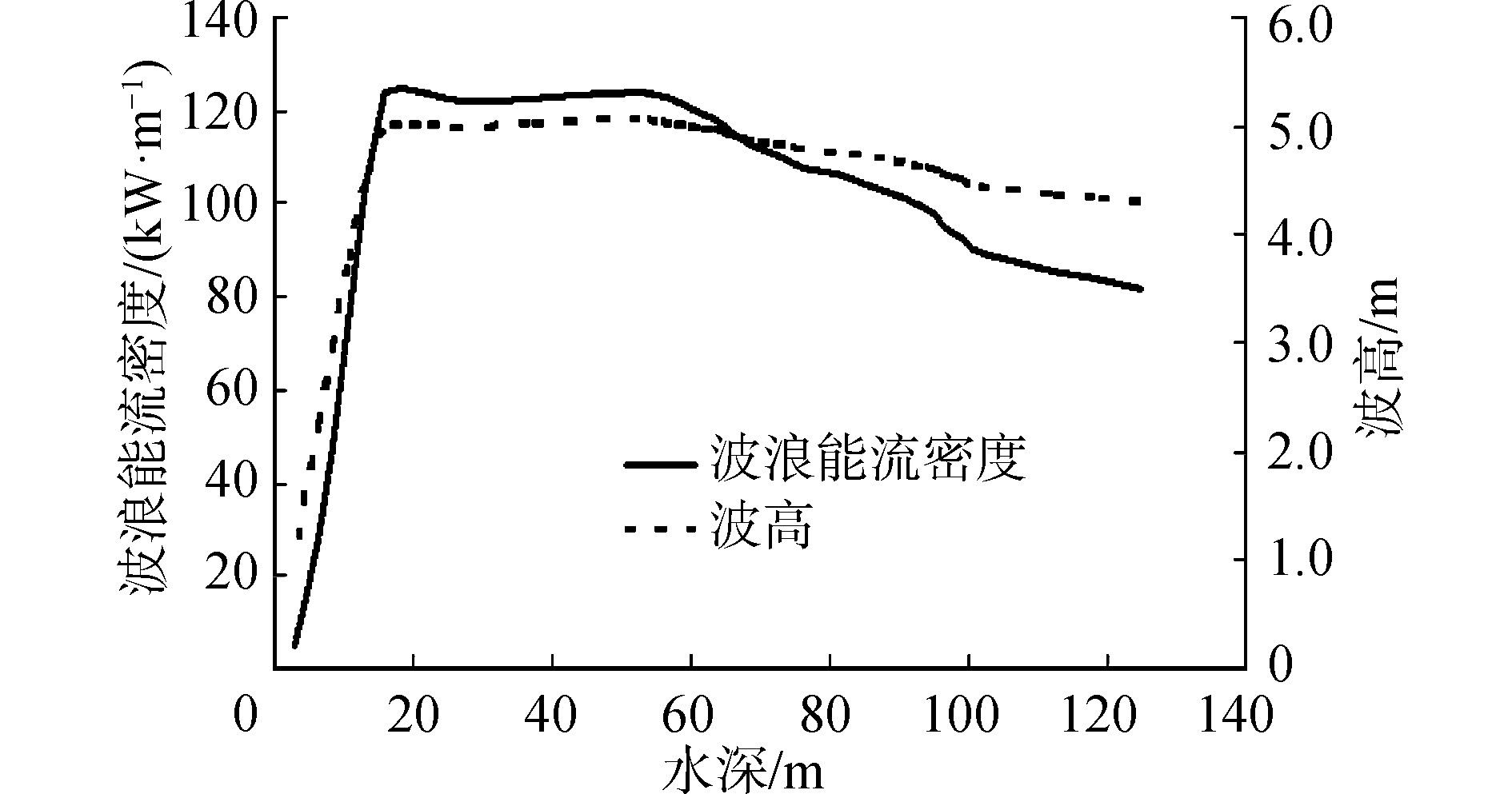
持续采用20 m/s风速定常风(东南风)直至波浪充分成长后,绘制第20 h时刻线段AD的能量变化如图 4。采用20 m/s风速定常风(东南见)持续5 h,波浪尚未达到充分成长状态,绘制第20 h时刻线段AD的能量变化如图 5。
|
Download:
|
| 图 4 充分成长状态下能流密度随水深的变化 Fig. 4 The change of energy flow density with water depth under full growth condition | |
|
Download:
|
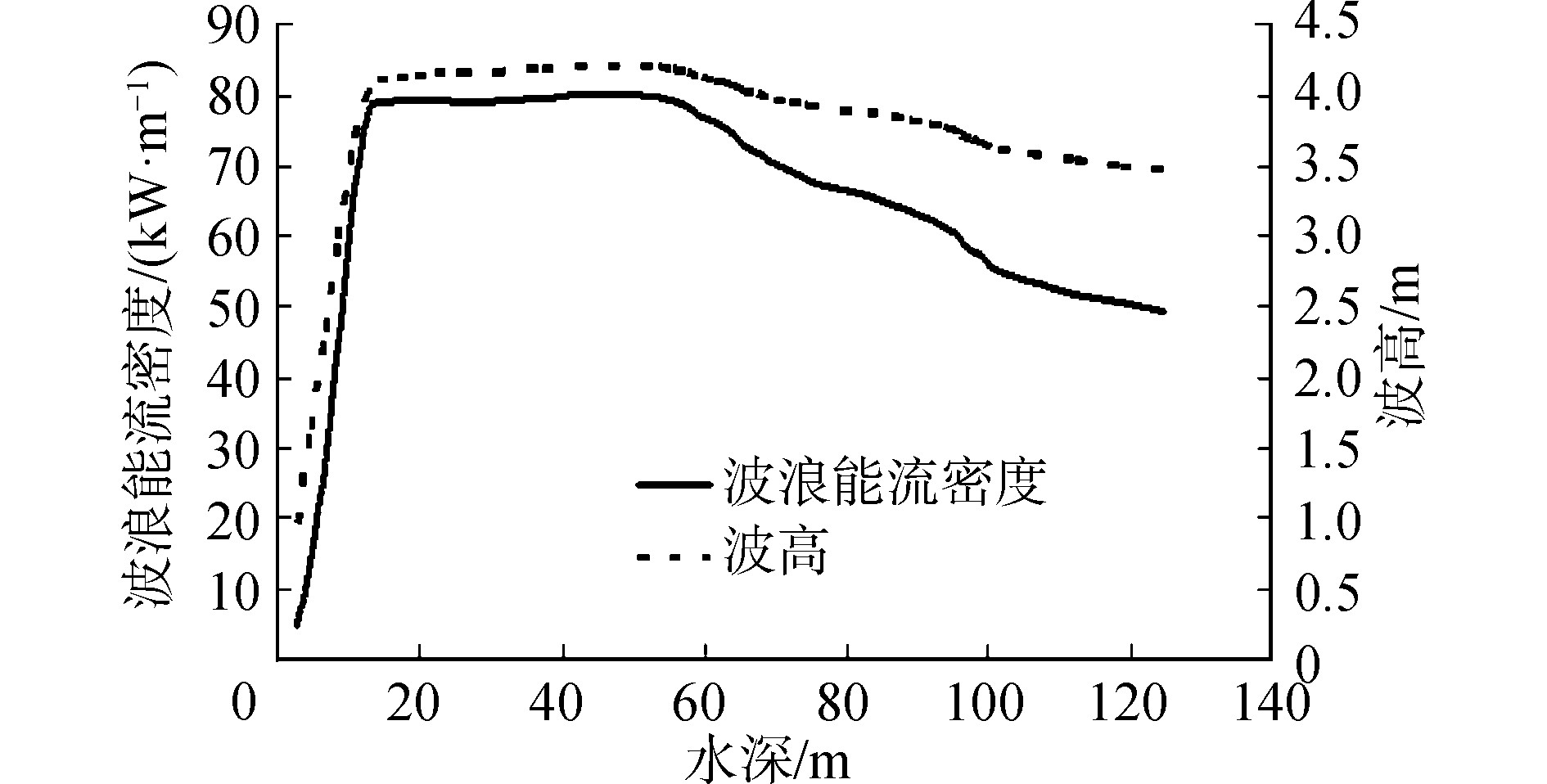
| 图 5 未充分成长状态下能流密度随水深的变化 Fig. 5 The change of energy flow density with water depth under the condition of insufficient growth | |
由图 4可以看出,波浪能流密度与波高随水深变化大体一致,直到水深大于60 m时,波浪能衰减速率大于波高。由图 4和图 5可以看到波浪充分成长与其未充分成长,波浪能随水深的变化形势基本一致,仅大小数值不同。波浪能最大值均出现在水深为20~60 m,与图 3结论一致。
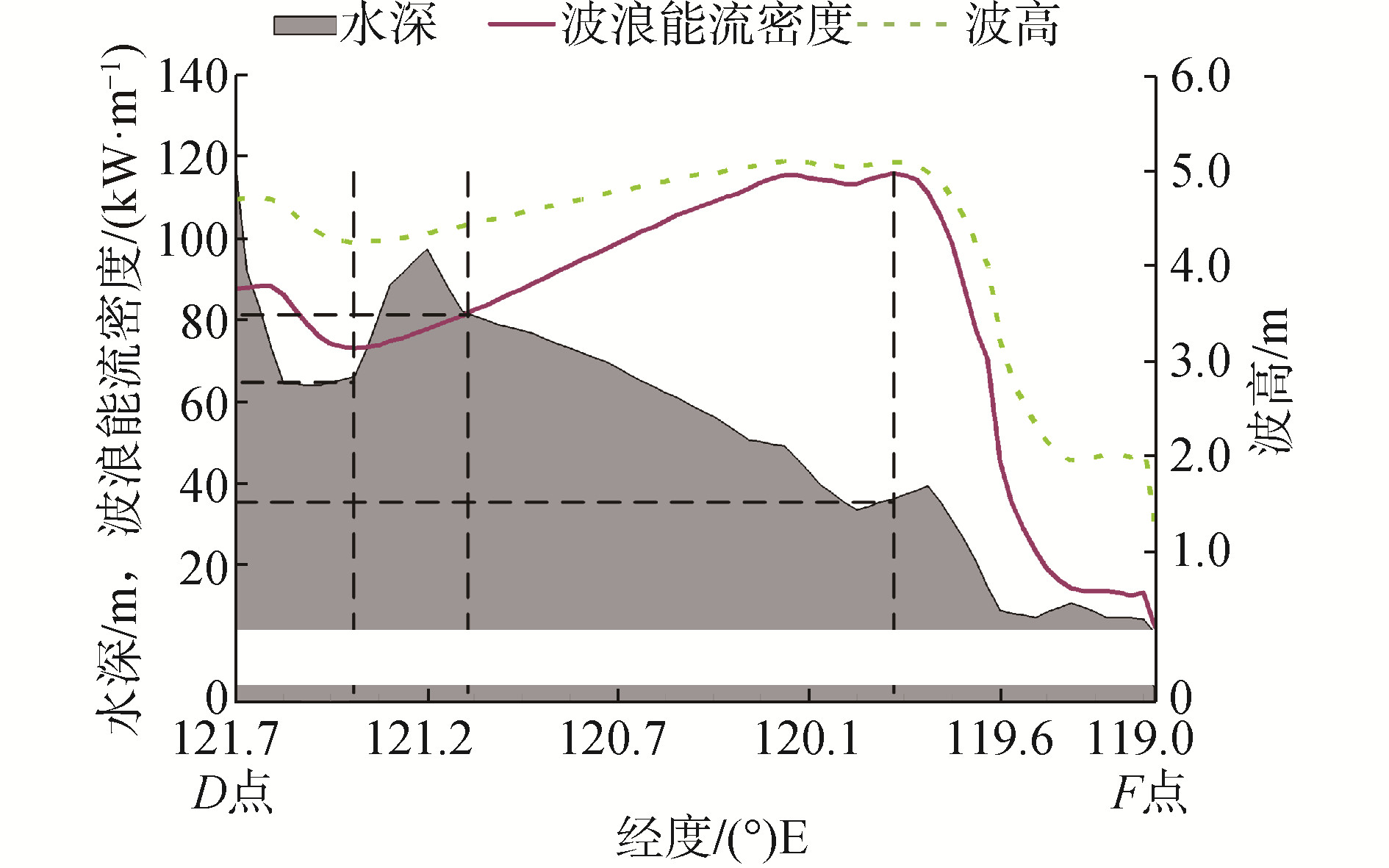
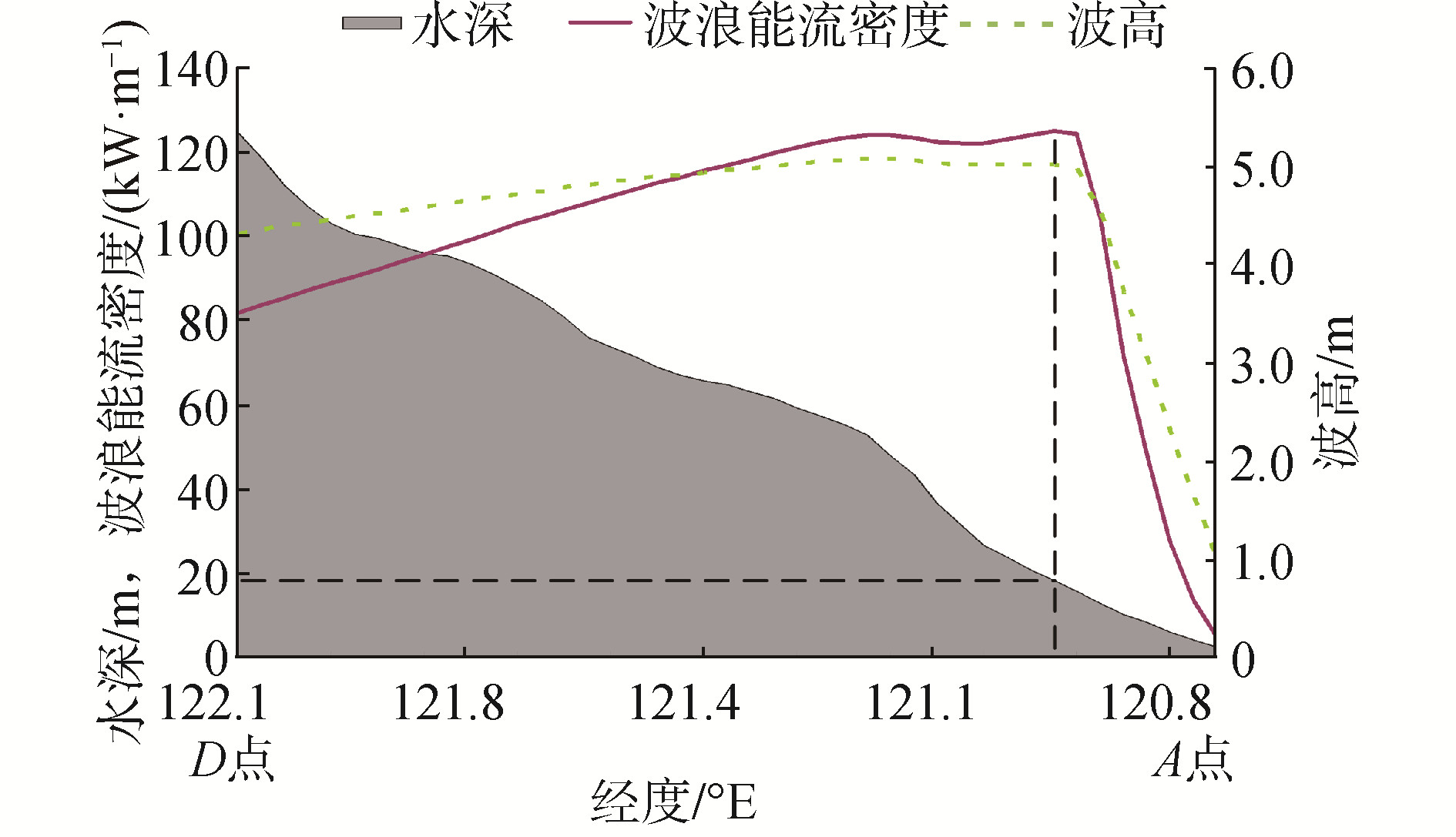
3.4 不同传播方向的能量传播取20 m/s定常风,风向与水深等值线成45°(东风)直至波浪达到充分成长状态,取线段DF上的能量变化,如图 6;风向与等深线成90°(东南风),取线段DA上的能量变化,如图 7。
|
Download:
|
| 图 6 风向与水深等值线成45°时能流密度随水深的变化 Fig. 6 The variation of energy flow density with water depth when the wind direction and the water depth contour are at an angle of 45° | |
|
Download:
|
| 图 7 未定常风向与水深等值线成45°时能流密度随水深的变化 Fig. 7 The change of energy flow density with water depth when the unsteady wind direction and the water depth contour are at an angle of 45° | |
从图 6可以看出,风向与等深线成45°时,随着水深的减小,水深位于60~120 m,波浪能呈下降趋势。水深位于40~80 m,随着水深的减小波浪能呈现增长趋势,水深约为40 m时波浪能达到最大。水深小于40 m时波浪能又随着水深的减小而迅速衰减。图 7可以看出,风向与海岸垂直时,随着水深的减小,能量逐渐增大,20 m水深时能量达到最大,之后迅速衰减,可见过去所认为的水深越深能量越大(外海能量大于近岸)的认识是值得商榷的,这与Folley[4]的结论相一致。因此对本文研究的福建海岸,若其盛行风向与海岸近乎垂直,波力电站适宜建在离岸距离较近的水深20 m左右海域,若盛行风向与海岸成45°角,则适合建在离岸水深40 m的海域。
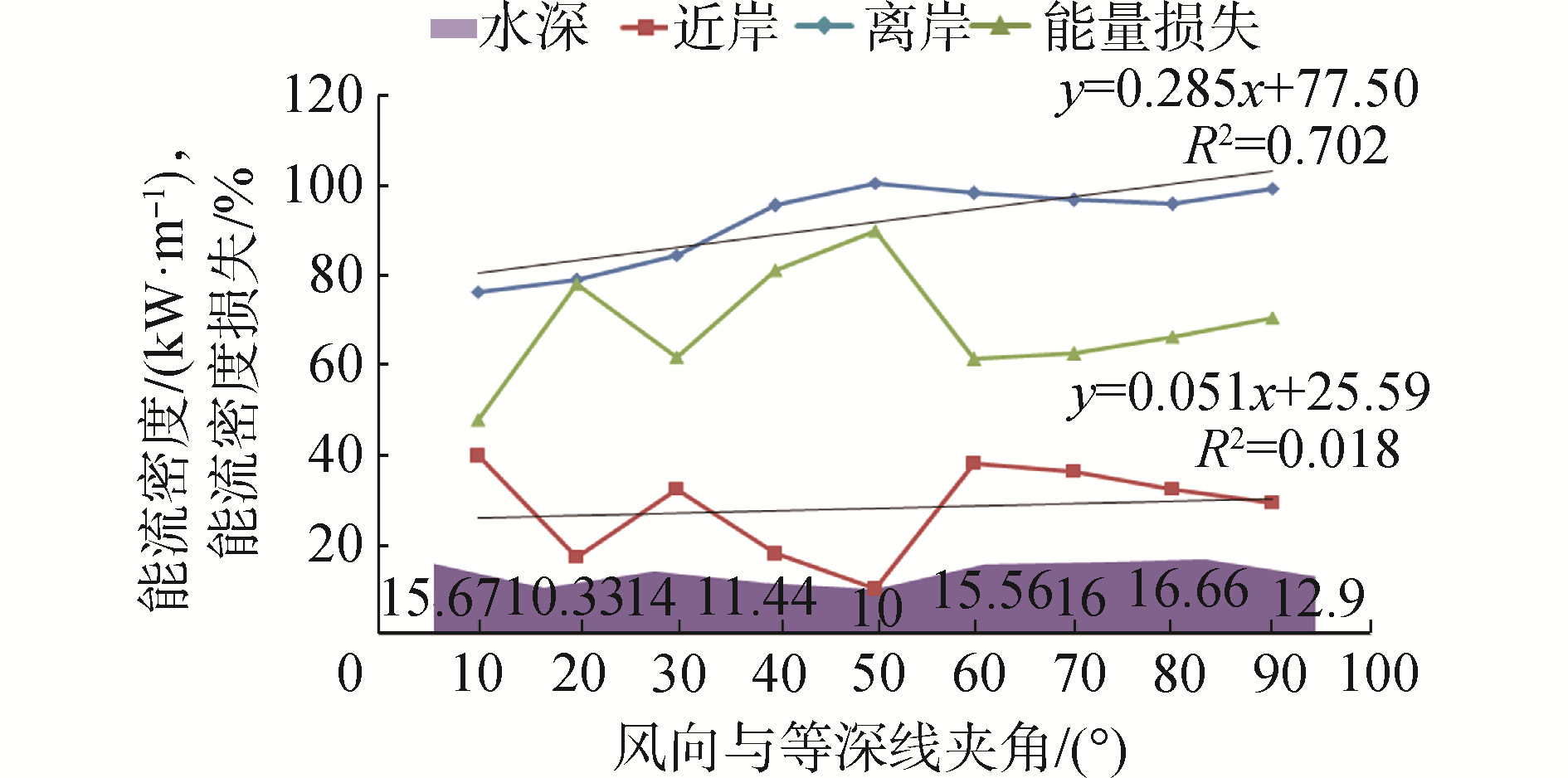
3.5 不同传播方向的能量损失考虑风向与等深线成不同角度时离岸传播到近岸的能量损失情况。如图 2中,取线段BG→BE→…→BH→BA,其风向与等深线夹角角度依次为10°→20°→…→80°→90°,将不同角度下的离岸(点2, B点)能量和近岸(G→E→…→H→A)能量绘制为图 8,其中能量损失率计算公式为:
| $ {P_l} = \frac{{{P_o} - {P_n}}}{{{P_o}}} $ | (3) |
|
Download:
|
| 图 8 不同传播方向离岸到近岸的能量损失 Fig. 8 Energy loss from offshore to near shore in different directions of propagation | |
式中:Pl为能量损失率;Po为离岸能量;Pn为近岸能量。由图 8可以看出,离岸波浪能流密度随着风向与等深线夹角的增大,能量逐渐增大,其回归系数可达0.285,可见风向对离岸的波浪能大小有很重要的影响,对近岸影响较小,且风向与海岸近似垂直时,吹程内波浪能最大。由离岸(B点,水深63 m)到近岸(G点、E点…A点,水深为10~16.7 m)的传播过程中,波浪能的能量损失率在48%~90%,平均损失率为68%。(比Folley等[7]的结果偏大,其为水槽理想化实验,而本文为实际水深,模式中包含波破碎、摩擦等作用,故损失率相比其结果偏大)。
3.6 能量随时间的变化垂直于水深等值线的20 m/s定常风(东南风)持续时间5 h后,风场立即张驰(停吹),考虑其后4天的波浪能衰减过程。图 9给出了上述实验条件下P点1(图 9(a)),P点2(图 9(b)),P点3(图 9(c))共3个点的波高、周期及波浪能流密度随时间的变化。可以看出,不同水深波浪能变化规律基本相似,其中深水最先达到波浪能最大值。近岸由30 kW/m衰减到5 kW/m(衰减83.3%),离岸120~10 kW/m(衰减91.7%),深水90~10 kW/m(衰减88.9%)均需约2天时间,可见近岸能量衰减相对较慢,离岸能量衰减最快。
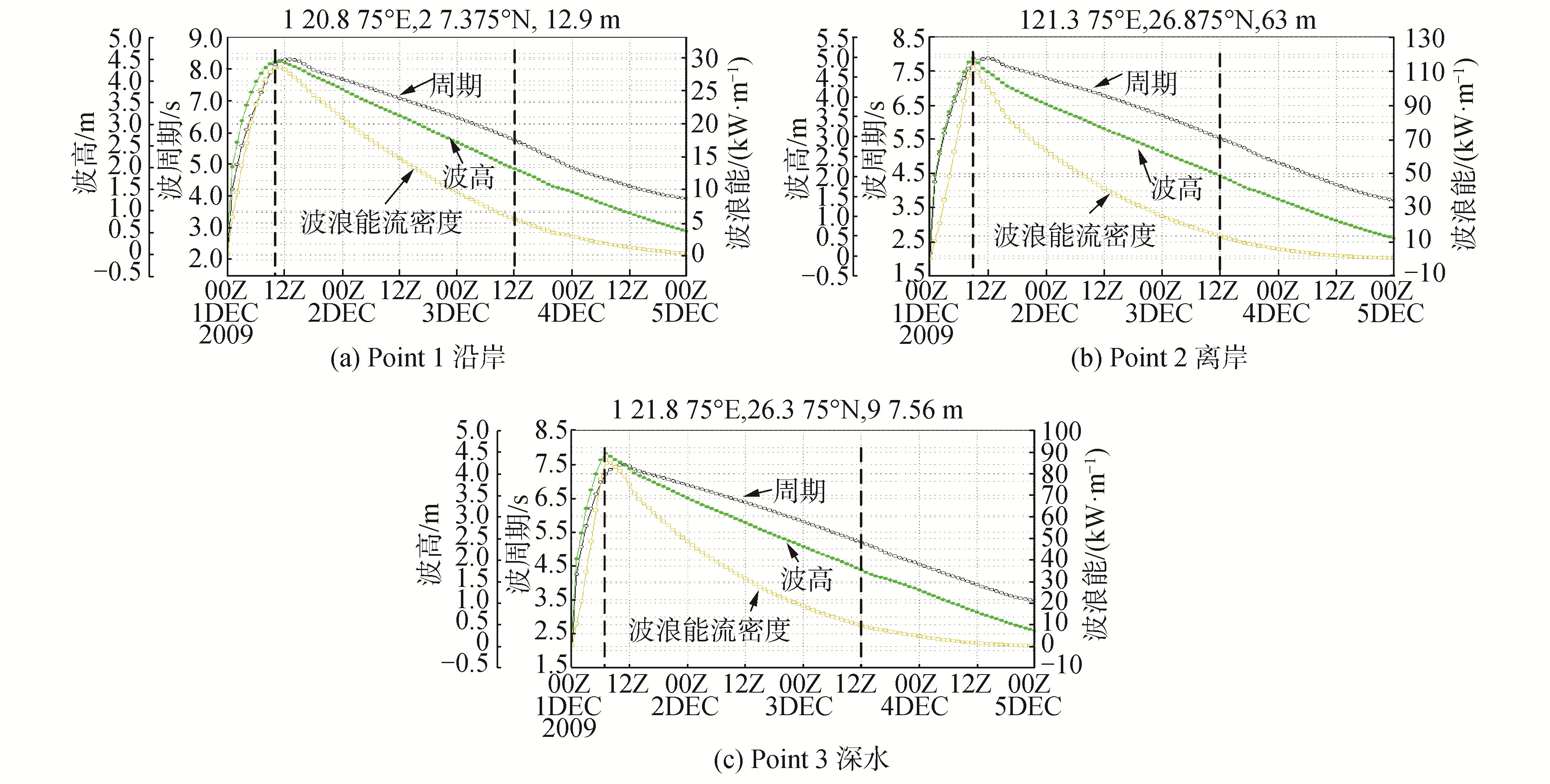
|
Download:
|
| 图 9 不同水深的波浪能流密度随时间变化 Fig. 9 Wave energy flow density at different water depths changes with time | |
二维波谱由描述在频率域以及方向域能量分布的频率谱和方向谱组成,其形状与波浪的生成机理有关,主要取决于风速、风区和风时3个要素。WW3模式采用的为Jonswap谱,其可精确描述平均波要素、频率(方向)谱等[15]。在3.6节基础上,绘制了能量衰减过程中1日7时、2日11时、3日17时和4日23时4个时次近岸的极坐标谱图(由于篇幅限制,图略),3点均在线段AC上,共同受东南定常风影响谱形较为一致。在波浪能量的传播过程中,风能输入项作用最大,非线性相互作用次之,波破碎带来的耗散作用最小。风能输入项和波破碎耗散项的最大值集中出现在西北方向,与风向相对应,而非线性作用项最大值中心则出现在风向的两侧。谱值均为由两侧向中心逐渐衰减,当波高小于1.5 m时,非线性波波相互作用和破碎耗散作用较小。7 h和11 h时,方向谱的大值中心频率基本均位于0.1~0.15 Hz,方向为东南向与风向一致。23 h时方向谱大值中心位于0.15~0.25 Hz,北偏东15°出现另一个大值中心。17 h和23 h时,风能输入等各项几乎消失殆尽。离岸谱图中(图略),相比近岸,离岸各项谱值均较大,且范围更广,到17 h方向谱最大值中心仍为东南向,频率位于0.15~0.2 Hz,23 h时方向谱最大值中心频率位于0.2~0.25 Hz,其间在北偏东30°均出现另一个明显大值中心。深水谱图中,23 h时大值中心位置为北偏东45°。吸波装置频率与波能量集中频率一致,可大大提高波浪能的采集效率,因此对于福建海岸,常年波高较大(2 m以上)的大浪区,主要吸收频率宜设在0.1~0.15 Hz;对于常年波高较小(小于2 m)的海域,其主要吸收频率宜设在0.15~0.2 Hz。
4 结论1) 在风向与等深线垂直时,不同风速下波浪能最大值均集中在水深为20~60 m,即对于我国福建海岸的大陆架坡度而言,离岸20~60 m为定常东南风产生最大波浪能密度带,离岸小于20 m时则波浪能流密度迅速减小。波浪能流密度与波高随水深变化大体一致,直到水深大于60 m时,波浪能衰减速率大于波高。波浪充分成长与否,其能流密度随水深的变化形势基本一致,仅大小数值不同。波浪能并非过去所认为的水深越深能量越大(外海能量大于近岸),当风向与海岸垂直时,随着水深的减小,能量逐渐增大,20 m水深时能量达到最大,之后迅速衰减;当风向与等深线成45°角时,水深约为40 m时波浪能达到最大,因此对福建海岸,若其盛行风向与海岸近乎垂直,波力电站适宜建在离岸距离较近的水深20 m左右海域,若盛行风向与海岸成45°角,则适合建在离岸水深40 m的海域。
2) 风向对离岸的波浪能大小有很重要的影响,对近岸影响较小,且风向与海岸近似垂直时,吹程内波浪能最大。本文模拟分析中包含了波破碎及摩擦等作用,波浪能由离岸传播到近岸过程中,能量平均损失率为68%,用水槽等设备做理想实验其值有望降低。不同的水深其波浪能变化规律基本相似,其中深水处其最先达到波浪能最大值,但近岸能量衰减相对较慢。对本文选择的福建海岸而言,对于常年波高较大(2 m以上)的大浪区,主要吸收频率宜设在0.1~0.15 Hz;对于常年波高较小(小于2 m)的海域,主要吸收频率宜设在0.15~0.2 Hz。
3) 本文采用真实水深利用“模式+模型”方法进行波浪能传播规律研究,旨在更接近真实情况,但也未将地形折射对波浪能辐聚辐散、吹程对浅水区能量累积效应等影响能量传播的因素剥离出来,对波浪能传播规律研究还存在一定局限性,后续拟设计理想地形(如平整水深坡度)、不同风向(如由近岸吹向离岸)等情况对波浪能传播规律进一步深入研究。
| [1] |
褚同金. 海洋能资源开发利用[M]. 北京: 化学工业出版社, 2005: 103-105. CHU Tongjin. Development and utilization of marine energy resources[M]. Beijing: Chemical Industry Press, 2005: 103-105. (  0) 0)
|
| [2] |
郑崇伟, 苏勤, 刘铁军. 1988-2010年中国海域波浪能资源模拟及优势区域划分[J]. 海洋学报, 2013, 35(3): 104-111. ZHENG Chongwei, SU Qin, LIU Tiejun. Wave energy resources assessment and dominant area evaluation in the China sea from 1988 to 2010[J]. Acta oceanologica sinica, 2013, 35(3): 104-111. DOI:10.3969/j.issn.0253-4193.2013.03.012 (  0) 0)
|
| [3] |
游亚戈, 马玉久. 海洋能在海洋环境测量标上的应用[J]. 气象水文海洋仪器, 2003(3): 32-35. YOU Yage, MA Yujiu. The sea energy source application in the sea environment[J]. Meteorological, hydrological and marine instruments, 2003(3): 32-35. DOI:10.3969/j.issn.1006-009X.2003.03.005 (  0) 0)
|
| [4] |
WAN Yong, ZHANG Jie, MENG Junmin, et al. Study on wave energy resource assessing method based on altimeter data-A case study in Northwest Pacific[J]. Acta oceanologica sinica, 2016, 35(3): 117-129. DOI:10.1007/s13131-016-0804-2 (  0) 0)
|
| [5] |
韩林生, 王静, 高佳, 等. 山东褚岛北部海域波浪能资源分析[J]. 太阳能学报, 2020, 41(2): 165-171. HAN Linsheng, WANG Jing, GAO Jia, et al. Analysis of wave energy resources in northern waters of Chudao island in Shandong province[J]. Acta energiae solaris sinica, 2020, 41(2): 165-171. (  0) 0)
|
| [6] |
万勇, 范陈清, 戴永寿, 等. 山东半岛周边近岸海域波浪能开发潜力研究[J]. 太阳能学报, 2018, 39(12): 3311-3318. WAN Yong, FAN Chenqing, DAI Yongshou, et al. Wave energy development potential assessment in nearshore sea area around Shandong peninsula[J]. Acta energiae solaris sinica, 2018, 39(12): 3311-3318. (  0) 0)
|
| [7] |
FOLLEY M, ELSAESSER B, WHITTAKER T. Analysis of the wave energy resource at the European Marine Energy Centre, Institution of Civil Engineers Coasts[C]//Marine Structures and Breakwaters Conference. Edinburgh. 2009: 1-10.
(  0) 0)
|
| [8] |
谢媛媛, 梁丙辰, 马得培. 近岸流对波浪传播影响的数值分析[J]. 海洋科学, 2010, 34(5): 73-78. XIE Yuanyuan, LIANG Bingchen, MA Depei. Numerical study of the influence of coastal current on wave propagation[J]. Marine sciences, 2010, 34(5): 73-78. (  0) 0)
|
| [9] |
The WAVEWATCH Ⅲ Development Group. User manual and system documentation of WAVEWATCH Ⅲ version 5.16. Tech. Note 329[EB/OL]. [2019-04-17]. College Park, MD, USA: NOAA/NWS/NCEP/MMAB, 2016. https://polar.ncep.noaa.gov/waves/wavewatch/manual.v5.16.pdf.
(  0) 0)
|
| [10] |
郑崇伟. 利用WW3模式实现中国周边海域波浪能流密度数值预报——以2次冷空气过程为例[J]. 亚热带资源与环境学报, 2014, 9(2): 18-25. ZHENG Chongwei. Wave energy density forecast in China Seas by WW3 wave model: a study based on two cold air events[J]. Journal of subtropical resources and environment, 2014, 9(2): 18-25. DOI:10.3969/j.issn.1673-7105.2014.02.004 (  0) 0)
|
| [11] |
张沥, 郑崇伟, 刘铁军, 等. 两种海浪模式对一次台风浪过程的模拟分析[J]. 广东海洋大学学报, 2013, 33(6): 72-76. ZHANG Li, ZHENG Chongwei, LIU Tiejun, et al. Contrast simulation of typhoon waves in the China Sea[J]. Journal of Guangdong Ocean University, 2013, 33(6): 72-76. (  0) 0)
|
| [12] |
BADIEI P, MOUSAVI S M S. The third generation spectral wave model, WAVEWATACH-Ⅲ, enhanced for use in nearshore regions[J]. Journal of civil and surveying engineering, faculty of engineering, 2010, 44(2): 289-302. (  0) 0)
|
| [13] |
WAN Yong, ZHANG Jie, MENG Junmin, et al. A wave energy resource assessment in the China's seas based on multi-satellite merged radar altimeter data[J]. Acta oceanologica sinica, 2015, 34(3): 115-124. DOI:10.1007/s13131-015-0627-6 (  0) 0)
|
| [14] |
王传崑, 卢苇. 海洋能资源分析方法及储量评估[M]. 北京: 海洋出版社, 2009: 9-11. WANG Chuankun, LU Wei. Analytical methods and reserves assessment of ocean energy resources[M]. Beijing: Ocean Press, 2009: 9-11. (  0) 0)
|
| [15] |
高加云. 波浪谱数学模型初步应用研究[D]. 南京: 河海大学, 2006: 15-26. GAO Jiayun. Rudiment research in application of wave spectral numerical models[D]. Nanjing: Hohai University, 2006: 15-26. (  0) 0)
|
 2021, Vol. 42
2021, Vol. 42


