2. 甘肃流体机械及系统重点实验室, 甘肃 兰州 730050;
3. 上海凯泉泵业(集团)有限公司, 上海 201804
2. Key Laboratory of Fluid Machinery and Systems of Gansu Province, Lanzhou 730050, China;
3. Shanghai Kaiquan Pump Industry(Group) Company, Ltd., Shanghai 201804, China
低比转速离心泵具有高扬程,结构紧凑的优点。然而,由于其叶片流道狭窄且较长,更容易存在效率不高,汽蚀性能差以及内部流动不稳定等现象[1]。
空化的发展是流动不稳定性的来源,会诱发振动[2-3]、噪声[4-5]、载荷分布不均衡,伴随流体冲击材料表面所形成的巨大破坏[6-7],这些均会扰乱系统的正常运行,减小能量转换率,降低机组性能,减少泵体的使用寿命。充分理解空化的产生、发展和演变特点,才能更好地对其进行控制。Pouffary等[8]采用数值模拟的方法对离心泵内空化流动进行了全流场分析,结果表明空化发生时空泡破裂过程中形成并释放的激波影响了离心泵的能量转换,对外表现为扬程骤降;Medvitz等[9]基于Kunz空化模型研究了小空化数下离心泵内的空化流动,并分析了离心泵在偏离工况点时的扬程下降机理;Lu等[10]模拟研究了低比转速离心泵在小流量工况下的空化不稳定性现象,结果表明叶轮与蜗壳间的动静干涉及叶轮内的空化现象是产生不稳定流动的主导因素;Coutier-Delgosha等[11]利用数值和试验研究了二维离心叶轮中空泡的发生形式和空间形态分布;Fu等[12]数值模拟了离心泵在不同工况下的空化流动,发现设计工况下空泡范围、尺度、持续时间、压力脉动幅值均最小;Kanwanami等[13]通过水翼试验提出了一种云空化的控制方法,即在水翼表面布置障碍物,结果表明布置在水翼中部的障碍物可以有效阻挡回射流,降低水翼阻力系数和噪声强度;陈红勋等[14]对带有缝隙引流叶轮的低比转速离心泵进行了研究,发现缝隙引流叶片可以提高泵的空化性能,较大程度的改善离心泵的振动特性;Lee等[15]发现在水翼尾缘注入的回射流能够有效延迟梢涡空化的初生,还可降低噪声强度,然后将其应用于螺旋桨发现有相同的抑制效果;王巍等[16]提出在水翼吸力面布置凹槽的方法,研究表明适当的凹槽位置和表面构型可以使水翼边界层厚度减小,边界层分离点滞后,对空化有明显的抑制效果,但也会触发凹槽附近区域回射流的加速;Reisman等[17]将非冷凝气体注入水翼表面,通过试验发现空气射流不仅可以减小噪声,同时可以对云空化产生有效的抑制作用;赵伟国等[18]提出了一种在离心泵叶片表面布置障碍物抑制空化的主动控制方法,发现适当高度的障碍物可以改变压力分布,增大近壁面湍动能,对空化发展各个阶段均有明显抑制效果;袁寿其等[19]模拟研究了分流叶片对低比转速离心泵空化性能和叶轮内流场的影响,其结果表明分流叶片增大扬程的同时明显提高了泵的抗汽蚀性能。
本文提出了一种在离心泵叶轮后盖板布置小叶片来抑制空化发展的新方法,该方法有区别于目前研究较成熟的分流叶片。将通过数值模拟和试验相结合的手段,分析小叶片对空化流动的影响及其控制空化的机理。
1 研究模型与数值方法 1.1 计算与试验模型所选模型为一比转速ns=32、转速n=500 r/min的低比转速离心泵,其设计性能参数如下:流量Q0=8.6 m3/h,扬程H0=4.2 m,叶轮入口直径D1=85 mm,叶轮出口直径D2=310 mm,叶轮出口宽度b2=12 mm,叶片进出口角度β1=β2=37°,叶片数Z=6。
通过Pro/E 5.0软件建立三维流场计算域,包括进口延长段、叶轮、蜗壳3部分,如图 1(a)所示。该离心泵叶轮,包括原叶片、后盖板和小叶片。小叶片是基于原型叶片型线减厚降高设计的,厚度为原叶片的1/3,高度为原叶片的1/4,布置在叶轮后盖板且靠近进口。与原叶片数量相同,沿叶轮圆周方向,偏置一定角度后与原叶片交错且均匀布置,如图 1(b)、图 1(c)所示。

|
Download:
|
| 图 1 三维流场计算域 Fig. 1 The 3D stream for calculation domain | |
网格划分在ICEM中完成,对叶轮进口添加进口延长段,以减小边界条件对泵内部流场的影响。设计了3种不同密度的网格,完成了原型泵在设计工况下的网格无关性分析,见表 1。
| 表 1 网格无关性检查 Table 1 Check of grid independence |
由表 1可知,随着网格数的不断减小,扬程误差不大于1%;综合考虑计算资源及数值精度影响,最终网格数确定为1 967 816。
1.3 基本方程流体运动基本控制方程为基于Reynolds平均的Navier-Stokes方程。
连续性方程及动量方程分别为:
| $ \frac{{\partial {\rho _m}}}{{\partial t}} + \frac{{\partial \left( {{\rho _m}{u_i}} \right)}}{{\partial {x_i}}} = 0 $ | (1) |
| $ \;\;\;\;\;\;\; \frac{{\partial \left( {{\rho _m}{u_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {{\rho _m}{u_i}{u_j}} \right)}}{{\partial {x_j}}}{\rm{ }} = - \frac{{\partial p}}{{\partial {x_i}}} + \\ \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + {\mu _t}} \right)\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {u_i}}} - \frac{2}{3}\frac{{\partial {u_k}}}{{\partial {x_k}}}{\delta _{ij}}} \right)} \right] $ | (2) |
混合相密度可以表示为:
| $ {\rho _m} = {\alpha _v}{\rho _v} + {\rho _l}(1 - {\alpha _v}) $ | (3) |
式中:ρm为混合相密度;ui、uj、uk为速度分量;μ、μt分别为混合介质动力粘度、湍流粘度;ρv、ρl分别为气相和液相密度,αv为气相体积分数,δij为克罗内克常数。
1.4 湍流模型湍流模型选用SST k-ω,不同的湍流模型对近壁区网格数量要求不同。常用Y+值保证近壁面区域有足够的节点数,从而能更好的捕捉边界层内的流动情况[20-21]。Y+值表示离壁面最近的网格节点到壁面的距离:
| $ {Y^ + } = {\rm{ }}\frac{{\sqrt {{\tau _\omega }/\rho } \Delta n}}{{{\rm{ }}v}} $ | (4) |
式中:τω为壁面切应力,Pa;ρ为流体密度,kg/m3;Δn为与壁面最近2个网格节点间距离,m;v为运动粘度,m2/s。
本文中模拟的近壁网格Y+值能够保证在离心泵流场模拟中有较好的适用性。
1.5 空化模型Zwart-Gerber-Belamri空化模型[22]基于简化的Rayleigh-Plesset方程,忽略二阶项和表面张力,重点考虑空化初生和发展时空泡体积变化的影响:
| $ {{R_e} = {F_{{\rm{vap}}}}\frac{{3{\alpha _{{\rm{ruc}}}}\left( {1 - {\partial _v}} \right){\rho _v}}}{{{R_B}}}\sqrt {\frac{2}{3}} \frac{{{P_v} - P}}{{{\rho _l}}}, P < P} $ | (5) |
| $ {{R_c} = {F_{{\rm{cond}}}}\frac{{3{\alpha _\imath }{\rho _v}}}{{{R_B}}}\sqrt {\frac{2}{3}} \frac{{P - {P_v}}}{{{\rho _l}}}, P > {P_v}} $ | (6) |
式中:源项Re、Rc分别表示汽泡的产生(汽化)和溃灭(凝结)。根据文献[23-24],成核位置体积分数αruc=5×10-4;RB为空泡半径取1.0×10-6;P为流场压力,Pv为饱和蒸汽压力,一般取25 ℃下纯水的饱和蒸汽压力为3 169 Pa;Fvap为蒸发过程中经验系数,取50;Fcond为凝结过程中经验系数,取0.01。
1.6 边界条件采用ANSYS CFX软件对计算域进行数值求解,固体壁面设置为绝热无滑移壁面,边界条件设为压力进口、质量流量出口。以定常计算结果为初始值,进行非定常模拟,动静交界面由冻结转子修改为瞬态冻结转子,收敛精度为10-5。叶轮每旋转3°作为1个时间步长,每个时间步长迭代20次,共旋转8圈,为保证叶轮内部流体进入稳定流动状态,选取最后一圈的模拟结果进行非定常分析。
2 数值模拟验证 2.1 试验装置在甘肃省流体机械及工程重点实验室的离心泵闭式实验台上进行离心泵外特性和空化实验。试验系统如图 2所示。
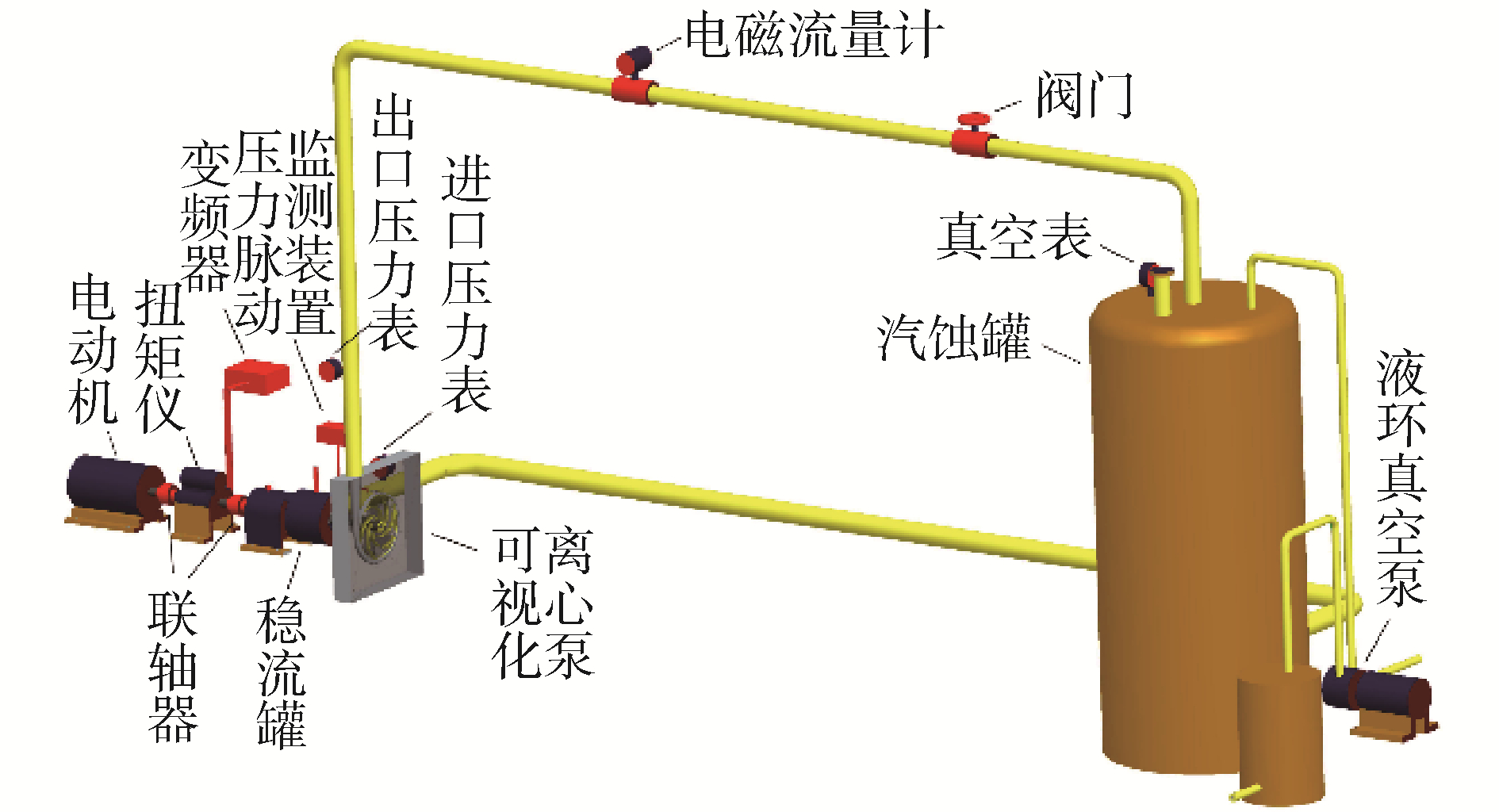
|
Download:
|
| 图 2 闭式试验台示意 Fig. 2 Sketch map of closed test bench | |
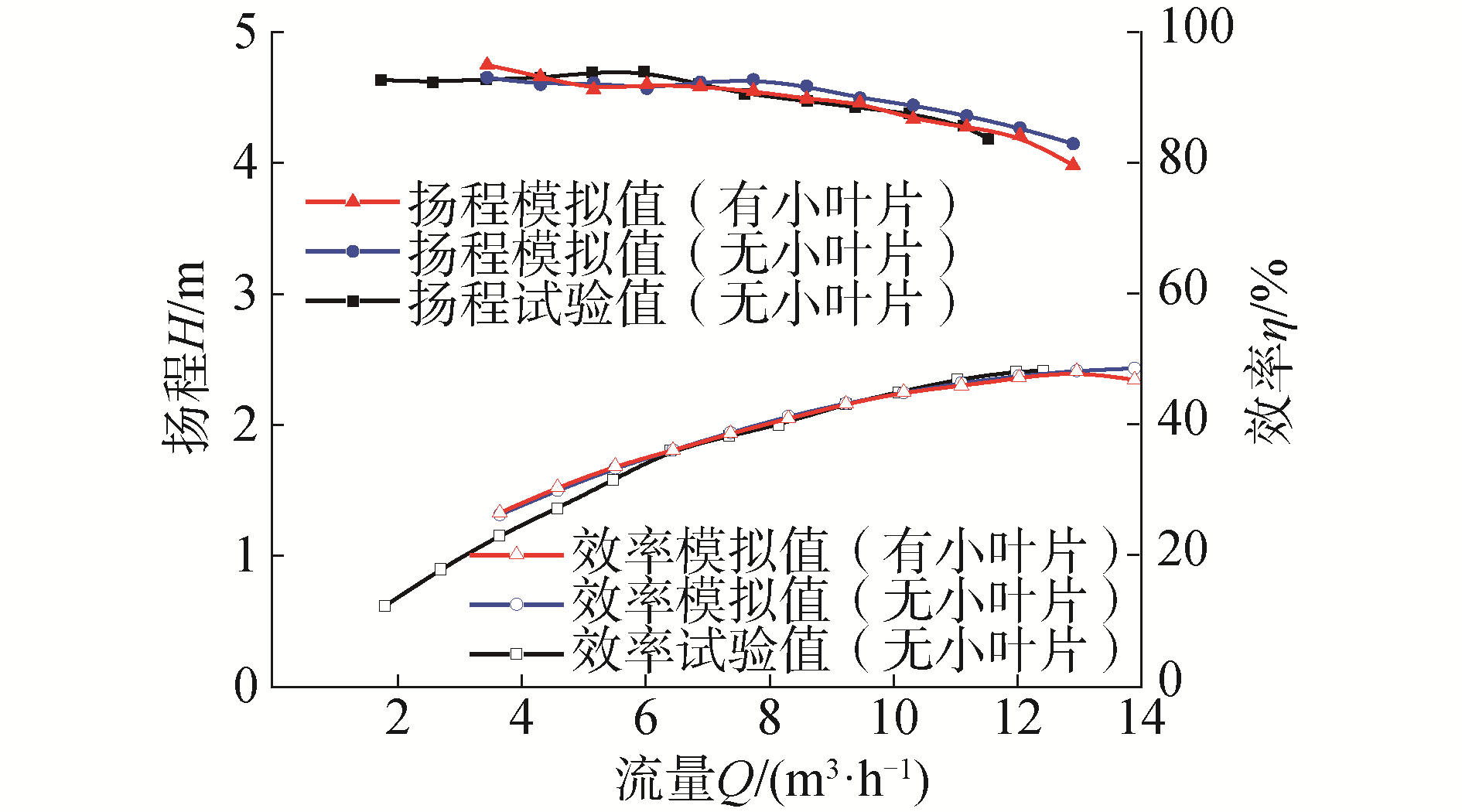
图 3为不同工况下有、无小叶片的离心泵模拟值与试验值的对比曲线。
|
Download:
|
| 图 3 数值模拟与试验性能曲线 Fig. 3 Performance curves of numerical and experiment values | |
原型泵的扬程试验曲线与模拟曲线变化趋势接近,误差在3%以内;效率试验值略低于其模拟值,主要原因是由于数值计算中并未考虑机械损失及水力损失。布置的小叶片几乎不影响离心泵的外特性性能,进一步验证了所选湍流模型对内部流场有较好的适应性。
2.3 空化模型验证常采用无量纲空化数来描述空化发生的可能性和严重程度:
| $ \sigma = ({P_1} - {P_v})/(0.5\rho {U^2}) $ | (7) |
式中:P1是参考压力也是泵的进口压力;Pv是饱和蒸汽压力,3 169 Pa;U是叶片和前盖板交接处的圆周速度:
| $ U = n\pi {D_0}/60 $ | (8) |
式中:n是叶轮的转速;D0是叶片进口和前盖板交界处的直径。
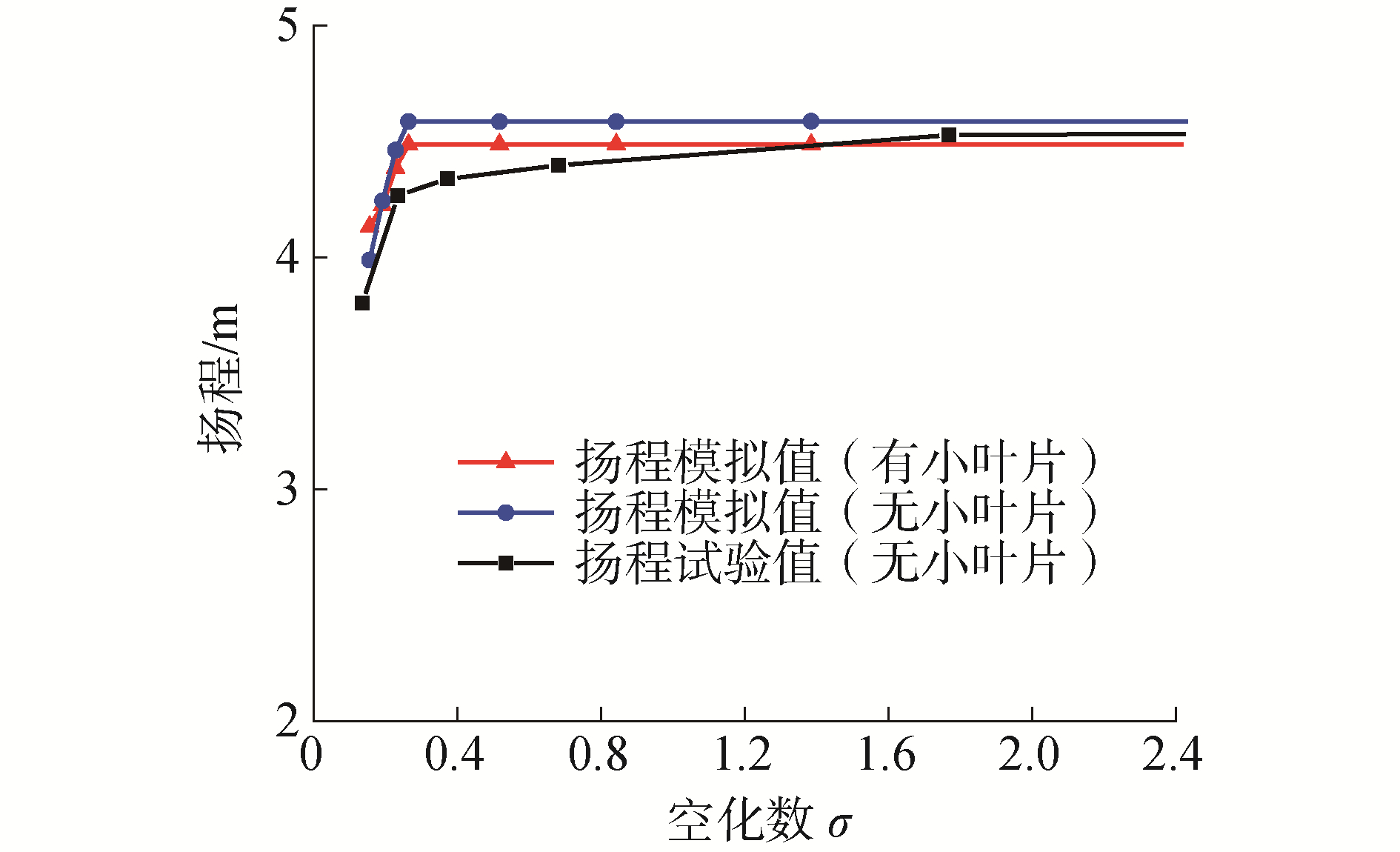
如图 4所示,在不同空化数下,无小叶片的扬程试验曲线均位于其模拟曲线下方,这是因为数值计算中忽略了部分空化流动的影响因素,例如水质、气核数以及加工误差等;随着空化数的减小,扬程试验曲线较模拟曲线下降更为明显;当空化数为0.15时,试验值和模拟值分别为3.80 m和3.99 m,误差为4.5%。有无小叶片的扬程模拟曲线变化趋势更为接近,小叶片还可提高低空化数时离心泵的扬程。由此验证了空化模型对流场分析的可靠性。
|
Download:
|
| 图 4 空化性能曲线 Fig. 4 Curves of cavitation performance | |
湍动能

|
Download:
|
| 图 5 湍动能分布 Fig. 5 Turbulence kinetic energy distributions | |
图 6为不同空化数下叶轮中间截面流线分布。可以看出,空化数σ为0.84时,小叶片对流线分布基本无影响。原型叶轮中,随着空化数减小,叶轮流道中开始产生漩涡,漩涡强度逐渐增大且集中在叶片吸力面附近。特别是当空化数σ为0.15时,流道内充满了空泡,流线分布较紊乱,旋涡表现出脱落特征,会导致较大的流动损失与能量耗散;而布置小叶片的叶轮在空化发展各个阶段内,旋涡强度明显减弱的同时,有效抑制了空泡的脱落并改善了空泡形态。小叶片并不会堵塞叶轮入口流道,其作用类似于分流叶片,通过对流体做功,减小了叶片背面上的流动分离,进而改善叶轮内流场结构。

|
Download:
|
| 图 6 流线分布 Fig. 6 Streamlines distributions | |
图 7是叶片压力面与吸力面在设计工况下的不同位置处的静压分布。横坐标表示叶片上某点在中间流线上的相对位置,其中0为叶片进口,1为叶片出口,纵坐标表示叶片表面静压力。叶片表面载荷定义为同一叶片相同半径处压力面与吸力面压力之差。可以看出,叶片中间流线表面载荷总体呈现先增大后减小的趋势,静压最低点位于叶片进口吸力面处。空化数σ为0.84时,小叶片基本不影响叶片中间流线上载荷分布。随着空化数减小,空泡开始形成于叶片吸力面附近,泵内空化加剧,叶片表面压力随之减小。而布置小叶片后压力面和吸力面的静压均明显升高,尤其是当空化数σ为0.15时,效果更为显著,进一步说明小叶片在一定程度上能够改善离心泵的空化性能,这与前面分析结果相一致。

|
Download:
|
| 图 7 叶片中间流线上载荷分布 Fig. 7 Blade loading distribution on middle streamline | |
定义叶轮内空泡体积为:
| $ {V_{{\rm{cav}}}} = \sum\limits_{i = 1}^N {{\alpha _{v, i}}{V_i}} {\rm{ }} $ | (9) |
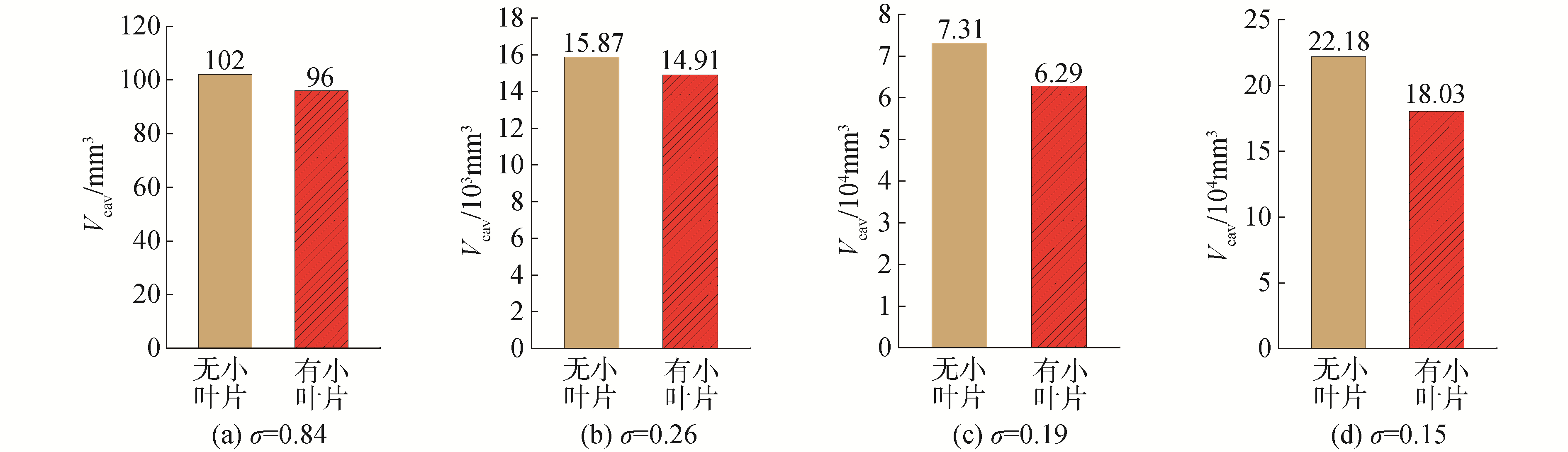
式中:N是计算域中控制单元总数量,αv, i是每一个控制体积中的蒸汽体积分数;Vi是每个控制单元体积,mm3。图 8为不同空化数下周期内叶轮中空泡体积的平均值Vcav。当空化数σ为0.84时,叶轮内空泡极少,此时有无小叶片的叶轮内空泡体积分别为96 mm3和102 mm3;当空化数σ为0.26、0.19时,叶片吸力面附近空化区突然增大,并向流道中部扩展,此时小叶片较大程度地减少了叶轮内空泡体积,减少量分别为6.0%和14.2%,抑制空化效果明显;空化数减小为0.15时,空泡积累严重,堵塞流道并导致过流面积受限,影响流体的正常流动和能量转换,对外表现为扬程曲线大幅下降。对比布置小叶片的叶轮,可以发现小叶片使叶轮内的空泡体积从22.18×104 mm3减少到18.03×104 mm3,减少量为18.7%,抑制效果最佳。
|
Download:
|
| 图 8 空泡体积变化 Fig. 8 Variations of the cavity volume | |
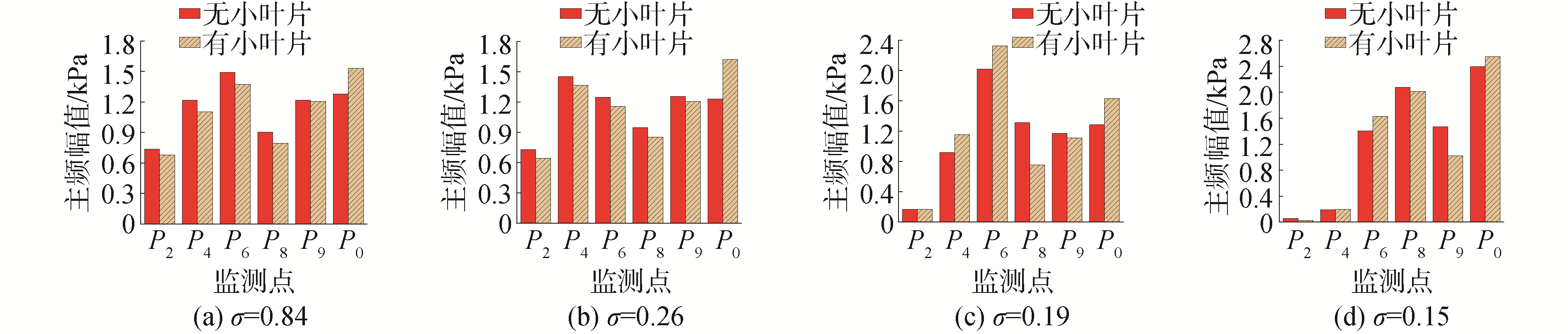
叶轮流道内及蜗壳隔舌处设置监测点如图 1(a)所示。选择P2、P4、P6、P8、P9、V0,其中V0是蜗壳隔舌处的点,其余为叶轮流道内的点。
本文中叶轮转速n=500 r/min,轴频为8.3 Hz,叶片通过频率为50 Hz。通过快速傅里叶变换,得到各监测点的压力脉动频域分布,此处并未展示。频域结果表明,最大压力幅值位于叶频处,且随叶频倍数增加而快速衰减。小叶片并不会改变不同空化状态下不同位置处的压力脉动分布,但会略微增加比原型叶轮更为明显的宽频脉动和轴频脉动,说明小叶片的存在会对流场产生小幅扰动。
将压力脉动频域分布中主频处的压力值提取出来,可得到不同空化状态下各监测点的主频压力幅值。图 9可以看出,空化数σ为0.84、0.26时,小叶片抑制空化的同时,明显降低了叶轮内各个监测点处的压力幅值,但对隔舌处产生了一定扰动,表现为幅值增大。空化数σ为0.19时,叶轮进口区域被空泡覆盖,因此P2处压力幅值变化很小;而P4、P6监测点处压力脉动由于受到小叶片的干扰,幅值因此变大。小叶片降低了P8、P9处的压力幅值,是因为P8、P9监测点位于叶轮出口区域,不会受到其干扰作用。空化数为0.15时,叶轮流道进口及附近区域几乎被空泡占据,空化发展严重,P2、P4监测点处压力幅值很小;小叶片降低了叶轮出口处P8、P9处的压力幅值,但会增大P6、V0处的压力幅值。综上所述,空化发展初期,小叶片能够降低叶轮内各个监测点处的压力幅值。空化严重阶段,小叶片对压力脉动的影响较为复杂,压力幅值变化紊乱;对隔舌处的扰动随着空化的加剧越来越大。
|
Download:
|
| 图 9 压力主频幅值 Fig. 9 Amplitudes of dominate frequency of pressure | |
1) 叶轮盖板布置小叶片后,扬程小幅下降,效率基本不变,且模拟结果与试验结果吻合较好;小叶片可提高低空化数时泵的扬程。
2) 在不同空化数下,小叶片缩小了高湍动能的分布区域,并降低了叶轮内湍动能强度,使流动趋于稳定。这是因为小叶片具有分流作用,通过对流体做功,有效减少了叶片背面上的流动分离,削弱了吸力面附近的漩涡强度,进而改善了离心泵的空化性能。
3) 有小叶片的叶轮内空泡体积远小于无小叶片的叶轮内空泡体积,且空化发展严重时,空泡体积减少量可达18.7%,小叶片抑制空化效果较好。
4) 空化初生及发展阶段,小叶片抑制空化的同时减小了叶轮内压力脉动主频幅值。但在空化严重阶段,小叶片会对流场造成小幅扰动,同时对隔舌处的扰动随空化数减小而增大。
| [1] |
ZHANG Jinfeng, LI Guidong, MAO Jieyun, et al. Effects of the outlet position of splitter blade on the flow characteristics in low-specific-speed centrifugal pump[J]. Advances in mechanical engineering, 2018, 10(7): 1-12. DOI:10.1177/1687814018789525 (  0) 0)
|
| [2] |
CHUDINA M. Noise as an indicator of cavitation in a centrifugal pump[J]. Acoustical physics, 2003, 49(4): 463-474. DOI:10.1134/1.1591303 (  0) 0)
|
| [3] |
王松林, 谭磊, 王玉川. 离心泵瞬态空化流动及压力脉动特性[J]. 振动与冲击, 2013, 32(22): 168-173. WANG Songlin, TAN Lei, WANG Yuchuan. Characteristics of transient cavitation flow and pressure fluctuation for a centrifugal pump[J]. Journal of vibration and shock, 2013, 32(22): 168-173. DOI:10.13465/j.cnki.jvs.2013.22.024 (  0) 0)
|
| [4] |
WEI Yingsan, SHEN Yang, JIN Shuanbao, et al. Scattering effect of submarine hull on propeller non-cavitation noise[J]. Journal of sound and vibration, 2016, 370: 319-335. DOI:10.1016/j.jsv.2016.01.027 (  0) 0)
|
| [5] |
FRIEDRICHS J, KOSYNA G. Rotating cavitation in a centrifugal pump impeller of low specific speed[J]. Journal of fluids engineering, 2002, 124(2): 356-362. DOI:10.1115/1.1457451 (  0) 0)
|
| [6] |
LIU Houlin, LIU Dongxi, WANG Yong, et al. Experimental investigation and numerical analysis of unsteady attached sheet cavitating flows in a centrifugal pump[J]. Journal of hydrodynamics, series B, 2013, 25(3): 370-378. DOI:10.1016/S1001-6058(11)60375-3 (  0) 0)
|
| [7] |
黎慧青.离心泵汽蚀磨损失效分析对策措施研究[D].广州: 华南理工大学, 2011. LI Huiqing. Studies on cavitation and fretting wear of centrifugal pump and counter measures[D]. Guangzhou: South China University of Technology, 2011. (  0) 0)
|
| [8] |
POUFFARY B, PATELLA R F, REBOUD J L, et al. Numerical simulation of 3D cavitating flows:analysis of cavitation head drop in turbomachinery[J]. Journal of fluids engineering, 2008, 130(6): 061301. DOI:10.1115/1.2917420 (  0) 0)
|
| [9] |
MEDVITZ R B, KUNZ R F, BOGER D A, et al. Performance analysis of cavitating flow in centrifugal pumps using multiphase CFD[J]. Journal of fluids engineering, 2002, 124(2): 377-383. DOI:10.1115/1.1457453 (  0) 0)
|
| [10] |
卢加兴, 袁寿其, 任旭东, 等. 离心泵小流量工况不稳定空化特性研究[J]. 农业机械学报, 2015, 46(8): 54-58. LU Jiaxing, YUAN Shouqi, REN Xudong, et al. Investigation of instabilities of cavitation at low flow rate of centrifugal pump[J]. Transactions of the Chinese society for agricultural machinery, 2015, 46(8): 54-58. DOI:10.6041/j.issn.1000-1298.2015.08.009 (  0) 0)
|
| [11] |
COUTIER-DELGOSHA O, FORTES-PATELLA R, REBOUD J L. Evaluation of the turbulence model influence on the numerical simulations of unsteady cavitation[J]. Journal of fluids engineering, 2003, 125(1): 38-45. DOI:10.1115/1.1524584 (  0) 0)
|
| [12] |
FU Qiang, YUAN Shouqi, ZHU Rongsheng, et al. Notice of retraction: numberical simulation of low-specific-speed centrifugal pump cavitation influence of pressure pulsation under different conditions[C]//Proceedings of 2010 International Conference on Computer Application and System Modeling (ICCASM 2010). Taiyuan, China, 2010, DOI: 10.1109/ICCASM.2010.5619008.
(  0) 0)
|
| [13] |
KAWANAMI Y, KATO H, YAMAGUCHI H, et al. Mechanism and control of cloud cavitation[J]. Journal of fluids engineering, 1997, 119(4): 788-794. DOI:10.1115/1.2819499 (  0) 0)
|
| [14] |
陈红勋, 林育战, 朱兵. 缝隙引流叶轮离心泵空化试验研究[J]. 排灌机械工程学报, 2013, 31(7): 570-574. CHEN Hongxun, LIN Yuzhan, ZHU Bing. Experimental study on cavitation performance of centrifugal pump with impeller having leading edge slots[J]. Journal of drainage and irrigation machinery engineering, 2013, 31(7): 570-574. DOI:10.3969/j.issn.1674-8530.2013.07.004 (  0) 0)
|
| [15] |
LEE C S, AHN B K, HAN J M, et al. Propeller tip vortex cavitation control and induced noise suppression by water injection[J]. Journal of marine science and technology, 2018, 23(3): 453-463. DOI:10.1007/s00773-017-0484-4 (  0) 0)
|
| [16] |
王巍, 唐滔, 卢盛鹏, 等. 水翼吸力面布置凹槽抑制空化研究[J]. 农业工程学报, 2019, 35(2): 40-47. WANG Wei, TANG Tao, LU Shengpeng, et al. Investigation of cavitation suppression by arranging pits on hydrofoil suction side[J]. Transactions of the Chinese society of agricultural engineering, 2019, 35(2): 40-47. DOI:10.11975/j.issn.1002-6819.2019.02.006 (  0) 0)
|
| [17] |
REISMAN G E, DUTTWEILER M E, BRENNEN C E. Effect of air injection on the cloud cavitation of a hydrofoil[C]//Proceedings of 1997 ASME Fluids Engineering Division Summer Meeting. 1997.
(  0) 0)
|
| [18] |
赵伟国, 赵国寿, 咸丽霞, 等. 离心泵叶片表面布置障碍物抑制空化的数值模拟与实验[J]. 农业机械学报, 2017, 48(9): 111-120. ZHAO Weiguo, ZHAO Guoshou, XIAN Lixia, et al. Effect of Surface-fitted obstacle in centrifugal pump on cavitation suppression[J]. Transactions of the Chinese society for agricultural machinery, 2017, 48(9): 111-120. DOI:10.6041/j.issn.1000-1298.2017.09.014 (  0) 0)
|
| [19] |
张云蕾, 袁寿其, 张金凤, 等. 分流叶片对离心泵空化性能影响的数值分析[J]. 排灌机械工程学报, 2015, 33(10): 846-852. ZHANG Yunlei, YUAN Shouqi, ZHANG Jinfeng, et al. Numerical analysis on effects of splitter blades on cavitation performance in a centrifugal pump[J]. Journal of drainage and irrigation machinery engineering, 2015, 33(10): 846-852. DOI:10.3969/j.issn.1674-8530.14.0142 (  0) 0)
|
| [20] |
张德胜, 吴苏青, 施卫东, 等. 不同湍流模型在轴流泵叶顶泄漏涡模拟中的应用与验证[J]. 农业工程学报, 2013, 29(13): 46-53. ZHANG Desheng, WU Suqing, SHI Weidong, et al. Application and experiment of different turbulence models for simulating tip leakage vortex in axial flow pump[J]. Transactions of the Chinese society of agricultural engineering, 2013, 29(13): 46-53. DOI:10.3969/j.issn.1002-6819.2013.13.007 (  0) 0)
|
| [21] |
JI Bin, LUO Xianwu, WANG Xin, et al. Unsteady numerical simulation of cavitating turbulent flow around a highly skewed model marine propeller[J]. Journal of fluids engineering, 2011, 133(1): 011102. DOI:10.1115/1.4003355 (  0) 0)
|
| [22] |
ZWART P J, GERBER A G, BELAMRI T. A two-phase flow model for predicting cavitation dynamics[C]//Proceedings of the 5th International Conference on Multiphase Flow. Yokohama, Japan, 2004: 152.
(  0) 0)
|
| [23] |
王柏秋, 王聪, 黄海龙, 等. 空化模型中的相变系数影响研究[J]. 工程力学, 2012, 29(8): 378-384. WANG Baiqiu, WANG Cong, HUANG Hailong, et al. Study of the influence of phase-change coefficients in the cavitation model[J]. Engineering mechanics, 2012, 29(8): 378-384. DOI:10.6052/j.issn.1000-4750.2011.09.0592 (  0) 0)
|
| [24] |
JI Bin, LUO Xianwu, WU Yulin, et al. Numerical analysis of unsteady cavitating turbulent flow and shedding horse-shoe vortex structure around a twisted hydrofoil[J]. International journal of multiphase flow, 2013, 51: 33-43. DOI:10.1016/j.ijmultiphaseflow.2012.11.008 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


