2. 自然资源部海岛(礁)测绘技术重点实验室, 山东 青岛 266590
2. Key Laboratory of Surveying and Mapping Technology on Island and Reef, Ministry of Natural Resources, Qingdao 266590, China
多波束测深技术是当前水下地形地貌探测的主要手段,能够对海底实现条带式的全覆盖测量,具有高精度、高密度和高效率等特点[1-3]。波束归位即利用多波束采集波束信息与各辅助设备采集的数据,通过一定的数学模型将波束脚印由换能器坐标系转化到地理坐标系和某一深度基准面下的水深的过程,是多波束数据处理的关键问题之一[4],其涉及的参数包括发射和接收导向角、发射时刻发射换能器姿态、接收时刻接收换能器姿态、发射和接收换能器安装偏差角等共14个角度。
针对多波束测深波束归位模型问题,国内外学者做了大量的研究。赵建虎等[5]结合航向、潮位、声速、姿态等数据对波束脚印计算的影响,建立了一定的假设条件,并给出了波束归位的详细过程与步骤;黄谟涛等[6]研究了多波束测深系统与机载激光测深系统在位置归算上存在的共性,给出了2者位置归算模型,推导了相应的精度评定模型;阳凡林[7]、何林帮等[8]考虑到水下声线弯曲对波束归位的影响,指出瞬时波束向量为安装偏差和姿态影响的综合产物,并据此推导了顾及安装偏差角和姿态角影响的瞬时波束向量的数学计算模型,提高了多波束测深点的计算精度;杨绍海等[9]、朱小辰等[10]推导了波束脚印位置归算模型,并利用实测浅水多波束测深数据对模型的有效性进行了验证。
上述研究成果在波束归位模型上存在一定的假设或局限性,即将发射换能器和接收换能器近似作为一个整体,忽略了2个换能器各自静态角度偏差和声波在往返海底与换能器期间发射换能器与接收换能器存在的姿态和航向变化。因此,上述模型一般适用于处理浅水型多波束测深仪获取的数据,如R2Sonic2024、SeaBat7125等,该类多波束的收发换能器体积小,通常集成安装,可近似作为整体;且由于浅水作业,发射Ping率较高,波束旅行时极短,发射与接收时刻收发换能器状态变化也可近似忽略。然而,对于中深水型多波束测深仪而言,波束旅行时较长,收发换能器姿态变化则难以忽略,采用上述模型必然在计算过程中引入误差,尤其为横摇方向的变化,使得边缘波束水深误差易超出1%的测深精度[11]。为解决该局限性,Beaudion等[12]提出一种虚拟同心阵(virtual concentric array,VCCA)模型,该模型将收发换能器作为2个独立单元,不仅考虑了收发换能器静态角度偏差,还考虑了波束往返期间换能器的姿态变化,计算精度较高,已应用于开源多波束数据处理软件MB-system中;Hamilton[13]在VCCA模型的基础上,考虑了发射换能器和接收换能器间的位置偏移对波束脚印的影响,并提出一种通过迭代解算波束脚印的收发分置模型,更接近发射与接收波束在海水中的传播状态。尽管2个模型有较高的计算精度,但其波束向量推导过程相对复杂、不易理解。
为此,本文基于VCCA模型,提出一种基于同心双曲线相交的波束归位算法,以虚拟同心阵中心与2个双曲线交点的连线方向构建波束向量,将VCCA模型中复杂的波束向量推导过程转化为求解相交双曲线方程的形式,在确保计算精度的同时获得更为直观且更接近实际的波束归位模型。
1 同心双曲线相交模型构建 1.1 相关坐标系定义为构建同心双曲线相交(co-concentric hyperbolic intersection,CHI)模型,首先需要定义相关坐标系。本文算法坐标系定义参照VCCA模型中坐标系的定义方式,主要包括虚拟换能器坐标系和当地水平坐标系。其中,虚拟换能器坐标系的定义方式如下:1)利用发射时刻t1的发射换能器瞬时状态向量Tx和接收时刻t2的接收换能器瞬时状态向量Rx对波束收发期间换能器状态变化进行记录;2)将2个向量平移到2个位置的中点;3)定义中点位置为坐标系原点O,Tx为Xa轴,Za轴正交于包含Tx和Rx的平面,Ya轴正交于Xa轴和Za轴,坐标系符合右手法则。
其中,Tx可由发射时刻姿态数据与发射换能器安装偏差推导得到,Rx可由接收时刻姿态数据与接收换能器安装偏差推导得到[12]。为将在虚拟换能器坐标系下计算得到的波束脚印坐标归算至当地水平坐标系下,需建立2个坐标系之间的旋转矩阵RGeo[13]。
当地水平坐标系的定义与三轴指向的选择顺序有关,主要有东北天(ENU)和北东地(NED)2种形式,本文算法采用北东地形式,其定义过程可参见文献[4]。
1.2 双曲线相交归位原理波束脚印为发射波束与接收波束声学能量在海底投影的交叉区域,若无波束导向时,发射与接收波束声学能量可抽象为扇形平面;若存在波束导向时,发射和接收声学能量则可抽象为圆锥面[14]。因此,波束脚印可抽象为发射圆锥面与接收圆锥面在海底投影形成的2个曲线的交点。由于发射圆锥面与接收圆锥面顶点重合,即为虚拟换能器坐标系原点[12-13],故圆锥面顶点至波束脚印之间的连线即为待求波束向量。
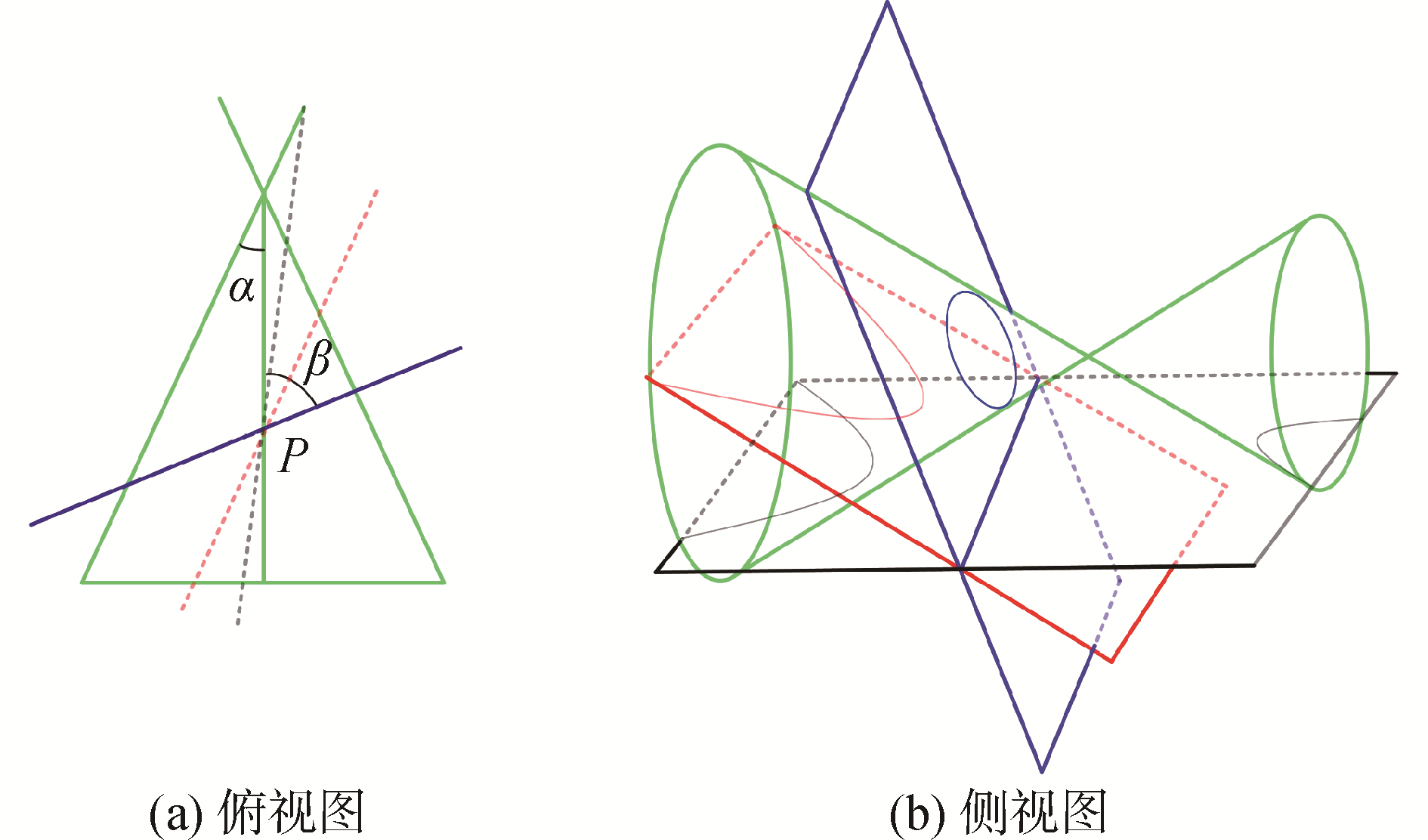
根据平面与圆锥面截线定理[15]可得,平面与圆锥面相交可形成双曲线、抛物线和椭圆,如图 1。由于虚拟换能器坐标系是由发射时刻发射换能器状态和接收时刻接收换能器状态构建得到,发射圆锥面中轴线与接收圆锥面中轴线均位于虚拟换能器坐标系XaOYa面内。因此,在虚拟换能器坐标系下,波束脚印所在交点平面始终平行于XaOYa平面,即交点平面与两圆锥面中轴线夹角β始终为0°。因此,发射和接收圆锥面在该平面上的投影曲线始终为双曲线[15],波束脚印即为2个双曲线的交点,从而避免了其他圆曲线同时出现而给解算过程带来的困难。
|
Download:
|
| 图 1 平面与圆锥面相交得到不同的圆曲线 Fig. 1 Different curves formed with different planes intersecting the cone | |
由1.2节可知,在虚拟换能器坐标系下,波束脚印为发射和接收圆锥面在海底投影形成的2个双曲线的交点。因此,发射圆锥面与接收圆锥面在交点平面中所形成的两双曲线之间的几何关系可如图 2所示。

|
Download:
|
| 图 2 本文算法中波束脚印表示方式 Fig. 2 Description of footprints formed by the intersection of two hyperbolas in this paper | |
计算波束向量需要解算双曲线方程,为便于求解,以双曲线参数方程形式分别对发射和接收双曲线进行定义:
| $ {\left\{ {\begin{array}{*{20}{l}} {{x_t} = {a_t}\cosh {t_1}}\\ {{y_t} = {b_t}\sinh {t_1}} \end{array}} \right.} $ | (1) |
| $ {\left\{ {\begin{array}{*{20}{l}} {{x_r} = {a_r}\cosh {t_2}}\\ {{y_r} = {b_r}\sinh {t_2}} \end{array}} \right.} $ | (2) |
式中:at和bt为发射双曲线参数;ar和br是接收双曲线参数;t1和t2为未知量,其物理意义为用于描述发射向量和接收向量在各自圆锥面上的方位。参数a本质为双曲线顶点,其具体数值与波束导向角和交点平面所在深度有关,如图 3所示。

|
Download:
|
| 图 3 双曲线参数定义 Fig. 3 Parameter definition of the hyperbola | |
由于2个圆锥面顶点相同,因此发射向量与接收向量重合,且不随水深变化,如图 3所示,当水深增加后,虚拟换能器中心(圆锥面顶点)至波束脚印之间构成的波束向量方向不变,故可将2个圆锥面在单位水深下的交点平面上的投影所形成的2个双曲线交点与圆锥面顶点之间的连线作为波束向量。因此令R=1,根据文献[15-16]可得,发射和接收双曲线参数为:
| $ \left\{\begin{array}{l} a_{t}=\tan T_{\text {steer }} \\ b_{t}=1 \\ a_{r}=\tan R_{\text {steer }} \\ b_{r}=1 \end{array}\right. $ | (3) |
式中:Tsteer和Rsteer分别为发射导向角和接收导向角,2角度分别与发射圆锥面与接收圆锥面的圆锥半角互余。
受发射和接收2个时刻换能器姿态变化的影响,接收双曲线轴线与发射双曲线轴线存在一定的角度偏差,大小为δ,如图 2所示。由于本文算法采用VCCA算法中虚拟换能器坐标系的定义方式,故δ具体数值可得到:
| $ \delta=\arccos \left(\boldsymbol{T}_{x} \cdot \boldsymbol{R}_{x}\right)-\frac{\pi}{2} $ | (4) |
对接收双曲线进行角度为δ的二维旋转,并联立发射双曲线参数方程,得到具体方程组为:
| $ \left\{\begin{array}{l} x_{t}=a_{t} \cosh t_{1} \\ y_{t}=b_{t} \sinh t_{1} \\ x_{r}=b_{r} \cos \delta \sinh t_{2}-a_{r} \sin \delta \cosh t_{2} \\ y_{r}=b_{r} \sin \delta \sinh t_{2}+a_{r} \cos \delta \cosh t_{2} \end{array}\right. $ | (5) |
然后将式(3)、(4)中定义的参数代入式(5),利用牛顿迭代法进行求解得到在虚拟换能器坐标系下波束点坐标Va(xa, ya, 1);进而根据旋转矩阵RGeo将其归算到当地水平坐标系下,即VL=RGeo·Va。VL(xL, yL, zL)则为所求波束向量,其用于声线跟踪的波束入射角θ1和计算侧向距、航向距的方位角θ2可进一步表示为[17-18]:
| $ \left\{\begin{array}{l} \theta_{1}=\arctan \left(\sqrt{\left(x_{L}^{2}+y_{L}^{2}\right)} / z_{L}\right) \\ \theta_{2}=\arctan \left(x_{L} / y_{L}\right) \end{array}\right. $ | (6) |
最后,利用上述波束向量进行声线跟踪,并将跟踪结果进行吃水改正、GNSS偏心改正等步骤,归算至地理坐标即完成波束归位过程。
3 实验与分析为验证本文算法的有效性,实验分析分别选取某海区多波束测量获取的浅水(小于500 m)数据和中深水(大于500 m)数据,利用本文算法、常规波束归位算法[19]和VCCA算法对实测数据进行处理并对数据处理结果进行比对,同时利用条带重叠区进行深度不符值的计算。由于VCCA算法已被开源多波束数据处理软件MB-system采用,故以该算法数据处理结果作为基准对本文算法的有效性进行验证。
浅水实测数据测量采用的多波束测深仪为Kongsberg EM2040,该多波束测深仪为浅水型测深仪,其可探测水深最大范围为635 m,每Ping波束数为400,波束开角为80°。
深水实测数据测量采用的多波束测深仪为Kongsberg EM302,该多波束测深仪为全水深型测深仪,其可探测水深范围为10~7 000 m,采用4个扇区,每Ping波束数为432,波束开角为125°。
3.1 浅水数据实验分析选取浅水区某2条重叠测线数据,使用开源多波束数据处理软件MB-system(即VCCA算法)对测线数据进行处理,得到的光照地形图如图 4所示,选择其中一条测线数据进行分析,该测线水深在18~28 m范围,测深点总数为369 200个,共923 Ping。

|
Download:
|
| 图 4 MB-system处理后得到的浅水区光照地形图 Fig. 4 Sun illuminate, depth colored grid of the shallow water data processed by MB-system | |
分别使用本文算法和常规波束归位算法对该测线数据进行处理,并计算本文算法与VCCA算法数据处理结果以及常规算法与VCCA算法数据处理结果之间的差值,其中,水深偏差统计结果如图 5所示。

|
Download:
|
| 图 5 浅水数据水深偏差统计 Fig. 5 Statistics of the depth deviations with shallow water data | |
从图 5(a)可见,本文算法与VCCA算法水深偏差值可近似为0,即本文算法与VCCA算法计算结果基本一致,因此体现了本文算法的有效性;从图 5(b)可见,常规波束归位算法与VCCA算法数据处理结果存在一定的差异,即忽略发射时刻换能器的姿态变化给计算结果带来了误差。
对2种算法与VCCA算法之间的数据处理比对结果进行分析,并按水运工程测量规范[20]中水深测量精度要求(1%水深)对水深差值中超限测深点数进行统计,统计结果如表 1所示。
| 表 1 浅水数据测深点误差统计 Table 1 Error statistics of the soundings form the shallow water data |
由表 1可以看出,本文算法与VCCA算法平面位置偏差与水深偏差最大值均为0.2 cm,最小值均为0,平均相对误差可近似为0,且不存在超出1%测深精度要求的测深点;常规算法与VCCA算法平面位置偏差最大值和最小值分别为0.2 m和0,水深差值最大值为0.341 m,最小值为0,平均相对误差为0.22%,其中约有805个超限点,占总测深点数的0.21%。
为进一步验证算法有效性,使用面面叠置法计算部分测线重叠区域数据处理结果的深度不符值,并统计出深度不符值的总数、均值、中误差及分布情况,并参照水运工程测量规范[20]对主检比对互差的相关要求(大于2%水深)统计超限点比例,结果如表 2所示。
| 表 2 深度不符值统计分析 Table 2 Statistical analysis of depth discrepancy |
由表 2可知,常规波束归位算法深度不符值中误差以及均值较VCCA算法大,而本文算法与VCCA算法不符值统计结果近似一致,表明本文算法计算结果较常规算法精度更高。
综合图 5和表 1、2可见,本文算法计算结果与VCCA算法计算结果差值较小,可近似为0,证明了本文算法具有有效性;常规算法与VCCA算法数据计算结果之间存在偏差,且存在不满足1%测深精度的超限点,但超限点数相对较少仅占总数的0.38%,且参照规范要求可知,3种算法处理的浅水区数据未存在超出2%水深的测深点,表明数据质量良好。因此,对于浅水数据,可认为波束往返期间换能器的姿态变化所带来的影响并不明显。
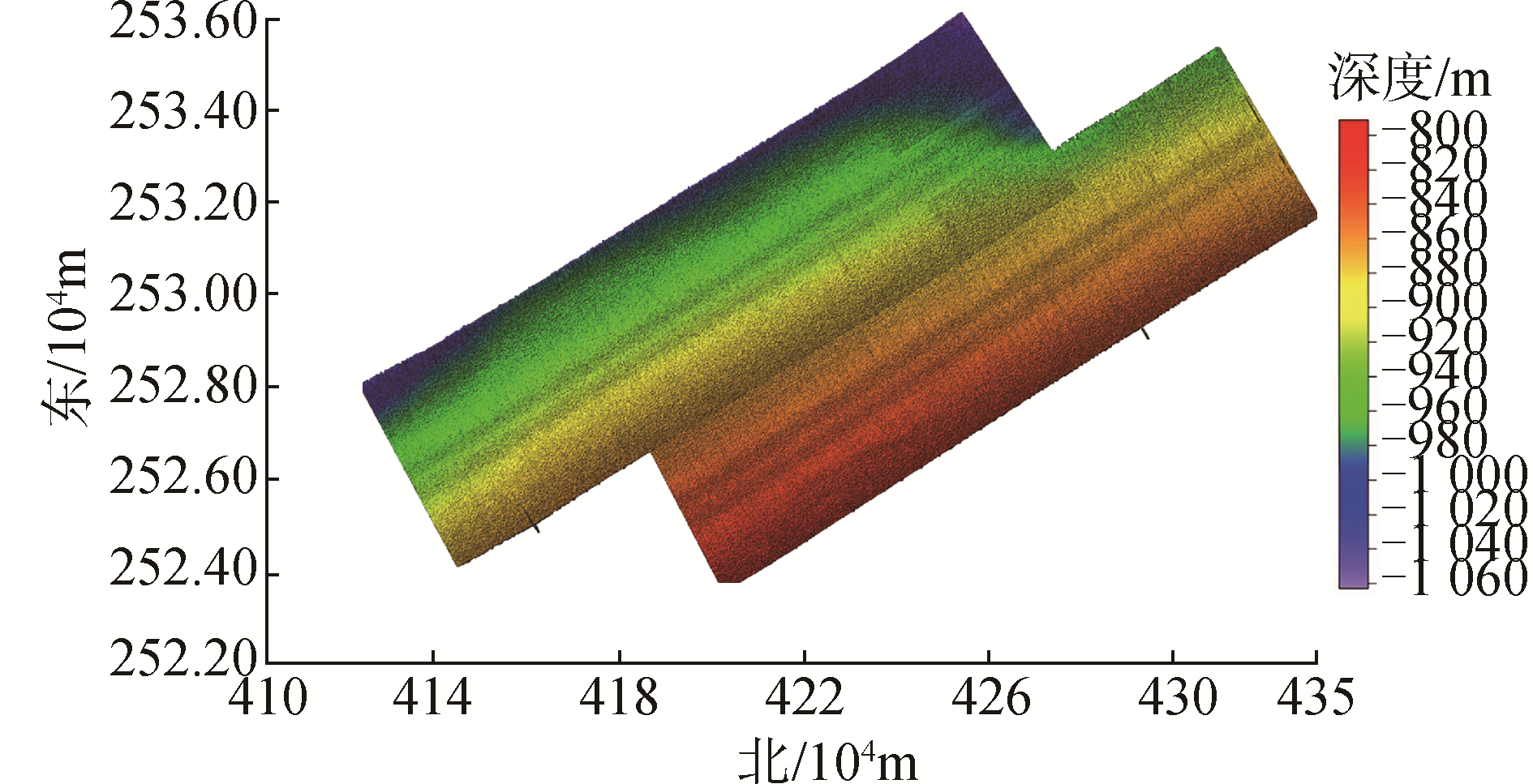
3.2 深水数据实验分析选取深水区某2条相邻测线数据,使用开源多波束数据处理软件MB-system对数据进行处理,得到的光照地形图如图 6所示。选择其中一条测线数据进行分析,该测线水深在795~1 060 m范围,测深点总数为704 160个,共1 630 Ping。
|
Download:
|
| 图 6 MB-system处理后得到的深水区光照地形图 Fig. 6 Sun illuminate, depth colored grid of the deep water data processed by MB-system | |
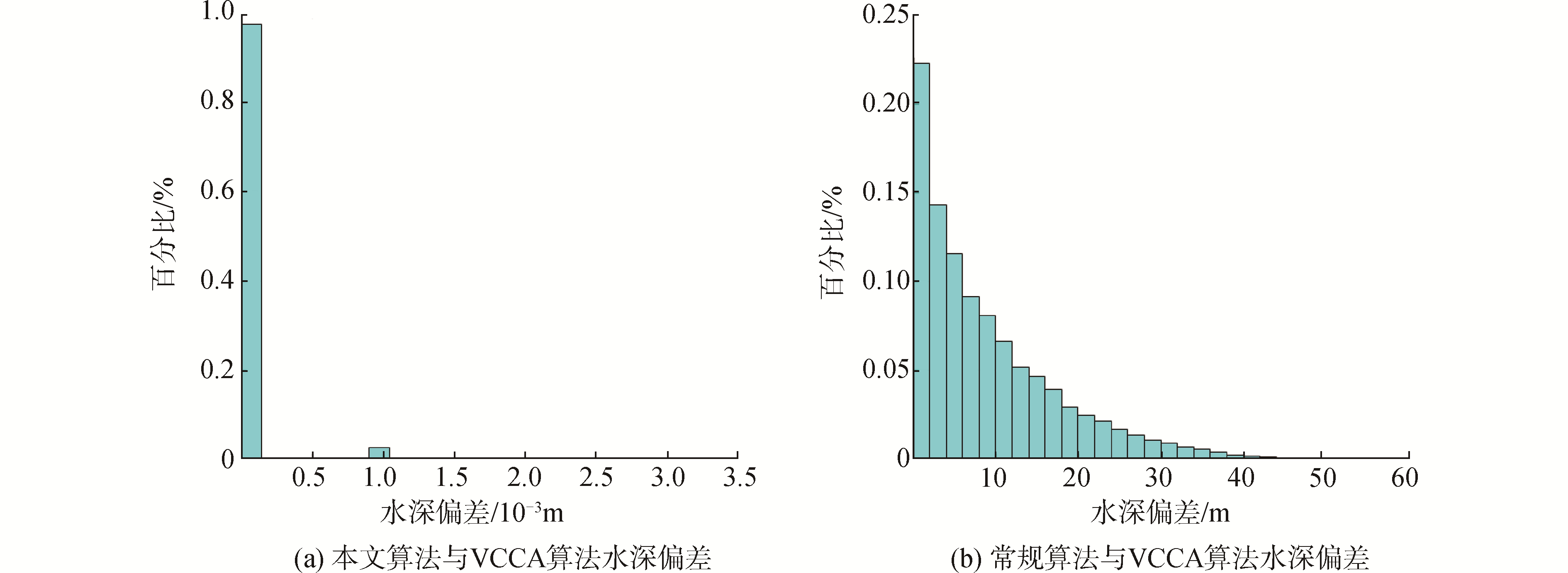
同样使用本文算法和常规波束归位算法对该测线数据进行处理,并计算本文算法与VCCA算法数据处理结果以及常规算法与VCCA算法数据处理结果之间的差值,其中,水深偏差统计结果如图 7所示。
|
Download:
|
| 图 7 深水数据水深偏差统计 Fig. 7 Statistics of the depth deviations with deep water data | |
对2种算法与VCCA算法之间的数据处理比对结果进行统计,并按1%的测深精度对水深差值中超限测深点数进行统计,统计结果如表 3所示。
| 表 3 深水数据测深点误差统计 Table 3 Error statistics of the soundings form the deep water data |
由表 3可以看出,本文算法与VCCA算法平面位置偏差与水深偏差最大值均为0.3 cm,最小值均为0,误差平均值可近似为0,且不存在超限点;常规算法与VCCA算法平面位置偏差最大值为44.44 m,最小值为1.1 cm,水深差值最大值为51.0 m,最小值为0,平均相对误差为0.95%,其中超限点数为263 427个,约占测深点总数的37.4%。
同样计算2个测线部分重叠区域的深度不符值,并统计出深度不符值的总数、均值、中误差、分布情况及超限点占比,如表 4所示。
| 表 4 深度不符值统计分析 Table 4 Statistical analysis of depth discrepancy |
由表 4可知,本文算法结果与VCCA算法深度不符值结果仍可近似一致,而常规算法深度不符值结果较浅水数据明显增大,且存在超出2%水深精度要求的测深点。
结合图 7和表 3、4可知,本文算法计算结果与VCCA算法计算结果差值仍可近似为0,再次证明了本文算法的有效性;同时,随着水深的增加,常规算法与VCCA算法间的偏差值逐渐增大,波束脚印坐标整体发生偏移且水深结果也超出1%的测深精度要求,同时数据质量也不再满足规范要求。因此,对于深水数据,由波束往返期间换能器的姿态变化对测深结果带来的影响则较为明显。
综合浅水与深水数据处理结果可以看出:常规波束归位算法在数据处理过程中忽略了波束往返期间换能器的姿态变化,给数据处理结果带来了误差,在浅水区域,该误差较小,但随着水深增加,误差也逐渐增大,并超出1%的测深精度,因此,常规波束归位算法仅仅适用于处理浅水多波束测量数据;本文算法数据处理结果与VCCA算法数据处理结果基本一致,且在浅水和深水区域存在的水深偏差均满足1%的水深测量精度要求,同时,通过计算条带重叠区的深度不符值,表明本文算法与VCCA算法在同一精度水平,因此本文算法对于处理浅水和深水多波束测量数据较常规算法均有较高的精度,从而更具有普适性。
4 结论1) 多波束测深波束往返期间发射换能器的姿态变化产生的影响在浅水区相对较小,因此,常规模型只适用于浅水区;当测区水深增加时,该影响产生的误差逐渐增大,使用常规模型易导致测深点位置整体出现偏差且水深误差易超出1%的测深精度要求。
2) 本文基于VCCA算法,提出一种同心双曲线相交的波束归位算法,将波束脚印作为发射圆锥面和接收圆锥面与交点平面投影形成的两双曲线交点,并推导了双曲线参数定义与解算方法,从而将VCCA算法中复杂的波束向量推导过程转化为求解相交双曲线方程的形式,模型更加直观且易于理解。
3) 使用实测数据对本文算法进行验证,结果表明,常规波束归位算法由于忽略波束往返期间换能器的姿态变化,使得数据处理结果存在误差,且随着水深的逐渐增加误差也逐渐增大,因此常规算法仅适用于处理浅水多波束测量数据;本文算法对浅水与深水多波束数据的计算结果与VCCA算法数据处理结果基本一致,计算结果满足1%的水深测量精度要求,因此本文算法具有有效性,对后续多波束数据处理研究具有很好的参考性。
| [1] |
赵建虎, 刘经南. 精密多波束测深系统位置修正方法研究[J]. 武汉大学学报(信息科学版), 2002, 27(5): 473-477. ZHAO Jianhu, LIU Jingnan. Development of method in precise multibeam acoustic bathymetry[J]. Geomatics and Information Science of Wuhan University, 2002, 27(5): 473-477. (  0) 0)
|
| [2] |
李家彪. 多波束勘测原理技术与方法[M]. 北京: 海洋出版社, 1999.
(  0) 0)
|
| [3] |
赵建虎, 沈文周, 吴永亭, 等. 现代海洋测绘[M]. 武汉: 武汉大学出版社, 2011.
(  0) 0)
|
| [4] |
阳凡林, 暴景阳, 胡兴树, 等. 水下地形测量[M]. 武汉: 武汉大学出版社, 2017.
(  0) 0)
|
| [5] |
赵建虎, 刘经南. 多波束测深系统的归位问题研究[J]. 海洋测绘, 2003, 23(1): 6-7, 12. ZHAO Jianhu, LIU Jingnan. Problems on the conformity to the real sounding points from the multi-beam sounding system[J]. Hydrographic surveying and charting, 2003, 23(1): 6-7, 12. DOI:10.3969/j.issn.1671-3044.2003.01.002 (  0) 0)
|
| [6] |
黄谟涛, 翟国君, 谢锡君, 等. 多波束和机载激光测深位置归算及载体姿态影响研究[J]. 测绘学报, 2000, 29(1): 82-88. HUANG Motao, ZHAI Guojun, XIE Xijun, et al. The influence of carrier's attitude and the position reduction in multibeam echosounding and airborne laser depth sounding[J]. Acta geodaetica et cartographica sinica, 2000, 29(1): 82-88. DOI:10.3321/j.issn:1001-1595.2000.01.014 (  0) 0)
|
| [7] |
阳凡林, 李家彪, 吴自银, 等. 多波束测深瞬时姿态误差的改正方法[J]. 测绘学报, 2009, 38(5): 450-456. YANG Fanlin, LI Jiabiao, WU Ziyin, et al. The methods of removing instantaneous attitude errors for multibeam bathymetry data[J]. Acta geodaetica et cartographica sinica, 2009, 38(5): 450-456. DOI:10.3321/j.issn:1001-1595.2009.05.012 (  0) 0)
|
| [8] |
何林帮, 赵建虎, 张红梅, 等. 顾及姿态角的多波束声线精确跟踪方法[J]. 哈尔滨工程大学学报, 2015, 36(1): 46-50. HE Linbang, ZHAO Jianhu, ZHANG Hongmei, et al. A precise multibeam sound ray tracking method taking into account the attitude angle[J]. Journal of Harbin Engineering University, 2015, 36(1): 46-50. (  0) 0)
|
| [9] |
杨绍海, 张彦昌. 多波束测量中海底测点三维坐标计算方法研究[J]. 气象水文海洋仪器, 2011, 28(2): 1-3, 19. YANG Shaohai, ZHANG Yanchang. Study on coordinate calculation of seabed point on multi-beam surveying[J]. Meteorological, hydrological and marine instruments, 2011, 28(2): 1-3, 19. DOI:10.3969/j.issn.1006-009X.2011.02.001 (  0) 0)
|
| [10] |
朱小辰, 刘雁春, 肖付民, 等. 多波束测深波束脚印位置归算模型研究[J]. 海洋测绘, 2011, 31(5): 24-27. ZHU Xiaochen, LIU Yanchun, XIAO Fumin, et al. The research of footprint location determination model of multibeam echosoundings[J]. Hydrographic surveying and charting, 2011, 31(5): 24-27. DOI:10.3969/j.issn.1671-3044.2011.05.008 (  0) 0)
|
| [11] |
阳凡林, 卢秀山, 李家彪, 等. 多波束勘测运动传感器偏移的改正方法[J]. 武汉大学学报(信息科学版), 2010, 35(7): 816-820. YAN Fanlin, LU Xiushan, LI Jiabiao, et al. Correction of imperfect alignment of MRU for multibeam bathymetry data[J]. Geomatics and Information Science of Wuhan University, 2010, 35(7): 816-820. (  0) 0)
|
| [12] |
BEAUDOIN J D, HUGHES CLARKE J E, BARTLETT J E. Application of surface sound speed measurements in post-processing for multi-sector multibeam echosounders[J]. The international hydrographic review, 2004, 5(3): 17-32. (  0) 0)
|
| [13] |
HAMILTON T, BEAUDOIN J, CLARKE J H. A more precise algorithm to account for non concentric multibeam array geometry[C]//Proceedings of Canadian Hydrographic Conference.[S.l.], 2014.
(  0) 0)
|
| [14] |
TENG Y. Sector-specific beam pattern compensation for multi-sector and multi-swath multibeam sonars[D]. New Brunswick: University of New Brunswick, 2011.
(  0) 0)
|
| [15] |
罗才忠. 关于Dandelin定理的证明[J]. 数学通报, 2004(10): 6. LUO Caizhong. Proof of Dandelin's theorem[J]. Bulletin des sciences mathematics, 2004(10): 6. DOI:10.3969/j.issn.0583-1458.2004.10.004 (  0) 0)
|
| [16] |
郭启淳. 圆锥曲线的学习总结[J]. 中国校外教育, 2018(3): 120-121. GUO Qichun. Learning summary of conic curves[J]. Education for Chinese after-school, 2018(3): 120-121. DOI:10.3969/j.issn.1004-8504.2018.03.094 (  0) 0)
|
| [17] |
卜宪海, 王明伟, 阳凡林, 等. 多波束测深波束归位近似转换模型研究[J]. 山东科技大学学报(自然科学版), 2016, 35(5): 28-34. BU Xianhai, WANG Mingwei, YANG Fanlin, et al. Research on approximate conversion model of beam homing in multibeam echosounding[J]. Journal of Shandong University of Science and Technology (natural science), 2016, 35(5): 28-34. DOI:10.3969/j.issn.1672-3767.2016.05.004 (  0) 0)
|
| [18] |
曲萌, 樊妙, 卜宪海, 等. 基于严密波束归位模型的多波束测深点不确定度改进方法[J]. 海洋通报, 2018, 37(6): 643-651. QU Meng, FAN Miao, BU Xianhai, et al. Uncertainty calculation of multibeam echo sounder based on accurate reduction model of footprints[J]. Marine science bulletin, 2018, 37(6): 643-651. (  0) 0)
|
| [19] |
卜宪海.基于激光点云约束的多波束低掠射波束几何改正[D].青岛: 山东科技大学, 2017. BU Xianhai. Geometric calibration method for the multibeam bathymetric data at large incidence angles based on the laser tie points[D]. Qingdao: Shandong University of Science and Technology, 2017. (  0) 0)
|
| [20] |
中华人民共和国交通运输部. JTS 131-2012, 水运工程测量规范[S].北京: 人民交通出版社, 2013. Ministry of Transport of the People's Republic of China. JTS 131-2012, Specifications for port and waterway engineering survey[S]. Beijing: People's Communications Press, 2013. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


