2. 一汽轿车股份有限公司, 吉林 长春 130012
2. FAW CAR Co., Ltd., Changchun 130012, China
轻量化技术是减轻汽车自重,降低燃油消耗、改善环境污染的有效方法。管材内高压成形技术因其具有众多优点而受到科研工作者的广泛重视[1]。它以管材为加工对象,在内压力和轴向进给的共同作用下,在一道工序内完成复杂几何形状零件的成形,生产出高质量的无缝复合变径管以及复合管接头,有效降低零件重量、提高生产效率,同时减少后续机械加工及组装焊接量。该技术被广泛应用于车辆进气系统、飞机管路系统、海水管道系统、核工业等高质量的无缝异型管和复杂截面管件的制造[2-3]。
影响金属管材内高压成形最终成形质量的因素有很多,如轴向进给、内压力、背向位移、材料的性能、摩擦及模具的几何结构等,各个因素之间相互制约又相互关联[4-5]。许多学者研究了加载路径对T形管、X形管、Y形管等典型管材内高压成形性能的影响[6-7]。Zadeh等[8]研究了不同加载路径对三通管壁厚分布的影响。Alaswad等[9]比较了单层管和双层管在相同的内高压成形工艺下支管高度和厚度分布情况等。但很多研究由于实验条件受限,背向位移这一重要参数经常被忽略,而仅仅考虑内压力和轴向进给会导致加载路径优化结果不理想;另一方面,目前加载路径大多设计为单线性或双线性条件,这样会大大降低加载路径对产品成形性能调整的灵活性。到目前为止,关于加载路径对管材成形性能的影响还没有一致明确的结论,因此,研究内高压成形加载路径对管材成形性能的影响规律,采用智能控制方法寻找适合多种典型形状管材的加载路径优化方法,完善管材内高压成形工艺研究体系,对于减少零件废品率,降低生产成本,缩短产品开发周期具有重要意义[10-11]。
由于T形管在内高压成形过程中变形的不对称性,控制T形管的加载路径相对较难。因此,本文选择T形管作为研究对象,研究其在内高压成形过程中加载路径的优化方法。
1 材料和方法首先,利用UG建模软件建立T形管的几何模型,并将导出的IGES标准格式导入DYNAFORM软件中;其次,在DYNAFORM软件中完成管坯,模具,冲头的装配并划分网格,设置边界条件,采用LS-DYNA求解器进行求解;然后,将智能控制方法嵌入DYNAFORM求解器(LS-DYNA)进行计算,直到成形零件的结果满足计算要求。最后,将结果导入DYNAFORM后处理器进行结果分析,并与实验结果进行对比。
1.1 材料特性本文选用的实验材料为SS304不锈钢,SS304不锈钢管的力学性能按照GB/T228-2002的规定在室温下测试,采用INSTRON4206电子万能材料试验机开展拉伸试验,得到性能参数如表 1所示。由于r值为1.02,该材料可视为各向同性。
| 表 1 材料性能参数 Table 1 Material performance parameters |
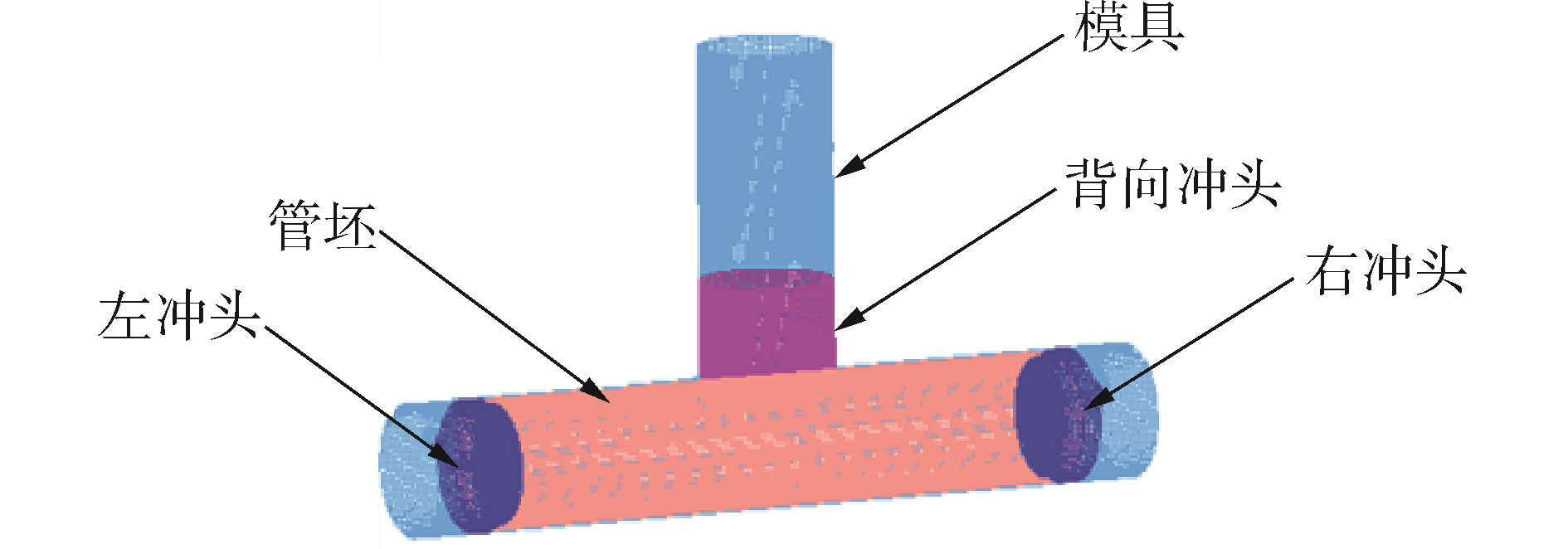
管材内高压成形模拟中采用壳体模型进行建模。管体长度为200 mm,外径为42 mm,壁厚为1 mm。T形管有限元模型的网格划分包括5个部分:管坯、模具、左冲头、右冲头、背向冲头,如图 1所示。冲头被设定为刚体,管坯为可变形的壳体。
|
Download:
|
| 图 1 T形管有限元分析模型 Fig. 1 Finite element analysis model of T tube | |
应用DYNAFORM软件计算仿真结果,采用比例缩减时间,将成形时间设定为0.01 s。
1.3 加载路径的智能控制方法工艺参数的匹配关系对成形结果有很大影响,而将背向位移纳入到加载路径的组成中,会使工艺参数的匹配关系更加复杂。因此,采用智能控制方法来优化加载路径关键因素(包括轴向进给、内压力和背向位移)的匹配,并且增加了支管顶部与背向冲头之间接触面积这一成形结果评价因素以优化加载路径。根据得到的优化后的相关参数和成形结果(包括壁厚最大值、壁厚最小值、支管高度以及支管和背向冲头之间的接触面积)指导生产实践[12-13],优化生产工艺。
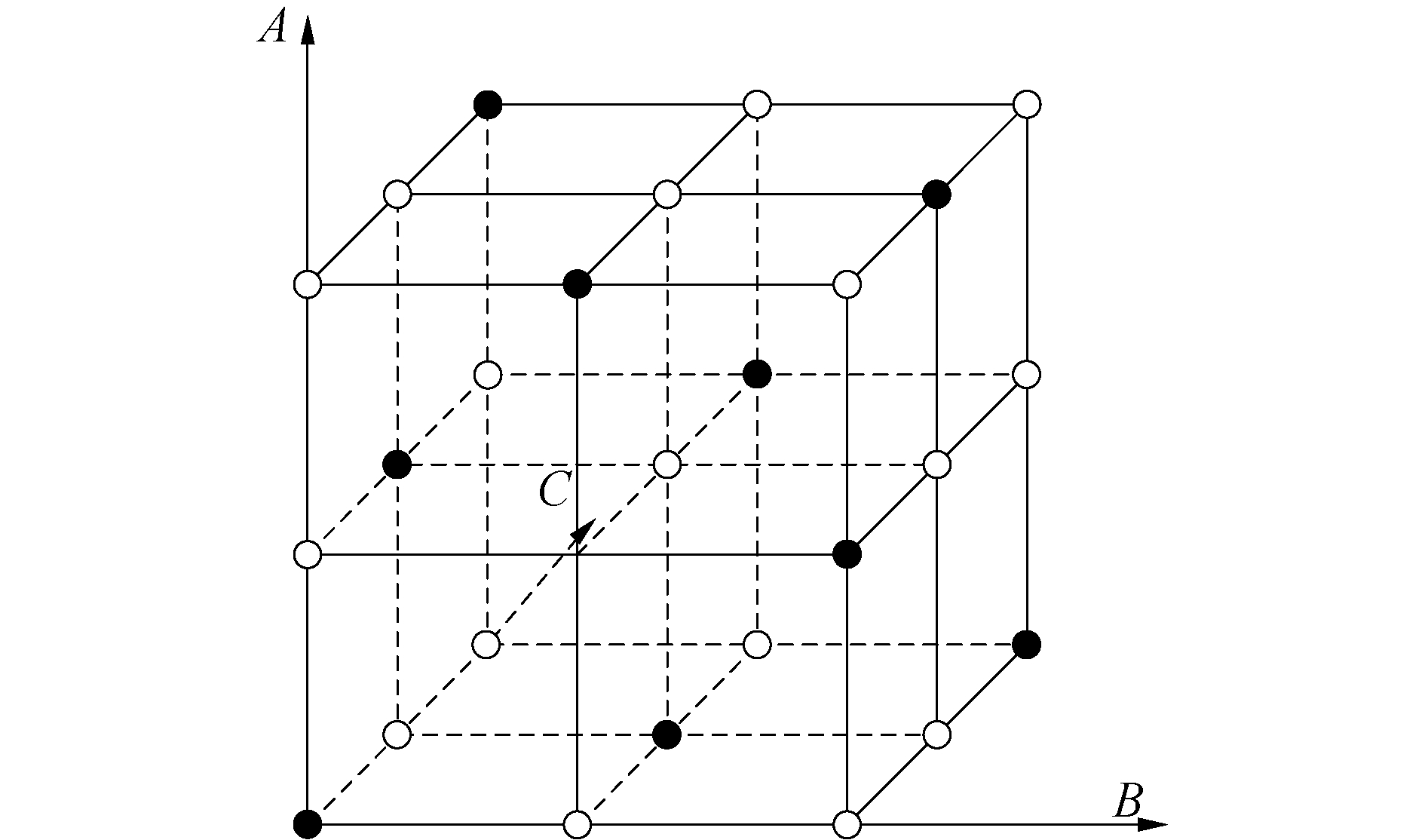
1.3.1 加载路径初始值的确定初始值的确定通过正交试验法从综合试验中选取一些代表点,采用三因素三水平值的方法。其中,3个因素是轴向进给、背向位移和内压力。同时,每个因素的3个等级被定义为3个参考值或3个设定路径,因此,3个因素组合的总体数量是33=27。3个因素的优选面积由图 2的立方体表示,共有9个试验被筛选出来,并用“·”表示。每个平面代表一个级别,总共有9个平面,每个平面有3个“·”点,并且在立方体的每一行上都有一个“·”,表明这些点是以均衡的方式分布,具有很强的代表性,可以全面反映实验结果。因此选择这9个加载路径作为初始值是合理的。
|
Download:
|
| 图 2 正交试验优选区域 Fig. 2 The drawing of orthogonal test preferred area | |
基于遗传算法的BP神经网络具有任意非线性逼近能力、自学习能力以及概括推广能力,使系统具有自适应性、可自动调节控制参数、提高控制性能和可靠性,所以采用此智能控制方法对加载路径(包括轴向进给、内压力、背向位移)进行合理匹配和优化[14-17]。针对内高压成形加载路径优化系统,搭建BP神经网络结构。采用3层BP神经网络,网络输入层的输入为:
| $ Q_j^{(1)} = x(j),j = 1,2, \cdots ,M $ | (1) |
式中:输入神经元个数M选为4,输入的4个量分别为轴向进给、内压力、背向位移以及阈值。网络隐含层的输入、输出为:
| $ {\rm{ net}} _i^{(2)}(k) = \sum\limits_{j = 1}^M {\omega _{ij}^{(2)}} Q_j^{(1)} $ | (2) |
| $ Q_i^{(2)}(k) = f({\rm{ net }}_i^{(2)}(k)),i,j = 1,2, \cdots ,M $ | (3) |
式中ωij(2)为隐含层加权系数。
网络输出层的输入、输出为:
| $ { {\rm{net}} _l^{(3)}(k) = \sum\limits_{i = 1}^Q {\omega _{li}^{(3)}} \cdot Q_i^{(2)}(k)} $ | (4) |
| $ {Q_l^{(3)}(k) = g( {\rm{net}} _l^{(3)}(k))} $ | (5) |
| $ \begin{array}{l} Q_1^{(3)}(k) = {T_{{\rm{max}}}};Q_2^{(3)}(k) = {T_{{\rm{min}}}};\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} Q_3^{(3)}(k) = H;Q_4^{(3)}(k) = S \end{array} $ | (6) |
输出层输出节点分别对应4个可调参数,即Tmax(最大壁厚)、Tmin(最小壁厚)、H(支管高度)、S(支管与背向冲头的接触面积)。
应用遗传算法将BP网络各层的权值和阈值按顺序级联起来,随机产生N个染色体。通过计算适应度,依据交叉概率和变异概率[18-19],产生并选择最优个体作为BP神经网络的初始权值和阈值。通过遗传算法确定隐含层神经元个数为5。至此,确定出神经网络结构为4-5-4。
根据相关工艺经验建立加载路径的评价规则,在管坯不发生破裂、屈曲、褶皱等缺陷的前提下,满足以下4个条件:1)使管坯最小壁厚尽可能达到更大;2)使管坯最大壁厚尽可能达到更小;3)使管坯壁厚分布更加均匀;4)使管坯的支管高度尽可能达到更大。针对不同规格的管坯确定内高压成形后管坯的最大壁厚、最小壁厚以及支管高度的理想范围值,分别对Tmax、Tmin、H和S建立性能指标函数为:
| $ {E{{(k)}_1} = \frac{1}{2}{{({r_1}(k) - {y_1}(k))}^2}} $ | (7) |
| $ {E{{(k)}_2} = \frac{1}{2}{{({r_2}(k) - {y_2}(k))}^2}} $ | (8) |
| $ {E{{(k)}_3} = \frac{1}{2}{{({r_3}(k) - {y_3}(k))}^2}} $ | (9) |
| $ {E{{(k)}_4} = \frac{1}{2}{{({r_4}(k) - {y_4}(k))}^2}} $ | (10) |
式中:E(k)1、E(k)2、E(k)3和E(k)4分别为Tmax、Tmin、H和S对应的性能指标函数;r1(k)、r2(k)、r3(k)、r4(k)为第k个周期Tmax、Tmin、H、S的设定值;y1(k)、y2(k)、y3(k)、y4(k)为第k个周期Tmax、Tmin、H、S的实际反馈值。
考虑以上4个因素理想值的相互关联性,取平均性能指标函数为:
| $ E(k) = \frac{1}{4}(E{(k)_1} + E{(k)_2} + E{(k)_3} + E{(k)_4}) $ | (11) |
按照梯度下降法修正网络的权系数,即按E(k)对加权系数的负梯度方向搜索调整,并附加一个使搜索快速收敛全局极小的惯性项:
| $ \Delta \omega _{{\rm{li}}}^{(3)}(k) = - \eta \cdot \frac{{\partial E(k)}}{{\partial \omega _{{\rm{li}}}^{(3)}}} + \alpha \Delta \omega _{{\rm{li}}}^{(3)}(k - 1) $ | (12) |
式中:η为学习速率;α为惯性系数。
根据经典的增量PID控制算法和上述分析,获得网络输出层的加权系数学习算法:
| $ \Delta \omega _{li}^{(3)}(k) = \alpha \Delta \omega _{li}^{(3)}(k - 1) + \eta \delta _1^{(3)}Q_i^{(2)}(k) $ | (13) |
| $ \begin{array}{l} \delta _l^{(3)} = {\rm{error}} (k) \cdot {\rm{sgn}} \left( {\frac{{\partial y(k)}}{{\partial \Delta u(k)}}} \right) \cdot \frac{{\partial \Delta u(k)}}{{\partial Q_l^{(3)}(k)}} \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {g^\prime }( {\rm{net}} _l^{(3)}(k)),l = 1,2,3 \end{array} $ | (14) |
| $ {g^\prime }( \cdot ) = g(x) \cdot (1 - g(x)) $ | (15) |
同理可得隐含层的加权系数的算法。
1.3.3 智能控制方法在有限元仿真中的应用上述智能控制方法采用Matlab软件编程,得到一个独立的子程序,嵌入DYNAFORM的求解器(LS-DYNA)中完成仿真计算。首先,通过子程序提取LS-DYNA的求解结果,壁厚最大值、壁厚最小值、支管高度可以直接提取,支管顶部和背向冲头之间的接触面积可表示为:
| $ S = \pi {\left( {\frac{{{D_1}}}{2} - {R_2}} \right)^2} $ | (16) |
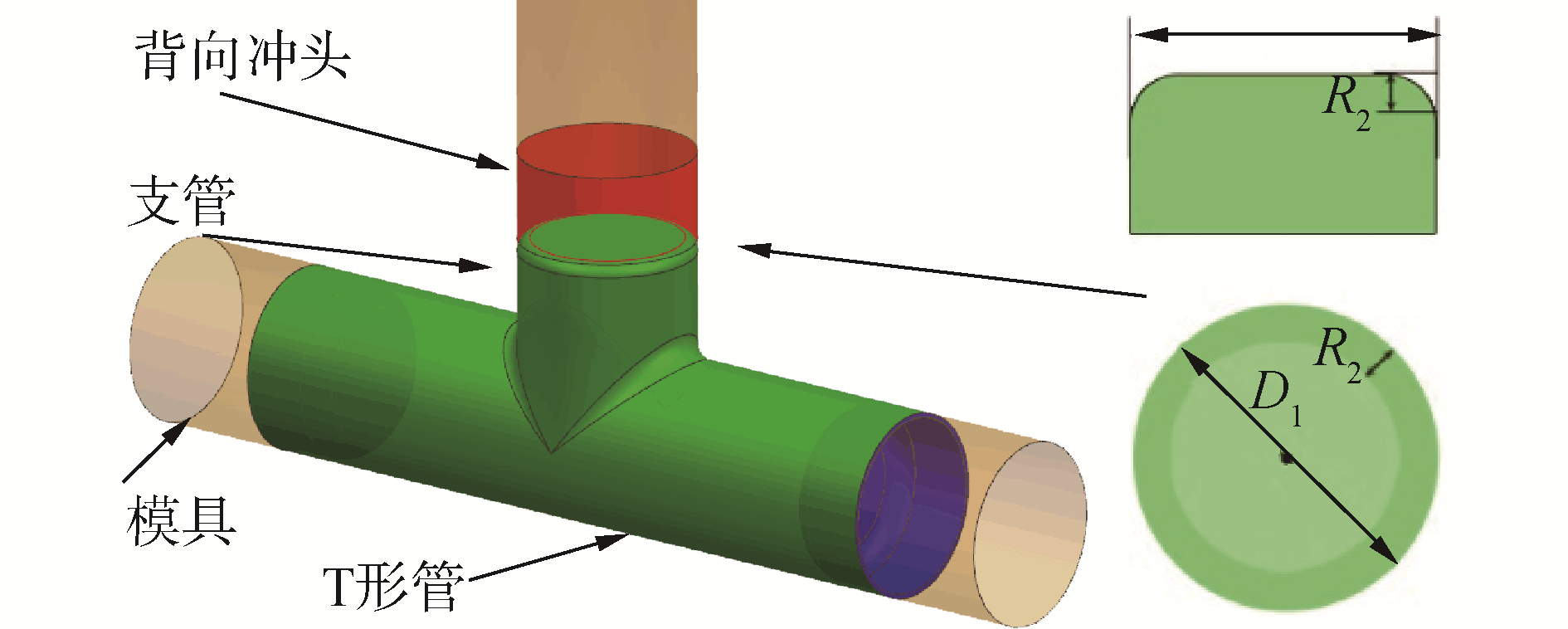
式中:D1是支管的直径,mm;R2是支管的圆角半径,mm。主要由支管的直径和支管圆角半径确定。T形管支管与背向冲头之间的接触面积示意图如图 3所示。
|
Download:
|
| 图 3 T形管示意图以及支管与背向冲头之间的接触面积 Fig. 3 The schematic of T shaped tube and contact area between branch tube and back punch | |
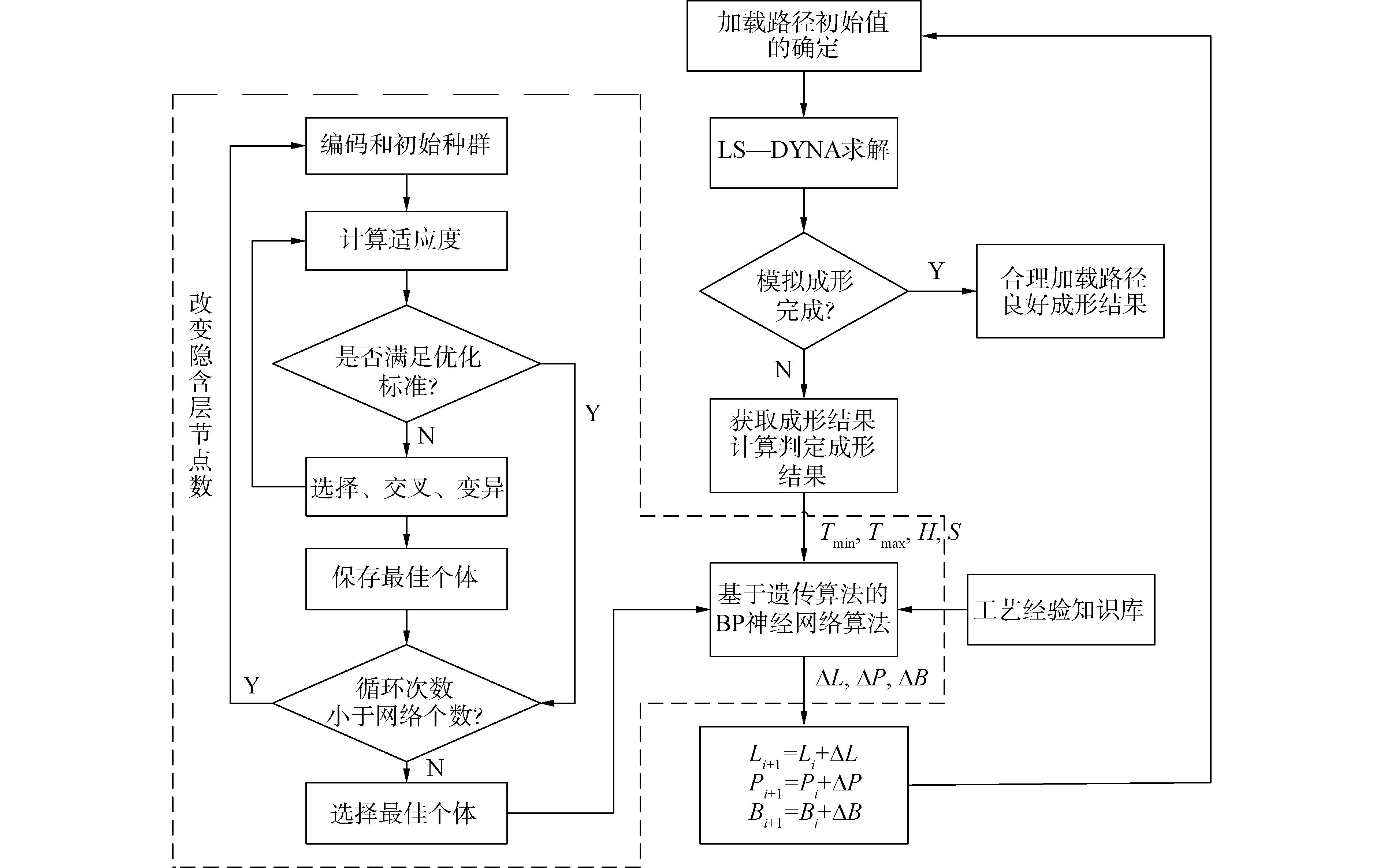
其次,利用BP神经网络控制器,根据加载路径控制的评价规则调整负载,采用遗传算法寻找理想的解决方案。最后,通过自适应仿真修改和计算*.Dyn文件的负载大小。如此反复,直到成形零件结果满足计算要求,并且获得合理地加载路径。基于遗传算法的自适应仿真和BP神经网络控制算法流程图如图 4所示。
|
Download:
|
| 图 4 自适应仿真与基于遗传算法的BP神经网络控制算法流程 Fig. 4 Flow chart of adaptive simulation and BP neural network control algorithm based on genetic algorithm 注:L为轴向进给;P为内压力;B为背向位移;S为支管顶部和背向冲头的接触面积。 | |
根据经验公式[20],依据表 1中材料性能,将内高压成形过程中管材的初始内压设定为30 MPa,最大成形内压为140 MPa,最大轴向进给为52 mm,最大背向位移为35 mm。通过正交试验法筛选出9组加载路径,有限元模拟结果如表 2所示。由于第9组的最大减薄率过大,已超过60%,管子会破裂,因此无法计算接触面积的结果。综合考虑较好的成形性和理想的支管高度,第2组数据被选为下一步优化的加载路径参数。将这组加载路径命名为路径A,并通过基于遗传算法的自适应仿真和BP神经网络控制算法对其进一步优化,表 3中显示了优化前加载路径A的参数,为简单的三折线式结构。在所有研究工作之前,通过模拟与实验结果的对比,确定模具与管材之间的摩擦系数为0.125[21]。优化前后加载路径的三因素对比曲线如图 5所示。
| 表 2 正交试验法选择的9组加载路径的有限元模拟结果 Table 2 The finite element simulation results of 9 groups of loading paths selected by orthogonal |
| 表 3 优化前加载路径A的参数 Table 3 The parameters of loading path A before optimization |

|
Download:
|
| 图 5 优化前后加载路径A的对比图 Fig. 5 Comparison chart of loading path A before and after optimization | |
本文将背向位移纳入加载路径的主要因素,将加载路径以三因子图的形式呈现。优化后的加载路径A不再是折线,而是围绕在优化前路径周围的自动调整曲线。根据智能控制方法的优化准则,自适应地调整加载路径。为了获得支管的最小圆角半径并确保T形管壁厚的均匀性,在成形末期,背向位移的增长速度将减慢;同时也要实现与其他因素的协同调整,以达到优化管坯成形效果的目的。在优化前后的加载路径下,T形管内高压成形有限元模拟结果分别如图 6~9所示。

|
Download:
|
| 图 6 优化前后路径A的管材内高压成形极限 Fig. 6 Tube hydroforming limit diagram of path A before and after optimization | |

|
Download:
|
| 图 7 优化前后圆角切线两点与支管高度之间的距离 Fig. 7 The distance between two points of the fillet tangent and height of branch tube before and after optimization | |

|
Download:
|
| 图 8 加载路径A优化前后的壁厚度分布 Fig. 8 The tube wall thickness distribution of path A before and after optimization | |

|
Download:
|
| 图 9 加载路径A优化前后的主应变分布 Fig. 9 The tube principal strain distribution of path A before and after optimization | |
比较路径A优化前后加载路径对管材成形性能的影响,可以看出优化后的路径A对提高管材的成形性起到重要作用。从图 6的成形极限图可得,优化后的加载路径使管坯的成形趋势更加合理,管材两侧的进给更加及时和充分。同时,管材中心部分的有褶皱趋势区域明显减小,即减少了起皱和弯曲变形的可能性。而且支管顶部有破裂风险的区域面积明显减小,这意味着支管顶部开裂的趋势被有效地缓解了。内高压成形后管材的轮廓如图 7所示,由此可以观察到支管顶部和背向冲头的接触情况。通过测量圆角切线的2个点之间的距离(l)来确定支管的圆角半径R2,采用公式
根据图 8中加载路径A优化前后的壁厚分布图可知,优化后的加载路径使壁厚分布更加均匀。T形管的最大减薄率从22.890%降低到16.877%,最大增厚率从156.448%降低到130.997%。因此,优化后的加载路径,可以有效地调整管材壁厚的最大值和最小值。
由图 9可知,在优化后的加载路径下,最大主应变从0.819增加到0.844,成形后的T形管的主应变分布也得到了改善;管坯中部最大主应变的分布面积显著减小,并且管坯的应变分布更均匀。
3 模拟结果验证实验将该智能控制方法应用于由东北大学轧制技术及连轧自动化国家重点实验室自主研发的200 MPa内高压成形机,如图 10所示。采用与加载路径A相同的工艺参数进行实验测试,并在管坯轴向剖面的不同位置取7个点测量管壁壁厚,对管材壁厚和支管高度的结果进行比较。如表 4和图 11所示。实验结果与有限元模拟结果非常吻合,模拟结果与实验结果的误差在±5%以内,准确度较高,可行性较好。综合考虑该加载路径优化方法的灵活性和适用性,可将其作为其他典型形状管材内高压成形加载路径的优选控制方法。

|
Download:
|
| 图 10 200 MPa内高压成形机 Fig. 10 The 200 MPa hydroforming machine | |
| 表 4 管坯轴向剖面7个典型位置的模拟和实验所得壁厚值 Table 4 The wall thickness of simulation and experiment at seven typical locations of tube blank axial profile |

|
Download:
|
| 图 11 有限元模拟的截面厚度分布图和实验样品的截面 Fig. 11 The axial section thickness distribution of finite element simulation and experimental sample | |
1) 将背向位移纳入加载路径的主要因素,有效缓解了支管顶端边部减薄,避免支管破裂等缺陷的发生。
2) 采用正交试验方法确定加载路径的初始值,采用基于遗传算法的BP神经网络控制方法优化T形管的加载路径,通过建立平均性能指标函数,优化了学习效率,提高了计算精度。此方法可以有效解决T形管内高压成形过程加载路径的匹配和优化问题。
3) 通过实验验证,模拟与实验结果的误差精度在±5%以内,说明此方法具有较高的精度和可行性。
| [1] |
SORINE M, SIMHA C H M, RIEMSDIJK I V, et al. Prediction of necking of high strength steel tubes during hydroforming-multi-axial loading[J]. International journal of mechanical sciences, 2008, 50(9): 1411-1422. DOI:10.1016/j.ijmecsci.2008.07.003 (  0) 0)
|
| [2] |
ABDESSALEM A B, PAGNACCO E, EL-HAMI A. Increasing the stability of T-shape tube hydroforming process under stochastic framework[J]. The international journal of advanced manufacturing technology, 2013, 69(5/6/7/8): 1343-1357. (  0) 0)
|
| [3] |
OLABI A G. Developments in sustainable energy and environmental protection[J]. Simulation modelling practice and theory, 2012, 19(4): 1139-1142. (  0) 0)
|
| [4] |
ALASWAD A, BENYOUNIS K Y, OLABI A G. Tube hydroforming process:a reference guide[J]. Materials & design, 2012, 33: 328-339. (  0) 0)
|
| [5] |
SIANO D. Three-dimensional/one-dimensional numerical correlation study of a three-pass perforated tube[J]. simulation modelling practice and theory, 2011, 19(4): 1143-1153. DOI:10.1016/j.simpat.2010.04.005 (  0) 0)
|
| [6] |
GUO Xunzhong, LIU Zhongli, WANG Hui, et al. Hydroforming simulation and experiment of clad T-shapes[J]. The international journal of advanced manufacturing technology, 2016, 83(1/2/3/4): 381-387. (  0) 0)
|
| [7] |
NAKAMORI T, SHUKUNO K, MANABE K. In-process controlled Y-shape tube hydroforming with high accurate built-in sensors[J]. Procedia engineering, 2017, 184: 43-49. DOI:10.1016/j.proeng.2017.04.069 (  0) 0)
|
| [8] |
ZADEH H K, MASHHADI M M. Finite element simulation and experiment in tube hydroforming of unequal T shapes[J]. Journal of materials processing technology, 2006, 177(1/2/3): 684-687. (  0) 0)
|
| [9] |
ALASWAD A, BENYOUNIS K Y, OLABI A G. Finite element comparison of single and bi-layered tube hydroforming processes[J]. Simulation modelling practice and theory, 2011, 19(7): 1584-1593. DOI:10.1016/j.simpat.2011.03.007 (  0) 0)
|
| [10] |
FENG Yingying, ZHANG Hongge, LUO Zongan, et al. Loading path optimization of T tube in hydroforming process using response surface method[J]. The international journal of advanced manufacturing technology, 2019, 101(5/6/7/8): 1979-1995. (  0) 0)
|
| [11] |
BIHAMTA R, BUI Q H, GUILLOT M, et al. Global optimisation of the production of complex aluminium tubes by the hydroforming process[J]. CIRP journal of manufacturing science and technology, 2015, 9: 1-11. DOI:10.1016/j.cirpj.2015.02.001 (  0) 0)
|
| [12] |
HUANG Tianlun, SONG Xuewei, LIU Xinyang. The multi-objective robust optimization of the loading path in the T-shape tube hydroforming based on dual response surface model[J]. The international journal of advanced manufacturing technology, 2016, 82(5/6/7/8): 1595-1605. (  0) 0)
|
| [13] |
MANABE K I, SUETAKE M, KOYAMA H, et al. Hydroforming process optimization of aluminum alloy tube using intelligent control technique[J]. International journal of machine tools and manufacture, 2006, 46(11): 1207-1211. DOI:10.1016/j.ijmachtools.2006.01.028 (  0) 0)
|
| [14] |
ZHANG Fuzhi, ZHOU Quanqiang. Ensemble detection model for profile injection attacks in collaborative recommender systems based on BP neural network[J]. IET information security, 2014, 9(1): 24-31. (  0) 0)
|
| [15] |
JIN K K, ZHAO R X, XU K L, et al. Research on optical character recognition based on BP neural network[J]. International journal of computational and engineering, 2018, 3(4): 17-20. (  0) 0)
|
| [16] |
WANG Long, TIAN Xinli, WANG Wanglong, et al. Evaluation of machined surface quality of Si3N4 ceramics based on neural network and grey-level co-occurrence matrix[J]. The international journal of advanced manufacturing technology, 2017, 89(5/6/7/8): 1661-1668. (  0) 0)
|
| [17] |
REN Ting, LIU Shi, YAN Gaocheng, et al. Temperature prediction of the molten salt collector tube using BP neural network[J]. IET renewable power generation, 2016, 10(2): 212-220. DOI:10.1049/iet-rpg.2015.0065 (  0) 0)
|
| [18] |
LI Tianyang, WANG Ruihe, WANG Zizhen, et al. Prediction of fracture density using genetic algorithm support vector machine based on acoustic logging data[J]. Geophysics, 2018, 83(2): D49-D60. (  0) 0)
|
| [19] |
杨兵.管件液压成形的加载路径理论与试验研究[D].上海: 上海交通大学, 2006: 96-120. YANG Bing. Study on the loading paths of the tube hydroforming process[D]. Shanghai: Shanghai Jiao Tong University, 2006: 96-120. (  0) 0)
|
| [20] |
苑世剑. 轻量化成形技术[M]. 北京: 国防工业出版社, 2010: 20-21. YUAN Shijian. Lightweight forming technologies[M]. Beijing: National Defense Industry Press, 2010: 20-21. (  0) 0)
|
| [21] |
FIORENTINO A, CERETTI E, GIARDINI C. Tube hydroforming compression test for friction estimation-numerical inverse method, application, and analysis[J]. The international journal of advanced manufacturing technology, 2013, 64(5/6/7/8): 695-705. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


