2. 燕山大学 河北省重型机械流体动力传输与控制重点实验室, 河北 秦皇岛 066004;
3. 燕山大学 先进锻压成形技术与科学教育部重点实验室, 河北 秦皇岛 066004
2. Hebei Provincial Key Laboratory of Heavy Machinery Fluid Power Transmission and Control, Yanshan University, Qinhuangdao 066004, China;
3. Key Laboratory of Advanced Forging & Stamping Technology and Science, Ministry of Education of China, Yanshan University, Qinhuangdao 066004, China
液压泵是液压系统的“心脏”,它被广泛地应用于各个涉及国计民生的工业领域[1]。液压泵所面临的工作环境也趋向于高温、高压、高速、重负载等恶劣工况,加速了液压泵健康状态的劣化,如果发生故障,将会产生严重的人员伤亡和财产损失。液压泵发生故障时,通常表现为机械振动和流体冲击共同使泵体的振动加剧,导致振动信号时域形态特征和频域频率成分发生改变。不同故障产生不同的激励,如何有效地采集故障信号是液压泵故障诊断的难点之一;某些故障信号的频域特征频率及其谐波存在重合或部分重合现象,因而其时域和频域特征信息存在一定相似性,使得液压泵故障特征提取和诊断存在一定难度。因此,对液压泵的智能故障诊断具有十分重要的意义。
目前,国内外一些学者对液压泵故障诊断进行了大量研究。王鹏飞等[2]利用K-SVD算法对液压泵故障信号进行样本字典学习,并基于正交匹配追踪算法,进行分解与特征信息重构,成功实现对液压泵的故障诊断。孙健等[3]利用液压泵多通道振动信号进行改进CS算法融合,并分别提取信息熵作为特征向量,成功地对其进行了故障诊断。Jiang等[4]利用局部均值分解(local mean decomposition, LMD)方法对液压泵故障信号进行分解处理,并利用数学形态学对其进行解调分析,成功地实现了液压泵故障信号的特征提取。Lu等[5]基于two-step的经验模态分解方法,对液压泵故障信号进行分解分析,进而利用模糊C均值聚类方法实现了液压泵的故障诊断。
SGMD是一种基于辛几何的非线性时间序列分析方法。SGMD的核心在于利用辛几何QR分解(辛矩阵相似变换)求解Hamilton矩阵的特征值,求解过程会保留相空间的结构特性和时间序列的完整性,可有效重构模态、去除噪声影响,且SGMD较传统模态分解方法在抑制模态分解和端点效应等方面具有明显优势[6]。
数学形态学又称为形态学,国立巴黎高等矿业学院Matheron教授及其博士生Serra于1964年提出该理论,之后Maragos将其应用到信号处理领域[7-8]。在此基础上,形成了GMFD方法,相比传统分形维数和单一形态分形维数,它能降低网格位置和尺寸变化对估计结果的不稳定影响,且能够全面和准确地反映信号的非线性和复杂程序信息[9-10]。
本文针对液压泵的松靴和滑靴磨损故障诊断问题,提出了一种基于能量的辛几何模态分解(symplectic geometry mode decomposition, SGMD)和广义形态分形维数(generalized morphological fractal dimensions, GMFD)相结合的新方法。
通过对比分析仿真和实测液压泵故障振动信号,该新方法成功地克服了SGMD的过分解缺陷所导致的故障特征信息分布过于分散问题,进而成功地利用GMFD实现了高精度故障诊断。
1 辛几何模态分解SGMD具体算法如下[6]。
1) 相空间重构。
设一维离散原信号s=(x1, x2, …, xn),则有:
| $ \mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{x}}_1}}&{{\mathit{\boldsymbol{x}}_{1 + \tau }}}& \cdots &{{\mathit{\boldsymbol{x}}_{1 + (d - 1)\tau }}}\\ {{\mathit{\boldsymbol{x}}_2}}&{{\mathit{\boldsymbol{x}}_{2 + \tau }}}& \cdots &{{\mathit{\boldsymbol{x}}_{2 + (d - 1)\tau }}}\\ \vdots & \vdots &{}& \vdots \\ {{\mathit{\boldsymbol{x}}_m}}&{{\mathit{\boldsymbol{x}}_{m + \tau }}}& \cdots &{{\mathit{\boldsymbol{x}}_{m + (d - 1)\tau }}} \end{array}} \right] $ | (1) |
设m=n-(d-1)τ,其中d为差值维数,τ为延迟时间。
2) 辛正交矩阵QR分解。
令A=XTX构造M为Hamilton矩阵,即:
| $ \mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}^{\rm{T}}}}&0\\ 0&{ - \mathit{\boldsymbol{A}}} \end{array}} \right] $ | (2) |
令N=M2,则M和N都为Hamilton矩阵。构造辛正交矩阵Q,使得:
| $ {\mathit{\boldsymbol{Q}}^{\rm{T}}}\mathit{\boldsymbol{NQ}} = \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{B}}&\mathit{\boldsymbol{R}}\\ 0&{{\mathit{\boldsymbol{B}}^{\rm{T}}}} \end{array}} \right] $ | (3) |
式中:B为上三角矩阵,bij=0(i>j+1)。B可通过定义的2类辛正交矩阵对N进行变换得到,其特征值为λ1, λ2, …, λd。根据性质有
3) 对角平均。
该步骤可将任一组分Xk(1≤k≤d)转化为一组长度为n的时间序列,因此d组长度为n的时间序列和即为原始时间序列s。
令Xm×d=(xij)m×d、d*=min(m, d)、m*=max(m, d)、n=m+(d-1)τ。
| $ {y_k} = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{k}\sum\limits_{p = 1}^k {y_{p,k - p + 1}^*} ,}&{1 \le k \le {d^*}}\\ {\frac{1}{d}\sum\limits_{p = 1}^{{d^*}} {y_{p,k - p + 1}^*} ,}&{{d^*} \le k \le {m^*}}\\ {\frac{1}{{n - k + 1}}n\sum\limits_{p = k - {m^*} + 1}^{n - {m^*} + 1} {y_{p,k - p + 1}^*} ,}&{{m^*} < k \le n} \end{array}} \right. $ | (4) |
由式(4),可根据Xi求得一组时间序列Yi=(y1, y2, …, yn),进而得到原信号在时域内的d组独立叠加成分,即d个SGC (symplectic geometry component, SGC)分量。
2 广义形态分形维数基于传统分形维数的盒覆盖法思想,给定GMFD的局部度量分布函数:
| $ {u_i}(\lambda ) = \frac{{(s \oplus \lambda g - s\Theta \lambda g)(i)}}{{{A_g}(\lambda )}} $ | (5) |
式中:g为结构元素;λ为结构元素尺度,i=1, 2, …, n;Ag(λ)为尺度为λ对信号的覆盖面积。
形态学广义信息熵的表达式为:
| $ {K_q}(\lambda ) = \alpha (\lambda )\frac{{{\rm{lg}}\mathop \sum \limits_{i = 1}^n {{[{\mu _i}(\lambda )]}^q}}}{{1 - q}} $ | (6) |
式中:q为给定参数;α(λ)为系数,其表达式为:
| $ \alpha (\lambda ) = \frac{{{\rm{lg}}{\kern 1pt} {A_g}(\lambda )/{\lambda ^2}}}{{{\rm{lg}}{\kern 1pt} {\kern 1pt} n(\lambda )}} = \frac{{{\rm{lg}}[n(\lambda )]}}{{{\rm{lg}}[n(\lambda )]}} = 1 $ | (7) |
定义划分函数为:
| $ \chi (\lambda ,q) = {[\sum\limits_{i = 1}^n {{u_i}^q} (\lambda )]^{\alpha (\lambda )}} $ | (8) |
因此,GMFD的表达式为:
| $ {D_q} = \frac{1}{{q - 1}}\mathop {{\rm{lim}}}\limits_{\lambda \to 0} \frac{{{\rm{lg}}{\kern 1pt} {\kern 1pt} \chi (\lambda ,q)}}{{{\rm{lg}}{\kern 1pt} {\kern 1pt} \lambda }} $ | (9) |
对lg[Ag(λ)/λ2]和lg[1/λ]进行最小二乘拟合,实现对Dq的估计[10]。
3 方法流程针对液压泵信号的辛几何模态分解方法的重度过分解、故障诊断问题,提出了一种基于能量的SGMD和GMFD相结合的新方法。
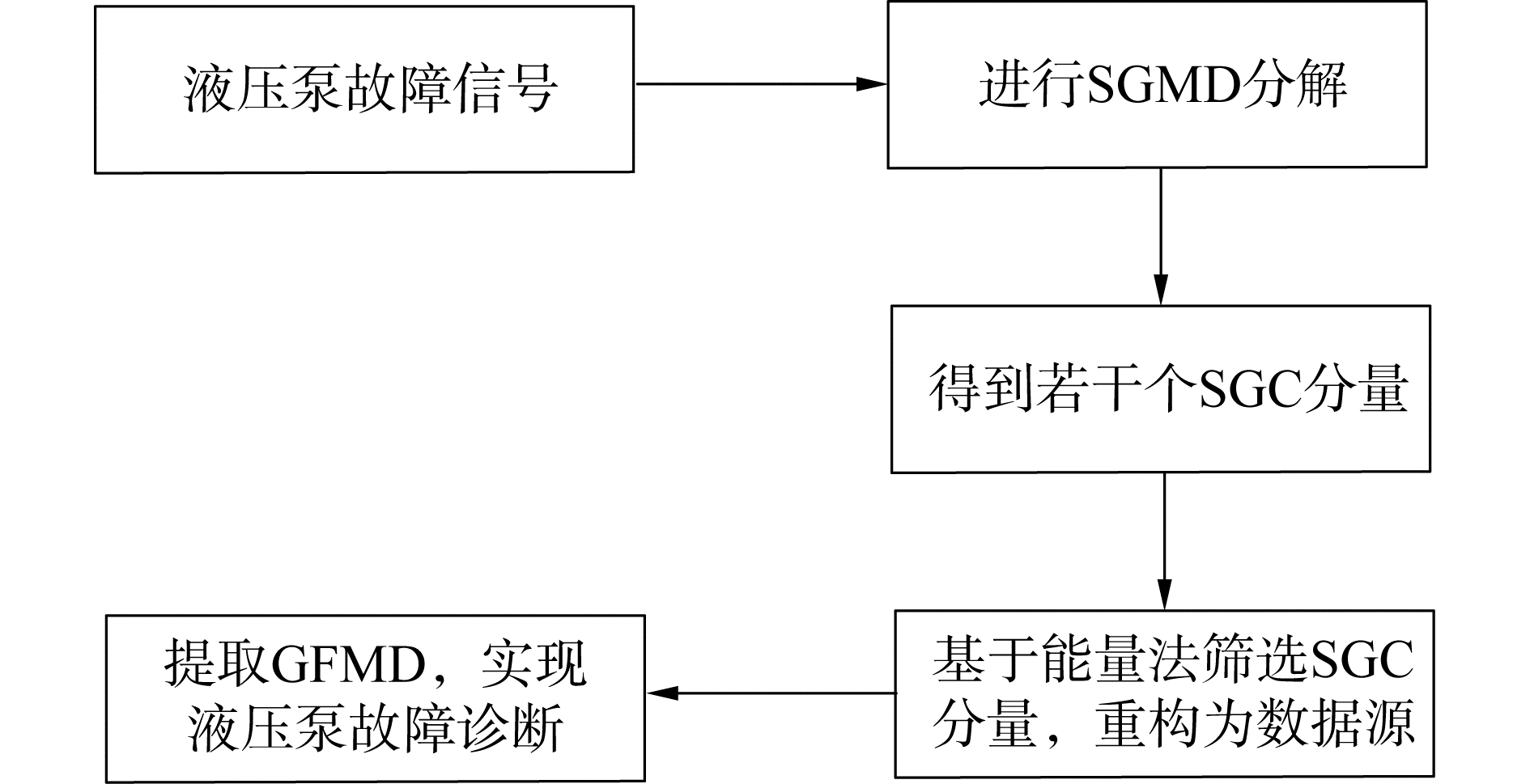
首先,利用SGMD对液压泵实际故障振动信号进行分解;其次,针对分解过程中产生的重度过分解现象,提出基于能量法选取含有丰富运行特征信息的SGC分量,将其重构为数据源;最后,基于数据源提取GMFD,实现对液压泵不同故障的诊断。
所提方法流程如图 1所示。
|
Download:
|
| 图 1 方法流程 Fig. 1 The flow chart of the proposed method | |
仿真信号设计如下:
| $ {x(t) = {x_1}(t) + {x_2}(t) + {x_3}(t)} $ | (10) |
| $ {x(t) = {\rm{sin}}(30\pi t) + 0.5{\rm{sin}}(50\pi t) + {\rm{ noise }}} $ | (11) |
式中:x1(t)是频率为15 Hz的正弦信号;x2(t)是频率为25 Hz的正弦信号;x3(t)是标准差为0.5的高斯白噪声。采样频率为1 000 Hz,采样时间为1 s。
设15 Hz和25 Hz正弦信号x1(t)和x2(t)为感兴趣信号,标准差为0.5的高斯白噪声x3(t)模拟强背景干扰噪声。
原信号x(t)、正弦信号x1(t)和正弦信号x2(t)的时域如图 2所示。仿真的目的是为了分别提取出15 Hz和25 Hz的正弦信号的模态分量。

|
Download:
|
| 图 2 仿真信号 Fig. 2 The simulation signals | |
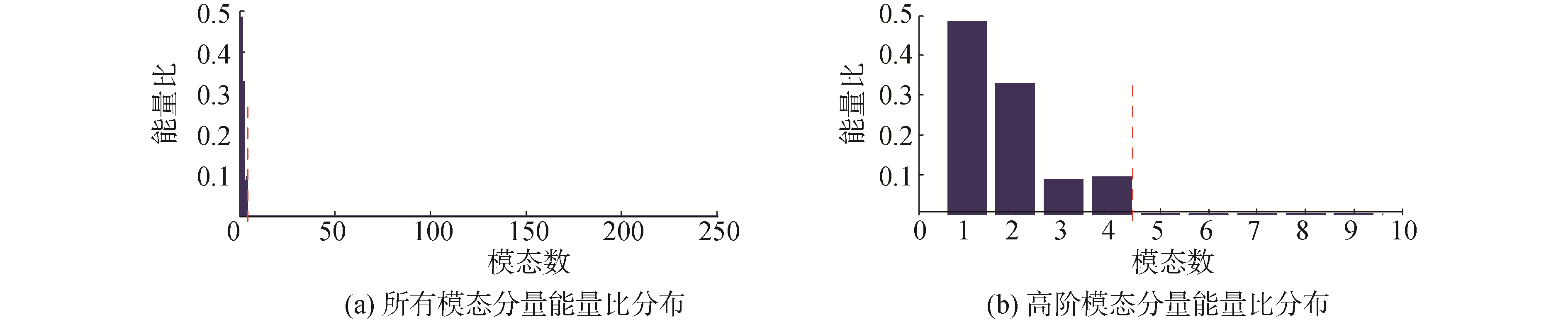
利用SGMD对仿真信号x(t)进行分解,根据文献[10]可知,参数d设置为n/3,其中n为信号长度,即得到255个SGC分量,并对上述分量进行能量分析,模态分量能量比分布如图 3所示。由图 3可知,绝大部分能量集聚在前4个SGC分量,剩余其他251个SGC分量所含能量极少。由此可知,15 Hz和25 Hz正弦信号x1(t)和x2(t)包含在上述4个分量中。
|
Download:
|
| 图 3 基于仿真信号的模态分量能量比分布 Fig. 3 Power ratio distribution of mode components based on simulation signal | |
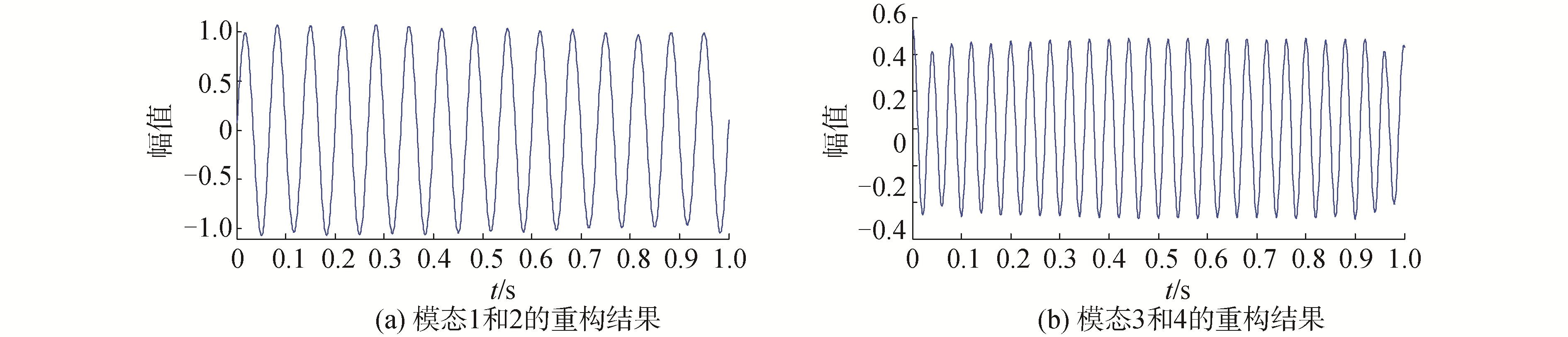
对上述4个分量进行相似性分析,结果如表 1所示。由表 1可知,模态1和2具有极高的相似性、模态3和4具有极高的相似性,其他模态之间相似性极低。因此,将模态1和模态2进行重构、模态3和模态4进行重构,结果如图 4所示。
|
Download:
|
| 图 4 重构结果 Fig. 4 Merge result | |
| 表 1 前4个SGC分量相似性分析结果 Table 1 Similarity analysis results among the first 4 SGCs |
对比图 2(b)的15 Hz正弦信号x1(t)和图 4(a)所重构信号可知,二者的形态特征具有高度相似性。因此,图 4(a)所示的重构结果即为SGMD从原始信号x(t)中所分解的15 Hz正弦信号。
对比图 2(c)的25 Hz正弦信号x2(t)和图 4(b)所重构信号可知,二者的形态特征具有高度相似性。因此,图 4(b)所示的重构结果即为SGMD从原始信号x(t)中所分解的25 Hz正弦信号。
因此,文中所提的基于能量法可以有效地从原信号中分别选取感兴趣的15 Hz和20 Hz正弦信号。
4.3 基于传统模态分解方法的仿真信号分析为了对比说明SGMD方法的优越性和有效性,本文将上述仿真信号进行传统的LMD分析。
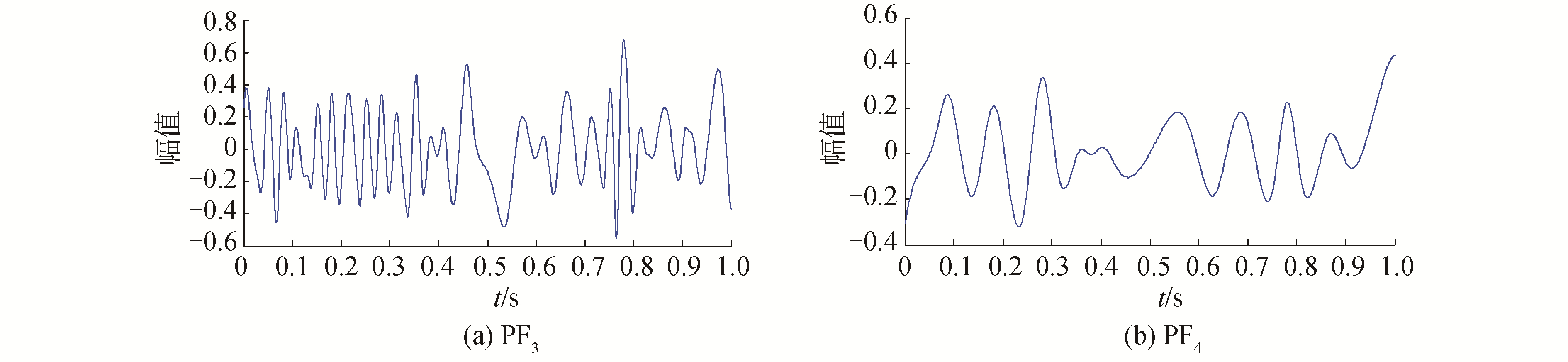
将3模态组成的仿真信号进行LMD分解,可得到10个PF(Product Function)分量和1个剩余分量,因此LMD方法出现了过分解现象。经过分析可知,和15 Hz和25 Hz的正弦信号最相近的2个模态分量分别为PF3和PF4,如图 5所示。
|
Download:
|
| 图 5 基于仿真信号的LMD分解结果 Fig. 5 Decomposition results based on LMD based on simulation signal | |
对比图 2(b)、图 2(c)和图 5可知,基于LMD所得到PF3、PF4相较于15 Hz、25 Hz正弦信号都产生了严重畸变。因此,LMD无法有效地实现从原信号中提取15 Hz和25 Hz正弦信号。
LMD分解缺陷原因为多模态信号形态特征具有复杂性,使得PF分量的瞬时频率与幅值失去信号原本应有物理意义,导致信号的时频分布的可读性变差,由此产生分解缺陷[11]。
通过上述对仿真信号分析可知,文中基于SGMD和所提能量法能够有效地从多模态信号中选取出频率为15 Hz和25 Hz的正弦信号,且较LMD具有有效性和优越性。
5 液压泵故障信号分析 5.1 实验方法为了验证所提方法的有效性和优越性,以柱塞数为7的MCY14-1B型斜盘式轴向柱塞泵为实验对象,利用10 kHz的采样频率采集正常、松靴和滑靴磨损的Z轴振动信号,其中额定转速为1 470 r/min,泵出口压力调定为12 MPa。实验系统图如图 6所示。

|
Download:
|
| 图 6 斜盘式轴向柱塞泵的实验系统 Fig. 6 The swashplate axial plunger pump experiment system | |
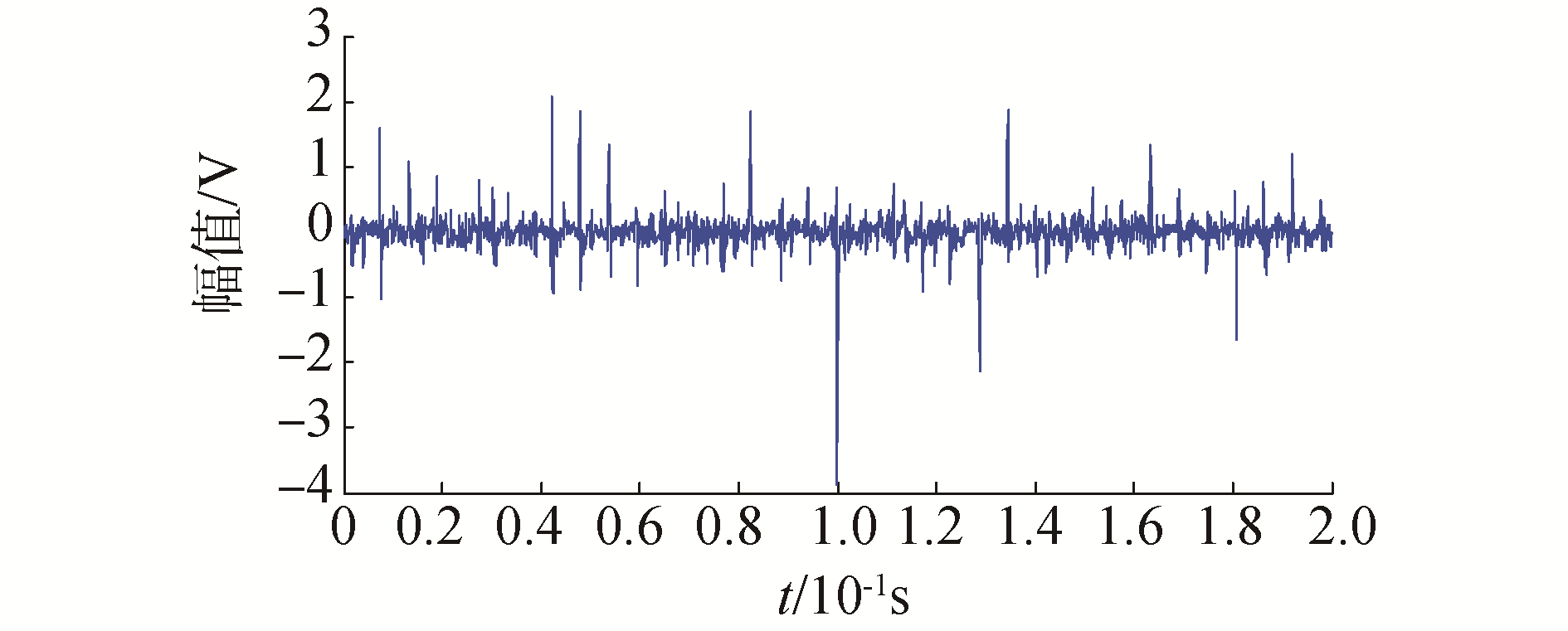
截取0.2 s(n=2 000点)数据进行分析,图 7为松靴故障信号。
|
Download:
|
| 图 7 松靴故障信号 Fig. 7 The signal of loose slipper fault | |
利用SGMD对松靴故障信号进行分解,即得到d=n/3=666个SGC分量,并对上述分量进行能量分析,模态分量能量比分布如图 8所示。大部分能量集聚在前10%(前66个)SGC分量,剩余其他600个SGC分量所含能量很少。由此可知,前10%SGC分量包含了丰富松靴故障特征信息。

|
Download:
|
| 图 8 基于松靴故障的模态分量能量比分布 Fig. 8 Power ratio distribution of mode components based on central loose slipper fault signal | |
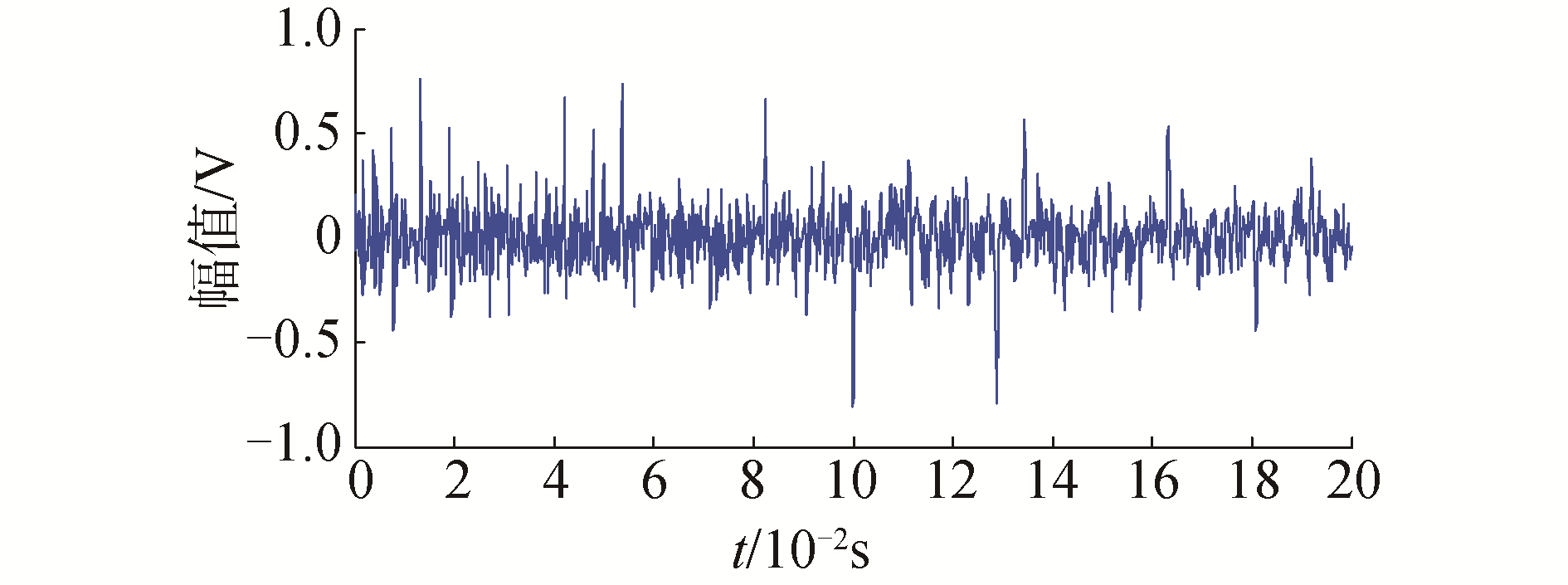
因此,将前10%SGC分量进行重构,即可得到松靴故障信号源,如图 9所示。
|
Download:
|
| 图 9 松靴故障信号源 Fig. 9 Data source of loose slipper fault | |
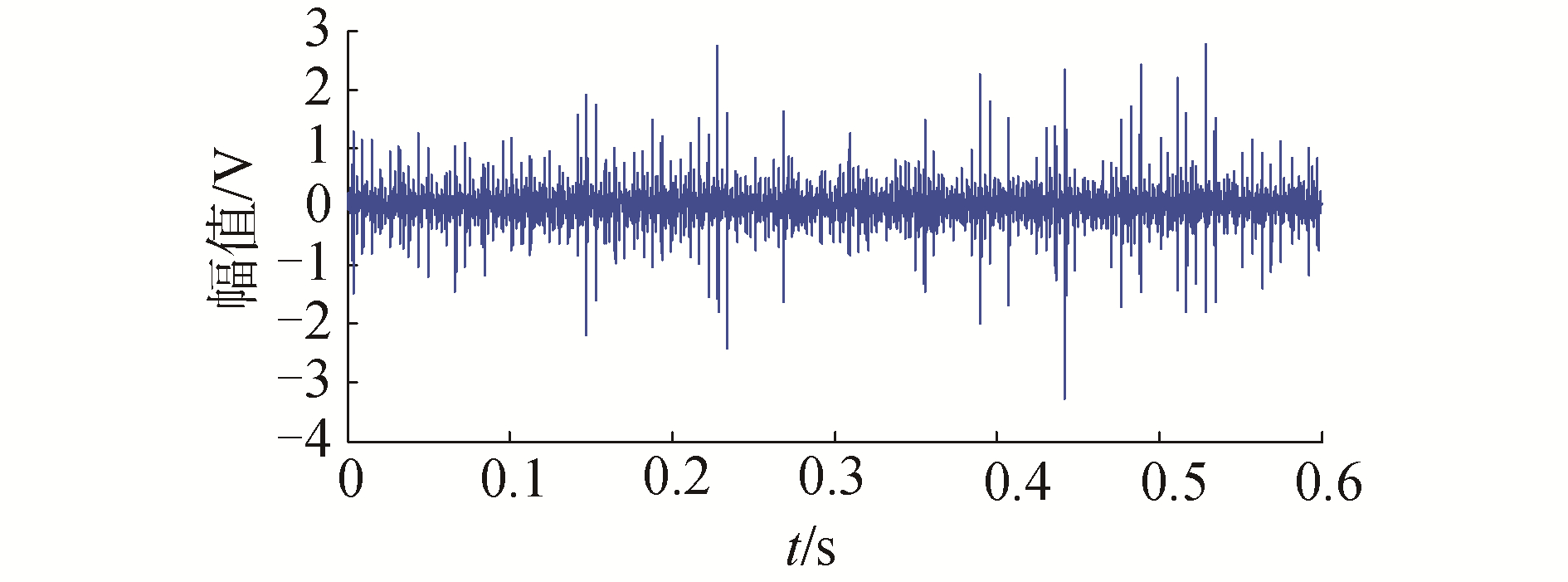
截取0.2 s(n=2 000点)数据进行分析,图 10为滑靴磨损故障信号。
|
Download:
|
| 图 10 滑靴磨损故障信号 Fig. 10 The signal of slipper wear fault | |
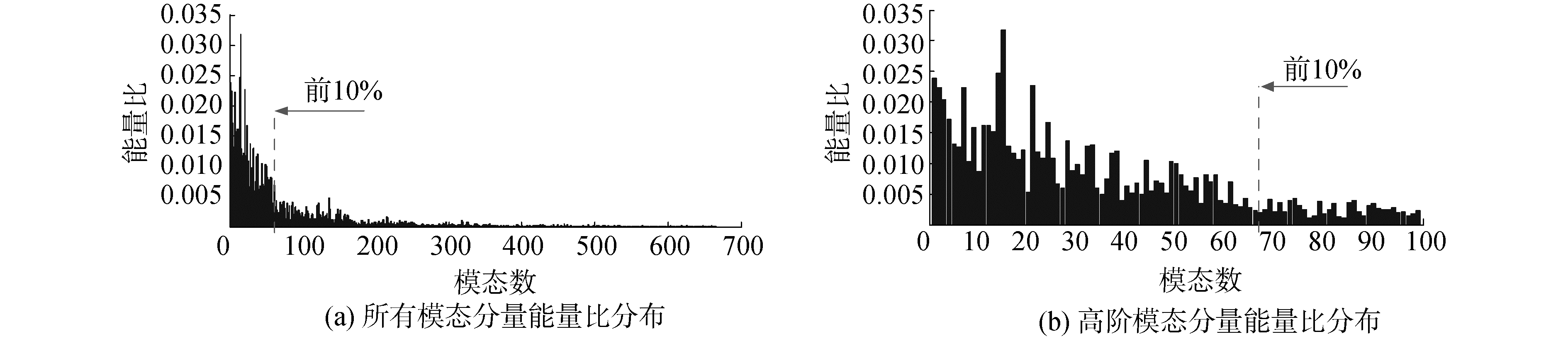
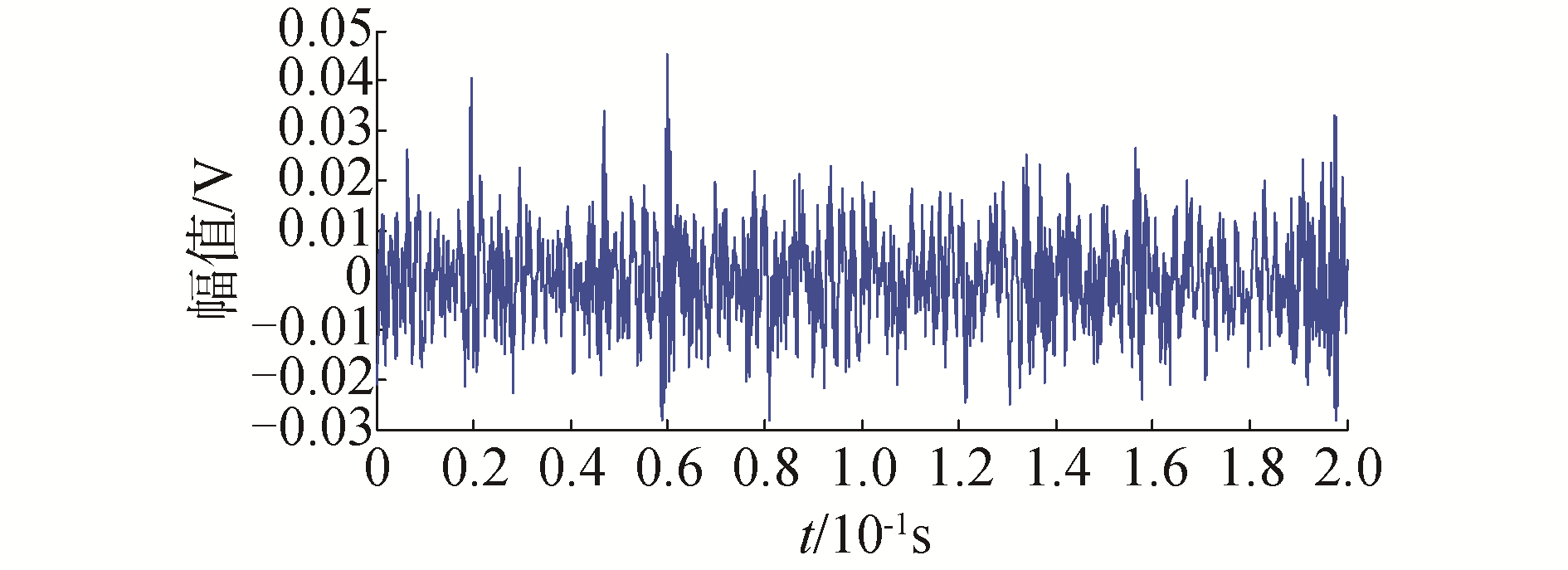
利用SGMD对滑靴磨损故障信号进行分解,即得到d=n/3=666个SGC分量,并对上述分量进行能量分析,模态分量能量比分布如图 11所示。
|
Download:
|
| 图 11 基于滑靴磨损故障的模态分量能量比分布 Fig. 11 Power ratio distribution of mode components based on central slipper wear fault signal | |
|
Download:
|
| 图 12 滑靴故障信号源 Fig. 12 Data source of slipper wear fault signal | |
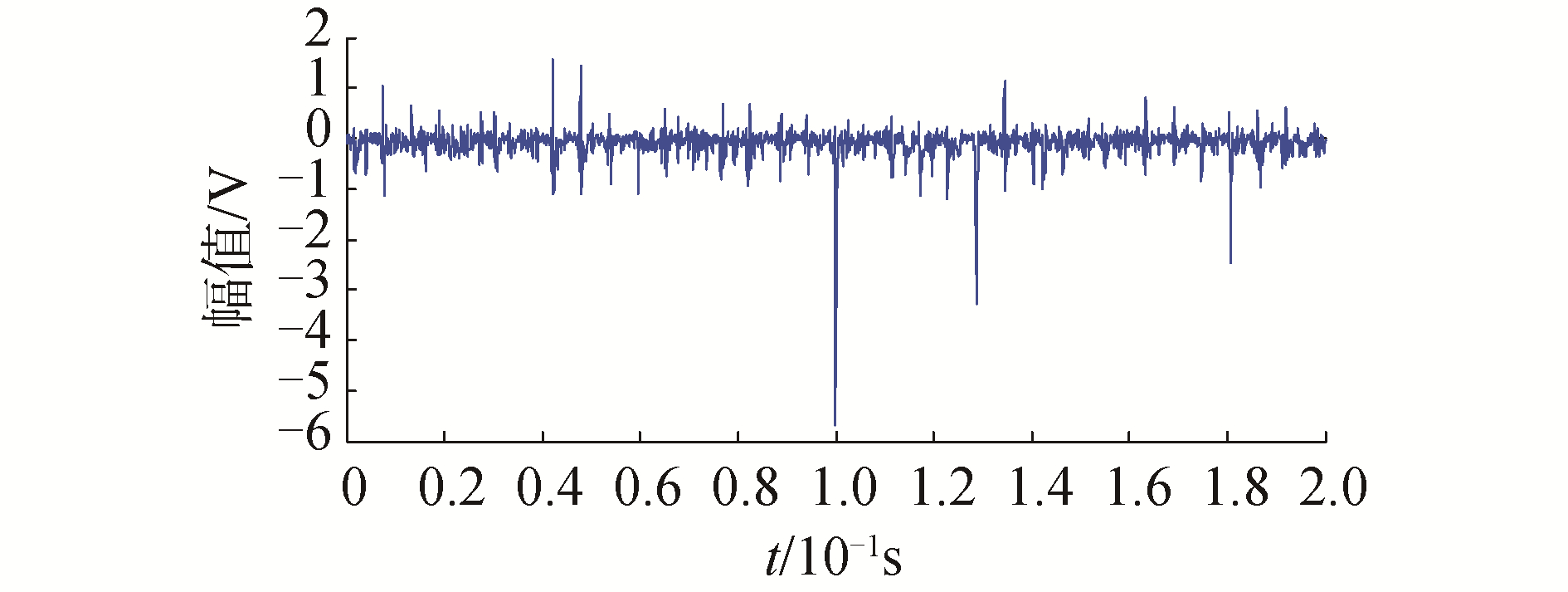
将松靴故障信号进行LMD分解,可得到6个PF分量和1个剩余分量R。将上述分量进行能量分析,模态分量能量比分布如图 13所示。由图 13所示,PF1在所有分量中能量最大,因此将其作为数据源进行分析,其波形图如图 14所示。

|
Download:
|
| 图 13 基于松靴故障的模态分量能量比分布 Fig. 13 Power ratio distribution of mode components based on loose slipper fault signal | |
|
Download:
|
| 图 14 基于松靴故障信号的LMD分解结果 Fig. 14 Decomposition results based on LMD based on loose slipper fault signal | |
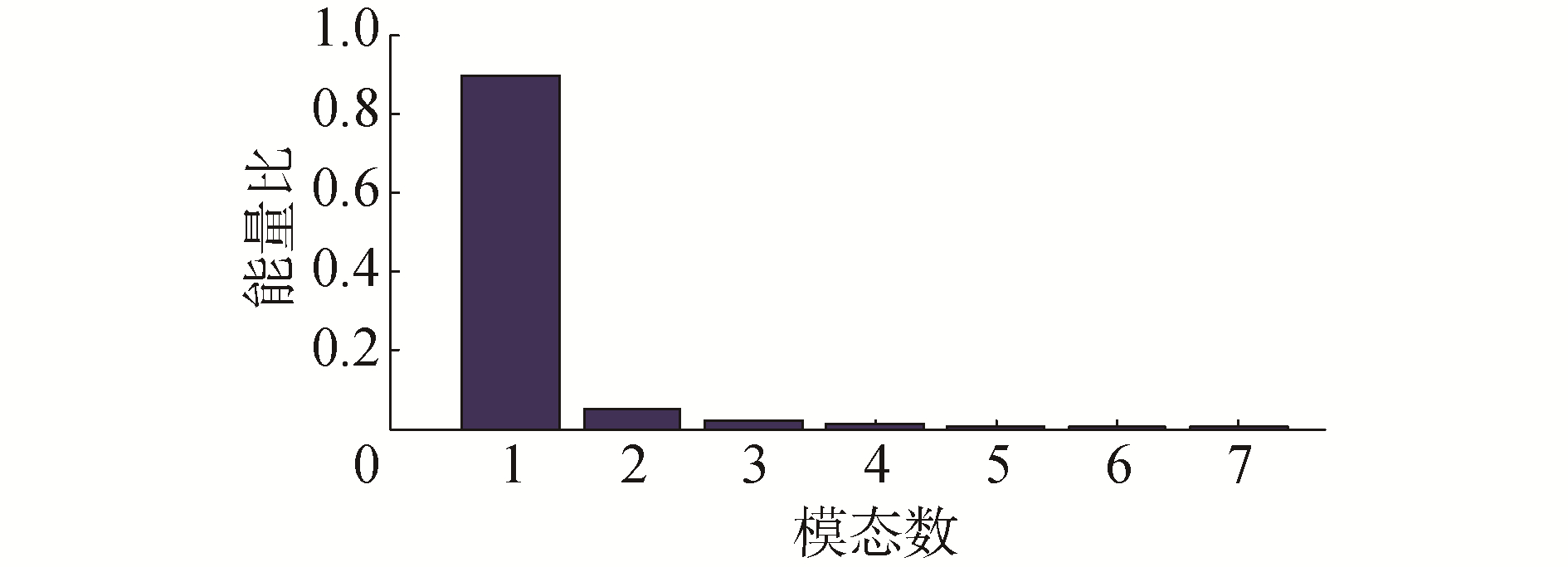
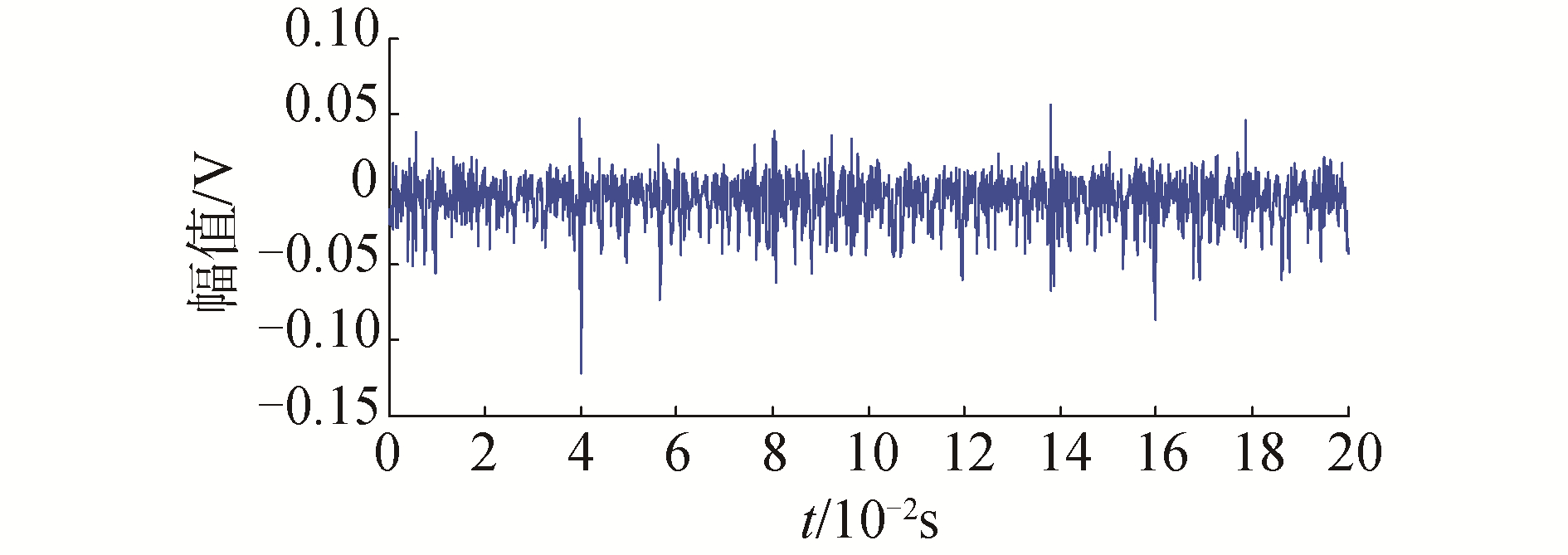
将滑靴故障信号进行LMD分解,可得到6个PF分量和1个剩余分量R将上述分量进行能量分析,模态分量能量比分布如图 15所示。由图 15所示,PF1在所有分量中能量最大,因此将其作为数据源进行分析,其波形图如图 16所示。
|
Download:
|
| 图 15 基于滑靴故障的模态分量能量比分布 Fig. 15 Power ratio distribution of mode components based on slipper wear fault signal | |
|
Download:
|
| 图 16 基于滑靴故障信号的LMD分解结果 Fig. 16 Decomposition results based on LMD based on slipper | |
对SGMD和LMD的数据源占信号总能量比例进行分析,结果如表 2所示。
| 表 2 数据源能量占比分析 Table 2 Energy ratio of data source |
文献[4]提出,基于能量法均可从PF分量中选取出含有特征信息丰富的分量作为数据源。由表 2可知,基于SGMD所提取数据源能量占比和基于LMD的相差不大,所以初步确定为基于能量法选取SGC重构分量方法合理有效。
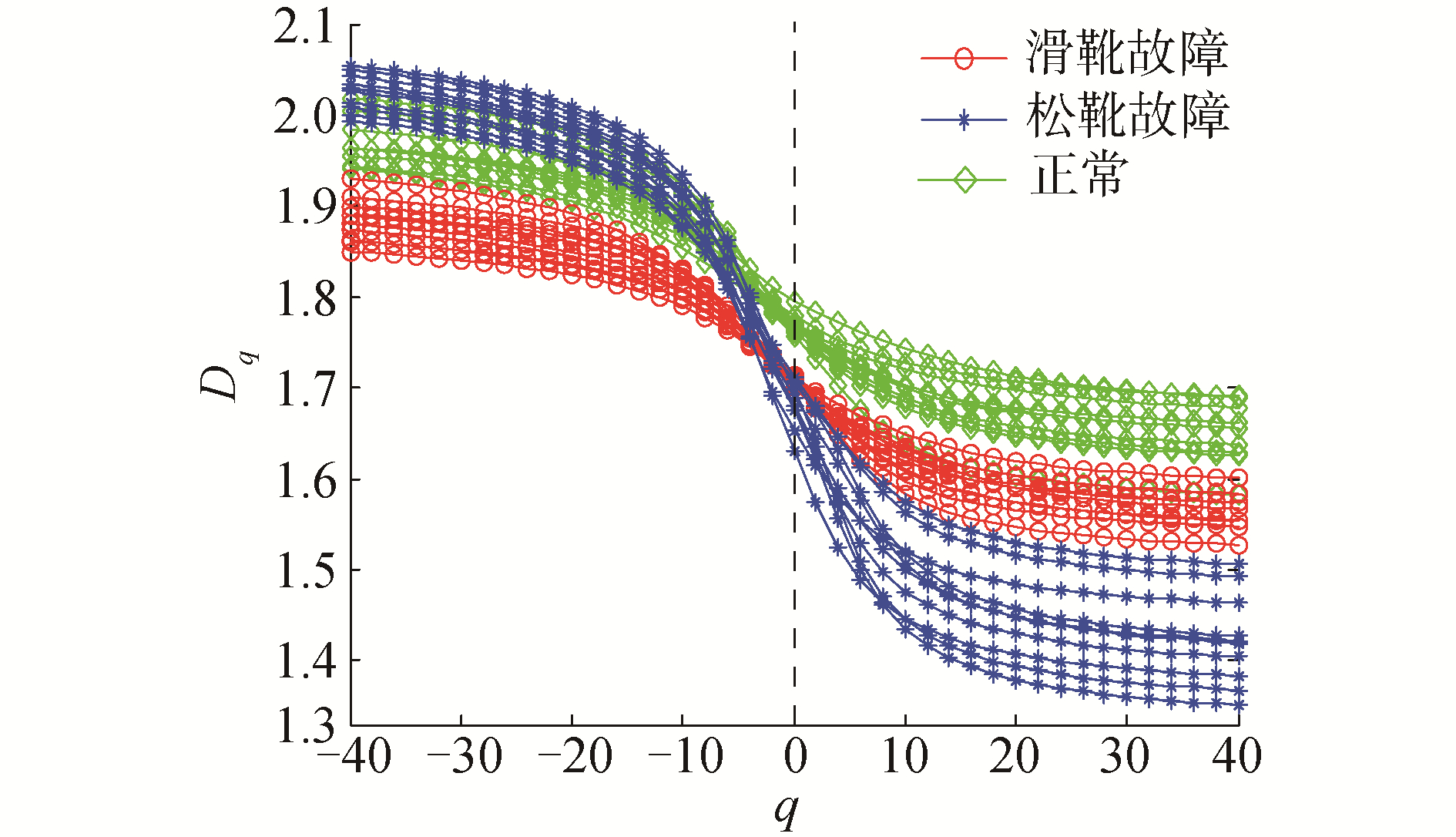
5.4 广义形态分形维数提取 5.4.1 基于SGMD的广义形态分形维数提取将正常信号、SGMD所提取的滑靴磨损故障信号和松靴故障信号作为数据源,进行GMFD提取,参数q设为[-40 :2 :40],单位结构元素设为(0 0 0),尺度参数范围设为2~20。结果如图 17所示。
|
Download:
|
| 图 17 基于SGMD的GMFD分布 Fig. 17 The GMFD diagrams based on SGMD | |
正常信号接近于随机噪声,其波形形态特征具有随机性;故障信号波形形态特征具有明显的周期性冲击特征。因此,基于正常信号所提取的GMFD较基于故障信号所提取的值要大[9]。
在图 17中,当0≤q≤40时,正常信号和故障信号的GMFD之间都不存在混叠现象,且正常状态的GMFD值也较松靴故障和滑靴磨损故障的值大;当-40≤q < 0时,正常状态和松靴故障的GMFD不存在混叠现象,但和滑靴磨损故障存在混叠现象,且正常状态GMFD值也不是最大。
因此,只有在0≤q≤40时,3种运行状态的GMFD能够定量和全面地表征液压泵运行状态的非线性信息、可实现松靴和滑靴的故障诊断。
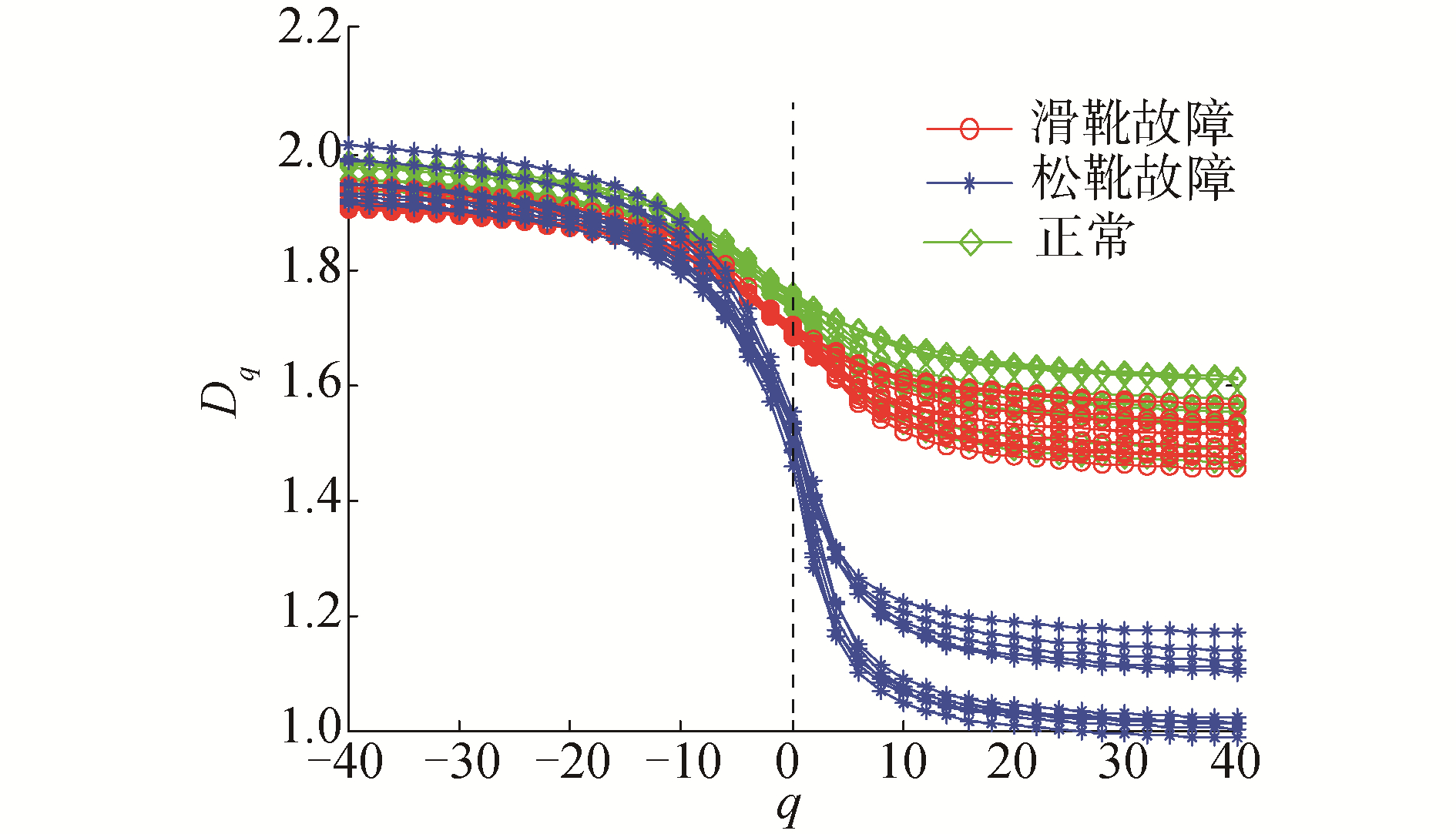
5.4.2 基于LMD的广义形态分形维数提取为了说明所提方法的优越性,本文还将LMD对信号进行分解,并提取GMFD,结果如图 18所示。由图 18可知,在-40≤q≤40,基于LMD所提取3种运行状态GMFD都存在不同程度的混叠现象,无法实现松靴和滑靴的故障诊断。
|
Download:
|
| 图 18 基于LMD的GMFD分布 Fig. 18 The GMFD diagrams based on LMD | |
对比图 17、图 18可知,只有针对SGMD分解后的信号,在0≤q≤40时所提取的GMFD能够定量和全面地表征液压泵运行状态的非线性信息、可实现松靴和滑靴的故障诊断。
6 结论1) 基于所提能量法,可以有效地筛选含有丰富运行特征信息的SGC分量,并将其重构作为高质量数据源;
2)在0≤q≤40,基于SGMD所提取的GMFD能够定量和全面地表征液压泵运行状态的非线性特征信息、可实现松靴和滑靴的故障诊断;
3) SGMD较LMD能提取出更多的故障特征信息,为故障诊断提供高质量数据源。
| [1] |
高宇, 冯培恩, 彭贝, 等. 液压挖掘机分阶段功率匹配控制技术[J]. 哈尔滨工程大学学报, 2017, 38(9): 1461-1469. GAO Yu, FENG Peien, PENG Bei, et al. Stage-based power matching control of hydraulic excavator[J]. Journal of Harbin Engineering University, 2017, 38(9): 1461-1469. (  0) 0)
|
| [2] |
王鹏飞, 王新晴, 朱会杰, 等. 液压泵故障诊断稀疏编码方法研究[J]. 北京理工大学学报, 2017, 37(5): 451-454, 465. WANG Pengfei, WANG Xinqing, ZHU Huijie, et al. A fault diagnosis method based on sparse coding for hydraulic pump[J]. Transactions of Beijing Institute of Technology, 2017, 37(5): 451-454, 465. (  0) 0)
|
| [3] |
孙健, 李洪儒. 一种基于复合谱与关联熵融合的特征提取方法[J]. 机械工程学报, 2017, 53(24): 96-103. SUN Jian, LI Hongru. Method for feature extraction based on composite spectrum and relative entropy fusion[J]. Journal of mechanical engineering, 2017, 53(24): 96-103. (  0) 0)
|
| [4] |
JIANG Wanlu, ZHENG Zhi, ZHU Yong, et al. Demodulation for hydraulic pump fault signals based on local mean decomposition and improved adaptive multiscale morphology analysis[J]. Mechanical systems and signal processing, 2015, 58-59: 179-205. DOI:10.1016/j.ymssp.2014.10.017 (  0) 0)
|
| [5] |
LU Chuanqi, WANG Shaoping, ZHANG Chao. Fault diagnosis of hydraulic piston pumps based on a two-step EMD method and fuzzy C-means clustering[J]. Proceedings of the institution of mechanical engineers, part C:journal of mechanical engineering science, 2016, 230(16): 2913-2928. DOI:10.1177/0954406215602285 (  0) 0)
|
| [6] |
PAN Haiyang, YANG Yu, LI Xin, et al. Symplectic geometry mode decomposition and its application to rotating machinery compound fault diagnosis[J]. Mechanical systems and signal processing, 2019, 114: 189-211. DOI:10.1016/j.ymssp.2018.05.019 (  0) 0)
|
| [7] |
MARAGOS P, SCHAFER R. Morphological filters-part Ⅱ:their relations to median, order-statistic, and stack filters[J]. IEEE transactions on acoustics, speech, and signal processing, 1987, 35(8): 1170-1184. DOI:10.1109/TASSP.1987.1165254 (  0) 0)
|
| [8] |
MARAGOS P, SUN F K. Measuring the fractal dimension of signals:morphological covers and iterative optimization[J]. IEEE transactions on signal processing, 1993, 41(1): 108. (  0) 0)
|
| [9] |
MARAGOS P, SUN F K. Measuring the fractal dimension of signals:morphological covers and iterative optimization[J]. IEEE transactions on signal processing, 1993, 41(1): 108. (  0) 0)
|
| [10] |
LI Bing, ZHANG Peilin, WANG Zhengjun, et al. Morphological covering based generalized dimension for gear fault diagnosis[J]. Nonlinear dynamics, 2012, 67(4): 2561-2571. DOI:10.1007/s11071-011-0169-1 (  0) 0)
|
| [11] |
何志坚, 周志雄. 基于ELMD的样本熵及Boosting-SVM的滚动轴承故障诊断[J]. 振动与冲击, 2016, 35(18): 190-195. HE Zhijian, ZHOU Zhixiong. Fault diagnosis of roller bearings based on ELMD sample entropy and Boosting-SVM[J]. Journal of vibration and shock, 2016, 35(18): 190-195. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


