随着科学技术的不断发展以及对能源和生活资源需求的不断增加,人们也愈重视对深海的探索和开发。带有动力定位系统的船舶是深海资源开发的重要工程装备之一[1]。动力定位船通常安装多个推进器,其在执行定点定位和路径跟踪等任务时,动力定位控制器首先计算出抵抗环境载荷和跟踪期望路径所需要的纵向力、横向力和艏摇力矩, 然后将控制指令传递给推力分配模块,将合力和力矩分配给每一台推进器。推力分配方法是推力分配模块的核心内容,而考虑推进器限制的推力分配方法则是动力定位技术未来研究的主要挑战之一[2],推进器的限制包括推进器的推力大小限制和回转禁止域。因此研究考虑了推进器回转禁止域的推力分配方法具有重要的意义。
推力分配问题是属于动力定位控制领域内的控制分配问题,迄今为止,分配算法也经历了从简单到复杂,从静态优化到动态优化,从单目标优化到多目标优化的发展过程。Sadenlen[3]提出利用滤波法和奇异分解法来约束全回转推进器推力回转角度。该方法既能避免发生奇异结构的现象,还能避免推进器的磨损。Berg[4]还提出了阻尼方差最小化方法解决奇异值问题。其优化目标是总功率最小化,使船舶的油耗能够显著降低。Wicher等[5]提出分组分配法,将临近的2个或多个推进器归为一组,将控制器计算得到的力矩分配给多个推进器组,简化了计算过程。Webster等[6]应用线性规划方法,解决多变量多约束的线性规划问题。Johansen等[7]在众多相关的研究基础上对控制分配算法的研究现状做了非常全面的总结,根据控制分配选用的模型的不同将控制分配算法分为线性分配和非线性分配2类。其中线性分配又分为无约束线性控制分配和有约束线性控制分配,线性控制分配为静态分配问题。采用线性的分配模型可以避免复杂的非线性最优化求解,简化计算的难度,但在处理推进器的约束上显得比较复杂。非线性分配主要采用的算法有非线性规划法、混合整数规划法、动态寻优法和直接非线性分配,但这些算法设计复杂,计算时间长,很难应用于实时系统。
近年来,许多研究者尝试运用智能优化算法解决具有复杂约束条件的推力分配问题[8]。黄炜[9]将模拟退火算法与全局人工鱼群算法相结合用来解决基于功率管理为目标函数的推力分配问题,该方法能够快速、精确地求解推力分配问题,但为了获得更高的寻优精度,牺牲了一部分时间性能。刘明等[10]提出一种将伪逆算法与混沌粒子群算法相融合的推力分配算法,该方法能兼顾能量消耗的同时,能有效降低推进器的磨损,解决推进器系统奇异结构问题,但较伪逆法相对耗时。付海军等[11]提出一种基于自适应遗传算法的加权伪逆推力分配策略,通过仿真实验表明,虽然该方法能在一定程度上改善推进器角度饱和问题,但并未能完全有效解决推进器角度饱和问题。可以看出现有的推力分配方法很难全方位地考虑推进器的推力饱和、推进器的回转禁止域以及推力分配计算的实时性等问题。
针对这些问题,本文从工程实际应用的角度出发,并较全面地考虑推进器的回转角禁止域约束和推力饱和约束条件,提出了一种将控制量归一化处理、直接分配法和伪逆法相结合的改进推力分配方法。该推力分配方法能够有效地解决回转禁止角约束、推力饱和等问题,同时由于算法步骤简单,因而具有良好的实时性。
1 船舶运动数学模型及动力定位船仿真模型为了研究动力定位船的推力分配方法,首先需要研究船舶的运动数学模型和动力学模型,并根据实际动力定位系统的组成和工作原理建立动力定位船的仿真模型。
1.1 船舶运动数学模型对于水面航行的船舶,通常使用北东坐标系(NED)来描述船舶在海面上的位置,而船舶的运动速度、加速度、角速度和角加速度则在本体坐标系{b}下进行描述[12]。当考虑水面动力定位船舶的运动时,船舶的升沉、横摇和纵摇运动是可以忽略的,因此只需要考虑船舶的纵荡u、横荡v和艏摇r。船舶的三自由度运动学和动力学公式为:
| $ {\mathit{\boldsymbol{\dot \eta }} = \mathit{\boldsymbol{J}}(\psi )\mathit{\boldsymbol{v}}} $ | (1) |
| $ {\mathit{\boldsymbol{M\dot v}} + \mathit{\boldsymbol{C}}(\mathit{\boldsymbol{v}})\mathit{\boldsymbol{v}} + \mathit{\boldsymbol{D}}(\mathit{\boldsymbol{v}})\mathit{\boldsymbol{v}} = \mathit{\boldsymbol{\tau }}} $ | (2) |
式中:η=[x y ψ]T表示船舶在北东坐标系下的位置和艏向角;υ=[u v r]T表示船舶在本体坐标系下的速度向量; M=MRB+MA为系统惯性矩阵;MRB为船舶刚体惯性矩阵;MA为水动力附加质量矩阵,M∈R3×3;C(υ)=CRB(υ)+CA(υ)为作用于船舶的科里奥利向心力矩阵;CRB(υ)为船舶刚体的科里奥利向心力矩阵;CA(υ)为由水动力附加质量产生的科里奥利向心力矩阵,C(υ)∈R3×3;D(υ)=D+ Dn(υ)为水阻尼矩阵;D为线性水阻尼矩阵;Dn为非线性水阻尼矩阵,D(υ)∈R3×3;τ=τthr+w为作用于船舶的合力及合力矩,τthr为推进器产生的推力,w为作用于船舶的环境力,即风、浪、流对船舶的作用力,τ∈R3。
船舶运动数学模型是建立动力定位船仿真模型中水动力学模块的基础,式(1)表示船舶在本体坐标系下的运动速度和旋转角速度转化到北东坐标系下,式(2)表示船舶的运动速度和加速度与所受的外力之间的关系。
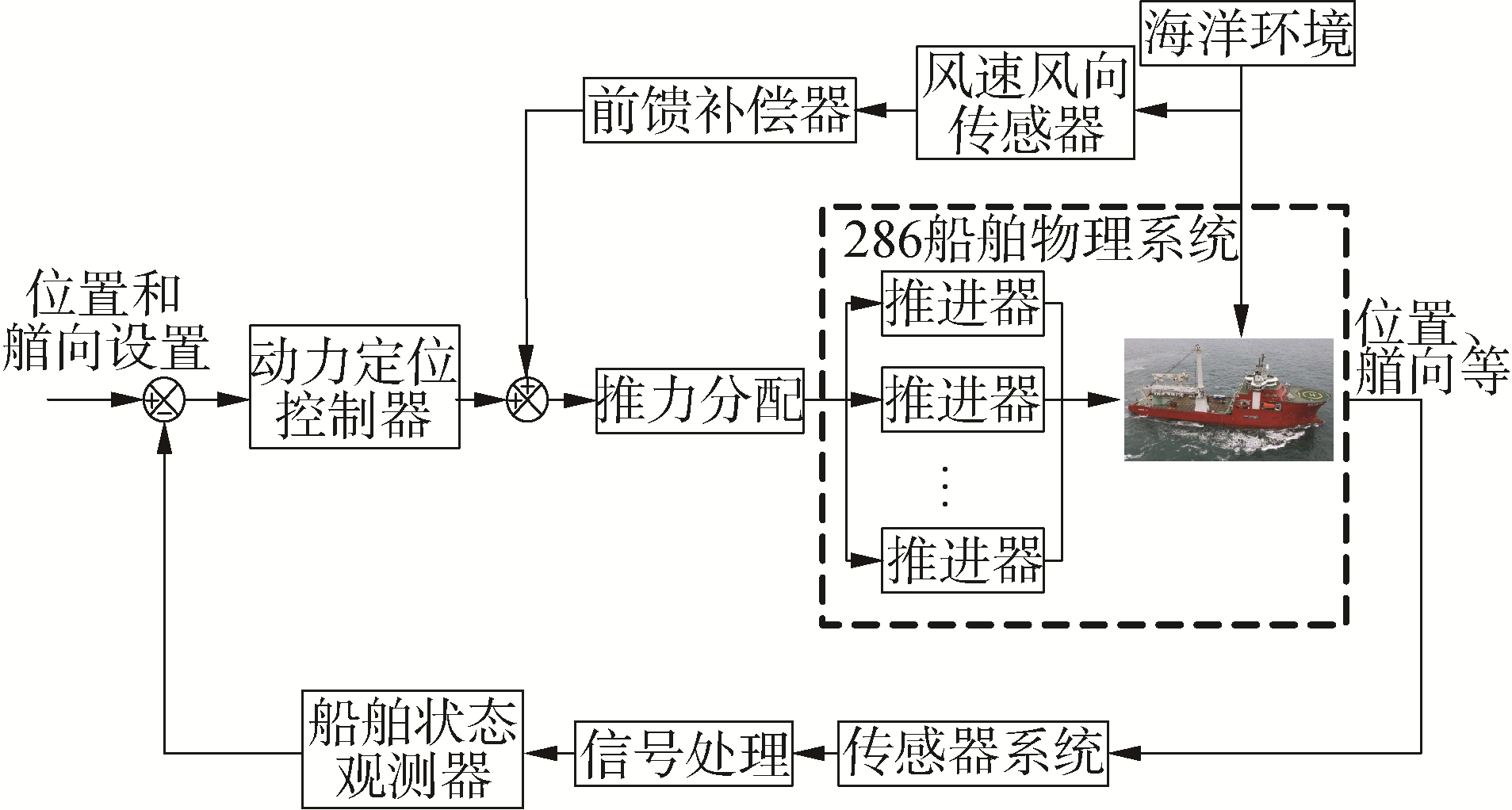
1.2 动力定位船仿真模型动力定位船是指带有动力定位系统的船舶,动力定位船具有优异的操纵性、耐波性。动力定位系统能够帮助船舶完成位置移动、位置保持和目标跟踪等任务。其基本的原理是利用船舶自身的推进器产生抵抗环境力和跟踪期望航迹所需的纵向力、横向力和艏摇力矩。其运动控制系统的组成及工作原理如图 1所示。
|
Download:
|
| 图 1 动力定位船运动控制系统组成及其工作原理 Fig. 1 Composition and working principle of motion control system for dynamic positioning ship | |
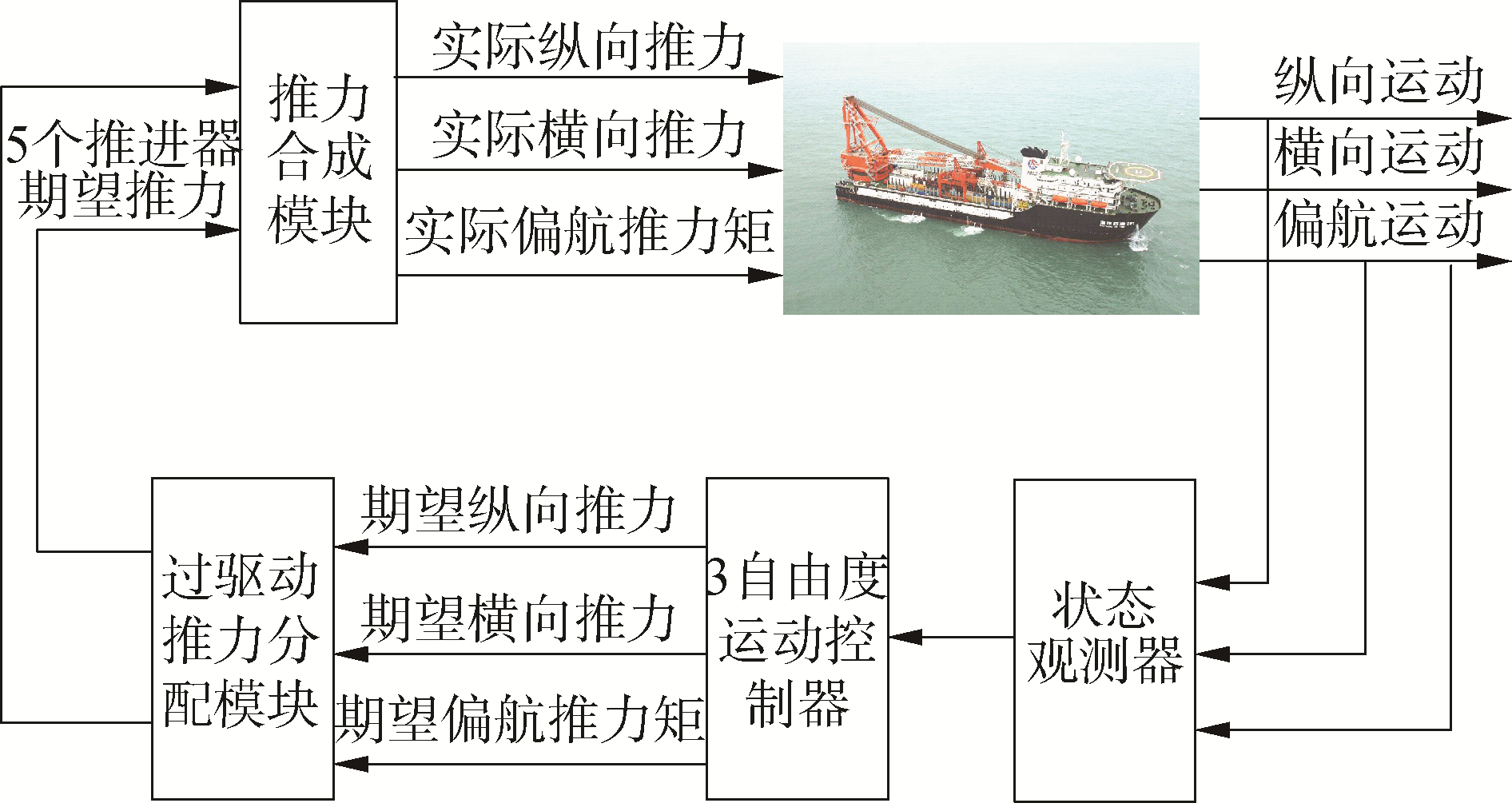
根据实际的动力定位船舶运动控制系统的组成和工作原理,在Matlab软件中建立动力定位船运动控制仿真模型。其Simulink仿真模型如图 2所示。
|
Download:
|
| 图 2 动力定位船运动控制系统仿真模型 Fig. 2 Simulation model of motion control system of dynamic positioning ship | |
动力定位船运动控制系统仿真模型由水动力学模块、状态观测器模块、3自由度运动控制器模块、过驱动推力分配模块和推力合成模块组成。动力定位系统是一个闭环控制系统,首先3自由度运动控制器根据期望的位置、速度和艏向,计算出所需要的推力和力矩。过驱动推力分配模块将该合力指令按照一定的分配原则分配给每一台推进器,确定每一台推进器需产生的推力大小和方向。推力合成模块将推进系统实际产生的推力合成,并输入到船舶水动力学模块,驱动船舶运动。
2 动力定位船推进系统建模 2.1 推进系统参数及其数学模型海洋石油286船装有定位能力为3级的动力定位系统,配备有5台推进器,推进器的布置及编号如图 3所示。

|
Download:
|
| 图 3 海洋石油286船的推进器布置 Fig. 3 Propellers layout of CNOOC′s 286 ship | |
其中船艏布置了2台槽道推进器和一台全回转推进器,船艉布置了2台全回转推进器。这5台推进器均为瓦锡兰公司生产,1号和2号为CT300 M-D型槽道式变螺距四桨叶推进器,直径2 750 mm,推力范围-336≤T1≤336 kN;3号为CS1510-350MNR型变螺距四叶全回转推进器,直径2 500 mm,推力范围0≤T3≤338 kN;4号和5号为FS3510-571/WN型固定螺距四叶全回转推进器,直径3 900 mm,推力范围0≤T4≤780 kN。其主要的安装技术参数如表 1所示。
| 表 1 海油286船推进器的安装位置及角度 Table 1 Installation position and angle of CNOOC′s 286 ship propellers |
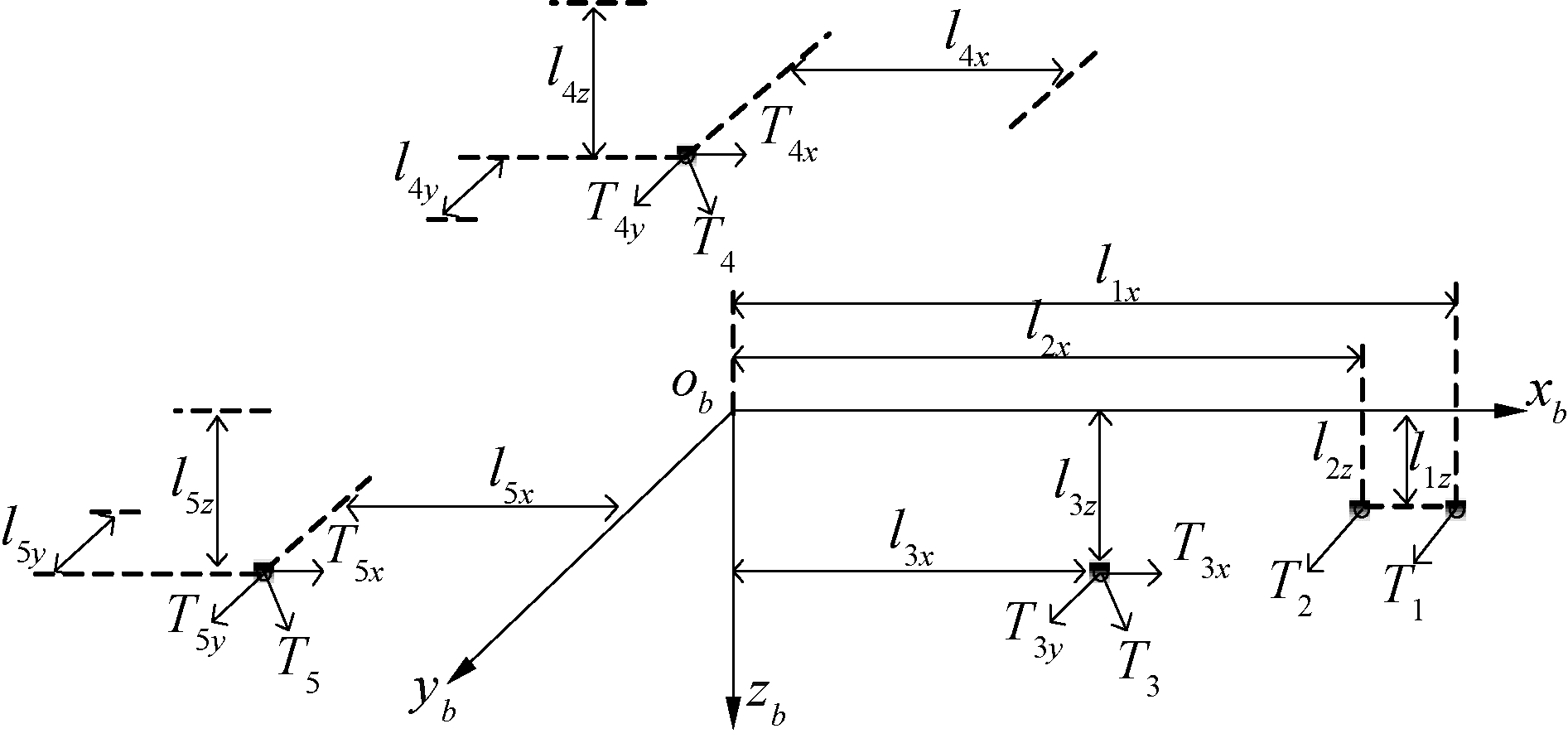
假设船舶的5台推进器均平行于ob-xbyb平面,将每台推进器产生力沿obxb和obyb轴进行分解。每个分力都会相对船舶重心产生相应的力矩。规定全回转推进器的回转角度以顺时针为正,其0°方位角与obxb一致。推进器的纵向推力以向艏为正,横向推力以向右舷为正。船体受到各台推进器推力作用在各轴的分力如图 4所示。
|
Download:
|
| 图 4 海油286船推进器的推力矩示意 Fig. 4 Thrust and moment of propellers of CNOOC′s 286 ship | |
图 4中各物理量表示的含义及计算公式如下所述T3x=T3 cosα3,T3y=T3 sinα3,T4x=T4 cosα4,T4y=T4 sinα4,T5x=T5 cosα5,T5y=T5 sinα5。l3x表示T3距离平面ob-ybzb的距离,l3z表示T3距离平面ob-xbyb的距离;l4x表示T4距离平面ob-ybzb的距离,l4y表示T4距离平面ob-xbzb的距离,l4z表示T4距离平面ob-xbyb的距离;l5x表示T5距离平面ob-ybzb的距离,l5y表示T5距离平面ob-xbzb的距离,l5z表示T5距离平面o-xbyb的距离。
则5台推进器对船舶产生的纵向合力、横向合力和绕Z轴的艏摇的力矩为:
| $ \left\{ {\begin{array}{*{20}{l}} {{X_T} = {T_3}{\kern 1pt} {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _3} + {T_4}{\kern 1pt} {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _4} + {T_5}{\kern 1pt} {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _5}}\\ {{Y_T} = {T_1} + {T_2} + {T_3}{\kern 1pt} {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _3} + {T_4}{\kern 1pt} {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _4} + {T_5}{\kern 1pt} {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\alpha _5}}\\ {{N_T} = {T_1}{l_{1x}} + {T_2}{l_{2x}} + {T_{3y}}{l_{3x}} + {T_{4x}}{l_{4y}} - }\\ {{T_{4y}}{l_{4x}} - {T_{5y}}{l_{5x}} - {T_{5x}}{l_{5y}}} \end{array}} \right. $ | (3) |
由式(3)可将船舶推进器产生的合力及合力矩写为:
| $ \mathit{\boldsymbol{\tau }} = \mathit{\boldsymbol{B}}(\alpha )\mathit{\boldsymbol{T}} $ | (4) |
式中:τ=[XT YT NT]T为推进器产生的三自由度合力;XT表示纵向力;YT表示横向力;NT表示转艏力矩;T=[T1 T2 T3 T4 T5]T为推进器输出的推力向量;B(α)表示推进器的矢量布置矩阵,其完整形式为:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{B}}(\alpha ) = \\ \left[ {\begin{array}{*{20}{c}} 0&0&{{\rm{c}}{\alpha _3}}&{{\rm{c}}{\alpha _4}}&{{\rm{c}}{\alpha _5}}\\ 1&1&{{\rm{s}}{\alpha _3}}&{{\rm{s}}{\alpha _4}}&{{\rm{s}}{\alpha _5}}\\ {{l_{1x}}}&{{l_{2x}}}&{{\rm{s}}{\alpha _3}{l_{3x}}}&{{\rm{c}}{\alpha _4}{l_{4y}} - {\rm{s}}{\alpha _4}{l_{4x}}}&{ - {\rm{c}}{\alpha _5}{l_{5y}} - {\rm{s}}{\alpha _5}{l_{5x}}} \end{array}} \right] \end{array} $ | (5) |
式中:c代表cos(·);s代表sin(·);αi(i=3, 4, 5)表示3号~5号推进器产生推力的方向角。
2.2 全回转推进器回转禁止域确定当动力定位船舶处于工作状态时,各全回转推进器也在不停绕其回转轴发生转动。若一个推进器处于另一推进器的尾流场中,尾流中推进器的推力可能会降低。在研究桨-桨干扰问题时,对于动力定位船这类低速船舶,螺旋桨进速系数的变化对推力减额的影响基本可忽略。而螺旋桨之间的距离和回转角度是影响推进器推力下降的主要因素。
在286船的这5台推进器中,4号和5号推进器之间容易发生桨-桨干扰。两推进器回转轴之间的距离为18 m,其螺旋桨直径均为3.9 m。轴距约为螺旋桨直径的4.6倍。经查阅相关的资料,当桨间距离在4倍螺旋桨直径以上时,将推进器禁止角设置为±10°~±20°,控制螺旋桨偏转时不进入这一区域,可以有效减小推力减额[13]。将禁止角作为约束条件应用在推力分配算法中,可以更好地优化推力分配结果。因此,4号推进器的回转禁止域为[70°,110°],5号推进器的回转禁止域为[250°,290°]。推进器的回转禁止域如表 2所示。
| 表 2 推进器回转禁止域 Table 2 Propeller azimuth forbidden zones |
对于考虑了回转禁止域(如表 2)的动力定位船推力分配,本文提出了一种将直接分配与伪逆算法相结合的分配方法。在使用该方法进行推力分配之前,需要对控制器输出的三自由度合力指令进行归一化处理。然后根据船舶推进系统的推进能力确定纵向力、横向力和艏摇力矩的放大权重系数,计算得到用于船舶实际的期望推力。对归一化处理后的期望推力进行一次直接分配,直接分配计算出每台推进器的推力大小及方向。直接分配没有考虑推进器之间的禁止角约束。因此接下来判断每台推进器的回转方位角是否超出了回转禁止域,若有一台及以上的推进器的方位角超出约束范围,则以与该角度相近的约束边界值作为该推进器的方位角。没有超出的推进器则保留原来的方位角。直接分配后,可以确定出推进器矢量布置矩阵中的角度变量,然后利用伪逆算法进行二次分配。最后得到每台推进器的实际推力大小及方向。
其具体的分配步骤如下。
1) 对控制器的合力指令进行归一化处理。
当船舶在水平面的三自由度的期望推力或期望推力对应的控制电压同时输出时,可能导致某个或几个推进器的推力饱和[14]。为了避免这种现象,首先需要将水平面内的3个期望控制电压进行归一化处理,归一化期望控制电压为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\delta _1} = |{u_X}|/{u_H}}\\ {{\delta _2} = |{u_Y}|/{u_H}}\\ {{\delta _3} = |{u_Y}|/{u_H}} \end{array}} \right. $ | (6) |
式中:uH=|uX|+|uY|+|uN|为水平方向推力对应的控制电压的绝对值之和;δ1、δ2、δ3分别为归一化后纵向控制电压、横向控制电压和偏航控制电压。
然后根据纵向、横向和偏航力矩的权重,分别将归一化后的期望控制电压进行放大:
| $ \left\{ {\begin{array}{*{20}{l}} {{X_d} = {k_1}{u_X}{\delta _1}}\\ {{Y_d} = {k_2}{u_Y}{\delta _2}}\\ {{N_d} = {k_3}{u_N}{\delta _3}} \end{array}} \right. $ | (7) |
式中:Xd、Yd、Nd为分别为期望的纵向推力、期望的横向推力和期望偏航力矩;k1、k2、k3为分别为纵向、横向推力和偏航力矩对应权重系数。
2) 利用直接分配法进行第1次分配。
根据归一化放大后的合力指令τd=[Xd Yd Nd]直接计算出各个推进器的横向力和纵向力分量,直接分配须保证分配后的合力与控制器的期望合力指令相一致。即满足:
| $ {\mathit{\boldsymbol{\tau }}_d} = \mathit{\boldsymbol{B}}(\alpha )\mathit{\boldsymbol{T}} $ | (8) |
根据以上的原则,并结合实际的经验,假定推进器的横向和纵向推力具有如下形式,同时为了保证系统具有较好的冗余度,在直接分配时,令3号推进器的推力为零。
最后构造的直接推力分配公式为:
| $ \left\{ {\begin{array}{*{20}{l}} {{T_1} = {T_2} = \alpha {Y_d} + \lambda {N_d}}\\ {{T_3} = 0}\\ {{T_{4x}} = \gamma {X_d} + \lambda {N_d}}\\ {{T_{5x}} = \gamma {X_d} - \lambda {N_d}}\\ {{T_{4y}} = {T_{5y}} = c{Y_d} - \lambda {N_d}} \end{array}} \right. $ | (9) |
式中系数满足:
| $ \left\{ {\begin{array}{*{20}{l}} {\alpha = 0.5({l_{4x}} + {l_{5x}})/({l_{1x}} + {l_{2x}} + {l_{4x}} + {l_{5x}})}\\ {c = 0.5 - \alpha }\\ {\gamma = 0.5}\\ {\lambda = 1/({l_{1x}} + {l_{2x}} + {l_{4x}} + {l_{4y}} + {l_{5x}} + {l_{5y}})} \end{array}} \right. $ | (10) |
3) 全回转推进器的方位角判断。
根据分配后的推力计算出4号和5号推进器的方位角θ4和θ5。
| $ {\theta _4} = \left\{ \begin{array}{l} {\rm{arccos}}({T_{4x}}/\sqrt {({T_{4x}}^2 + {T_{4y}}^2)} ),\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {T_{4y}} \ge 0,{T_{4x}} \ne 0\\ \pi /2,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {T_{4y}} \ge 0,{T_{4x}} = 0\\ 2\pi - {\rm{arccos}}({T_{4x}}/\sqrt {({T_{4x}}^2 + {T_{4y}}^2)} ),\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {T_{4y}} < 0 \end{array} \right. $ | (11) |
| $ {\theta _5} = \left\{ \begin{array}{l} {\rm{arccos}}({T_{5x}}/\sqrt {({T_{5x}}^2 + {T_{5y}}^2)} ),\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {T_{5y}} \ge 0,{T_{5x}} \ne 0\\ \pi /2,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {T_{5y}} \ge 0,{T_{5x}} = 0\\ 2\pi - {\rm{arccos}}({T_{5x}}/\sqrt {({T_{5x}}^2 + {T_{5y}}^2)} ),\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {T_{5y}} < 0 \end{array} \right. $ | (12) |
然后判断是否出现在回转角禁止域内,将进入禁止域方位角替换为与之相近的禁止域边界值。若没有进入则保留原值。
| $ {\theta _4} = \left\{ \begin{array}{l} {\theta _4},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (0 \le {\theta _4} \le 0.389\pi ) \cup \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (0.611\pi \le {\theta _4} < 2\pi )\\ 0.389\pi ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.389\pi < {\theta _4} \le 0.5\pi \\ 0.611\pi ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.5\pi < {\theta _4} < 0.611\pi \end{array} \right. $ | (13) |
| $ {\theta _5} = \left\{ \begin{array}{l} {\theta _5},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le {\theta _5} \le 1.389\pi {\kern 1pt} {\kern 1pt} {\kern 1pt} \cup \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (1.611\pi \le {\theta _5} < 2\pi )\\ 1.389\pi ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1.389\pi < {\theta _5} \le 1.5\pi \\ 1.611\pi ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1.5\pi < {\theta _5} < 1.611\pi \end{array} \right. $ | (14) |
4) 更新推进器的矢量布置矩阵B,运用伪逆算法进行第2次求解。
选用的推力分配模型为二次无约束的推力分配模型[15]:
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{min}}}&{f(\mathit{\boldsymbol{x}}) = \frac{1}{2}{\mathit{\boldsymbol{u}}^{\rm{T}}}\mathit{\boldsymbol{Wu}}}\\ {{\rm{s}}{\rm{.t}}{\rm{. }}}&{\mathit{\boldsymbol{\tau }} - \mathit{\boldsymbol{Bu}} = 0} \end{array}} \right. $ | (15) |
式中:W为正定权值矩阵;B为推进器矢量布置矩阵;f为推进器的功率函数;τ为控制器输出的合力指令;u为各个推力器输出的推力指令;
由于推进器的回转方位角θ与推力的方向角α在大小上是相等的,因此,在推进器的矢量布置矩阵中只需用对应θi替换αi(i=3, 4, 5)即可。
每个推进器产生的推力:
| $ \mathit{\boldsymbol{T}} = {[{T_1}{\kern 1pt} {\kern 1pt} {T_2}{\kern 1pt} {\kern 1pt} {T_3}{\kern 1pt} {\kern 1pt} {T_4}{\kern 1pt} {\kern 1pt} {T_5}]^{\rm{T}}} = {\mathit{\boldsymbol{W}}^1}{\mathit{\boldsymbol{B}}^{\rm{T}}}{(\mathit{\boldsymbol{B}}{\mathit{\boldsymbol{W}}^1}{\mathit{\boldsymbol{B}}^{\rm{T}}})^{ - 1}}\mathit{\boldsymbol{\tau }} $ | (16) |
为了验证该推力分配方法的有效性,将直接分配与伪逆法结合的分配算法转化为程序写入到动力定位船仿真模型的推力分配模块中。该仿真模型完整地模拟了动力定位系统定点定位的能力。因此用该仿真模型来测试改进推力分配方法具有一定的实际参考价值。
4.1 仿真初始条件仿真初始条件:船舶位于北东坐标系的原点处,艏向角为0°,且船舶的纵向运动速度、横向运动速度和艏摇角速度均为0。
仿真的环境参数设为:风速32.1 kn,风向40°;浪高3 m,浪向40°;流速2 kn, 流向40°;仿真时间500 s。
仿真目标:将船舶维持在(0, 0)处,即所选位置参考系,北东坐标系的原点处,维持艏向为角为0°。
4.2 船舶运动的仿真结果及分析从图 5可以看出,在风浪流的联合作用下,应用该推力分配算法可以成功的将船位保持在原点处,艏向维持在0°。程序实际运行时间为30 s。北向和东向位置在200 s左右时趋于稳定,艏向角在250 s左右时趋于稳定。满足了船舶实际运动控制的要求。

|
Download:
|
| 图 5 船舶位置及艏向角响应 Fig. 5 The response of ship′s position and heading | |
图 6中的Xt、Yt、Nt分别表示纵向推力、横向推力和转艏力矩。图 6中反映了由控制器计算的期望推力和力矩与实际推进系统所产生的推力和力矩之间的关系。从上图可以看出,纵向期望推力和实际推力在100 s时开始吻合一致,横向期望推力和实际推力在200 s左右时开始吻合一致,转艏期望力矩和实际力矩在200 s时开始吻合。推进系统产生的推力与期望推力在100~200 s之后才开始吻合,是由于推进系统在初始时刻执行推进指令时不能立即产生相应的推力,而是逐渐增大直到与期望推力一致。表明在仿真模型中所建立的推进系统符合实际推进系统的物理特性。滞后的时间在200 s以内表明推进系统能较好地执行由控制器发出合力指令。综合以上仿真结果可验证矢量推进系统数学模型的准确性。

|
Download:
|
| 图 6 推进系统推力响应 Fig. 6 thrust response of the propulsion system | |
对于各个推进器,其期望推力与实际产生的推力,期望的回转角与实际的回转角如图 7所示。

|
Download:
|
| 图 7 推进器推力和方位角响应 Fig. 7 Thrust and azimuth response of propellers | |
从图 7可以看出,各推进器实际产生的推力与期望的推力指令能在较短的时间相吻合并趋于相应的稳定值。1号推进器约在150 s时实际推力与期望推力相吻合,最后稳定在196 kn处;2号推进器在120 s左右时实际推力与期望推力相吻合,最后稳定在190 kn处;4号推进器在80 s时实际推力与期望推力相吻合,最后稳定在139 kn;5号推进器在160 s时实际推力与期望推力相吻合,最后稳定在51 kn处。表明该推力分配方法具有良好的实时性,使推进系统能快速地响应并执行期望推力指令。从各推进器的期望推力最大值来看,1号、2号、4号、5号推进器对应期望推力最大值分别为253.7、247、296.5、161.3 kn,均被有超出其推力范围,表明对控制变量的归一化处理能有效解决推进器推力饱和问题。
图 7中(e)和(f)反映了4号和5号全回转推进器的回转角变化趋势,其中实际回转角与期望回转角基本相重合。4号推进器的回转方位角稳定在21.6°,5号推进器的回转方位角稳定在93.5°处。全回转推进器的回转方位角都在其回转域内,表明该算法有效的解决了推进器回转禁止域的问题。
5 结论1) 根据过驱动动力定位船总体结构中推进器的空间分布关系,推导出推进器输出推力和作用到船体上推力合力及合力矩之间的关系,进而建立过驱动动力定位船推进系统的数学模型,仿真结果证明了本文所建立模型的准确性,为船舶的运动控制和推力分配方法的研究奠定基础。
2) 在对过驱动动力定位船进行推力分配时,先将水平面控制电压进行归一化处理,再分别按照权重进行放大,然后进行推力分配,可有效解决推进器的饱和输出问题。
3) 针对考虑推进器回转禁止域的推力分配问题,提出了一种将直接分配与伪逆算法相结合的分配方法。通过仿真分析表明该方法能够有效解决推进器回转禁止角约束问题。同时,由于直接分配和伪逆分配具有算法简单和计算效率高等特点,使得结合后的分配方法具有良好的实时性,能够满足实际动力定位船舶的定位要求。
综合以上的特点该推力分配方法可以应用于动力定位船舶和水下机器人等海洋工程装备上,具有较强的工程应用价值。
| [1] |
魏玉石.船舶动力定位系统推力估计与推力分配研究[D].哈尔滨: 哈尔滨工程大学, 2013: 1-13. WEI Yushi. Research on thrust estimation and thrust allocation for dynamic positioning system of ships[D]. Harbin: Harbin Engineering University, 2013: 1-13. http://cdmd.cnki.com.cn/Article/CDMD-10217-1017241165.htm (  0) 0)
|
| [2] |
边信黔, 付明玉, 王元慧. 船舶动力定位[M]. 北京: 科学出版社, 2011: 1-7. BIAN Xinqian, FU Mingyu, WANG Yuanhui. Ship dynamic positioning[M]. Beijing: Science Press, 2011: 1-7. (  0) 0)
|
| [3] |
SØRDALEN O J. Optimal thrust allocation for marine vessels[J]. Control engineering practice, 1997, 5(9): 1223-1231. DOI:10.1016/S0967-0661(97)84361-4 (  0) 0)
|
| [4] |
BERGE S P. Robust control allocation of actuated ships. Experiments with a model ship[N]. Trondheim, Norway: Norwegian University of Science and Technology, Department of Engineering Cybernetics, 1996.
(  0) 0)
|
| [5] |
WICHERS J, BULTEMA S, MATTEN R. Hydrodynamic research on and optimizing dynamic positioning system of a deep water drilling vessel[C]//Offshore Technology Conference. Houston, Texas, 1998.
(  0) 0)
|
| [6] |
WEBSTER W C, SOUSA J. Optimum allocation for multiple thrusters[C]//Proceedings of the 9th International Offshore and Polar Engineering Conference. Brest, France, 1999: 201-381.
(  0) 0)
|
| [7] |
JOHANSEN T A, FOSSEN T I. Control allocation-a survey[J]. Automatica, 2013, 49(5): 1087-1103. DOI:10.1016/j.automatica.2013.01.035 (  0) 0)
|
| [8] |
吴德烽, 杨国豪. 船舶动力定位关键技术研究综述[J]. 舰船科学技术, 2014, 36(7): 1-6. WU Defeng, YANG Guohao. Review on key techniques for ship dynamic positioning system[J]. Ship science and technology, 2014, 36(7): 1-6. DOI:10.3404/j.issn.1672-7649.2014.07.001 (  0) 0)
|
| [9] |
黄炜.基于改进人工鱼群算法的动力定位系统推力分配研究[D].哈尔滨: 哈尔滨工程大学, 2016. HUANG Wei. Research on thrust allocation of dynamic positioning system based on improved artificial fish swarm algorithm[D]. Harbin: Harbin Engineering University, 2016. (  0) 0)
|
| [10] |
刘明, 华亮, 周俊, 等. 动力定位船舶伪逆法与混沌粒子群法相融合的推力分配算法研究[J]. 海洋工程, 2016, 34(4): 100-106. LIU Ming, HUA Liang, ZHOU Jun, et al. Research on dynamic positioning thrust allocation algorithm based on pseudo inverse method and CPSO algorithm[J]. The ocean engineering, 2016, 34(4): 100-106. (  0) 0)
|
| [11] |
付海军, 徐海祥, 冯辉.基于自适应遗传算法的加权伪逆推力分配策略及仿真[C]//聚焦应用支撑创新——船舶力学学术委员会测试技术学组2016年学术会议论文集.武汉, 2016: 8. FU Haijun, XU Haixiang, FENG Hui. Strategy and simulation of weighted pseudo-inverse based on adaptive genetic algorithm for thrust allocation[C]//Focus on Application Support Innovation——Testing Technology Group of Academic Committee of Ship Mechanics 2016 Proceedings of the Conference. Wuhan, 2016: 8. (  0) 0)
|
| [12] |
FOSSEN T I. Handbook of marine craft hydrodynamics and motion control[M]. New York: John Wiley & Sons Ltd, 2011: 1-10.
(  0) 0)
|
| [13] |
李想. DP船推进系统水动力干扰及推力分配方法研究[D].哈尔滨: 哈尔滨工程大学, 2017. LI Xiang. Research on hydrodynamic interference of propulsion system and thrust allocation of DP ship[D]. Harbin: Harbin Engineering University, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10217-1018288649.htm (  0) 0)
|
| [14] |
李新飞, 马强, 袁利毫, 等. 矢量推进水下机器人的推力分配方法[J]. 哈尔滨工程大学学报, 2018, 39(10): 1605-1611. LI Xinfei, MA Qiang, YUAN Lihao, et al. Thrust allocation method of underwater robots with vector propelling system[J]. Journal of Harbin Engineering University, 2018, 39(10): 1605-1611. (  0) 0)
|
| [15] |
郭峰.铺管起重船动力定位系统推力分配方法研究[D].哈尔滨: 哈尔滨工程大学, 2012. GUO Feng. Research on the control allocation of pipe laying crane dynamic positioning system[D]. Harbin: Harbin Engineering University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10217-1012516795.htm (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


