2. 西安建筑科技大学 土木工程学院, 陕西 西安 710055
2. School of Civil Engineering, Xi'an University of Architecture & Technology, Xi'an 710055, China
钢筋混凝土剪力墙以其较大的抗侧移刚度,较好的抗震性能而广泛应用于高层建筑结构。然而,根据现行规范设计和建造的钢筋混凝土剪力墙结构,尽管经受了地震的考验,保护了人民的生命安全,但在强震作用下会经历较大的非弹性形变,其非弹性性能在一定程度上难以预测和控制,从而导致严重的直接和间接经济损失。
长期以来,国内外抗震设计规范都是以承载力控制结构的性能,即基于力的抗震设计。然而近年来世界各地的强震经验表明,这种理论在保证人的生命安全方面确实具有一定的可靠性,但对结构变形导致的损伤以及由此导致的经济损失却不能进行有效控制。鉴于此,20世纪90年代由美国学者提出了基于性能(performance based seismic design)的地震工程设计方法。基于性能的抗震设计通常采用变形或位移作为衡量建筑结构性能和损伤的指标,并把控制建筑结构在地震中的变形作为抗震设计追求的基本目标。因此,在高层建筑结构中,作为第1道抗震防线的剪力墙,其变形能力的确定就十分重要。文献[1-3]介绍了剪力墙构件变形指标计算方法,这些方法的总体思路是:首先根据力的平衡方程求出剪力墙截面受压区高度,或者相对受压区高度,然后利用几何关系或者回归方法求得剪力墙构件的截面曲率,最后求出所需要的剪力墙边缘构件配箍特征值和约束边缘构件长度。而我国现行《高层建筑混凝土结构技术规程》[4]中对结构不同性能水准有不同的变形能力要求,文献[5]对塑性铰区采用纤维增强混凝土剪力墙进行了试验研究,并推导了剪力墙构件在水平力作用下侧移计算公式。
尽管一些学者[1-3, 6-11]已经建立了剪力墙的非弹性形变或位移计算经验公式,但是这些公式大多只适用于与试验剪力墙特性完全匹配的剪力墙构件。因此,有必要建立一种能够合理地描述剪力墙非弹性形变的分析模型。本文基于竖向悬臂梁纵向伸长量计算的桁架模型,建立了中高墙、高墙带端柱I形截面剪力墙的峰值位移计算模型和计算公式。
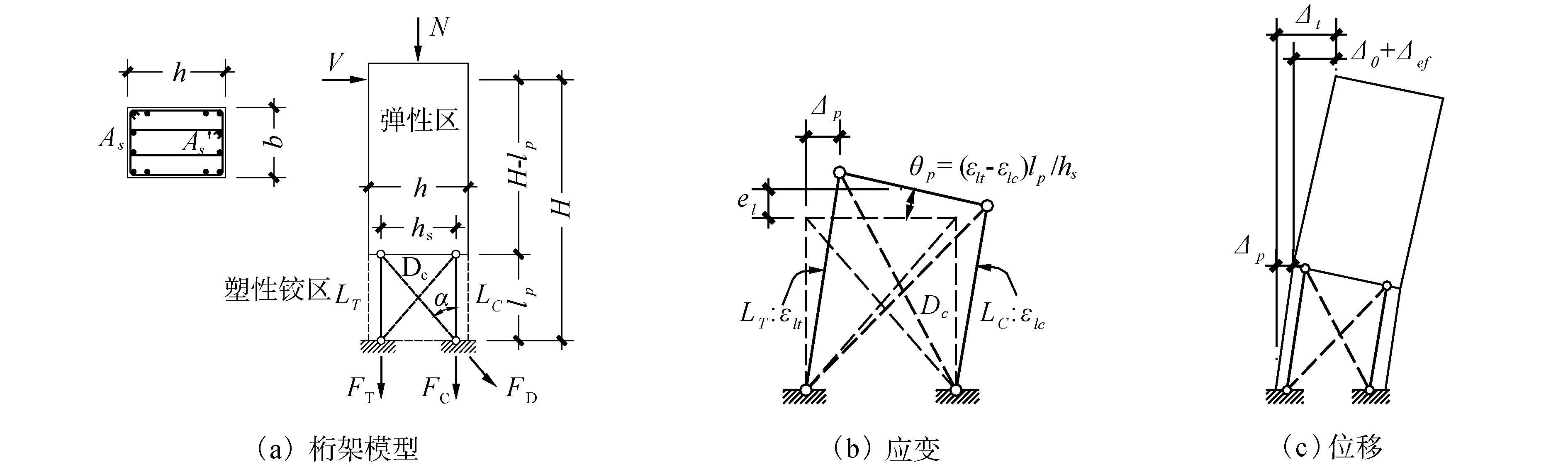
1 竖向悬臂梁纵向伸长量计算桁架模型为了建立竖向悬臂梁纵向伸长量与侧移之间的相关关系,同时为了考虑不同设计参数的影响,将竖向悬臂梁的塑性铰理想化为桁架模型(如图 1(a))。该桁架模型包含混凝土斜压杆DC,纵向受拉钢筋构件LT和纵向受压钢筋构件LC。构件的纵向伸长定义为纵向钢筋构件LT和LC的平均值。考虑位移协调性、力的平衡条件和这些构件的本构关系,推导构件的纵向伸长量。
|
Download:
|
| 图 1 竖向悬臂梁纵向伸长量计算 Fig. 1 Longitudinal elongation calculation of vertical cantilever beam | |
定义构件侧移以及塑性铰区桁架杆件的应变如图 1(b)所示。构件顶点侧移Δt定义为:
| $ \Delta_{t}=\Delta_{p}+\Delta_{\theta}+\Delta_{e f} $ | (1) |
式中:Δp为构件塑性铰区的侧移;Δθ为弹性区刚体转动引起的侧移;Δef为构件弹性区弯曲变形引起的侧移;Δp包含弯曲变形和剪切变形。
由于DC的压应变远小于另一方向斜拉杆的拉应变[12],故忽略其压应变。因此,在如图 1(b)所示模型中有:
| $ -\Delta_{p} \sin \alpha+\varepsilon_{l t} l_{p} \cos \alpha \approx 0 $ | (2) |
式中:εlt为LT的应变;lp为塑性铰的长度≈h0[13-14];h0为截面有效高度;α为DC与纵轴的夹角。
由纵筋应变定义塑性铰区的纵向伸长el为:
| $ e_{l}=\left(\varepsilon_{l t}+\varepsilon_{l c}\right) l_{p} / 2 $ | (3) |
式中εlc为LC的应变。根据式(2)和(3),则:
| $ \Delta_{p}=\varepsilon_{l t} l_{p} \cot \alpha=\left(2 e_{l}-\varepsilon_{l c} l_{p}\right) l_{p} / h_{s} $ | (4) |
式中hs为纵向钢筋构件LT和LC的间距。
| $ \Delta_{\theta}=\theta_{p}\left(H-l_{p}\right)=\left(\varepsilon_{u}-\varepsilon_{l c}\right) l_{p}\left(H-l_{p}\right) / h_{s} $ |
式中:H为悬臂梁的剪跨;θp为塑性铰的转角。用式(3)消掉εlt:
| $ \Delta_{\theta}=2\left(e_{l}-\varepsilon_{l c} l_{p}\right)\left(H-l_{p}\right) / h_{s} $ | (5) |
由式(1)、(4)和(5),定义el为构件顶点侧移:
| $ e_{l}=\frac{\left(\Delta_{t}-\Delta_{e f}\right) h_{s}}{2 H}+\varepsilon_{l c} l_{p}\left(1-\frac{l_{p}}{2 H}\right) $ | (6) |
Δef可采用Δef=ϕy(H-lp)2/3计算。根据Priestley[15],梁截面的屈服曲率近似估计为ϕy=1.7εyield/h,式中εyield为纵筋的屈服应变,h为梁截面高度。由式(6)可知,el为Δt和εlc的函数。
1.2 力的平衡条件由图 1(a)可得出塑性铰区的力平衡条件为:
| $ \left\{\begin{array}{l}{F_{D} \sin \alpha+V=0} \\ {F_{D} \cos \alpha+F_{C}+F_{T}+N=0} \\ {V H-N h_{s} / 2=F_{T} h_{s}}\end{array}\right. $ |
式中:FT、FC和FD分别为LT、LC和DC的内力;N为构件上的轴力(压力为正,拉力为负)。则
| $ \left\{ \begin{array}{l} {F_C} = - {F_T}\left( {1 - \frac{{{h_s}\cot \alpha }}{H}} \right) - N\left( {1 - \frac{{{h_s}\cot \alpha }}{{2H}}} \right) = \\ - {F_T}\left( {1 - \frac{{{l_p}}}{H}} \right) - N\left( {1 - \frac{{{l_p}}}{{2H}}} \right)\\ {\sigma _{lc}} = - {\sigma _{lt}}\left( {\frac{{{A_s}}}{{{{A'}_s}}}} \right)\left( {1 - \frac{{{l_p}}}{H}} \right) - \frac{N}{{{{A'}_s}}}\left( {1 - \frac{{{l_p}}}{{2H}}} \right) \approx \\ - {f_y}\left( {\frac{{{A_s}}}{{{{A'}_s}}}} \right)\left( {1 - \frac{{{l_p}}}{H}} \right) - \frac{N}{{{{A'}_s}}}\left( {1 - \frac{{{l_p}}}{{2H}}} \right) \end{array} \right. $ | (7) |
式中:σlt(=FT/As),σlc(=FC/A′s)分别为LT和LC的应力;As和A′s分别为LT和LC的面积(图 1(a));fy为纵向钢筋的屈服强度。
1.3 钢筋的本构关系图 2给出了LC的滞回应力-应变关系。为了计算方便,考虑Bauschinger效应的卸载再加载应力-应变关系,采用三折线曲线加以简化(见图 2)。

|
Download:
|
| 图 2 钢筋应力-应变关系 Fig. 2 Stress-strain relationship of steel bars | |
在该简化曲线中,相应于σlc的εlc可计算为:
| $ \varepsilon_{l c}=\varepsilon_{1}-\varepsilon_{\text { yield }}-\left(-\eta \frac{\sigma_{l c}}{f_{y}}\right) \varepsilon_{1}=\varepsilon_{1}\left(1+\eta \frac{\sigma_{l c}}{f_{y}}\right)-\varepsilon_{\text { yield }} $ | (8) |
式中:η为考虑Bauschinger效应的系数;ε1为LC在前一次加载循环中的最大拉应变。近似假定η=0.6。若式(7)计算的σlc < -fy,则混凝土的压力需满足截面纵向拉力和压力的平衡条件,因此纵向受压钢筋构件的受拉塑性应变减小到0。由此,若式(7)中的σlc < -fy,则εlc则可假定为0。
1.4 构件纵向伸长的分步求解在考虑加载历史的条件下,该方法需要逐步求解计算,如图 3。由式(7)和(8)计算LC的σlc和εlc,然后由式(6)计算el。一旦el确定,则可由式(3)计算LT的拉应变εlt。在下一次加载循环中,荷载反向加载。根据构件的内力符号,纵向钢筋构件可重新指定为LT和LC。同样地,采用前一次加载循环中的方法可计算出这次加载循环下的el。

|
Download:
|
| 图 3 构件纵向伸长分步计算的流程 Fig. 3 Flow chart of the stepwise calculation of the longitudinal elongation of the component | |
对于对称配筋(As=A′s)的构件,在第n次加载循环下el以及LT和LC的应变可指定为el(n)、εlt(n)和εlc(n)。根据式(2),则el(n)可定义为:
| $ e_{l(n)}=\frac{\left(\Delta_{t}-\Delta_{e f}\right) h_{s}}{2 H}+\varepsilon_{l c(n)} l_{p}\left(1-\frac{l_{p}}{2 H}\right) $ | (9) |
由式(3)和(9),εlt(n)定义为el(n)的函数,即:
| $ \varepsilon_{l t(n)}=\frac{2\left(H-l_{p}\right)}{l_{p}\left(2 H-l_{p}\right)} e_{l(n)}+\frac{\left(\Delta_{t}-\Delta_{e f}\right) h_{s}}{l_{p}\left(2 H-l_{p}\right)} $ | (10) |
对于第n+1次加载循环,当荷载反向时,el(n+1)和εlc(n+1)之间的关系可表述为:
| $ e_{l(n+1)}=\frac{\left(\Delta_{t}-\Delta_{e f}\right) h_{s}}{2 H}+\varepsilon_{l c(n+1)} l_{p}\left(1-\frac{l_{p}}{2 H}\right) $ | (11) |
根据式(7),εlc(n+1)可以由第n次加载循环下的应变εlt(n)来计算:
| $ \begin{array}{*{20}{c}} {{\varepsilon _{lc(n + 1)}} = {\varepsilon _1}\left( {1 + \eta \frac{{{\sigma _{lc}}}}{{{f_y}}}} \right) - {\varepsilon _{{\rm{yield}}}} = }\\ {{\varepsilon _{lt(n)}}\left( {1 + \eta \frac{{{\sigma _{lc}}}}{{{f_y}}}} \right) - {\varepsilon _{{\rm{ yield }}}}} \end{array} $ | (12) |
联合式(10)、(11)和(12),有:
| $ \begin{array}{*{20}{c}} {{e_{l(n + 1)}} = \left( {1 - \frac{{{l_p}}}{H}} \right)\left( {1 + \eta \frac{{{\sigma _{lc}}}}{{{f_y}}}} \right){e_{l(n)}} + }\\ {\frac{{\left( {{\Delta _t} - {\Delta _{ef}}} \right){h_s}}}{H}\left( {1 + \eta \frac{{{\sigma _{lc}}}}{{2{f_y}}}} \right) - {\varepsilon _y}{l_p}\left( {1 - \frac{{{l_p}}}{{2H}}} \right)} \end{array} $ | (13) |
式(1)为构件伸长数列的一般表达式。该数列可以求解为:
| $ e_{l(n)}=f\left(\Delta_{t}\right)+\beta^{n-1}\left[e_{l(1)}-f\left(\Delta_{t}\right)\right] $ | (14) |
| $ \left\{ \begin{array}{l} f\left( {{\Delta _t}} \right) = \frac{{\frac{{\left( {{\Delta _t} - {\Delta _{ef}}} \right){h_s}}}{H}\left( {1 + \eta \frac{{{\sigma _{lc}}}}{{2{f_y}}}} \right) - {\varepsilon _{{\rm{yield}}}}{l_p}\left( {1 - \frac{{{l_p}}}{{2H}}} \right)}}{{1 - \left( {1 - \frac{{{l_p}}}{H}} \right)\left( {1 + \eta \frac{{{\sigma _{lc}}}}{{{f_y}}}} \right)}}\\ \beta = \left( {1 - \frac{{{l_p}}}{H}} \right)\left( {1 + \eta \frac{{{\sigma _{lc}}}}{{{f_y}}}} \right)\\ {e_l} = \frac{{\frac{{\left( {{\Delta _t} - {\Delta _{ef}}} \right){h_s}}}{H}\left( {1 + \eta \frac{{{\sigma _{lc}}}}{{2{f_y}}}} \right) - {\varepsilon _{{\rm{yield}}}}{l_p}\left( {1 - \frac{{{l_p}}}{{2H}}} \right)}}{{1 - \left( {1 - \frac{{{l_p}}}{H}} \right)\left( {1 + \eta \frac{{{\sigma _{lc}}}}{{{f_y}}}} \right)}} \end{array} \right. $ |
构件的纵向伸长应变定义为:
| $ \varepsilon_{l}=e_{l} / l_{p} $ |
那么
| $ {\varepsilon _l} = \frac{{\frac{{\left( {{\Delta _t} - {\Delta _{ef}}} \right){h_s}}}{{{l_p}H}}\left( {1 + \eta \frac{{{\sigma _{lc}}}}{{2{f_y}}}} \right) - {\varepsilon _{{\rm{yield}}}}\left( {1 - \frac{{{l_p}}}{{2H}}} \right)}}{{1 - \left( {1 - \frac{{{l_p}}}{H}} \right)\left( {1 + \eta \frac{{{\sigma _{lc}}}}{{{f_y}}}} \right)}} $ | (15) |
| $ {\varepsilon _l} = \frac{{\left( {{\Delta _t} - {\Delta _{ef}}} \right){h_s}}}{{2{l_p}H}}\;当\;{\sigma _{lc}} < - {f_y}\;或\;{\varepsilon _{lc}} = 0 $ | (16) |
钢筋混凝土剪力墙桁架模型的内力及荷载作用如图 4所示。

|
Download:
|
| 图 4 钢筋混凝土剪力墙桁架模型的内力及荷载作用 Fig. 4 Internal force and load of reinforced concrete shear wall truss model | |
剪力墙构件顶点侧移Δm为:
| $ \Delta_{m}=\Delta_{p}+\Delta_{\theta}+\Delta_{e f}+\Delta_{e s} $ |
式中:Δes为构件弹性区剪切变形引起的侧移,有:
| $ \Delta_{e s}=\mu V H / G A $ |
式中:H为剪力墙的高度;G为混凝土的剪切模量,取G=0.4E;μ为剪应力分布不均匀系数。
由此,式(15)和(16)可改写为:
| $ {\varepsilon _l} = \frac{{\frac{{\left( {{\Delta _m} - {\Delta _{ef}} - {\Delta _{es}}} \right){h_s}}}{{{l_p}H}}\left( {1 + \eta \frac{{{\sigma _{lc}}}}{{2{f_y}}}} \right) - {\varepsilon _{{\rm{yield}}}}\left( {1 - \frac{{{l_p}}}{{2H}}} \right)}}{{1 - \left( {1 - \frac{{{l_p}}}{H}} \right)\left( {1 + \eta \frac{{{\sigma _{lc}}}}{{{f_y}}}} \right)}} $ | (17) |
| $ {\varepsilon _l} = \frac{{\left( {{\Delta _t} - {\Delta _{ef}} - {\Delta _{es}}} \right){h_s}}}{{2{l_p}H}},{\sigma _{lc}} < - {f_y}\;或\;{\varepsilon _{lc}} = 0 $ | (18) |
由图 4得出剪力墙构件的内力须满足平衡条件:
| $ F_{D} \cos \alpha+F_{C}+F_{T}+F_{W}+N=0 $ |
| $ F_{D} \sin \alpha+V=0 $ |
| $ V H-\frac{N h_{s}}{2}=F_{T} h_{s}+F_{W}\left(\frac{h_{s}}{2}\right) $ |
式中:FW为剪力墙腹板钢筋构件LW的内力。有:
| $ F_{C}=-F_{T}\left(1-\frac{l_{p}}{H}\right)-\left(F_{W}+N\right)\left(1-\frac{l_{p}}{2 H}\right) $ |
拉力FW全部由腹板竖向钢筋承担。
| $ \begin{array}{*{20}{c}} {{\sigma _{lc}} = - {\sigma _{lt}}\left( {\frac{{{A_s}}}{{{{A'}_s}}}} \right)\left( {1 - \frac{{{l_p}}}{H}} \right) - \left( {{\sigma _{lw}}\frac{{{A_w}}}{{{{A'}_s}}} + \frac{N}{{{{A'}_s}}}} \right)\left( {1 - \frac{{{l_p}}}{H}} \right) \approx }\\ { - {f_y}\left( {\frac{{{A_s}}}{{{{A'}_s}}}} \right)\left( {1 - \frac{{{l_p}}}{H}} \right) - \left( {{f_{yw}}\frac{{{A_w}}}{{{{A'}_s}}} + \frac{N}{{{{A'}_s}}}} \right)\left( {1 - \frac{{{l_p}}}{H}} \right)} \end{array} $ | (19) |
式中:σlw=(FW/AW)为剪力墙腹板竖向钢筋构件的应力;AW为剪力墙腹板竖向钢筋的面积;fyw为腹板竖向钢筋的屈服强度。
剪力墙纵向伸长计算如图 5所示。

|
Download:
|
| 图 5 剪力墙纵向伸长计算 Fig. 5 Longitudinal elongation calculation of wall | |
图 5(a)给出了I形截面剪力墙构件的桁架模型。该桁架模型包含纵向构件LT、LC和LW,斜向受压构件DC,以及横向构件T。混凝土斜压杆的截面面积可由混凝土截面的受压区高度以及塑性铰的长度来确定[16]。
| $ {A_{Dc}} = {h_d}{b_w} = \left( {3{l_p} + 2{l_c}} \right){b_w}\sin \alpha /4 $ |
| $ l_{c}=\frac{\left(x_{c}-\alpha_{s}^{\prime}\right) l_{p}}{2\left(h_{s}-x_{c}+\alpha_{s}^{\prime}\right)} \geqslant 0 $ |
式中:ADc为混凝土斜压杆的截面面积;bw为剪力墙的厚度;xc为混凝土截面的受压区高度;α′s为截面受压边缘至纵向受压钢筋构件的距离。
图 5(b)给出了塑性铰区桁架杆件的内力和应变。Vecchio等[17]的研究表明,混凝土斜压杆的有效抗压强度fce随主拉应变εt的增大而减小(如图 6)。因此,在混凝土截面边缘压碎时,混凝土斜压杆DC的受力FD可表示为垂直于斜压杆的主拉应变εt的函数。

|
Download:
|
| 图 6 有效抗压强度fce-主拉应变εt相关关系 Fig. 6 Effective compressive strength fce-primary tensile strain εt correlation | |
| $ F_{D}=-f_{c e} A_{D c}=-\frac{f_{c} A_{D c}}{0.8+0.34\left(\varepsilon_{t} / \varepsilon_{c o}\right)} \geqslant-f_{c} A_{D_{c}} $ | (20) |
式中:fce为混凝土斜压杆的有效抗压强度;fc为混凝土的抗压强度;εco为混凝土的峰值应变(0.002+0.001×(fck-20)/80)[18];εt为垂直于斜压杆的主拉应变。
当混凝土截面边缘压碎时,剪力墙的最大受剪承载力为:
| $ {V_{wc}} = \frac{{{f_{ce}}{A_{Dc}}\sin \alpha }}{{0.8 + 0.34\left( {{\varepsilon _t}/{\varepsilon _{co}}} \right)}} \le {f_c}{A_{Dc}}\sin \alpha $ | (21) |
从式(21)可以看出,随着主拉应变εt的增大,剪力墙的受剪承载力减小。εt可以采用剪力墙的纵向伸长应变εl来确定。
图 5给出了塑性铰区桁架杆件的应变分布,假设其平均应变满足条件:
| $ \varepsilon_{x}=\varepsilon_{v} / 2, \varepsilon_{y}=\left(\varepsilon_{l t}+\varepsilon_{l c}\right) / 2 $ |
式中:εx、εy为作用于x-y平面的正应变;εv为横向构件T的拉应变。
根据Oesterle[19]和Wood[20]的研究,εv≈εvy,εvy为水平钢筋的屈服强度。这样,εx、εy可以改写为:
| $ \varepsilon_{x}=\varepsilon_{v y} / 2, \varepsilon_{y}=\varepsilon_{l} $ | (22) |
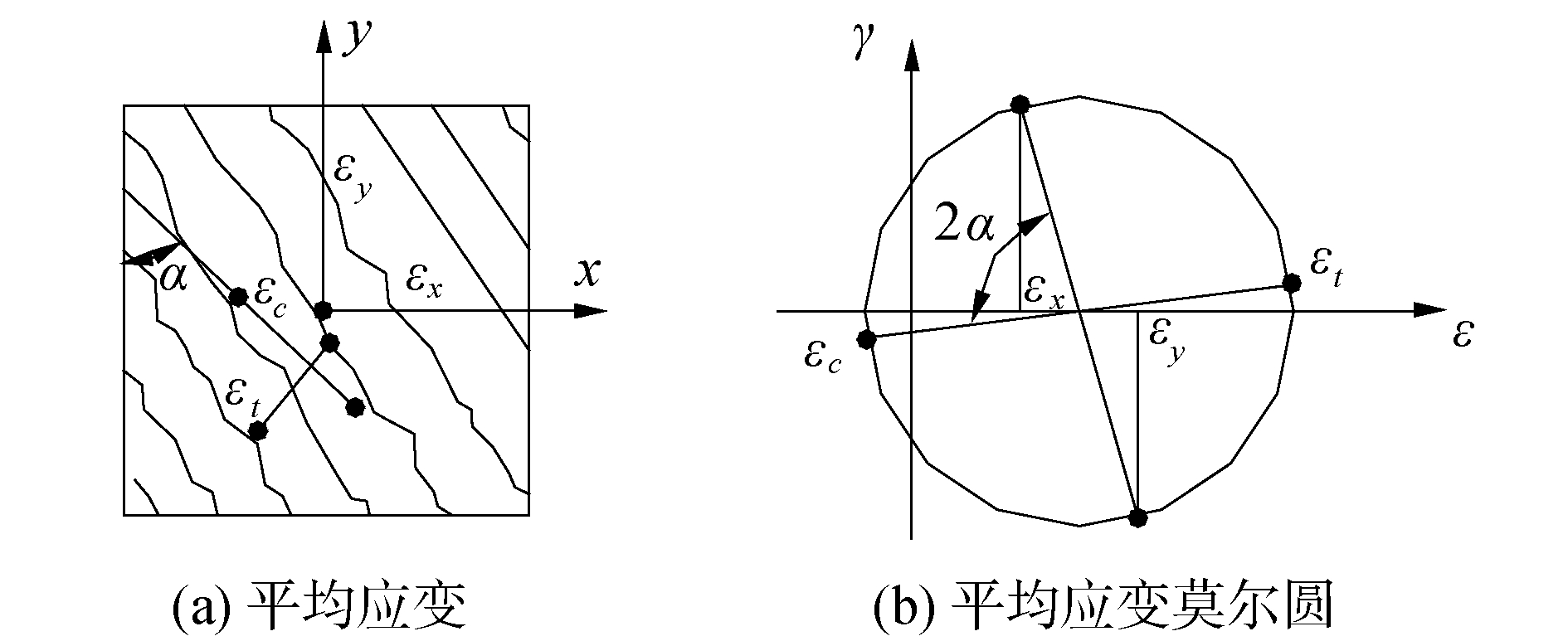
根据图 7所示的应变莫尔圆以及材料的第一应变不变量可以给出关系为:
|
Download:
|
| 图 7 开裂混凝土平均应变及平均应变莫尔圆 Fig. 7 Average strain and average strain of cracked concrete | |
| $ \boldsymbol{\varepsilon}_{x}+\boldsymbol{\varepsilon}_{y}=\boldsymbol{\varepsilon}_{t}+\boldsymbol{\varepsilon}_{c} $ | (23) |
式中:εc、εt为混凝土斜压杆的压应变和拉应变(图 5)。
将式(22)代入式(23)可得:
| $ \varepsilon_{t}=\varepsilon_{l}+\varepsilon_{v y} / 2-\varepsilon_{c} $ |
当剪力墙截面受压区边缘混凝土压应变达到极限压应变而发生破坏时,εc=-εco。水平钢筋的屈服应变近似取为0.002。则εt简化为:
| $ \varepsilon_{t} \approx \varepsilon_{l}+3 \varepsilon_{c o} / 2 $ | (24) |
由式(21)和(24)得剪力墙的受剪承载力为:
| $ {V_{wc}} = \frac{{{f_c}{A_{Dc}}\sin \alpha }}{{1.31 + 0.34\left( {{\varepsilon _l}/{\varepsilon _{co}}} \right)}} \le {f_c}{A_{Dc}}\sin \alpha $ | (25) |
由上述推导,当剪力墙达到极限承载力时,存在关系:
| $ \frac{{{f_{ck}}{A_{Dc}}\sin \alpha }}{{1.31 + 0.34\left( {{\varepsilon _l}/{\varepsilon _{co}}} \right)}} = {F_m} $ | (26) |
式中Fm为剪力墙的峰值荷载。
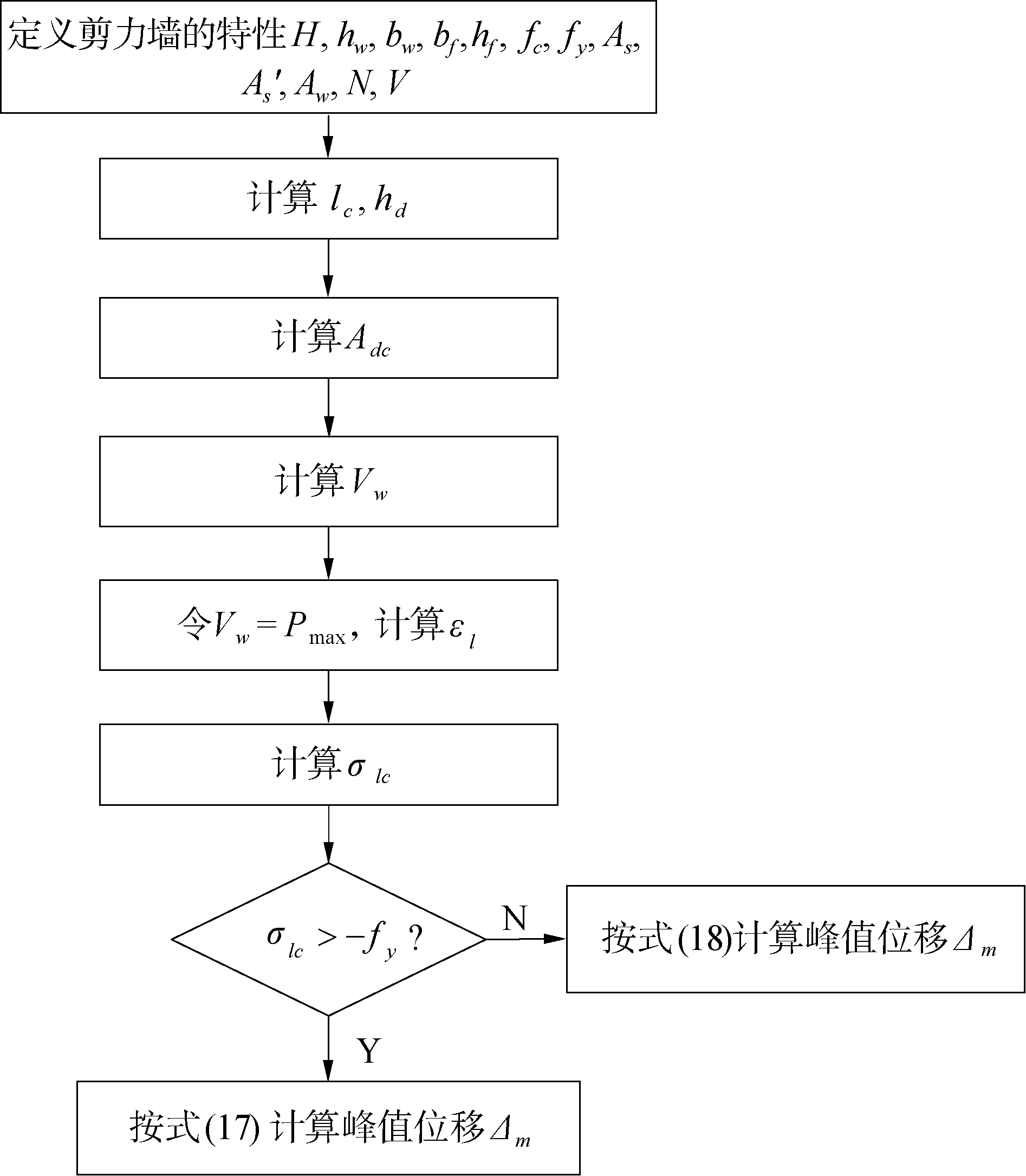
钢筋混凝土剪力墙峰值位移的计算流程如图 8所示。
|
Download:
|
| 图 8 钢筋混凝土剪力墙峰值位移的计算流程 Fig. 8 Calculation process of peak displacement of reinforced concrete shear wall | |
本文收集的钢筋混凝土剪力墙试验数据只包含带端柱的I形截面剪力墙,且以发生弯曲破坏为主的剪力墙。I形截面剪力墙数据库试验测得的峰值包含34片不同尺寸的剪力墙试件。这34片剪力墙的试验数据分别来自文献[21-27]关于试验的构件截面尺寸、混凝土强度、荷载等数据可参见以上文献。弯曲破坏I形截面剪力墙试验数据见表 1。
| 表 1 弯曲破坏I形截面剪力墙试验数据及计算峰值位移 Table 1 Test data of curved fracture I-section shear wall and calculation of peak displacement |
从表 1可以看出,试验数据库中剪力墙的高宽比为1.4~3.0。其中梁兴文的4片剪力墙均为高强混凝土剪力墙,其余的皆为普通混凝土剪力墙。表 1给出了34片带端柱I形截面剪力墙的峰值位移试验值,由式(28)和(29)得到的计算值。峰值位移试验值与计算值之比大致在1.83~0.50,平均值为1.20。对于Rothe试件和Huang试件,式(17)和(18)低估了剪力墙的峰值位移。从表 1还可以看出,计算值与试验值相差20%以内的有15组,计算值与试验值相差30%以内的有20组。可见,采用本文所提公式计算的峰值位移与试验值基本吻合,基本验证了本文所提方法的有效性。
4 结论1) 与文献[1-3]介绍的剪力墙构件变形指标计算方法相比该模型只要给定剪力墙的截面设计信息、剪力墙的高度以及轴力和剪力就可以直接求解得到与该剪力对应的峰值位移。无需再计算受压区高度或相对受压区高度。
2) 采用本文提出的方法,对收集的34片I形截面剪力墙的峰值位移进行了计算,计算值与试验值相差20%以内的有15组,计算值与试验值相差30%以内的有20组,基本验证了本文所提方法的有效性。
3) 本文所建立模型是基于单片剪力墙,且塑性铰区部位是规则的,可对塑性铰部位不规则的剪力墙做进一步研究。
| [1] |
钱稼茹, 徐福江. 钢筋混凝土剪力墙基于位移的变形能力设计方法[J]. 清华大学学报(自然科学版), 2007, 43(3): 305-308. QIAN Jiaru, XU Fujiang. Displacement-based deformation capacity design method of RC cantilever walls[J]. Journal of Tsinghua University (science and technology), 2007, 43(3): 305-308. DOI:10.3321/j.issn:1000-0054.2007.03.002 (  0) 0)
|
| [2] |
钱稼茹, 吕文, 方鄂华. 基于位移延性的剪力墙抗震设计[J]. 建筑结构学报, 1999, 20(3): 42-49. QIAN Jiaru, LYU Wen, FANG Ehua. Displacement ductility-based aseismic design for shear walls[J]. Journal of building structures, 1999, 20(3): 42-49. (  0) 0)
|
| [3] |
马恺泽, 梁兴文.基于性能的高性能混凝土剪力墙变形能力分析研究[C]//第七届全国土木工程研究生学术论坛论文集.南京, 2009: 1-6. MA Kaize, LIANG Xingwen. Nonlinear finite element analysis on high performance concrete structural walls[C]//The 7th National Civil Engineering Forum for Graduate Students (NCFEGS). Nanjing, 2009: 1-6. (  0) 0)
|
| [4] |
中华人民共和国住房和城乡建设部. JGJ 3-2010, 高层建筑混凝土结构技术规程[S].北京: 中国建筑工业出版社, 2011. Ministry of Housing and Urban-Rural Development of the People's Republic of China. JGJ 3-2010, Technical Specification for concrete structures of tall building[S]. Beijing: China Architecture & Building Press, 2011. (  0) 0)
|
| [5] |
梁兴文, 郑雨, 邓明科, 等. 塑性铰区采用纤维增强混凝土剪力墙的变形性能研究[J]. 工程力学, 2013, 30(3): 256-262. LIANG Xingwen, ZHENG Yu, DENG Mingke, et al. An investigation of deformation behavior of the shear wall with fiber-reinforced concrete in plastic hinge region[J]. Engineering mechanics, 2013, 30(3): 256-262. (  0) 0)
|
| [6] |
TAKAHASHI S, YOSHIDA K, ICHINOSE T, et al. Flexural drift capacity of reinforced concrete wall with limited confinement[J]. ACI structural journal, 2013, 110(1): 95-104. (  0) 0)
|
| [7] |
EOM T S, PARK H G, KIM J Y. Evaluation of deformation capacity of slender reinforced concrete walls with thin web[J]. Journal of the Korea concrete institute, 2010, 22(1): 59-68. (  0) 0)
|
| [8] |
KANG S M, KIM J Y. Evaluation of deformation capacity including yield deformation in displacement-based design of special RC shear wall[J]. The structural design of tall and special buildings, 2014, 23(3): 181-209. (  0) 0)
|
| [9] |
GRAMMATIKOU S, BISKINIS D, FARDIS M N. Strength, deformation capacity and failure modes of RC walls under cyclic loading[J]. Bulletin of earthquake engineering, 2015, 13(11): 3277-3300. (  0) 0)
|
| [10] |
黄志华, 吕西林, 周颖. 钢筋混凝土剪力墙的变形能力及基于性能的抗震设计[J]. 地震工程与工程振动, 2009, 29(5): 86-91. HUANG Zhihua, LYU Xilin, ZHOU Ying. Deformation capacity and performance-based seismic design for reinforced concrete shear walls[J]. Earthquake engineering and engineering vibration, 2009, 29(5): 86-91. (  0) 0)
|
| [11] |
剡理祯.剪力墙截面变形能力计算方法研究[D].西安: 西安建筑科技大学, 2014. YAN Lizhen. Research on calculation method of deformation capacity of shear wall[D]. Xi'an: Xi'an University of Architecture and Technology, 2014. (  0) 0)
|
| [12] |
EOM T S, PARK H G. Elongation of reinforced concrete members subjected to cyclic loading[J]. Journal of structural engineering, 2010, 136(9): 1044-1054. (  0) 0)
|
| [13] |
LEE J Y, WATANABE F. Shear deterioration of reinforced concrete beams subjected to reversed cyclic loading[J]. ACI structural journal, 2003, 100(4): 480-489. (  0) 0)
|
| [14] |
LEE J Y, WATANABE F. Predicting the longitudinal axial strain in the plastic hinge regions of reinforced concrete beams subjected to reversed cyclic loading[J]. Engineering structures, 2003, 25(7): 927-939. (  0) 0)
|
| [15] |
PRIESTLEY MJN. Performance based seismic design[C]//Proceedings of the 12th World Conference on Earthquake Engineering. Auckland, New Zealand, 2000.
(  0) 0)
|
| [16] |
PARK H, EOM T. Truss model for nonlinear analysis of RC members subject to cyclic loading[J]. Journal of structural engineering, 2007, 133(10): 1351-1363. (  0) 0)
|
| [17] |
VECCHIO F J, COLLINS M P. The modified compression-field theory for reinforced concrete elements subjected to shear[J]. ACI structural journal, 1986, 83(2): 219-231. (  0) 0)
|
| [18] |
FOSTER S J, GILBERT R I. The design of nonflexural members with normal and high-strength concretes[J]. ACI structural journal, 1996, 93(1): 3-10. (  0) 0)
|
| [19] |
OESTERLE R G, FIORATO A E, JOHAL L, et al. Earthquake resistant structural walls-tests of isolated walls[R]. Illinois: Illinois: Construction Technology Laboratories, Portland Cement Association, 1976.
(  0) 0)
|
| [20] |
WOOD S L. Minimum tensile reinforcement requirements in walls[J]. ACI structural journal, 1989, 86(5): 582-591. (  0) 0)
|
| [21] |
ROTHE D, KONIG G. Behavior and modeling of reinforced concrete structural wall elements[C]//Proceedings of 9WCEE. Tokyo-Kyoto, Japan, 1988.
(  0) 0)
|
| [22] |
HUANG C L, LI Y F, LIN C T, et al. Analytical and pushover analysis for predicting nonlinear force-displacement relationships of slender RC walls[J]. Journal of the Chinese institute of engineers, 2011, 34(3): 415-428. (  0) 0)
|
| [23] |
SITTIPUNT C, WOOD S L. Development of reinforcement details to improve the cyclic response of slender structural walls[C]//Proceedings of 12 WCEE. Auckland, New Zealand, 2000.
(  0) 0)
|
| [24] |
梁兴文, 杨鹏辉, 崔晓玲, 等. 带端柱高强混凝土剪力墙抗震性能试验研究[J]. 建筑结构学报, 2010, 31(1): 23-32. LIANG Xingwen, YANG Penghui, CUI Xiaoling, et al. Experimental studies on seismic behavior of high strength concrete shear wall with boundary columns[J]. Journal of building structures, 2010, 31(1): 23-32. (  0) 0)
|
| [25] |
龚治国, 吕西林, 姬守中. 不同边缘构件约束剪力墙抗震性能试验研究[J]. 结构工程师, 2006, 22(1): 56-61. GONG Zhiguo, LYU Xilin, JI Shouzhong. Experimental study on seismic behavior of R. C. shear walls with different boundary restraints[J]. Structural engineers, 2006, 22(1): 56-61. DOI:10.3969/j.issn.1005-0159.2006.01.013 (  0) 0)
|
| [26] |
祖亚丽.轻骨料混凝土剪力墙抗震性能的试验研究与有限元分析[D].天津: 河北工业大学, 2007. ZU Yali. Experiment study and finite element analysis on seismic behaviour of lightweight concrete shear-wall[D]. Tianjin: Hebei University of Technology, 2007. (  0) 0)
|
| [27] |
SHAINGCHIN S, LUKKUNAPRASIT P, WOOD S L. Influence of diagonal web reinforcement on cyclic behavior of structural walls[J]. Engineering structures, 2007, 29(4): 498-510. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


