2. 哈尔滨工程大学 自动化学院, 黑龙江 哈尔滨 150001
2. College of Automation, Harbin Engineering University, Harbin 150001, China
传递对准算法在机载武器、舰载机以及空间武器平台等系统中应用广泛[1-3]。传递对准算法利用精度较高的主惯导系统来校准未对准好的子惯导系统,算法设计的关键就是如何准确而快速地估计出失准角,包括静态安装、动态变形误差角等[4-5]。为了准确地估计出失准角,必然要求模型有一定的准确度,也就是说应尽量包含所有的状态量;但过多的状态变量,在有限的激励条件又不一定都能得到有效分离,即不一定都能有很好的估计效果[6]。传递对准理论研究比较成熟,但在实际工程应用中经常遇见理论与实际不符的情况。在某型车载武器系统中,车上装备高精度定位定向系统作为主惯导,发射武器中装有低精度惯导(受体积和成本的限制)作为子惯导,发射前一般采用传递对准方式,保证子惯导快速对准[1-2]。理想情况下,认为传递对准中的主、子惯导是刚性连接,两者存在一定的静态失准角。而实际上,由于安装杆臂较长(米级)及使用材料的特性,使得在传递对准机动过程中(比如发射架起竖时)主、子惯导之间产生额外的动、静态变形角,若无法对该变形角进行准确的建模、估计,造成传递对准结果严重失真,滤波器发散,导致任务失败[7]。比如,通常的传递对准方案中使用二阶马尔可夫过程来模拟这种挠曲变形角,这种情况下一般需反复调节马尔可夫过程的相关时间参数来达到一个满意效果,且时间参数调节方法也多依靠经验,没有具体的理论依据可循。而若无法对动态变形角进行正确的估计则会导致在机动期间产生的动态变形角被错误的估计至失准角内从而导致失准角估计精度下降。
通过对动力学和材料学进行研究可发现通过理论建模已经不合适实际情况,至少不适合大型车载武器系统。从而,尝试从实验的角度,采用应变片的方式,测量主、子惯导安装基座的变形角,用实际数据反推状态方程相关参数,以此建立起更接近真实情况的变形角模型,从而提高传递对准的准确性和试验成功的概率。
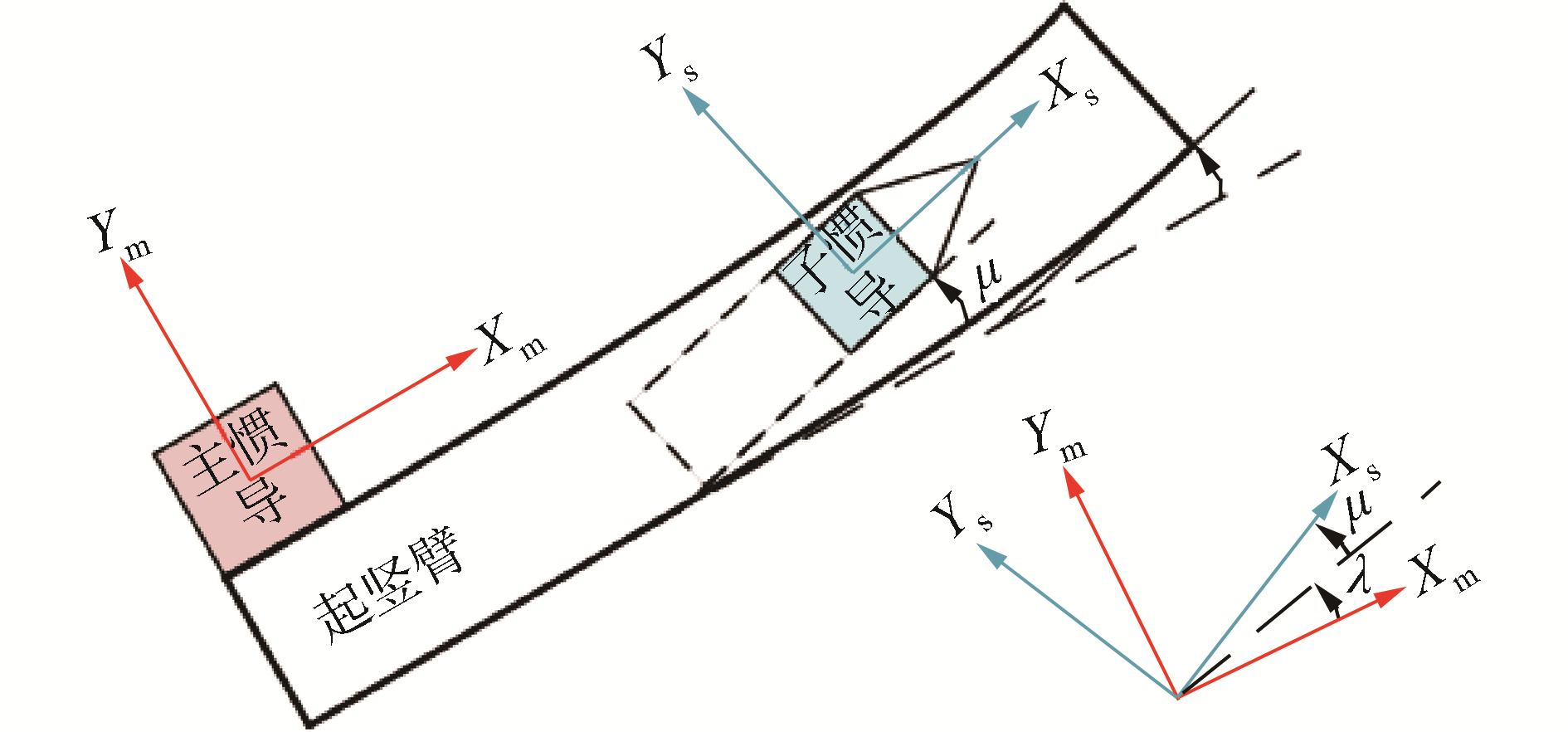
1 传递对准基础模型 1.1 传统的传递对准模型在传递对准要求较高的场合,除安装误差角外还需要考虑挠曲变形的影响。如图 1所示,载体变形可以分为2类:1)静态变形,由于其变化周期较长,通常认为在传递对准的相对较短的时间内,这个值变化很小,将其归入到安装误差角μ中;2)在传递对准过程中变化较快的挠曲变形角λ。通常传递对准根据匹配参数的不同可分为量测参数匹配法和计算参数匹配法[8]。由于量测参数匹配法对挠曲变形角过于敏感,在同等条件下精度一般要低于计算参数匹配法[9]。因此本文拟采用“速度+姿态”的计算参数匹配方法。
|
Download:
|
| 图 1 传递对准的2种变形角示意 Fig. 1 Two types deformation angles of transfer alignment | |
对于速度匹配传递对准,系统一般仅通过估计姿态误差角ϕ来计算子惯导姿态的最优估计值,不需要考虑变形角的影响[11]。对于姿态匹配传递对准中,系统通过估计安装误差角μ和挠曲变形角λ的值来计算子惯导的最优估计姿态。因此,在姿态匹配传递对准中,通常是先对挠曲变形角进行建模,然后根据建立的模型,把挠曲变形角作为状态量加入到传递对准的状态方程中,建立更精确的状态方程,再对其进行最优估计,以进一步消除误差[11-12]。
设定“速度+姿态”匹配传递对准的系统状态量为X=[ϕ, δV, ε, ∇, μ],其中ϕ为子惯导东向、北向和天向的平台失准角,δV为子惯导东向和北向的速度误差,ε为子惯导陀螺的常值漂移,∇为子惯导加速度计的常值偏置误差,μ为子惯导的安装误差角,则由姿态误差方程与速度误差方程可以得到系统的状态方程为[13]:
| $ \begin{gathered} \mathit{\boldsymbol{\dot X}} = \left[ {\begin{array}{*{20}{c}} { - \left( {\omega _{in}^n \times } \right)}&{{{\bf{0}}_{3 \times 3}}}&{ - \mathit{\boldsymbol{C}}_{bs}^n}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}} \\ {{\mathit{\boldsymbol{M}}_1}}&{{\mathit{\boldsymbol{M}}_2}}&{{{\bf{0}}_{3 \times 3}}}&{{\mathit{\boldsymbol{M}}_3}}&{{{\bf{0}}_{3 \times 3}}} \\ {{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}} \\ {{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}} \\ {{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}} \end{array}} \right]\mathit{\boldsymbol{X}} + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}} { - \mathit{\boldsymbol{C}}_{bs}^n\mathit{\boldsymbol{\varepsilon }}} \\ {{\mathit{\boldsymbol{M}}_3}\nabla } \\ {{{\bf{0}}_{3 \times 1}}} \\ {{{\bf{0}}_{3 \times 1}}} \\ {{{\bf{0}}_{3 \times 1}}} \end{array}} \right] = {\mathit{\boldsymbol{F}}_1}\mathit{\boldsymbol{X}} + {\mathit{\boldsymbol{W}}_1} \hfill \\ \end{gathered} $ | (1) |
式中:
| $\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_1} = \left[ {\begin{array}{*{20}{c}} 0&{{f_U}}&{{f_N}} \\ {{f_U}}&0&{ - {f_E}} \end{array}} \right];} \\ {{\mathit{\boldsymbol{M}}_2} = \left[ {\begin{array}{*{20}{c}} {\frac{{{V_N}\tan L - {V_U}}}{{{R_N} + h}}}&{2{\omega _{ie}}\sin L + \frac{{{V_E}}}{{{R_N} + h}}\tan L} \\ { - 2{\omega _{ie}}\sin L - \frac{{{V_E}}}{{{R_N} + h}}\tan L}&{\frac{{{V_U}}}{{{R_M} + h}}} \end{array}} \right];} \\ {{\mathit{\boldsymbol{M}}_3} = \left[ {\begin{array}{*{20}{l}} {{C_{11}}}&{{C_{12}}}&{{C_{13}}} \\ {{C_{21}}}&{{C_{22}}}&{{C_{23}}} \end{array}} \right]。} \end{array} $ |
设主惯导输出的速度为Vmn,子惯导输出的速度为Vsn,由子惯导输出计算得到的杆臂速度为Vrn,采用东向和北向主子惯导速度误差作为速度量测,姿态量测采用量测失准角作为匹配量[14]。量测量选取:
| $ \mathit{\boldsymbol{Z}} = \left[ {\begin{array}{*{20}{l}} {{Z_\theta }} \\ {{Z_V}} \end{array}} \right] $ |
式中:Zθ=ϕ-Cbsnμ;ZV=Vsn-Vmn-Vrn。
系统的量测方程为:
| $ \mathit{\boldsymbol{Z}} = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{I}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 2}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{ - C_{bs}^n} \\ {{{\bf{0}}_{2 \times 3}}}&{{{\bf{I}}_{2 \times 2}}}&{{{\bf{0}}_{2 \times 3}}}&{{{\bf{0}}_{2 \times 3}}}&{{{\bf{0}}_{2 \times 3}}} \end{array}} \right]\mathit{\boldsymbol{X}} + \left[ {\begin{array}{*{20}{c}} {{V_\theta }} \\ {{V_v}} \end{array}} \right] $ | (2) |
式中:VV为零均值高斯白噪声;Vθ为未知的量测噪声信号。
1.2 基于马尔可夫过程的动态变形角建模传统传递对准方案认为,载体的动态变形是随机扰动干扰的随机变量,因此通常把相应的动态结构变形视为白噪声驱动的二阶马尔可夫过程[1]。
在该前提下设动态变形角为λ(t),它是白噪声激励的二阶马尔科夫过程,另取动态变形角速率为ωf(t),即有:
| $ \left\{ {\begin{array}{*{20}{l}} {{w_{{fx}}}(t) = {{\dot \lambda }_x}(t)} \\ {{w_{fy}}(t) = {{\dot \lambda }_y}(t)} \\ {{w_{fz}}(t) = {\dot \lambda _z}(t)} \end{array}} \right. $ | (3) |
动态变形角速率运动方程为:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot w}_{{fx}}}(t) = - \beta _x^2{\lambda _x}(t) - 2{\beta _x}{w_{fx}}(t) + {W_x}(t)} \\ {{{\dot w}_{{fy}}}(t) = - \beta _y^2{\lambda _y}(t) - 2{\beta _y}{w_{fy}}(t) + {W_y}(t)} \\ {{{\dot w}_{{fz}}}(t) = - \beta _z^2{\lambda _z}(t) - 2{\beta _z}{w_{fy}}(t) + {W_z}(t)} \end{array}} \right. $ | (4) |
式中:βx=2.146 /τi(i=x, y, z);τi为相关时间,可以视具体的载体情况而定;Wi(t)一般认为是具有一定方差的白噪声,如果是有色噪声,则需要进行白化处理,其方差满足:Qi=4βi3σi2(i=x, y, z),σi2(i=x, y, z)为3个弹性变形角λx, λy, λz的方差。
则此时扩展后的传递对准系统状态量可写作X=[ϕ, δV, ε, ▽, μ, λ, ωf],其状态方程可按式(3)与式(4)进行扩展为:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot X}} = \mathit{\boldsymbol{FX}} + \mathit{\boldsymbol{W}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_1}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}} \\ {{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{\mathit{\boldsymbol{I}}_{3 \times 3}}} \\ {{{\bf{0}}_{3 \times 3}}}&{{\mathit{\boldsymbol{B}}_1}}&{{\mathit{\boldsymbol{B}}_2}} \end{array}} \right]\mathit{\boldsymbol{X}} + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{W}}_1}} \\ {{{\bf{0}}_{3 \times 1}}} \\ {{\sigma _{3 \times 1}}} \end{array}} \right]} \\ {{\mathit{\boldsymbol{B}}_1} = \left[ {\begin{array}{*{20}{c}} { - \beta _x^2}&0&0 \\ 0&{ - \beta _y^2}&0 \\ 0&0&{ - \beta _z^2} \end{array}} \right]} \\ {{\mathit{\boldsymbol{B}}_2} = \left[ {\begin{array}{*{20}{c}} { - 2{\beta _x}}&0&0 \\ 0&{ - 2{\beta _y}}&0 \\ 0&0&{ - 2{\beta _s}} \end{array}} \right]} \end{array} $ | (5) |
同时量测方程中也应扩展为:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{Z}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 2}}}&{{{\bf{0}}_{3 \times 2}}}&{{{\bf{0}}_{3 \times 3}}}&{ - \mathit{\boldsymbol{C}}_{bs}^n}&{ - \mathit{\boldsymbol{C}}_{bs}^n}&{{{\bf{0}}_{3 \times 3}}} \\ {{{\bf{0}}_{2 \times 3}}}&{{\mathit{\boldsymbol{I}}_{2 \times 2}}}&{{{\bf{0}}_{2 \times 3}}}&{{{\bf{0}}_{2 \times 3}}}&{{{\bf{0}}_{2 \times 3}}}&{{{\bf{0}}_{2 \times 3}}}&{{{\bf{0}}_{2 \times 3}}} \end{array}} \right] + } \\ {\left[ {\begin{array}{*{20}{l}} {{V_\theta }} \\ {{V_V}} \end{array}} \right]} \end{array} $ | (6) |
需要注意的是,在该种方法下动态变形角被认为遵循马尔可夫过程的变换函数,但是对于其相关参数的选定并未形成一套成熟可靠的理论体系,通常仍为经验或反复调节所致,因而极有可能导致所建模型与实际相差过大以致影响对准精度的问题。
2 应变片量测改进后模型 2.1 采用应变片测量动态变形角及建模系统挠曲变形的模型和载体类型、所在环境和机动方式等因素相关,通过理论分析建立系统的挠曲变形模型是比较困难的。1.2节中的二阶马尔可夫过程虽可一定程度上逼近动态变形角规律,但是由于缺乏真实参照,在实际试验中往往需要反复调节相关时间参数才可获得较满意的估计结果。
若此时在主、子惯导安装基座嵌入2组应变片,通过应变片测量值对挠曲变形角进行综合建模,可能是一种简单有效的方式。在主、子惯导附近所贴的应变片如图 2所示。通过两者形变角度差值即可估出某一时刻主子惯导间因形变引起的误差角。

|
Download:
|
| 图 2 使用应变片测量挠曲变形角 Fig. 2 Measuring deflection angle with strain gauge | |
为获取传递对准的动态变形角特性,可把子惯导到主惯导之间的杆臂和子惯导组成的系统看作一个有阻尼系统[15],假设有一个平动加速度
则此时系统的微分方程为:
| $ \begin{array}{*{20}{c}} {J\left( {\ddot \theta - {{\ddot \theta }_t}} \right) = c{{\dot \theta }_t} - mgl\sin \left( {\theta - {\theta _t}} \right) - } \\ {ml\left( {\ddot y\sin \left( {\theta - {\theta _t}} \right) + \ddot x\cos \left( {\theta - {\theta _t}} \right)} \right)} \end{array} $ | (7) |
式中:c为阻尼系数;l为子惯导与主惯导间杆臂的长度;m为子惯导质量;J为转动惯量。由于主、子惯导失准角通常为小角度,因此可以近似得到sin(θ-θt)≈θ-θt, cos(θ-θt)≈1,由于此时
| $ J\left( {\ddot \theta - {{\ddot \theta }_t}} \right) = c{\dot \theta _t} - mgl\left( {\theta - {\theta _t}} \right) - ml\ddot x $ | (8) |
如果定义α1≡c/J, α2≡mgl/J, γ1≡α2/g, 并且β0=1, β1=0, β2=α2, 则此系统运动状态的线性化方程的传递函数有以下形式:
| $ {\mathit{\Theta} _t}(s) = \frac{{{\beta _0}{s^2} + {\beta _1}s + {\beta _2}}}{{{s^2} + {\alpha _1}s + {\alpha _2}}}\mathit{\Theta} (s) + \frac{{{\gamma _1}}}{{{s^2} + {\alpha _1}s + {\alpha _2}}}X(s) $ | (9) |
式中Θt(s)、Θ(s)和X(s)分别为θt(t)、θ(t)和
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} {{{\dot x}_1}} \\ {{{\dot x}_2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - {\alpha _1}}&1 \\ { - {\alpha _2}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{x_1}} \\ {{x_2}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\beta _1} - {\beta _0}{\alpha _1}} \\ {{\beta _2} - {\beta _0}{\alpha _2}} \end{array}} \right]\theta + \left[ {\begin{array}{*{20}{c}} 0 \\ {{\gamma _1}} \end{array}} \right]\ddot x} \\ {{{\dot \theta }_t} = \left[ {\begin{array}{*{20}{l}} 1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{x_1}} \\ {{x_2}} \end{array}} \right] + {\beta _0}\theta + {w_t}} \end{array} $ | (10) |
式中wt为应变片量测噪声,而对于该状态空间由于α1、α2、γ1、β0、β1、β2均有定义,θ、θt可通过应变片直接量测得到,因此未知量x1、x2也是可解析的[15]。对于式(10),其展开后可得到:
| $\left\{ {\begin{array}{*{20}{l}} {{{\dot x}_1} = - {\alpha _1}{x_1} + {x_2} - {\alpha _1}\theta = {x_2} - {\alpha _1}\left( {{x_1} + \theta } \right)} \\ {{{\dot x}_2} = - {\alpha _2}{x_1} + {\gamma _1}\ddot x} \\ {{{\dot \theta }_t} = \left( {{x_1} + \theta } \right) + {w_t}} \end{array}} \right. $ | (11) |
此时将应变片量测与传递对准形变进行对应,即认为θt为动态挠曲变形角,则动态挠曲变形角速度的微分应为
将2.1节得到的动态变形角相关微分方程带回传递对准相关方程中,此时上节中的θt等价于挠曲变形角λ,则式(5)中的B1、B2可定义为:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1} = \left[ {\begin{array}{*{20}{c}} {{A_{1x}}}&0&0 \\ 0&{{A_{1y}}}&0 \\ 0&0&{{A_{1z}}} \end{array}} \right]} \\ {{\mathit{\boldsymbol{B}}_2} = \left[ {\begin{array}{*{20}{c}} {{A_{2x}} - {\alpha _{1x}}}&0&0 \\ 0&{{A_{2y}} - {\alpha _{1y}}}&0 \\ 0&0&{{A_{2z}} - {\alpha _{1z}}} \end{array}} \right]} \end{array} $ | (12) |
式中A1x,A1y, A1z, A2x, A2y, A2z为起竖臂xyz轴动态变形角微分方程相关参数,可通过式(10)反推得到,则在该模型下式(5)中的σ对应的量应为应变片量测标准差。
由于此处仅对动态变形角进行精确建模,因而量测方程仍为传统量测方程。
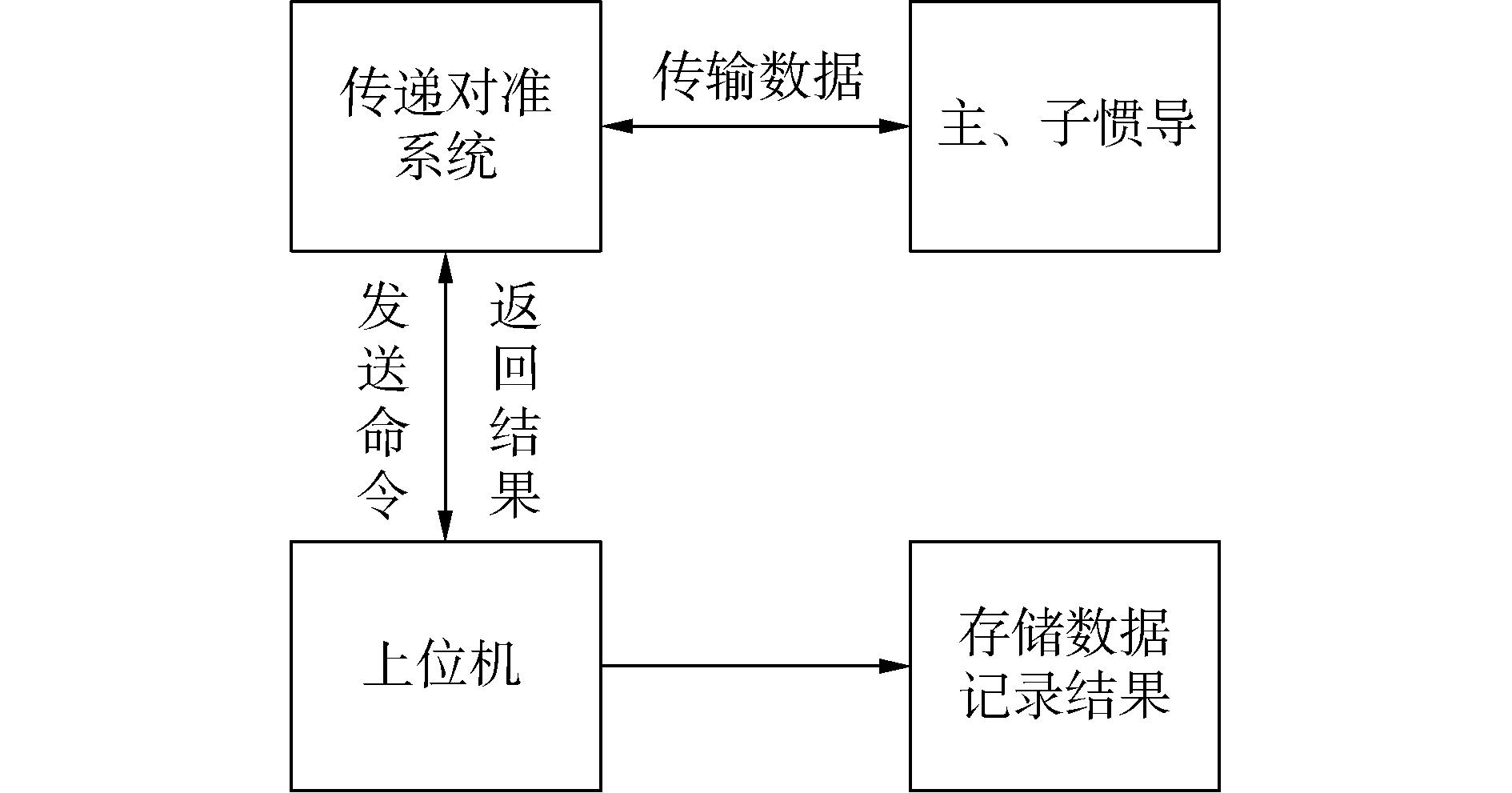
3 实验结果及分析 3.1 实验方法为了验证系统的实际使用,分别完成了室内和野外车载试验验证,验证流程如图 3所示,传递对准综合信息处理系统(图 4)实时接收主、子惯导的导航信息,同时接收上位机软件发出的开始对准命令、装订的参数信息等;系统接收到开始对准命令后系统开始进行传递对准解算,同时把计算结果和主、子惯导的导航信息等数据实时发送给上位机,上位机则将数据实时存储,用于事后分析、评估。
|
Download:
|
| 图 3 车载试验验证流程 Fig. 3 The verification process of vehicle test | |

|
Download:
|
| 图 4 传递对准综合信息处理系统 Fig. 4 The CPU of transfer alignment test | |
传递对准试验的高、低精度光纤陀螺导航系统的主要性能指标分别如表 1~3所示。
| 表 1 主惯导导航性能指标 Table 1 The navigation performance indicator of MINS |
| 表 2 子惯导加速度计性能指标 Table 2 The performance of accelerometer used in SINS |
| 表 3 子惯导光纤陀螺性能指标 Table 3 The performance of FOG used in SINS |
车载试验时的主、子惯导具体安装如图 5所示,主惯导和子惯导安装在起竖臂上,图中1和2分别为主、子惯导,3和4分别为安装在主、子惯导周边的量测应变片,5和6分别为安装在主、子惯导上的基准面棱镜,试验开始前用高精度陀螺经纬仪瞄准主、子惯导的基准面棱镜,获取两套系统的方位安装失准角,认为在水平状态下子惯导的水平姿态可以作为参考,因此水平安装失准角也可以获得。最终获取的安装失准角参考值为:1.083°、0.379°、0.005°(方位,俯仰,横滚)。主、子惯导北向杆臂距离1.5 m,东向和天向的杆臂长度为0,因此杆臂长度设置为rn=[0 1.5 0]T。

|
Download:
|
| 图 5 车载试验安装示意 Fig. 5 The installation diagram of vehicle test | |
试验时,系统先通上位机给传递对准系统发送开始计算命令,然后让起竖臂分别抬起30°、60°和90°,等待起竖臂抬起结束后静止10 s,记录传递对准系统输出的值。
精度检验采用高精度陀螺经纬仪。如图 6所示,其主要功能是提供北向方位基准。该产品的寻北精度不大于10″(1σ),寻北时间不大于10 min,采用全自动工作方式。每次试验前,使用陀螺经纬仪瞄准贴合在主、子惯导上的高精密棱镜,获取主、子惯导的方位参考值,同时可获取主、子惯导的方位误差角。

|
Download:
|
| 图 6 高精度寻北仪作为精度检验基准设备 Fig. 6 The high precision gyro north finder | |
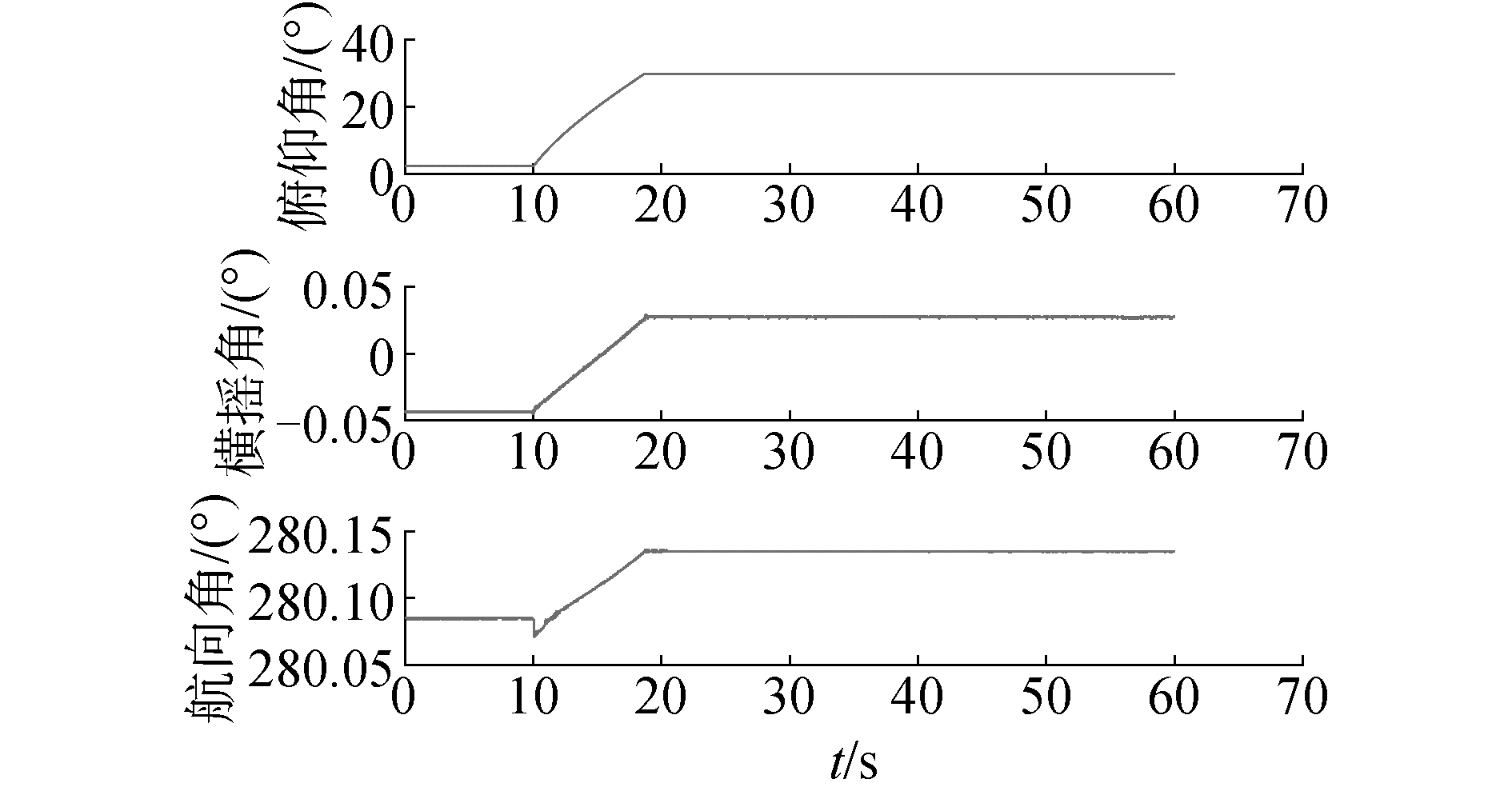
为进行传统传递对准模型和基于应变片量测建模模型之间的精度对比,选取一组起竖臂上抬至30°后静止的数据进行计算对比, 如图 7所示,起竖臂在10 s内上抬至30°并在之后保持静止一段时间。
|
Download:
|
| 图 7 主惯导姿态角变化 Fig. 7 The angle changes of MINS | |
对比结果如图 8所示,传统马尔可夫过程建模对于动态变形角估计情况较不理想,这种估计的错误会直接导致其在机动结束后需花费较多时间进行静态失准角的进一步收敛,而使用本文建模的传递对准算法在动态变形角跟踪上则明显优于前者。

|
Download:
|
| 图 8 方位、俯仰和横滚动态变形角估计结果 Fig. 8 The estimation result of dynamic deformation angle | |
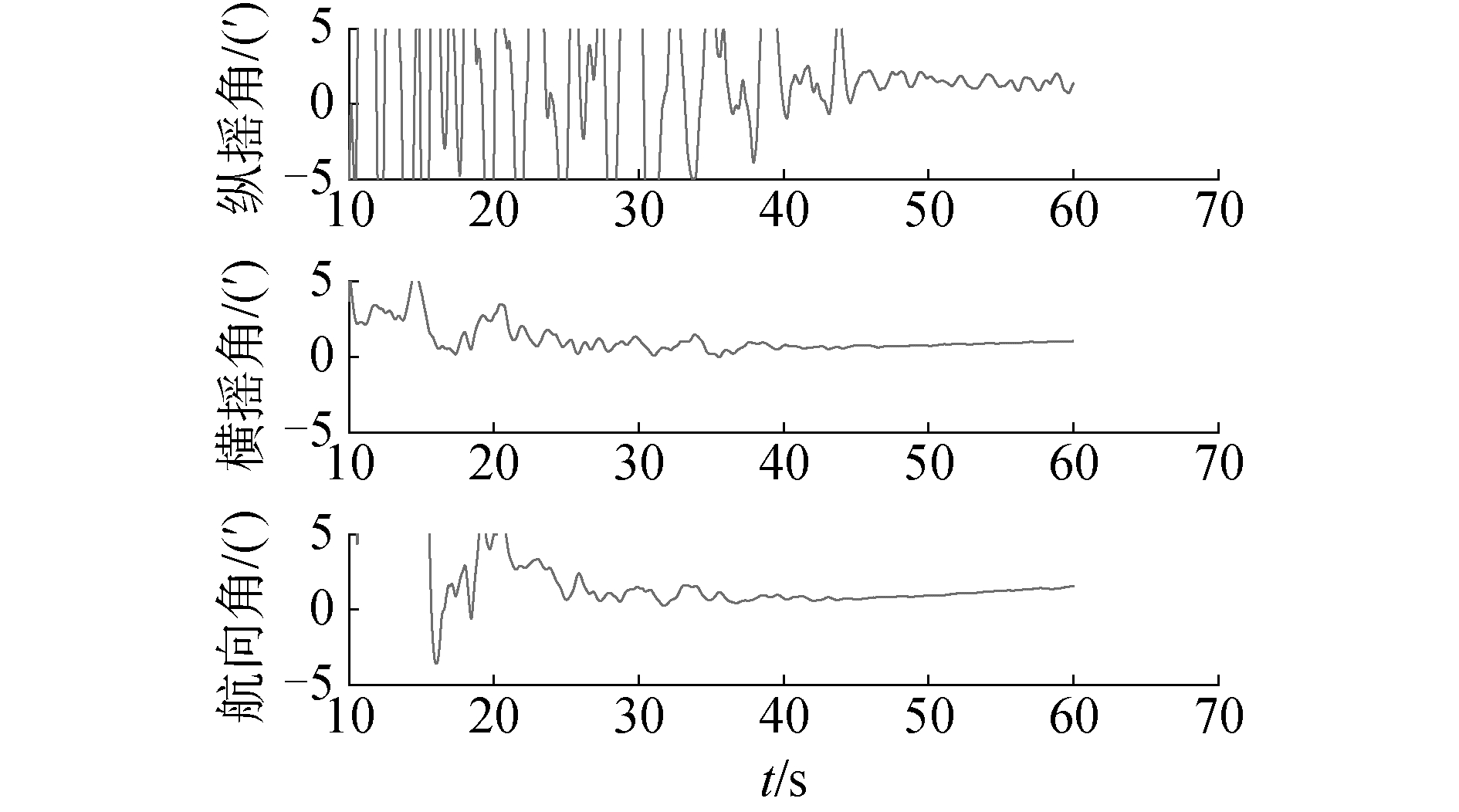
从图 9中可以看到,机动结束后,传统传递对准仍需要额外的30 s来对失准角进行进一步估计和收敛,且最终估计误差均达到3′以上。
|
Download:
|
| 图 9 方位、俯仰和横滚失准角估计误差 Fig. 9 The estimation error of misalignment angle | |
同样选取起竖臂上抬至30°而后静止的数据,则选用了文中模型的传递对准算法估计结果如图 10、11所示。
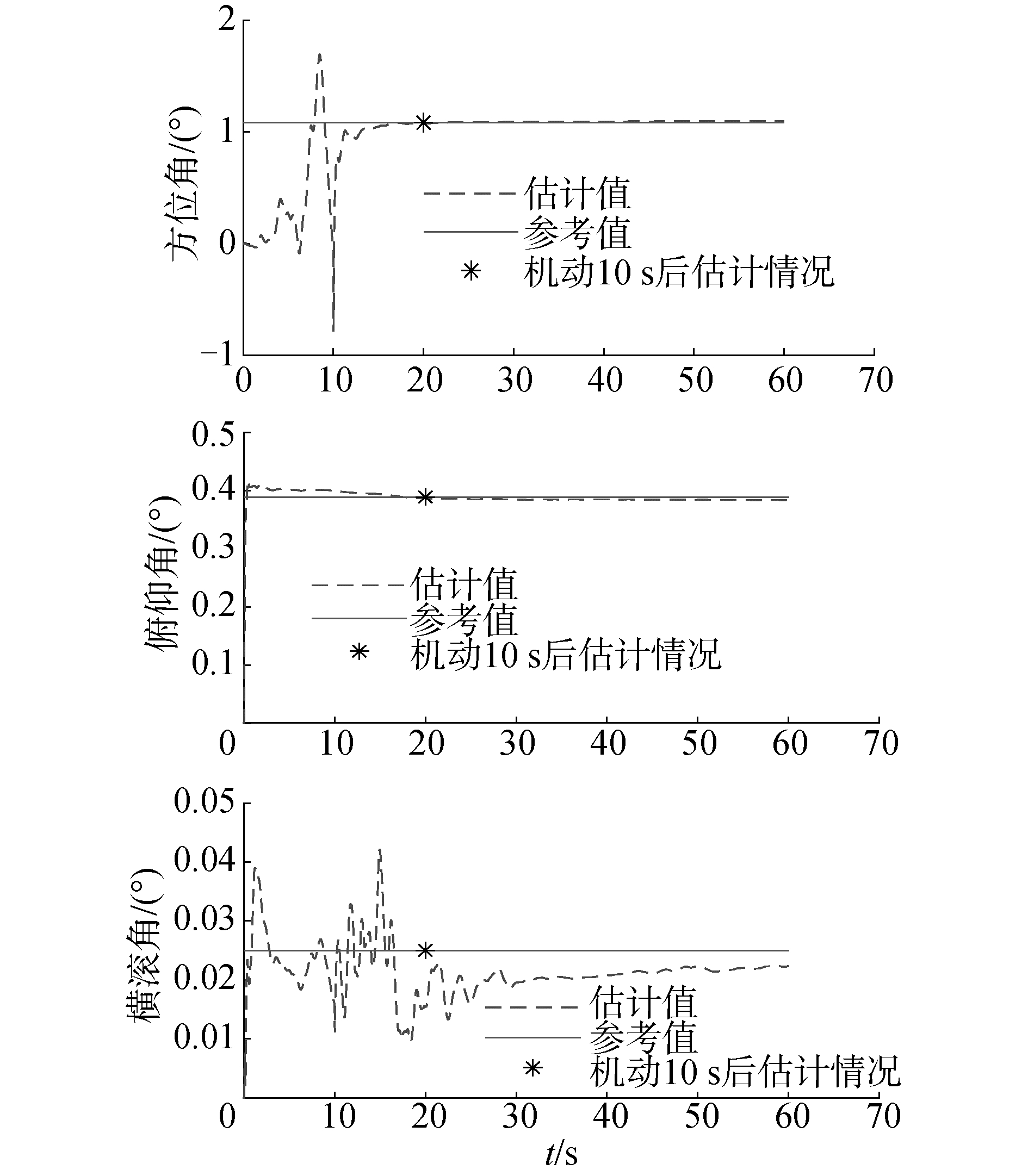
|
Download:
|
| 图 10 方位、俯仰和横滚失准角估计结果 Fig. 10 The estimation result of misalignment angle | |
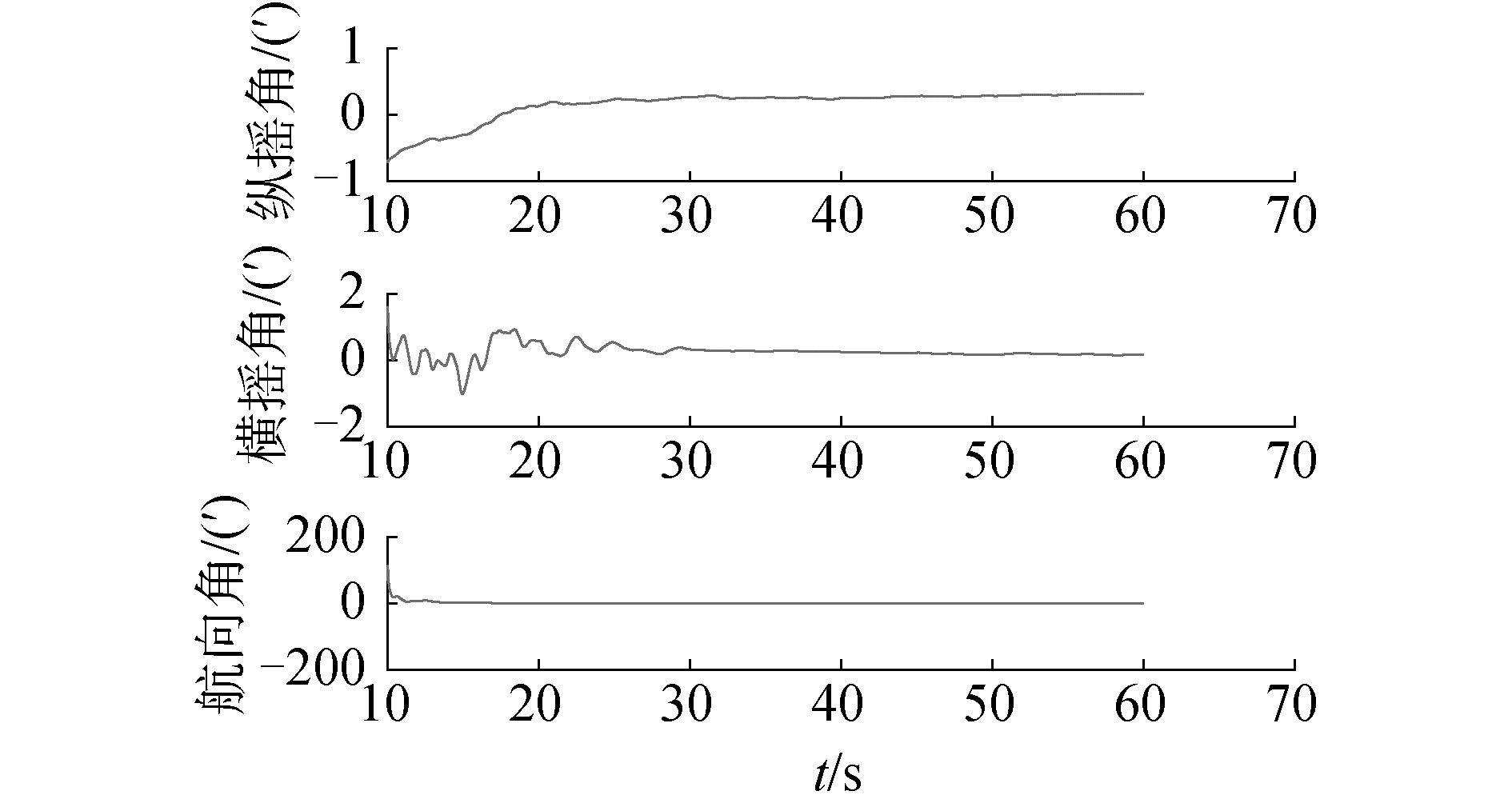
|
Download:
|
| 图 11 方位、俯仰和横滚失准角估计误差 Fig. 11 Test system structure | |
从图 10的估计结果和图 11的误差曲线中可以看出起竖臂保持在30°状态静止10 s后,系统的失准角估计结果已经收敛,且最终方位失准角估计误差小于3′,俯仰和横滚失准角估计误差小于2′,比较传统传递对准结果,可发现使用了新模型的传递对准算法不仅在速度上优于传统算法,同时在准确性上也有较好的提升。
为验证该建模的适用性,起竖臂依次在30°、60°和90°起竖环境下做了多组实验,其在不同环境下估计结果如下表所示,并统计了其在机动结束10 s后的收敛结果,从表 4中可以看到仅在90°起竖实验中方位失准角估计误差超过了2′,其余各组数据失准角误差估计均保持在2′以内。
| 表 4 试验记录结果 Table 4 Results of test records |
1) 使用了应变片估计动态变形角的传递对准模型有效解决了传统传递对准模型中因经验建模参数不匹配导致的失准角估计无法收敛问题,可在机动结束10 s内将失准角估计收敛至一个较高精度;
2) 在机动结束后,传递对准系统估计的方位失准角误差小于3′,俯仰和横滚失准角误差小于2′,其精度等级基本达到了该精度子惯导系统的理想结果。
因此,增加应变片测量动态变形角的方案,能有效地避免动态变形模型失真,带来估计不准确的风险,并且能提升传递对准估计精度。一般情况下,如果不更换主子惯导安装基座,只要在试验开始前,对所用环境进行一次数据采集,即可完成动态变形建模,这样提高了后续传递对准试验的可靠性。需注意的是,为方便建模及计算,在实际计算及反推中省略了一部分二阶小量,即使用模型与实际模型仍存在一定误差关系。
| [1] |
管叙军, 王新龙. 捷联惯导系统动基座传递对准匹配方法[J]. 航空兵器, 2014(2): 3-8, 15. GUAN Xujun, WANG Xinlong. Transfer alignment match methods for strapdown inertial navigation system on moving bases[J]. Aero weaponry, 2014(2): 3-8, 15. DOI:10.3969/j.issn.1673-5048.2014.02.001 (  0) 0)
|
| [2] |
宫晓琳, 房建成, 郭雷. SINS快速精确传递对准技术研究[J]. 宇航学报, 2008, 29(4): 1228-1232. GONG Xiaolin, FANG Jiancheng, GUO Lei. Study on the rapid and accurate transfer alignment for SINS[J]. Journal of astronautics, 2008, 29(4): 1228-1232. DOI:10.3873/j.issn.1000-1328.2008.04.026 (  0) 0)
|
| [3] |
SHORTELLE K J, GRAHAM W R, RABOURN C. F-16 flight tests of a rapid transfer alignment procedure[C]//IEEE 1998 Position Location and Navigation Symposium. Palm Springs, CA, USA, 1998: 379-386.
(  0) 0)
|
| [4] |
陈凯, 鲁浩, 闫杰. 传递对准中一种新的姿态匹配算法[J]. 西北工业大学学报, 2007, 25(5): 691-694. CHEN Kai, LU Hao, YAN Jie. A different and better algorithm for attitude match of transfer alignment[J]. Journal of Northwestern Polytechnical University, 2007, 25(5): 691-694. DOI:10.3969/j.issn.1000-2758.2007.05.016 (  0) 0)
|
| [5] |
KAIN J E, CLOUTIER J R. Rapid transfer alignment for tactical weapon applications[C]//Guidance, Navigation and Control Conference. Boston, 1989: 1290-1300.
(  0) 0)
|
| [6] |
LIM Y C, LYOU J. An error compensation method for transfer alignment[C]//Proceedings of IEEE Region 10 International Conference on Electrical and Electronic Technology. Singapore, 2001: 850-855.
(  0) 0)
|
| [7] |
HONG S, LEE M H, CHUN H H, et al. Experimental study on the estimation of lever arm in GPS/INS[J]. IEEE transactions on vehicular technology, 2006, 55(2): 431-448. DOI:10.1109/TVT.2005.863411 (  0) 0)
|
| [8] |
顾冬晴, 秦永元. 传递对准中主惯导速度匹配量的实时构造算法[J]. 西北工业大学学报, 2004, 22(5): 666-670. GU Dongqing, QIN Yongyuan. On-line algorithm for constructing velocity matching data of master INS for transfer alignment[J]. Journal of Northwestern Polytechnical University, 2004, 22(5): 666-670. DOI:10.3969/j.issn.1000-2758.2004.05.029 (  0) 0)
|
| [9] |
李良君.传递对准误差补偿及精度评估方法研究[D].哈尔滨: 哈尔滨工程大学, 2008. LI Liangjun. Research of the transfer alignment error compensation and precision estimation[D]. Harbin: Harbin Engineering University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10217-2009058845.htm (  0) 0)
|
| [10] |
WANG Zhen, GAO Min, GAO Fengqi, et al. Study on transfer alignment stable targeting method of moving base based on velocity plus attitude matching algorithm[C]//2015 International Industrial Informatics and Computer Engineering Conference. Shaanxi, 2015.
(  0) 0)
|
| [11] |
ABUBAKAR A, DOW R S. Simulation of ship grounding damage using the finite element method[J]. International journal of solids and structures, 2013, 50(5): 623-636. DOI:10.1016/j.ijsolstr.2012.10.016 (  0) 0)
|
| [12] |
杨功流, 郭蔚林, 袁二凯. 姿态匹配法测量船体变形角中时间延迟的补偿[J]. 光学精密工程, 2015, 23(5): 1409-1415. YANG Gongliu, GUO Weilin, YUAN Erkai. Compensation of time delay in ship deformation measured by attitude matching[J]. Optics and precision engineering, 2015, 23(5): 1409-1415. (  0) 0)
|
| [13] |
杨鹏翔, 秦永元, 严恭敏. 捷联惯导系统简化非线性对准研究[J]. 系统仿真学报, 2010, 22(12): 2817-2820. YANG Pengxiang, QIN Yongyuan, YAN Gongmin. Simplified strapdown INS nonlinear alignment research[J]. Journal of system simulation, 2010, 22(12): 2817-2820. (  0) 0)
|
| [14] |
LEAVITT J, SIDERIS A, BOBROW J E. High bandwidth tilt measurement using low-cost sensors[J]. IEEE/ASME transactions on mechatronics, 2006, 11(3): 320-327. DOI:10.1109/TMECH.2006.875571 (  0) 0)
|
| [15] |
何昆鹏. MEMS惯性器件参数辨识及系统误差补偿技术[D].哈尔滨: 哈尔滨工程大学, 2009. HE Kunpeng. Parametric identification and error compensation of MEMS inertial sensors and IMU[D]. Harbin: Harbin Engineering University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10217-2009154504.htm (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


