近空间可变翼飞行器又称高超声速可变翼飞行器,是指在近空间区域内飞行且飞行器机翼外形结构具可变化的飞行器。近空间可变翼飞行器采用翼身融合,外形结构呈三角形。由于近空间可变翼飞行器在军事装备、科学探索和未来航天运输领域均具有重要的潜在应用价值,因此对于可变翼飞行器的研究得到了国内外众多学者和研究机构的重视[1]。
近空间可变翼飞行器爬升段的轨迹研究是一个复杂的、高度非线性的、多变量、多约束条件下的最优控制问题。由于高超声速下系统对气动参数的敏感性,爬升段的状态参数变化的跨越性,爬升段可变翼的小翼伸缩对系统造成的扰动性,这些都无形中增加了优化求解的难度。因此其成为了航空航天领域极具挑战性的研究课题,具有重要的理论研究意义和工程应用价值[2-3]。
对于最优控制问题求解的基本方法,一般分成直接法和间接法两大类。1)间接法:间接法将最优控制问题转换为Hamilton边值问题,然后通过数值方法求解,存在收敛域小、难以估计共轭变量初值等不足。这种方法的优点是解的精度高,且解满足最优性的一阶必要条件;2)直接法:采用参数化方法,将连续空间的最优控制问题求解转化为非线性规划(non linear programming,NLP)问题,通过数值求解非线性规划问题来获得最优解[4-5]。直接法克服了间接法的缺点,因为它不需要计算协态的信息,但是解的精度较低,缺少协态,不能检验最优性的一阶必要条件[6]。近年来,直接法中的伪谱法由于其高精度、高效率,在轨迹优化方面得到了广泛的应用[7]。文献[8]基于高斯伪谱法(GPM)研究了助推-滑翔飞行器多阶段轨迹优化问题;如文献[9]采用基于HP自适应伪谱法解决助推-滑翔飞行器的多阶段多约束轨迹优化问题;文献[10]提出了一种基于点位经纬度变换条件改进GPM的方法,跳出了时域变换的限制,进行2点间的航迹规划。文献[11]研究了空天飞机上升段最优轨迹设计问题,提出了分段优化的策略并将攻角与推力阀门进行离散化,利用配点法求解得到最优控制量。文献[12]提出一种基于高斯伪谱法的上升段轨迹优化策略,依据发动机的推力特性将上升轨迹合理分段,使原最优控制问题转化为多段最优控制问题后,采用高斯伪谱法进行并行优化计算。
本文针对近空间可变翼飞行器小翼伸缩燃料最省轨迹优化,采用GMP高斯伪谱法,先将连续时间问题转化为离散点,在离散点上用状态量和控制量等未知变量表示出性能指标函数、微分方程和约束条件等,再将其转化为非线性规划(NLP)问题,然后通过SQP算法进行NLP问题求解。最后利用该方法能够在较短的时间对近空间可变翼飞行器爬升段小翼伸缩量进行优化,得到燃料最优轨迹及小翼在爬升段的伸缩变化过程。
1 非线性最优控制问题的高斯伪谱法一般的Bolza问题[13],统一形式为:
| $ \left\{ \begin{gathered} \min :J = \mathit{\Phi} \left( {x\left( {{t_0}} \right), {t_0}, x\left( {{t_f}} \right), {t_f}} \right) + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\int_{{t_0}}^{{t_f}} g (x(t), u(x), t){\text{d}}t \hfill \\ {\text{s}}{\text{.t}}{\text{.}}\left\{ \begin{array}{l} \dot x(t) = f(x(t), u(t), t) \hfill \\ E\left( {x\left( t \right), {\text{ }}u\left( t \right), {\text{ }}t} \right) = 0 \hfill \\ C(x(t), u(t), t) \leqslant 0, t \in \left[ {{t_0}, {t_f}}\right] \end{array} \right. \\ \end{gathered} \right. $ | (1) |
式中: x(t)、u(t)分别表示状态变量和控制变量,t0、tf分别表示最优控制问题的起始时间和末端时间,E和C分别表示等式约束和不等式约束。本文采用非等间距的Gauss伪谱法,首先把上述Bolza问题转化到时间定义在[-1, 1]上的标准最优控制问题。首先需要引入时间变量τ,将时间区间[t0,tf]投影变换到[-1, 1]内[14]:
| $ t = \frac{{{t_f} - {t_0}}}{2}\tau + \frac{{{t_f} + {t_0}}}{2}, \tau \in [ - 1, 1] $ | (2) |
将无穷维的连续最优控制问题转换得到有限维的非线性规划(NLP)问题:
| $ \left\{ \begin{array}{l} \min :J = \mathit{\Phi} \left( {x( - 1), {t_0}, x(1), {t_f}} \right) + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{t_f} - {t_0}}}{2}\int_{ - 1}^1 g \left( {x(\tau ), u(\tau ), \tau ;{t_0}, {t_f}} \right){\text{d}}\tau \hfill \\ {\text{s}}{\text{.t}}{\text{.}}\left\{ \begin{array}{l} \dot x(t) = \frac{{{t_f} - {t_0}}}{2}f\left( {x(\tau ), u(\tau ), \tau ;{t_0}, {t_f}} \right) \hfill \\ E\left( {x( - 1), u( - 1), {t_0};x(1), u(1), {t_f}} ;\right. \hfill \\ x(\tau ), u(\tau ), \tau ) = 0 \hfill \\ C\left( {x(\tau ), u(\tau ), \tau ;{t_0}, {t_f}} \right) \leqslant 0 \end{array} \right.\\ \end{array} \right. $ | (3) |
利用高斯伪谱法得到的N个配点,一般采用Lagrange插值的方法,将连续状态变量通过离散状态变量插值拟合:
| $ y(\tau ) \approx Y(\tau ) = \sum\limits_{i = 0}^N {{L_i}} (\tau )y\left( {{\tau _i}} \right) $ | (4) |
其中N次Lagrange插值多项式表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {{L_i}(\tau ) = \prod\limits_{j = 0, j \ne i}^N {\frac{{\tau - {\tau _j}}}{{{\tau _i} - {\tau _j}}}} = \frac{{b(\tau )}}{{\left( {\tau - {\tau _i}} \right)\dot b\left( {{\tau _i}} \right)}}} \\ {b(\tau ) = \prod\limits_{i = 0}^N \tau - {\tau _i}} \end{array}} \right. $ | (5) |
插值多项式在离散点上特点:
| $ {L_i}(\tau ) = {\delta _{ij}} = \left\{ {\begin{array}{*{20}{l}} {1, }&{i = j} \\ {0, }&{i \ne j} \end{array}} \right. $ | (6) |
高斯伪谱法中,状态变量和控制变量属于未知参数。选用N个LG配点进行状态变量和控制变量离散化:
| $ x(\tau ) \approx X(\tau ) = \sum\limits_{i = 0}^N {{L_i}} (\tau )X\left( {{\tau _i}} \right) $ | (7) |
| $u(\tau ) \approx U(\tau ) = \sum\limits_{i = 1}^N {{{\tilde L}_i}} (\tau )U\left( {{\tau _i}} \right) $ | (8) |
为了将标准的Bolza问题转化为NLP,需要把状态方程中的状态变量的导数进行离散化:
| $ \dot x(\tau ) \approx \dot X(\tau ) = \sum\limits_{i = 0}^N {{{\dot L}_i}} (\tau )X\left( {{\tau _i}} \right) = \sum\limits_{i = 0}^N {{D_{k, i}}} (\tau )X\left( {{\tau _i}} \right) $ | (9) |
| $ {D_{k, i}} = \left\{ {\begin{array}{*{20}{l}} {\frac{{\dot b\left( {{\tau _k}} \right)}}{{\left( {{\tau _k} - {\tau _i}} \right)\dot b\left( {{\tau _i}} \right)}}, }&{k \ne i} \\ {\frac{{\dot b\left( {{\tau _k}} \right)}}{{2\dot b\left( {{\tau _k}} \right)}}, }&{k = i} \end{array}} \right. $ | (10) |
D是一个N×(N+1)的状态微分矩阵,可以提前计算获得。因此状态微分方程可以由约束条件替代:
| $ \left\{ {\begin{array}{*{20}{l}} {\sum\limits_{i = 0}^N {{D_{k, i}}} (\tau ){X_k} = \frac{{{t_f} - {t_0}}}{2}f\left( {{X_k}, {U_k}, {\tau _k};{t_0}, {t_f}} \right)} \\ {k = 1, 2, \cdots , N} \end{array}} \right. $ | (11) |
由状态量和控制量的近似,可以对路径约束,和边界约束在LG配点上进行离散化,得到:
| $ C\left( {{X_k}, {U_k}, {\tau _k};{t_0}, {t_f}} \right)0, k = 1, 2, \cdots , N $ | (12) |
| $ \left\{ {\begin{array}{*{20}{l}} {E\left( {x( - 1), u( - 1), {t_0};} \right) = 0} \\ {E\left( {x(1), u(1), {t_f}} \right) = 0} \end{array}} \right. $ | (13) |
由于最优控制问题存在终端状态约束,因此需要对终端状态进行计算,根据高斯积分公式,终端状态可以表示为:
| $ \begin{gathered} {X_f} = {X_{N + 1}} = {X_0} + \frac{{{t_f} - {t_0}}}{2}\int_{{\tau _0}}^{{\tau _f}} f \left( {x(\tau ), u(\tau ), \tau ;{t_0}, {t_f}} \right){\text{d}}\tau \approx \hfill \\ \;\;\;\;\;{X_0} + \frac{{{t_f} - {t_0}}}{2}\sum\limits_{k = 1}^N {{w_k}} f\left( {x\left( {{\tau _k}} \right), u\left( {{\tau _k}} \right), {\tau _k};{t_0}, {t_f}} \right) = \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;{X_0} + \frac{{{t_f} - {t_0}}}{2}\sum\limits_{k = 1}^N {{w_k}} f\left( {{X_k}, {U_k}, {\tau _k};{t_0}, {t_f}} \right) \hfill \\ \end{gathered} $ | (14) |
其中
性能指标函数中的Lagrange项需要计算函数的积分,并且高斯积分表达精度最高,因此性能指标函数进行如下精确近似:
| $ \begin{array}{*{20}{c}} {J = \mathit{\Phi} \left( {x( - 1), {t_0}, x(1), {t_f}} \right) + } \\ {\frac{{{t_f} - {t_0}}}{2}\sum\limits_{k = 1}^N {{{\hat w}_k}} g\left( {{X_k}, {U_k}, {\tau _k};{t_0}, {t_f}} \right)} \end{array} $ | (15) |
| $ {\hat w_k} = \frac{2}{{\left( {1 - \tau _k^2} \right){{\left( {{{\dot p}_N}\left( {{\tau _k}} \right)} \right)}^2}}} $ | (16) |
式中pN是N次Legendre多项式。
1.4 NLP问题的建立原最优控制Bolza问题可以转化为离散形式的NLP问题。基于上述的数值近似方法,高斯伪谱法将连续最优控制问题离散[15]。综合表示为:
| $\begin{gathered} \;\;\;\;\;\;\;\;\;\;\;\min :J = \mathit{\Phi} \left( {x( - 1), {t_0}, x(1), {t_f}} \right) + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\frac{{{t_f} - {t_0}}}{2}\sum\limits_{k = 1}^N {{{\hat w}_k}} g\left( {{X_k}, {U_k}, {\tau _k};{t_0}, {t_f}} \right) \hfill \\ \left\{ {\begin{array}{*{20}{l}} {\sum\limits_{k, i}^N {{D_{k, i}}} (\tau ){X_k} - \frac{{{t_f} - {t_0}}}{2}f\left( {{X_k}, {U_k}, {\tau _k};{t_0}, {t_f}} \right) = 0} \\ {C\left( {{X_k}, {U_k}, {\tau _k};{t_0}, {t_f}} \right) \leqslant 0, k = 1, 2 \cdots , N} \\ {{E_1}\left( {x( - 1), u( - 1), {t_0};} \right) = 0} \\ {{E_2}\left( {x(1), u(1), {t_f}} \right) = 0} \\ {{X_f} - {X_0} + \frac{{{t_f} - {t_0}}}{2}\sum\limits_{k = 1}^N {{w_k}} f\left( {{X_k}, {U_k}, {\tau _k};{t_0}, {t_f}} \right) = 0} \end{array}} \right. \hfill \\ \end{gathered} $ | (17) |
针对近空间可变翼飞行器爬升段小翼伸缩最省燃料飞行器轨迹优化问题, 综合考虑飞行器在近空间飞行声速变化、密度变化、地球引力及发动机推力变化等因素对飞行爬升轨迹的影响。因此该问题的数学模型包括动力学模型、发动机模型、大气模型与气动力模型等。
2.1 近空间可变翼飞行器构型参数本文的研究对象为近空间可变翼飞行器,与一般的近空间飞行器相比,加入可变小翼,在飞行器的机翼翼梢装有可伸缩小翼,通过伸出和收回小翼来改变机翼浸润面积和展长。相关外形参数如表 1。
| 表 1 近空间可变翼飞行器参数 Table 1 Parameters of near space morphing hypersonic aircraft |
可伸缩小翼的特点是使该飞行器具有更好的自适应能力,可通过改变机翼外形更好地实现水平起降和高超声速远程巡航,增加起飞和爬升段的升力,减小近空间区域超高速飞行的阻力,从而提高飞行效率。通过改变飞行器的气动特性更好地适应复杂的飞行条件和飞行状态,从而完成飞行任务。
本文针对在飞行器爬升段会消耗大量的燃油,配合飞行器小翼可伸缩这一特点,以最佳省油爬升为目标进行爬升段的优化,力求得出爬升段最优的小翼伸缩方式。
2.2 动力学模型近空间可变翼飞行器爬升段数学模型[16]描述可表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {\dot V = \frac{{T\cos \alpha - D}}{m} - \frac{\mu }{{{r^2}}}\sin \gamma } \\ {\dot h = V\sin \gamma } \\ {\dot \gamma = \frac{{L + T\sin \alpha }}{{mV}} - \frac{{\left( {\mu - {V^2}r} \right)\cos \gamma }}{{V{r^2}}}} \\ {\dot m = - \frac{T}{{{I_\text{sp}}{g_0}}}} \end{array}} \right. $ | (18) |
| $ {I_\text{sp}} = \left\{ {\begin{array}{*{20}{l}} {4700 - \frac{h}{{100}}, }&{Ma < 4} \\ {5680 - 245Ma - \frac{h}{{100}}, }&{Ma \geqslant 4} \end{array}} \right. $ | (19) |
式中:V为飞行速度;h为飞行高度;γ为航迹角;m为飞行器质量;α为迎角;L为升力;D为阻力;T为发动机推力;Isp为燃料比冲;g0为海平面重力加速度;r为地球半径;μ为地球引力参数;Ma为马赫数。
2.3 发动机模型发动机推力计算公式为:
| $ T = 0.5\rho {V^2}\left( {S + {S_\text{s}}} \right){C_{\text{T}}} $ | (20) |
式中:S为飞行器有效参考面积,Ss小翼的伸缩面积。CT为推力系数,且:
| $ {C_{\text{T}}} = \left\{ {\begin{array}{*{20}{l}} {0.02576\beta , }&{\beta \geqslant 1} \\ {0.0224 + 0.00336\beta , }&{\beta < 1} \end{array}} \right. $ | (21) |
式中β为发动机节流阀调定值状态。
2.4 大气环境模型与气动力模型近空间可变翼飞行器在爬升段时,从地球表面跨越大气层到达近空间区域的过程中,重力加速度按规律变化的。当飞行器到达一定高度时,重力加速度会随着高度的增大而减少。重力加速度的表达式为:
| $ g = {g_0}{\left( {\frac{{{r_0}}}{{{r_0} + h}}} \right)^2} $ | (22) |
式中:r0为地球半径;g0为标准重力加速度。
在飞行器爬升整个飞行过程中,大气密度是不断变化的,随着高度的增加而减小。大气密度表达式为:
| $ \rho = {\rho _0}{{\text{e}}^{ - h/7315.2}} $ | (23) |
式中ρ0=1.226 6 kg/m3,即地球表面的大气密度。本文数值仿真验证中采用的标准重力加速度g0=9.806 65 m/s2,地球半径r0=6 356 766 m。
飞行器飞行过程中受到阻力D和升力L的计算公式如下:
| $ \left\{ {\begin{array}{*{20}{l}} {L = 0.5\rho {V^2}\left( {S + {S_{\text{s}}}} \right){C_L}} \\ {D = 0.5\rho {V^2}\left( {S + {S_{\text{s}}}} \right){C_D}} \end{array}} \right. $ | (24) |
式中:CL和CD分别为升力系数和阻力系数,其中小翼伸缩时的升阻力系数通过插值法得到。图 1给出了小翼完全伸出和小翼全部收回时的升力系数CL和阻力系数CD与马赫数Ma、迎角α的关系。

|
Download:
|
| 图 1 小翼伸缩前后升阻力系数 Fig. 1 Wing lift drag coefficient before and after expansion | |
本文结合近空间飞行环境模型,可变翼飞行器在小翼伸缩时气动参数采用高精度的插值方法获得,对飞行器轨迹优化问题进行研究,能较好地反映飞行器的真实飞行环境。气动参数的获取如图 2所示。

|
Download:
|
| 图 2 气动数据获取流程 Fig. 2 Flow chart of pneumatic parameter acquisition | |
近空间飞行器一般通过助推器助推到达预定的高度和速度后,飞行器的发动机开始工作,因此飞行器给定飞行器初始爬升的状态和爬升末端的状态:
| $ \left\{ {\begin{array}{*{20}{l}} {h\left( {{t_0}} \right) = {h_0}, }&{h\left( {{t_f}} \right) = {h_f}} \\ {V\left( {{t_0}} \right) = {V_0}, }&{V\left( {{t_f}} \right) = {V_f}} \\ {\gamma \left( {{t_0}} \right) = {\gamma _0}, }&{\gamma \left( {{t_f}} \right) = {\gamma _f}} \\ {m\left( {{t_0}} \right) = {m_0}}&{} \end{array}} \right. $ | (25) |
近空间飞行器在加速爬升的过程中,由于速度很快,会严重受到因大气层而产生的阻力,在大气的强压及摩擦下,飞行器的表面温度迅速升高,同时,大气压的作用也会对飞行器外形产生影响。所以,要使飞行器顺利爬升而且不会对飞行器造成损坏,必须对飞行过程中的动压、热流率、过载等做一定的约束,因此爬升过程中必须满足的路径约束条件[17]。
1) 热流率约束。
| $ \dot Q = C{\rho ^p}{V^q} $ | (26) |
式中:C=7.968 6×10-5;p=0.5;q=3.15。
2) 动压约束。
根据爬升任务的要求,考虑动压对控制系统的影响,存在动压约束:
| $ {q_{\min }} \leqslant q = \frac{1}{2}\rho {v^2} \leqslant {q_{{\text{max}}}} $ | (27) |
3) 过载约束。
为了使机体结构部受到破坏,其所承受的过载不超出允许的范围,需对过载进行约束:
| $ n = \frac{{qS\sqrt {\left( {C_L^2 + C_D^2} \right)} }}{{mg}} \leqslant {n_{\max }} $ | (28) |
飞行器在爬升过程中,由于执行机构的限制,控制量必须约束在一定范围内,同时,由于爬升段某些特殊要求和机动性能的影响,要满足一定的状态量约束,以保证飞行器正常的飞行,本文针对的是可变翼飞行器,存在3个控制变量分别是迎角、发动机节流阀、小翼伸缩面积,u=[α β Ss]; 4个状态变量分别是速度、高度、航迹角、质量,x=[V h γ m]。
| $ \left\{ \begin{array}{l} {\alpha _{\min }} \leqslant \alpha \leqslant {\alpha _{\max }}, \;\;\;\;{V_{\min }} \leqslant V \leqslant {V_{\max }} \hfill \\ {\beta _{\min }} \leqslant \beta \leqslant {\beta _{\max }}, \;\;\;\;{h_{\min }} \leqslant h \leqslant {h_{\max }} \hfill \\ {S_{\operatorname{sinin} }} \leqslant {S_{\text{s}}} \leqslant {S_{{\text{smax}}}}, \;\;\;\;{\gamma _{\min }} \leqslant \gamma \leqslant {\gamma _{{\text{max}}}} \hfill \\ \end{array} \right. $ | (29) |
基于本文所研究的近空间可变翼飞行器,其在爬升过程中,消耗大量燃料,其在爬升过程中质量的减少近似为燃料的消耗。由于飞行器本身所携带的燃料有限,为了能够有较多的燃料用于巡航段的飞行,所以要求飞行器以最省燃料进行爬升,即爬升末端飞行器的质量保持最大。其性能指标函数为:
| $ J = - {m_{{t_f}}} = \mathop {\max }\limits_t \left( {m\left( {{t_0}} \right) - \int_{{t_0}}^{{t_f}} m (\tau ){\rm{d}}\tau } \right) $ | (30) |
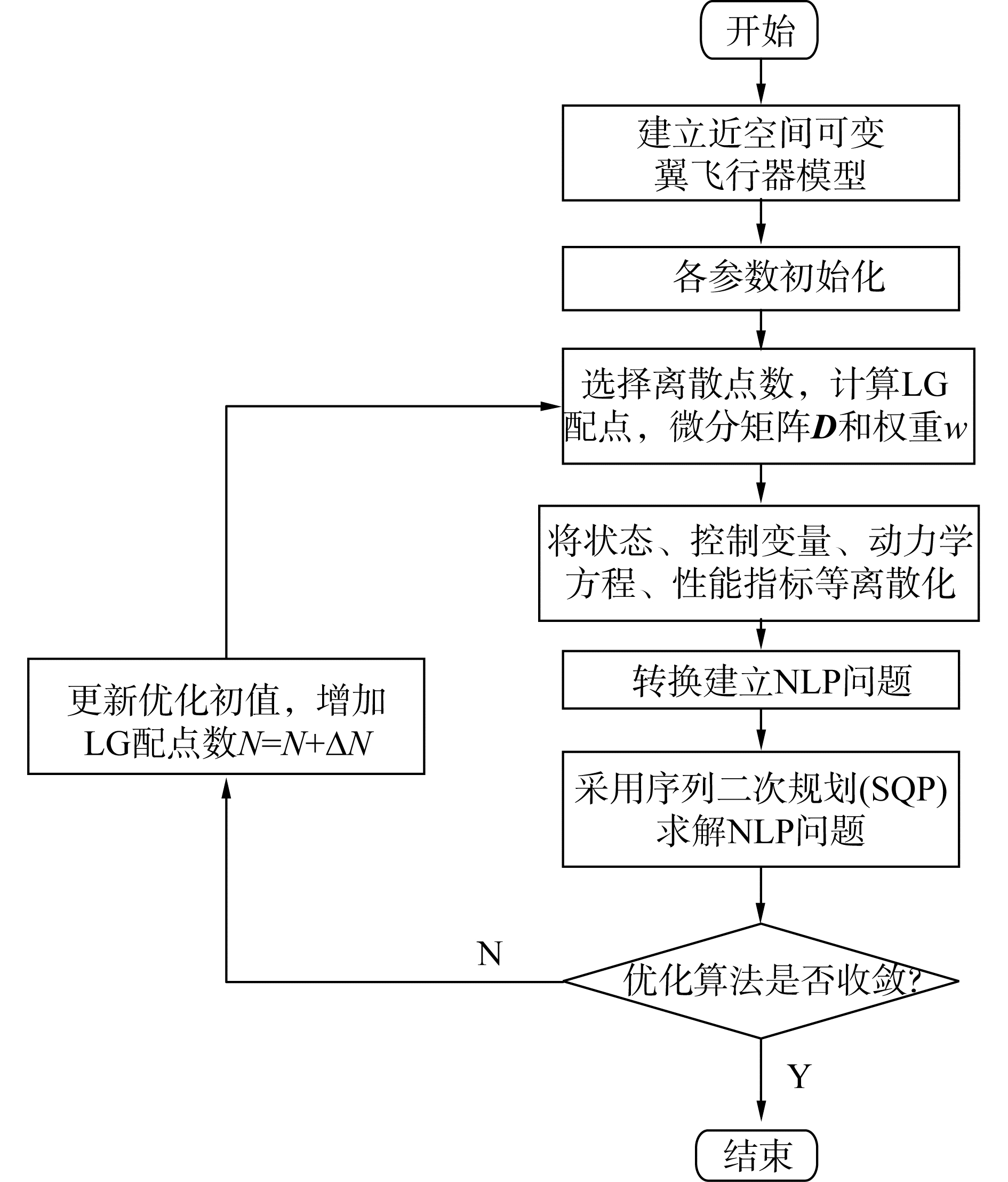
应用高斯伪谱法对爬升段可变翼飞行器小翼伸缩轨迹优化时,由于初值选取个数和LG配点个数成正比关系,为了保证能收敛到最优解及减少计算时间,本文提出一种初值选取改进的高斯伪谱法。
1) 选取配点个数n,针对飞行器爬升段爬升走廊约束选取合适的初值。
2) GPM法离散转化为NLP问题,利用SQP算法优化求解。
3) 将所得的控制变量代入系统状态方程,进行仿真,将仿真优化结果进行线性插值,作为下一步的初值。
4) 若爬升末端质量不再增加,则获得最优轨迹。否则取配点个数n=n+5,返回步骤2),初值由步骤3)获取得到的。
其优化策略流程如图 3所示。
|
Download:
|
| 图 3 优化策略算法流程 Fig. 3 Flow chart of the optimization strategy algorithm | |
利用上述优化策略,首先选取少量的LG配点进行优化,减少变量个数,为更多LG配点初值获取更精确的信息,也可以保证优化的收敛性,减少优化计算时间。
3 仿真分析 3.1 仿真初始条件与参数设置针对上述改进的高斯伪谱法优化策略,对近空间可变翼飞行器小翼伸缩面积进行最省燃油轨迹优化仿真实验。
给定可变翼飞行器初始总质量m0=100 200 kg,爬升段初始高度h0=17 000 m,初始速度V0=1 200 m/s,初始航迹角γ0=0.035 rad。爬升终端高度htf=26 000 m,终端速度Vtf=2 400 m/s,终端航迹角γtf=0,飞行器参考面积S=360 m2。控制量范围限定:迎角αmin=-3°, αmax=8°,油门开合状态βmin=0, βmax=1。小翼伸缩控制面积大小Ssmin=0 m2, Ssmax=30 m2。约束条件有:动压约束qmin=4×104 Pa, qmax=1.6×104 kPa,热流约束,
将高斯伪谱法计算出的控制变量代入运动微分方程,用Matlab的ode45命令数值积分可以获得飞行器爬升段的状态曲线,将高斯伪谱法得到的最优轨迹与此轨迹进行对比。仿真最优结果为选取插值点个数35,总优化计算时间为78.9 s。仿真效果如图 4所示。

|
Download:
|
| 图 4 状态量、控制变量优化曲线 Fig. 4 Optimization curves of state and control variable | |
由图 4(a)~(d)状态优化仿真曲线看出,飞行器在小翼伸缩变化的同时,对比ODE得到的轨迹,整个爬升高度误差优化精度控制在±3.5 m内,速度误差精度控制在±0.2 m/s内。从航迹角优化曲线图 4(e)看出,在爬升的同时,航迹角缓慢变化,最终收敛到终端约束条件。其中航迹倾斜角先增大后减小,说明速度矢量先是朝垂直方向增加,然后往水平方向移动,先加速向上爬升而后爬升趋于缓慢。
图 4(g)~(i)分别表示控制变量迎角、发动机节流阀状态、小翼伸缩面积变化曲线。从仿真图中可以看出小翼从初始时刻开始收回,由于在低速段小翼的伸出使得阻力系数增加,此时小翼收回有利于飞行器在低速段加速爬升。迎角、发动机节流阀状态在100 s后突然增大,此时小翼正好从收缩状态向伸出状态进行切换。小翼的伸出一方面增加了升力效应,使得油门可以小翼伸出过程中状态保持较小的恒定值,对于加速爬升油量控制具有可观的影响。飞行器在爬升至100 s左右时,速度加速到高超声速阶段,由于高超声速段发动机推力进行转换,且气动参数上小翼伸出对升阻比存在较大的影响,小翼的伸出使得气动焦点往后移动,为爬升阶段增加一定的稳定与机动特性。在高超声速阶段,小翼伸出对升力系数影响较大,因此小翼在100 s处从收回到缓慢伸出,此过程对飞行器油量节省也具有可观的影响。虽然此时发动机有一定幅度的跳转,但很快就趋于较小的稳定值。
图 4(f)质量变化曲线,小翼实时伸缩变化与小翼恒定不变爬升时的燃油消耗进行对比,可以得出,小翼进行实时伸缩有利于爬升段燃油的节省,在高超声速阶段,小翼的伸缩量使得阻力变化较为明显,因此合适的小翼伸缩会使影响燃料的消耗。从仿真图中可以看出,在100 s之后小翼伸出量与对应燃油消耗量有显著的影响关系,整个200 s的爬升过程中,消耗燃料约为10 t,相比爬升段全程小翼收回节省了燃油约700~900 kg,相比小翼全部伸出节省燃料约1 400~2 000 kg,可节省爬升段耗油量的10%,为飞行器下一阶段提供了充足的油量。
4 结论1) 为了能够较好地反映飞行器的真实飞行环境,综合考虑可变翼飞行器在近空间飞行声速变化、密度变化、地球引力及发动机推力变化等众多因素对飞行爬升轨迹的影响,使得建立的模型更为准确有效。
2) 设计并改进优化策略,有效解决爬升段的小翼伸缩轨迹优化,并且提高优化收敛速度与减少计算时长,使得优化效率进一步提高。
3) 对于可变翼飞行器利用可伸缩小翼这一特性,对飞行器在耗油量较大的爬升段进行优化,可以节省燃油消耗,具有一定的工程应用价值。
| [1] |
吴雨珊, 江驹, 甄子洋, 等. 基于回馈递推的可变翼高超声速飞行器智能非线性控制[J]. 哈尔滨工程大学学报, 2016, 37(7): 963-968. WU Yushan, JIANG Ju, ZHEN Ziyang, et al. Intelligent nonlinear control for the hypersonic morphing vehicle based on the backstepping method[J]. Journal of Harbin Engineering University, 2016, 37(7): 963-968. (  0) 0)
|
| [2] |
宗群, 田栢苓, 窦立谦. 基于Gauss伪谱法的临近空间飞行器上升段轨迹优化[J]. 宇航学报, 2010, 31(7): 1775-1781. ZONG Qun, TIAN Bailing, DOU Liqian. Ascent phase trajectory optimization for near space vehicle based on Gauss pseudospectral method[J]. Journal of astronautics, 2010, 31(7): 1775-1781. DOI:10.3873/j.issn.1000-1328.2010.07.012 (  0) 0)
|
| [3] |
GARCÍA I M. Nonlinear trajectory optimization with path constraints applied to spacecraft reconfiguration maneuvers[D]. Massachusetts: Massachusetts Institute of Technology, 2005.
(  0) 0)
|
| [4] |
杨希祥, 张为华. 基于Gauss伪谱法的固体运载火箭上升段轨迹快速优化研究[J]. 宇航学报, 2011, 32(1): 15-21. YANG Xixiang, ZHANG Weihua. Rapid optimization of ascent trajectory for solid launch vehicles based on Gauss pseudospectral method[J]. Journal of astronautics, 2011, 32(1): 15-21. DOI:10.3873/j.issn.1000-1328.2011.01.003 (  0) 0)
|
| [5] |
邱丰, 宋征宇. 采用联立法求解大姿态终端约束的上升段轨迹优化[J]. 宇航学报, 2017, 38(1): 18-25. QIU Feng, SONG Zhengyu. Large terminal attitude constrained trajectory optimization of ascent stage via simultaneous method[J]. Journal of astronautics, 2017, 38(1): 18-25. DOI:10.3873/j.issn.1000-1328.2017.01.003 (  0) 0)
|
| [6] |
周树静.高超声速飞行器爬升段轨迹优化与跟踪[D].哈尔滨: 哈尔滨工业大学, 2012. ZHOU Shujing. Ascent phase trajectory optimization and tracking for hypersonic vehicles[D]. Harbin: Harbin Institute of Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10213-1013036083.htm (  0) 0)
|
| [7] |
胡松启, 陈雨. 伪谱法在飞行器轨迹优化中应用分析[J]. 火箭推进, 2014, 40(5): 61-68. HU Songqi, CHEN Yu. Analysis of pseudospectral methods applied to aircraft trajectory optimization[J]. Journal of rocket propulsion, 2014, 40(5): 61-68. DOI:10.3969/j.issn.1672-9374.2014.05.011 (  0) 0)
|
| [8] |
HUNTINGTON G T, BENSON D, RAO A V. A comparison of accuracy and computational efficiency of three pseudospectral methods[C]//Proceedings of AIAA Guidance, Navigation and Control Conference and Exhibit. Hilton Head, South Carolina, 2007: 20-23.
(  0) 0)
|
| [9] |
邱文杰, 孟秀云. 基于HP自适应伪谱法的飞行器多阶段轨迹优化[J]. 北京理工大学学报, 2017, 37(4): 412-417. QIU Wenjie, MENG Xiuyun. Multi-phase trajectory optimization of vehicle based on HP-adaptive pseudospectral method[J]. Transactions of Beijing Institute of Technology, 2017, 37(4): 412-417. (  0) 0)
|
| [10] |
张重阳, 舒健生, 姚群, 等. 基于改进Gauss伪谱法的高超声速飞行器航迹规划[J]. 飞行力学, 2017, 35(5): 53-56, 61. ZHANG Chongyang, SHU Jiansheng, YAO Qun, et al. Trajectory planning for hypersonic vehicle based on improved GPM[J]. Flight dynamics, 2017, 35(5): 53-56, 61. (  0) 0)
|
| [11] |
黄国强, 陆宇平, 南英. 飞行器轨迹优化数值算法综述[J]. 中国科学:技术科学, 2012, 55(9): 2538-2560. HUANG Guoqiang, LU Yuping, NAN Ying. A survey of numerical algorithms for trajectory optimization of flight vehicles[J]. Science China technological sciences, 2012, 55(9): 2538-2560. (  0) 0)
|
| [12] |
张佩俊, 刘鲁华, 王建华. 基于高斯伪谱法的空天飞机上升段最优轨迹设计[J]. 空间控制技术与应用, 2017, 43(2): 13-20. ZHANG Peijun, LIU Luhua, WANG Jianhua. Optimal ascent trajectory design for single-stage-to-orbit space planes based on gauss pseudospectral method[J]. Aerospace control and application, 2017, 43(2): 13-20. DOI:10.3969/j.issn.1674-1579.2017.02.003 (  0) 0)
|
| [13] |
孙勇.基于改进Gauss伪谱法的高超声速飞行器轨迹优化与制导[D].哈尔滨: 哈尔滨工业大学, 2012. SUN Yong. Trajectory optimization and guidance of hypersonic vehicle based on improved Gauss pseudospectral method[D]. Harbin: Harbin Institute of Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10213-1013035314.htm (  0) 0)
|
| [14] |
张志国, 余梦伦, 耿光有, 等. 应用伪谱法的运载火箭在线制导方法研究[J]. 宇航学报, 2017, 38(3): 262-269. ZHANG Zhiguo, YU Menglun, GENG Guangyou, et al. Research on application of pseudo-spectral method in online guidance method for a launch vehicle[J]. Journal of astronautics, 2017, 38(3): 262-269. DOI:10.3873/j.issn.1000-1328.2017.03.006 (  0) 0)
|
| [15] |
陶超. 基于高斯伪谱法的高超声速飞行器轨迹优化与跟踪控制[J]. 系统仿真学报, 2017, 29(4): 865-872, 879. TAO Chao. Trajectory optimization and tracking controller based on gauss pseudo spectral method for hypersonic vehicle[J]. Journal of system simulation, 2017, 29(4): 865-872, 879. (  0) 0)
|
| [16] |
顾臣风, 江驹, 吴雨珊. 近空间飞行器爬升段跟踪控制[J]. 哈尔滨工程大学学报, 2016, 37(11): 1526-1531. GU Chenfeng, JIANG Ju, WU Yushan. Tracking control for a near-space vehicle in the ascent phase[J]. Journal of Harbin Engineering University, 2016, 37(11): 1526-1531. (  0) 0)
|
| [17] |
姚寅伟, 李华滨. 基于Gauss伪谱法的高超声速飞行器多约束三维再入轨迹优化[J]. 航天控制, 2012, 30(2): 33-38, 45. YAO Yinwei, LI Huabin. The generation of three-dimensional constrained entry trajectories for hypersonic vehicle based on the gauss pseudospectral method[J]. Aerospace control, 2012, 30(2): 33-38, 45. DOI:10.3969/j.issn.1006-3242.2012.02.007 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


