2. 河北工业大学 能源与环境工程学院, 天津 300401;
3. 青岛理工大学 环境与市政工程学院, 山东 青岛 266033
2. School of Energy and Environmental Engineering, Hebei University of Technology, Tianjin 300401, China;
3. School of Environmental and Municipal Engineering, Qingdao Technological University, Qingdao 266033, China
我国的风电总装机容量在过去十多年间快速增长,2010年以来高居世界第一,但同时也面临着无法忽视的弃风问题[1-2]。在基于热电联产实现区域供热的北方大部分地区,部分煤电机组在供暖季以热定电运行,电出力调节范围严重下降。在风电出力高峰且电负荷较低时,可能出现严重弃风[3-6]。
适度发展电供热,提高热电联产机组的运行灵活性是促进风电消纳的有效手段[7-8]。Chen等[9]提出利用电锅炉和蓄热罐促进风电消纳的方法,研究表明电热设备能够更有效地消纳风电。Hedegaard等[10]认为分布式热泵配合小型蓄热罐能够有效促进风电消纳。然而分布式小型热泵的供热系数在室外温度较低时非常有限,大规模推广应用的经济性存在争议。吕泉等[11]提出热电厂集中配置电热锅炉的弃风消纳方案,该方案的国民经济性取决于电网的弃风功率延续曲线和电热锅炉的装机容量。邓佳乐等[12]提出二级网配置分布式电热锅炉提升风能整合的方案。李群英等[13]提出利用电动热泵回收火电厂乏汽余热,扩大系统供热能力的同时促进风能利用。
尽管文献[11-13]都包含有一定的经济性分析,但均未明确提出新增电热设备最优装机容量的定量计算方法,且未能比较电热设备在不同组合条件下的经济性。本文以区域能源系统改造项目整个供暖季的净收益最大为目标,提出新增电热设备的最优装机容量优化配置模型,并在案例系统中实现了遗传优化计算。
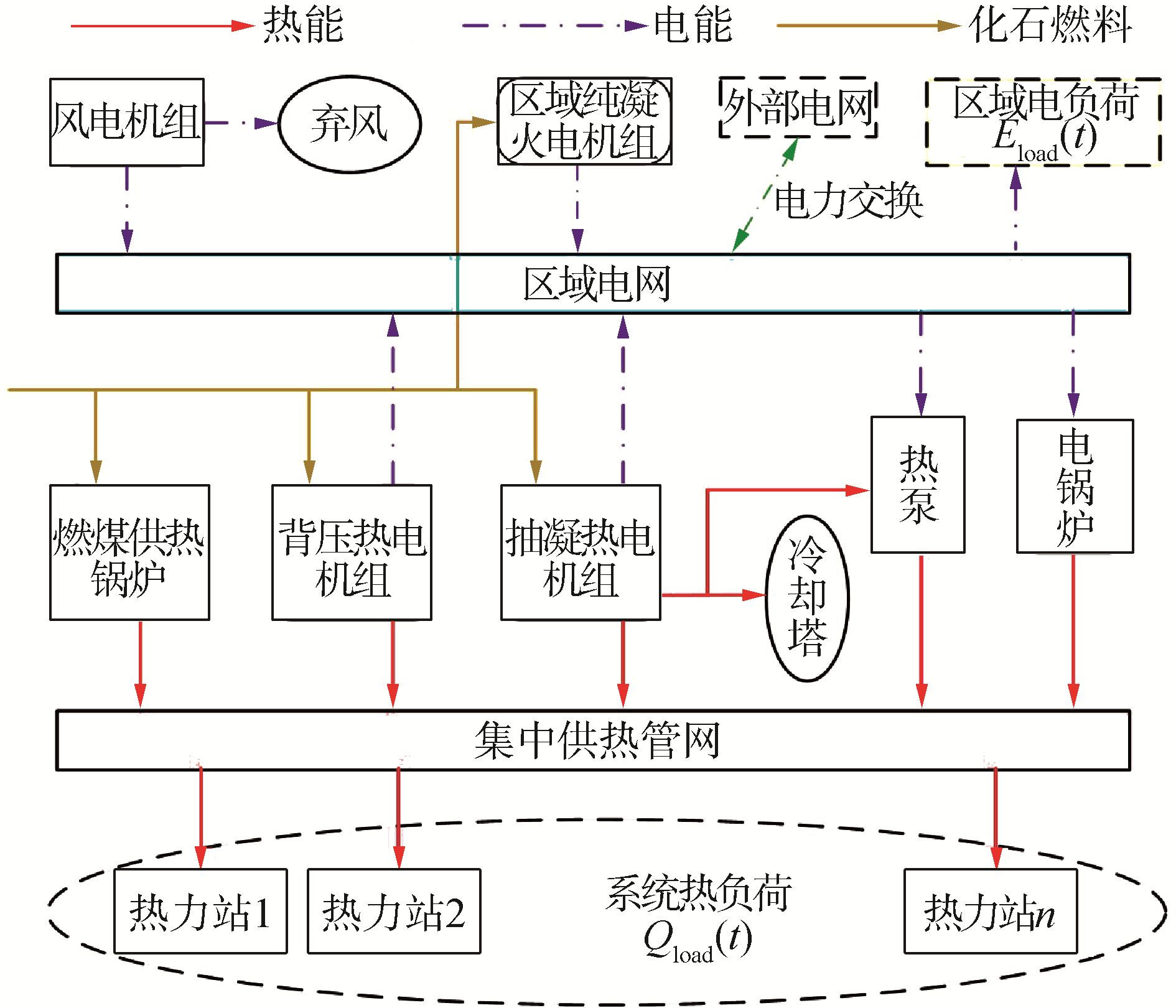
1 区域能源系统的构建确定区域能源系统的组成结构,厘清生产、输配和消费等环节的能流走向是能源系统逐时优化调度的基础,也是电热设备经济性优化配置研究的必要前提。“区域”在本文中特指由某区域供热系统所覆盖的小型城区,且该城区同时接入某小型区域电网。为反映区域电、热能源系统的宏观结构,并提高本研究的通用性和实用性,本文区域能源系统的典型组成结构和能流关系如图 1所示。
|
Download:
|
| 图 1 区域能源系统的典型结构及能量流向 Fig. 1 Typical configuration of a district energy system and the corresponding energy flow | |
考虑到我国北方地区电力系统的实际状况(水电等其他灵活电源的比例较小),区域能源系统中的电源仅包含风电机组、纯凝火电机组和热电联产机组。此外,由于供热机组的乏汽余热温度较高(相比室外空气、地下水和土壤),本文考虑配置一定容量的余热回收热泵来促进风电消纳。同时,电锅炉启停灵活、供热参数高,同样是理想的电热设备。
2 电热设备的经济优化配置 2.1 电热设备优化配置的目标函数从工程经济的角度看,配置余热回收热泵和电锅炉促进风电消纳是对原有区域能源系统的改造,适合采用“增量比较法”进行分析[14]。
将区域热、电系统看作一个整体,额外配置电热设备的宏观经济收益体现为区域能源系统在整个供热季总煤耗费用的降低(由于弃风减少、更多风电得到了有效利用);新增成本则为电热设备初投资分摊到某个供暖季内的费用。为定量分析电热设备在整个生命周期内的经济效益,本文以改造项目的供暖季“净收益(net profits,NP)”作为定量评价指标,其表达式为:
| $ {\rm{NP}} = [{\rm{TF}}{{\rm{C}}_{{\rm{ref}}}} - {\rm{TFC}}({\rm{I}}{{\rm{C}}_m})] - \sum\limits_m {{\rm{COS}}{{\rm{T}}_m}} $ | (1) |
式中:TFCref为区域能源系统供暖季的基准总煤耗费用,元;TFC(ICm)为配置一定容量电热设备后系统的总煤耗费用,元;COSTm为电热设备m的初投资分摊到寿命期每年内的成本费用(与设备的装机容量成正比),元。
考虑到资金的时间价值,COSTm的表达式如下:
| $ {\rm{ COST}}{ _m} = ({F_m} + {V_m} \cdot {\rm{I}}{{\rm{C}}_m}) \cdot \frac{{i{{(1 + i)}^n}}}{{{{(1 + i)}^n} - 1}} $ | (2) |
式中:Fm为电热设备m的固定投资成本,元;Vm为电热设备m的可变投资成本,元/MW;ICm为电热设备m的配置容量,MW;i为社会折现率;n为电热设备的预期使用寿命,a。
结合式(1)、(2),促进风电消纳的电热设备经济性优化配置的目标函数可表示为:
| $ \begin{array}{*{20}{l}} {{\rm{maxNP}} = {\rm{TF}}{{\rm{C}}_{{\rm{ref}}}} - {\rm{TFC}} ({\rm{I}}{{\rm{C}}_m}) - }\\ {({F_m} + {V_m} \cdot {\rm{I}}{{\rm{C}}_m}) \cdot \frac{{i{{(1 + i)}^n}}}{{{{(1 + i)}^n} - 1}}} \end{array} $ | (3) |
由式(3)可以看到,新增一定容量电热设备所能带来的年经济收益与区域能源系统改造前后供热季的总煤耗费用有关。因此,定量计算基准工况和新增电热设备后区域能源系统整个供热季的总煤耗费用是实现经济优化配置的关键。
2.2.1 目标函数当区域能源系统中热电设备的类型及装机容量确定后,理论上存在一组最优的机组运行调度计划,使区域能源系统在整个供暖季的总煤耗费用最低,由于最小化总煤耗费用与最小化风电场弃风在逻辑上的一致性,区域能源系统供暖季逐时优化调度的目标函数(优化结果可同时实现最大程度的风电消纳):
| $ \begin{array}{l} {\rm{ minTFC = }}\xi \cdot \Delta \tau \cdot \sum\limits_t {[{P_{{\rm{BP}}}}(t) + {P_{{\rm{EC}}}}(t) + } \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {P_{{\rm{HOB}}}}(t) + {P_{\rm{C}}}(t)] + \zeta \cdot \Delta \tau \cdot {\rm{PE}}(t) \end{array} $ | (4) |
式中:ξ为不同机组单位供能的燃煤成本,元/(MW·h);Δτ为系统优化调度的计算时间间隔,1 h;PBP(t)、PEC(t)、PHOB(t)和PC(t)分别为背压供热机组、抽凝供热机组、燃煤供热锅炉和纯凝火电机组t时刻的能耗(由各机组t时刻的电、热出力所决定),MW;ζ为区域电网与外部电网的电能交易费用,元/MW;PE(t)为t时刻区域电网与外部电网的交换功率(输入电能为正,输出电能为负),MW。
假设抽凝供热机组的热力循环由“背压循环”和“凝汽循环”线性组合而成,能源系统中不同机组的逐时能耗可计算得到:
| $ \left\{ {\begin{array}{*{20}{l}} {{P_{{\rm{BP}}}}(t) = \frac{{{Q_{{\rm{BP}}}}(t)}}{{{\eta _{{\rm{boiler}}}}}}(1 + \alpha )}\\ {{P_{{\rm{EC}}}}(t) = \frac{{{E_{{\rm{EC}}}}(t) + {c_v} \cdot {Q_{{\rm{EC}}}}(t)}}{{{\eta _{{\rm{CO}}}} \cdot {\eta _{{\rm{boiler}}}}}}}\\ {{P_{{\rm{HOB}}}}(t) = \frac{{{Q_{{\rm{HOB}}}}(t)}}{{{\eta _{{\rm{boiler}}}}}}}\\ {{P_{\rm{C}}}(t) = \frac{{{E_{\rm{C}}}(t)}}{{{\eta _{{\rm{CO}}}} \cdot {\eta _{{\rm{boiler}}}}}}} \end{array}} \right. $ | (5) |
式中:QBP(t)、QEC(t)和QHOB(t)分别为背压机、抽凝机和供热锅炉在t时刻的供热功率,MW;EEC(t)和EC(t)分别为抽凝机和纯凝发电机组在t时刻的发电功率,MW;ηboiler为燃煤锅炉的热效率;ηco为纯凝热力循环的发电效率;α为背压热力循环的电-热比;cv为抽凝机组的比发电损失。α和cv的表达式为:
| $ \left\{ {\begin{array}{*{20}{l}} {\alpha = \frac{{{\eta _{{\rm{bp}}}}}}{{1 - {\eta _{{\rm{bp}}}}}}}\\ {{c_v} = \frac{{{\eta _{{\rm{co}}}} - {\eta _{{\rm{bp}}}}}}{{1 - {\eta _{{\rm{bp}}}}}}} \end{array}} \right. $ | (6) |
式中ηbp为背压热力循环的发电效率。
2.2.2 约束条件区域热电系统在进行整个供热季的逐时优化调度时,需保证系统的电、热供需平衡;同时还需满足机组的容量及调节能力约束。
1) 电平衡约束
| $ \begin{array}{*{20}{c}} {\alpha \cdot {Q_{{\rm{BP}}}}(t) + {E_{{\rm{EC}}}}(t) + {E_{\rm{C}}}(t) + W(t) + {\rm{PE}}(t) = }\\ {{E_{{\rm{HP}}}}(t) + {E_{{\rm{EB}}}}(t) + {E_{{\rm{load}}}}(t)} \end{array} $ | (7) |
式中:W(t)为风电场在t时刻的并网发电功率,MW;EHP(t)和EEB(t)分别为余热回收热泵和电锅炉在t时刻的耗电功率,MW;Eload(t)为区域电网t时刻的电负荷,MW。
2) 热平衡约束
当不考虑供热管网及末端建筑物的蓄热,区域能源系统的逐时供热量要与系统的逐时热负荷相等,即:
| $ \begin{array}{*{20}{l}} {{Q_{{\rm{BP}}}}(t) + {Q_{{\rm{EC}}}}(t) + {Q_{{\rm{HOB}}}}(t) + {\rm{CO}}{{\rm{P}}_{{\rm{HP}}}} \cdot {E_{{\rm{HP}}}}(t) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\eta _{{\rm{EB}}}} \cdot {E_{{\rm{EB}}}}(t) = {Q_{{\rm{load}}}}(t)} \end{array} $ | (8) |
式中:COPHP为热泵的供热系数;ηEB为电锅炉的热效率;Qload(t)为区域供热系统t时刻的实际热负荷(与室、内外温差成正比),MW。
3) 供热机组的装机容量及调节能力约束
| $ \left\{ {\begin{array}{*{20}{l}} {{Q_{{\rm{BP,min}}}} \le {Q_{{\rm{BP}}}}(t) \le {Q_{{\rm{BP,max}}}}}\\ {[{E_{{\rm{EC}}}}(t),{Q_{{\rm{EC}}}}(t)] \in {\varOmega _{{\rm{EC}}}}} \end{array}} \right. $ | (9) |
式中:QBP, min和QBP, max分别为背压机组的最小、最大供热功率,MW;ΩEC为抽凝式供热机组的热电出力区间。
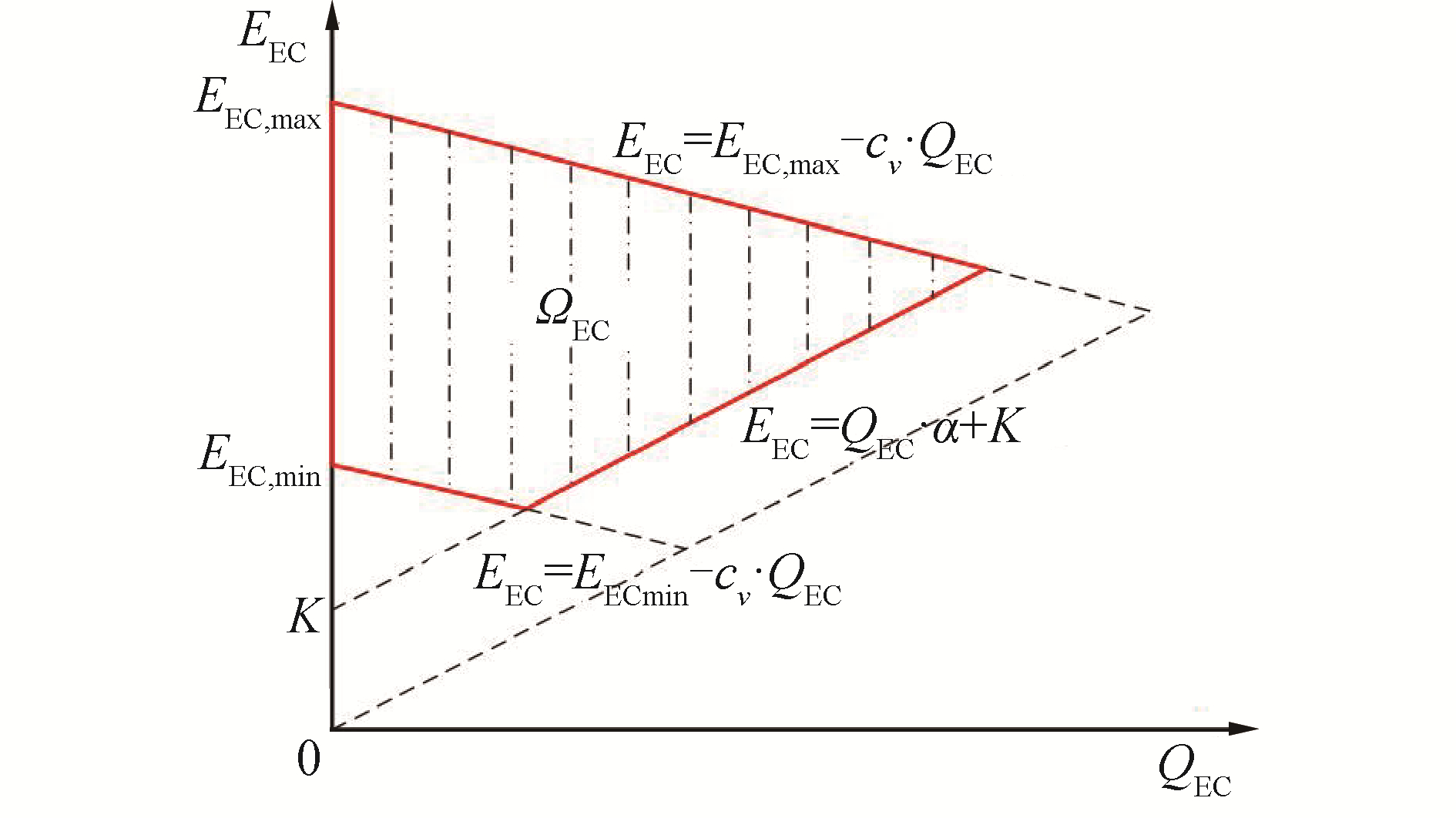
为保证抽凝供热机组运行的稳定性和安全性,抽凝机组并不能以背压工况运行,因此必然存在一定量的乏汽余热损失,因此抽凝供热机组热电出力的可行域如图 2所示。
4) 风电出力约束
| $ 0 \le W(t) \le {W_{{\rm{max}}}}(t) $ | (10) |
|
Download:
|
| 图 2 抽凝供热机组热电出力可行域 Fig. 2 Feasible region of heat and power output for extraction-condensing CHP units | |
式中:Wmax(t)为风电场t时刻的理论最大电出力,MW;Wmax(t)可由t时刻风电场的平均风速和风机总容量所确定[15],其表达式为:
| $ {W_{{\rm{max}}}}(t) = \left\{ {\begin{array}{*{20}{l}} {0,}&{0 \le v \le {v_i}}\\ {\frac{{v{{(t)}^3} - v_i^3}}{{v_r^3 - v_i^3}} \cdot {P_r},}&{{v_i} < v \le {v_r}}\\ {{P_r},}&{{v_r} < v \le {v_c}}\\ {0,}&{v > {v_c}} \end{array}} \right. $ | (11) |
式中:v(t)为风电场t时刻的平均风速,m/s;vi为风机的切入风速,m/s;vr为风机的额定风速,m/s;vc为风机的切出风速,m/s;Pr为风机的总装机容量,MW。
5) 纯凝火电机组和区域锅炉房的装机容量及调节范围约束
| $ \left\{ {\begin{array}{*{20}{l}} {{E_{{\rm{C,min}}}} \le {E_C}(t) \le {E_{{\rm{C,max}}}}}\\ {{Q_{{\rm{HOB,min}}}} \le {Q_{{\rm{HOB}}}}(t) \le {Q_{{\rm{HOB}}}}} \end{array}} \right. $ | (12) |
式中:ICHP和ICEB分别为余热回收热泵和电锅炉的装机容量,MW。
6) 余热回收热泵和电锅炉的装机容量约束
| $ \left\{ {\begin{array}{*{20}{l}} {0 \le {E_{{\rm{HP}}}}(t) \le {\rm{I}}{{\rm{C}}_{{\rm{HP}}}}}\\ {0 \le {E_{{\rm{EB}}}}(t) \le {\rm{I}}{{\rm{C}}_{{\rm{EB}}}}} \end{array}} \right. $ | (13) |
式中:ICHP和ICEB分别为余热回收热泵和电锅炉的装机容量,MW。
7) 抽凝机组的乏汽余热量约束
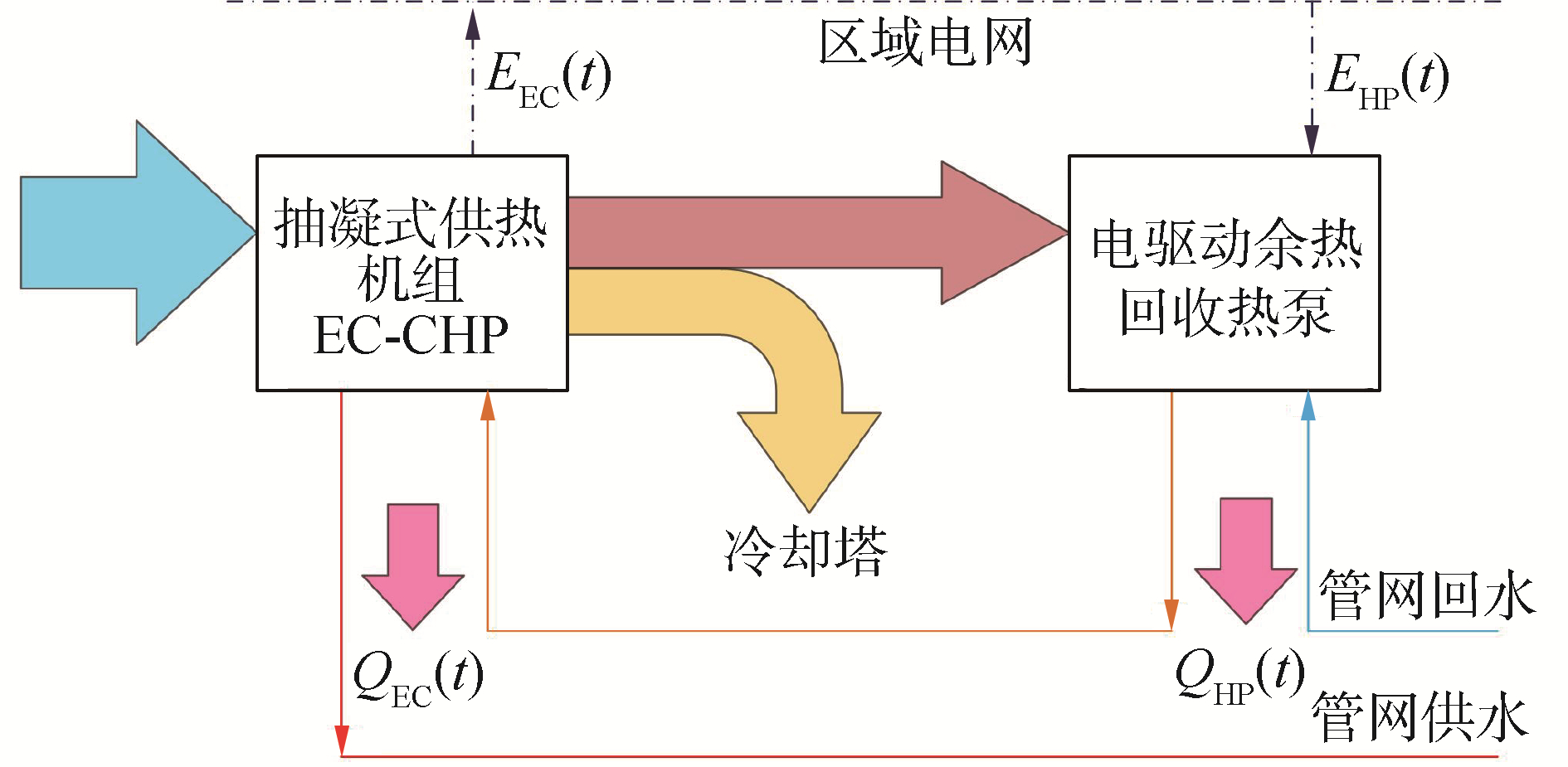
根据能量守恒,电热泵t时刻所回收的乏汽余热量必然要小于抽凝供热机组的总乏汽余热量,该约束可表示为(图 3为电热泵回收抽凝机组乏汽余热的示意图):
| $ ({\rm{CO}}{{\rm{P}}_{{\rm{HP}}}} - 1) \cdot {E_{{\rm{HP}}}}(t) \le \frac{{1 - {\eta _{co}}}}{{{\eta _{co}}}}\left[ {\begin{array}{*{20}{c}} {{E_{{\rm{EC}}}}(t)}\\ { - \alpha \cdot {Q_{{\rm{EC}}}}(t)} \end{array}} \right] $ | (14) |
|
Download:
|
| 图 3 电热泵回收供热机组的乏汽余热 Fig. 3 Exhaust heat recycling by using electric heat pump | |
8) 电网间输送能力约束:
| $ - {\rm{P}}{{\rm{E}}_{{\rm{max}}}} \le {\rm{PE}}(t) \le {\rm{P}}{{\rm{E}}_{{\rm{max}}}} $ | (15) |
式中PEmax(t)为电力联络线的最大输送功率,MW。
对于本文图 1所示的区域能源系统,供暖季逐时优化调度的决策变量见表 1。需要指出,由于背压热力循环的热电比恒定,因此背压机组的逐时发电量EBP(t)并非独立的决策变量。另外,热泵和电锅炉的逐时供热量QHP(t)和QEB(t)可由其逐时耗电量EHP(t)和EEB(t)直接计算得到,并非独立的决策变量。
| 表 1 长输管线与供热系统的相关设计参数 Table 1 Design parameters of long transmission pipelines and district heating system |
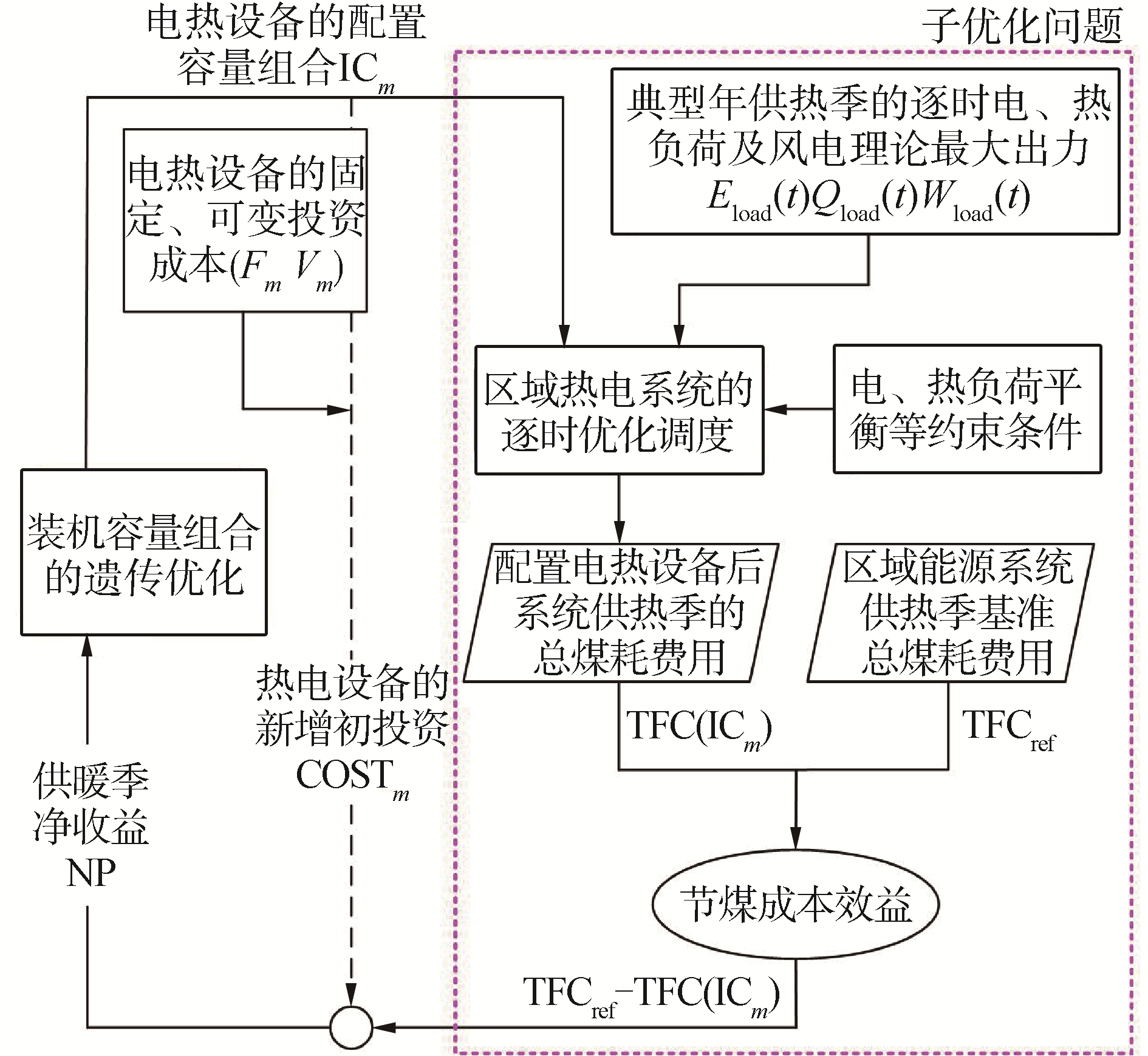
如图 4所示,电热设备装机容量的经济性优化配置可看作2类优化问题的组合:1)当电热设备的配置容量确定后,能源系统整个供暖季的净收益可由逐时优化调度计算得到(供热季系统的逐时电、热负荷及风电场逐时理论最大电出力采用最近几年的实测数据);2)由于决策变量(设备装机容量组合ICm)与目标函数NP之间的复杂耦合关系,本文采用遗传算法进行寻优计算。算法收敛后便可得到经济性最优的电热设备装机容量组合。
|
Download:
|
| 图 4 电热设备的经济性优化配置流程 Fig. 4 Solving progress of economy optimizing for electric heating devices | |
利用遗传算法对电热设备的装机容量进行优化计算,还需要对决策变量的搜索范围进行限定,其显式约束条件为:
| $ \left\{ {\begin{array}{*{20}{l}} {0 \le {\rm{I}}{{\rm{C}}_{{\rm{HP}}}} \le {\rm{I}}{{\rm{C}}_{{\rm{HP,max}}}}}\\ {0 \le {\rm{I}}{{\rm{C}}_{{\rm{EB}}}} \le {\rm{I}}{{\rm{C}}_{{\rm{EB,max}}}}} \end{array}} \right. $ | (16) |
式中:ICHP, max和ICEB, max分别为热泵和电锅炉装机容量的搜索上限,MW。
3 电热设备经济优化配置的案例计算本文以吉林省白城市某小型区域热电系统为例,对本文提出的电热设备优化配置模型及遗传算法的有效性进行验证;并计算在不同经济性参数条件下,电热设备的最优配置容量。
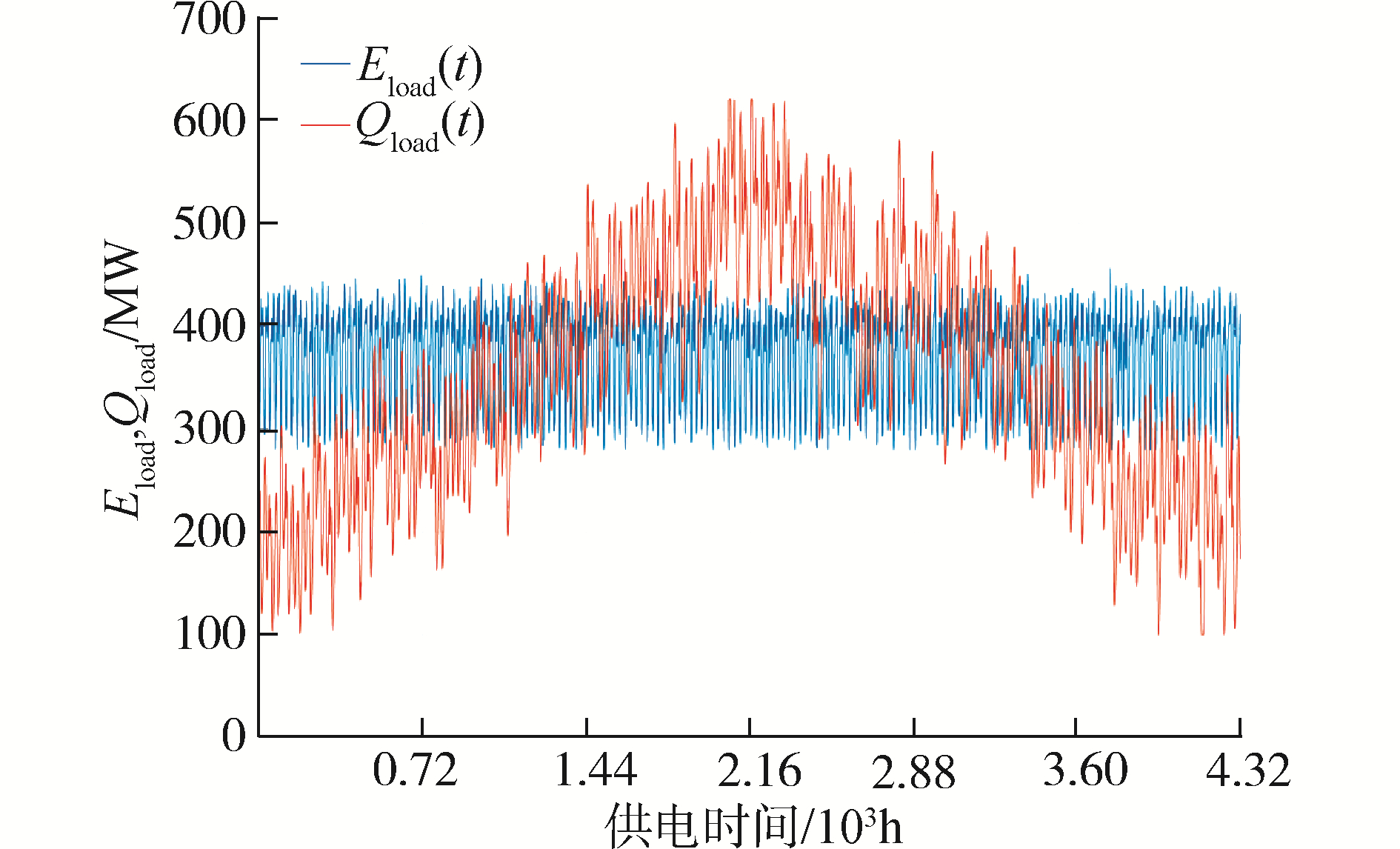
3.1 区域能源系统的电、热负荷及风电资源状况在该区域能源系统中,逐时电负荷Eload(t)具有明显的日内变化规律,且电负荷的日平均值在整个供热季较为平稳,没有显著的季节性变化;与逐时电负荷不同,系统的逐时热负荷不仅具有显著的日内波动,且在整个供暖季有明显的变化规律(供热初末期较小而严寒期较大)。由实测数据,能源系统2017—2018年供暖季(共180 d、4 320 h)的逐时电、热负荷变化曲线如图 5所示。
|
Download:
|
| 图 5 区域能源系统供暖季的逐时电、热负荷 Fig. 5 Hourly power and heat load of the district energy system during the heating season | |
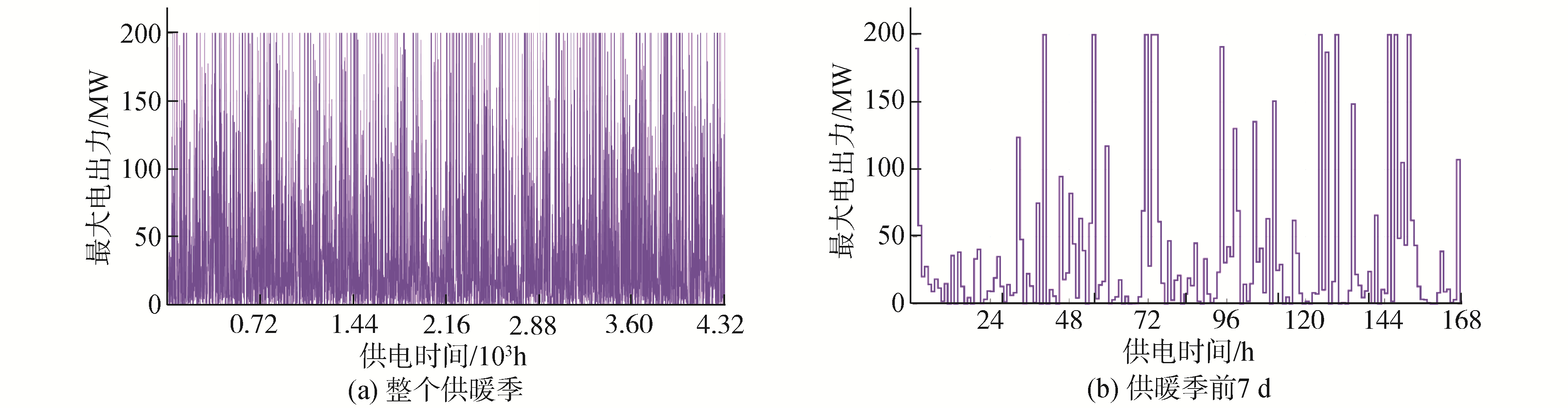
该区域能源系统接入总装机容量200 MW的风电机组(风机的切入风速、额定风速和切出风速分别为3、16和25 m/s)。同一时期、风电场逐时平均风速的频数分布与风电场的逐时理论最大电出力见图 6、图 7。

|
Download:
|
| 图 6 供暖季小时平均风速的分布 Fig. 6 Distribution of hourly mean wind speed during the heating season | |
|
Download:
|
| 图 7 风电场的逐时理论最大电出力 Fig. 7 Hourly theoretical power output from the district wind farm | |
区域能源系统中各设备的装机容量和调节性能参数见表 2,用于经济性分析的相关参数取值见表 3。
| 表 2 能源设备的技术参数取值 Table 2 Technical parameters of each energy devices |
| 表 3 经济性参数取值 Table 3 Values of the economical parameters |
电热设备的初投资成本受技术、市场、政策导向、政府补贴等多种因素的共同影响,在不同地区、不同时期可能存在较大的变化。为考察设备最优装机容量与建设成本的定量关系,本文假设电热设备的固定投资费用Fm恒定,而可变投资费用Vm则根据已有的工程案例限定在一个较大的变化区间内。
3.3 供暖季的基准运行工况为定量评估新增一定容量电热设备的经济收益,需要对区域能源系统整个供暖季的运行情况进行逐时优化计算,并以未配置电热设备时系统的总煤耗费用TFCref作为净收益计算的基准。
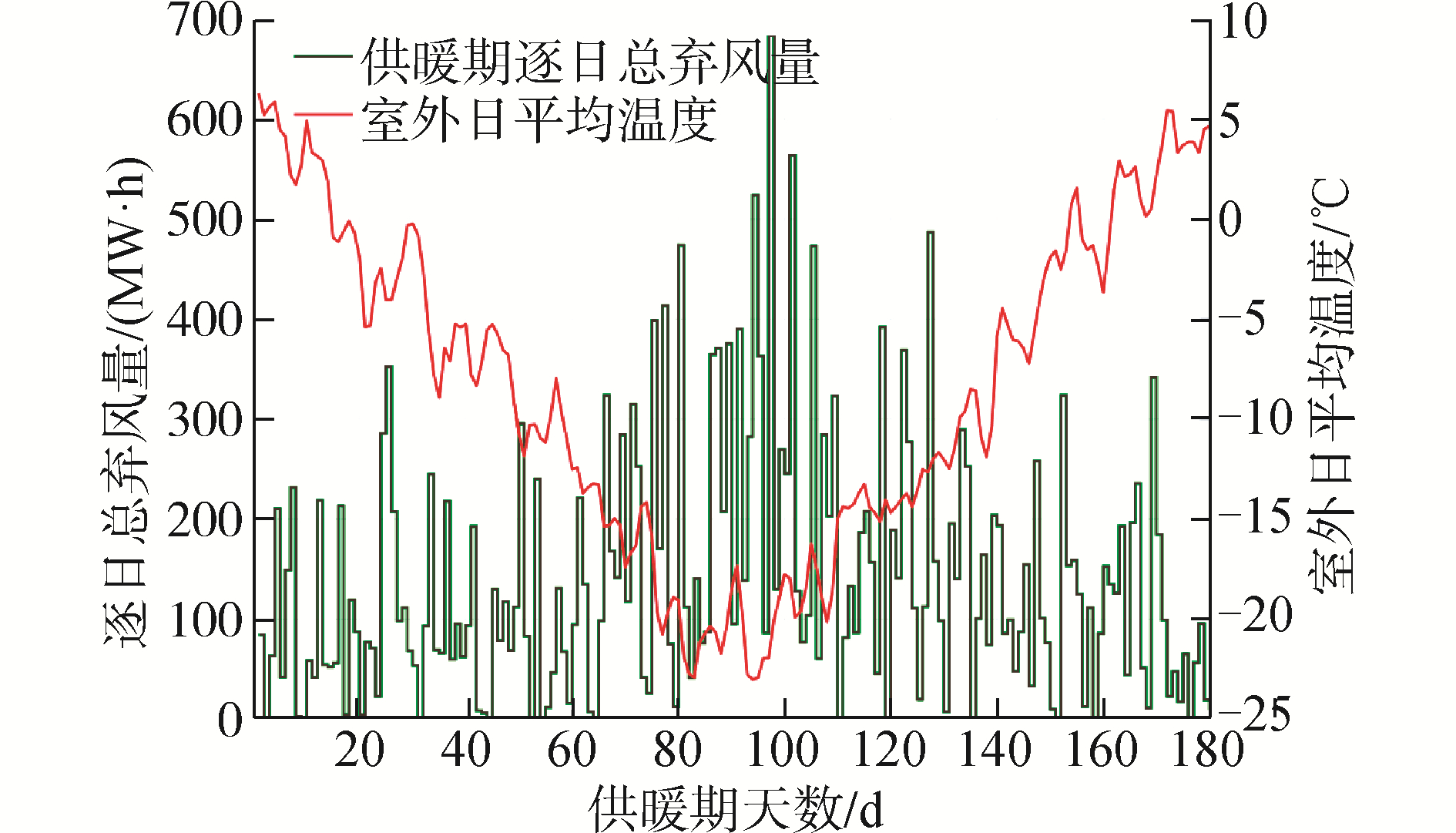
当未配置电热设备时,经本文2.2节的逐时优化调度计算可得:区域能源系统整个供暖季的基准总弃风量为25 485.2 MW·h(弃风率14.18 %),系统总煤耗费用42 383万元。风电场逐日总弃风量与室外日平均温度在供暖季不同时期的变化曲线见图 8。
|
Download:
|
| 图 8 基准工况下区域能源系统的逐日总弃风量与室外日平均温度 Fig. 8 Total daily curtailed wind power of district energy system under reference scenario and the daily mean outdoor temperature | |
如图 8所示,供暖季逐日总弃风量的变化规律与室外平均温度的变化趋势相反。严寒期供热系统的热需求较大、热电联产机组的最小供热量增加,因此区域电网的电力调峰能力受限、弃风增大。
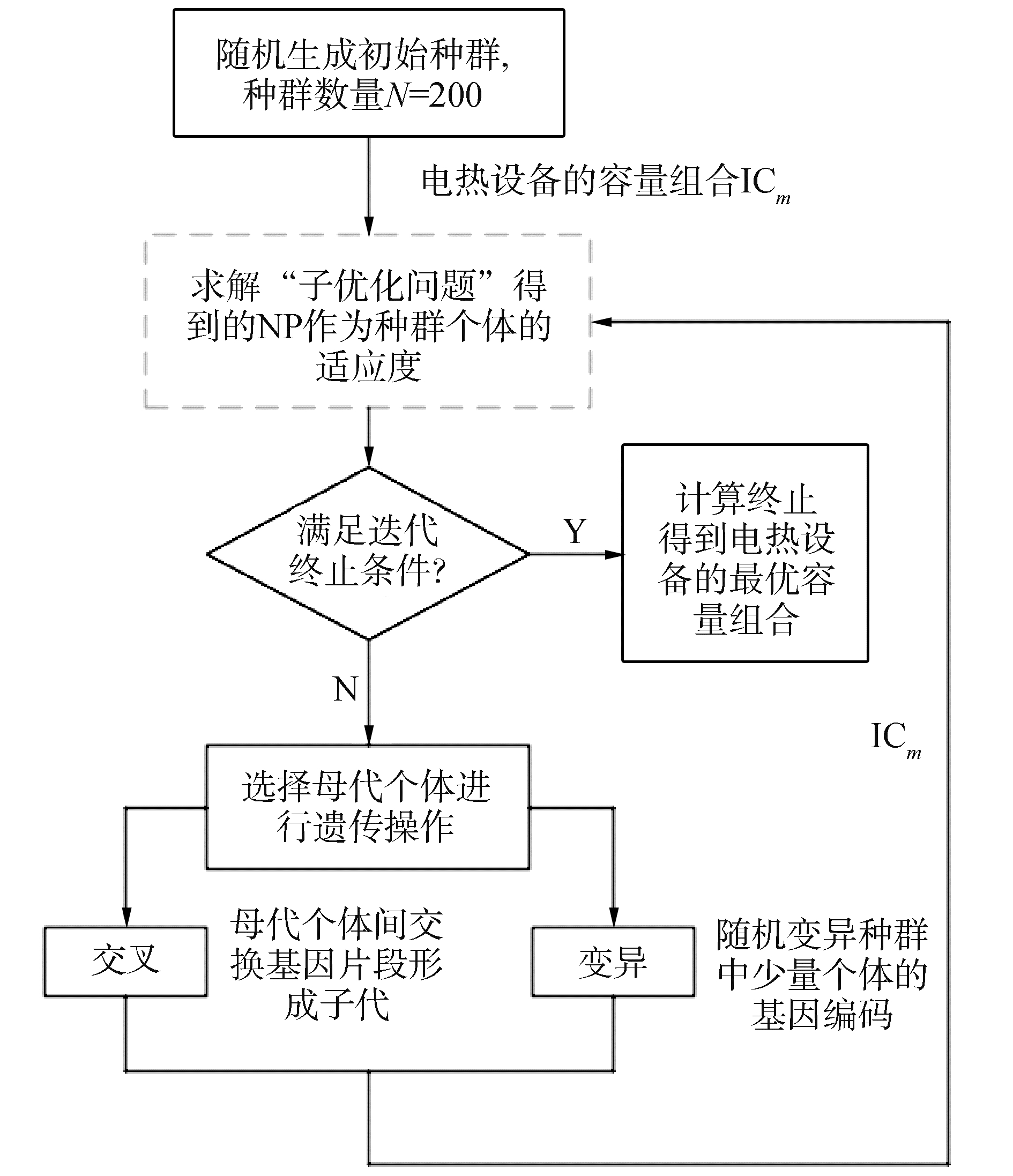
3.4 电热设备最优配置容量的遗传优化本文使用Matlab遗传算法工具箱(gatool)对电热设备的最优经济容量配置进行全局搜索,遗传算法的简易流程见图 9。
|
Download:
|
| 图 9 遗传优化的计算流程 Fig. 9 Solving process of the genetic algorithm | |
当仅在区域热电系统中引入余热回收热泵或电锅炉时,则不同可变投资成本所对应的遗传优化结果见表 4、表 5。
| 表 4 仅引入热泵的经济优化配置结果 Table 4 Optimal economic results of only introducing the electric heat pumps |
| 表 5 仅引入电锅炉的经济优化配置结果 Table 5 Optimal economic results of only introducing the electric boilers |
从表 4、表 5中可以看到,当只引入热泵或电锅炉促进弃风消纳时,不同电热设备的经济性最优配置容量均随可变投资成本的升高而降低,供暖季净收益也显著降低。特别地,当VEB≥50万元/MW时,配置任意容量电锅炉所带来的经济收益都将小于设备的安装投资成本,因此优化计算的结果为0。另一方面,由于低品位余热的回收利用、热泵可以提供超出耗电量数倍的供热量。对比表 4、表 5中的数据,可以看到新增热泵设备所带来的供暖季净收益显著高于电锅炉。
当在区域能源系统中同时引入热泵和电锅炉,不同投资成本组合条件下电热设备的最优配置容量见表 6。
| 表 6 同时引入热泵和电锅炉的经济优化配置结果 Table 6 Optimal economic results of introducing both the heat pumps and the electric boilers |
从表 6可以看到,热泵和电锅炉的综合优化配置能够带来更好的经济效益。供暖季净收益NP相比配置单一种类的电热设备有了进一步的提升,同时弃风总量和弃风率达到更低的水平。
根据边际效益递减的经济学原理,当新增电热设备所带来的边际收益(促进弃风消纳的系统节煤费用)与投资费用增量相等时,容量配置达到最优。因此,实现100%的风电消纳可能并不经济。从表 4~6的优化计算结果可以看到,新增电热设备能够显著降低弃风率,但并没有完全消除弃风。
4 结论1) 当仅配置单一种类的电热设备时,其最优装机容量随可变投资成本的增大而减少,当可变投资成本大于某临界值后,配置任何容量的电热设备都无法带来经济收益。
2) 由于大量乏汽余热的回收利用,单独配置电热泵的供暖季净收益远高于单独配置电锅炉;同时组合配置热泵和电锅炉能够达到最佳的经济收益,并最大程度上消纳弃风电能。
3) 由于风电出力的随机性和波动性,完全消纳弃风电能既无必要也不经济,因此在电热设备的最优容量配置条件下,依然存在一定比例的弃风。
区域能源系统逐时优化调度的计算负荷较大,当参与遗传优化的种群数量较多时,优化配置计算的收敛速度很慢,如何降低计算负荷、提高优化计算效率有待进一步的研究。
| [1] |
中国风能协会(CWEA). 2016年中国风电装机容量简报[EB/OL]. (2016-02-17). http://www.escn.com.cn/news/show-397308.html.Chinese Wind Energy Association (CWEA). Brief report of the installed capacity of all wind power units in China 2016[EB/OL]. (2016-02-17). http://www.escn.com.cn/news/show-397308.html. (  0) 0)
|
| [2] |
张宁, 周天睿, 段长刚, 等. 大规模风电场接入对电力系统调峰的影响[J]. 电网技术, 2010, 34(1): 152-158. ZHANG Ning, ZHOU Tianrui, DUAN Changgang, et al. Impact of large-scale wind farm connecting with power grid on peak load regulation demand[J]. Power system technology, 2010, 34(1): 152-158. (  0) 0)
|
| [3] |
LUO Guoliang, LI Yanling, TANG Wenjun, et al. Wind curtailment of China's wind power operation: evolution, causes and solutions[J]. Renewable and sustainable energy reviews, 2016, 53: 1190-1201. DOI:10.1016/j.rser.2015.09.075 (  0) 0)
|
| [4] |
周强, 汪宁渤, 冉亮, 等. 中国新能源弃风弃光原因分析及前景探究[J]. 中国电力, 2016, 49(9): 7-12, 159. ZHOU Qiang, WANG Ningbo, RAN Liang, et al. Cause analysis on wind and photovoltaic energy curtailment and prospect research in China[J]. Electric power, 2016, 49(9): 7-12, 159. (  0) 0)
|
| [5] |
冯泽深, 张曙光, 郭雁珩, 等. 东北地区风电"弃风"现状及分析[J]. 电气技术, 2014(2): 1-3. FENG Zeshen, ZHANG Shuguang, GUO Yanheng, et al. Status and analysis of abandoned wind power in northeast of China[J]. Electrical engineering, 2014(2): 1-3. (  0) 0)
|
| [6] |
王赵宾. 中国弃风限电报告[J]. 能源, 2014(7): 42-48. WANG Zhaobin. Wind energy curtailment list[J]. Energy, 2014(7): 42-48. (  0) 0)
|
| [7] |
LUND H. Large-scale integration of wind power into different energy systems[J]. Energy, 2005, 30(13): 2402-2412. DOI:10.1016/j.energy.2004.11.001 (  0) 0)
|
| [8] |
MEIBOM P, KIVILUOMA J, BARTH R, et al. Value of electric heat boilers and heat pumps for wind power integration[J]. Wind energy, 2007, 10(4): 321-337. DOI:10.1002/we.224 (  0) 0)
|
| [9] |
CHEN Xinyu, KANG Chongqing, O'MALLEY M, et al. Increasing the flexibility of combined heat and power for wind power integration in China: Modeling and implications[J]. IEEE transactions on power systems, 2015, 30(4): 1848-1857. (  0) 0)
|
| [10] |
HEDEGAARD K, MATHIESEN B V, LUND H, et al. Wind power integration using individual heat pumps-analysis of different heat storage options[J]. Energy, 2012, 47(1): 284-293. (  0) 0)
|
| [11] |
吕泉, 姜浩, 陈天佑, 等. 基于电锅炉的热电厂消纳风电方案及其国民经济评价[J]. 电力系统自动化, 2014, 38(1): 6-12. LYU Quan, JIANG Hao, CHEN Tianyou, et al. Wind power accommodation by combined heat and power plant with electric boiler and its national economic evaluation[J]. Automation of electric power systems, 2014, 38(1): 6-12. (  0) 0)
|
| [12] |
邓佳乐, 胡林献, 李佳佳. 采用二级热网电锅炉调峰的消纳弃风机理及经济性分析[J]. 电力系统自动化, 2016, 40(18): 41-47. DENG Jiale, HU Linxian, LI Jiajia. Analysis on mechanism of curtailed wind power accommodation and its economic operation based on electric boiler for peak-load regulation at secondary heat supply network[J]. Automation of electric power systems, 2016, 40(18): 41-47. DOI:10.7500/AEPS20151001001 (  0) 0)
|
| [13] |
李群英, 冯利民, 许宇辉, 等. 基于水源热泵技术的风电消纳模式[J]. 电力系统自动化, 2012, 36(17): 25-27, 61. LI Qunying, FENG Limin, XU Yuhui, et al. Accommodation mode of wind power based on water source heat pump technology[J]. Automation of electric power systems, 2012, 36(17): 25-27, 61. (  0) 0)
|
| [14] |
刘玉明.工程经济学[M].北京: 清华大学出版社, 北京交通大学出版社, 2006. LIU Yuming. Engineering economics[M]. Beijing: Tsinghua University Press, Beijing JiaoTong University Press, 2006. (  0) 0)
|
| [15] |
LI Pai, GUAN Xiaohong, WU Jiang, et al. Modeling dynamic spatial correlations of geographically distributed wind farms and constructing ellipsoidal uncertainty sets for optimization-based generation scheduling[J]. IEEE transactions on sustainable energy, 2015, 6(4): 1594-1605. DOI:10.1109/TSTE.2015.2457917 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


