2. 石家庄铁道大学 河北省交通应急保障工程技术研究中心, 河北 石家庄 050043
2. Hebei Engineering Research Center for Traffic Emergency and Guarantee, Shijiazhuang TieDao University, Shijiazhuang 050043, China
斜拉桥因其力学性能好且跨越能力强,在过去几十年中得到快速发展。基于行车安全和震后修复等因素的考虑,规范[1-2]中要求其在E1地震作用下结构应保持在弹性范围内,而在E2地震作用下主塔等重要受力构件产生的局部损伤也应当可修复。然而,1995年神户地震[3]及1999年我国台湾省集集镇地震[4]中斜拉桥均观测到明显的震害,因而研究其在地震作用下的响应特性及损伤模式有重要意义。
目前在实际工程中为改善斜拉桥抗震性能,通常采取减隔震设计。不同学者对大跨度桥梁中减隔震体系的应用已展开了深入的研究。Sharabash等[5]分析了一种使用形状记忆合金(SMAs)的新型被动减震装置,研究表明其能改善斜拉桥的抗震性能;Soneji等[6]研究了在双向地震作用下斜拉桥隔震的有效性与局限性。此外,还有学者对减隔震装置的混合使用以及参数设置进行了深入的研究[7-10]。以上研究主要通过对减隔震装置的技术创新和优化设计来控制桥梁的地震响应,忽略了可以通过对斜拉桥主塔结构形式的优化设计提升主塔的抗震性能,以达到桥梁抗震设计的目标要求。
低重心斜拉桥由于其重心高度非常低,导致结构动力特性会有很大不同[11-12]。目前关于不同结构体系低重心斜拉桥地震响应特性和强震损伤模式的研究还相对较少。为此,本文以某双塔半漂浮体系斜拉桥为工程背景,设计了3个不同的低重心斜拉桥试验模型,通过模拟地震振动台试验,研究了不同结构体系、不同形式桥塔模型的动力特性和破坏模式。
1 振动台试验模型设计本文选取某双塔双索面组合梁斜拉桥为振动台试验原型桥。主桥全长为636.6 m,跨径组合为32.9 m+115.4 m+340 m+115.4 m+32.9 m。该斜拉桥为半漂浮体系,桥塔采用纵向1字形索塔,索塔高为119.629 m,塔柱采用空心箱型断面,桥梁全宽36.6 m。主桥各塔均布置13对索及横、竖向限位装置。
在本次试验模型的设计中,由于试验设备中振动台台面尺寸仅为3 m×3 m,为满足全桥模型的长度要求,采用钢梁将振动台台面加长至5 m,并参照加长后台面尺寸设计了3个双塔三跨低重心斜拉桥试验模型。3个模型主塔材料均为钢筋混凝土,主梁和辅助墩则采用钢材模拟,斜拉索采用2 mm钢丝模拟,并对原型桥斜拉索进行并索处理以满足索距要求[13]。
考虑到振动台尺寸及承载能力,试验模型的几何相似比为1/75,加速度相似比为1。由于钢主梁在试验过程中并不是重点研究对象,且受限于振动台尺寸,因此对其长度适当缩减,几何相似比按1/120进行设计,钢主梁的弹性模量相似比为1。本次试验的跨径组合为1.23 m+2.8 m+1.23 m,总长度为5.26 m。表 1为混凝土主塔的相似比设计。
| 表 1 混凝土主塔相似比设计 Table 1 Similarity relation design of concrete towers |
本次试验模型为小比例缩尺模型,不同于大比例振动台试验模型可以直接参照几何相似系数缩尺的设计方法,小比例模型截面缩尺若严格按照几何相似比,则模型加工困难。因此,选取主要而忽略次要相似系数,采用刚度等效原则,对主塔、主梁截面设计按抗弯刚度严格等效,并忽略抗扭刚度和抗压刚度。
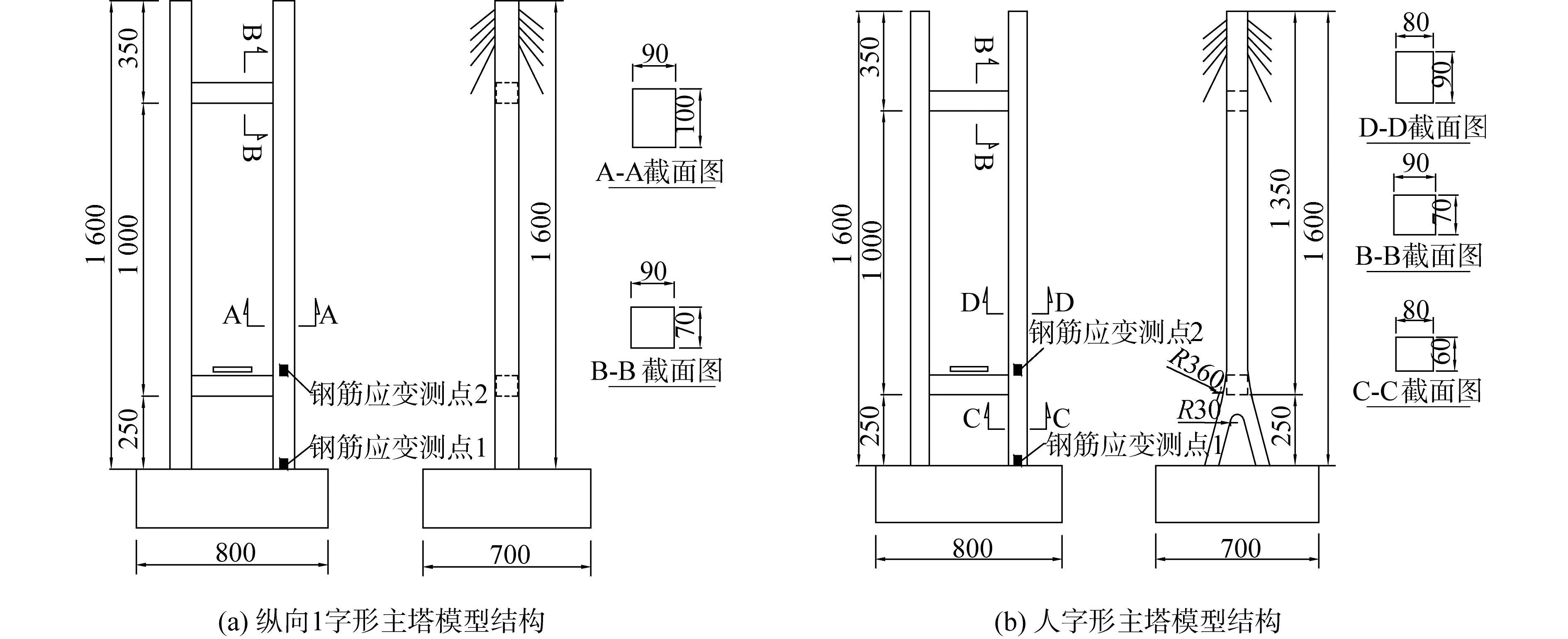
试验模型主塔分为2种不同形式:纵向1字形主塔和塔底分叉的纵向人字形主塔。人字形主塔塔柱自上而下分为3个不同区段:上部直线段、分叉点处圆弧过渡段和底部斜腿段[14],底部斜腿段的倾斜度为1/6。在相似比设计中,3个振动台试验模型采用相同相似关系进行设计,并且在设计中遵循材料用量一致的原则,即单个主塔的钢筋和混凝土总用量相同。试验模型中单个主塔钢筋用量约为6.59 kg,混凝土浇筑量约为0.033 m3。纵向1字形主塔和纵向人字形主塔模型设计如图 1所示。模型配重采用实验室中标准铁块,并通过质量相似系数得出模型质量,与模型自重之差即为所需配重。模型主塔共配重280 kg,主梁配重320 kg。
|
Download:
|
| 图 1 试验模型设计 Fig. 1 Design of test model | |
本次试验中的3个低重心斜拉桥模型均为双塔三跨。模型1的A塔和B塔均采用原桥中的纵向1字形,其中A塔与主梁间采用固定支座连接,B塔与主梁间无纵向约束;模型2的A塔结构形式为纵向人字形,B塔为原桥中的纵向1字形,其中A塔与主梁间采用固定支座连接,B塔与主梁间无纵向约束;模型3的A塔和B塔均采用原桥中的纵向1字形,塔梁间无纵向约束。全桥试验模型如图 2所示。

|
Download:
|
| 图 2 振动台全桥试验模型 Fig. 2 Test model in shaking tables | |
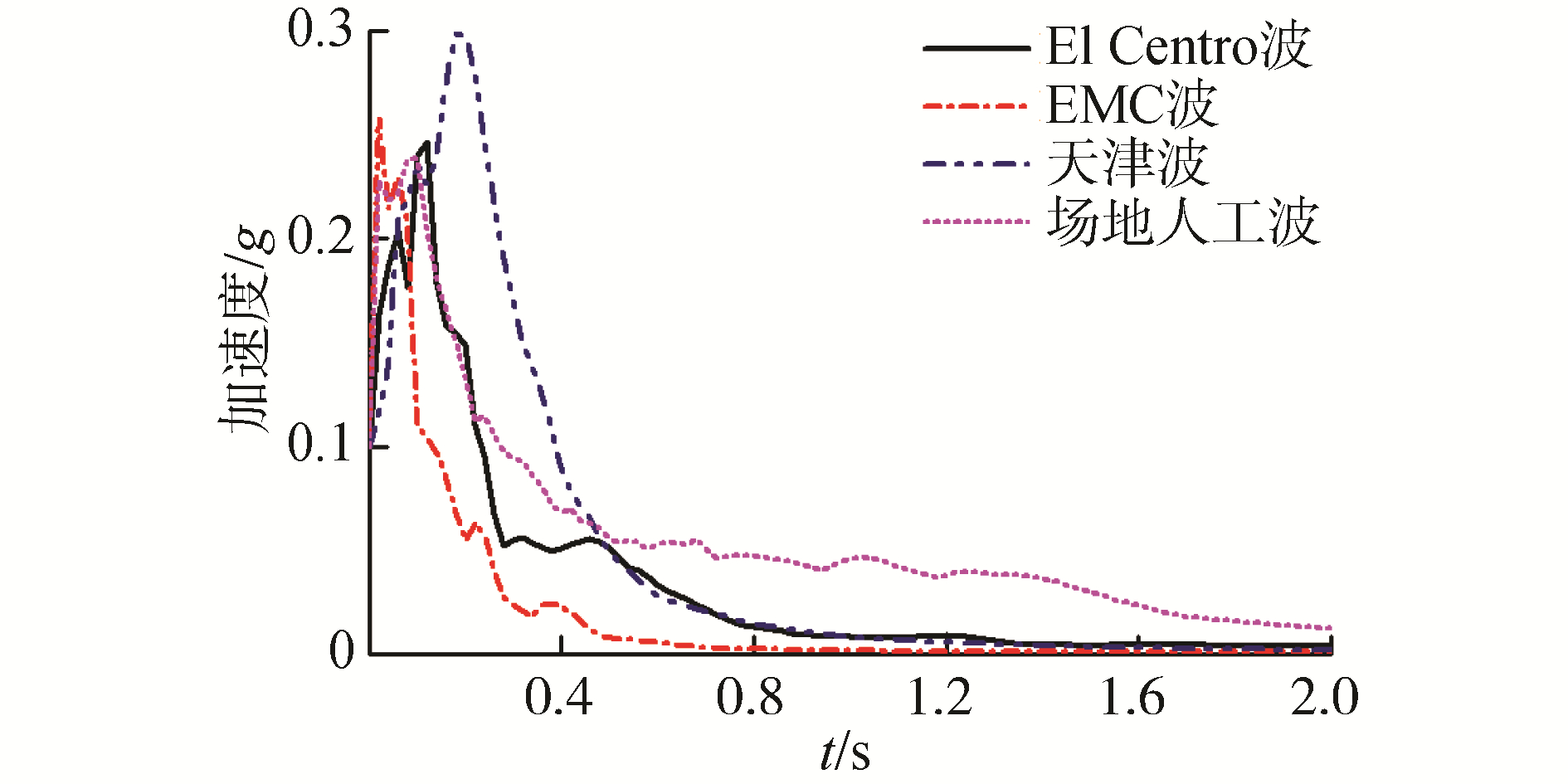
选取3条实测地震波(分别为El Centro波、天津波、EMC_FAIRVIEW AVE波)和一条场地人工波沿纵桥向(如图 2所示)进行地震激励。将上述4条地震波的峰值加速度(PGA)统一调整为0.1g,并将台面输入的试验波周期压缩为原始波的1/5。本次试验主要目的是探究低重心斜拉桥的地震响应特性及在强震作用下的损伤模式,并不强求反推回原形桥结构,因此地震波周期的压缩并未严格按照相似比设计中的时间相似常数,以保证试验模型有一定的地震反应时间。台面输入地震波的加速度响应谱如图 3所示。可以看出,El Centro波和天津波包含更多的低频成分,会对长周期结构产生明显的影响。相比之下,EMC波则包含较多的高频成分。
|
Download:
|
| 图 3 台面输入地震波的加速度响应谱 Fig. 3 Acceleration response spectrum of input earthquake waves | |
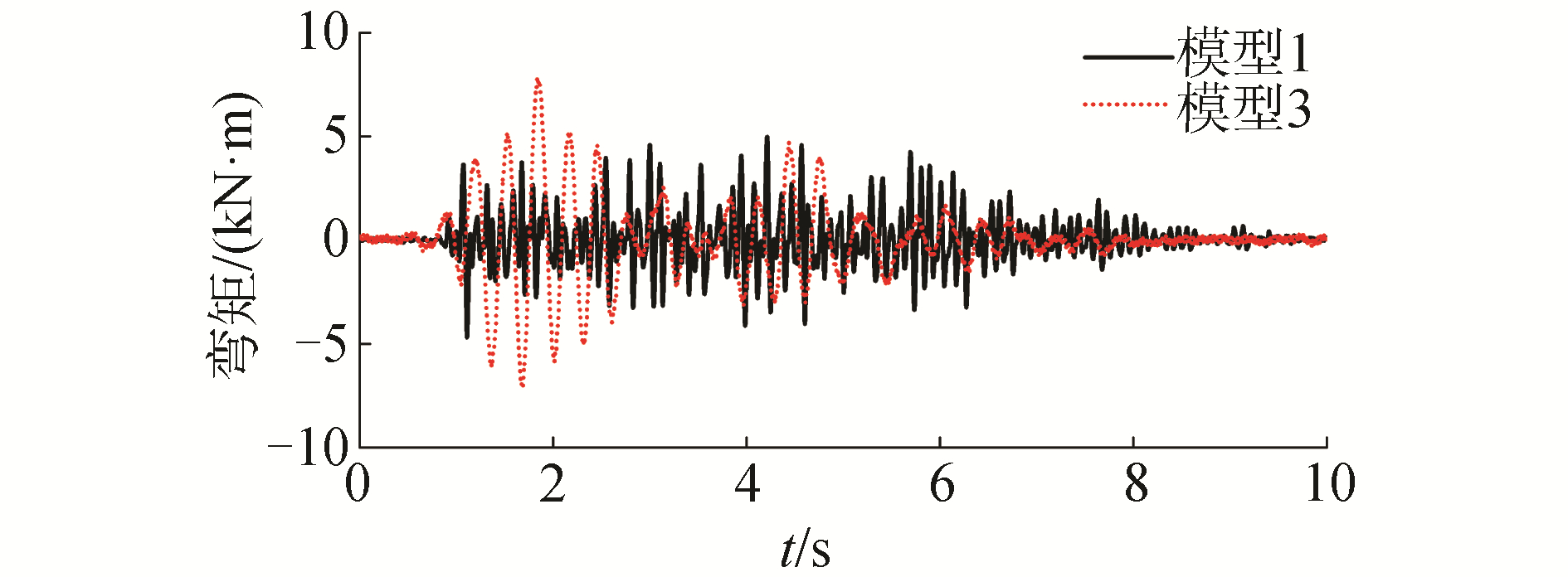
在实际工程中,为满足温度效应的影响,固结体系斜拉桥通常只在一侧桥塔中设置纵向固定支座。在本次试验中,对于模型1,仅在A塔处设置纵向固定支座与主梁连接。依据张文学等[11]提出的低重心斜拉桥判定方法,选取模型1和模型3中A塔塔底弯矩,若按漂浮体系设计的模型3塔底弯矩M3与按固定铰接体系设计的模型1塔底弯矩M1的比值γ=M3/M1≥1,则判定试验模型符合低重心特征。图 4为PGA为0.1g时,模型1和模型3在场地人工波作用下的塔底弯矩对比。可以看出,模型1的塔底弯矩峰值明显小于模型3,符合低重心的特征。
|
Download:
|
| 图 4 塔底弯矩对比 Fig. 4 Comparison of bending moment at tower bottom | |
选取模型1和模型2对混凝土主塔的破坏模式进行分析。本次试验在加载时台面输入PGA由0.1g递增,4条地震波按相同PGA依次输入(先后顺序为El Centro波、天津波、EMC_FAIRVIEW AVE波和场地人工波)。当PGA增大至1.1g后,仅采用一条地震波(天津波)加载至1.5g。
沿纵桥向输入地震波时,随着台面输入PGA逐级增大,2个模型A塔均产生破坏,而模型B塔均未有任何可以观察到的裂缝出现。下文描述的破坏现象均为2个模型中A塔。PGA小于0.7g时,模型1中纵向1字形主塔和模型2中纵向人字形主塔均无可观察到的裂缝。PGA增大至0.7g时,模型1主塔底部侧面出现45°剪切斜裂缝,裂缝宽度在0.1 mm左右,裂缝长度约为3 cm,同时A塔下横梁固定支座位置处有斜裂缝出现,裂缝向塔梁连接处延伸。PGA增加至0.8g时,模型1中主塔下横梁原有裂缝延展,在固定支座位置处有混凝土局部压碎并剥落;模型2中人字形主塔下横梁与塔柱连接处有裂缝出现,裂缝长度在4 cm左右,人字形主塔底部斜腿段没有出现可观察到的裂缝。PGA增大至0.9g时,模型2中主塔下横梁与塔柱连接处出现有部分混凝土剥落,并在固定支座底部沿45°斜向有新的裂缝产生。PGA达到1.1g时,模型1中塔底柱脚处有大块混凝土的剥落,塔柱主筋外露。PGA增加至1.4g时,模型1中主塔下横梁竖向支座处有大面积混凝土剥落,塔下横梁钢筋露出。此外,主塔底部有水平弯曲裂缝产生,下塔柱侧面出现多条交叉斜裂缝,并同时伴随竖向裂缝产生,由此判断此时模型1中固定支座侧的主塔已经发生严重破坏;模型2中的人字形塔下横梁支座位置处混凝土剥落导致配筋外露,根部与塔柱连接处有混凝土剥落,并形成塑性铰,塔下横梁发生严重破坏,此时人字形主塔塔柱底部分叉段与上部直线段并无任何可观察裂缝,主塔塔柱无明显破坏。模型1中纵向1字形主塔和模型2中纵向人字形主塔破坏情况见图 5。

|
Download:
|
| 图 5 模型主塔破坏情况 Fig. 5 Observed damage of main tower | |
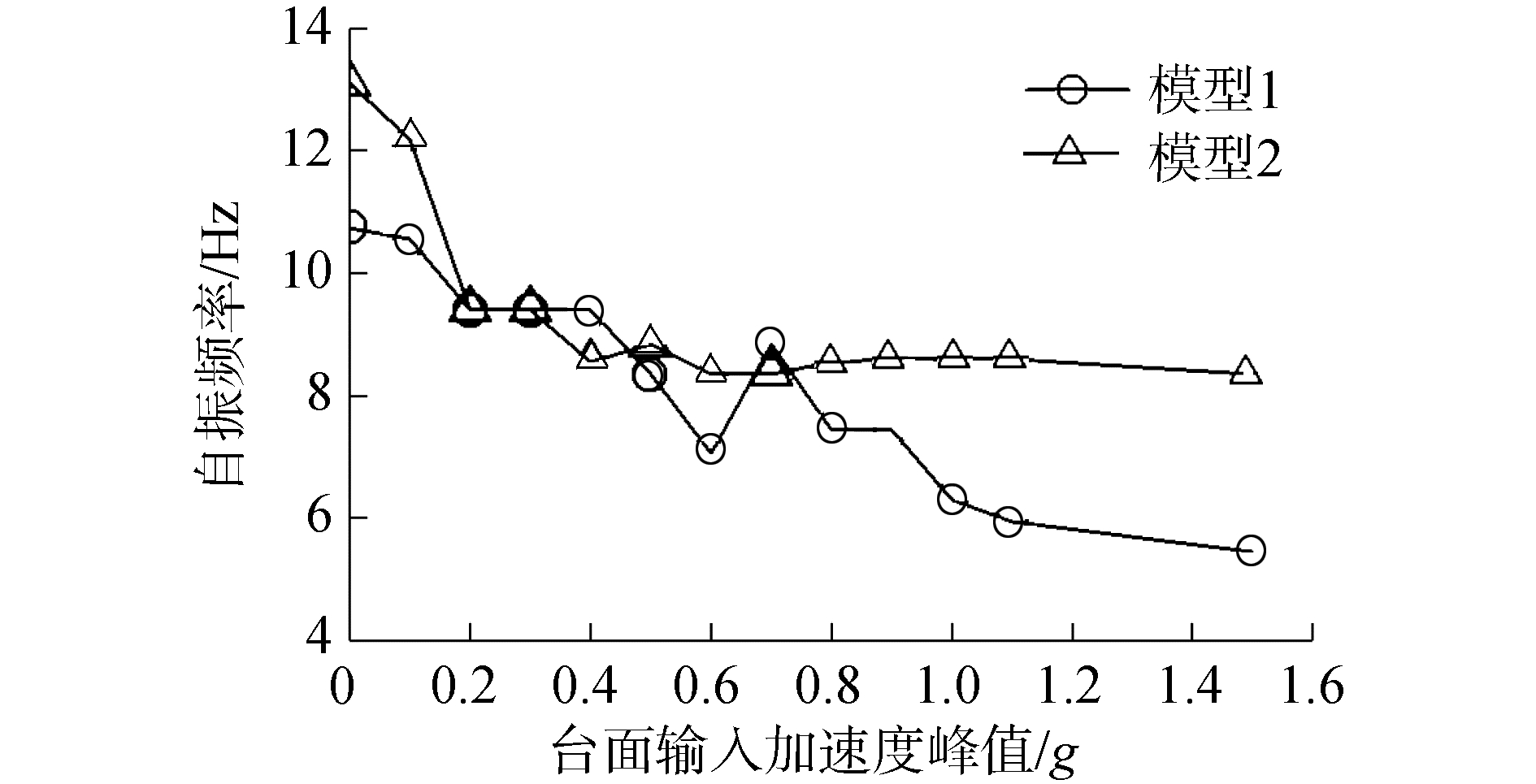
动力特性如自振频率、阻尼比等是分析模型结构在地震过程中损伤的重要参数,本次试验选用加速度峰值为0.05g,频率范围0.1~45 Hz的白噪声信号激励,对主塔顶部加速度时程信号进行频谱分析得到结构自振频率,模型1和模型2结构自振频率变化如图 6所示。
|
Download:
|
| 图 6 模型自振频率对比 Fig. 6 Comparison of model natural frequency | |
模型1初始自振频率为10.74 Hz,全部工况加载完成后的自振频率为5.45 Hz,降低了49.26%;模型2初始自振频率为13.09 Hz,全部工况加载完成后的自振频率为8.34 Hz,降低了36.26%。与模型1相比,模型2结构的初始自振频率更大,表明结构初始刚度更大;随着地震波的逐级加载,2个模型的基频都出现降低,这说明2个模型在地震作用下结构都产生损伤。与模型1相比,模型2结构的基频降低更少,且全部工况加载完成后其自振频率也远大于模型1,表明模型2的人字形主塔震后破坏更小。
2.4 加速度响应对比分析选取El Centro波作用下模型1和模型2的A塔塔顶纵桥向(x向)加速度响应进行分析(如图 7)。由图 7(a)分析可知,PGA逐级加至0.3g后,模型1中A塔塔顶加速度放大系数呈明显下降趋势,并在PGA为0.6g时降至最小值,为1.837。从模型1结构自振周期的变化角度分析,当输入PGA从0.1g增至0.6g过程中,模型1自振周期由0.093 s增加至0.142 s,其对应图 3中El Centro波加速度响应谱中的曲线为先增加至最大值后又减小,加速度放大系数的变化是由结构损伤导致自振周期改变所引起。模型2中的加速度放大系数变化规律与其自振周期对应的加速度响应谱曲线规律一致。
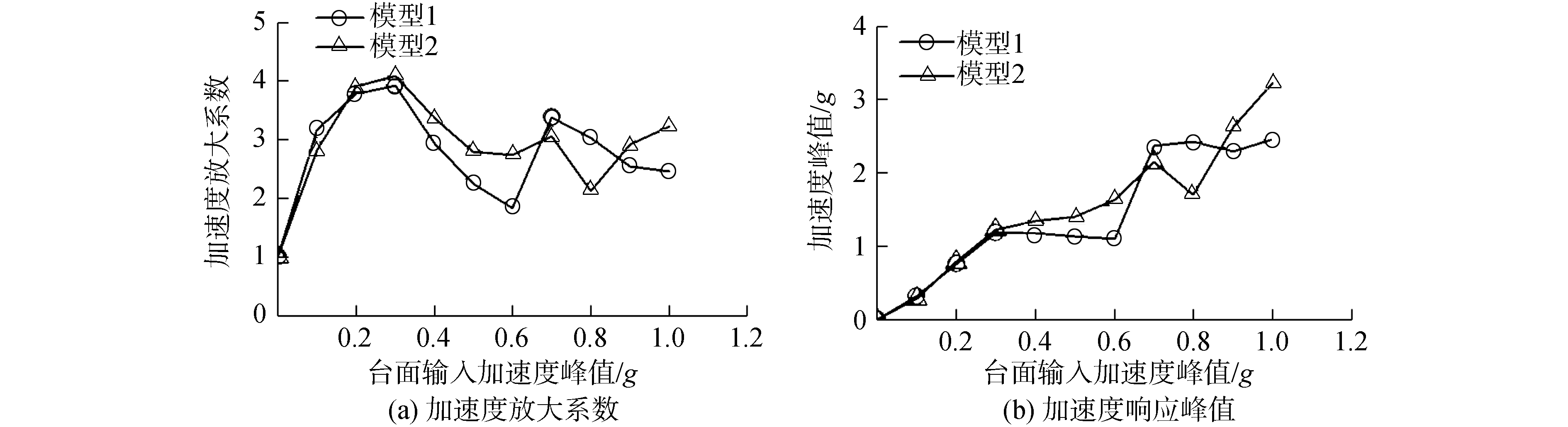
|
Download:
|
| 图 7 模型塔顶加速度响应对比(El Centro波) Fig. 7 Comparison of the acceleration response at model tower top (El Centro wave) | |
由图 7(b)可以看出,2个模型中A塔塔顶加速度响应峰值随着输入PGA的增大而增大。在PGA≤0.3g时,El Centro波作用下A塔塔顶加速度响应峰值与输入PGA呈线性关系,说明此时桥塔仍处于弹性反应阶段,并未出现塑性破坏;在PGA>0.3g时,受混凝土主塔损伤的影响,模型塔顶加速度响应峰值与输入PGA呈现出明显的非线性关系。
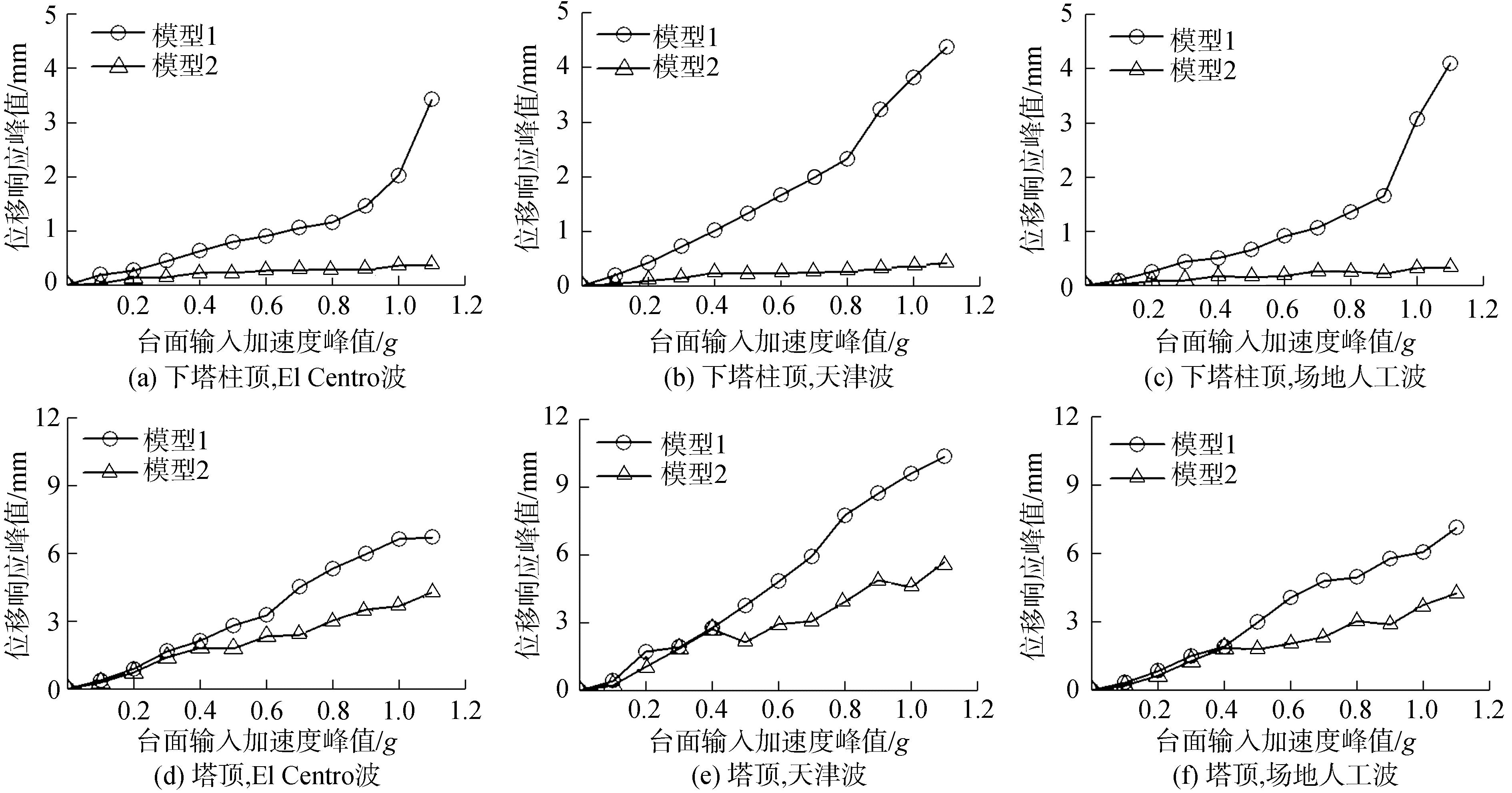
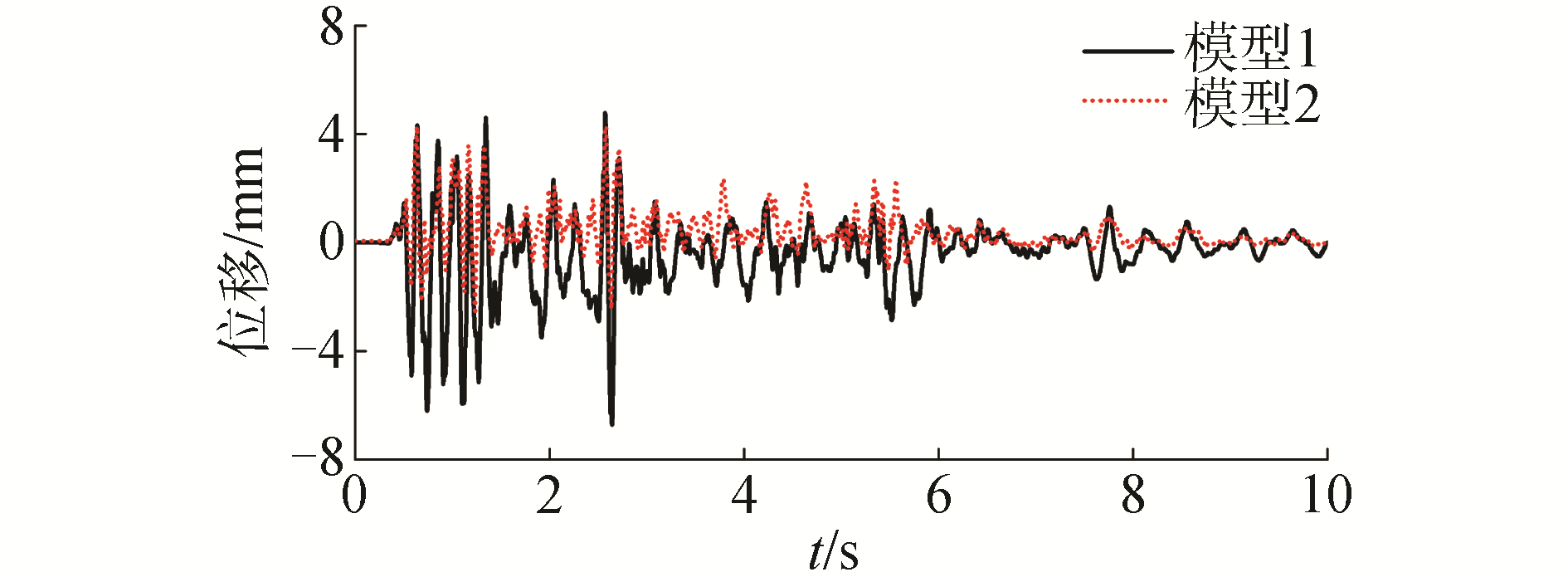
2.5 主塔位移响应对比分析选取El Centro波、天津波和场地人工波作用下模型1和2中A塔关键位置沿纵桥向(x向)的位移响应分析(如图 8)。图 9为El Centro波作用下A塔塔顶位移时程曲线。分析图 8和图 9可知:
|
Download:
|
| 图 8 模型位移响应峰值对比 Fig. 8 Comparison of peak displacement response of test model | |
|
Download:
|
| 图 9 模型塔顶位移响应时程曲线对比(El Centro波PGA=1.1g) Fig. 9 Comparison of displacement response time history curves of tower top (El Centro wave PGA=1.1g) | |
1) 模型2个关键位置处的位移响应峰值均随输入PGA的逐级增大而递增。在输入PGA超出0.9g时,模型1中下塔柱顶的位移响应峰值增长速率要明显加快,结合模型1的试验破坏现象可知,这是由于输入PGA超出0.9g后,模型1中纵向1字形主塔塔底开裂严重,混凝土主塔刚度退化明显;模型2中人字形主塔下塔柱顶在各工况地震波作用下均保持较小的位移响应。在天津波输入PGA为1.1g时,模型1中下塔柱顶位移响应峰值为4.36 mm,对应工况下模型2相同位置处的位移响应峰值仅为0.42 mm,模型2位移响应峰值仅为模型1的1/10。
2) 模型1和模型2中塔顶位移响应峰值在天津波作用下要大于El Centro波和场地人工波。在天津波输入PGA为1.1g时,模型1中塔顶的位移响应峰值为10.34 mm,模型2中塔顶的位移响应峰值为5.68 mm,模型2的塔顶处位移响应峰值仅为模型1的54.93%,表明与纵向1字形相比,纵向人字形能够有效降低主塔在罕遇地震作用下的位移响应。
3) 由图 9分析可知,模型1和模型2在地震作用后其位移时程曲线仍然可以归零,说明主塔并未倒塌,也没有残余变形产生。结合试验现象的观察,此时2个模型的主塔虽然均进入塑性破坏状态并且下横梁损伤严重,但主塔在地震波加载后仍然能够恢复原位。
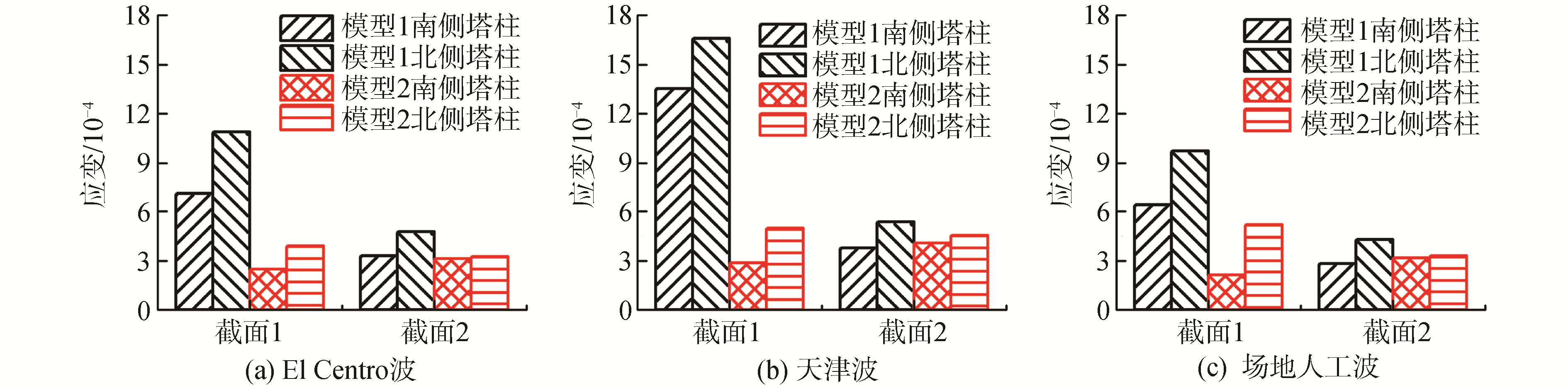
2.6 主塔钢筋应变响应对比分析选取模型1和模型2中A塔的2个关键位置处所测钢筋应变响应分析。截面1位于A塔塔底,截面2位于A塔塔柱的下横梁高度处,具体位置见图 1。图 10为台面输入PGA为0.7g时,在El Centro波、天津波和场地人工波作用下,2个模型的A主塔塔柱不同截面处钢筋应变响应峰值对比。由图 10分析可知:
|
Download:
|
| 图 10 模型主塔钢筋应变响应峰值对比(PGA=0.7g) Fig. 10 Comparison of steel strain peak response at main tower (PGA=0.7g) | |
1) 输入PGA相同时,天津波作用下,模型1塔底应变响应峰值最大,最大值为1 658.38×10-6,而在El Centro波和场地人工波作用下,模型1塔底应变响应峰值相差不大,分别为1 088.29×10-6和972.93×10-6,这主要是由于天津波能量较大且主要富集在低频范围,故激起结构沿纵桥向地震响应较大。
2) 对比模型1和模型2塔底钢筋应变响应峰值可以看出,PGA相同时,在3条不同类型地震波的分别作用下,模型1塔底钢筋应变响应峰值为模型2应变响应峰值的1.5~4.7倍;模型1和模型2在截面2处的钢筋应变响应峰值差别不大。分析模型1和模型2主塔钢筋应变产生原因可知,模型1中主塔为纵向1字形,其钢筋应变由主塔受弯引起,应变响应峰值越大,说明结构在此处所受弯矩越大;模型2中的主塔为人字形,分叉点以上直线段以受弯为主,而分叉点以下斜腿段所受纵向弯矩较小,其塔底钢筋应变主要是由轴力引起。
3) 综上分析可知,模型1中纵向1字形主塔所受弯矩最大处位于塔底,模型2中人字形主塔弯矩最大值则出现在塔柱分叉点处,底部斜腿段受力以轴力为主。相对比于模型1中纵向1字形主塔,模型2中人字形主塔在地震动作用下可以改善下塔柱的受力特性和抗震性能。
3 结论1) 在天津波PGA为0.7g时,模型1中纵向1字形主塔的下横梁和塔柱底部出现可见裂缝;在天津波PGA为0.8g时,模型2人字形主塔的下横梁处有可见裂缝产生;在PGA增至1.4g时,模型1主塔的下横梁及下塔柱破坏严重,而模型2主塔塔柱无明显破坏。
2) 在强震作用下,模型2主塔下横梁损伤严重,但通过下横梁的损伤有效地保护了塔柱,避免了不可修复破坏模式的发生,提高了震后结构的可修复性。
3) 双塔低重心斜拉桥在固定支座侧采用空间结构设计的人字形主塔,可有效控制主塔的纵向位移响应,避免塔柱在强震下发生剪切破坏,是一种比较合理的低重心斜拉桥桥塔结构形式。
| [1] |
中华人民共和国交通运输部. JTG/T B02-01-2008, 公路桥梁抗震设计细则[S].北京: 人民交通出版社, 2008. Ministry of Transport of the People's Republic of China. JTG/T B02-01-2008, Guidelines for seismic design of highway bridges[S]. Beijing: China Communications Press, 2008. (  0) 0)
|
| [2] |
中华人民共和国住房和城乡建设部. CJJ 166-2011, 城市桥梁抗震设计规范[S].北京: 中国建筑工业出版社, 2012. Ministry of Housing and Urban-Rural Development of the People's Republic of China. CJJ 166-2011, Code for seismic design of urban bridges[S]. Beijing: China Architecture and Building Press, 2012. (  0) 0)
|
| [3] |
GANEV T, YAMAZAKI F, ISHIZAKI H, et al. Response analysis of the Higashi-Kobe bridge and surrounding soil in the 1995 Hyogoken-Nanbu earthquake[J]. Earthquake engineering and structural dynamics, 1998, 27(6): 557-576. DOI:10.1002/(SICI)1096-9845(199806)27:6<557::AID-EQE742>3.0.CO;2-Z (  0) 0)
|
| [4] |
CHANG K C, MO Y L, CHEN C C, et al. Lessons learned from the damaged Chi-Lu cable-stayed bridge[J]. Journal of bridge engineering, 2004, 9(4): 343-352. DOI:10.1061/(ASCE)1084-0702(2004)9:4(343) (  0) 0)
|
| [5] |
SHARABASH A M, ANDRAWES B O. Application of shape memory alloy dampers in the seismic control of cable-stayed bridges[J]. Engineering structures, 2009, 31(2): 607-616. (  0) 0)
|
| [6] |
SONEJI B B, JANGID R S. Response of an isolated cable-stayed bridge under bi-directional seismic actions[J]. Structure and infrastructure engineering, 2010, 6(3): 347-363. DOI:10.1080/15732470701596833 (  0) 0)
|
| [7] |
燕斌, 杜修力, 韩强, 等. 减隔震混合装置在独塔斜拉桥抗震设计中的应用[J]. 桥梁建设, 2014, 44(6): 101-106. YAN Bin, DU Xiuli, HAN Qiang, et al. Application of hybrid seismic mitigation and isolation device to seismic design of single-pylon cable-stayed bridge[J]. Bridge construction, 2014, 44(6): 101-106. (  0) 0)
|
| [8] |
袁万城, 屈小伟. 减隔震装置在飘浮体系斜拉桥纵桥向的应用[J]. 同济大学学报(自然科学版), 2015, 43(2): 199-204. YUAN Wancheng, QU Xiaowei. Application analysis of seismic isolation devices on longitudinal seismic response of floating system cable-stayed bridge[J]. Journal of Tongji University (natural science), 2015, 43(2): 199-204. DOI:10.11908/j.issn.0253-374x.2015.02.006 (  0) 0)
|
| [9] |
王志强, 胡世德, 范立础. 东海大桥粘滞阻尼器参数研究[J]. 中国公路学报, 2005, 18(3): 37-42. WANG Zhiqiang, HU Shide, FAN Lichu. Research on viscous damper parameters of Donghai bridge[J]. China journal of highway and transport, 2005, 18(3): 37-42. DOI:10.3321/j.issn:1001-7372.2005.03.008 (  0) 0)
|
| [10] |
郭进, 王冠, 杜彦良, 等. 桥梁限位型减隔震支座试验及其参数敏感性分析[J]. 哈尔滨工程大学学报, 2017, 38(7): 1114-1120. GUO Jin, WANG Guan, DU Yanliang, et al. Test and parameter sensitivity analysis on seismic isolation bearing with the function of displacement limitation used in bridges[J]. Journal of Harbin Engineering University, 2017, 38(7): 1114-1120. DOI:10.11990/jheu.201610012 (  0) 0)
|
| [11] |
张文学, 李建中, 李怀峰. 低重心斜拉桥地震响应特性研究[J]. 桥梁建设, 2007(5): 21-23, 41. ZHANG Wenxue, LI Jianzhong, LI Huaifeng. Study of seismic response characteristics of low gravity center cable-stayed bridge[J]. Bridge construction, 2007(5): 21-23, 41. DOI:10.3969/j.issn.1003-4722.2007.05.006 (  0) 0)
|
| [12] |
张文学, 王景景, 陈士通. 重心高度对不同体系斜拉桥地震响应特性影响研究[J]. 公路, 2015, 60(1): 72-76. ZHANG Wenxue, WANG Jingjing, CHEN Shitong. Study of seismic response characteristics of gravity center's height to different structure system cable-stayed bridge[J]. Highway, 2015, 60(1): 72-76. (  0) 0)
|
| [13] |
王瑞龙, 徐艳, 李建中. 一致激励下的混凝土斜拉桥振动台试验[J]. 同济大学学报(自然科学版), 2015, 43(3): 357-363. WANG Ruilong, XU Yan, LI Jianzhong. Shake table test of a concrete cable-stayed bridge subjected to uniform seismic excitation[J]. Journal of Tongji University (natural science), 2015, 43(3): 357-363. DOI:10.11908/j.issn.0253-374x.2015.03.006 (  0) 0)
|
| [14] |
王忠彬, 万田保. 泰州长江公路大桥三塔两跨悬索桥结构行为特征[J]. 桥梁建设, 2008(2): 38-40, 59. WANG Zhongbin, WAN Tianbao. Characteristics of structural behavior of three-tower and two-span suspension bridge of Taizhou Changjiang river highway bridge[J]. Bridge construction, 2008(2): 38-40, 59. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


