2. 中交第一公路勘察设计研究院有限公司, 陕西 西安 710075
2. First Highway Survey and Design Institute, China Communications Construction Group, Xi'an 710075, China
寒区隧道围岩和衬砌易产生冻融循环现象,冻融循环作用降低了混凝土的强度,加速其劣化过程,严重影响隧道衬砌结构稳定和行车安全。如新疆玉希莫勒盖隧道衬砌由于受到反复冻融破坏而报废[1]。
许多学者对围岩和衬砌在冻融循环作用环境下的劣化规律进行了研究。黎岩[2]进行了混凝土衬砌冻融循环试验,得到混凝土相对动弹性模量、抗压强度等物理力学参数随冻融循环次数劣化的规律。周宇翔[3]得到板岩冻融循环作用下劣化规律。以上关于冻融循环条件下围岩和衬砌劣化研究为冻融循环条件下寒区隧道衬砌的服役性能研究提供了参考。
为了保证寒区隧道衬砌性能,目前国内寒区隧道大多采用铺设隔热保温材料的方式来减少洞内气体和围岩的热交换量,从而达到减小冻融圈,减轻衬砌劣化的目的。
在保温层铺设方式方面,我国寒区隧道保温层铺设方式主要有表面铺设[4]、夹层铺设[5]、双层铺设3种。现有的研究成果多是从使用耐久性、防火性能等方面进行分析各种铺设方式的优缺点[6],但不同保温层铺设方式对于衬砌服役性能影响有待研究。
各国学者提出的隔热(保温)层厚度的计算方法归纳起来可分为解析计算法和有限元计算法两大类。陈建勋等[7-8]推导出了铺设在初期支护和二衬之间以及铺设在二衬表面时隔热(保温)层厚度的解析计算公式;夏才初等[9]通过计算铺设隔热(保温)层后指定位置处的温度来确定隔热(保温)层的厚度。目前解析法计算保温层厚度均基于稳态传热的基本假定进行推导,寒区隧道与洞内气温热交换是一个瞬态分析的过程,其计算出的保温层厚度一般偏小。
有限元计算法是利用有限元软件试算铺设不同厚度的隔热(保温)层后围岩的温度分布,直至围岩温度满足防冻或防融要求。晏启祥等[10]采用有限元计算法对某隧道工程不设保温层和铺设0.03 m保温层的围岩温度进行了计算,验证了保温层的保温效果;Lai等[11]采用有限元计算法对大坂山隧道铺设保温材料后的隧道围岩温度场进行了研究。
无论是采用解析法还是数值法计算寒区隧道保温层铺设厚度,更多从多年冻土段围岩不融化和非冻土段围岩不冻结角度分析,大多未考虑到衬砌由于受到冻融循环作用劣化现象。此外,寒区隧道往往并不是从单一的冻土层中穿过。根据经验表明,隧道洞口至中央、寒区隧道围岩一般呈现季节冻结、常年冻结和常年不冻结等状态。因此在计算保温层铺设厚度时需针对隧道穿越的不同冻土段进行区别分析。
本文依托青海知亥代公路隧道,考虑寒区隧道中受洞内气温影响引起的衬砌冻融循环程度不同,从衬砌劣化和安全性能角度,采用数值模拟计算手段开展了冻融循环条件下寒区隧道衬砌的服役性能,分析了保温层铺设与否以及3种保温层铺设方式对于衬砌服役性能的影响,并在此基础上,对知亥代隧道保温层的铺设厚度进行了优化。
1 青海知亥代公路隧道工程情况与计算模型 1.1 青海知亥代公路隧道工程情况知亥代隧道位于青海省海南州,里程桩号ZK58+440-ZK63+010,全长4 550 m,隧道穿越多年冻土段和非冻土段。隧道轴线通过路段地标高4 808.25~4401.83 m,相对高差约407 m,最大埋深约346 m。
隧址年平均气温-4.0 ℃,年温度振幅12.5 ℃,隧址区多年冻土年平均地温Tcp=-0.1 ℃。多年冻土上限一般2.0~2.5 m,为衔接型多年冻土,洞身段围岩为冰水沉积碎块石和板岩,隧道洞口前200 m为多年冻土段,200 m后为非冻土段。

|
Download:
|
| 图 1 知亥代隧道穿越地段 Fig. 1 Profile of ZHIHAI tunnel | |
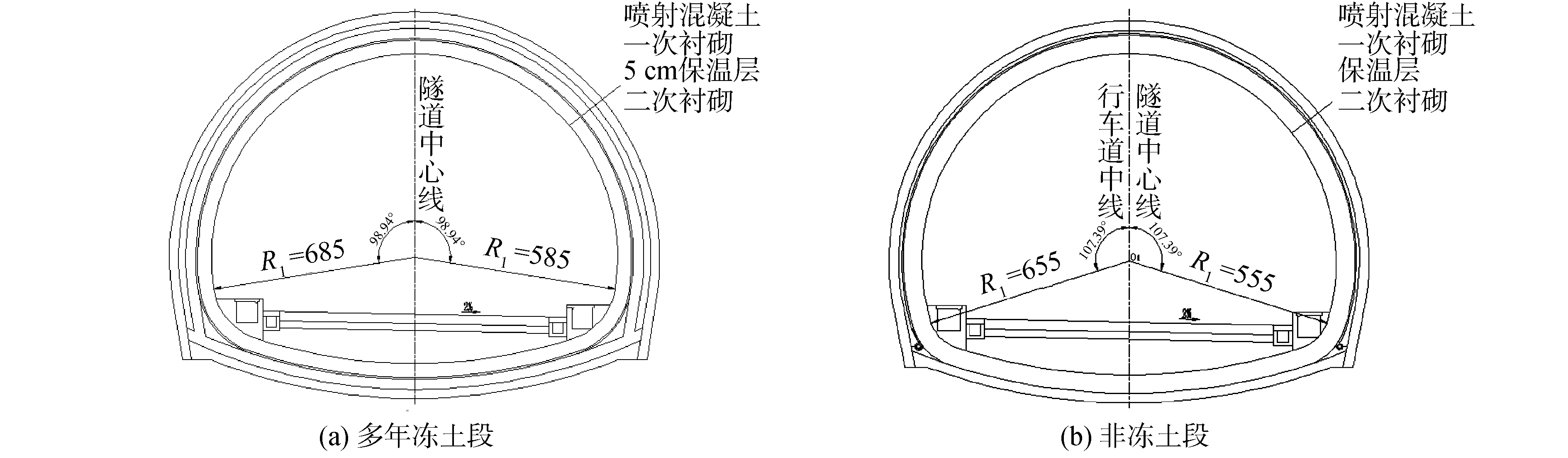
依托知亥代隧道多年冻土段ZK58+470断面和非冻土段ZK58+640作为典型断面进行计算。隧道断面设计情况如图 2所示。
|
Download:
|
| 图 2 多年冻土和非冻土段断面衬砌 Fig. 2 Permafrost and non-frozen soil section lining | |
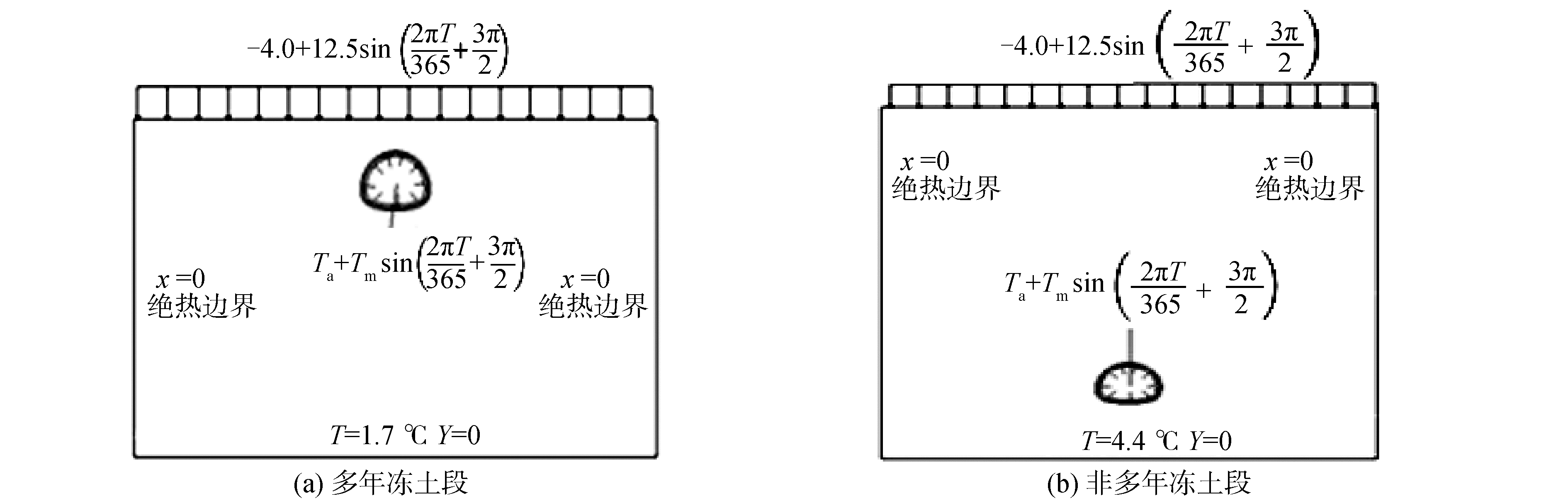
模型边界按照3~5倍洞径选取,多年冻土段和非冻土段计算边界条件如图 4、图 5所示,上部边界受到外界气温作用,底部温度边界条件按照每100 m上升3 ℃的规律计算底部温度边界条件,模型两侧为绝热边界。计算模型中各材料的物理力学参数如表 1所示。
|
Download:
|
| 图 3 多年冻土和非多年冻土段计算边界条件 Fig. 3 Calculating boundary conditions for permafrost and non-permafrost regions | |
|
Download:
|
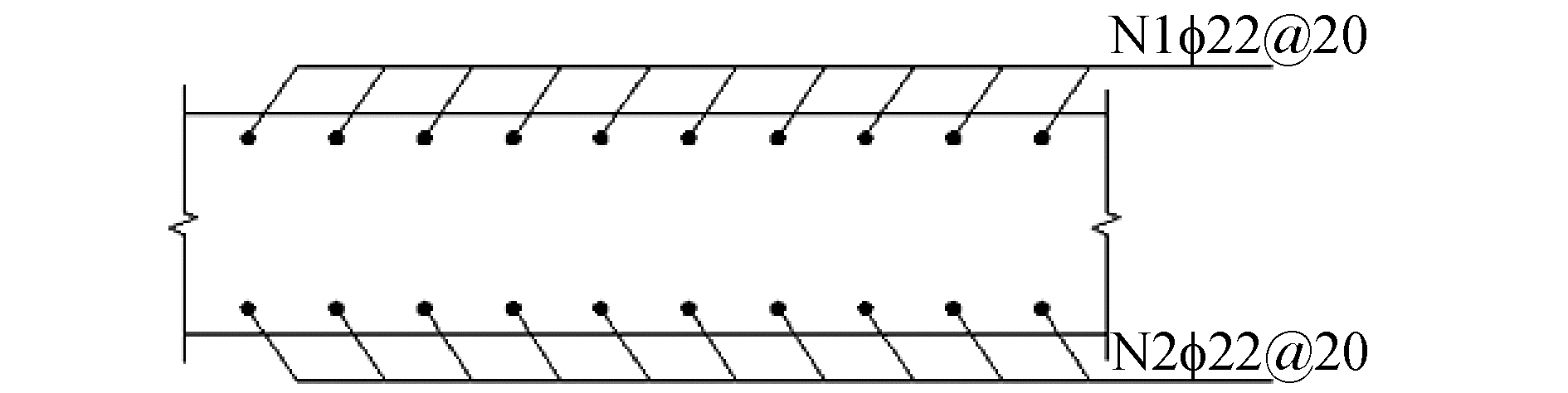
| 图 5 二衬配筋环向图 Fig. 5 Circumferential diagram of secondary lining with reinforcement | |
| 表 1 计算参数选取 Table 1 Calculation parameter selection |
在计算衬砌安全系数时需考虑到衬砌材料物理力学性质会发生劣化,根据黎岩[2]混凝土衬砌冻融循环试验结果得到混凝土相对动弹性模量、抗压强度随冻融循环次数N的劣化规律为:
| $ {{P_t} = 96.299{{\rm{e}}^{ - 0.004N}}} $ | (1) |
| $ {{f_{ct}} = {f_{c0}}{{\rm{e}}^{ - 0.008N}}} $ | (2) |
式中:Pt为混凝土相对动弹性模量;fc0为混凝土的初始抗压强度;fct为混凝土的受到动容循环后的抗压强度。
以上变化规律为室内试验规律,现场冻融循环条件下温度变化速率和条件与室内试验有所不同。文献[13]基于Miner法则推导得到与现场冻融循环次数Ni相对应的等效试验室内的冻融循环次数Neq为:
| $ {{N_{eq}} = \sum\limits_i {k_i^\xi } {N_i}} $ | (3) |
式中:ki为现场温度冻融循环产生的静水压与室内快冻试验温度冻融循环产生的静水压的比例系数。
刘西拉[14]根据Powers的静水压假说[15]推导得到现场温度冻融循环产生的静水压与室内快冻试验温度冻融循环产生的静水压的比例系数ki近似等于现场降温速率与室内快冻试验降温速率之比:
| $ {{k_i} = {{\dot T}_I}/\dot T} $ | (4) |
式中:
本文用混凝土结构截面安全系数评价衬砌服役性能,安全系数按《铁路隧道设计规范》[13]中规定方法计算得来。衬砌安全系数越低,衬砌服役性能越差。
为分析衬砌劣化对其承载安全性的影响,需要根据二衬各位置内力结果计算衬砌结构的安全系数,分析衬砌劣化后的承载安全性。
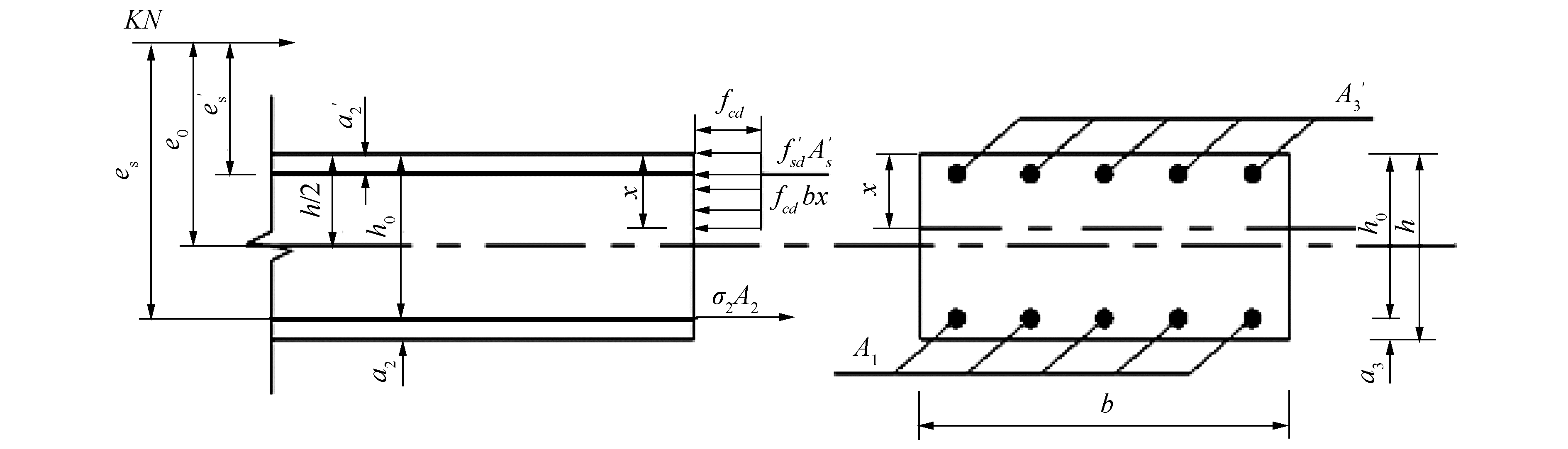
知亥代隧道二衬均为45 cm厚C45钢筋混凝土,环向配筋如图 5所示。二衬各断面为对称配筋的矩形偏心受压构件,取纵向方向上单位长度进行分析,矩形断面偏心受压构件的安全系数计算示意图如图 6所示。
|
Download:
|
| 图 6 矩形断面偏心受压构件正断面承载力计算 Fig. 6 Calculation diagram of bearing capacity of rectangular section eccentric compression member | |
构件纵轴方向的内外力之和为零,有:
| $ {KN \le {N_U} = {f_{cd}}bx + f_{sd}^\prime A_S^\prime - {\sigma _s}{A_S}} $ | (5) |
式中:KN为偏心压力;x为受压区高度;fcd为混凝土的轴心抗压强度;AS、A′S分别为离偏心压力较远一侧和较近一侧的钢筋面积;σs为钢筋混凝土截面破坏时受拉区钢筋应力;fsd、f′sd分别为钢筋的抗拉强度和抗压强度,对HRB335钢筋,均为280 MPa。
断面上所有对钢筋AS合力点的力矩之和等于零,有:
| $ {KN{e_s} \le {M_U} = {f_{cd}}bx\left( {{h_0} - \frac{x}{2}} \right) + f_{sd}^\prime A_S^\prime ({h_0} - a_s^\prime )} $ | (6) |
式中:h、h0分别为截面的高度和有效高度;es为偏心压力KN作用点至钢筋AS合力作用点的距离。
断面上所有对钢筋A′S合力点的力矩之和等于零,有:
| $ {KNe_s^\prime \le {M_U} = - {f_{cd}}bx\left( {\frac{x}{2} - a_s^\prime } \right) + {\sigma _s}{A_s}({h_0} - a_S^\prime )} $ | (7) |
式中e′s为偏心压力KN作用点至钢筋A′S合力作用点的距离。
断面上所有力对KN作用点力矩之和为零,有
| $ {{f_{cd}}bx\left( {{e_s} - {h_0} + \frac{x}{2}} \right) = {\sigma _s}{A_s}{e_s} - f_{sd}^\prime A_S^\prime ({h_0} - a_s^\prime )e_s^\prime } $ | (8) |
式中:as、a′s分别为钢筋AS、A′S形心距截面相应边缘的距离。
| $ {\left\{ {\begin{array}{*{20}{l}} {{e_0} = M/N}\\ {{e_s} = {e_0} + \frac{h}{2} - {a_s}}\\ {e_s^\prime = {e_0} - \frac{h}{2} + {a_s}} \end{array}} \right.} $ | (9) |
式中:e0为轴向力对截面重心轴的偏心距;M、N分别为截面所受弯矩和轴力。
对称配筋的矩形截面偏心受压构件,AS=A′S,计算安全系数时,先假设为大偏心受压,此时σs=fsd,由式(8)得到:
| $ {{f_{cd}}bx\left( {{e_s} - {h_0} + \frac{x}{2}} \right) = {f_s}{A_s}{e_s} - f_{sd}^\prime A_S^\prime e_s^\prime } $ | (10) |
由式(10)解得受压区x高度为
| $ {\xi = \left\{ {\begin{array}{*{20}{l}} {\frac{x}{{{h_0}}} \le {\xi _b}}&{{\rm{大偏心受压}}}\\ {\frac{x}{{{h_0}}} > {\xi _b}}&{{\rm{小偏心受压}}} \end{array}} \right.} $ | (11) |
式中:ξ为相对受压区高度;ξb为相对界限受压区高度,对于HRB335钢筋取0.56。
1) 当ξ≤ξb时,构件为大偏心受压构件。构件破坏时,受拉区钢筋达到屈服强度。
若2a′s≤x≤ξbh0,由式(10)计算得到的x即为大偏心受压构件断面受压区高度,按式(5)可求得断面安全系数K。
若x < 2a′s,受压钢筋A′S的应力可能达不到f′sd,此时近似取x=2a′s,受压区混凝土承担的压力作用位置与受压区钢筋承担的压力作用位置重合,按式(7)可得:
| $ {KNe_s^\prime \le {M_U} = {f_{sd}}{A_S}({h_0} - a_s^\prime )} $ | (12) |
按式(12)可求得安全系数K。
2) 当ξ>ξb时,构件属于为大偏心受压构件。构件破坏时,受拉区钢筋未屈服,受压区高度需重新计算。
构件破坏时,受拉区钢筋应力σs:
| $ {{\sigma _s} = {\varepsilon _{cu}}{E_S}\left( {\frac{{\beta {h_0}}}{x} - 1} \right)} $ | (13) |
式中:εcu为混凝土的极限压应变,对于C45混凝土取0.003 3;β为与εcu相对应的系数,对于C45混凝土取0.8;Es为受拉钢筋的弹性模量。
联合式(8)和式(13),得到:
| $ \left\{ {\begin{array}{*{20}{l}} {A{x^3} + B{x^2} + Cx + D = 0}\\ {A = 0.5{f_{cd}}b}\\ {B = {f_{cd}}b({e_s} - {h_0})}\\ {C = {\varepsilon _{cu}}{E_s}{A_S}{e_s} + f_{sd}^\prime A_S^\prime e_s^\prime }\\ {D = - \beta {\varepsilon _{cu}}{E_s}{A_S}{e_s}{h_0}} \end{array}} \right. $ | (14) |
由式(14)解得小偏心受压构件断面受压区高度。
当x < h时,断面部分受压,部分受拉,将x代入式(13)可得受拉区钢筋应力σs,按式(5)可求得断面安全系数K。
当x>h时,断面全部受压,取x=h代入式(13)可得受拉区钢筋应力,按式(5)可求得断面安全系数K。
2 不铺设保温层情况下隧道衬砌服役性能在我国建设寒区隧道的地区,其年平均气温的范围约在-2 ℃~-6 ℃范围,年温度振幅一般在9~15 ℃范围。多年冻土段计算依托知亥代隧道多年冻土段ZK58+470断面,选取不同的年平均气温(-2 ℃、-4 ℃、-6 ℃)和不同的年温度振幅(9.5 ℃、12.5 ℃、15.5 ℃)组合出的5个洞内气温边界荷载作为5种运营期工况,对比分析5种工况下隧道多年冻土段运营期衬砌服役性能变化。各工况下施加和气温函数荷载如表 2所示。
| 表 2 多年冻土段不同工况下温度边界函数 Table 2 Temperature boundary function of permafrost under different working conditions |
非冻土段洞内年平均气温高于多年冻土段洞内年平均气温,年温度振幅小于多年冻土段的洞内气温年温度振幅。非冻土段计算依托知亥代隧道多年冻土段ZK58+断面。在非冻土段负年平均气温段选取不同洞内年平均气温(-0.5 ℃、-1.0 ℃、-1.5 ℃)和不同年温度振幅(3.1 ℃、5.1 ℃、7.1 ℃)组合出的5个洞内气温边界荷载作为5种运营期工况,对比分析5种工况下非冻土段衬砌服役性能变化。各工况下施加和气温函数荷载如表 3所示。
| 表 3 非冻土段正年平均气温段不同工况下温度边界函数 Table 3 Temperature boundary function under different working conditions of the normal annual mean temperature section of the non-frozen soil section |
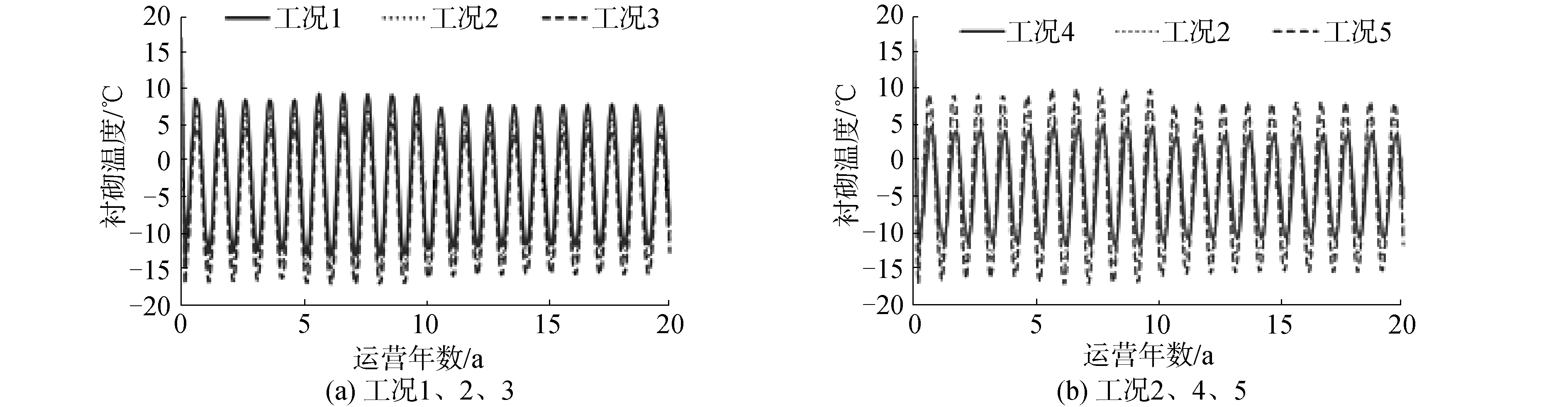
隧道衬砌由于与外界气温直接对流,隧道衬砌每年均承受周期性冻融循环作用,各工况下运营期衬砌温度变化如图 7,利用式(3)和式(4)结合现场资料得到室内等效冻融循环次数如表 4所示。
|
Download:
|
| 图 7 5种工况条件下衬砌温度 Fig. 7 Lining temperature under five working conditions | |
| 表 4 多年冻土段衬砌等效室内冻融循环次数 Table 4 The lining of permafrost section is equivalent to the number of indoor freeze-thaw cycles |
如表 5所示,在运营期,多年冻土段衬砌轴力和弯矩均略微减小,但变化不大。
| 表 5 多年冻土段运营期拱顶衬砌处轴力弯矩值 Table 5 Axial moment at the vault lining in permafrost section during operation |
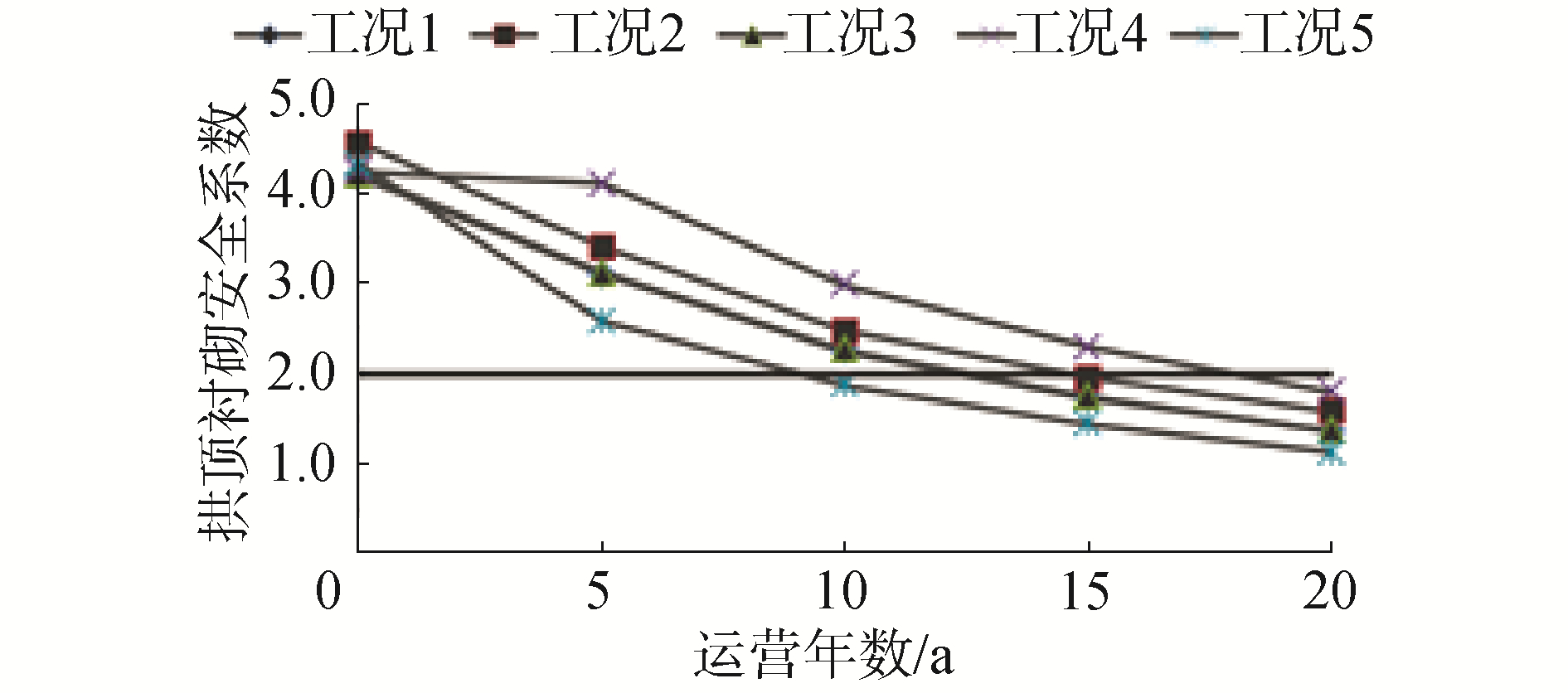
如图 8所示,在运营期开始时,各工况下拱顶衬砌安全系数均大于5,随着运营时间的增加,周期性冻融循环作用下衬砌性质不断劣化,隧道衬砌各处安全系数不断减小。当年平均振幅为12.5 ℃时,年平均温度为-2 ℃、-4 ℃和-6 ℃条件下衬砌的服役年数分别为16、16和12 a,年平均温度越低,衬砌服役性能下降越快。当年平均温度为-4 ℃时,年温度振幅为9.5 ℃、12.5 ℃和15.5 ℃条件下,17、16、9 a,年温度振幅越大,衬砌服役性能下降越快。
|
Download:
|
| 图 8 多年冻土段运营期拱顶衬砌承载安全系数 Fig. 8 Bearing safety factor of vault lining in permafrost section during operation | |
|
Download:
|
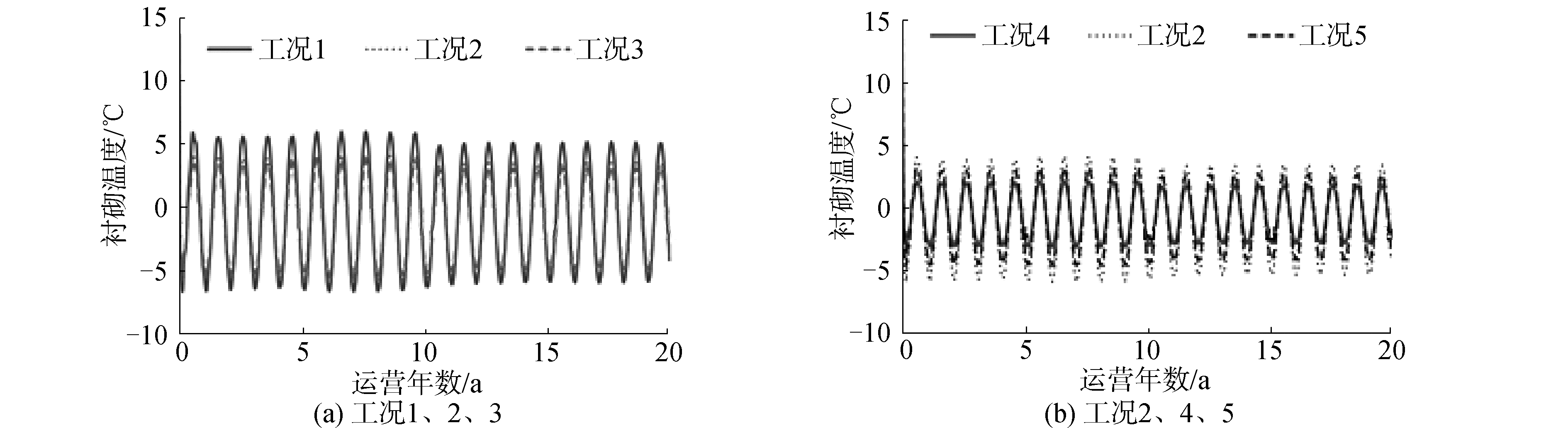
| 图 9 5种工况条件下衬砌温度 Fig. 9 Lining temperature under five working conditions | |
非冻土段选取了表 6中5种工况进行计算,各工况下计算结果如图 9所示。
| 表 6 非冻土段等效室内冻融循环次数 Table 6 The equivalent number of indoor freeze-thaw cycles in the non-frozen soil section |
非冻土段由于洞内气温温度振幅小于多年冻土段,因此非冻土段衬砌受到的冻融循环作用小于多年冻土段衬砌受到的冻融循环作用。
2.4 非冻土段衬砌内力和衬砌服役性能变化如表 7所示,各工况下衬砌拱顶轴力均为压力,运营期轴力变化不大。随着运营期的增长,冻胀作用存在,各工况下拱顶衬砌弯矩逐渐增大。
| 表 7 非冻土段运营期拱顶衬砌处轴力弯矩值 Table 7 The axial moment at the vault lining in the operation period of the non-frozen soil section |
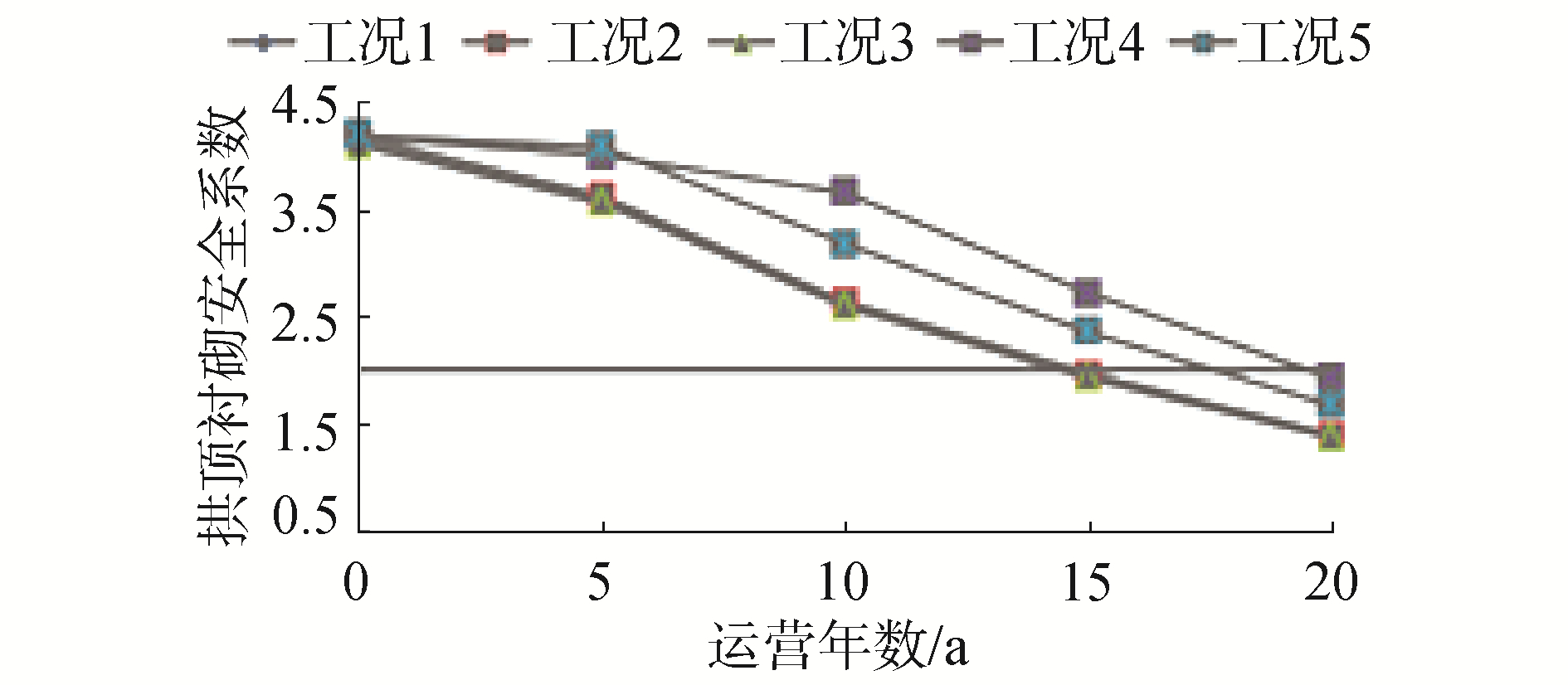
如图 10所示,非冻土段拱顶衬砌安全系数初始值均在5左右。随着运营年数增加,隧道衬砌不断受到冻融循环作用发生劣化,衬砌的轴力保持稳定,弯矩略微增加,衬砌安全系数不断减小。
|
Download:
|
| 图 10 非冻土段运营期拱顶衬砌承载安全系数 Fig. 10 Bearing safety factor of vault lining in operation period of non-frozen soil section | |
当年平均振幅为7.1 ℃时,年平均温度为-0.5 ℃、-1.0 ℃和-1.5 ℃条件下衬砌的服役年数为15 a。当年平均温度为-1.0 ℃时,年温度振幅为7.1 ℃、5.1 ℃和3.1 ℃条件下衬砌的服役年数分别为15、18和19 a,年温度振幅越大,衬砌服役性能下降越快。
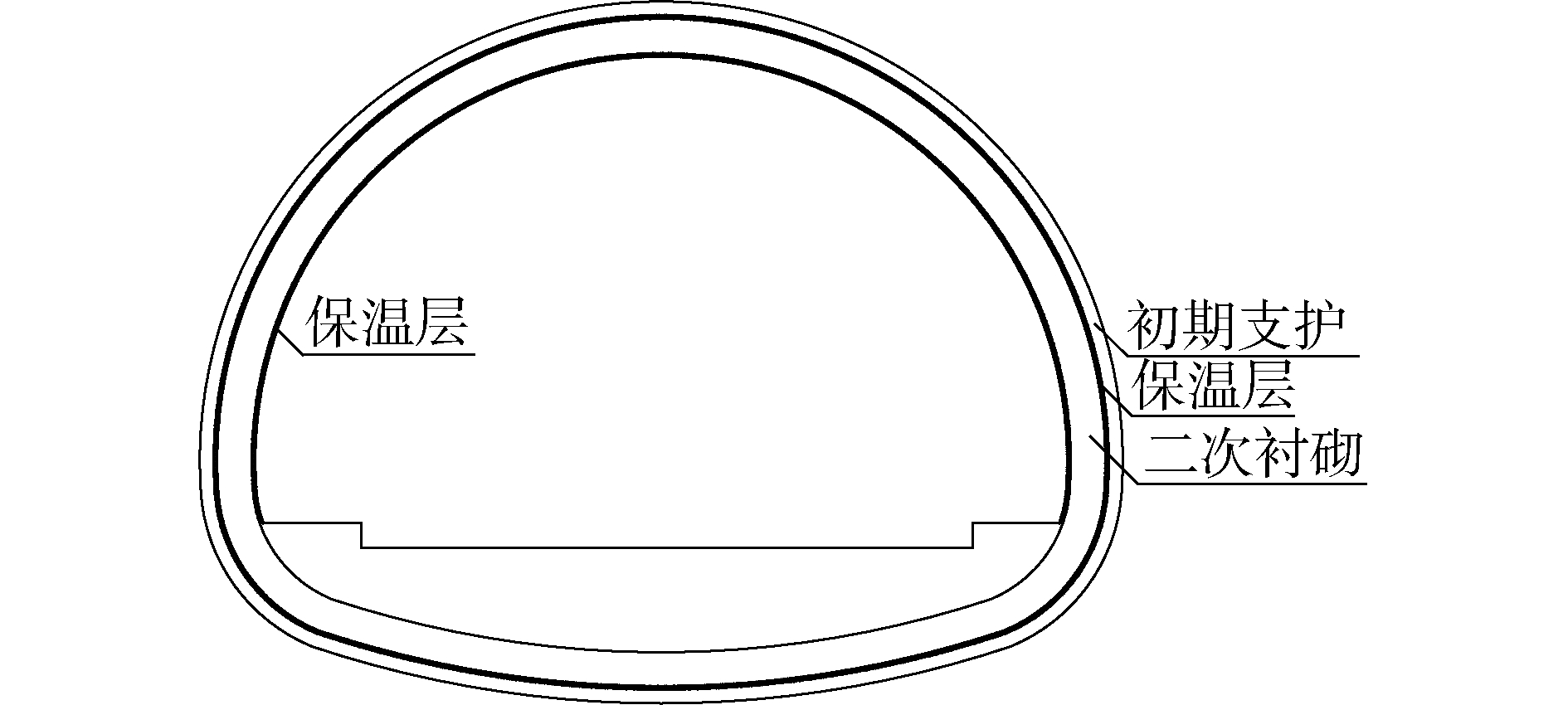
3 铺设保温层情况下隧道衬砌服役性能知亥代隧道采取铺设保温层的方式降低外界气温对于衬砌的影响。在多年冻土段,铺设2层5 cm厚保温层,一层铺设于一衬和二衬之间,另一层铺设在二衬表面,如图 11所示。非冻土段在二衬表面铺设一层5 cm厚保温层,如图 12所示。
|
Download:
|
| 图 11 多年冻土段双层铺设保温层 Fig. 11 The permafrost section is covered with a double insulation layer | |

|
Download:
|
| 图 12 非冻土段表面铺设保温层 Fig. 12 The surface insulation layer is laid on the non-frozen soil section | |
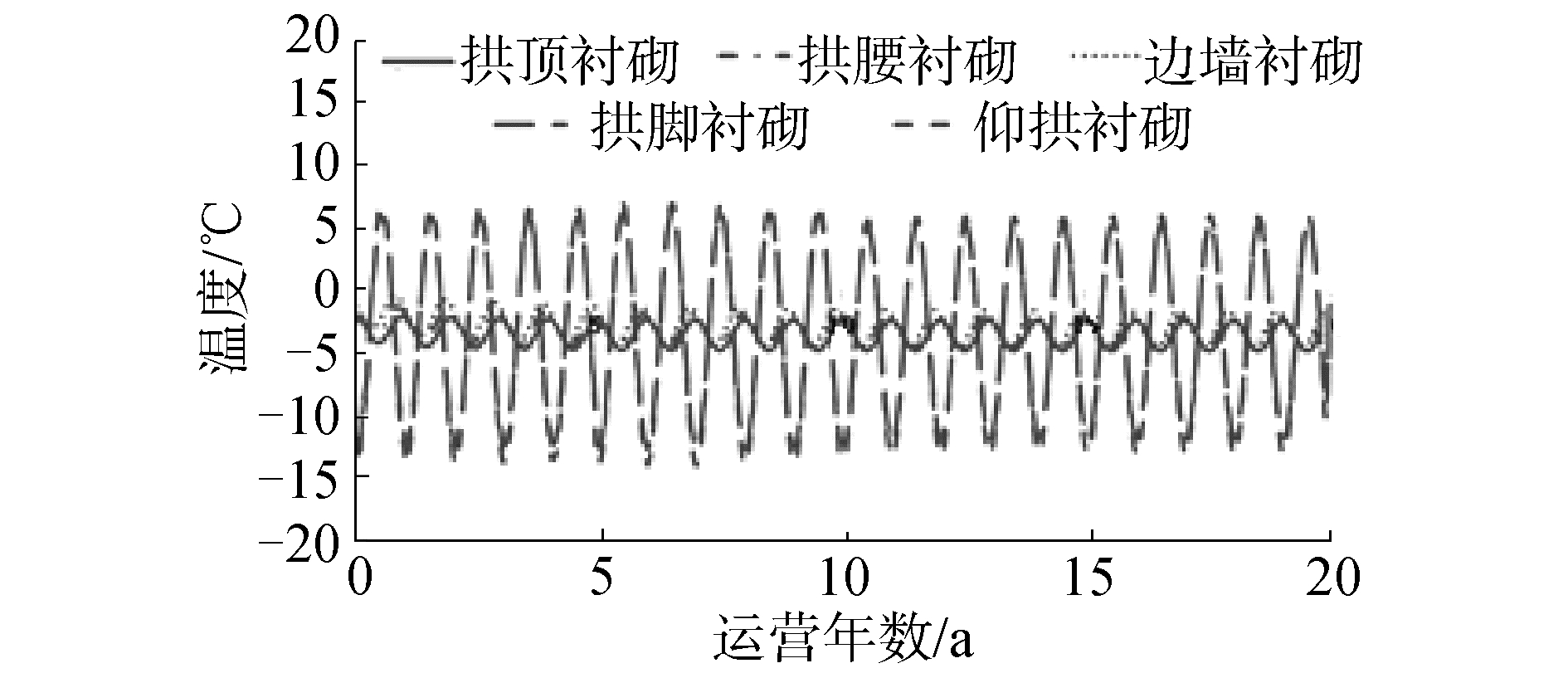
由图 13可知,在铺设两层保温层情况下,隧道拱顶、拱腰和边墙衬砌均不受冻融循环作用,但是拱脚和仰拱处衬砌仍然受到气温引起的冻融作用。
|
Download:
|
| 图 13 知亥代隧道多年冻土段衬砌温度变化 Fig. 13 Temperature variation of lining of permafrost section of ZHIHAI tunnel | |
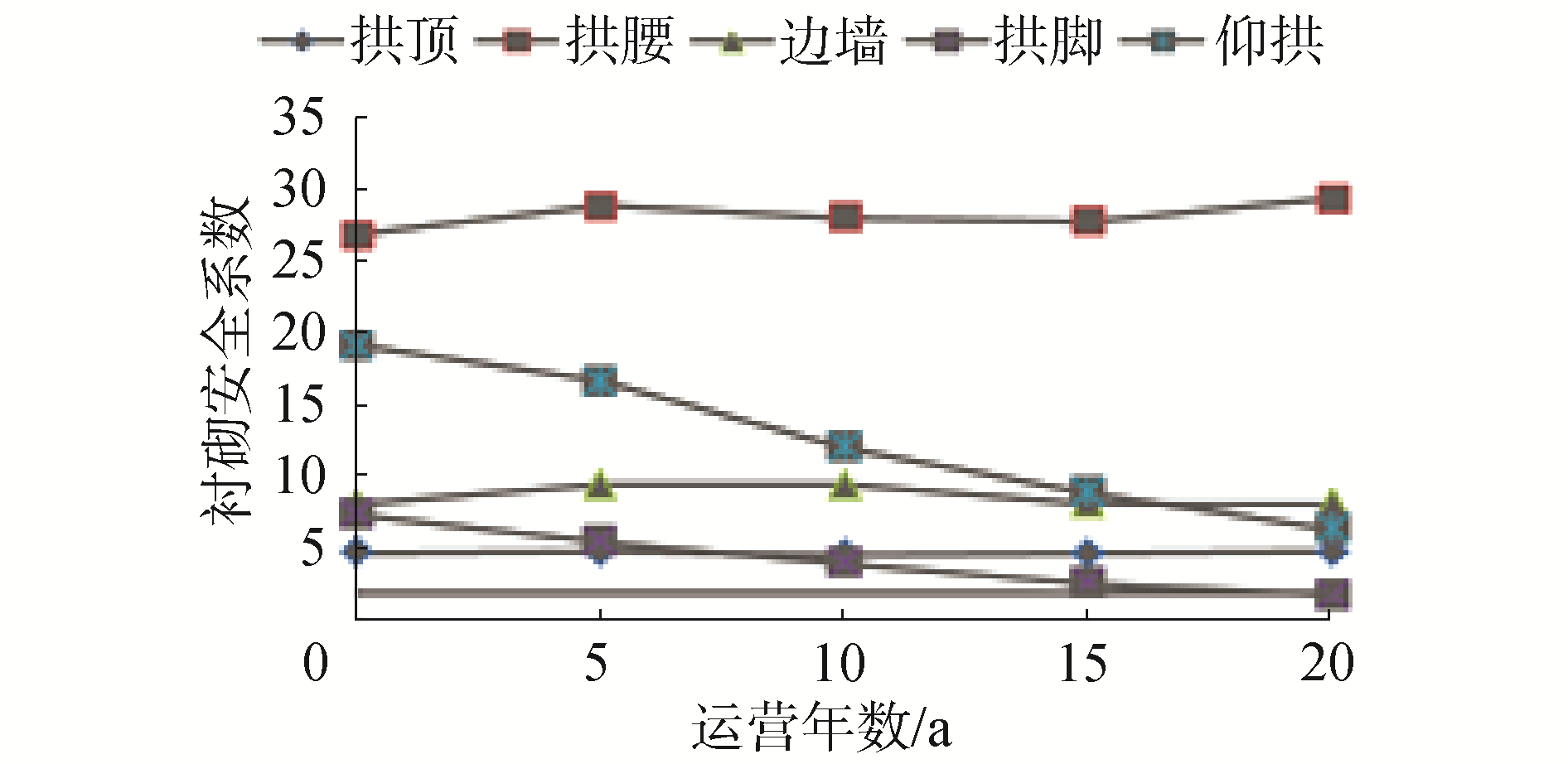
如表 8所示,铺设2层保温层后,运营期多年冻土段衬砌轴力和弯矩值十分稳定。如图 14所示,其拱顶、拱腰和边墙衬砌安全系数也较稳定,无减小趋势。但拱脚和仰拱处衬砌由于受到冻融循环作用,其衬砌安全系数不断减小,拱脚处衬砌安全系数约20 a后已小于2.0,而20 a后仰拱衬砌安全系数也由运营开始时19.16减小至6.42,衬砌服役性能大大降低。
| 表 8 多年冻土段铺设两层保温层下运营期拱顶衬砌处轴力弯矩值 Table 8 The axial moment at the lining of the vault in the permafrost section under the two layers of insulation |
|
Download:
|
| 图 14 知亥代隧道多年冻土段衬砌安全系数变化 Fig. 14 Variation of lining safety coefficient of permafrost section of ZHIHAI tunnel | |
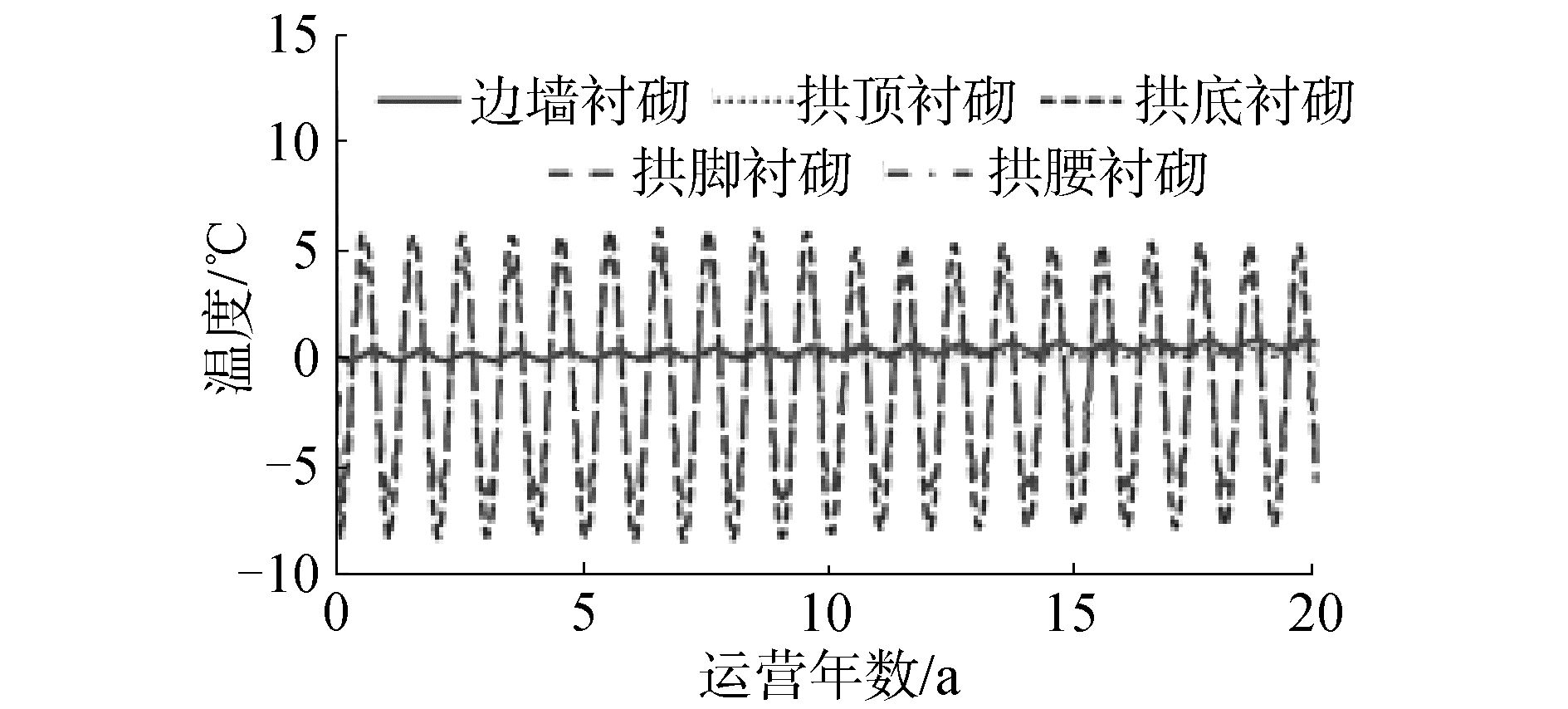
如图 15所示,与多年冻土段双层铺设保温层相似,表面铺设保温层无法阻止洞内气温对于拱脚和仰拱处衬砌的冻融循环作用,同时,在运营期前期,边墙、拱顶和边墙处衬砌仍受到冻融循环作用。
|
Download:
|
| 图 15 知亥代隧道非冻土段衬砌温度变化 Fig. 15 Temperature variation of lining in non-frozen soil section of ZHIHAI tunnel | |
如表 9所示,非冻土段表面铺设一层5 cm厚保温层运营期各处衬砌弯矩较为稳定,拱顶、拱腰和边墙处衬砌轴力变化不大,拱脚和仰拱处衬砌轴力略微增大,表明非冻土段拱脚和仰拱处围岩冻结使轴力增加。
| 表 9 非冻土段铺设一层保温层下运营期拱顶衬砌处轴力弯矩值 Table 9 The axial moment at the lining of the vault during the operation period under the thermal insulation layer is laid in the non-frozen soil section |
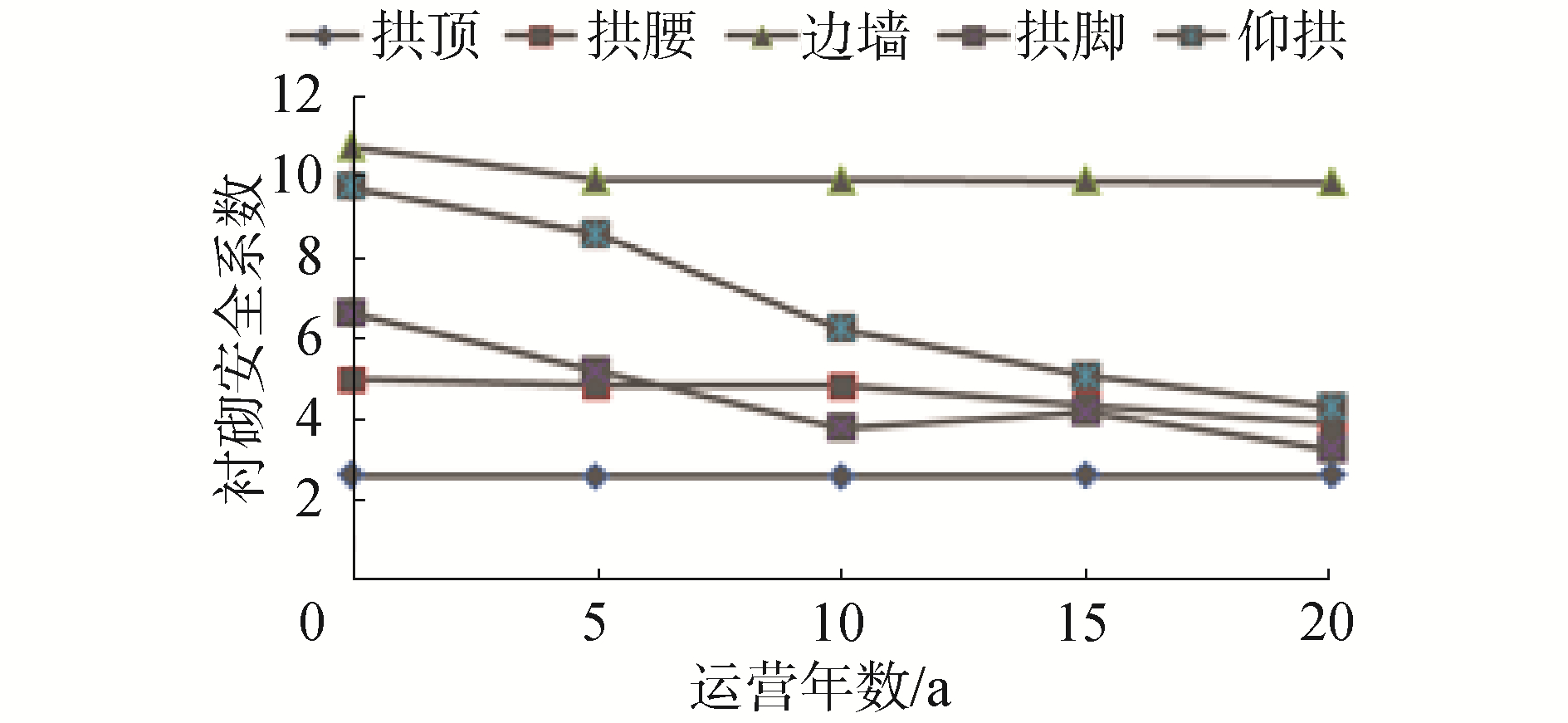
如图 16所示,非冻土段铺设一层5 cm厚保温层后,由于拱脚和仰拱处衬砌受到冻融循环作用,拱脚和仰拱衬砌安全系数不断下降,拱脚处和仰拱处衬砌运营20 a后安全系数分别下降了51%、56%,拱顶、拱腰和边墙处衬砌安全系数都一定程度下降。
|
Download:
|
| 图 16 知亥代隧道非冻土段衬砌安全系数变化 Fig. 16 Variation of lining safety coefficient in non-frozen soil section of ZHIHAI tunnel | |
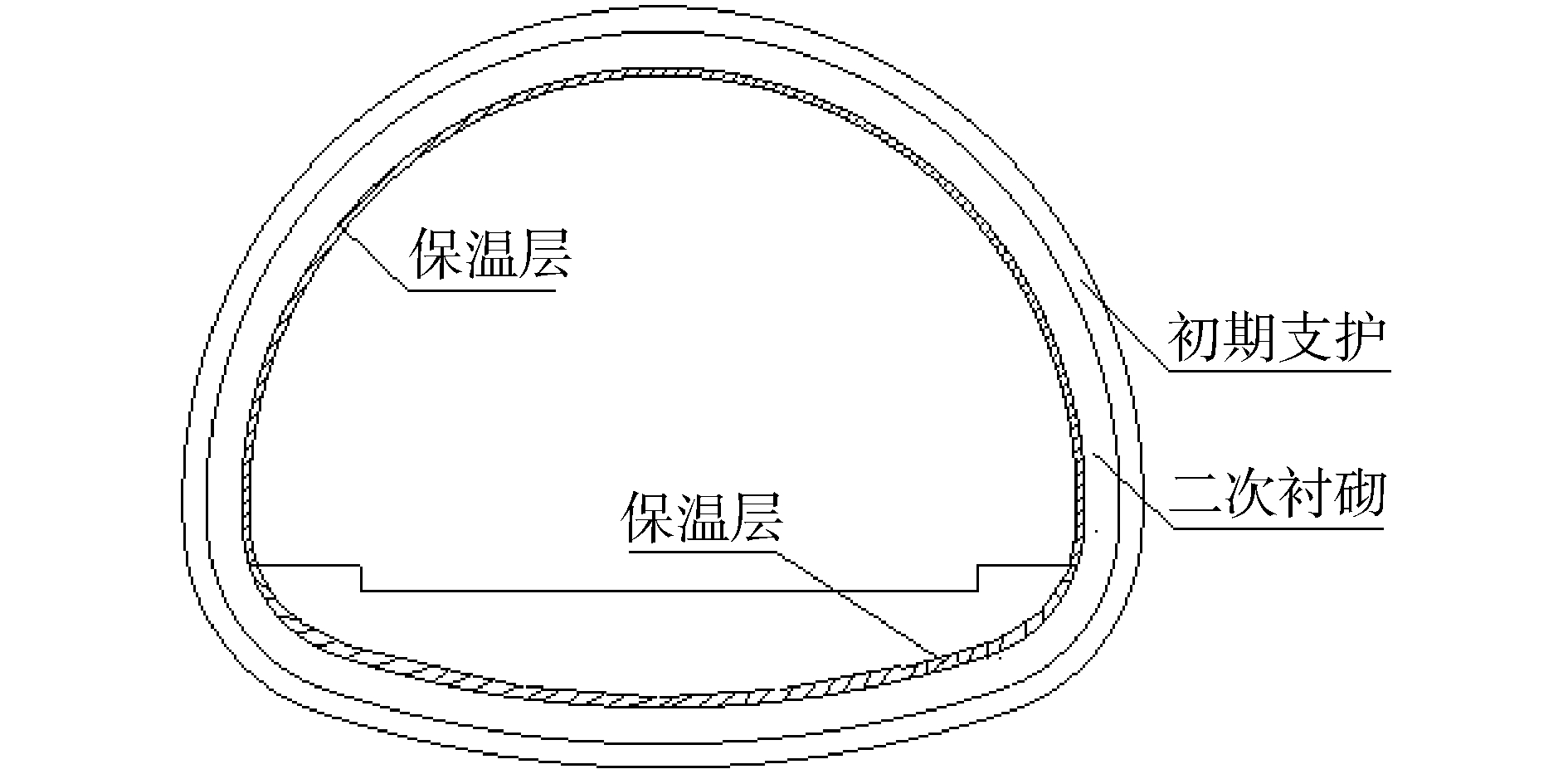
由3.1和3.2计算结果可知,双层铺设保温层和表面铺设保温层时,拱脚和仰拱处衬砌受到洞内气温引起的冻融循环作用而导致衬砌不断劣化,安全系数逐渐减小,服役性能不断降低。此外,常见的夹层铺设保温层方式更是将整个二衬暴露在洞内气温下,其衬砌服役性能势必不断降低。因此,应对拱脚处和仰拱进行保温处理和加固。建议在表面铺设保温层基础上,在仰拱和拱脚处加设一层5 cm厚保温层,如图 17所示,并计算该种保温层方式下多年冻土段衬砌安全系数。
|
Download:
|
| 图 17 加设保温层示意 Fig. 17 Schematic diagram of insulation layer | |
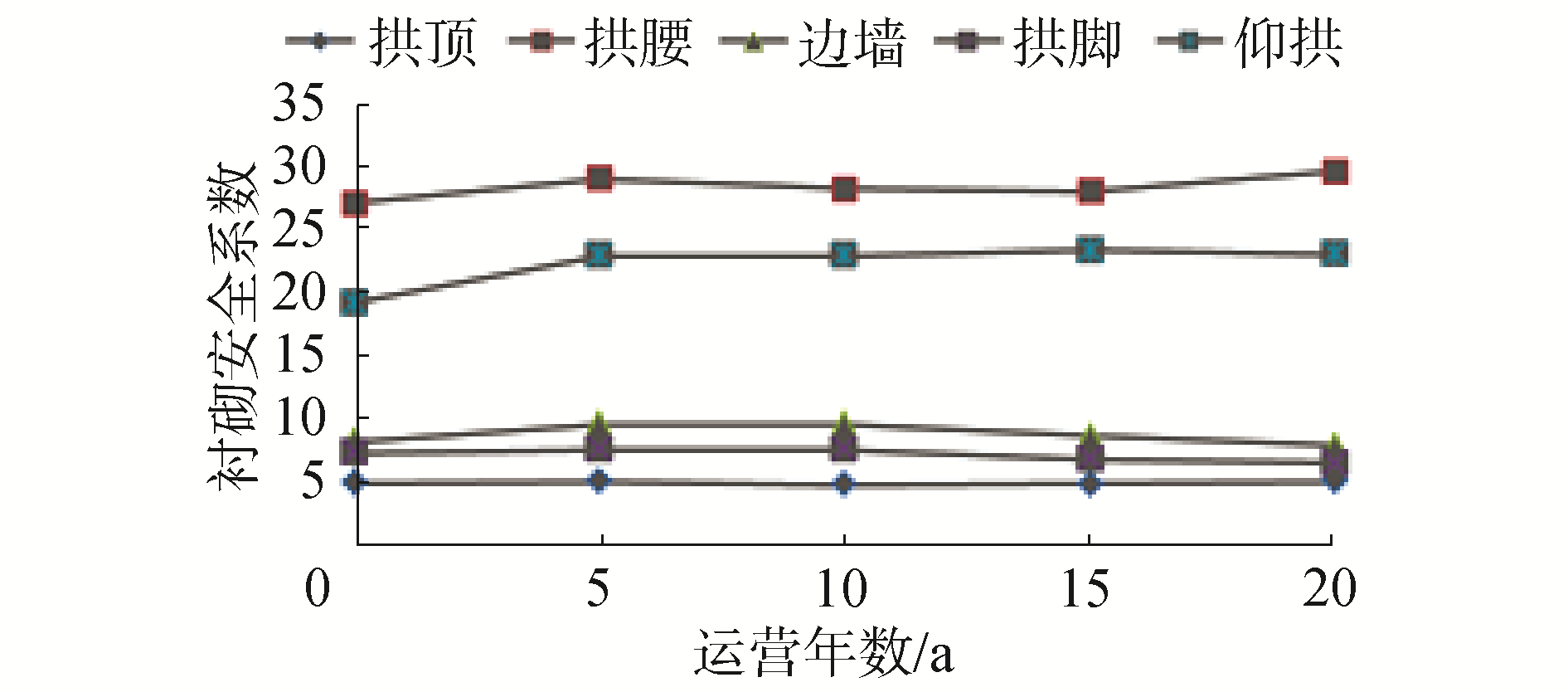
由图可知,加设铺设保温层情况下各处衬砌安全系数较稳定,无减小趋势,表明加设铺设保温层能使衬砌服役性能不下降。
4 寒区隧道保温层铺设厚度优化由多年冻土段和非冻土段在洞内气温条件下衬砌服役性能研究可知,衬砌安全系数减小主要是由于衬砌受到冻融循环劣化引起,因此寒区隧道保温层铺设厚度应使得隧道衬砌不受冻融循环作用。
本节基于ANSYS热力耦合瞬态计算,以衬砌在运营期不受到冻融循环作用为标准,依托知亥代隧道对多年冻土段ZK58+470断面(年平均温度-3.3 ℃,温度振幅11.6 ℃)、非冻土段ZK58+640断面(年平均温度-1.65 ℃,温度振幅9.45 ℃)进行计算,得出隧道各段保温层的最小铺设厚度。
其计算模型、边界条件和温度函数等均按照实际条件选取,计算不同保温层厚度下运营期衬砌所受冻融循环情况。
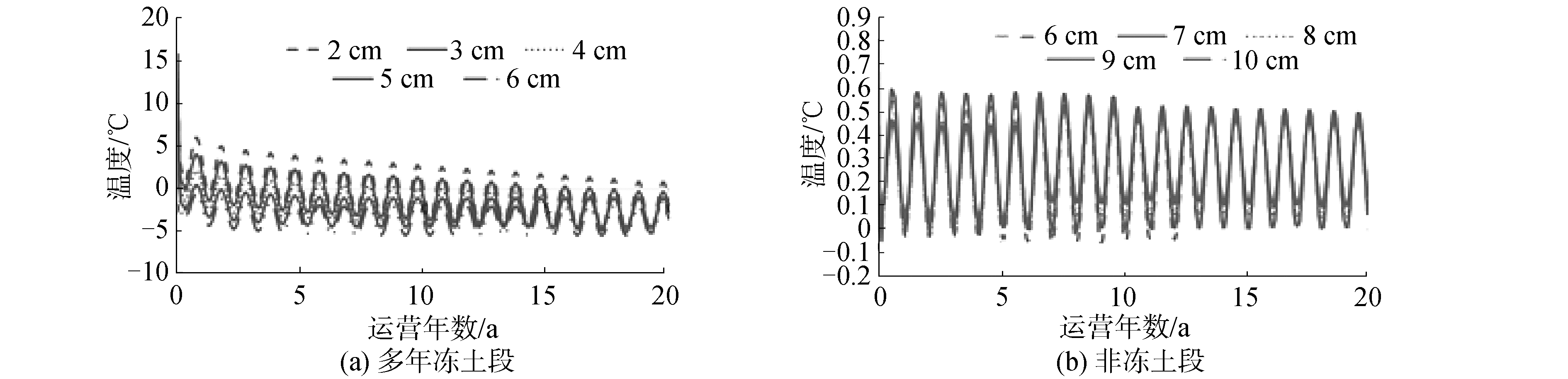
如图 19所示,多年冻土段计算断面在铺设2、3、4、5、6 cm厚保温层情况下运营100 a期间前20 a衬砌受到冻融循环作用年数为19、14、6、1、1 a。非冻土段计算断面在铺设6、7、8、9、10 cm厚保温层情况下运营100 a期间前20 a衬砌受到冻融循环作用年数为12、8、3、1、1 a。因此,对于知亥代隧道,多年冻土段隧道保温层最小铺设厚度应为5 cm,其非冻土段渐冻段保温层铺设厚度应为9 cm。
|
Download:
|
| 图 18 加设保温层下多年冻土段衬砌安全系数变化 Fig. 18 Variation of lining safety coefficient of permafrost section with insulation layer | |
|
Download:
|
| 图 19 多年冻土段及非冻土段不同保温层厚度下衬砌温度变化 Fig. 19 Variation of lining temperature in permafrost and non-frozen soil section under different insulation thickness | |
1) 在不铺设保温层情况下,寒区隧道衬砌受到冻融循环作用,其物理力学性质不断劣化,从而导致衬砌承载安全系数降低,衬砌服役性能下降。对于多年冻土段,当年平均振幅为12.5 ℃时,年平均温度为-2 ℃、-4 ℃和-6 ℃条件下衬砌的服役年数分别为16、16、12 a,年平均温度越低,衬砌服役性能下降越快。当年平均温度为-4 ℃时,年温度振幅为9.5 ℃、12.5 ℃和15.5 ℃条件下,服役年数为17、16、9 a,且年温度振幅越大,衬砌服役性能下降越快。对于非冻土段,当年平均振幅为7.1 ℃时,年平均温度为-0.5 ℃、-1.0 ℃和-1.5 ℃条件下衬砌的服役年数为15、15、15 a。当年平均温度为-1.0 ℃时,年温度振幅为7.1 ℃、5.1 ℃和3.1 ℃条件下衬砌的服役年数分别为15、18、19 a,年温度振幅越大,衬砌服役性能下降越快。
2) 知亥代隧道多年冻土段双层铺设2层5 cm厚保温层,能使拱顶、拱腰和边墙处衬砌不受到冻融循环作用。但该种保温层铺设方式下,拱脚和仰拱处衬砌不断受到冻融循环作用,多年冻土段拱脚和仰拱处衬砌服役年数下降到20 a。非冻土段铺设一层5 cm厚保温层后,由于拱脚和仰拱处衬砌受到冻融循环作用,拱脚和仰拱衬砌安全系数不断下降,拱脚处和仰拱处衬砌运营20 a后安全系数分别下降了51%、56%,拱顶、拱腰和边墙处衬砌由于运营期前期仍受到冻融循环作用,运营期其安全系数都一定程度下降。
3) 对于知亥代隧道,建议在表面铺设保温层基础上加设一层5 cm厚保温层于仰拱和拱脚上,计算结果表明,该种保温层铺设方式下隧道衬砌服役年数不减少。
4) 若要保证知亥代隧道衬砌服役性能不降低,多年冻土段保温层铺设厚度至少为5 cm,非冻土段保温层铺设厚度至少为9 cm。
| [1] |
吴楚钢.新疆天山地区高速公路隧道防冻技术研究[D].重庆: 重庆交通大学, 2007. WU Chugang. Anti-freezing technology of highway tunnel in xinjiang tianshan area[D]. Chongqing: Chongqing Jiaotong University, 2007. (  0) 0)
|
| [2] |
黎岩.寒区隧道围岩融化圈控制技术及衬砌劣化规律研究[D].上海: 同济大学, 2013. LI Yan. Study on the technique of controlling surrounding rock thawing depth and the law of tunnel lining deterioration[D]. Shanghai: Tongji University, 2013. (  0) 0)
|
| [3] |
周宇翔.西藏高海拔地区冻岩冻融循环过程中劣化规律研究[D].西南交通大学, 2015. ZHOU Yuxiang. The deterioration law of frozen rock during freeze-thaw cycles in the TIBETAN high altitude[D]. Chengdu: Southwest Jiaotong University, 2015. (  0) 0)
|
| [4] |
马忠英, 范增莲. 大坂山公路隧道保温层的作用与冻害防治[J]. 公路, 1997(11): 43-45. MA Zhongyin, FAN Zenglian. Effect of thermal insulation and frost damage control of highway tunnel at Dabanshan[J]. Highway, 1997(11): 43-45. (  0) 0)
|
| [5] |
游泳, 徐伟杰, 张业学. 风火山隧道结构防排水施工技术[J]. 公路, 2003(11): 116-119. YOU Yong, XU Weijie, Zhang Yexue. Construction technology of Fenghuoshan tunnel structure waterproof and drainage[J]. Highway, 2003(11): 116-119. DOI:10.3969/j.issn.0451-0712.2003.11.032 (  0) 0)
|
| [6] |
刘小刚. 青藏铁路多年冻土隧道隔热保温研究[J]. 隧道建设, 2010, 30(3): 225-230. LIU Xiaogang. Study on thermal insulation of tunnels in perma-frost soil on Qinghai-Tibet railway[J]. Tunnel construction, 2010, 30(3): 225-230. (  0) 0)
|
| [7] |
陈建勋, 罗彦斌. 寒冷地区隧道防冻隔温层厚度计算方法[J]. 交通运输工程学报, 2007(02): 76-79. CHEN Jianxun, LUO Yanbin. Calculation method of anti-freezing layer thickness in cold region tunnel[J]. Journal of traffic and transportation engineering, 2007(02): 76-79. DOI:10.3321/j.issn:1671-1637.2007.02.016 (  0) 0)
|
| [8] |
陈建勋. 寒冷地区隧道防冻隔温层设计计算方法及应用[J]. 土木工程学报, 2004(11): 85-88. CHEN Jianxun. Design method and application for anti-freezing thermal-protective layers in cold-area tunnels[J]. China civil engineering journal, 2004(11): 85-88. DOI:10.3321/j.issn:1000-131X.2004.11.014 (  0) 0)
|
| [9] |
夏才初, 张国柱, 肖素光. 考虑衬砌和隔热层的寒区隧道温度场解析解[J]. 岩石力学与工程学报, 2010, 29(9): 1767-1773. XIA Caichu, zhang Guozhu, XIAO Suguang. Analytical solution to temperature fields of tunnel in cold region considering lining and insulation layer[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(9): 1767-1773. (  0) 0)
|
| [10] |
晏启祥, 何川, 曾东洋. 寒区隧道温度场及保温隔热层研究[J]. 四川大学学报(工程科学版), 2005(3): 24-27. YAN Qixiang, HE Cuan, ZENG Dongyang. Study of temperature field and heat preservation and insulation layer for tunnel in cold area[J]. Journal of sichuan university (engineering science edition), 2005(3): 24-27. DOI:10.3969/j.issn.1009-3087.2005.03.006 (  0) 0)
|
| [11] |
LAI Y M, SUN A L, ZHU Y L, et al. Geometrically nonlinear analysis of a simply-supported hip-truncated combined parabolical cylinder roof (SCI)[J]. Engineering Structures, 1999, 21(3): 267-276. (  0) 0)
|
| [12] |
中华人民共和国交通部. TB 10003-2005铁路隧道设计规范[S]. Ministry of Communications of PRC. TB 10003-2005 Code for Design of Railway Tunnel. (  0) 0)
|
| [13] |
刘西拉, 唐光普. 现场环境下混凝土冻融耐久性预测方法研究[J]. 岩石力学与工程学报, 2007, 26(12): 2412-2419. LIU Xila, TANG Guangpu. Research on prediction method of concrete freeze-thaw durability under field environments[J]. Chinese journal of rock mechanics and engineering, 2007, 26(12): 2412-2419. DOI:10.3321/j.issn:1000-6915.2007.12.005 (  0) 0)
|
| [14] |
张德华, 王梦恕, 任少强. 青藏铁路多年冻土隧道围岩季节性活动层温度及响应的试验研究[J]. 岩石力学与工程学报, 2007, 26(3): 614-619. ZHANG Dehua, WANG Mengsu, REN Shaoqiang. Experimental study on temperature and response of seasonal active layer of tunnel surrounding rock in perma-frost region on Qinghai-TIBET plateau[J]. Chinese journal of rock mechanics and engineering, 2007, 26(3): 614-619. DOI:10.3321/j.issn:1000-6915.2007.03.025 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


