中比转速离心泵广泛用于城市供水、农业灌溉、石油化工和船舶等领域。一般传统设计的中比转速离心泵轴功率随流量增加而增大,导致离心泵在大流量区工作时容易引起配套电机过载或电机烧毁。因此研究中比转速离心泵无过载性能具有重要意义。
目前国内外研究者对离心泵的无过载性能进行了大量研究,但主要集中于低比转速离心泵范围。研究内容涉及进口条件及压水室结构研究、叶轮关键参数优化、有无过载设计判别理论及方法[1-3]等。文献[4]根据公式,通过推导得出低比转速离心泵功率备用系数K的表达公式并验证公式的准确性;文献[5]指出无过载离心泵的功率备用系数K值(即最大轴功率与额定工况下轴功率的比值)一般小于1.2;文献[6]通过对叶轮增加分流叶片的方式验证离心泵无过载设计;文献[7]通过数值模拟发现前置导叶安放角的取值范围决定了功率曲线是否有极值;文献[8]总结了离心泵的比转速和叶轮出口宽度系数和出口直径系数的比值的关系,得到了中比转速多级离心泵无过载的设计方程组;文献[9-10]采用正交优化的方法,通过数值模拟和试验都能达到无过载设计要求,对离心泵无过载设计具有一定的参考价值;文献[11]通过数值模拟方法验证了叶轮叶片出口角、出口宽度和叶片包角是影响离心泵无过载的因素。
综上,离心泵无过载的研究已取得了一些研究成果,但对于中比转速离心泵无过载理论的研究甚少。如何根据比转速和功率备用系数选取合适的叶轮参数,保证中比转速离心泵无过载且高效率方面的研究还是空白。因此本文在中比转速离心泵无过载性能与叶轮几何参数设计关系方面进行研究。
1 中比转速离心泵无过载叶轮设计方法在文献[12]中,将功率备用系数K值(即最大轴功率与额定功率的比值)表示成叶轮滑移系数、叶片出口角和流量系数的函数:
| $ K=\frac{P_{\max }}{P}=\frac{\mathit{\Phi}_{\max } h_{0}-\frac{\mathit{\Phi}_{\max }^{2}}{\tan \beta_{2}}}{\mathit{\Phi} h_{0}-\frac{\mathit{\Phi}^{2}}{\tan \beta_{2}}} $ | (1) |
式中:
将Φmax和h0代入式(1)并化简得[13]:
| $ \begin{array}{c} K=\frac{P_{\max }}{P}=\frac{1}{4}\left(1-\frac{\pi}{Z} \sin \beta_{2}\right)^{2}\left[\frac{\mathit{\Phi}}{\tan \beta_{2}}(1-\right. \\ \left.\left.\frac{\pi}{Z} \sin \beta_{2}\right)-\left(\frac{\mathit{\Phi}}{\tan \beta_{2}}\right)^{2}\right]^{-1} \end{array} $ | (2) |
对于比转速为80≤ns≤150的中比转速离心泵中有经验公式[12]:
| $ \frac{b_{2}}{D_{2}}=0.000147 n_{s}^{\frac{4}{3}} $ | (3) |
一般离心泵出口排挤系数[13]φ2=0.8~0.9,为研究方便,取φ2=0.85。再通过一元理论计算得到流量系数的关系式:
| $ \begin{array}{c} n_{s}^{\frac{4}{3}} \eta_{h}^{3}\left(h_{0}-\frac{\mathit{\Phi}}{\tan \beta_{2}}\right)^{3}- \\ 3435.287022\left(\frac{1}{1+0.68 n_{s}^{-2 / 3}}\right)^{2} \mathit{\Phi}^{2}=0 \end{array} $ | (4) |
其中水力效率:
| $ \eta_{h}=1+0.0835 \lg \sqrt[3]{\frac{Q}{n}} $ | (5) |
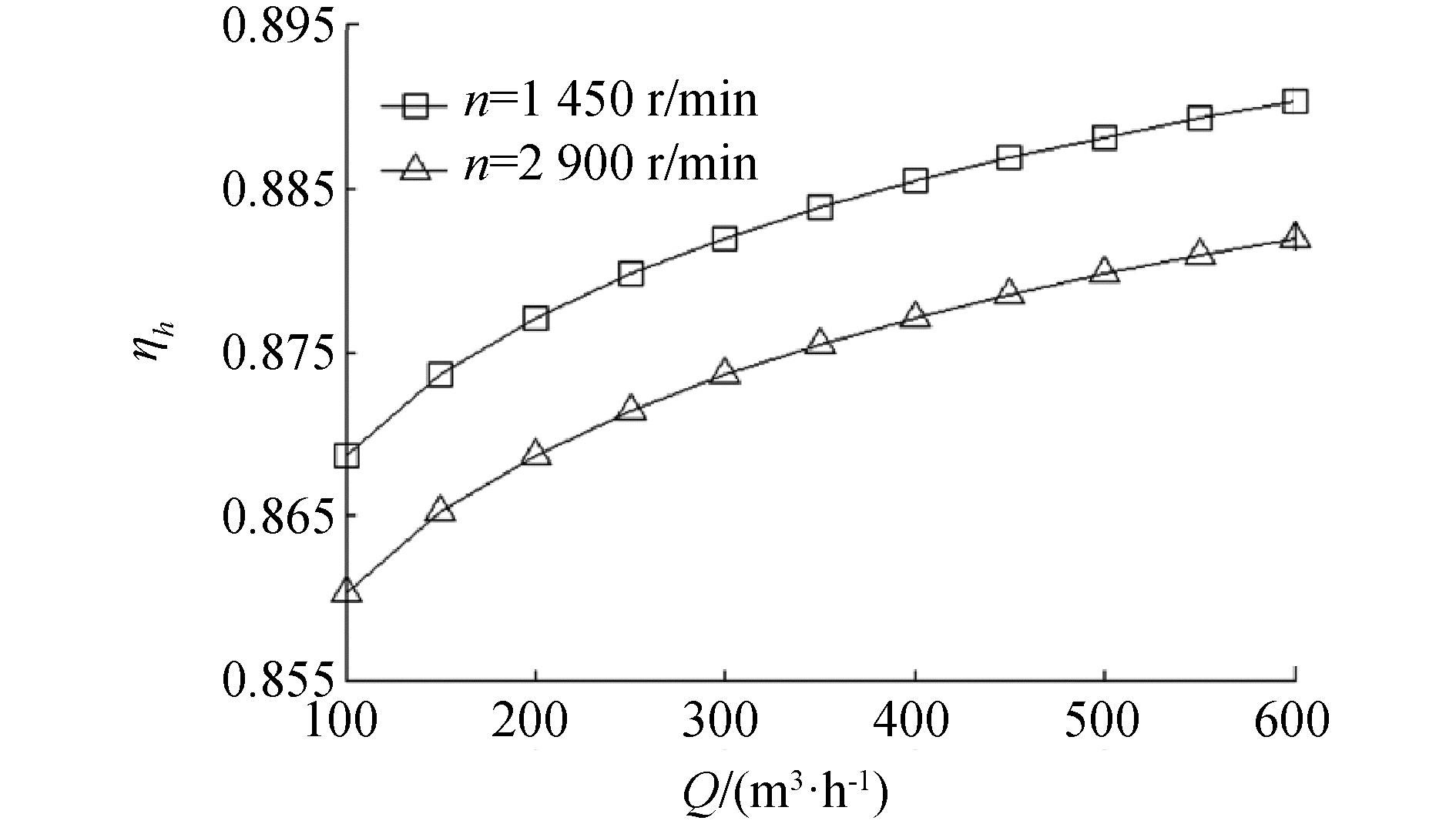
由水力效率公式可绘出ηh-Q图像,如图 1所示。大部分中比转速离心泵(即80≤ns≤150)的转速为1 450 r/min或2 900 r/min。
|
Download:
|
| 图 1 流量—水力效率曲线 Fig. 1 Curves of hydraulic efficiency and flow rate | |
从图 1中可以看出当流量Q发生变化时,ηh变化很小,可取ηh=0.875。这样ηh的上下浮动不会超过0.015,不会影响计算的精度,将ηh=0.875代入到式(4)中得:
| $ \begin{array}{c} 0.6585 n_{s}^{4 / 3}\left(h_{0}-\frac{\mathit{\Phi}}{\tan \beta_{2}}\right)^{3}- \\ 3435.287022\left(\frac{1}{1+0.68 n_{s}^{-2 / 3}}\right)^{2} \mathit{\Phi}^{2}=0 \end{array} $ | (6) |
由式(6)可以将流量系数Φ表示为:Φ=
| $ \begin{aligned} K=\frac{P_{\max }}{P} =\frac{1}{4}\left(1-\frac{\pi}{Z} \sin \beta_{2}\right)^{2}\left[\frac{f\left(n_{s}, \beta_{2}, Z\right)}{\tan \beta_{2}}(1-\right.\\ \left.\left.\frac{\pi}{Z} \sin \beta_{2}\right)-\left(\frac{f\left(n_{s}, \beta_{2}, Z\right)}{\tan \beta_{2}}\right)^{2}\right]^{-1} \end{aligned} $ | (7) |
这样功率备用系数即K值就是ns、β2、Z的函数。
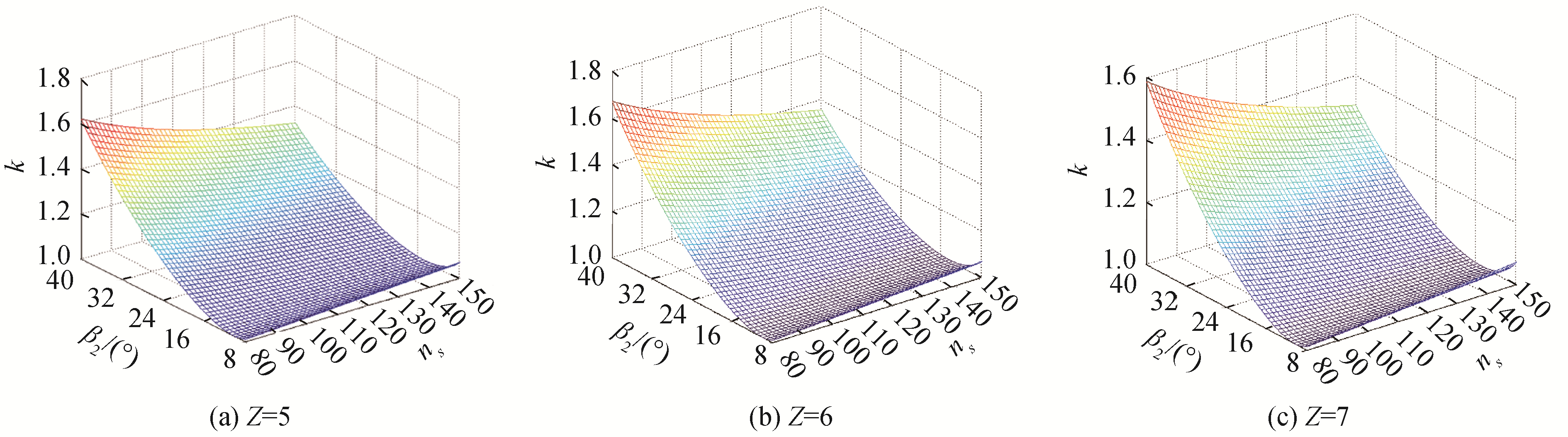
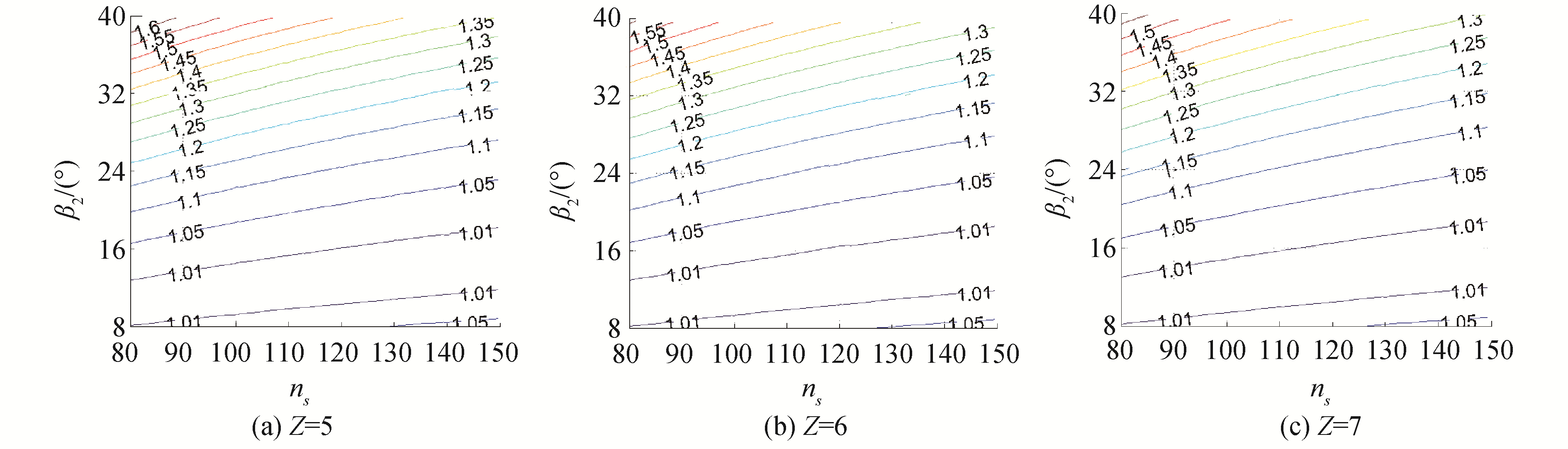
2 不同参数对功率备用系数的影响 2.1 利用Matlab软件绘制图像根据式(7)利用Matlab计算并绘制出K值关于ns、β2、Z的三维函数图像[14]。为了更具体地看出在叶片数不变的情况下K值与ns、β2的关系,将叶片数Z看作常数,绘制出K值关于ns、β2的等高线图。对于中比转速而言,叶片数Z一般赋值为5、6、7,绘制图像如图 2、3所示。
|
Download:
|
| 图 2 不同叶片数下K值三维函数 Fig. 2 Three-dimensional image of K under the different number of blades | |
|
Download:
|
| 图 3 不同叶片数下K值等高线 Fig. 3 Contour chart of K under the different number of blades | |
从图 3中可以看出:对于中比转速离心泵,当叶片数和泵的比转速一定时,功率备用系数K值越大,叶轮叶片出口角越大;当泵的比转速和叶轮叶片出口角一定时,叶片数的增加对K值影响较小;当K值一定时,比转速越大,选取的最大叶片出口角也越大;随泵比转速增大,叶片出口角度范围的最小值和最大值也在增大,以K=1.15为例,在80~150变化的比转速过程中,可选取的最大叶片出口角也从23°增加到32°左右。可见比转速、叶片出口角对离心泵功率备用系数影响较大。
在进行中比转速离心泵无过载叶轮设计时,就可以根据不同的功率备用系数和比转速结合关系式(7)以及图 2、3快捷准确地选取合适的叶片出口角,对于叶轮、蜗壳等其他参数的计算和选择与普通离心泵设计相同。这种理论设计创新不仅避免了传统设计方法中叶片出口角选择的盲目性,同时还提高了设计效率。
3 中比转速离心泵无过载设计及数值预测 3.1 无过载离心泵设计根据上述的理论方法,设计了2台不同的中比转速无过载离心泵,其设计要求如表 1所示。
| 表 1 无过载离心泵设计要求 Table 1 Centrifugal pump non-overload design requirements |
根据表 1中的要求,根据离心泵设计理论及K值等高线图,设计时ns=84.5无过载离心泵要求最大轴功率与额定功率的比值K≤1.13,取叶轮叶片数为Z=6,根据比转速ns=84.5和叶片数从图 3(2)中查得叶片出口角β2≤22°,取β2=22°。同理ns=125.3离心泵叶片数Z=5,要求K≤1.17,从图 3(1)中查得叶片出口角β2≤29°取β2=29°。叶轮及蜗壳的其他参数根据泵的设计理论通过计算可以得到,设计的这2种中比转速无过载离心泵叶轮、蜗壳的主要参数如表 2所示。
| 表 2 离心泵主要几何参数 Table 2 The main geometrical parameters of centrifugal pumps |
根据表 2及叶轮、蜗壳其他几何参数对这2台中比转速离心泵三维建模,如图 4所示。

|
Download:
|
| 图 4 离心泵三维图 Fig. 4 Three-dimensional image of centrifugal pump | |
对设计的无过载离心泵进行性能预测时,利用ICEM软件采用非结构化四面体对该模型进行网格划分,利用Fluent软件选取RNGK-ε模型,对速度与压力耦合方式选择SIMPLE,进口采用速度进口、出口采用自由出流方式进行性能预测[15]。首先对2台中比转速离心泵进行网格无关性检查,然后再对2台中比转速离心泵多个工况点进行性能预测。
为了验证数值模拟的准确性,对其中一台比转速为84.5的无过载离心泵进行外特性实验,图 5为离心泵试验台。试验台包括模型泵;进出水管路;型号为AMF-80-2.5-1000-COA,精度等级为0.5级的电磁流量计;型号为3351DP7E22M3B3C2,精度等级为0.25级的压力传感器;型号为NJ1,精度等级为0.2级的转矩转速传感器;ZA2.T调节阀型号。泵实验时,对该泵在小流量、额定流量、大流量等11个工况点进行测试。

|
Download:
|
| 图 5 离心泵试验台 Fig. 5 Centrifugal pump test bench | |
本文只是模拟了离心泵的水力效率,对于ns=84.5的离心泵为了和实验进行对比,通过数值模拟得到的水力效率ηh,最终计算出总效率η:
| $ \eta=\eta_{\mathrm{h}} \eta_{\mathrm{m}} \eta_{\mathrm{v}} $ | (8) |
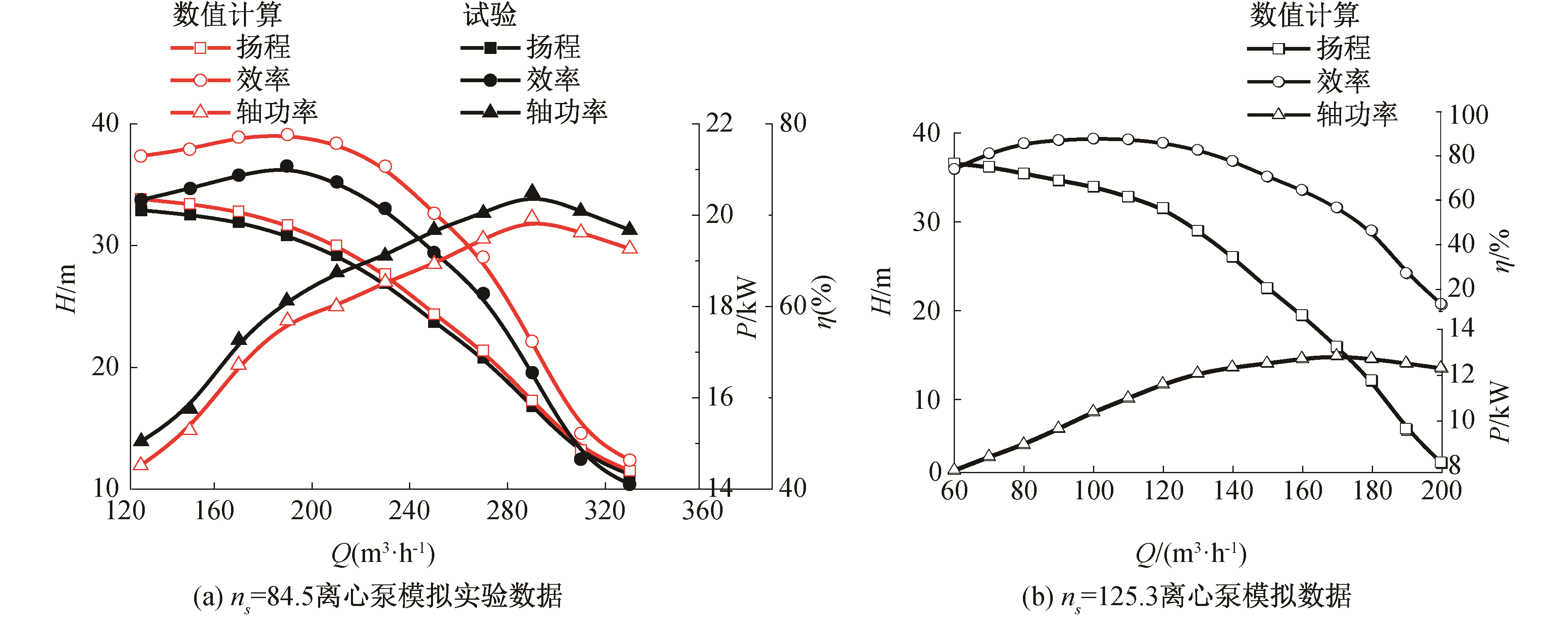
式中机械效率ηm和容积效率ηv取自文献[13]中的经验公式,将模拟数据和试验数据统计整理,如图 6所示[17]。同时又做出2台中比转速离心泵的模拟结果静压如图 7、8所示。
|
Download:
|
| 图 6 离心泵性能曲线 Fig. 6 Performance curves diagram of centrifugal pumps | |
|
Download:
|
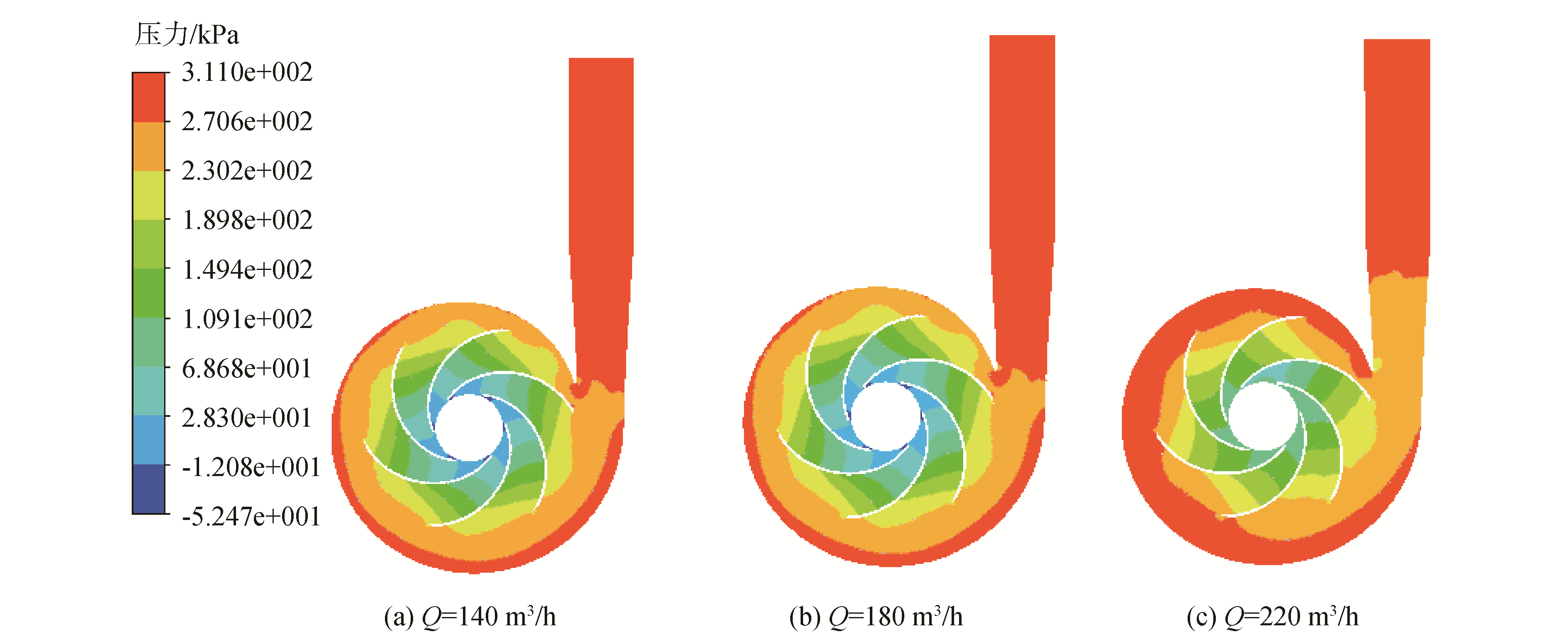
| 图 7 ns=84.5的离心泵在不同工况下中间截面上内部静压分布云图 Fig. 7 The static pressure distribution cloud diagram in the middle section of centrifugal pump withns=84.5 | |
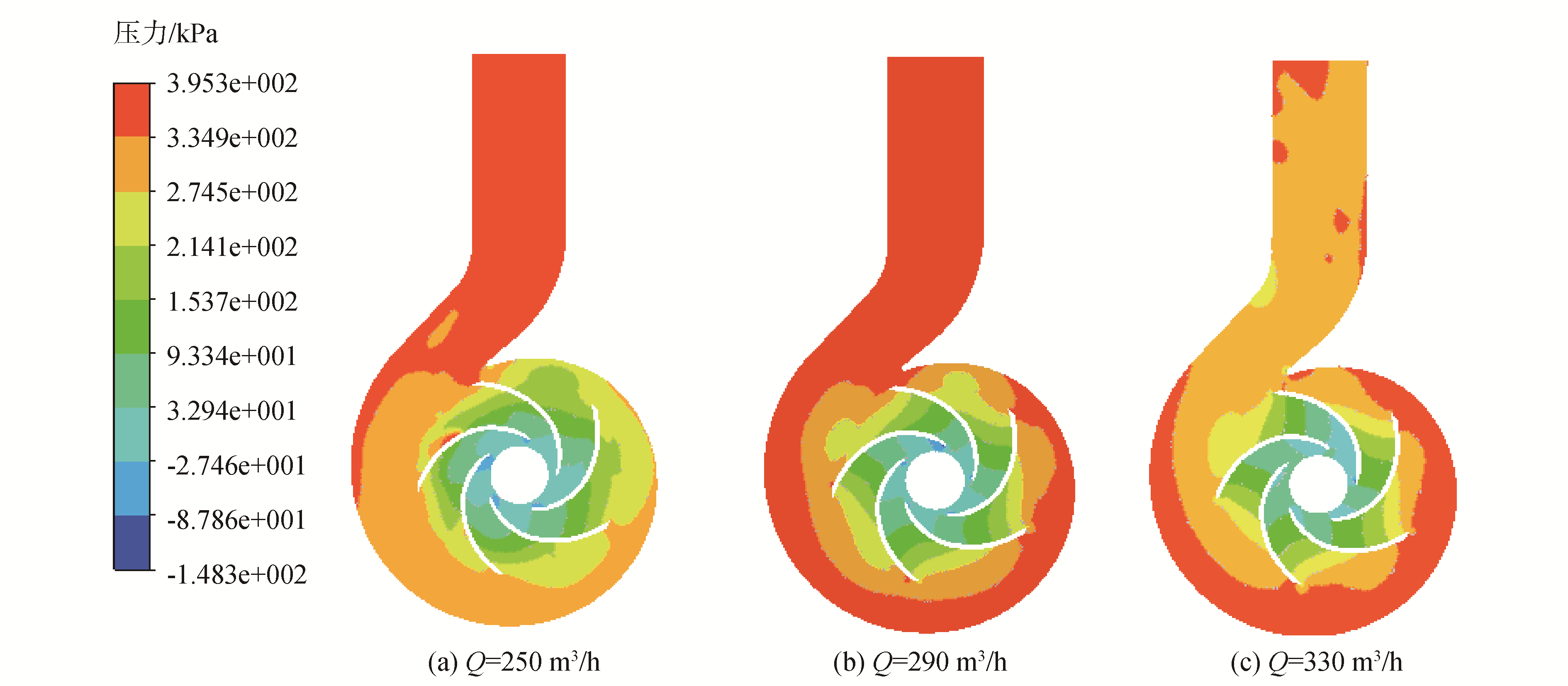
|
Download:
|
| 图 8 ns=125的离心泵在不同工况下中间截面上内部静压分布云图 Fig. 8 The static pressure distribution cloud diagram in the middle section of centrifugal pump withns=125 | |
将图 6中最大轴功率点和最高效率点的数据整理如表 3、4所示。
| 表 3 ns=84.5离心泵数值模拟和实验分析表 Table 3 Numerical simulation and experimental analysis table of centrifugal pump withns=84.5 |
| 表 4 ns=125.3离心泵数值模拟分析表 Table 4 Numerical simulation analysis table of centrifugal pump withns=125.3 |
由表 3可知,对于ns=84.5的离心泵,在最高效率点和最大轴功率点时,其实验数据和数值模拟数据相对误差都在5%以内,相对误差较小。通过数值模拟和实验可以计算出模拟中的功率备用系数K=1.127,实验的功率备用系数K=1.131,此离心泵设计要求的功率备用系数K=1.13。由表 4可知,对于ns=125.3的离心泵通过数值模拟计算得到功率备用系数K=1.168,设计要求K=1.17。可见2台中比转速离心泵通过模拟或实验与设计的功率备用系数相差很小。因此通过上述理论和功率备用系数等值图可以快速选取中比转速离心泵叶轮几何参数,从而能够得到无过载且高效率的中比转速离心泵。
图 7、8是2台中比转速无过载离心泵在不同流量工况下中间截面上内部静压分布云图[17]。从图中可以发现:泵在设计工况下运行时,叶轮内的流场分布更合理,流体的流态较好;叶片工作面和背面的压力差对流体做功使流体的动能和压力能从进口到出口逐渐增高;叶轮各流道内的静压分布并不均匀,尤其是靠近隔舌处,这主要是由于蜗壳的几何结构以及蜗壳与叶轮的相互作用造成的。
4 结论1) 本文通过理论推导得出中比转速离心泵功率备用系数能够表示成仅与比转速、叶片出口角和叶片数相关的函数。通过三维函数图和等高线图可知叶片出口角、比转速对功率备用系数K值影响较大,而叶片数对K值影响较小。
2) 中比转速离心泵无过载设计时,在已知叶片数下,可以利用图像根据比转速和功率备用系数直接选取最合适的叶片出口角,避免了叶片出口角选取的盲目性,简化了设计过程。
3) 实例表明:通过数值模拟及试验计算得到的功率备用系数K值与设计时要求的K值误差较小,在合理范围内。
| [1] |
ZHANG Hua, CHEN Bin, SHI Weidong, et al. Effects of contraction-type impeller on non-overloaded performance for low-specific-speed sewage pump[J]. Journal of mechanical science and technology, 2014, 28(3): 937-944. DOI:10.1007/s12206-013-1165-9 (  0) 0)
|
| [2] |
从小青, 袁寿其, 袁丹青, 等. 无过载排污泵理论与设计方法研究[J]. 农业机械学报, 2003, 34(6): 77-80. CONG Xiaoqing, YUAN Shouqi, YUAN Danqing, et al. Theory and hydraulic design of non-overload sewage pumps[J]. Transactions of the Chinese society for agricultural machinery, 2003, 34(6): 77-80. DOI:10.3969/j.issn.1000-1298.2003.06.022 (  0) 0)
|
| [3] |
SHAN S R, JAIN S V, PATEL R N, et al. CFD for centrifugal pumps: a review of the state-of-the-art[J]. Procedia engineering, 2013, 51: 715-720. DOI:10.1016/j.proeng.2013.01.102 (  0) 0)
|
| [4] |
杨军虎, 郭斌, 王玥, 等. 无过载离心泵设计参数与性能关系研究[J]. 农业机械学报, 2012, 43(11): 119-122, 128. YANG Junhu, GUO Bin, WANG Yue, et al. Relationship of performances and design parameters for non-overload centrifugal pumps[J]. Transactions of the Chinese society for agricultural machinery, 2012, 43(11): 119-122, 128. DOI:10.6041/j.issn.1000-1298.2012.11.022 (  0) 0)
|
| [5] |
SHI Weidong, LONG Fei, LI Yue, et al. Non-overload design of low specific speed submersible pump[C]//Proceedings of ASME 20103rd Joint US-European Fluids Engineering Summer Meeting collocated with 8th International Conference on Nanochannels, Microchannels, and Minichannels. Montreal: ASME, 2010: 563-567.
(  0) 0)
|
| [6] |
张帆, 袁寿其, 付强, 等. 带分流叶片低比转速无过载离心泵优化设计[J]. 流体机械, 2013, 41(6): 11-15, 21. ZHANG Fan, YUAN Shouqi, FU Qiang, et al. Non-overload optimization design on low specific speed centrifugal pump with splitter blades[J]. Fluid machinery, 2013, 41(6): 11-15, 21. DOI:10.3969/j.issn.1005-0329.2013.06.003 (  0) 0)
|
| [7] |
施卫东, 李辉, 陆伟刚, 等. 进口预旋对低比速离心泵无过载性能的影响[J]. 农业机械学报, 2013, 44(5): 50-54, 112. SHI Weidong, LI Wei, LU Weigang, et al. Effect of prewhirl flow on non-overload performance of low-specific-speed centrifugal pumps[J]. Transactions of the Chinese society for agricultural machinery, 2013, 44(5): 50-54, 112. (  0) 0)
|
| [8] |
马艺, 马中强, 张生昌, 等. 中比转速无过载多级离心泵的叶轮设计方法[J]. 上海交通大学学报, 2015, 49(5): 695-701. MA Yi, MA Zhongqiang, ZHANG Shengchang, et al. A novel design method for impeller of medium specific speed non-overload multistage centrifugal pumps[J]. Journal of Shanghai Jiao Tong University, 2015, 49(5): 695-701. (  0) 0)
|
| [9] |
马中强, 张生昌, 马艺, 等. 基于正交设计法的中比转速泵无过载优化设计[J]. 流体机械, 2015, 43(10): 42-46, 83. MA Zhongqiang, ZHANG Shengchang, MA Yi, et al. Non-overload optimization design of medium specific speed pump based on orthogonal design method[J]. Fluid machinery, 2015, 43(10): 42-46, 83. (  0) 0)
|
| [10] |
沈艳宁, 袁寿其, 陆伟刚, 等. 复合叶轮离心泵数值模拟正交试验设计方法[J]. 农业机械学报, 2010, 41(9): 22-26. SHEN Yanning, YUAN Shouqi, LU Weigang, et al. Orthogonal test design method based on numerical simulation for non-overload centrifugal pump with complex impeller[J]. Transactions of the Chinese society for agricultural machinery, 2010, 41(9): 22-26. (  0) 0)
|
| [11] |
HU Bo, YUAN Shouqi, LU Weigang, et al. Numerical optimal design of a non-overload centrifugal pump[C]//Proceedings of ASME 2012 Fluids Engineering Division Summer meeting Collocated with the ASME 2012 Heat Transfer Summer Conference and the ASME 201210th International Conference on Nanochannels, Microchannels, and Minichannels. Rio Grande, Puerto Rico, USA: American Society of Mechanical Engineers, 2012: 427-433.
(  0) 0)
|
| [12] |
袁寿其. 低比转速离心泵理论与设计[M]. 北京: 机械工业出版社, 1997. YUAN Shouqi. Theory and design of low specific speed centrifugal pump[M]. Beijing: China Machine Press, 1997. (  0) 0)
|
| [13] |
关醒凡. 现代泵理论与设计[M]. 北京: 中国宇航出版社, 2011. GUAN Xingfan. Modern pumps theory and design[M]. Beijing: China Astronautic Publishing House, 2011. (  0) 0)
|
| [14] |
郝文化. MATLAB图形图像处理应用教程[M]. 北京: 中国水利水电出版社, 2004. HAO Wenhua. MATLAB image processing application tutorial[M]. Beijing: China Water Power Press, 2004. (  0) 0)
|
| [15] |
杨军虎, 吴俊辉, 张人会. 无过载离心泵内部流场的三维数值模拟[J]. 兰州理工大学学报, 2009, 35(1): 41-45. YANG Junhu, WU Junhui, ZHANG Renhui. Three-dimensional numerical simulation of internal flow field in non-overloading centrifugal pump[J]. Journal of Lanzhou University of Technology, 2009, 35(1): 41-45. DOI:10.3969/j.issn.1673-5196.2009.01.011 (  0) 0)
|
| [16] |
林彬.中比转速离心泵无过载低空化设计方法研究[D].兰州: 兰州理工大学, 2019. LIN Bin. Research on design method of non-overload and low cavitation for medium specific speed centrifugal pump[D]. Lanzhou: Lanzhou University of Technology, 2019. (  0) 0)
|
| [17] |
徐鹏, 魏修亭, 李春花, 等. 离心泵内部流场数值模拟与性能分析[J]. 现代制造技术与装备, 2012(3): 72-73, 82. XU Peng, WEI Xiuting, LI Chunhua, et al. Inner flow field numerical simulation and performance analysis of centrifugal pump[J]. Modern manufacturing technology and equipment, 2012(3): 72-73, 82. DOI:10.3969/j.issn.1673-5587.2012.03.036 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


