2. 北京市建筑安全监测工程技术研究中心, 北京 100044
2. Beijing Engineering Research Center of Monitoring for Construction Safety, Beijing 100044, China
滚动轴承是旋转机械的关键部件之一,其健康状况直接影响整机的工作性能,因此对滚动轴承进行及时诊断具有重要意义。
对轴承进行故障诊断时,噪声的存在会对诊断结果产生很大影响,在轴承振动信号降噪方法中,小波阈值法降噪时阈值和小波基函数难以选取;奇异值分解(singular value decomposition,SVD)[1]降噪法在噪声强度较大时效果差;局部均值分解(local mean decomposition,LMD)、固有时间尺度分解(intrinsic time scale decomposition,ITD)、经验模态分解(empirical mode decomposition,EMD)[2]降噪需要对信号反复迭代,存在端点效应和虚假分量问题;变分模态分解(variational mode decomposition,VMD)[3]降噪时预先设定的模态分量个数会直接影响降噪效果。压缩感知(compressive sensing,CS)[4]降噪避免了阈值选取问题,通过对轴承振动信号进行压缩采样并重构实现信号的降噪。经验小波变换(empirical wavelet transform,EWT)[5]降噪通过自适应分割信号的频谱并构造合适的小波滤波器提取不同的模态函数,降噪结果更稳定。
在当今大数据时代,传统的基于“特征提取+模式识别”的轴承智能故障诊断模式越来越不能满足自动化诊断要求。深度学习[6]克服传统智能诊断方法的固有缺陷[7],很大程度上摆脱依赖诊断专家的信号处理与特征提取经验,一些深度学习技术已经进入机器健康监测系统。赵光权等[8]利用深度置信网络(deep belief network,DBN)直接对滚动轴承时域振动信号进行自动特征提取与分类。曲建岭等[9]将轴承原始时域振动信号直接输入卷积神经网络模型,从而实现对原始振动信号的逐层自适应特征提取。但在轴承故障诊断中广泛使用的DBN、堆栈自编码器等逐层深度学习技术所需要调整的参数众多,诊断过程耗时过长且极易受到噪声影响[10];而普通卷积神经网络一般对数据的行方向和列方向均进行卷积融合运算,对于图像来说合理,但对轴承振动信号这种一维信号采用卷积运算是不合理的。基于CS、EWT和深度学习的优势,本文提出一种改进EWT-CS(improved EWT-CS,IEWT-CS)联合降噪法结合导联卷积神经网络(lead convolution neural network,LCNN)的轴承故障诊断方法。本文提出方法通过CS和改进经验小波变换(improved empirical wavelet transform,IEWT)方法对轴承振动信号进行联合降噪,LCNN用于从降噪后的振动信号中自动提取特征并识别故障,避免了人工特征提取。实验结果表明,提出方法具有很好的可行性和有效性。
1 压缩感知降噪原理设N维纯净轴承振动信号为x,N维噪声信号为n,则轴承加噪振动信号可表示为xn=(x + n)。由压缩感知原理对其进行低维观测,设压缩感知观测矩阵为Φ (M×N维,M < N),则可得到M维压缩观测向量y为:
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{x}}_n} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {\mathit{\boldsymbol{x}} + \mathit{\boldsymbol{n}}} \right) $ | (1) |
构造稀疏字典矩阵ψ (N×N维),字典矩阵ψ可对信号x稀疏化,由于噪声信号不具备稀疏性,所以ψ无法将噪声信号n稀疏化。将原始振动信号x和噪声信号n在ψ中展开,可得:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{x}} = {\mathit{\boldsymbol{\psi }}^{ - 1}}{\mathit{\boldsymbol{\theta }}_x}}\\ {\mathit{\boldsymbol{n}} = {\mathit{\boldsymbol{\psi }}^{ - 1}}{\mathit{\boldsymbol{\theta }}_n}} \end{array}} \right. $ | (2) |
式中:θx和θn表示x和n在字典ψ上展开的系数向量,此时y可重写为:
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{\psi }}^{ - 1}}({\mathit{\boldsymbol{\theta }}_x} + {\mathit{\boldsymbol{\theta }}_n}) $ | (3) |
由ψ的选择原则可知θx是稀疏的,θn不是稀疏的,设θx的稀疏度为kx,θn的稀疏度为kn,则有kx≪kn < N。由CS信号重构条件可知,从M个测量量中能以较大概率重构出振动信号x,但是很难重构出噪声n,即在压缩投影中一部分噪声信息被丢弃,这就是CS降噪的基础。基于DFT、DCT、DWT等构造的完备稀疏字典和基于正交级联、精细采样、插值扩展、时频原子离散化等方法构造的超完备稀疏字典在对轴承振动信号分解时都有一定的稀疏表达能力,但是并不能进一步提高稀疏性能。而基于字典学习的方法充分考虑了轴承振动信号自身的特性,能更进一步提高稀疏性能。本文使用K-奇异值分解(K-singular value decomposition,K-SVD)算法求取稀疏字典,K-SVD方法直接使用采集得到的轴承振动数据作为训练样本来训练字典,具体步骤见文献[11]。CS观测矩阵选择高斯随机观测矩阵,信号重构算法使用正交匹配追踪[12](orthogonal matching pursuit,OMP)算法。
2 改进经验小波变换传统EWT算法自适应划分轴承振动信号频谱,并建立合适的小波滤波器提取不同频段的调幅-调频成分,从而将原始信号f(t)分解为N个单分量模态函数之和。为了找出频谱区间边界,Gilles[13]给出了4种边界检测法:局部极大值法、局部极大极小值法、自适应法和尺度空间法。前两种方法需要人为设置子分量个数;自适应法要考虑每个边界可能出现的位置;尺度空间法可能使得某些频率成分无法分离。朱永利等[14]提出一种双阈值筛选法来确定VMD中的分解模态数,较好的对局部放电信号进行了特征提取,鉴于VMD模态数k的确定方法,提出一种基于振动信号功率谱确定EWT分解模态数的幅值阈值筛选法。
功率谱表示信号功率和频率之间的关系。轴承振动信号由于易受噪声干扰,功率谱具有较强的随机性。采集到的轴承振动信号通常是复杂的非平稳信号,其中多振源激励和响应相互耦合,包含多种干扰成分,每种成分都有相应的频域特性,因此,可以将轴承振动信号的整个频段分成若干个具有窄带特性的带宽,并根据相应频带中的频率幅值判断该频带是否为有效频带,有效频带的个数即为调幅-调频分量个数。基于EWT分解模式和信号功率谱的特点,提出一种基于轴承振动信号功率谱幅值阈值筛选法以确定EWT分解模态数。幅值阈值T用以度量信号功率谱中相应频率的幅值,幅值超过T的频率被认为是原信号中的有用频率分量,被保留;幅值过小,则看做干扰忽略。使用幅值阈值筛选法确定模态数的具体实现步骤如下:
1) 基于被分析轴承振动信号的频域特性确定幅值阈值T。
2) 计算振动信号相应的功率谱。
3) 得到功率谱的局部极大值点以及相应的下标序列。
4) 基于幅值阈值T对步骤3)中得到的局部极值进行判断。幅值大于T的极值对应的下标视为有用边界,相应频带作为被分析信号的有效频带。
5) 统计有效边界,得到有效的频带区间,即得到分解模态数。
在本文中,幅值阈值T依据Otsu准则[15]自适应确定,即选择特定阈值T以最大化有用频率分量和干扰频率分量之间的方差,此时2类数据之间的差异也最大。基于Otsu准则确定幅值阈值T的基本原理如下:将轴承振动信号功率谱幅值视为长度为m的离散序列{xi},i=1,2,…,m,xmax、xmin分别为序列最大值和最小值。令灰度对应功率谱中频率幅值大小,L为灰度等级,另dx=(xmax-xmin)/L。统计幅值落在[(l-1)dx,ldx]内的值的数量为nl,l为灰度值,l=1,2,…,L。灰度值l出现的概率为pl=nl/N,N=n1+n2+…+nL。将序列{xi}的频率幅值分成2类,幅值落在[0,kdx]内的构成一类,记C0;幅值落在[(k+1)dx,Ldx]内的构成另一类,记C1。文献[16]给出2种灰度均值μ0(k)、μ1(k)和方差σ02(k)、σ12(k)的计算公式,则C0和C1的类内方差之和为:
| $ \begin{array}{*{20}{c}} {\sigma _b^2(k) = \sum\limits_{l = 1}^k {{p_l}} {{({\mu _0}(k) - \mu )}^2} + }\\ {\left( {1 - \sum\limits_{l = 1}^k {{p_l}} } \right){{({\mu _1}(k) - \mu )}^2}} \end{array} $ | (4) |
式中:μ为整个序列的灰度均值,计算式为:
| $ {\mu = {\mu _0}(k)\sum\limits_{l = 1}^k {{p_l}} + {\mu _1}(k)\left( {1 - \sum\limits_{l = 1}^k {{p_l}} } \right)} $ | (5) |
| $ {\sigma _b^2({k^*}) = \mathop {{\rm{max}}}\limits_{1 \le k < L} \sigma _b^2(k)} $ | (6) |
最终得到最优阈值T=k*dx。由此可得到所有的区间边界,则N个区间段中的每个区间都可表示为An=[Mn-1,Mn],Mn为第n个边界,经验小波的母小波定义为An上的带通滤波器,经验尺度函数
| $ {W_f^\varepsilon (n,t) = < f,{\psi _n} > = {F^{ - 1}}(\hat f(w){{\bar {\hat \psi }}_n}(w))} $ | (7) |
| $ {W_f^\varepsilon (0,t) = < f,{\varphi _1} > = {F^{ - 1}}(\hat f(w){{\bar {\hat \varphi }}_1}(w))} $ | (8) |
信号重建公式为:
| $ f(t) = W_f^\varepsilon (0,t) * {\varphi _1}(t) + \sum\limits_{n = 1}^{N - 1} {W_f^\varepsilon } (n,t) * {\psi _n}(t) $ | (9) |
信号f(t)可被分解为:
| $ {{f_0}(t) = W_f^\varepsilon (0,t) * {\varphi _1}(t)} $ | (10) |
| $ {{f_k}(t) = W_f^\varepsilon (k,t) * {\psi _k}(t)} $ | (11) |
式中k=1,2,…,N-1。
信号经IEWT分解为若干模态分量后,按相关系数-峭度准则[16]选出故障特征较为明显的模态分量并重构信号。模态分量所包含的冲击成分越多,峭度值越大;模态分量与原信号的相关性越大,相关系数越大。
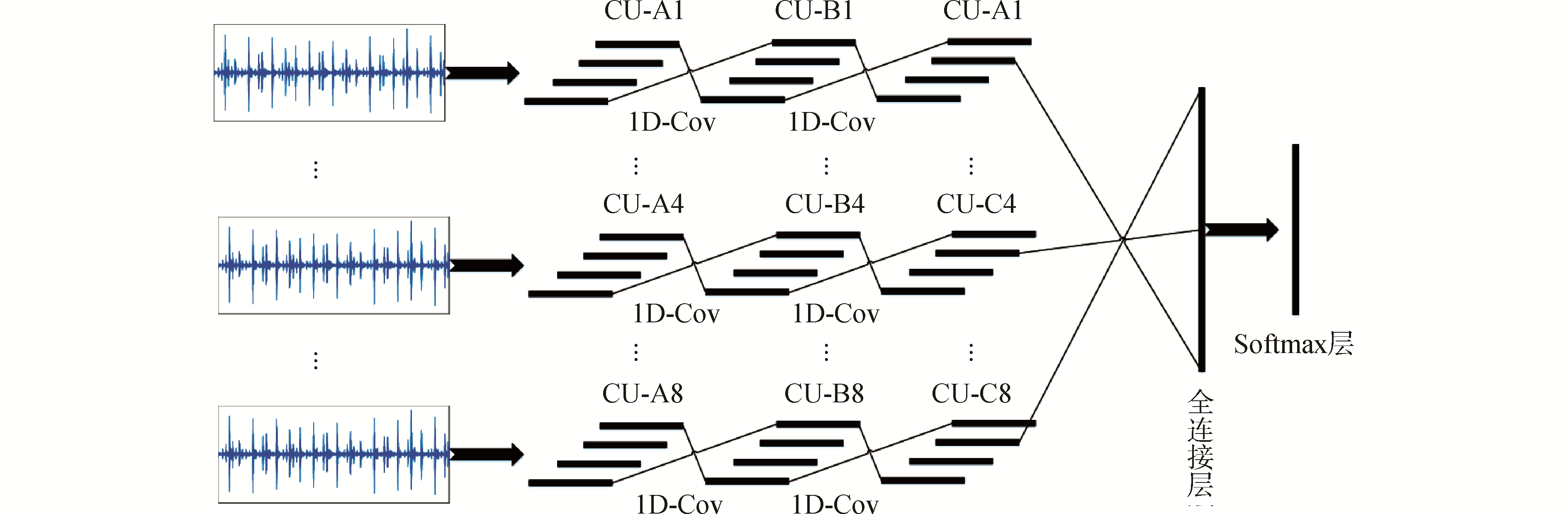
3 导联卷积神经网络采用多传感器对轴承进行监测,增加了信息的多样性和完整性,能够更全面地反映轴承运行的状态,进行故障诊断时可获得更高的准确度。多传感器数据结构类似于二维图像,但传感器间数据的相关性与传感器内数据的相关性程度不同,若采用普通卷积神经网络对数据的行方向和列方向均进行卷积运算,对图像来说合理,但是运用到多传感器振动数据,则不同传感器(列方向)同一时间段内(行方向)的轴承振动数据就会有卷积运算,同一传感器内的数据是时间相关的,采用卷积运算是合理的;但传感器间的数据是相互独立的,如果要进行卷积运算,则要考虑到不同传感器的所有不同组合情况。金林鹏等[18]基于多导联心电信号这种特殊的二维数据结构,提出了LCNN,而多导联心电信号与多传感器振动信号的数据结构相似,因此,针对多传感器数据结构,将LCNN引入轴承故障诊断中,LCNN结构如图 1。
|
Download:
|
| 图 1 导联卷积神经网络结构 Fig. 1 The structure of LCNN | |
卷积单元CU有多个特征面,1D-Cov为一维卷积运算,每只传感器通道均有3个卷积单元,不同传感器间的卷积单元互不相干,本文设置有8只传感器,则共有24个卷积单元。普通的卷积神经网络只要3个卷积单元,每只传感器通道的振动数据依次通过最适合自身的3个卷积单元,然后汇总所有传感器通道的信息做最后的分类。本文选择适用于多分类问题的Softmax回归层做最后的分类,下面给出导联卷积神经网络前向计算公式:
设输入样本为x =[x1,x2,…,x8],其中xi(1≤i≤8)为第i个传感器通道的数据,fc为卷积函数,fs为池化函数,则网络输出为:
| $ f(\mathit{\boldsymbol{x}}) = gE(gD(\bigcup\limits_{i = 1}^8 {g{C_i}(g{B_i}(g{A_i}({\mathit{\boldsymbol{x}}_i}))))} ) $ | (12) |
式中:gAi、gBi、gCi表达式均为fs(fc(x)),但计算权值不同,函数的计算公式为:
| $ {{f_c}(v) = \bigcup\limits_{j,x} {v_{ij}^x} = \bigcup\limits_{j,x} {({b_{ij}} + \sum\limits_m {\sum\limits_{p = 0}^{{P_i} - 1} {w_{ij,(i - 1)m}^p} } v_{(i - 1)m}^{(x + p)})} } $ | (13) |
| $ {{f}_{\text{s}}}(x)=\bigcup\limits_{\begin{smallmatrix} m \\ x=1,{{Q}_{i}}+1 \end{smallmatrix}}{v_{im}^{x}}=\bigcup\limits_{\begin{smallmatrix} m \\ x=1,{{Q}_{i}}+1 \end{smallmatrix}}{\varphi (\text{max}(\bigcup\limits_{q=0,1,\cdots ,{{Q}_{i}}-1}{v_{(i-1)m}^{(x+q)}}))} $ | (14) |
式中:第i层的卷积核大小为1×Pi;池化核大小为1×Qi;vijx为导联卷积神经网络中第i层第j个特征面且位置是x的神经元的输出值;wij, (i-1)mp为第i层第j个特征面到第i-1层第m个特征面的核权值;bij为第i层第j个特征面的偏置。
gD(·)为全连接层计算函数,表达式为:
| $ gD(\mathit{\boldsymbol{x}}) = \phi (\mathit{\boldsymbol{Wx}} + \mathit{\boldsymbol{b}}) $ | (15) |
式中:ф通常取ReLU函数,表达式为:
| $ {\rm{ReLU }}(x) = \left\{ {\begin{array}{*{20}{l}} {x,}&{x > 0}\\ {0,}&{x \le 0} \end{array}} \right. $ | (16) |
gE(·)为Softmax层计算函数,假设任务为K分类问题,则表达式为:
| $ gE(\mathit{\boldsymbol{x}}) = \frac{1}{{\sum\limits_{i = 1}^K {{\rm{exp}}} ({\mathit{\boldsymbol{W}}_j}\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{b}}_j})}} \cdot \left[ {\begin{array}{*{20}{c}} {{\rm{exp}}({\mathit{\boldsymbol{W}}_1}\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{b}}_1})}\\ \vdots \\ {{\rm{exp}}({\mathit{\boldsymbol{W}}_K}\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{b}}_K})} \end{array}} \right] $ | (17) |
式中Wj和bj为权重和偏置。
导联卷积神经网络采用和卷积神经网络相同的反向传播(back propagation,BP)训练算法,步骤见文献[17-18]。
综上,故障诊断步骤如下:
1) 获取轴承不同故障状态振动信号样本集,构造K-SVD字典矩阵。
2) 利用K-SVD字典矩阵对振动信号进行第1次降噪。
3) 利用IEWT方法和相关系数-峭度准则对信号进行第2次降噪并重构信号。
4) 从去噪样本集中选取80%作为训练样本,其余作为测试样本。
5) 根据实际样本数据大小确定卷积层、池化层、卷积核、特征平面、学习率等参数。
6) 将训练数据输入导联卷积神经网络中进行有监督网络训练,通过反向传播算法调整整个网络的权值和偏置等参数。
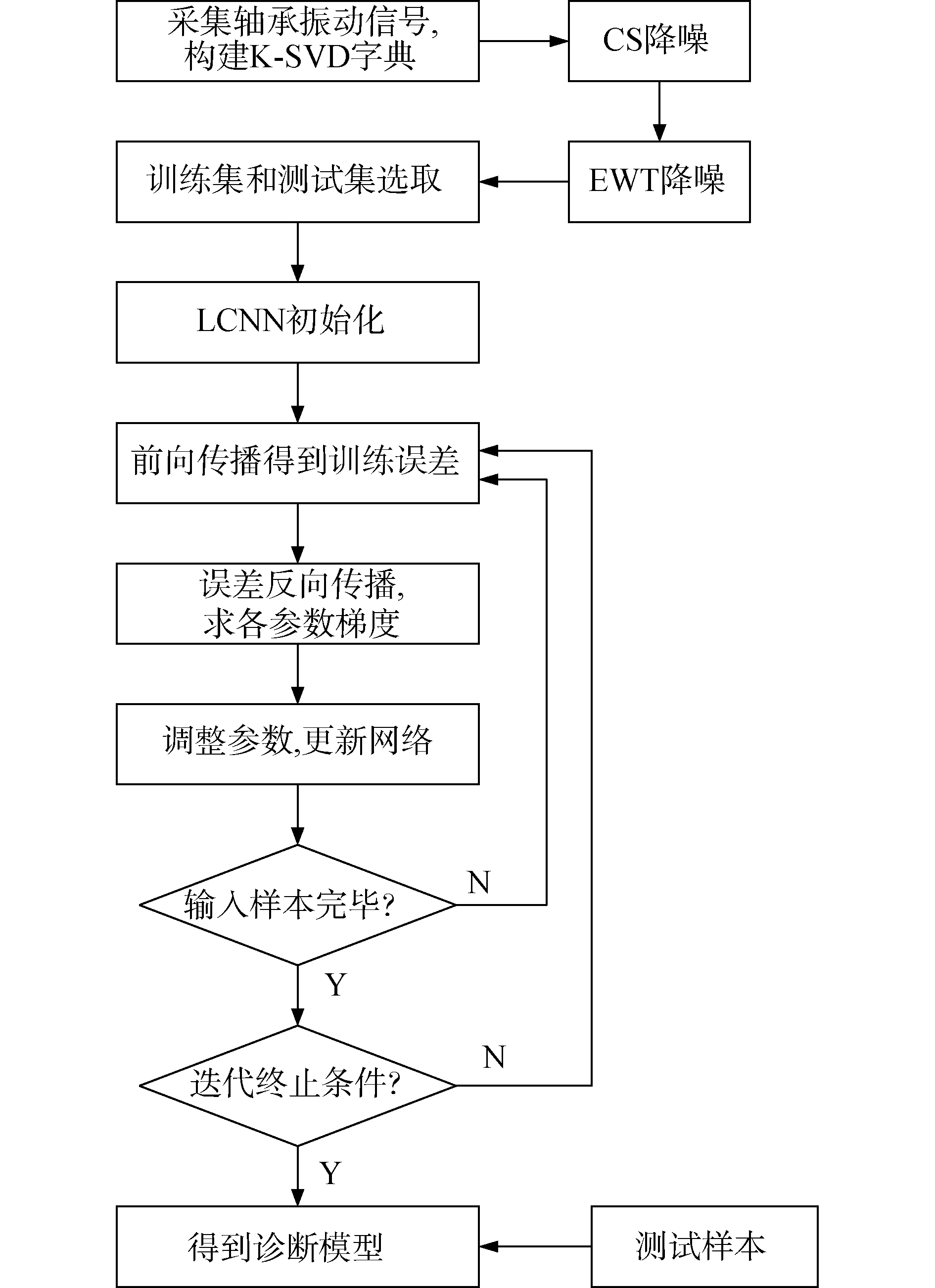
7) 根据测试样本集的结果判断是否满足实际期望的诊断效果,如果诊断正确率过低则修正网络,再重复步骤5)和步骤6),直到达到预期精度。图 2为总流程图。
|
Download:
|
| 图 2 故障诊断流程 Fig. 2 Fault diagnosis flow chart | |
在本实验中,滚动轴承的振动数据是从滚动轴承故障模拟实验台获得的,如图 3,实验台由驱动器、电磁制动器、测试轴承等组成。轴承型号为SKF,使用电火花技术在轴承内圈、外圈和滚动体上加工故障直径分别为0.18 mm和0.36 mm的切槽,用8只传感器采集不同故障状态下的滚动轴承振动信号。转轴转速设为1 500 r/min,采样频率为24 kHz,负载为0.73 kW,转轴转1圈,传感器采集约960(48 000×60/1 500≈960)个数据点。训练LCNN网络需要大量训练样本,采用文献[9]的方法对训练数据进行有重叠样本分割,从而实现数据扩充,这种分割方式既增加了训练样本数量,又可以使LCNN的学习更具鲁棒性。最后选择了不同故障类型、不同故障严重程度的7种状态,每种状态包含1 000个样本,随机选取800个作为训练样本,剩余作为测试样本,每个样本由1 900个采样数据点组成。表 1列出了7种轴承工况。为减少噪声干扰,将轴承原始信号归一化到[0, 1]:

|
Download:
|
| 图 3 轴承实验台 Fig. 3 The rolling bearing experimental setup | |
| 表 1 7种轴承状态 Table 1 Seven bearing working conditions |
| $ {x^\prime } = ({x_i} - {x_{{\rm{min}}}})/({x_{{\rm{max}}}} - {x_{{\rm{min}}}}) $ | (18) |
图 4为7种轴承工况下的时域波形。由图 4可知,早期故障信号中冲击成分能量低,噪声干扰严重,且部分冲击淹没在噪声中,振动情况较为复杂,难以区分故障类型及故障程度。且由于传统特征提取方法的不确定性和复杂性,使得轴承早期轻微故障特征不易提取,复合故障特征难以提取,致使故障诊断的难度很大。因此有必要引入深度学习技术以建立各种工况状态与输入信号之间的精确映射关系。

|
Download:
|
| 图 4 7种轴承状态的振动信号波形 Fig. 4 Vibration signals of the seven bearing conditions | |
取轴承7种状态振动样本各500个,每个样本数据点为1 900,使用K-SVD算法训练得到超完备字典。经反复试验,在字典训练中,字典原子个数设为3 000个,稀疏分解原子个数为20,循环次数30次,稀疏字典矩阵ψ ∈ R1 900×3 000,CS观测矩阵选择高斯随机观测矩阵,重构算法使用OMP算法,OMP算法稀疏度设置为10。
经反复试验,LCNN中卷积层A为8个特征面,卷积核大小1×18,池化核大小为1×3;卷积层B为14个特征面,卷积核大小为1×12,池化核大小为1×3;卷积层C为20个特征面,卷积核大小为1×4,无池化层,全连接层神经元个数为30,Softmax层神经元数为7,代表 7种故障类别。网络使用小批量随机梯度下降法来训练网络,其具体思路是在更新每一参数时都使用一部分样本来进行更新,从而使得梯度下降更加稳定,同时小批量的计算,也减少了计算资源的占用,本文设置小批量训练尺寸为30。代价函数选择交叉熵函数,最大训练迭代次数8 000次。每个卷积运算之后、激活函数之前,使用批归一化方法,该方法使得卷积提取后特征均值为0,方差为1,可以获得较大的学习速率,而且可以省去Dropout层,且会避免过拟合。网络训练时学习率为0.05,动量值为0.05。为了验证提出方法的有效性和鲁棒性,共进行5次试验。
4.3 实测信号降噪分析按照4.2节K-SVD算法得到超完备字典,以图 4内圈故障振动信号为例,经CS降噪后的结果如图 5所示。

|
Download:
|
| 图 5 压缩感知降噪结果 Fig. 5 CS noise reduction result | |
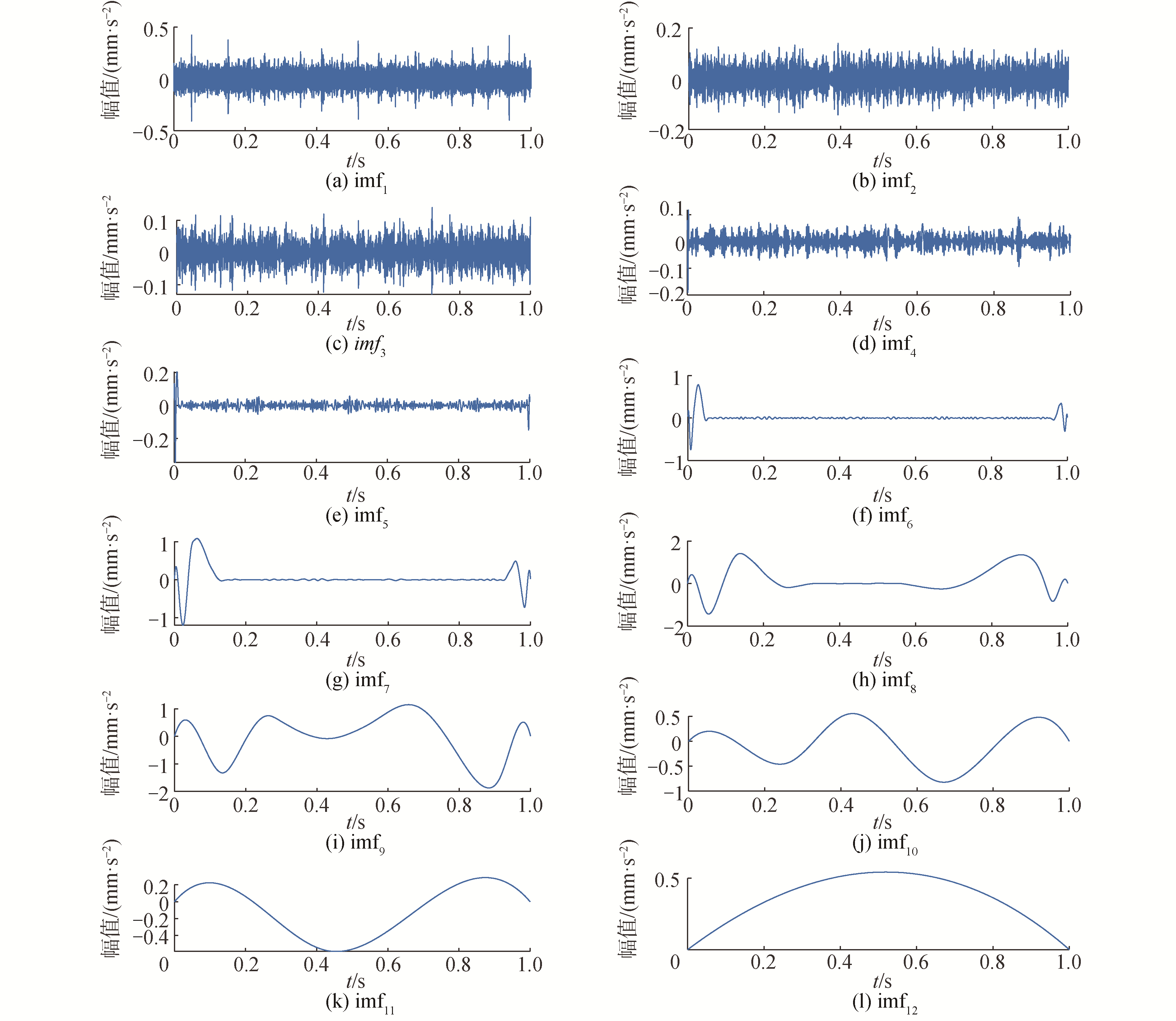
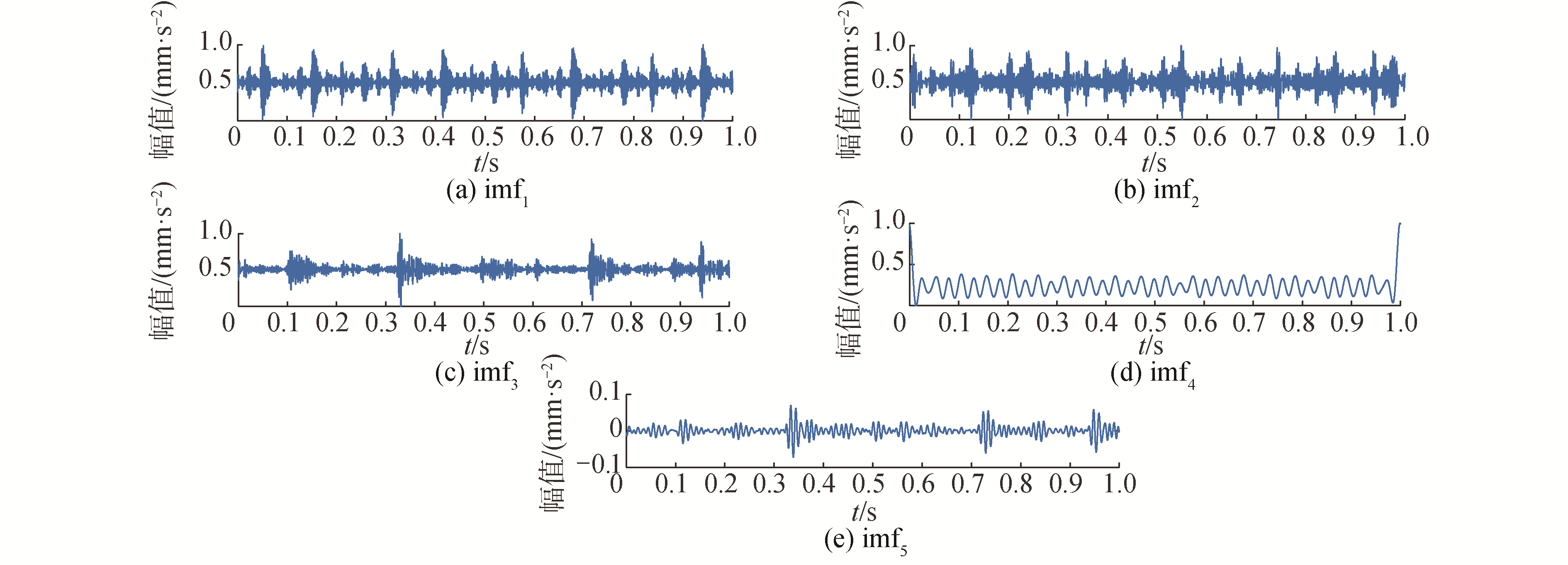
以均方根误差和信噪比衡量降噪效果,计算见文献[19]。均方根误差越小且信噪比越高,表明降噪效果越好。经计算,降噪前信号信噪比和均方根误差分别为1.751和0.698,经CS降噪后信号信噪比和均方根误差分别为4.67和0.402,这说明CS方法很好地实现了降噪。分别采用EMD和IEWT对经CS降噪后的信号进行分解,如图 6和图 7所示。
|
Download:
|
| 图 6 外圈故障信号EMD结果 Fig. 6 EMD result of outer ring fault signal | |
|
Download:
|
| 图 7 外圈故障信号IEWT结果 Fig. 7 IEWT result of outer ring fault signal | |
由图 6可以看出,EMD分解模态混叠严重,干扰过多。以IEWT分解结果为例,经计算,imf2和imf5分量峭度值和相关系数值最低,舍弃,将其余分量进行重构。经EMD和IEWT分解降噪后的重构信号如图 8。经计算,EMD降噪后信号信噪比和均方误差分别为5.12和0.389,经IEWT降噪后信号信噪比和均方误差为7.79和0.205,表明IEWT分解效果优于EMD,很好地实现了2次降噪。

|
Download:
|
| 图 8 EMD和IEWT降噪结果 Fig. 8 EMD and IEWT noise reduction result | |
为了验证提出方法的优越性,采用人工神经网络(artificial neural network,ANN)、支持向量机(support vector machine,SVM、DBN)、CNN、深度稀疏自动编码器(deep sparse auto-encoder,DSAE)等方法进行分析比较。本文提出的方法输入的是降噪后的振动数据(1 900维)。其中ANN、SVM的输入是24个特征(11个时域特征和13个频域特征),有关这24个特征参数见文献[20]。
方法1 (24个特征参数输入ANN) ANN结构为24-59-7,学习速率为0.1,迭代次数为500次。
方法2 (24个特征参数输入SVM) SVM采用RBF核函数,核函数的惩罚因子和半径分别为28和0.15,由10折交叉验证法确定。
方法3 (降噪数据输入DBN) DBN的结构为1 900-900-450-200-50-7,每个限制玻尔兹曼机的学习率、动量因子和迭代次数分别为0.04、0.1和200。
方法4 (降噪数据输入CNN) CNN输入层维数为8×1 900,有3个卷积层,第1卷积层有8个特征面,每个特征面使用1个3×18的卷积核,池化核大小为2×2;第2卷积层使用大小为3×12的卷积核,有14个特征面,池化核大小为2×2;第3卷积层使用3×8大小的卷积核,20个特征面,池化核大小为3×3,最后1层为Softmax分类器输出。
方法5 (降噪数据输入DSAE) DSAE的结构为1 900-900-450-200-50-7,每个稀疏自编码器的学习率为0.14,动量因子为0.1,迭代次数为200。
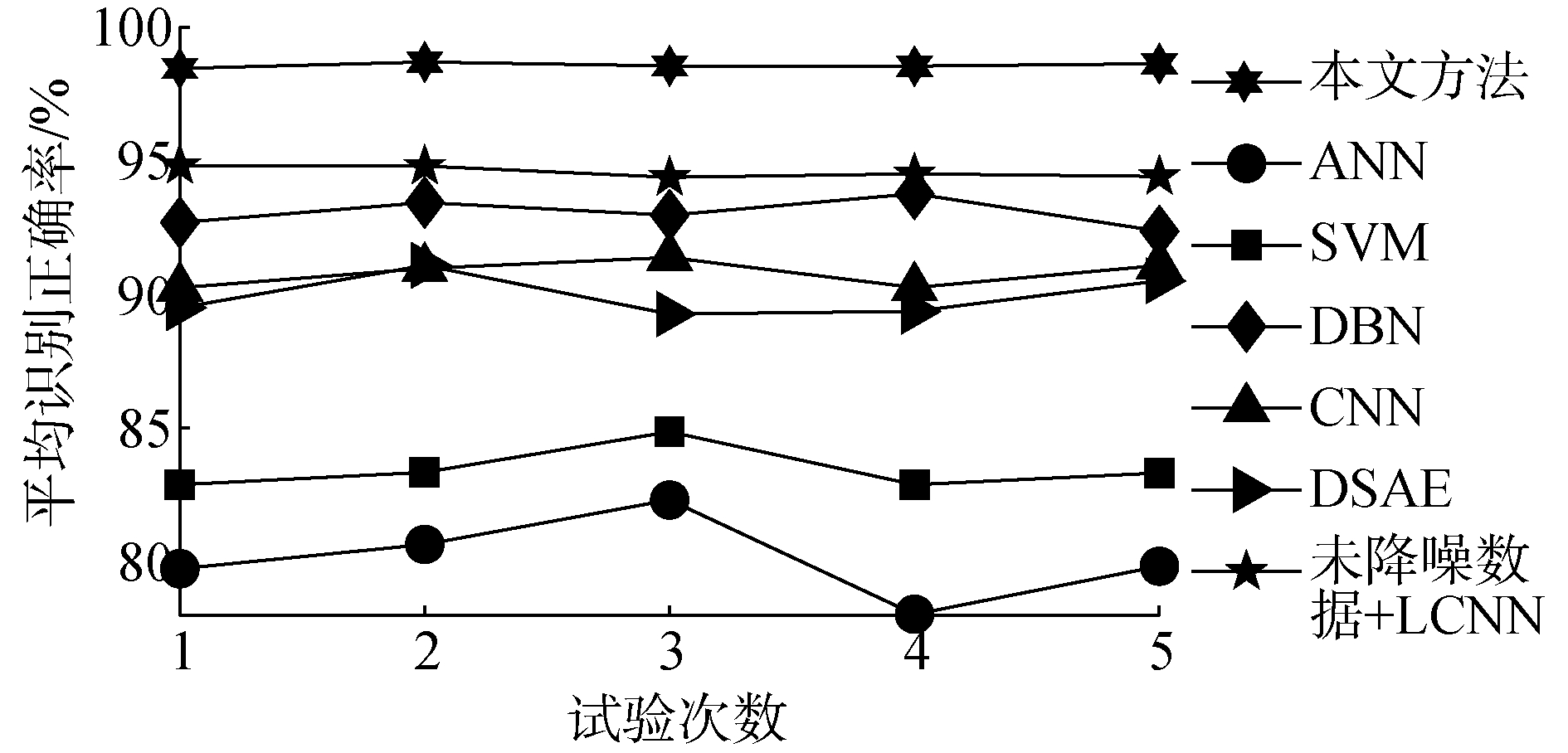
方法6 未降噪数据输入LCNN。表 2列出了测试阶段的平均诊断准确率与标准差,图 9列出了在每次试验中采用不同方法测试的详细诊断结果。
| 表 2 不同方法的诊断结果 Table 2 Diagnosis results of different methods |
|
Download:
|
| 图 9 不同方法的5次测试结果 Fig. 9 Detailed testing results of different methods for 5 trials | |
从表 2中可以看出,与其他方法相比,提出方法具有更高的测试准确率和最小的标准差,平均测试正确率达到98.58%,高于其他方法。与DBN、DSAE和普通CNN等深度学习方法相比,提出方法具有更好的稳定性,且信号降噪后的识别结果比未降噪信号的识别结果高出4个百分点,充分说明了降噪的必要性,提出方法能够稳定地区分滚动轴承的不同故障类型、不同故障严重程度。从图 9可以看出,提出方法每次测试的准确率分别为99.18%、99.73%、97.93%、97.55%和98.15%。比较结果表明,提出方法具有更高的故障识别精度和稳定性。主要原因是:1)提出方法能够通过多个非线性变换有效地从输入数据中提取特征,而ANN和SVM等传统方法的性能很大程度上依赖于人工特征提取。从原始特征集中选取敏感特征后,虽然诊断结果提高,然而,这是一项非常耗费时间的任务。2)提出方法考虑到了不同传感器的不同组合情况,使每个传感器振动数据都有最合适的滤波器。
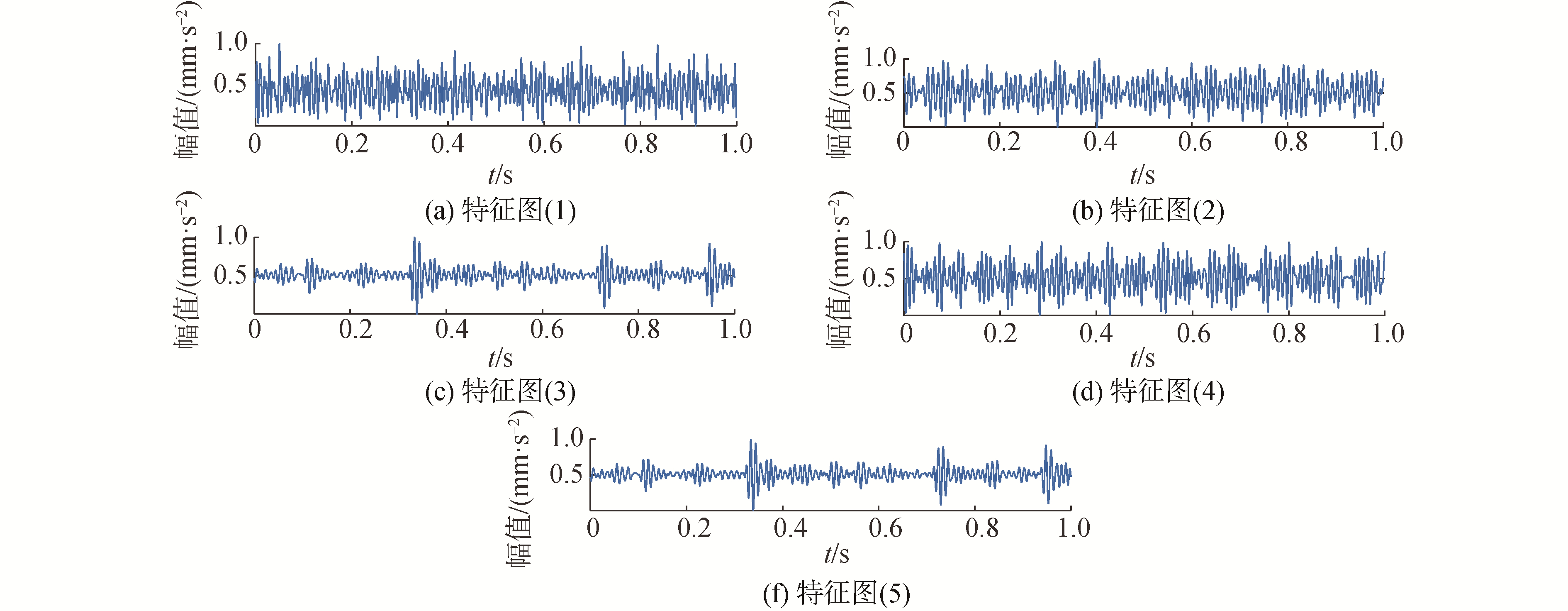
相比传统的故障识别算法,LCNN包含了自动特征提取过程,每一层对应一组特征输出,最后一层给出分类结果。以正常状态轴承振动信号为例,本文只给出LCNN提取的卷积单元A1的特征,如图 10所示。可以看出,LCNN提取的特征从不同角度表现原始信号,较好地满足了Fisher判别准则[21],更有利于最后的分类。
|
Download:
|
| 图 10 正常状态的所提取的A1层特征 Fig. 10 The extracted A1 layer feature diagram in normal condtion | |
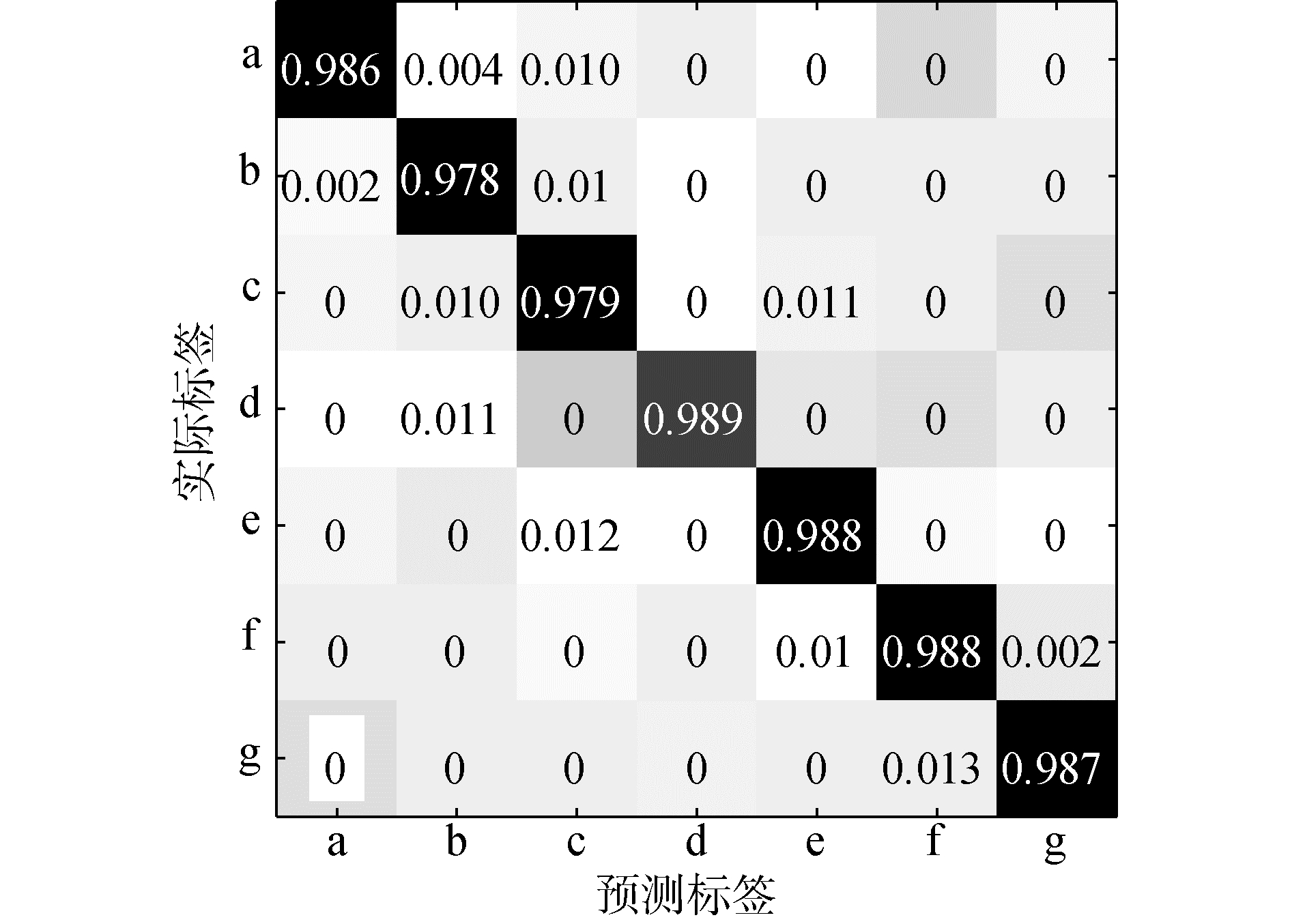
图 11给出了提出方法的第1次测试结果的多分类混淆矩阵,由图可得,复合故障状态b和c的分类正确率较低,这是由于滚动轴承复合故障发生时,产生故障的位置与程度各有不同,导致不同故障特征相互耦合在一起,相比单一故障形式,复合故障特征叠加在一起,彼此干扰,特征信息较微弱,导致复合故障特征提取的难度增加,后期考虑将先验知识加入LCNN,并对LCNN的结构做进一步改进。
|
Download:
|
| 图 11 多分类混淆矩阵 Fig. 11 Multi-class confusion matrix | |
1) 提出的IEWT-CS联合降噪法先对轴承振动信号样本自身构造CS字典,并进行第1次降噪,避免了阈值的人工选取;使用IEWT算法自适应的划分轴承振动信号谱的边界,从而自动确定分解模态数并利用相关系数-峭度准则进行第2次降噪,降噪效果优于EMD方法。
2) 将LCNN引入滚动轴承故障诊断领域,使不同的传感器通道数据配备不同的卷积核进而使每个传感器通道的振动数据都有合适的滤波器,克服了传统的CNN对振动数据特征提取与分类的缺陷。实验结果表明LCNN能有效地对滚动轴承进行多种故障状态的识别,取得了98.58%的平均识别准确率,较好地摆脱了对人工特征提取的依赖,特征提取能力和识别能力优于ANN、SVM、DBN、CNN、DSAE等方法。
后续将对神经元层数、神经元个数以及参数优化方法等方面进行进一步研究。
| [1] |
何田, 刘献栋, 李其汉. 噪声背景下检测突变信息的奇异值分解技术[J]. 振动工程学报, 2006, 19(3): 399-403. HE Tian, LIU Xiandong, LI Qihan. An improved method of detecting abrupt information based on singularity value decomposition in noise background[J]. Journal of vibration engineering, 2006, 19(3): 399-403. DOI:10.3969/j.issn.1004-4523.2006.03.020 (  0) 0)
|
| [2] |
周俊, 马建林, 徐华, 等. EMD降噪在高速铁路路基沉降预测中的应用[J]. 振动与冲击, 2016, 35(8): 66-72. ZHOU Jun, MA Jianlin, XU Hua, et al. Application of EMD denoising method in subgrade settlement prediction of high-speed railways[J]. Journal of vibration and shock, 2016, 35(8): 66-72. (  0) 0)
|
| [3] |
马增强, 张俊甲, 张安, 等. 基于VMD-SVD联合降噪和频率切片小波变换的滚动轴承故障特征提取[J]. 振动与冲击, 2018, 37(17): 210-217. MA Zengqiang, ZHANG Junjia, ZHANG An, et al. Fault feature extraction of rolling bearings based on VMD-SVD joint de-noising and FSWT[J]. Journal of vibration and shock, 2018, 37(17): 210-217. (  0) 0)
|
| [4] |
DONOHO D L. Compressed sensing[J]. IEEE transactions on information theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 (  0) 0)
|
| [5] |
李兵, 刘明亮, 杨平. EWT与GS-SVM在断路器机械故障诊断中的应用[J]. 哈尔滨工程大学学报, 2018, 39(8): 1422-1430. LI Bing, LIU Mingliang, YANG Ping. Application of EWT and GS-SVM in mechanical fault diagnosis of circuit breakers[J]. Journal of Harbin Engineering University, 2018, 39(8): 1422-1430. (  0) 0)
|
| [6] |
LECUN Y, BENGIO Y, HINTON G. Deep learning[J]. Nature, 2015, 521(7553): 436-444. DOI:10.1038/nature14539 (  0) 0)
|
| [7] |
SCHMIDHUBER J. Deep learning in neural networks: an overview[J]. Neural networks, 2015, 61: 85-117. DOI:10.1016/j.neunet.2014.09.003 (  0) 0)
|
| [8] |
赵光权, 葛强强, 刘小勇, 等. 基于DBN的故障特征提取及诊断方法研究[J]. 仪器仪表学报, 2016, 37(9): 1946-1953. ZHAO Guangquan, GE Qiangqiang, LIU Xiaoyong, et al. Fault feature extraction and diagnosis method based on deep belief network[J]. Chinese journal of scientific instrument, 2016, 37(9): 1946-1953. DOI:10.3969/j.issn.0254-3087.2016.09.004 (  0) 0)
|
| [9] |
曲建岭, 余路, 袁涛, 等. 基于一维卷积神经网络的滚动轴承自适应故障诊断算法[J]. 仪器仪表学报, 2018, 39(7): 134-143. QU Jianling, YU Lu, YUAN Tao, et al. Adaptive fault diagnosis algorithm for rolling bearings based on one-dimensional convolutional neural network[J]. Chinese journal of scientific instrument, 2018, 39(7): 134-143. (  0) 0)
|
| [10] |
张西宁, 向宙, 唐春华. 一种深度卷积自编码网络及其在滚动轴承故障诊断中的应用[J]. 西安交通大学学报, 2018, 52(7): 1-8, 59. ZHANG Xining, XIANG Zhou, TANG Chunhua. A deep convolutional auto-encoding neural network and its application in bearing fault diagnosis[J]. Journal of Xi'an JiaoTong University, 2018, 52(7): 1-8, 59. (  0) 0)
|
| [11] |
AHARON M, ELAD M, BRUCKSTEIN A M. K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE transactions on signal processing, 2006, 54(11): 4311-4322. DOI:10.1109/TSP.2006.881199 (  0) 0)
|
| [12] |
NEEDELL D, VERSHYNIN R. Signal recovery from Incomplete and inaccurate measurements via regularized orthogonal matching pursuit[J]. IEEE journal of selected topics in signal processing, 2010, 4(2): 310-316. (  0) 0)
|
| [13] |
GILLES J. Empirical wavelet transform[J]. IEEE transactions on signal processing, 2013, 61(16): 3999-4010. DOI:10.1109/TSP.2013.2265222 (  0) 0)
|
| [14] |
朱永利, 贾亚飞, 王刘旺, 等. 基于改进变分模态分解和Hilbert变换的变压器局部放电信号特征提取及分类[J]. 电工技术学报, 2017, 32(9): 221-235. ZHU Yongli, JIA Yafei, WANG Liuwang, et al. Feature extraction and classification on partial discharge signals of power transformers based on improved variational mode decomposition and Hilbert transform[J]. Transactions of China electrotechnical society, 2017, 32(9): 221-235. (  0) 0)
|
| [15] |
许向阳, 宋恩民, 金良海. Otsu准则的阈值性质分析[J]. 电子学报, 2009, 37(12): 2716-2719. XU Xiangyang, SONG Enmin, JIN Lianghai. Characteristic analysis of threshold based on Otsu criterion[J]. Acta electronica sinica, 2009, 37(12): 2716-2719. DOI:10.3321/j.issn:0372-2112.2009.12.020 (  0) 0)
|
| [16] |
胡爱军, 南冰, 任永辉. 基于PPCA-EWT的滚动轴承轻微故障诊断[J]. 振动、测试与诊断, 2018, 38(2): 365-370. HU Aijun, NAN Bing, REN Yonghui. Rolling bearing weak fault diagnosis based on PPCA and EWT[J]. Journal of vibration, measurement & diagnosis, 2018, 38(2): 365-370. (  0) 0)
|
| [17] |
LAUER F, SUEN C Y, BLOCH G. A trainable feature extractor for handwritten digit recognition[J]. Pattern recognition, 2007, 40(6): 1816-1824. DOI:10.1016/j.patcog.2006.10.011 (  0) 0)
|
| [18] |
金林鹏, 董军. 面向临床心电图分析的深层学习算法[J]. 中国科学:信息科学, 2015, 45(3): 398-416. JIN Linpeng, DONG Jun. Deep learning research on clinical electrocardiogram analysis[J]. Scientia sinica informationis, 2015, 45(3): 398-416. (  0) 0)
|
| [19] |
王亚萍, 匡宇麒, 葛江华, 等. CEEMD和小波半软阈值相结合的滚动轴承降噪[J]. 振动、测试与诊断, 2018, 38(1): 80-86. WANG Yaping, KUANG Yulin, GE Jianghua, et al. De-noising method for bearing vibration signal based on CEEMD and wavelet semi-soft threshold[J]. Journal of vibration, measurement & diagnosis, 2018, 38(1): 80-86. (  0) 0)
|
| [20] |
QU Jinxiu, ZHANG Zhousuo, GONG Teng. A novel intelligent method for mechanical fault diagnosis based on dual-tree complex wavelet packet transform and multiple classifier fusion[J]. Neurocomputing, 2016, 171: 837-853. DOI:10.1016/j.neucom.2015.07.020 (  0) 0)
|
| [21] |
于辉.基于Fisher判别法的模拟电路故障诊断[D].长沙: 湖南大学, 2014. YU Hui. Analog circuit fault diagnosis based on Fisher classifier[D]. Changsha: Hunan University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10532-1016070458.htm (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


