微创外科手术机器人技术是一种融合了先进机器人技术和微创手术医学的交叉学科研究。与传统手术相比,机器人微创外科手术具有手术精度高、患者创伤小、术后恢复快等优点[1-2]。手术器械的末端多自由度机构能够使其类似人手缝合一样灵活操作,提高手术效率。
目前已开发的多种手术器械可分为刚性连杆驱动式和柔性钢丝绳驱动式。例如,Arata等[3]研制出一款刚性连杆驱动的4-DOF手术器械。Hong等采用刚性连杆设计出一款2-DOF手术器械[4],并应用在刚性串联铰链驱动的4-DOF手术器械[5]。此外,Seibold等[6]研制了一款钢丝绳驱动式3-DOF手术器械。Haraguchi等[7]采用刚性弹簧实现腕部弯曲,研制出钢丝绳驱动式3-DOF手术器械。已经投入市场的da Vinci系统[8]的手术器械同样采用钢丝绳驱动方式。由于钢丝绳具有质量轻、空间占用少、操作灵活性高等优点,使得其在手术器械研制中应用更为广泛。
面对钢丝绳驱动式手术器械末端关节存在严重的运动耦合问题,Nishizawa等[9]采用旋转接触机构和齿轮组对手术器械进行了解耦设计。Zhao等[10-11]基于行星齿轮理论提出了一种运动解耦通用方案。然而,无法消除的齿侧间隙增大了末端执行器的运动误差。此外,国内学者也进行了大量研究,如Sang等[12]通过推导理论补偿公式进行运动解耦。Feng等[13]利用差动行星齿轮组设计出补偿机构,对4-DOF手术器械进行了运动解耦[14]。Xue等[15]提出在线补偿的控制算法,实现了绝对误差降低至4°以内。
综上分析可知,算法补偿式解耦是通过推导关节运动、钢丝绳形变和驱动信息之间映射关系的一种理论近似方法,其减少了机构设计和装配等难度,然而实际中钢丝绳形变和机械间隙等仍难以准确建模;机械式解耦是设计由刚性零件构建的机械机构对腕部与执行器进行单独控制,其解耦精度和可靠性相对更高,但该方式的手术器械的操作灵活性往往不如钢丝绳驱动式。鉴于此,本文结合对称式腕部机构设计与绳轨道平行对称式绕线布局,设计了一种运动解耦的钢丝绳驱动式3-DOF手术器械,仿真结果表明腕关节运动对驱动末端执行器的钢丝绳的影响非常小,且在弹性形变范围内钢丝绳仍可保持张紧状态。
1 钢丝绳驱动式手术器械 1.1 手术机器人床旁机械臂微创外科手术机器人系统是一种高度集成化的主从式机器人系统,主要包括外科医生主控制平台、床旁机械臂系统、主从控制系统、成像系统等[16]。医生在主控制台操纵主控制系统,以主从控制方式,控制床旁机械臂和持镜臂进行同步手术操作。床旁机械臂系统通常由2条或3条配备手术器械的机械臂和一条配备三维内窥镜的持镜臂组成。本文以手术机器人系统为研究对象,设计开发了一台8-DOF通用床旁机械臂,其实验样机如图 1所示。

|
Download:
|
| 图 1 手术机器人8-DOF通用机械臂样机 Fig. 1 8-DOF universal mechanical arm of surgical robot | |
该通用机械臂主要由主动控制部分和被动控制部分组成。其中主动控制部分包括一个实现套针管不动点控制的双平行四边形机构,以及2个旋转关节和一个移动关节,机械臂末端设计了快换机构可以实现3-DOF手术器械和三维高清内窥镜的快速安装与更换;被动控制部分包括3个被动旋转关节和一个升降关节,便于机械臂的术前摆位工作。
为实现手术的主从远程操作控制,医生的双手动作将同步映射到手术器械末端执行器,而手术器械作为代替人手的操作工具,在手术过程中不断与人体软组织接触,其工作空间大小、操作灵活性以及运动控制精度等都会关系到整个手术能否成功。
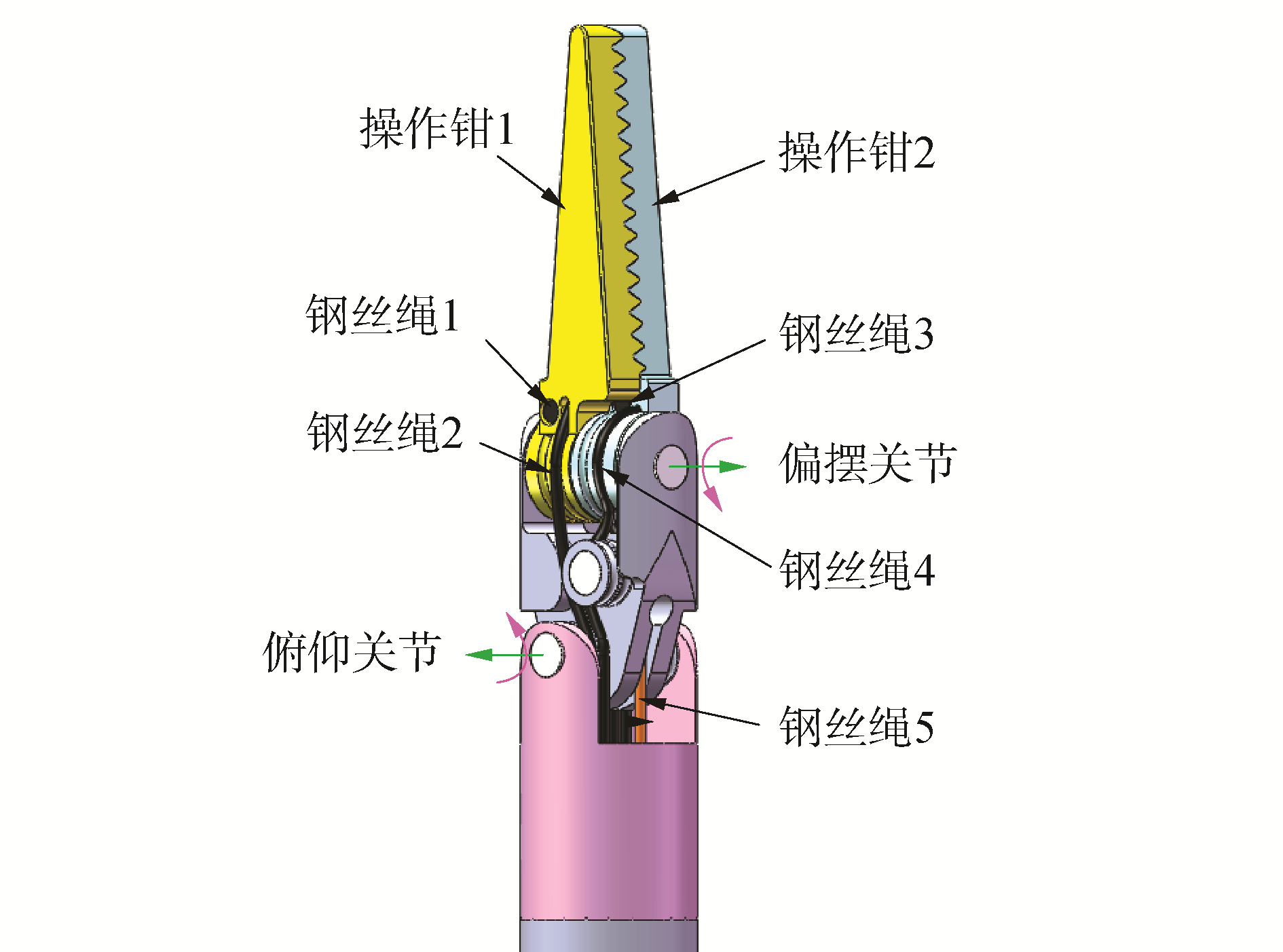
1.2 绳驱动式手术器械的运动耦合分析通常情况下,手术器械包括旋转、俯仰、偏摆和开合等4个自由度。考虑到围绕手术器械长轴线的旋转自由度在末端机构中难以实现,同时为了避免钢丝绳在长输导管中发生缠绕现象,因此,本文采用机械臂末端的旋转关节来控制手术器械整体的旋转运动,该方式也是诸多手术机器人系统中行之有效的常用方法。如图 2所示,为实验室内部加工制造的手术器械实验样机,其末端俯仰运动由一根带绳结的钢丝绳5独立驱动腕部实现,而末端执行器的操作钳1和操作钳2均由单一电机同时控制2根钢丝绳来独立驱动实现运动,即钢丝绳1和钢丝绳2驱动控制操作钳1,钢丝绳3和钢丝绳4驱动控制操作钳2,2片操作钳同方向控制可实现执行器的偏摆动作,反方向控制时可实现开合动作。3个直流电机安装在手术器械前端的驱动单元中。
|
Download:
|
| 图 2 常用的绳驱动式手术器械末端机构 Fig. 2 End mechanism of commonly used cable-driven surgical instrument | |
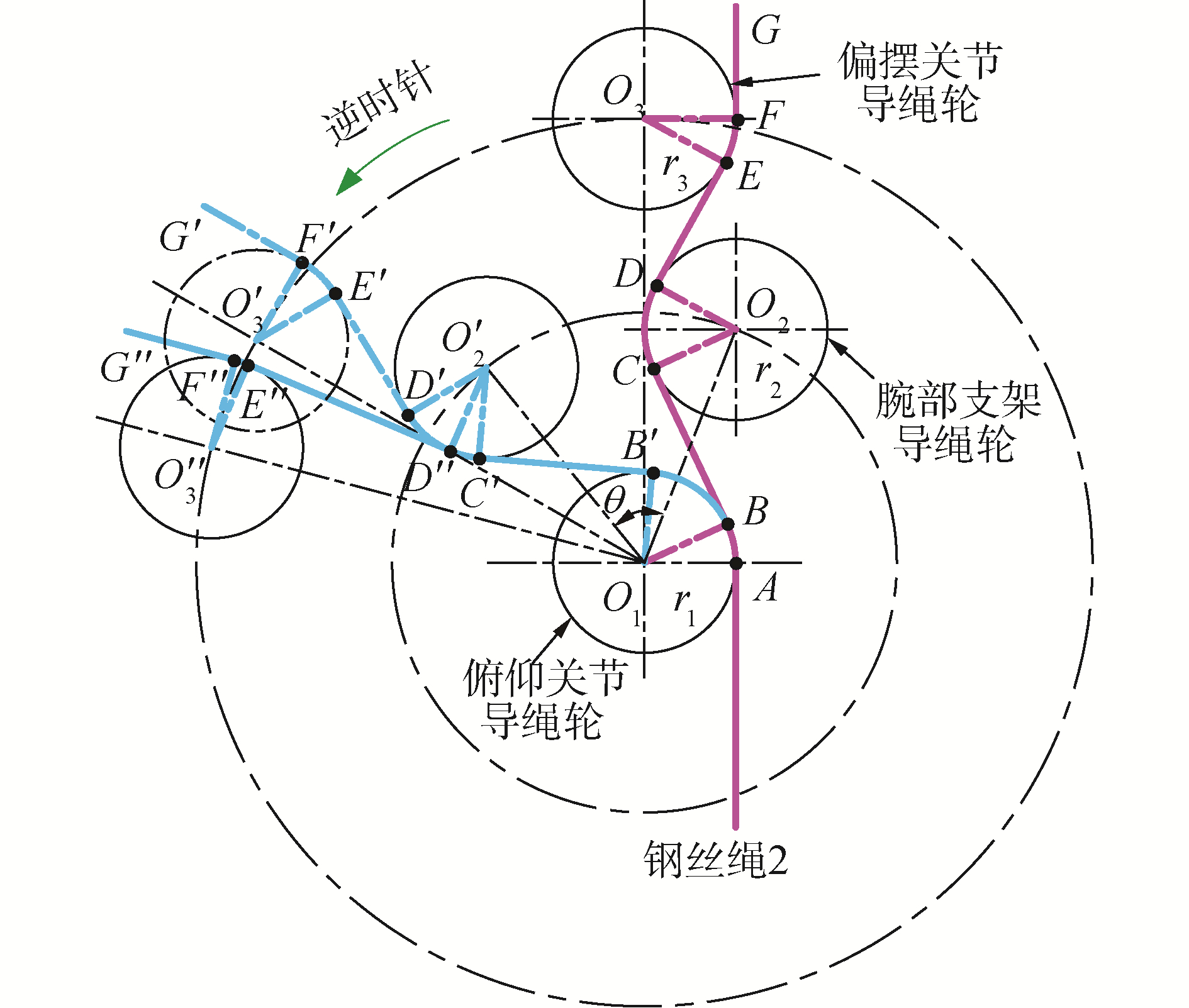
然而,由于驱动执行器2片操作钳的4根钢丝绳需要通过腕关节和俯仰关节处的导绳轮,当腕部关节单独进行俯仰运动时将会附加牵引2片操作钳产生受迫运动,即与常用的da Vinci手术器械的运动控制类似,末端关节同样存在俯仰和偏摆的运动耦合问题。为便于分析绳驱动式手术器械运动耦合问题,将手术器械的俯仰与偏摆关节的运动耦合示意图绘制在同一个平面内,如图 3所示。由于钢丝绳1与钢丝绳4绕线轨迹相同,钢丝绳2与钢丝绳3绕线轨迹相同,且耦合机理相同,因此,本文以钢丝绳2绕线轨迹为例进行阐述。
|
Download:
|
| 图 3 俯仰与偏摆关节运动耦合示意 Fig. 3 Schematic diagram of kinematic coupling between pitch and yaw joints | |
如图 3所示,AB、BC、CD、DE、EF、FG、BB′等为钢丝绳环绕在导绳轮间的绳段,A、B、C、D、E、F等为各绳段切点。当初始位置时,即操作钳处于闭合状态且俯仰关节转角θ=0°,俯仰和偏摆关节之间的钢丝绳长度可表示为:
| $ L=\overset\frown{AB}+\overset\frown{BC}+\overset\frown{CD}+\overset\frown{DE}+\overset\frown{EF}+\overset\frown{FG} $ | (1) |
当俯仰关节逆时针旋转θ时,即腕部支架导绳轮由O2运动到O′ 2位置,偏摆关节理想上由O3运动到O′ 3位置,此时,俯仰和偏摆关节之间的钢丝绳长度为:
| $ {{L}^{\prime}}=\overset\frown{AB}+\overset\frown{B{{B}^{\prime}}}+\overset\frown{{{B}^{\prime}}{{C}^{\prime}}}+\overset\frown{{{C}^{\prime}}{{D}^{\prime}}}+\overset\frown{{{D}^{\prime}}{{E}^{\prime}}}+\overset\frown{{{E}^{\prime}}{{F}^{\prime}}}+\overset\frown{{{F}^{\prime}}{{G}^{\prime}}} $ | (2) |
由几何关系可得:
| $ \left\{ \begin{array}{*{35}{l}} \overset\frown{BC}=\overset\frown{{{B}^{\prime }}{{C}^{\prime }}} \\ \overset\frown{CD}=\overset\frown{{{C}^{\prime }}{{D}^{\prime }}} \\ \overset\frown{DE}=\overset\frown{{{D}^{\prime }}{{E}^{\prime }}} \\ \overset\frown{EF}=\overset\frown{{{E}^{\prime }}{{F}^{\prime }}} \\ \overset\frown{FG}=\overset\frown{{{F}^{\prime }}{{G}^{\prime }}} \\ \end{array} \right. $ | (3) |
联立式(1)~(3)可知,当俯仰关节逆时针转动θ时,俯仰和偏摆关节之间钢丝绳形变量为:
| $ \Delta L=L-{{L}^{\prime }}=\overset\frown{B{{B}^{\prime}}}=\theta {{r}_{1}} $ | (4) |
由于存在关节运动耦合现象,使得偏摆关节实际上由O3运动到了O″ 3位置,此时钢丝绳长度为:
| $ {{L}^{\prime \prime}}=\overset\frown{AB}+\overset\frown{B{{B}^{\prime }}}+\overset\frown{{{B}^{\prime }}{{C}^{\prime }}}+\overset\frown{{{C}^{\prime }}{{D}^{\prime \prime}}}+\overset\frown{{{D}^{\prime \prime}}{{E}^{\prime \prime}}}+\overset\frown{{{E}^{\prime \prime}}{{F}^{\prime \prime}}}+\overset\frown{{{F}^{\prime \prime}}{{G}^{\prime \prime}}} $ | (5) |
从而使得L″=L。因此可得由于耦合作用产生的偏摆关节理论转角为:
| $ \varphi = \frac{{\Delta L}}{{{r_3}}} = \frac{{\theta {r_1}}}{{{r_3}}} $ | (6) |
依据上述分析可以看出,俯仰和偏摆关节的耦合作用主要是由于俯仰关节位置的导绳轮使钢丝绳绕线存在一个绳轮半径的偏心距,导致耦合度偏大甚至超出钢丝绳的弹性形变范围,这非常不利于驱动控制钢丝绳。此外,尽管运动耦合在理论上可以通过上述推导公式进行算法补偿,但是实际上钢丝绳张紧力大小、弹性形变范围和机械间隙等因素将导致单独的算法补偿无法到达高精度解耦效果,甚至会出现转角累积误差。
2 新型手术器械设计 2.1 末端机构设计与钢丝绳平行对称式绕线布局为了解决手术器械末端关节运动耦合问题,便于手术器械更高精度的运动控制研究,本文提出机械上低耦合度的对称式腕部机构设计与钢丝绳平行对称式绕线布局相结合的方法,该方法在实现末端关节运动解耦的同时,具有机构设计简单和易于装配等优点。
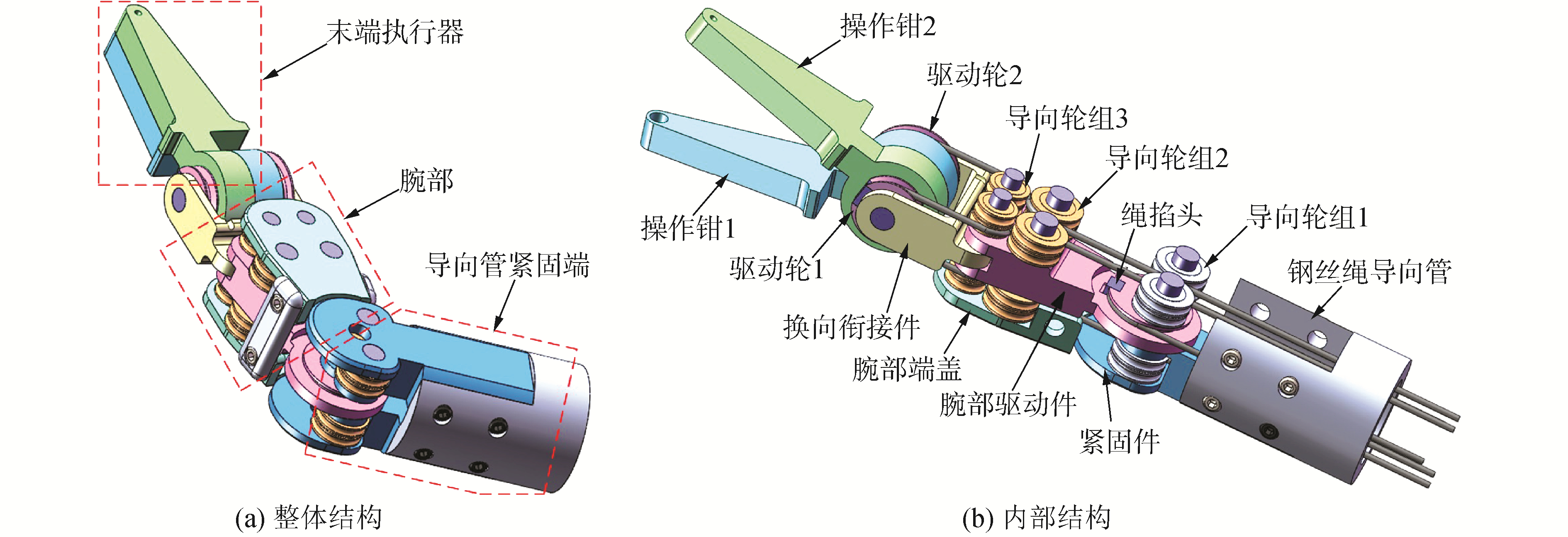
针对机械式运动解耦,设计的新型手术器械末端机构如图 4所示。主要由3个部分组成,末端执行器、腕部和导向管紧固端。其中,末端执行器的2片操作钳分别配备一个尺寸不同的驱动轮,可实现单片操作钳的独立驱动,钢丝绳通过独特设计的绳掐头安装在驱动轮上,可以将一根长钢丝绳在同一平面内分成2根,消除了钢丝绳打结不牢靠的问题。腕部机构主要采用导向轮组和腕部驱动件组成。导向轮组为双层轮对称布置形式,其中轮组2和轮组3安装在腕部机构内,用于将钢丝绳由两侧导向到微器械轴中线,上下端盖保证零件紧密连接;腕部驱动件实现俯仰运动,且腕部与末端执行器之间由换向衔接件连接。轮组1安装在导向管紧固端,便于将多根钢丝绳导向到长轴导向管中,避免发生碰撞和缠绕,此外,其与轮组2之间的距离以及腕部转轴位置是实现运动解耦的重要部分。
|
Download:
|
| 图 4 手术器械末端机构模型 Fig. 4 End mechanism model of surgical instrument | |
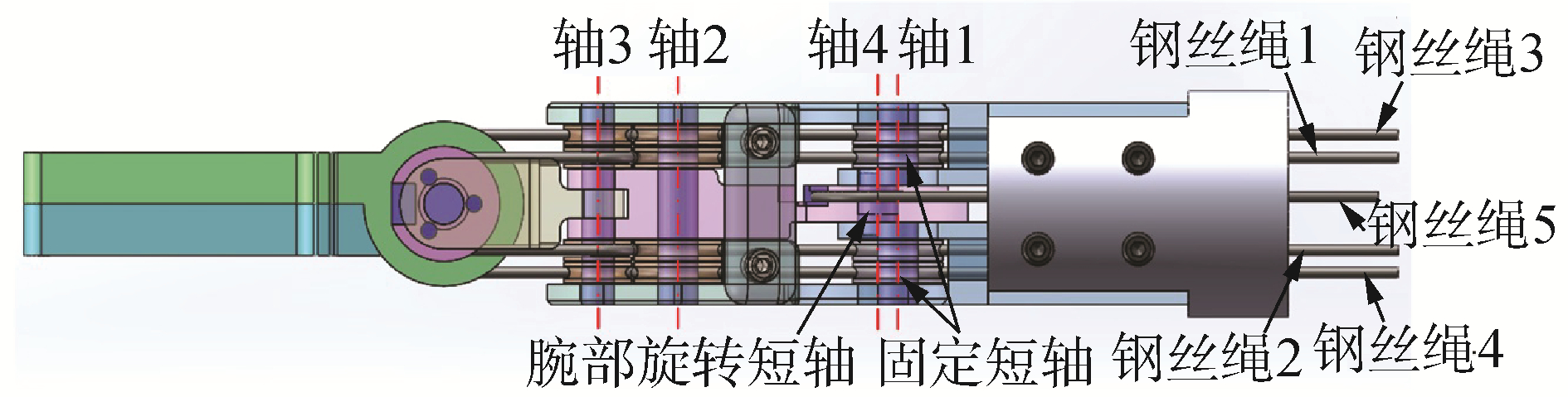
除了合理的机构设计之外,多根钢丝绳在腕部机构中的绕线布局也紧密关系到微器械末端各关节的运动解耦情况,而且合理的绕线布局可以便于关节控制、装配和拆卸等工作。目前,已设计或研制出的手术器械,其钢丝绳的绕线方式可以大体分为2种:当驱动同一片操作钳的2根钢丝绳的绕线轨迹相同时,关节耦合作用使得2个钢丝绳同时伸长或缩短;当绕线轨迹不同时,将会出现一根伸长,另一根缩短。无论哪种绕线方式,都要避免钢丝绳由于拉力过大而超出弹性极限发生断裂或拉力过小而发生松脱等问题。因此,本文提出钢丝绳绕线采用平行对称式布局,即驱动同一片操作钳的2根钢丝绳绕线轨迹相同且对称,如图 5所示。
|
Download:
|
| 图 5 末端机构前视图 Fig. 5 Front view of end mechanism | |
轴2和轴3均为安装在腕部机构的固定长转轴;转轴1为导向管紧固件上安装导向轮组1的2个固定短轴;中间为连接腕部驱动件与导向管紧固端的旋转短轴;俯仰运动通过轴4实现。钢丝绳1与钢丝绳2驱动操作钳2,绕线轨迹平行,绳3与绳4同理驱动操作钳1,4根钢丝绳在各自独立绕线轨道中运动,不会发生相互干扰;钢丝绳5独立控制腕部驱动件,实现末端整体俯仰运动。
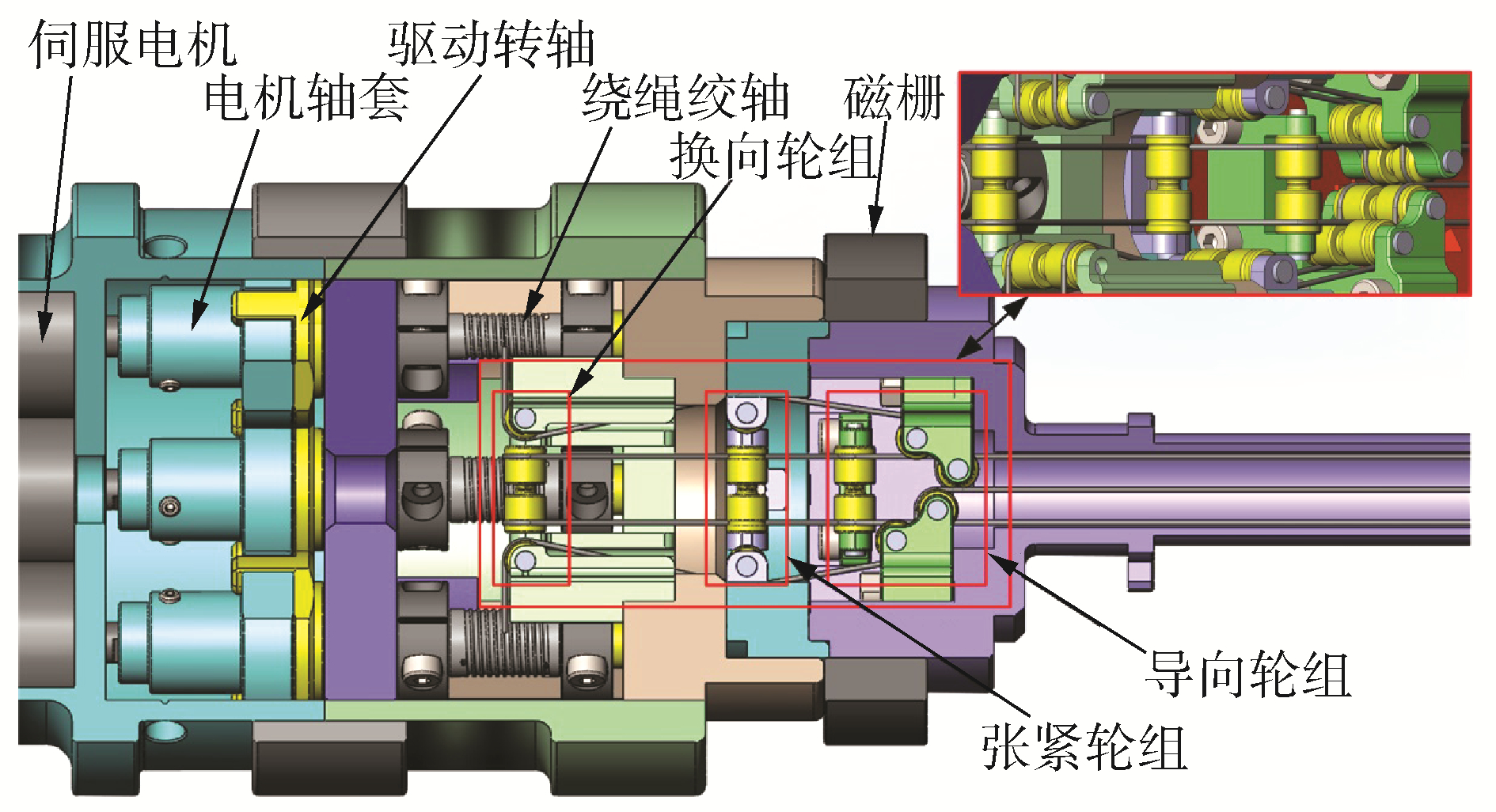
2.2 驱动单元机构新型手术器械的驱动单元机构如图 6所示,驱动末端机构的6根钢丝绳通过导向轮组、张紧轮组和换向轮组最终缠绕在驱动转轴上的绕绳绞轴上,并由3个小型maxon伺服电机提供动力来源。电机与驱动转轴由电机轴套连接,并且各绕绳轮组均安装在不同的支架上,便于各部分组件的拆卸更换。外层的磁栅为控制微器械整体旋转自由度的测量器件。由于6根钢丝绳不在同一平面内,为了使每根钢丝绳从末端腕部到绕绳绞轴能够处在同一平面轨道内而避免脱轨问题,每个绕绳轮组内的3个方向绕绳轮垂直布置。此外,张紧轮组通过配套旋转螺钉可以调节钢丝绳的张紧状态,便于装配完成后的微调工作。
|
Download:
|
| 图 6 驱动单元机构 Fig. 6 Mechanism of driving unit | |
通过新型腕部机构设计与钢丝绳轨道平行对称式绕线布局相结合可以实现手术器械末端机构的运动解耦功能,但是腕部关节的运动仍然使驱动末端执行器的钢丝绳产生微小的受迫形变。为了保证在整个运动范围内,腕关节运动使末端钢丝绳的受迫形变降低到最小,并避免由于受迫形变的伸长或缩短引起钢丝绳过张紧或松脱,需要对驱动末端执行器的钢丝绳受迫形变进行分析。
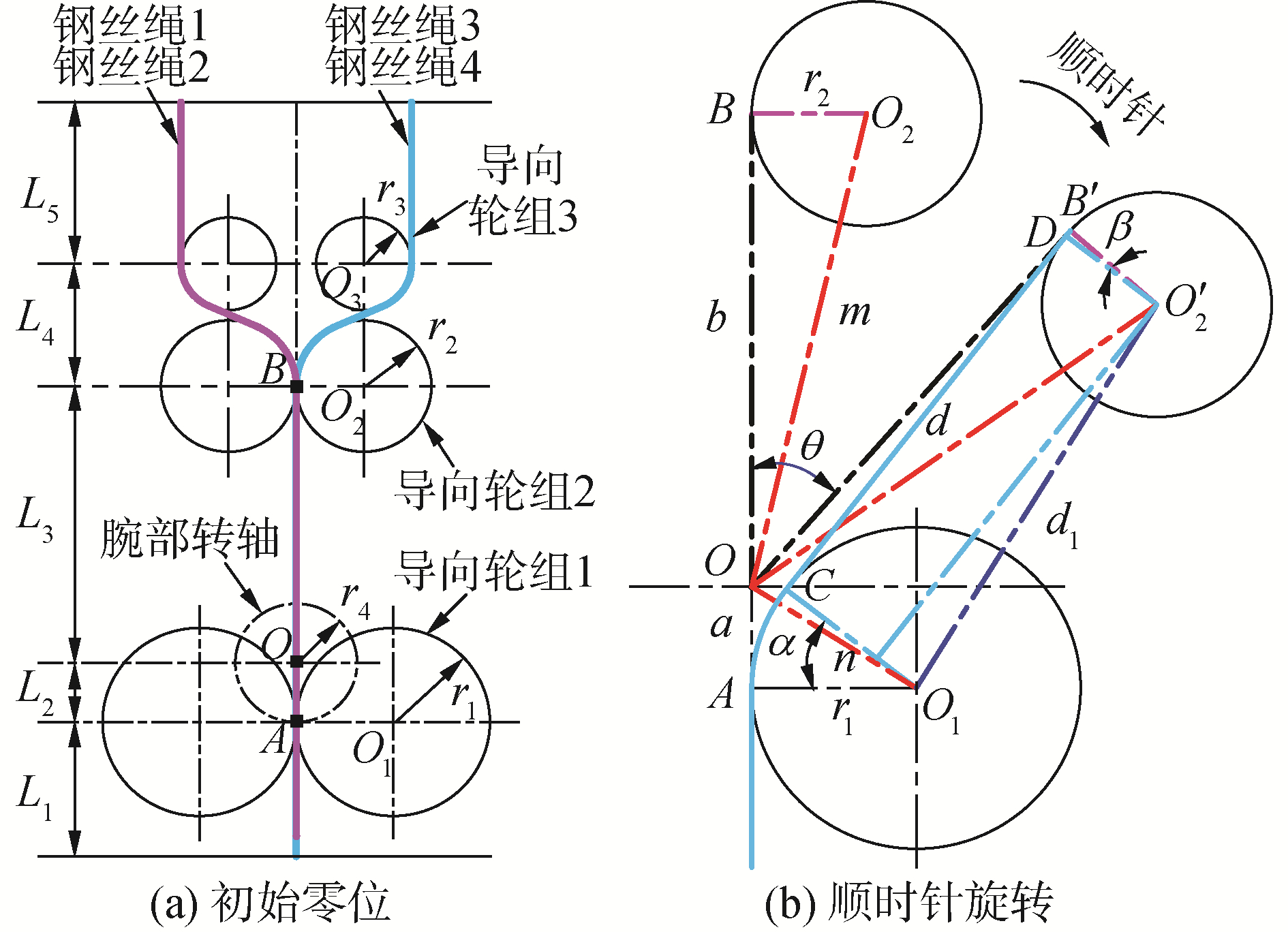
3.1 钢丝绳受迫形变数学模型由于新型手术器械末端机构为对称式,并且执行器的2个操作钳的驱动方式和运动分析相同,因此,本文选取驱动操作钳的一根钢丝绳进行绕线轨迹分析。以下分析的前提是:操作钳的偏摆和开合自由度固定不动,即驱动操作钳的钢丝绳不发生运动,令腕部俯仰自由度单独运动。如图 7所示,为腕部绳轮机构运动示意图,根据机构运动原理可知,导向轮中心距离L1、L4和L5以内的钢丝绳将不会随着运动而发生长度变化,因此,只需研究钢丝绳长度发生变化的L2和L3。
|
Download:
|
| 图 7 腕部绳轮机构运动示意 Fig. 7 Motion diagram of cable-pulley mechanism at the wrist | |
当腕部处于零位时,即腕关节转角θ=0°,钢丝绳长度可表示为:
| $ \hat L = {L_2} + {L_3} = a + b $ | (7) |
当腕部关节发生顺时针转动θ角度时,导向轮组2由O2运动到O′ 2位置,则钢丝绳长度为:
| $ {{\hat{L}}^{\prime }}=\overset\frown{AC}+\overset\frown{CD}+\overset\frown{DB}={{r}_{1}}\alpha +d+{{r}_{2}}\beta $ | (8) |
根据几何关系可得:
| $ \left\{ {\begin{array}{*{20}{l}} {\angle AO{O_1} = {\rm{arctan}}\frac{{{r_1}}}{a}}\\ {\angle BO{O_2} = {\rm{arctan}}\frac{{{r_2}}}{b}} \end{array}} \right. $ | (9) |
| $ \left\{ {\begin{array}{*{20}{l}} {m = \sqrt {{b^2} + r_2^2} }\\ {n = \sqrt {{a^2} + r_1^2} } \end{array}} \right. $ | (10) |
进而可得:
| $ \angle {O_1}OO_2^\prime = \mathsf{π} - \theta - \angle AO{O_1} - \angle BO{O_2} $ | (11) |
由式(9)~(11)可得:
| $ {d_1} = \sqrt {{m^2} + {n^2} - 2mn{\rm{cos}}\angle {O_1}OO_2^\prime } $ | (12) |
最终可得:
| $ \begin{array}{*{20}{c}} {d = \sqrt {d_1^2 - {{({r_1} - {r_2})}^2}} = }\\ {\sqrt {W + \sqrt {{{(2ab - 2{r_1}{r_2})}^2} + {{(2a{r_2} + 2b{r_1})}^2}} {\rm{sin}}(\theta + \varphi )} } \end{array} $ | (13) |
式中:W=b2+a2+2r1r2;tan φ=
根据三角形余弦定理可知:
| $ \left\{ {\begin{array}{*{20}{l}} {\angle O{O_1}O_2^\prime = {\rm{arccos}}\frac{{{n^2} + d_1^2 - {m^2}}}{{2n{d_1}}}}\\ {\angle C{O_1}O_2^\prime = {\rm{arccos}}\frac{{{r_1} - {r_2}}}{{{d_1}}}} \end{array}} \right. $ | (14) |
钢丝绳在导向轮组1上的转角为:
| $ \alpha = \frac{\mathsf{π} }{2} - \angle AO{O_1} + \angle O{O_1}O_2^\prime - \angle C{O_1}O_2^\prime $ | (15) |
联立式(9)~(11)、(14)、(15),并应用反三角函数公式可得:
| $ \begin{array}{l} \alpha = \theta + {\rm{arcsin}}\frac{{{r_1} - {r_2}}}{{{d_1}}} + {\rm{arcsin}}\frac{{{m^2} + d_1^2 - {n^2}}}{{2m{d_1}}} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{arctan}}\frac{b}{2} \end{array} $ | (16) |
此外,可得钢丝绳在导向轮组2上缠绕角度为:
| $ \begin{array}{*{20}{c}} {\beta = \angle {B^\prime }O_2^\prime O - \angle DO_2^\prime O = \frac{\mathsf{π} }{2} - \angle BO{O_2} - }\\ {\left( {\frac{\mathsf{π} }{2} - \left( {\angle OO_2^\prime {O_1} - \left( {\frac{\mathsf{π} }{2} - \angle C{O_1}O_2^\prime } \right)} \right)} \right) = \theta - \alpha } \end{array} $ | (17) |
联立式(8)~(17),可以得到此时钢丝绳长度为:
| $ \begin{array}{l} \hat L' = {r_1}\theta + ({r_1} + {r_2})\left( {{\rm{arcsin}}\sqrt {\frac{{{{({r_1} - {r_2})}^2}}}{{{a^2} + {b^2} + r_1^2 + r_2^2 + 2\sqrt {{a^2}{b^2} - r_1^2r_2^2 + {a^2}r_2^2 + {b^2}r_1^2} {\rm{sin}}(\theta + \varphi )}}} + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{arcsin}} \frac{{{b^2} + r_2^2 + \sqrt {{a^2}{b^2} - r_1^2r_2^2 + {a^2}r_2^2 + {b^2}r_1^2} {\rm{sin}}(\theta + \varphi )}}{{\sqrt {{b^2} + r_2^2} \sqrt {{b^2} + {a^2} + r_1^2 + r_2^2 + 2\sqrt {{a^2}{b^2} - r_1^2r_2^2 + {a^2}r_2^2 + {b^2}r_1^2}{\rm{sin}}(\theta + \varphi ) } }} - \\ {\kern 1pt} \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{arctan}}\frac{b}{{{r_2}}}} \right) + {b^2} + {a^2} + 2{r_1}{r_2} + 2\sqrt {{{(ab - {r_1}{r_2})}^2} + {{(a{r_2} + b{r_1})}^2}} {\rm{sin}}(\theta + \varphi ) \end{array} $ | (18) |
随着腕部关节转角θ的变化,驱动末端执行器的钢丝绳受迫形变数学模型为:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta L = \hat L' - \hat L = \\ {r_1}\theta + ({r_1} + {r_2})\left( {{\rm{arcsin}}\sqrt {\frac{{{{({r_1} - {r_2})}^2}}}{{{a^2} + {b^2} + r_1^2 + r_2^2 + 2\sqrt {{a^2}{b^2} - r_1^2r_2^2 + {a^2}r_2^2 + {b^2}r_1^2} {\rm{sin}}(\theta + \varphi )}}} + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{arcsin}} \frac{{{b^2} + r_2^2 + \sqrt {{a^2}{b^2} - r_1^2r_2^2 + {a^2}r_2^2 + {b^2}r_1^2} {\rm{sin}}(\theta + \varphi )}}{{\sqrt {{b^2} + r_2^2} \sqrt {{b^2} + {a^2} + r_1^2 + r_2^2 + 2\sqrt {{a^2}{b^2} - r_1^2r_2^2 + {a^2}r_2^2 + {b^2}r_1^2} {\rm{sin}}(\theta + \varphi )} }} - \\ {\kern 1pt} \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{arctan}}\frac{b}{{{r_2}}}} \right) + {b^2} + {a^2} + 2{r_1}{r_2} + 2\sqrt {{{(ab - {r_1}{r_2})}^2} + {{(a{r_2} + b{r_1})}^2}} {\rm{sin}}(\theta + \varphi ) - a - b \end{array} $ | (19) |
由上述推导可知,ΔL为驱动执行器的钢丝绳受迫形变量,该数值主要受腕部转角θ、导向轮组间距离a和b、以及导向轮半径r1和r2的影响,为使腕关节运动产生钢丝绳的受迫形变接近零,避免出现钢丝绳过张紧或松脱等现象,需要对a、b、r1和r24个机构尺寸参数进行分析,在寻求低受迫形变的尺寸参数的同时,追求整体尺寸小型化原则。
采用的分析策略是:在各参数取值范围内,令其中3个参数任取固定值,单独分析剩余一个参数取值不同时,ΔL随θ的变化情况。
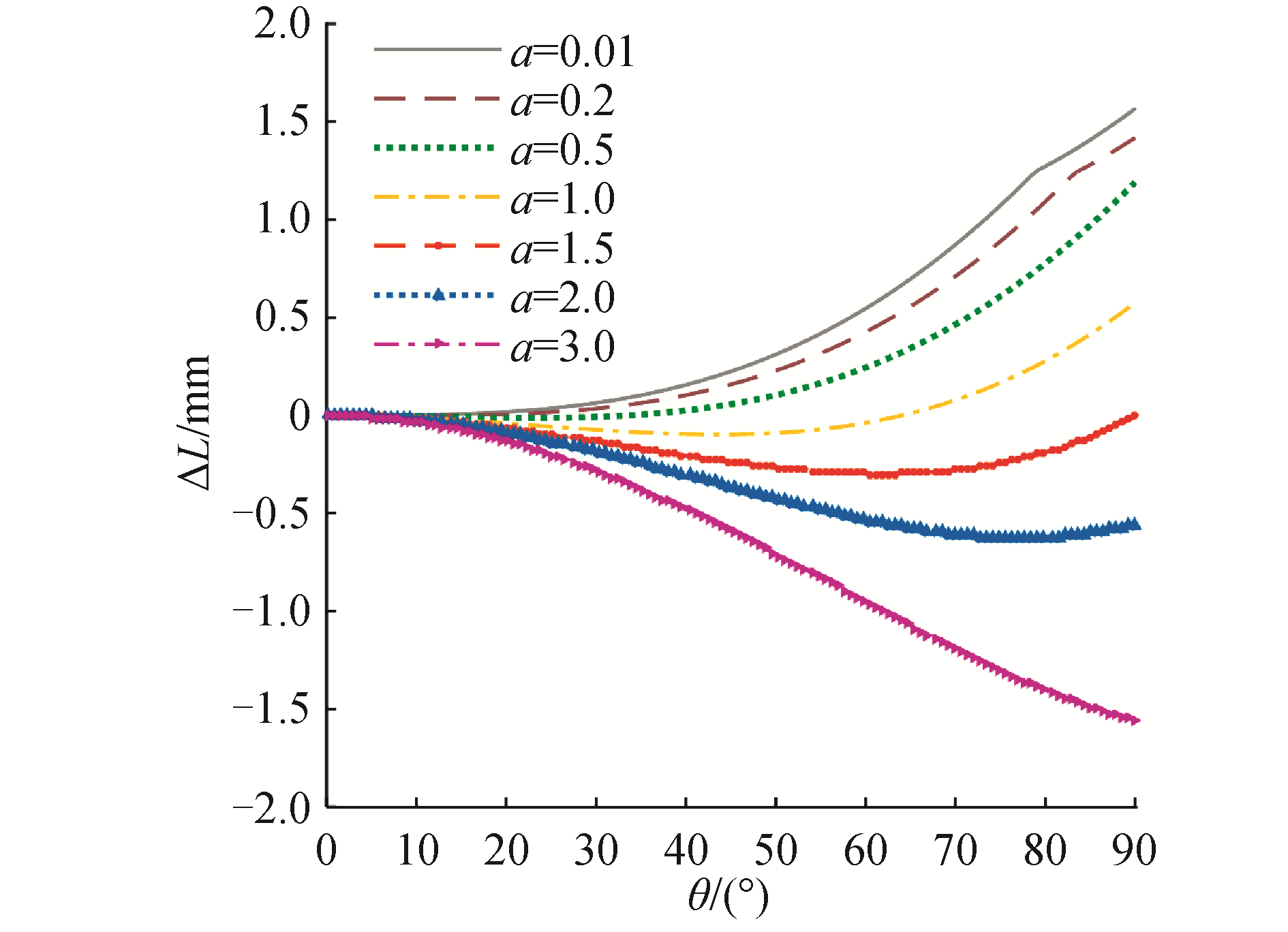
1) 令b、r1、r2取固定值,即b=10 mm,r1=2.5 mm,r2=2 mm,则参数a取不同值时,ΔL随θ的变化曲线如图 8所示。由图可以看出,随着a的增大,钢丝绳受迫形变量逐渐减小,即钢丝绳逐渐缩短,在此过程中,受迫形变量会出现接近零的情况,此时选择适当的a将减小钢丝绳的受迫形变量。
|
Download:
|
| 图 8 参数a取不同值时钢丝绳受迫形变 Fig. 8 Compelled deformation of cables for different a | |
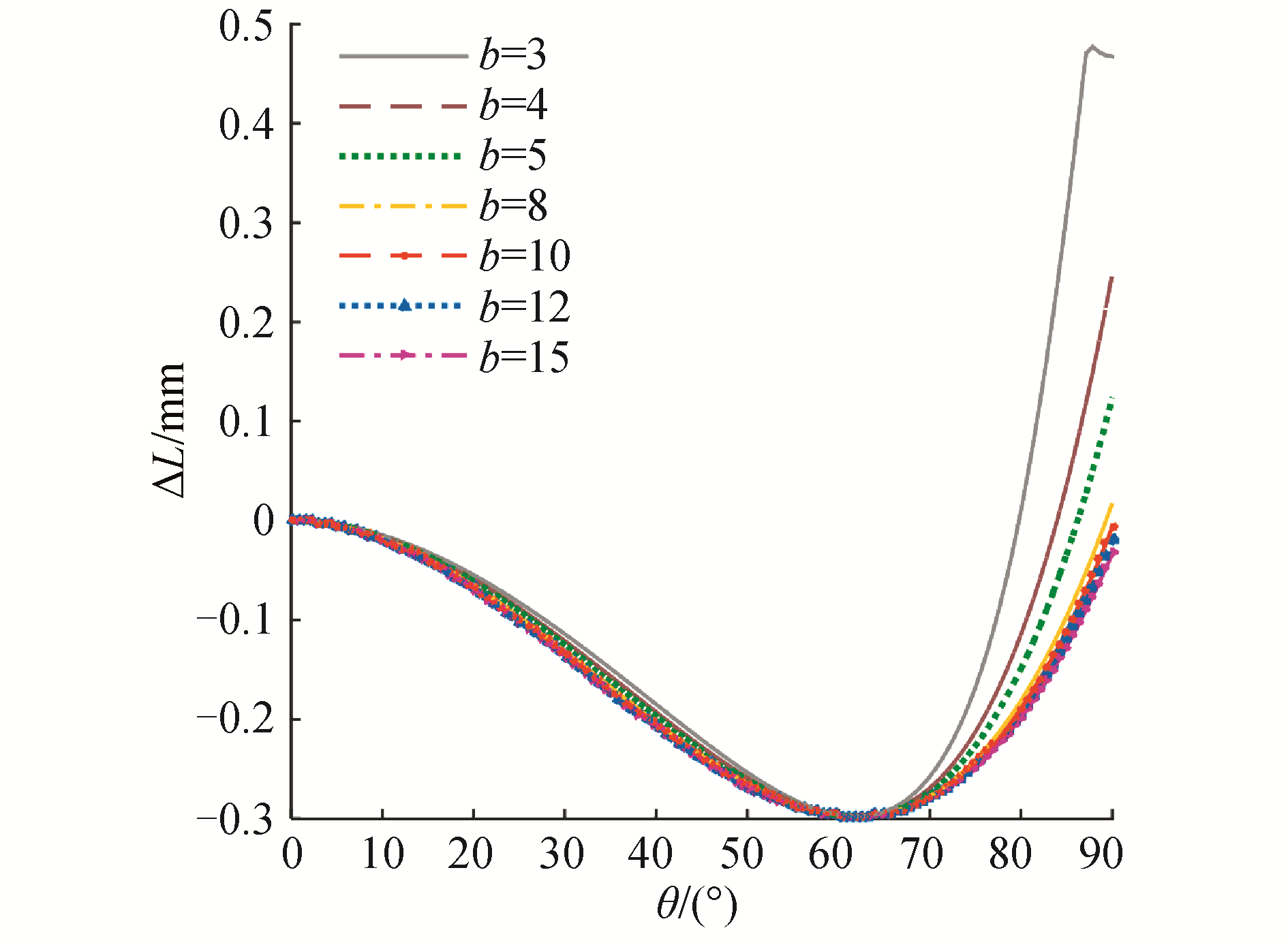
2) 当参数a、r1、r2取固定值时,即a=1.5 mm,r1=2.5 mm,r2=2 mm,则参数b取不同值时,ΔL随θ的变化曲线如图 9所示。由图可以看出,随着b的增大,受迫形变量逐渐减小,但减小的幅度越来越小。由此可知,当b增大到一定范围内后,钢丝绳的受迫形变量受参数b的影响作用非常小,这有利于降低腕部机构的设计尺寸。
|
Download:
|
| 图 9 参数b取不同值时钢丝绳受迫形变 Fig. 9 Compelled deformation of cables for different b | |
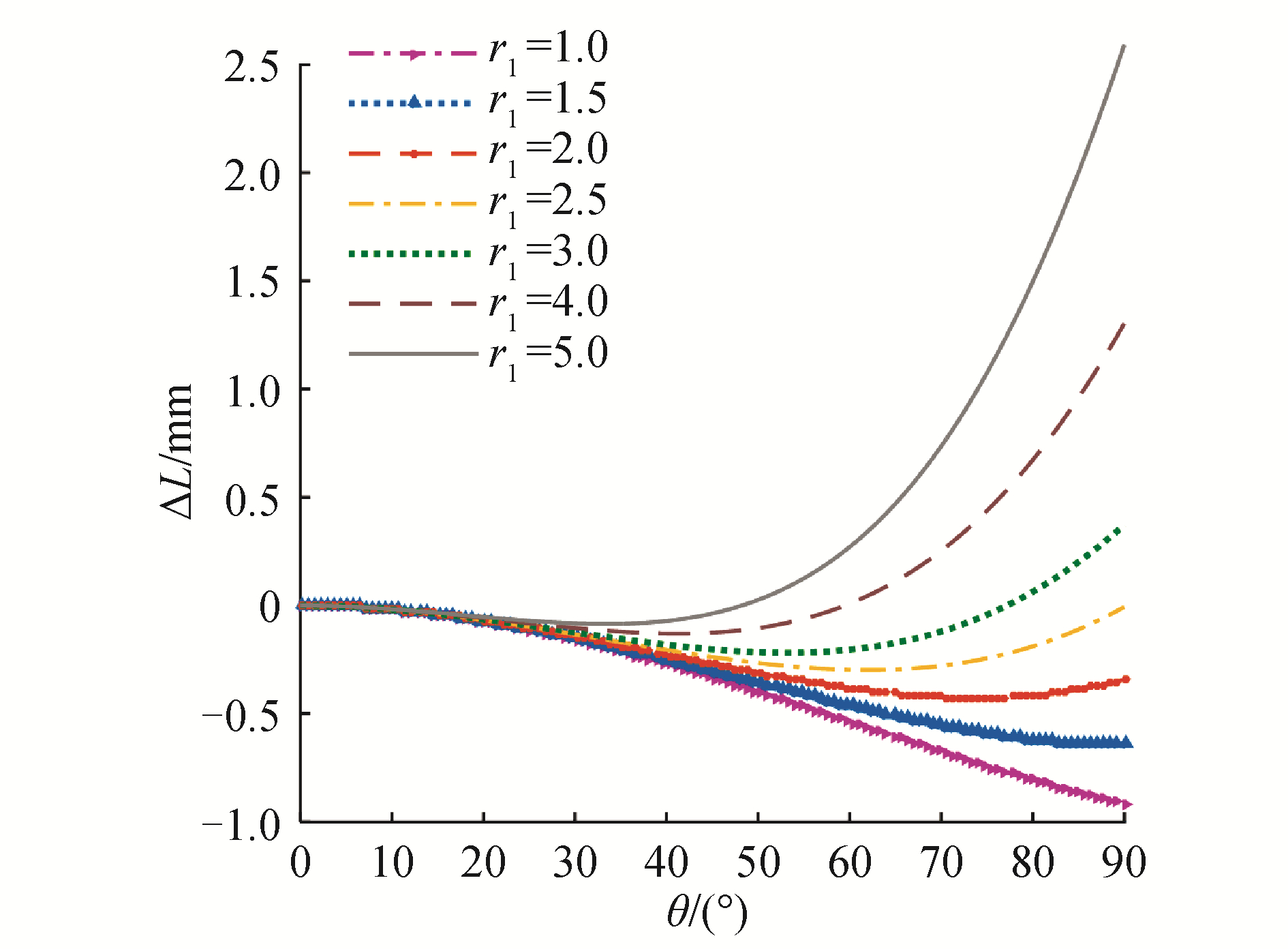
3) 当参数a、b、r2取固定值时,即a=1.5 mm,b=10 mm,r2=2.2 mm,则参数r1取不同值时,ΔL随θ的变化曲线如图 10所示。由图可以看出,随着r1的增大,受迫形变量逐渐减小,且减小幅度相对较大。由此可知,导向轮组1的半径r1对钢丝绳受迫形变量的影响作用较大,因此,该参数选取将增加腕部机构的整体外径尺寸。
|
Download:
|
| 图 10 r1取不同值时钢丝绳受迫形变 Fig. 10 Compelled deformation of cables for different r1 | |
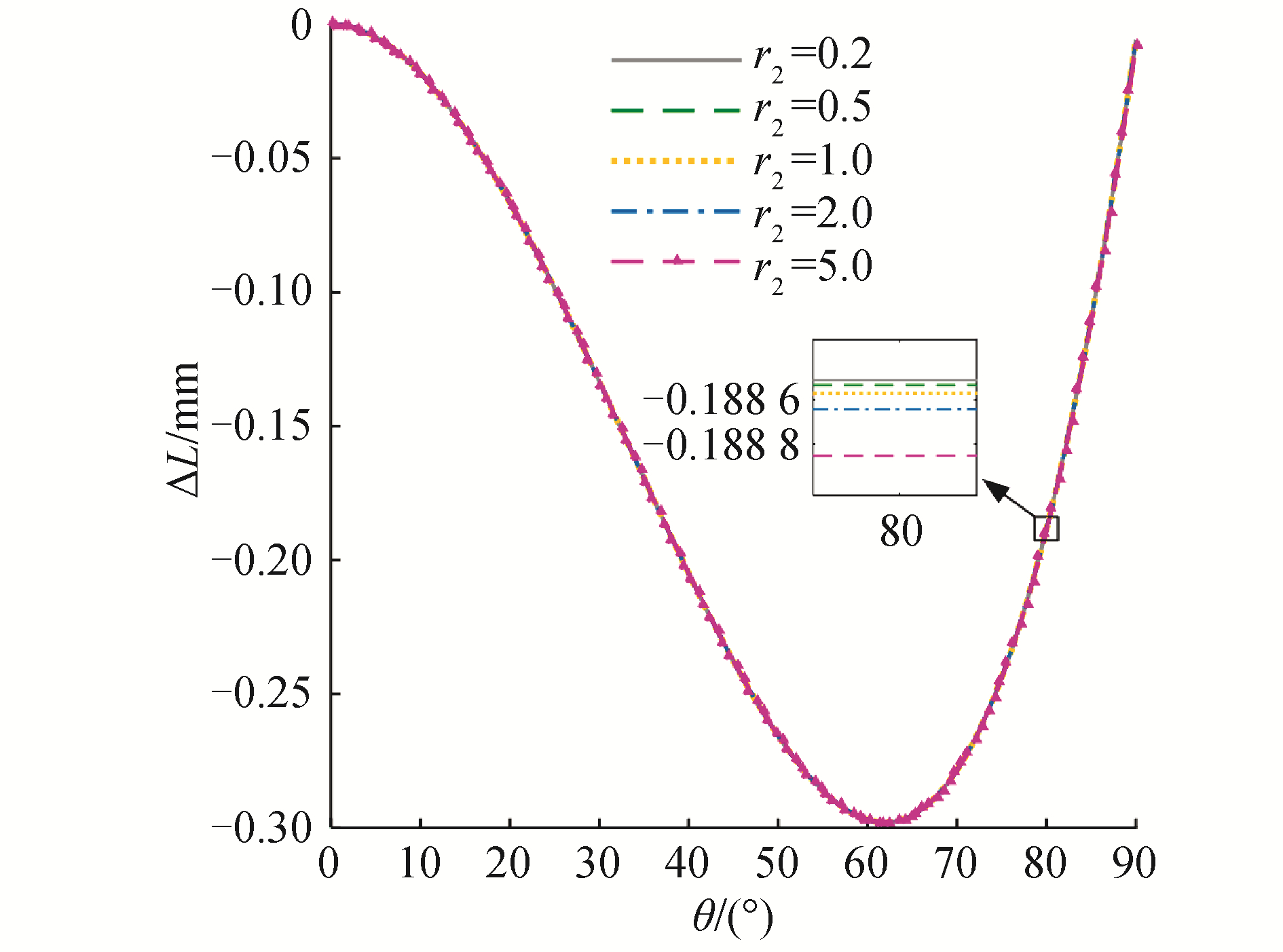
4) 当参数a、b、r1取固定值时,即a=1.5 mm,b=10 mm,r1=2.5 mm,则参数r2取不同值时,ΔL随θ的变化曲线如图 11所示。由图可以看出,随着r2的增大,受迫形变量几乎不发生改变。由此可知,导向轮组2半径r2的大小对钢丝绳的影响作用非常小,几乎可以忽略。因此,在可加工范围内,该参数的选取有利于降低零件在腕部机构中的空间占用率。
|
Download:
|
| 图 11 r2取不同值时钢丝绳受迫形变 Fig. 11 Compelled deformation of cables for different r2 | |
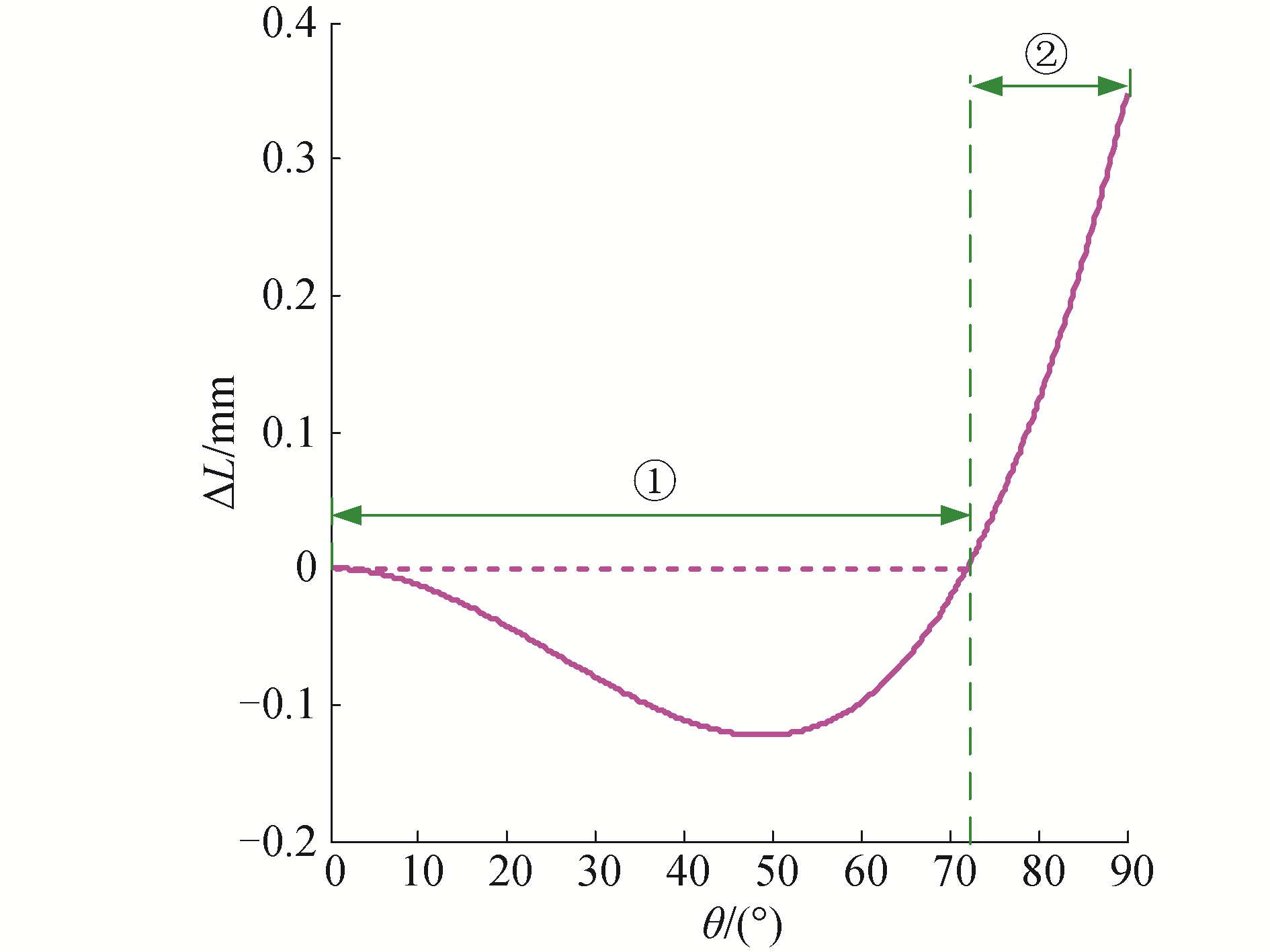
考虑到手术器械初始零位时钢丝绳处在一定的预张紧状态,且初始伸长形变量较小,为避免腕部运动过程中造成驱动执行器的钢丝绳出现松脱情况,应该使钢丝绳受迫产生的压缩形变量尽量降低,此外,为避免钢丝绳由于过张紧而导致的塑性变形或断裂现象,应该使钢丝绳产生受迫伸长形变量时仍然处在弹性形变范围内。综上分析,最终确定腕部机构的4个主要参数尺寸分别为:a=1 mm,b=10 mm,r1=2.2 mm,r2=2.2 mm。由于r3的大小只取决于驱动轮a和b的距离,不影响钢丝绳受迫形变,因此需尽可能降低该尺寸,为保证机构强度,本文选取r3=1.75 mm。并得到了驱动末端执行器的单根钢丝绳受迫形变量与腕关节转角关系曲线,如图 12所示。
|
Download:
|
| 图 12 单根钢丝绳随腕部转角的受迫形变量 Fig. 12 Compelled deformation of single cable by the rotation angle of wrist | |
由图 12可以看出,以初始零位为参考,曲线可以分成2个阶段:形变量缩短过程(①),形变量伸长过程(②)。随着腕关节转角的增加,钢丝绳先是发生缩短形变,之后再发生伸长形变,其中,正向最大形变量为0.348 mm,负向最大形变量为0.129 mm,平均形变量为负向0.024 mm。当θ在操作范围0°~80°内时,钢丝绳受迫形变量范围为-0.123~0.122 mm;当θ在操作范围80°~90°内时,钢丝绳受迫形变量范围为0.122~0.348 mm。经过实验可知,在手术器械初始状态下,预张紧力作用使0.65 m钢丝绳的初始伸长形变为1.5~2 mm[17],由此可知钢丝绳受迫形变量已经非常小,不会产生过张紧或松脱等现象。此外,腕部关节的±80°俯仰运动范围是手术器械操作最频繁的区间,手术过程中的绝大部分手术操作都会在该区间内完成,其已经达到了对于手术器械操作空间的需求,尽管在运动区间80°~90°内的手术动作非常少,但却增大了手术器械的可操作空间,便于整套手术操作的顺畅性和灵活性,而且对关节运动控制可以起到缓冲作用,从而有利于避免手术器械造成软组织额外损伤。
4 结论1) 通过分析手术机器人系统中手术器械末端机构的运动耦合问题,设计了对称式腕部机构,并提出了钢丝绳平行对称式绕线布局,确定了驱动单元内部布局。
2) 基于机构设计,对驱动末端执行器的钢丝绳受迫产生的形变进行建模,确定了导致末端关节运动耦合的主要参数。
3) 通过分析钢丝绳受迫形变数学模型,确定了末端机构主要参数的合理尺寸,运动耦合仿真验证结果表明本文提出的腕部机构与钢丝绳平行对称绕线布局相结合方法的正确性与合理性。
末端机构中的机械摩擦对关节运动耦合的影响以及机构尺寸进一步优化将是今后的研究工作。
| [1] |
YU Lingtao, YAN Yusheng, YU Xiaoyan, et al. Design and realization of forceps with 3-D force sensing capability for robot-assisted surgical system[J]. IEEE sensors journal, 2018, 18(21): 8924-8932. DOI:10.1109/JSEN.2018.2867838 (  0) 0)
|
| [2] |
LI Changsheng, GU Xiaoyi, XIAO Xiao, et al. A robotic system with multi-channel flexible parallel manipulators for single port access surgery[J]. IEEE transactions on industrial informatics, 2019, 15(3): 1678-1687. DOI:10.1109/TII.2018.2856108 (  0) 0)
|
| [3] |
ARATA J, MITSUISHI M, WARISAWA S, et al. Development of a dexterous minimally-invasive surgical system with augmented force feedback capability[C]//Proceedings of 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems. Edmonton, Alberta, Canada, 2005: 3207-3212. https://www.researchgate.net/publication/224623526_Development_of_a_dexterous_minimally-invasive_surgical_system_with_augmented_force_feedback_capability
(  0) 0)
|
| [4] |
HONG M B, JO Y H. Design and evaluation of 2-DOF compliant forceps with force-sensing capability for minimally invasive robot surgery[J]. IEEE transactions on robotics, 2012, 28(4): 932-941. (  0) 0)
|
| [5] |
HONG M B, JO Y H. Design of a novel 4-DOF wrist-type surgical instrument with enhanced rigidity and dexterity[J]. IEEE/ASME transactions on mechatronics, 2014, 19(2): 500-511. (  0) 0)
|
| [6] |
SEIBOLD U, KUBLER B, HIRZINGER G. Prototype of instrument for minimally invasive surgery with 6-axis force sensing capability[C]//Proceedings of 2005 IEEE International Conference on Robotics and Automation. Barcelona, Spain, 2005: 496-501. https://www.researchgate.net/publication/4210087_Prototype_of_Instrument_for_Minimally_Invasive_Surgery_with_6-Axis_Force_Sensing_Capability
(  0) 0)
|
| [7] |
HARAGUCHI D, TADANO K, KAWASHIMA K. A prototype of pneumatically-driven forceps manipulator with force sensing capability using a simple flexible joint[C]//Proceedings of 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems. San Francisco, USA, 2011: 931-936. https://www.researchgate.net/publication/221065125_A_prototype_of_pneumatically-driven_forceps_manipulator_with_force_sensing_capability_using_a_simple_flexible_joint
(  0) 0)
|
| [8] |
杜志江, 孙立宁, 富历新. 医疗机器人发展概况综述[J]. 机器人, 2003, 25(2): 182-187. DU Zhijiang, SUN Lining, FU Lixin. An overview of medical robots[J]. Robot, 2003, 25(2): 182-187. DOI:10.3321/j.issn:1002-0446.2003.02.020 (  0) 0)
|
| [9] |
NISHIZAWA K, KISHI K. Development of interference-free wire-driven joint mechanism for surgical manipulator systems[J]. Journal of robotics and mechatronics, 2004, 16(2): 116-121. (  0) 0)
|
| [10] |
ZHAO Baoliang, NELSON C A. Decoupled cable-driven grasper design based on planetary gear theory[J]. Journal of medical devices, 2013, 7(2): 020918. (  0) 0)
|
| [11] |
ZHAO Baoliang, NELSON C A. Sensorless force sensing for minimally invasive surgery[J]. Journal of medical devices, 2015, 9(4): 041012. (  0) 0)
|
| [12] |
SANG Hongqiang, MENG Jianjun, YUN Jintian. Kinematic analysis of a class of multi-DOF tendon-driven minimally invasive surgical instruments[C]//Proceedings of 2011 International Conference on Computer Science and Network Technology. Harbin, 2012: 607-612. https://www.researchgate.net/publication/254025528_Kinematic_analysis_of_a_class_of_multi-DOF_tendon-driven_minimally_invasive_surgical_instruments
(  0) 0)
|
| [13] |
FENG Mei, FU Yili, PAN Bo, et al. An improved surgical instrument without coupled motions that can be used in robotic-assisted minimally invasive surgery[J]. Proceedings of the institution of mechanical engineers, part H: journal of engineering in medicine, 2012, 226(8): 623-630. DOI:10.1177/0954411912447145 (  0) 0)
|
| [14] |
PAN Bo, NIU Guojun, FU Yili, et al. Design of a novel surgical instrument for minimally invasive robotic surgery[C]//Proceedings of 2014 IEEE International Conference on Robotics and Biomimetics. Bali, Indonesia, 2014: 223-228. https://www.researchgate.net/publication/282986532_Design_of_a_novel_surgical_instrument_for_minimally_invasive_robotic_surgery
(  0) 0)
|
| [15] |
XUE Renfeng, REN Bingyin, YAN Zhiyuan, et al. A cable-pulley system modeling based position compensation control for a laparoscope surgical robot[J]. Mechanism and machine theory, 2017, 118: 283-299. DOI:10.1016/j.mechmachtheory.2017.08.006 (  0) 0)
|
| [16] |
王伟, 王伟东, 闫志远, 等. 腹腔镜外科手术机器人发展概况综述[J]. 中国医疗设备, 2014, 29(8): 5-10, 35. WANG Wei, WANG Weidong, YAN Zhiyuan, et al. Development review of laparoscopic surgical robotic[J]. China medical devices, 2014, 29(8): 5-10, 35. (  0) 0)
|
| [17] |
王正雨.外科手术机器人腹腔镜视窗运动算法与微器械外力检测研究[D].哈尔滨: 哈尔滨工程大学, 2017: 126-127. WANG Zhengyu. Research on kinematic algorithms of laparoscope visual window and external force sensing of micro instrument for invasive surgical robot[D]. Harbin: Harbin Engineering University, 2017: 126-127. http://cdmd.cnki.com.cn/Article/CDMD-10217-1018074761.htm (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


