超短基线定位系统因其尺寸小、成本低、灵活性强等优点，在海洋工程、海洋矿产资源、水下考古、海洋国防等领域得到了广泛的应用^[1-24]。常见的超短基线定位系统多依赖于孔径小于半波长的三元或四元基阵，利用CW信号测量各通道间的相位差来估计目标的位置^[1]。传统的超短基线定位方法依靠阵元间的相位差来估计目标所在方位，其相位差估计精度取决于信噪比，因此，超短基线的远距离目标定位精度往往不高。喻敏等^[4-6]通过改进阵型增加了基阵的基线长度，有效提高了超短基线的定位精度；郑翠娥等^{[3, 6]}通过改变信标发射信号的形式，以达到提高超短基线定位精度的目的；赵安邦等^[8]提出了一种可用于任意声速分布的定位算法，并通过计算机仿真验证了算法的有效性。从实际使用上看这些方法在某些特定的应用场合是有效的，但对信噪比不高的情况，定位精度往往不能满足实际的需求。本文不同于上述方法，从传统方法定位误差的主要来源出发，理论推导了各种误差源对定位精度的影响。在不改变阵型和发射信号形式的前提下，充分利用深度信息，提出了一种提高超短基线定位精度的方法，并仿真验证了该方法的可行性与可靠性。

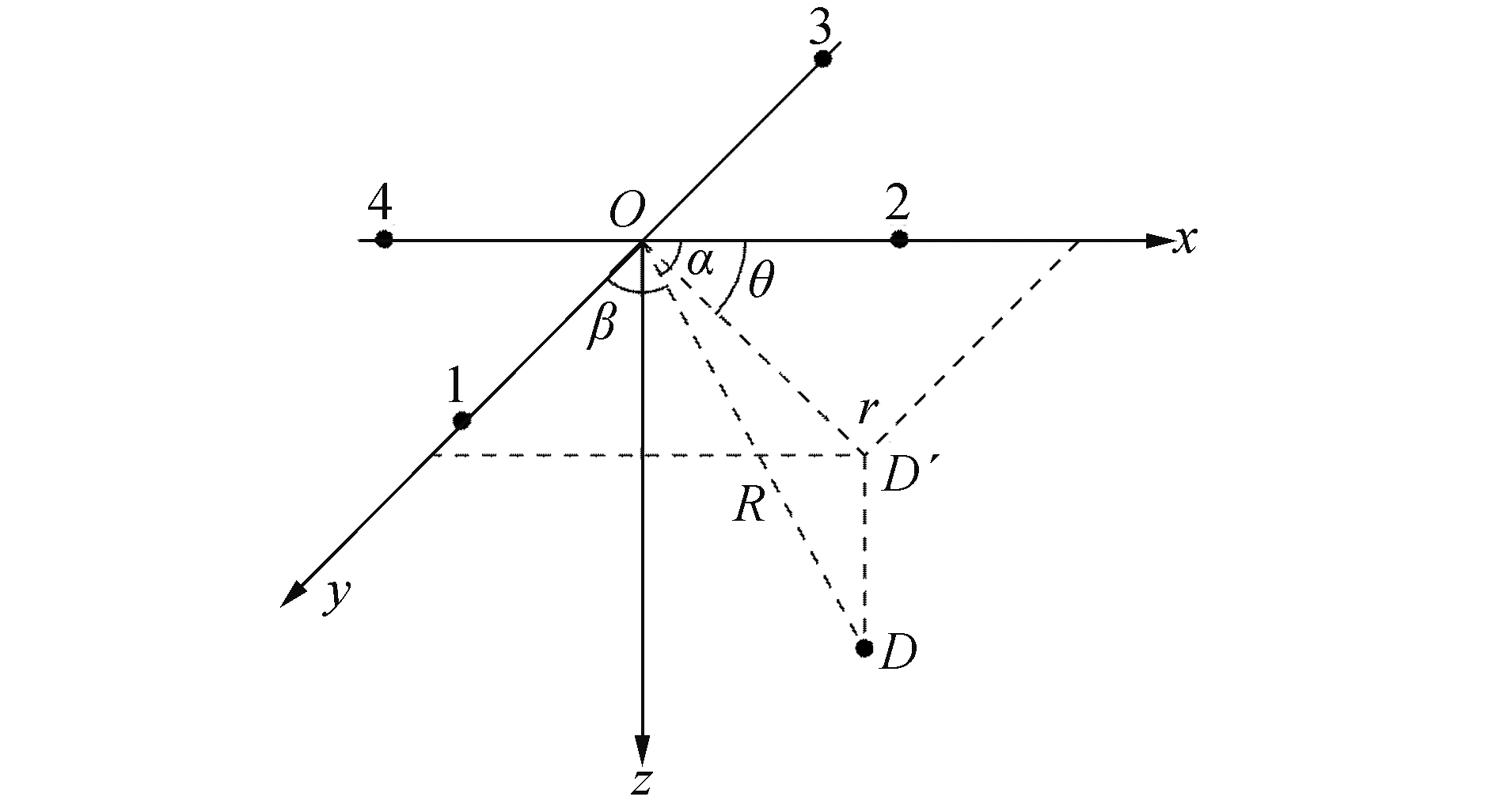
1 传统超短基线定位原理及误差分析 1.1 定位原理

传统超短基线定位方法是靠测量到达接收基阵阵元之间的相位差和测量目标到基阵中心的斜距来实现定位的^[8]。取“北东地”直角坐标系(x, y, z)，其定位原理几何图如图 1所示。

设目标位于D处，其坐标为(x, y, z)。2个正交直线阵分别置于x轴和y轴上，阵的中心为坐标原点。为了避免2种方法中的物理量混淆，现给出如下定义：传统方法中，目标与x轴夹角和y轴夹角分别为α₀和β₀；本文方法中，目标与x轴夹角和y轴夹角分别为α和β。

记1号水听器和3号水听器所接收声波的相位差为ϕ₁₃，2号水听器和4号水听器所接受声波的相位差为ϕ₂₄，当目标处于远场，根据平面波模型，可以得到^{[2-4, 9-11]}：

$ \cos {\beta _0} = {\phi _{13}}/kd $

(1)

$ \cos \alpha_{0}=\phi_{24} / k d $

(2)

式中：k为波数，k=2π/λ=2πf/c；d为基线长度。则目标的定位结果为：

$ y=R \cos \beta_{0}=R \phi_{13} / k d $

(3)

$ x=R \cos \alpha_{0}=R \phi_{24} / k d $

(4)

测量R、ϕ₁₃、ϕ₂₄，由式(3)、(4)可以确定目标位置。R为目标斜距，可通过回波测量测得具有很高的精度，ϕ₁₃和ϕ₂₄通常用自适应相位计测量。

1.2 定位误差分析

对式(3)和式(4)微分整理后得到定位误差的表达式为：

$ \sqrt{\overline{\Delta y^{2}} / R^{2}}=\sqrt{\left(\overline{\Delta R^{2}} / R^{2}\right) \cos ^{2} \beta_{0}+\sin ^{2} \beta_{0} \overline{\Delta \beta_{0}^{2}}} $

(5)

$ \sqrt{\overline{\Delta x^{2}} / R^{2}}=\sqrt{\left(\overline{\Delta R^{2}} / R^{2}\right) \cos ^{2} \alpha_{0}+\sin ^{2} \alpha_{0} \overline{\Delta \alpha_{0}^{2}}} $

(6)

对式(1)和式(2)进行微分，并代入式(5)、(6)，整理后可得：

$ \sqrt{\overline{\Delta y^{2}} / R^{2}}=\sqrt{\left(\overline{\Delta R^{2}} / R^{2}\right) \cos ^{2} \beta_{0}+\overline{\Delta \phi_{13}^{2}} /(k d)^{2}} $

(7)

$ \sqrt{\overline{\Delta x^{2}} / R^{2}}=\sqrt{\left(\overline{\Delta R^{2}} / R^{2}\right) \cos ^{2} \alpha_{0}+\overline{\Delta \phi_{24}^{2} /(k d)^{2}}} $

(8)

由式(7)、(8)可知，对于远距离目标，测距误差可以忽略。因此，对于给定的目标信号和阵型，传统超短基线的定位误差由相位差测量误差直接决定。区别于传统的改变信号形式和增加基线长度以减小相位差误差对定位误差的影响，本文通过利用深度信息，对传统定位方法进行改进，以减小相位差误差对定位误差的影响，从而达到提高定位精度的目的。

2 基于夹角几何关系的高精度定位算法及误差分析 2.1 定位原理

由夹角的几何关系，易知：

$ \cos \beta=\cos \gamma \cos \theta $

(9)

$ \cos \alpha=\cos \gamma \sin \theta $

(10)

式中：γ为目标俯仰角；θ为目标方位角。

$ y=R \cos \beta $

(11)

$ x=R \cos \alpha $

(12)

由式(11)和式(12)可以确定目标的位置，同时，可以得到定位误差的表达式为：

$ \sqrt{\overline{\Delta y^{2}} / R^{2}}=\sqrt{\left(\overline{\Delta R^{2}} / R^{2}\right) \cos ^{2} \beta+\sin ^{2} \beta \cdot \overline{\Delta \beta^{2}}} $

(13)

$ \sqrt{\overline{\Delta x^{2}} / R^{2}}=\sqrt{\left(\overline{\Delta R^{2}} / R^{2}\right) \cos ^{2} \alpha+\sin ^{2} \alpha \cdot \overline{\Delta \alpha^{2}}} $

(14)

由式(9)和式(10)可以得到：

$ \cos ^{2} \alpha+\cos ^{2} \beta=\cos ^{2} \gamma $

(15)

对式(15)进行微分，得：

$ \Delta \alpha \cos \alpha \sin \alpha+\Delta \beta \cos \beta \sin \beta=\Delta \gamma \cos \gamma \sin \gamma $

(16)

式中：

$ \sin \gamma=h / R $

(17)

式中：h为目标相对于基阵的深度，由压力传感器测量得到，其精度通常较高。式(19)对于均匀声场是成立的，对于非均匀声场需要先进行声线修正，实际中，声线修正的结果对本文方法有影响，这一部分内容将在以后的研究中做进一步讨论。

对式(17)进行微分可以得到：

$ \cos \gamma \cdot \Delta \gamma=(\Delta h \cdot R-h \cdot \Delta R) / R^{2} $

(18)

将式(17)、(18)代入式(16)，整理得：

$ \sin ^{2} \alpha \cdot \overline{\Delta \alpha^{2}}=r_{\beta}+p_{y}+q_{y} $

(19)

式中：${r_\beta } = {\left( {\frac{{\cos \beta }}{{\cos \alpha }}} \right)^2}{\sin ^2}\beta \cdot \overline {\Delta {\beta ^2}} ;{p_y} = {\left( {\frac{h}{{Ry}}} \right)^2}\overline {\Delta {h^2}} ;{q_y} = {\left( {\frac{{{h^2}}}{{{R^2}y}}} \right)^2}\overline {\Delta {R^2}} $。

假定Δϕ₁₃和Δϕ₂₄是相互独立的，且$\sqrt {\overline {\Delta \phi _{13}^2} } = \sqrt {\overline {\Delta \phi _{24}^2} } = \sqrt {\overline {\Delta {\phi ^2}} } $。由式(7)、(13)、(19)可知，若使$\sqrt {\frac{{\overline {\Delta {y^2}} }}{{{R^2}}}} $减小，即${\sin ^2}\alpha \cdot \overline {\Delta {\alpha ^2}} < \frac{{\overline {\Delta {\phi ^2}} }}{{{{(kd)}^2}}}$，则需满足：

$ \frac{h^{2} \overline{\Delta h^{2}}}{R^{4}}+\frac{h^{4} \overline{\Delta R^{2}}}{R^{6}}<\left(\cos ^{2} \alpha_{0}-\cos ^{2} \beta_{0}\right) \overline{\Delta \phi^{2}} /(k d)^{2} $

(20)

则当方向角和测量误差满足式(20)时，与y轴夹角β=β₀，与x轴夹角α可以计算得出为：

$ \left\{ {\begin{array}{*{20}{l}} {{{\cos }^2}\alpha = {{\cos }^2}\gamma - {{\cos }^2}\beta }\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}\min \left\| {\mathit{\boldsymbol{\alpha }} - {\mathit{\boldsymbol{\alpha }}_0}} \right\|} \end{array}} \right. $

(21)

同理，重新整理式(21)，得：

$ \sin ^{2} \beta \cdot \overline{\Delta \beta^{2}}=r_{\alpha}+p_{x}+q_{x} $

(22)

式中：${r_\alpha } = \frac{{{{\cos }^2}\alpha }}{{{{\cos }^2}\beta }}{\sin ^2}\alpha \cdot \overline {\Delta {\alpha ^2}} ;{p_x} = {\left( {\frac{h}{{Rx}}} \right)^2}\overline {\Delta {h^2}} ;{q_x} = {\left( {\frac{{{h^2}}}{{{R^2}x}}} \right)^2}\overline {\Delta {R^2}} $。

若使$\sqrt{\overline{\Delta x^{2}} / R^{2}}$减小，则需满足：

$ \frac{h^{2} \overline{\Delta h^{2}}}{R^{4}}+\frac{h^{2} \overline{\Delta R^{2}}}{R^{6}}<\left(\cos ^{2} \beta_{0}-\cos ^{2} \alpha_{0}\right) \overline{\Delta \phi^{2}} /(k d)^{2} $

(23)

则当方向角和测量误差满足式(23)时，与x轴夹角α=α₀与y轴夹角β可以计算得出为：

$ \left\{ {\begin{array}{*{20}{l}} {{{\cos }^2}\beta = {{\cos }^2}\gamma - {{\cos }^2}\alpha }\\ {{\mathop{\rm s}\nolimits} .{\rm{t.min}}\left\| {\mathit{\boldsymbol{\beta }} - {\mathit{\boldsymbol{\beta }}_0}} \right\|} \end{array}} \right. $

(24)

综上，当方向角和测量误差满足式(20)时，与y轴夹角β=β₀，与x轴夹角α可以由式(21)计算得出；当方向角和测量误差满足式(23)时，与x轴夹角α=α₀与y轴夹角β可以由式(24)计算得出。将计算出的α和β代入式(11)、(12)，得到目标的位置。

2.2 定位误差分析

当满足式(16)中的条件时，利用式(5)、(6)、(19)，得到：

$ \begin{array}{*{20}{c}} {\sqrt {\frac{{\overline {\Delta {x^2}} }}{{{R^2}}}} = \sqrt {{u_\beta } + \frac{{\overline {\Delta {\phi ^2}} }}{{{{(kd)}^2}}}} }\\ {\sqrt {\frac{{\overline {\Delta {y^2}} }}{{{R^2}}}} = \sqrt {{u_\alpha } + \frac{{{{\cos }^2}\beta }}{{{{\cos }^2}\alpha }}\frac{{\overline {\Delta {\phi ^2}} }}{{{{(kd)}^2}}} + {p_y} + {q_y}} } \end{array} $

(25)

式中：${u_\alpha } = \frac{{\overline {\Delta {R^2}} }}{{{R^2}}}{\cos ^2}\alpha ;{u_\beta } = \frac{{\overline {\Delta {R^2}} }}{{{R^2}}}{\cos ^2}\beta $，则此时定位误差为：

$ \sqrt{\frac{\overline{\Delta x^{2}}+\overline{\Delta y^{2}}}{R^{2}}}=\sqrt{\frac{\cos ^{2} \gamma}{\cos ^{2} \alpha} \frac{\overline{\Delta \phi^{2}}}{(k d)^{2}}+p_{y}+u_{\gamma}+q_{y}} $

(26)

式中${u_\gamma } = \frac{{\overline {\Delta {R^2}} }}{{{R^2}}}{\cos ^2}\gamma $。同理，当满足(23)中条件时，利用式(5)、式(6)和式(22)得到：

$ \left\{\begin{array}{l}{\sqrt{\frac{\overline{\Delta x^{2}}}{R^{2}}}=\sqrt{u_{\beta}+\frac{\cos ^{2} \alpha}{\cos ^{2} \beta} \frac{\overline{\Delta \phi^{2}}}{(k d)^{2}}+p_{x}+q_{x}}} \\ {\sqrt{\frac{\overline{\Delta y^{2}}}{R^{2}}}=\sqrt{u_{\alpha}+\frac{\overline{\Delta \phi^{2}}}{(k d)^{2}}}}\end{array}\right. $

(27)

则此时定位误差为：

$ \sqrt{\frac{\overline{\Delta x^{2}}+\overline{\Delta y^{2}}}{R^{2}}}=\sqrt{\frac{\cos ^{2} \gamma}{\cos ^{2} \beta} \frac{\overline{\Delta \phi^{2}}}{(k d)^{2}}+u_{\gamma}+p_{x}+q_{x}} $

(28)

3 仿真实验与分析

仿真实验1：在水平切面上，研究本文方法较传统方法定位性能的改善情况。

仿真条件：信号频率为30 kHz，声速为1 500 m/s，测距误差0.15 m，阵元间距300 mm，相位差估计误差为6°。如无特殊说明，均采用以上基本实验条件。

为便于分析说明仿真结果，将传统的定位方法和基于夹角几何关系的高精度算法进行定位性能比较。超短基线的定位范围为椎体，形状如图 2，其中，γ′为开角和h为深度。

图 3给出了图 2的横切面上2种方法的定位相对误差，仿真深度为4 000 m，开角从0°扩展到140°，色棒表示定位相对误差的百分比。为了便于说明，规定x的正方向为0°，由图 3(a)、3(d)、3(g)和图 3(b)、3(e)、3(h)对比可知，相比于传统算法，基于夹角几何关系的高精度算法，在x、y方向均能提高定位精度，定位精度最高可提高0.25%。当目标所在位置满足高精度算法的条件时，目标的定位精度将得到提高。由图 3(c)和图 3(f)可知，当目标越靠近坐标轴，则在该轴方向上的定位精度提高得就越明显, 但坐标轴及其附近的区域内，精度提高的程度下降，这是因为利用式(11)计算时，坐标轴附近函数的非线性使得计算夹角时精度下降，稳健性降低。

仿真实验2：在纵切面上，研究文方法较传统方法定位性能的改善情况。

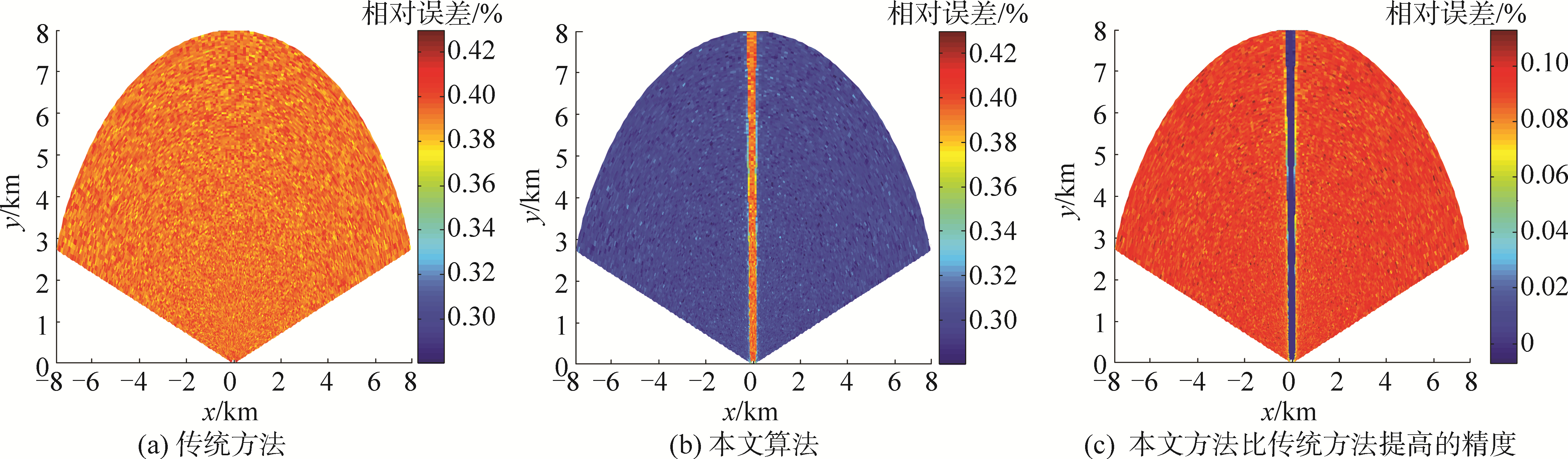
图 4(a)(b)给出了图 2纵切面上2种方法定位的相对误差，图 4(c)给出了在纵切面上新方法较传统方法提高的精度。仿真目标所在方位角为67.5°，目标距基线原点的距离R和开角γ′满足：R∈[100 m, 8 000 m]，γ′∈[0°, 140°]，其他仿真条件不变。由图 4(a)和图 4(b)对比可知，相比于传统方法，本文方法对于目标在开角稍大的位置有一定的改善。由图 4(c)可以清晰地看到新方法较传统方法提高的精度随开角的变化情况。其中，图 4(c)的中间区域表明相比于传统方法，本文方法的定位精度没有提高，这是因为当目标与2条基线夹角近似垂直时，不能满足本文方法的定位条件，仍用传统方法进行定位。图 4(c)的中间非蓝色区域表明当开角稍大时，新方法较传统方法提高定位精度，但提高精度与开角变化关系不明显，这与式(24)中的误差计算结果相一致，提高精度约为0.1%。因此，对目标位于稍大开角的情况，采用本文算法能够提高定位精度。

仿真实验3：在仿真1的基础上，研究传统方法和基于夹角几何关系的高精度算法的定位均方根误差随相位差估计误差的变化。

数值仿真条件：目标位置固定，目标方位角为67.5°，目标俯仰角为60°，目标距基线3 000 m，相位差估计误差由0.1°向10°变化，做1 000次蒙特卡洛实验，其他条件同仿真1。

图 5给出了2种方法的定位相对误差随相位差估计误差的变化。总体来看，2种方法定位相对误差均随着相位差估计误差的增加而增加，但相比于传统方法，本文算法随着相位差的增大对传统方法的改善情况越加明显。

4 结论

1) 相比于传统算法，基于夹角的高精度定位算法在和方向均能提高定位精度，定位精度最高可提高约0.25%。

2) 除坐标轴及其附近区域外，目标越靠近坐标轴，则基于夹角的高精度定位算法在该轴方向上的定位精度提高得就越明显。

3) 从总的定位误差的角度看，相比于传统算法，基于夹角的高精度定位算法的定位精度在绝大多数区域均有显著提高。

4) 当目标与两条基线近似垂直时，三者的几何关系难以满足基于夹角的高精度定位算法的适用条件，因此，该方法在这一条件下无法应用。

5) 在纵切面上看，当目标位于稍大开角的情况，采用基于夹角的高精度定位算法能够提高定位精度，且提高精度与开角变化关系不明显。

6) 对于以相位差为主要误差源的的超短基线定位问题，基于夹角的高精度定位算法提高的定位精度更为显著。