2. 江南大学 机器人技术与系统国家重点实验室, 江苏 无锡 214122;
3. 江南大学 江苏省食品先进制造装备技术重点实验室, 江苏 无锡 214122
2. State Key Laboratory of Robotics and System, Jiangnan University, Wuxi 214122, China;
3. Jiangsu Key Laboratory of Advanced Food Manufacturing Equipment and Technology, Jiangnan University, Wuxi 214122, China
并联机构的各零件在加工、使用及生产过程中由于误差的存在,导致连接各构件的关节处存在间隙,当机构工作时,运动关节处的磨损会产生,进而引起系统振动,稳定性降低。基于上述,关节元素间必然存在的关节间隙已成为国内外学者研究的热点问题[1-11]。
Koshy等[12]基于Hertz理论对一种平面连杆机构进行了转动关节处含间隙的动力学建模与实验研究。Bai等[13-14]利用混合非线性接触力模型对一种含间隙的双轴定位机构进行了动力学建模与数值分析。Marques等[15]提出一种具有径向和轴向间隙的空间转动关节数学模型,并通过实例对模型进行了验证。Luka等[16]对一种含间隙的滑槽机构进行了动力学建模,并将其作为验证模型与不同的接触模型进行比较,最后与实验结果进行对比。
在基于动力学模型的控制器设计中,关节间隙引起的关节效应等不确定因素会影响机构的控制效果,Li等[17]对一种2自由度并联机构进行动力学建模,并根据机构动力学模型设计了一种滑模变结构控制器,实验结果验证了其控制器设计的正确性;文献[18]基于平面2自由度并联机器人的位置控制,结合自适应控制设计了一种动态模糊神经网络控制器。上述控制方法需要满足对动力学模型进行参数化处理的要求或需建立在机构关节效应及模型参数不确定项上界已知的情况下。为此,许多学者将自适应控制、神经网络、模糊控制,遗传算法以及滑模控制等相互组合成混合控制器以提升控制效果[19-20]。
本文基于3-CPaRR机构,对该系统开展含间隙的动力学建模,比较了不同间隙量对其产生的影响,最后设计了该并联机构自适应滑模运动控制器,以提高控制系统的鲁棒性。
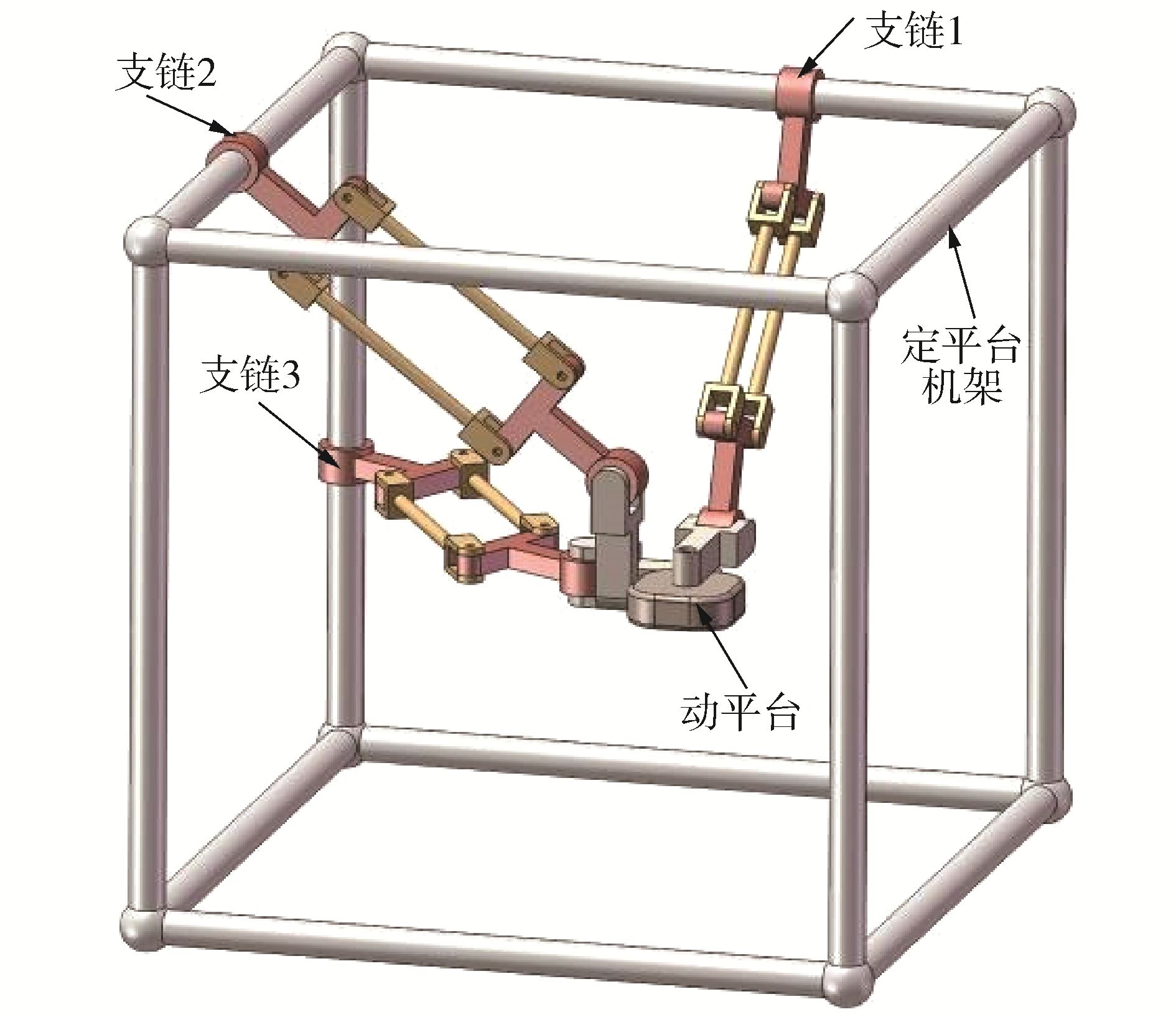
1 3-CPaRR机构含间隙关节运动学及接触力模型3-CPaRR样机模型如图 1所示,各支链间的位置约束方程及各构件参数与其铰接转动副处夹角之间的关系请参见文献[21]。
|
Download:
|
| 图 1 3-CPaRR机构样机简图 Fig. 1 Schematic of the 3-CPaRR mechanism prototype | |
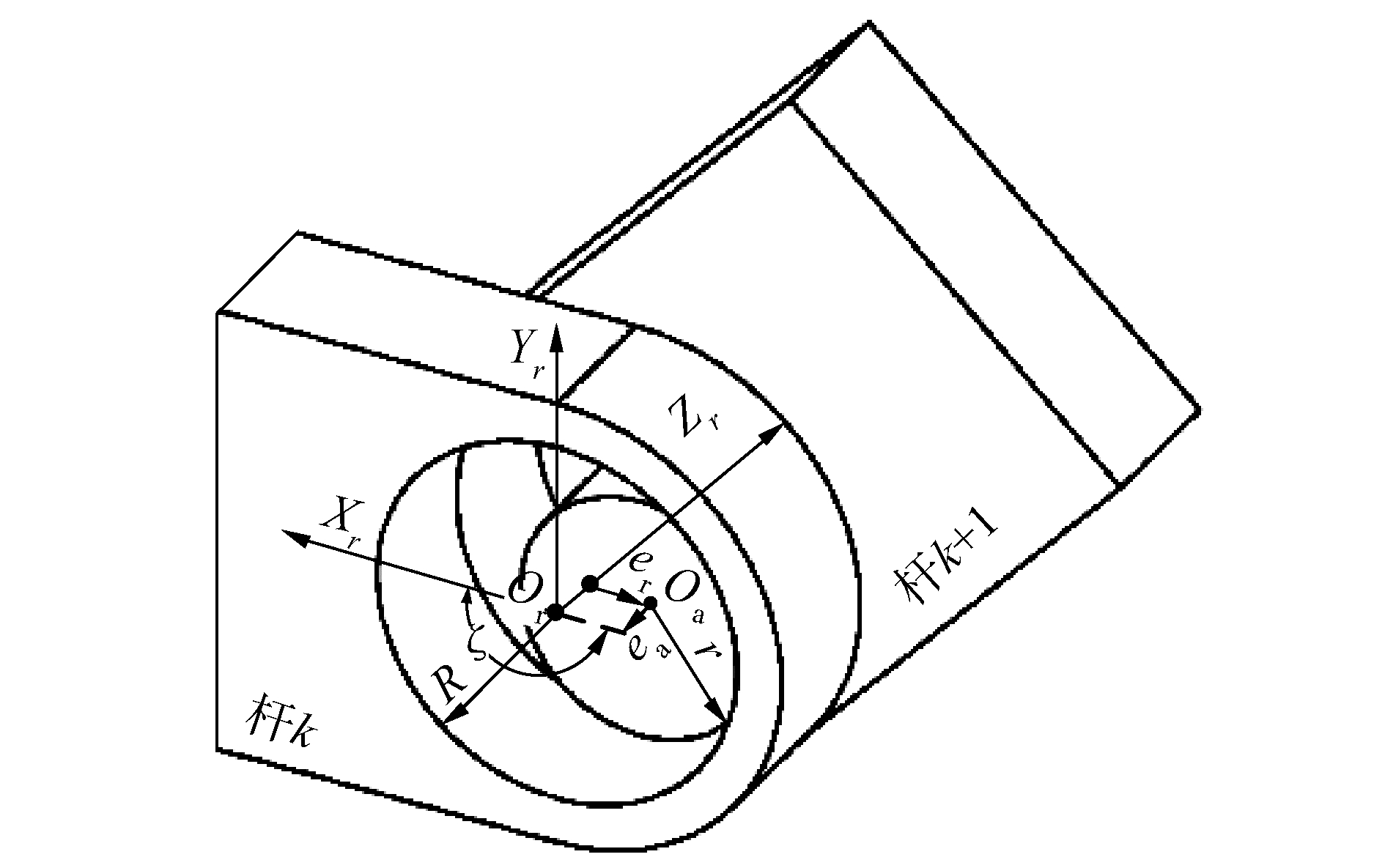
当考虑驱动构件与定机架铰接处的圆柱副中存在间隙时,驱动关节Ai及其运动模型如图 2所示,由于Ai处含间隙,当系统运动时,其在Or-XrYrZr坐标系中沿Xr、Yr、Zr方向做随机运动,故引入概率密度函数模型描述Ai关节处的矢量变化[22]。
| $ {e_r} = {e_{r\max }}\int {{f_r}} \left( {{r_r}\left( {{x_r},{y_r}} \right)} \right){\rm{d}}{r_r} $ |
|
Download:
|
| 图 2 间隙关节模型 Fig. 2 The model of joint with clearance | |
机构运动时,Ai关节中心Or在Or-XrYrZr中沿直径、轴方向上随机位置矢量值fr(rr)、fa(zr)可分别表示为:
| $ {f_r}\left( {{r_r}} \right) = \left\{ {\begin{array}{*{20}{l}} {k{{\rm{e}}^{ - {{\left( {\frac{{{r_r} - \mu }}{{\sqrt {2\sigma } }}} \right)}^2}}},}&{0 \le r_r^2 = x_r^2 + y_r^2 \le e_{r\max }^2}\\ {0,}&{其他} \end{array}} \right. $ | (1) |
| $ {f_a}\left( {{z_r}} \right) = \left\{ {\begin{array}{*{20}{l}} {k{{\rm{e}}^{ - {{\left( {\frac{{{z_r} - \mu }}{{\sqrt {2\sigma } }}} \right)}^2}}},}&{0 \le {z_r} \le {e_{a\max }}}\\ {0,}&{其他} \end{array}} \right. $ | (2) |
间隙引起的偏心距、轴向位移变化量分别为:
| $ {e_r} = {e_{r\max }}\int {{f_r}\left( {{r_r}\left( {{x_r},{y_r}} \right)} \right){\rm{d}}r} $ | (3) |
| $ {e_a} = {e_{a\max }}\int {{f_a}} \left( {{z_r}} \right){\rm{d}}{z_r} $ | (4) |
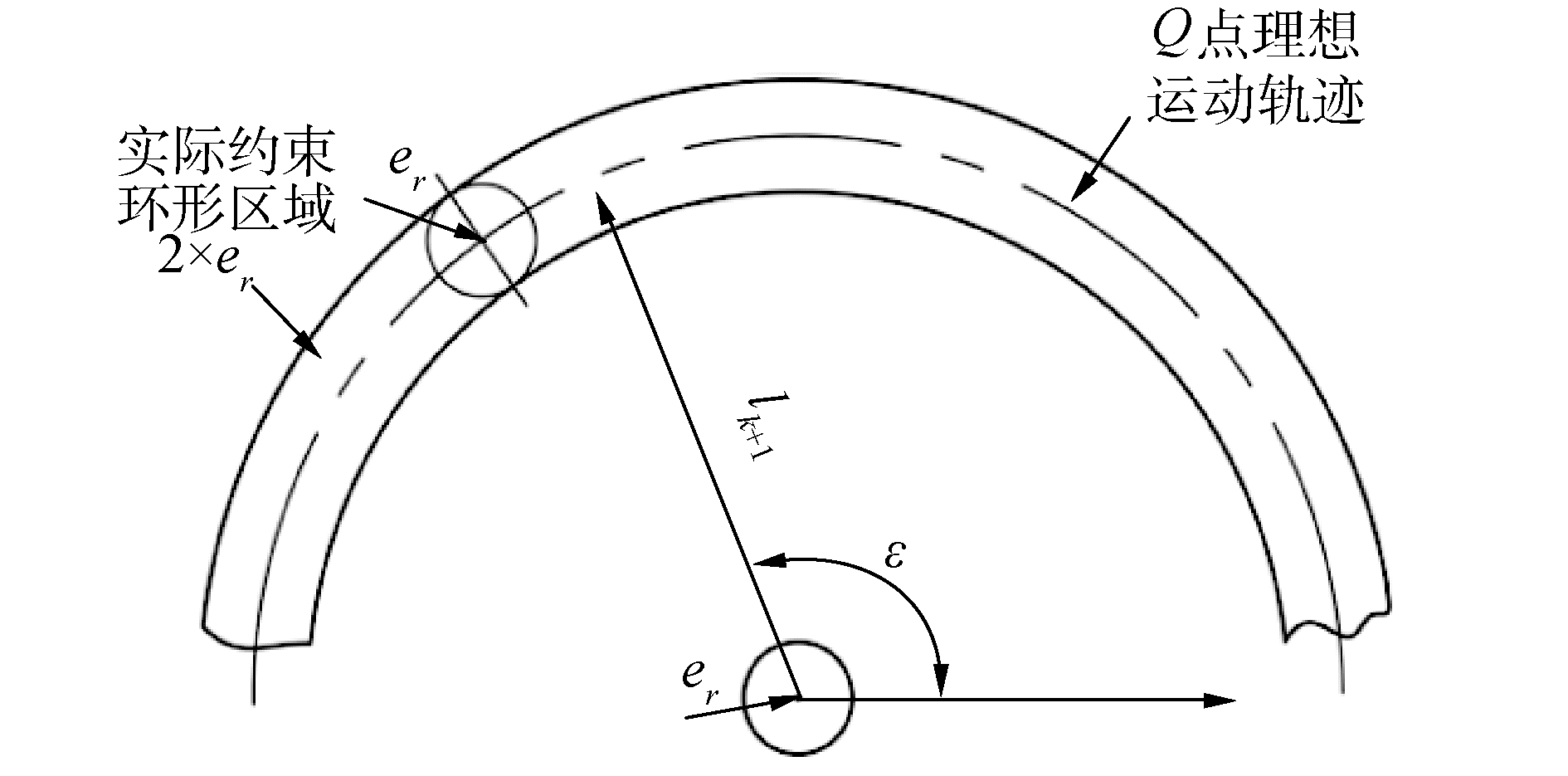
驱动关节Ai运动模型如图 3所示,Q为构件AiBi上的点,当AiBi伴随机构运动时,其在Or-XrYrZr坐标系中的坐标xQ、yQ、zQ为:
| $ \left\{ {\begin{array}{*{20}{l}} {{x_Q} = {e_r}\cos \zeta + {l_{k + 1}}\cos \varepsilon }\\ {{y_Q} = {e_r}\sin \zeta + {l_{k + 1}}\sin \varepsilon }\\ {{z_Q} = {z_r} + {e_a}} \end{array}} \right. $ | (5) |
|
Download:
|
| 图 3 间隙关节运动模型 Fig. 3 Kinematic model of the joint with clearance | |
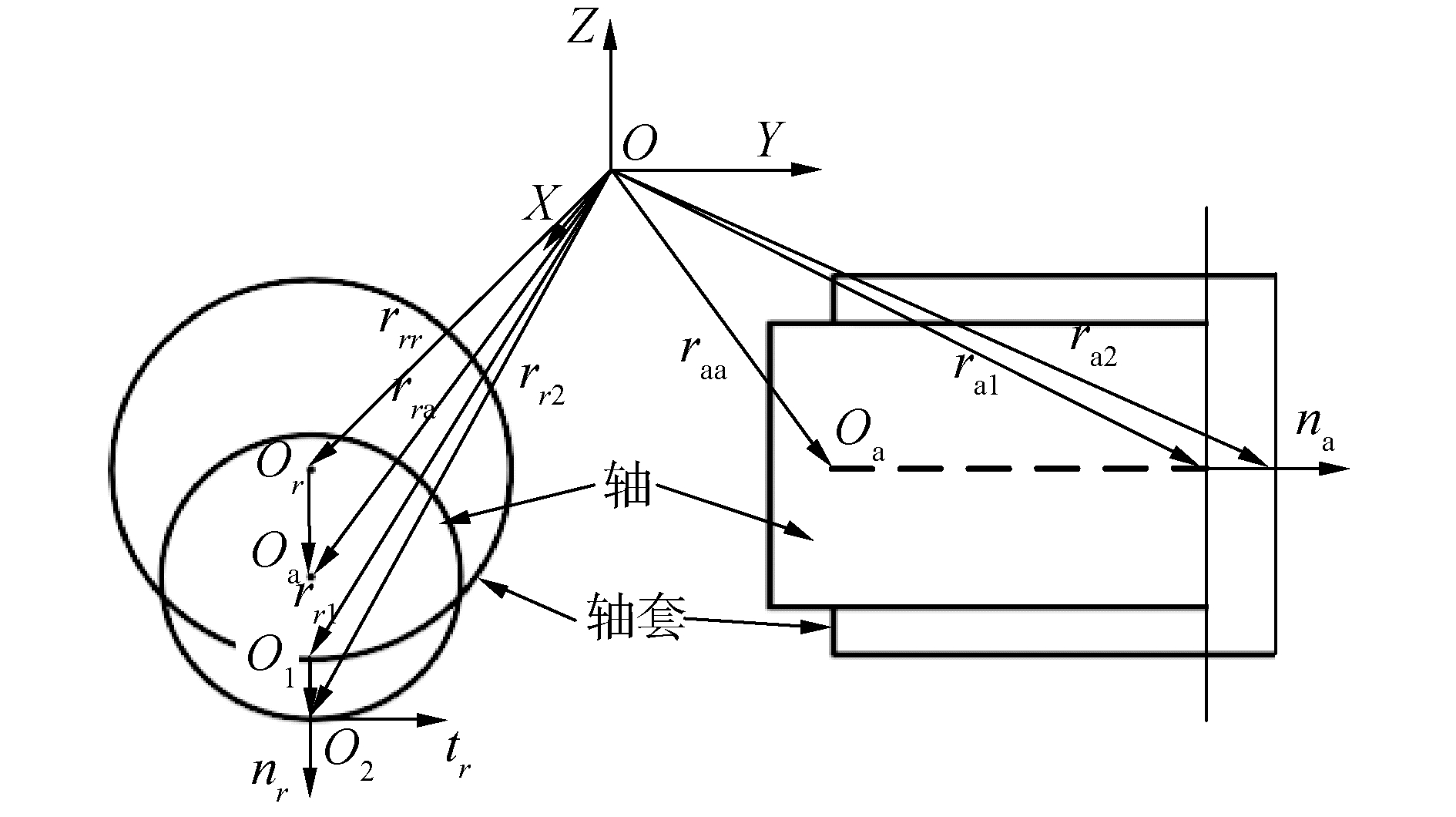
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{r}}_{r1}} = {\mathit{\boldsymbol{r}}_{rr}} + {\mathit{\boldsymbol{n}}_r}R}\\ {{\mathit{\boldsymbol{r}}_{r2}} = {\mathit{\boldsymbol{r}}_{ra}} + {\mathit{\boldsymbol{n}}_r}r} \end{array}} \right. $ | (6) |
|
Download:
|
| 图 4 关节接触运动模型 Fig. 4 Kinematic model of the joint with contact | |
关节Ai处的速度矢量可表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{v}}_{nr}} = \left[ {{{\left( {{{\mathit{\boldsymbol{\dot r}}}_{r1}} - {{\mathit{\boldsymbol{\dot r}}}_{r2}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{n}}_r}} \right]{\mathit{\boldsymbol{n}}_r}}\\ {{\mathit{\boldsymbol{v}}_{tr}} = \left( {{{\mathit{\boldsymbol{\dot r}}}_{r1}} - {{\mathit{\boldsymbol{\dot r}}}_{r2}}} \right) - {\mathit{\boldsymbol{v}}_{nr}}}\\ {{\mathit{\boldsymbol{v}}_{na}} = \left[ {{{\left( {{{\mathit{\boldsymbol{\dot r}}}_{a1}} - {{\mathit{\boldsymbol{\dot r}}}_{a2}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{n}}_a}} \right]{\mathit{\boldsymbol{n}}_a}} \end{array}} \right. $ | (7) |
在3-CPaRR并联机构中,其在刚性且Ai关节处存在间隙条件下时,关节处的接触力与摩擦力模型分别为:
| $ {\mathit{\boldsymbol{F}}_n} = K{\delta ^{1.5}}\left[ {1 + \frac{{8\left( {1 - {c_r}} \right)}}{{5{c_r}}}\frac{{\dot \delta }}{{{{\mathit{\boldsymbol{\dot \delta }}}^{( - )}}}}} \right] $ | (8) |
| $ {\mathit{\boldsymbol{F}}_t} = - {\mu _d}{c_d}{F_n}{\mathit{\boldsymbol{v}}_t} $ | (9) |
式(1)~(9)中相关变量意义及Ai处是否产生碰撞的条件判别等见文献[22]。
2 含关节间隙3-CPaRR并联机构的动力学模型 2.1 含间隙动力学模型因间隙而使关节Ai处产生的接触力Fif需向系统构件质心进行等效转化,设其为fi,则:
| $ {\mathit{\boldsymbol{F}}_{if}} = {F_{in}}\mathit{\boldsymbol{n}} + {F_{it}}\mathit{\boldsymbol{t}} + {F_{ia}}\mathit{\boldsymbol{n}},i = 1,2,3 $ | (10) |
| $ {\mathit{\boldsymbol{f}}_i} = \sum\limits_{i = 1}^3 {{\mathit{\boldsymbol{R}}_i}} {\mathit{\boldsymbol{F}}_{if}} = {\left[ {{f_{ix}}\quad {f_{iy}}\quad {f_{ix}}} \right]^{\rm{T}}},i = 1,2,3 $ | (11) |
构件l1i、l2i、l3i和l4i (i=1, 2, 3)在坐标系O-XYZ中质心坐标为(xjic, yjic, zjic),速度为vji=[ẋjic ẏjic żjic]T,转动惯量为Jji,动平台相对速度为
| $ \begin{array}{l} T = \frac{1}{2}\sum\limits_{j = 1}^4 {\sum\limits_{i = 1}^3 {\left[ {{m_{ji}}\left( {\dot x_{jic}^2 + \dot y_{jic}^2 + \dot z_{jic}^2} \right)} \right]} } + \frac{1}{2}\sum\limits_{i = 1}^3 {{J_{1i}}} \dot \theta _i^2 + \\ \;\;\;\;\;\frac{1}{2}\sum\limits_{i = 1}^3 {{J_{2i}}} \dot \theta _{(i + 3)}^2 + \frac{1}{2}\sum\limits_{i = 1}^3 {{J_{3i}}} \dot \theta _i^2 + \frac{1}{2}{m_0}\mathit{\boldsymbol{v}}_0^{\rm{T}}{\mathit{\boldsymbol{v}}_0} \end{array} $ | (12) |
| $ V = \sum\limits_{j = 1}^4 {\sum\limits_{i = 1}^3 {{m_{ji}}} } g{z_{jic}} + {m_0}g\left( {{Z_p} + {q_3}} \right) $ | (13) |
将式(12)、(13)代入非完整系统的Lagrange方程:
| $ \frac{d}{{dt}}\left( {\frac{{\partial T}}{{\partial {{\dot q}_i}}}} \right) - \frac{{\partial T}}{{\partial {q_i}}} + \frac{{\partial V}}{{\partial {q_i}}} = {F_i} + {Q_i},i = 1,2,3 $ | (14) |
化简后可得:
| $ \mathit{\boldsymbol{M}}\left( \mathit{\boldsymbol{q}} \right)\mathit{\boldsymbol{\ddot q}} + \mathit{\boldsymbol{C}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}})\mathit{\boldsymbol{\dot q}} + \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{q}}) = \mathit{\boldsymbol{F}} + \mathit{\boldsymbol{Q}} $ | (15) |
式中:
| $ \mathit{\boldsymbol{M}}\left( \mathit{\boldsymbol{q}} \right) = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat M}}}_{11}}}&{{{\mathit{\boldsymbol{\hat M}}}_{12}}}&{{{\mathit{\boldsymbol{\hat M}}}_{13}}}\\ {{{\mathit{\boldsymbol{\hat M}}}_{12}}}&{{{\mathit{\boldsymbol{\hat M}}}_{22}}}&{{{\mathit{\boldsymbol{\hat M}}}_{23}}}\\ {{{\mathit{\boldsymbol{\hat M}}}_{13}}}&{{{\mathit{\boldsymbol{\hat M}}}_{23}}}&{{{\mathit{\boldsymbol{\hat M}}}_{33}}} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{C}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}) = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{C}}_{11}}}&{{\mathit{\boldsymbol{C}}_{12}}}&{{\mathit{\boldsymbol{C}}_{13}}}\\ {{\mathit{\boldsymbol{C}}_{21}}}&{{\mathit{\boldsymbol{C}}_{22}}}&{{\mathit{\boldsymbol{C}}_{23}}}\\ {{\mathit{\boldsymbol{C}}_{31}}}&{{\mathit{\boldsymbol{C}}_{32}}}&{{\mathit{\boldsymbol{C}}_{33}}} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{q}}) = \left[ {\begin{array}{*{20}{l}} {\frac{{\partial V}}{{\partial {q_1}}}}&{\frac{{\partial V}}{{\partial {q_2}}}}&{\frac{{\partial V}}{{\partial {q_3}}}} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{Q}} = {\left[ {\begin{array}{*{20}{c}} {\sum\limits_{i = 1}^3 {{f_{ix}}} }&{\sum\limits_{i = 1}^3 {{f_{iy}}} }&{\sum\limits_{i = 1}^3 {{f_{iz}}} } \end{array}} \right]^{\rm{T}}}, $ |
| $ {\mathit{\boldsymbol{C}}_{11}} = \frac{1}{2}\frac{{\partial {{\hat M}_{11}}}}{{\partial {q_1}}}\dot q_1^2 + \frac{{\partial {{\hat M}_{11}}}}{{\partial {q_2}}}\dot q_2^2, $ |
| $ {\mathit{\boldsymbol{C}}_{12}} = \left( {\frac{{\partial {{\hat M}_{12}}}}{{\partial {q_2}}} - \frac{1}{2}\frac{{\partial {{\hat M}_{22}}}}{{\partial {q_1}}}} \right)\dot q_2^2 + \left( {\frac{{\partial {{\hat M}_{12}}}}{{\partial {q_3}}} + \frac{{\partial {{\hat M}_{13}}}}{{\partial {q_2}}} - \frac{{\partial {{\hat M}_{23}}}}{{\partial {q_1}}}} \right)\dot q_3^2, $ |
| $ {\mathit{\boldsymbol{C}}_{13}} = \left( {\frac{{\partial {{\hat M}_{13}}}}{{\partial {q_3}}} - \frac{1}{2}\frac{{\partial {{\hat M}_{33}}}}{{\partial {q_1}}}} \right)\dot q_3^2 + \frac{{\partial {{\hat M}_{11}}}}{{\partial {q_3}}}{{\dot q}_1}{{\dot q}_3}, $ |
| $ {\mathit{\boldsymbol{C}}_{21}} = \left( {\frac{{\partial {{\hat M}_{12}}}}{{\partial {q_1}}} - \frac{1}{2}\frac{{\partial {{\hat M}_{11}}}}{{\partial {q_2}}}} \right)\dot q_1^2 + \frac{{\partial {{\hat M}_{22}}}}{{\partial {q_1}}}\dot q_2^2, $ |
| $ {\mathit{\boldsymbol{C}}_{22}} = \frac{1}{2}\frac{{\partial {{\hat M}_{22}}}}{{\partial {q_2}}}\dot q_2^2 + \frac{{\partial {{\hat M}_{22}}}}{{\partial {q_3}}}\dot q_3^2, $ |
| $ {\mathit{\boldsymbol{C}}_{23}} = \left( {\frac{{\partial {{\hat M}_{23}}}}{{\partial {q_3}}} - \frac{1}{2}\frac{{\partial {{\hat M}_{33}}}}{{\partial {q_2}}}} \right)\dot q_3^2 + \left( {\frac{{\partial {{\hat M}_{12}}}}{{\partial {q_3}}} - \frac{{\partial {{\hat M}_{13}}}}{{\partial {q_2}}} + \frac{{\partial {{\hat M}_{23}}}}{{\partial {q_1}}}} \right)\dot q_1^2, $ |
| $ {\mathit{\boldsymbol{C}}_{31}} = \left( {\frac{{\partial {{\hat M}_{{\rm{13}}}}}}{{\partial {q_1}}} - \frac{1}{2}\frac{{\partial {{\hat M}_{{\rm{11}}}}}}{{\partial {q_3}}}} \right)\dot q_{\rm{l}}^2 + \left( {\frac{{\partial {{\hat M}_{{\rm{13}}}}}}{{\partial {q_2}}} - \frac{{\partial {{\hat M}_{{\rm{13}}}}}}{{\partial {q_3}}} + \frac{{\partial {{\hat M}_{{\rm{23}}}}}}{{\partial {q_1}}}} \right)\dot q_2^2, $ |
| $ {\mathit{\boldsymbol{C}}_{32}} = \left( {\frac{{\partial {{\hat M}_{23}}}}{{\partial {q_2}}} - \frac{1}{2}\frac{{\partial {{\hat M}_{22}}}}{{\partial {q_3}}}} \right)\dot q_2^2 + \frac{{\partial {{\hat M}_{33}}}}{{\partial {q_2}}}\dot q_3^2, $ |
| $ {\mathit{\boldsymbol{C}}_{33}} = \frac{1}{2}\frac{{\partial {{\hat M}_{33}}}}{{\partial {q_3}}}\dot q_3^2 + \frac{{\partial {{\hat M}_{33}}}}{{\partial {q_1}}}\dot q_1^2 $ |
基于上述模型,3-CPaRR机构具体参数如下:材料为碳素钢,密度ρ=7 800 kg/m3,弹性模量分别为E=210 GPa,G=80 GPa,l1i=160 mm,l2i=150 mm,l3i=160 mm,l4i=55 mm,截面尺寸为b=15 mm,h=10 mm,m0=0.875 kg,周期T=5 s,步长Δt=0.01 s。Jix、Jiy、Jiz为构件绕X、Y、Z转动惯量,如表 1所示。
| 表 1 杆l1i、l2i、l3i、l4i转动惯量 Table 1 Moment of inertia of components l1i, l2i, l3i, l4i |
给定轨迹如下:
| $ \left\{ {\begin{array}{*{20}{l}} {X = {x_0} - 5\sin (0.4{\rm{ \mathsf{ π} }}t)}\\ {Y = {x_0} - 6\sin (0.4{\rm{ \mathsf{ π} }}t)\quad (0 \le t \le 5)}\\ {Z = {z_0} - 5t} \end{array}} \right. $ | (16) |
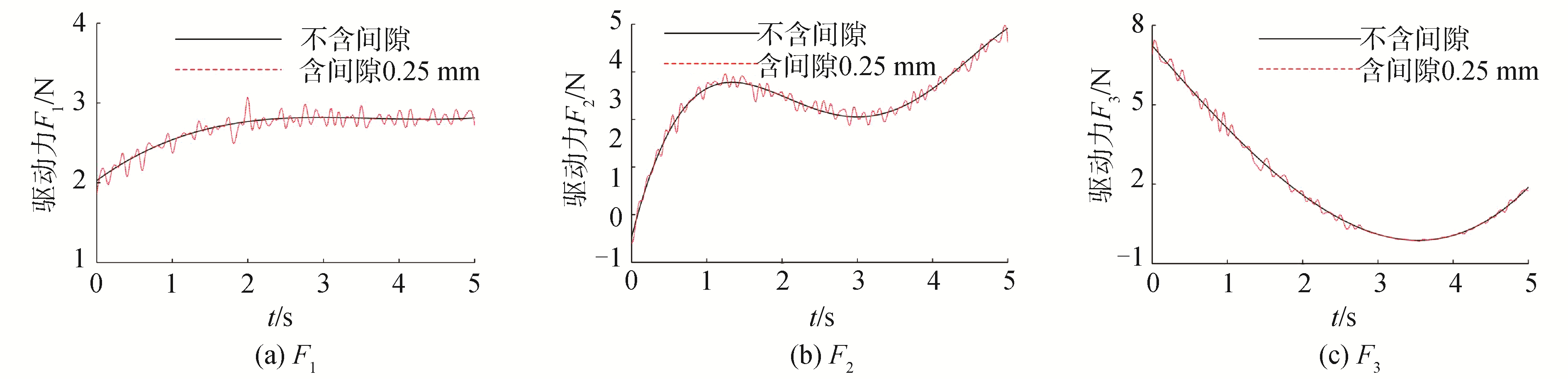
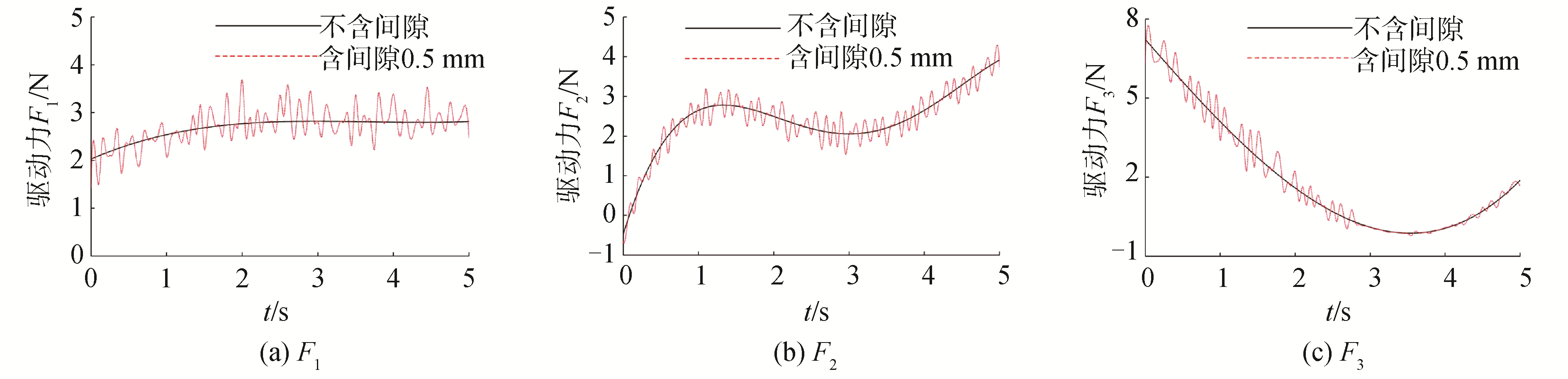
图 5、6为模型的求解结果,由图可得,当构件铰接Ai处为理想运动副时,该处的驱动力Fi为光滑曲线,且不产生波动。当考虑间隙的存在时,Fi开始产生不同幅值的震荡,这说明当机构运行时,间隙的存在使Ai处有碰撞产生,且随着间隙量的增大而愈加剧烈,降低系统稳定性,缩短构件的使用寿命。
|
Download:
|
| 图 5 间隙cr=ca=0.25 mm时,关节Ai处外力Fi曲线 Fig. 5 The forces of the Ai joint with clearance when cr=ca=0.25 mm | |
|
Download:
|
| 图 6 间隙cr=ca=0.5 mm时,关节Ai处外力Fi曲线 Fig. 6 The forces of the Ai joint with clearance when cr=ca=0.5 mm | |
为验证基于含关节间隙转动副模型所建立的支链运动副模型以及考虑关节间隙的并联机构动力学建模的合理性,本文基于ADAMS软件对含关节间隙的3-CPaRR并联机构虚拟样机仿真结果进行原理上的对比分析,以验证该方法的有效性与可参考性。
基于上述对该机构进行仿真验证时,需对间隙关节进行接触定义,在ADAMS软件中有如下2类接触模型:二维接触模型与三维接触模型。其中接触中的法向力模型有回归接触模型和碰撞函数接触模型。其中碰撞函数接触是指ADAMS/Solver运用函数库中Impact函数来计算接触力。对于3-CPaRR并联机构,根据其结构及加工制造时采用的不同材料,定义法向接触力模型参数与库伦摩擦力模型参数,如表 2所示。
| 表 2 ADAMS间隙建模参数 Table 2 ADAMS modeling parameters with clearance |
在进行了含关节间隙的该3自由度并联机构虚拟样机仿真后(定义关节间隙量cr=ca=0.5 mm),取运动副A3处的Z方向的广义驱动力F3作为对照,其广义驱动力变化曲线如图 7所示。

|
Download:
|
| 图 7 含关节间隙转动副A3广义驱动力仿真变化曲线 Fig. 7 ADAMS Simulation curve of generalized driving force of rotating joint A3 with clearance | |
由图 7可知,含关节间隙的3-CPaRR并联机构在运动过程中,含关节间隙的转动副关节元素间的相对运动存在随机性,基于此结论,验证了本文选取概率统计数学模型理论为基点来描述转动副关节元素在其径向与轴向运动规律数学模型的合理性,同时,图 7也可验证前述基于正态分布概率统计模型来计算分析含关节间隙3-CPaRR并联机构的运动学与动力学一定的正确性与合理性。
此外,可见提出的关关节间隙数学模型的分析结果与ADAMS仿真结果存在一定的偏差,经分析其原因有如下2点:1)含关节间隙运动副模型中的法向接触力模型与切向接触力模型与ADAMS软件中的接触力模型不完全一致,这是不可避免的原因;2)建模计算过程中,参考文献[23-24],定义了含关节间隙并联机构的各转动关节的广义坐标与封闭方程求得角θi近似相等;在本文含关节间隙并联机构的动力学方程建模过程中,因考虑机构动力学模型的计算复杂问题,为提高计算效率,进行了部分简化计算。
3 3-CPaRR并联机构控制系统设计本文以滑模控制理论为基础设计其运动控制器。如机构系统有模型参数误差以及间隙等关节效应,这些不确定项的存在均会导致未知扰动W,因此,式(15)可表示为:
| $ \left( {{\mathit{\boldsymbol{M}}_0} + \Delta \mathit{\boldsymbol{M}}} \right)\mathit{\boldsymbol{\ddot q}} + \left( {{\mathit{\boldsymbol{C}}_0} + \Delta \mathit{\boldsymbol{C}}} \right)\mathit{\boldsymbol{\dot q}} + \left( {{\mathit{\boldsymbol{G}}_0} + \Delta \mathit{\boldsymbol{G}}} \right) = \mathit{\boldsymbol{F}} + \mathit{\boldsymbol{W}} $ | (17) |
式中:M0、C0、G0、W0分别为M、C、G、W的名义值;ΔM=M-M0,ΔC=C-C0,ΔG=G-G0,ΔW=W-W0表示为建模误差。该动力学模型式(17)具有如下一些性质:1) M∈R3×3为正定矩阵,且有界;2)Ṁ-2C为反对称矩阵,即存在xT(Ṁ-2C)x=0其中x∈Rn。
由理想多体机构系统动力学方程中的参数不确定项和负载扰动集中起来作为总的不确定项,记为d∈R3×3,表达式为:
| $ \mathit{\boldsymbol{d}} = \Delta \mathit{\boldsymbol{M\ddot q}} + \Delta \mathit{\boldsymbol{C\dot q}} + \Delta \mathit{\boldsymbol{G}} + \Delta \mathit{\boldsymbol{f}} + \mathit{\boldsymbol{W}} $ | (18) |
式中:∣di∣≤bi,bi>0。
常规滑模控制的滑模面定义为:定义qd、
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{F}} = {\mathit{\boldsymbol{u}}_{eq}} - \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}{\rm{sgn}}(\mathit{\boldsymbol{s}})}\\ {{\mathit{\boldsymbol{u}}_{eq}} = {\mathit{\boldsymbol{M}}_0}\left( {{{\mathit{\boldsymbol{\ddot q}}}_d} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} \dot {\tilde q}}}} \right) + {\mathit{\boldsymbol{C}}_0}\left( {{{\mathit{\boldsymbol{\dot q}}}_d} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} \tilde q}}} \right) + {\mathit{\boldsymbol{G}}_0}\mathit{\boldsymbol{q}} - {\mathit{\boldsymbol{W}}_0}} \end{array} $ | (19) |
式中,控制律可分为2个部分:
1) ueq是基于机构系统建立的名义动力学模型,作为控制器前馈控制项,用于在线补偿各个构件的惯性力及运动关节之间的冲击力与摩擦力。
2) -ρsgn(s)是针对d的补偿项,sgn(s)是符号函数,ρ=diag(ρi)是正定切换增益矩阵,当ρi>bi时,系统可趋于稳定。
3.1 自适应滑模控制常规滑模控制律(19)存有以下问题:该并联机构运动过程中关节间隙的影响是复杂多变的,因不确定项的上界b难以准确预估。针对此问题,设计该并联机构的自适应滑模控制器,利用自适应算法进行实时补偿,可省去对不确定项b的不确定估计,提高控制器的准确性与鲁棒性。考虑并联机构的模型参数及外界扰动等不确定项,设定α、β和ε为并联机构物理参数常数。定义并联机构的系统参数为a,a=[α β ε]T,â为a的估计,
由上述可知α、β和ε为未知常数,运动轨迹误差
滑模函数为:
| $ \mathit{\boldsymbol{s}} = \mathit{\boldsymbol{\dot {\tilde q}}} - \mathit{\boldsymbol{ \boldsymbol{\varLambda} \tilde q}} $ | (20) |
设计控制器为:
| $ \mathit{\boldsymbol{F}} = \mathit{\boldsymbol{\hat M}}\left( \mathit{\boldsymbol{q}} \right){{\mathit{\boldsymbol{\ddot q}}}_r} + \mathit{\boldsymbol{\hat C}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}){{\mathit{\boldsymbol{\dot q}}}_r} + \mathit{\boldsymbol{\hat G}}(\mathit{\boldsymbol{q}}) - {\mathit{\boldsymbol{K}}_d}\mathit{\boldsymbol{s}} $ | (21) |
其中:Kd=diag(kd1 kd2 kd3),kd>0,i=1, 2, 3。
由于M为正定矩阵,设计稳定性判定的Lyapunov函数为:
| $ V = \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{Ms}} + \frac{1}{2}{\mathit{\boldsymbol{a}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} a}} $ | (22) |
其中:Γ=diag(γ1 γ2 γ3),γi>0,i=1, 2, 3。
因此,式(22)表示为:
| $ \begin{array}{l} \mathit{\boldsymbol{\dot V}} = \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{M\dot s}} + \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{\dot Ms}} + {{\mathit{\boldsymbol{\tilde a}}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} \dot {\tilde a}}} = \\ \;\;\;\;\;\;{\mathit{\boldsymbol{s}}^{\rm{T}}}\left( {\mathit{\boldsymbol{M\ddot q}} - \mathit{\boldsymbol{M}}{{\mathit{\boldsymbol{\ddot q}}}_r}} \right) + \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{\dot Ms}} + {{\mathit{\boldsymbol{\tilde a}}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} \dot {\tilde a}}} = \\ \;\;\;\;\;\;{\mathit{\boldsymbol{s}}^{\rm{T}}}\left( {\mathit{\boldsymbol{F}} - \mathit{\boldsymbol{C\dot q}} - \mathit{\boldsymbol{G}} - \mathit{\boldsymbol{M}}{{\mathit{\boldsymbol{\ddot q}}}_r}} \right) + \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{\dot Ms}} + {{\mathit{\boldsymbol{\tilde a}}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} \dot {\tilde a}}} = \\ \;\;\;\;\;\;{\mathit{\boldsymbol{s}}^{\rm{T}}}\left( {\mathit{\boldsymbol{F}} - \mathit{\boldsymbol{C}}\left( {\mathit{\boldsymbol{s}} + {{\mathit{\boldsymbol{\dot q}}}_r}} \right) - \mathit{\boldsymbol{G}} - \mathit{\boldsymbol{M}}{{\mathit{\boldsymbol{\ddot q}}}_r}} \right) + \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{\dot Ms}} + {{\mathit{\boldsymbol{\tilde a}}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} \dot {\tilde a}}} \end{array} $ | (23) |
将控制律式(19)代入式(22),可得:
| $ \begin{array}{l} \dot V = {\mathit{\boldsymbol{s}}^{\rm{T}}}\left( {\mathit{\boldsymbol{\hat M}}{{\mathit{\boldsymbol{\ddot q}}}_r} + \mathit{\boldsymbol{\hat C}}{{\mathit{\boldsymbol{\dot q}}}_r} + \mathit{\boldsymbol{\hat G}} - {\mathit{\boldsymbol{K}}_d}\mathit{\boldsymbol{s}} - \mathit{\boldsymbol{C}}\left( {\mathit{\boldsymbol{s}} + {{\mathit{\boldsymbol{\dot q}}}_r}} \right) - \mathit{\boldsymbol{G}} - } \right.\\ \;\;\;\;\;\;\left. {\mathit{\boldsymbol{M}}{{\mathit{\boldsymbol{\ddot q}}}_r}} \right) + \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{\dot Ms}} + {{\mathit{\boldsymbol{\tilde a}}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} \dot {\tilde a}}} = \\ \;\;\;\;\;\;{\mathit{\boldsymbol{s}}^{\rm{T}}}\left( {\mathit{\boldsymbol{\tilde M}}{{\mathit{\boldsymbol{\ddot q}}}_r} + \mathit{\boldsymbol{\tilde C}}{{\mathit{\boldsymbol{\dot q}}}_r} + \mathit{\boldsymbol{G}} - {\mathit{\boldsymbol{K}}_d}\mathit{\boldsymbol{s}} - \mathit{\boldsymbol{Cs}}} \right) + \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{\dot Ms}} + \\ \;\;\;\;\;\;{{\mathit{\boldsymbol{\tilde a}}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} \dot {\tilde a}}} \end{array} $ | (24) |
根据该并联机构动力学方程的线性化特性,有:
| $ \mathit{\boldsymbol{\tilde M}}{{\mathit{\boldsymbol{\ddot q}}}_r} + \mathit{\boldsymbol{\tilde C}}{{\mathit{\boldsymbol{\dot q}}}_r} + \mathit{\boldsymbol{\tilde G}} = \mathit{\boldsymbol{Y}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}},{{\mathit{\boldsymbol{\dot q}}}_r},{{\mathit{\boldsymbol{\ddot q}}}_r}} \right)\mathit{\boldsymbol{\tilde a}} $ | (25) |
| $ \begin{array}{l} \dot V = {\mathit{\boldsymbol{s}}^{\rm{T}}}\left( {\mathit{\boldsymbol{Y\tilde a}} - {\mathit{\boldsymbol{K}}_d}\mathit{\boldsymbol{s}} - \mathit{\boldsymbol{Cs}}} \right) + \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\mathit{\boldsymbol{\dot Ms}} + {{\mathit{\boldsymbol{\tilde a}}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} \dot {\tilde a}}} = \\ \;\;\;\;\;\;{\mathit{\boldsymbol{s}}^{\rm{T}}}\left( {\mathit{\boldsymbol{Y\tilde a}} - {\mathit{\boldsymbol{K}}_d}\mathit{\boldsymbol{s}}} \right) + \frac{1}{2}{\mathit{\boldsymbol{s}}^{\rm{T}}}\left( {\mathit{\boldsymbol{\dot M}} - 2\mathit{\boldsymbol{C}}} \right)\mathit{\boldsymbol{s}} + {{\mathit{\boldsymbol{\tilde a}}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\dot {\tilde a} = \\ \;\;\;\;\;\;{\mathit{\boldsymbol{s}}^{\rm{T}}}\left( {\mathit{\boldsymbol{Y\tilde a}} - {\mathit{\boldsymbol{K}}_d}\mathit{\boldsymbol{s}}} \right) + {{\mathit{\boldsymbol{\tilde a}}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} \dot {\tilde a}}} = \\ \;\;\;\;\;\;{{\mathit{\boldsymbol{\tilde a}}}^{\rm{T}}}\left( {{\mathit{\boldsymbol{Y}}^{\rm{T}}}\mathit{\boldsymbol{s}} + \mathit{\boldsymbol{ \boldsymbol{\varGamma} \dot {\tilde a}}}} \right) - {\mathit{\boldsymbol{s}}^{\rm{T}}}{\mathit{\boldsymbol{K}}_d}\mathit{\boldsymbol{s}} \end{array} $ | (26) |
设计自适应律为:
| $ \mathit{\boldsymbol{\dot {\hat a}}} = - {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{ - 1}}{\mathit{\boldsymbol{Y}}^{\rm{T}}}\mathit{\boldsymbol{s}} $ | (27) |
则
取
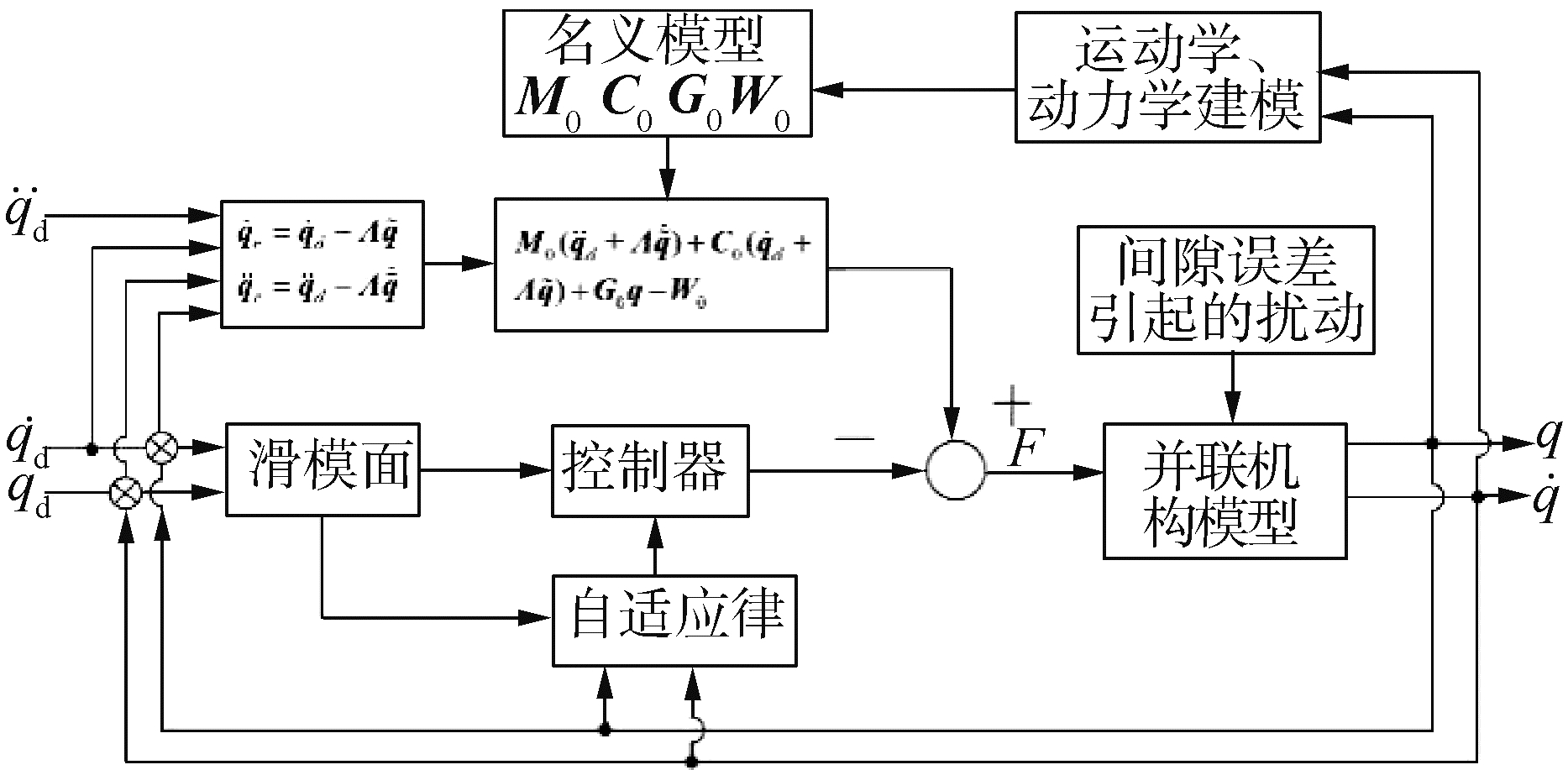
为实现3-CPaRR并联机构的高精度运动控制效果,本节将含关节间隙的转动副引起的并联机构冲击负载定义为外界扰动,基于上文的自适应滑模控制器,对含间隙的该并联机构进行数值仿真,该3自由度并联机构自适应滑模变结构控制的系统框图如图 8所示。
|
Download:
|
| 图 8 自适应滑模变结构控制的系统框图 Fig. 8 System block diagram of adaptive sliding mode variable structure control | |
基于上述,在该机构的自适应滑模控制仿真过程中,其参数取:Λ=diag(5 5 5),Kd=diag(10 10 10),Γ=diag(1 1 1)。为验证误差的收敛性,假设该机构存在初始误差。机构输出端在初始时刻的状态为:q1(0)=q2(0)=q3(0)=1.2 mm,
|
Download:
|
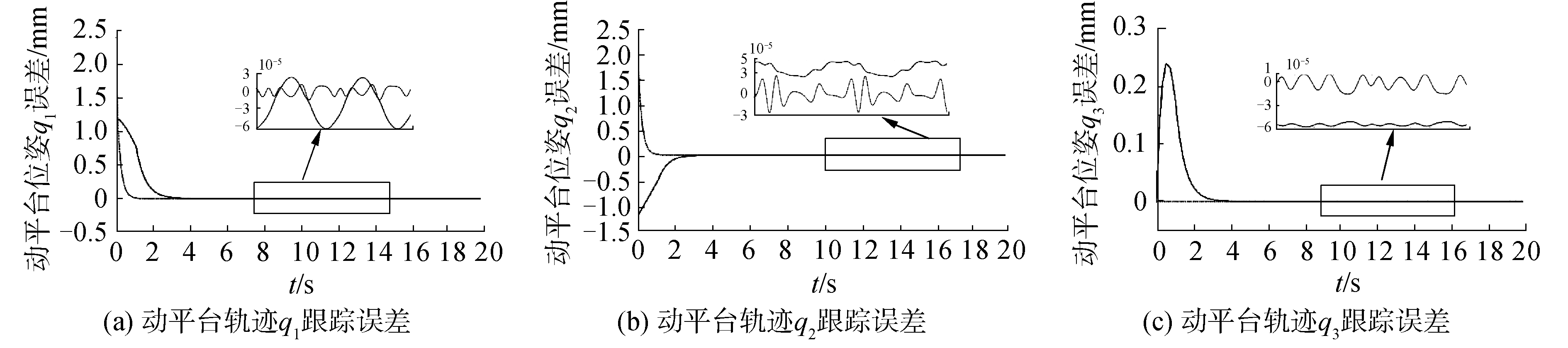
| 图 9 动平台轨迹跟踪误差 Fig. 9 The tracking error of moving platform trajectory | |
为评定控制器的控制效果,引入2项评定指标:平均控制误差AVE和最大控制误差MAX,其中将AVE表示为:
| $ {\rm{AVE}} = \frac{1}{{{t_m}}}\int_0^{{t_m}} {\left| {e\left( t \right)} \right|{\rm{d}}t} $ | (28) |
式中tm表示运行时间。
图 9对比了常规滑模控制和自适应滑模控制下3自由度并联机构动平台正交方向上运动控制误差曲线,尽管机构系统存在初始误差以及时变负载扰动影响,但系统依然可以保证在一定时间内趋近平稳,从而验证了上述的2种控制方法都可以使该并联机构的运动精度误差收敛至稳定值。自适应滑模控制下,动平台轨迹误差能在0.9 s内收敛到稳定状态,收敛的速度明显比前者控制更快。
表 3和表 4分别是2种控制方法的AVE指标和MAX指标的对比。在运动精度达到稳定状态后,采用常规滑模控制q1、q2、q3的平均跟踪误差(10-5 mm)分别为2.72、3.87、5.51,最大控制误差值(10-5 mm)分别为6.00、4.78、5.83,与之相比,采用自适应滑模控制时的误差值(10-5 mm)分别为0.53、1.34、0.67,最大控制误差值(10-5 mm)分别为1.35、2.82、1.72,说明了自适应滑模控制不仅收敛速度快,而且控制精度明显比常规滑模控制更高,对模型不确定性及外界扰动的抑制能力更强。
| 表 3 2种控制方法的平均误差指标对比 Table 3 Comparison of average error index between two control methods |
| 表 4 2种控制方法的最大误差指标对比 Table 4 Comparison of maximum error index between two control methods |
图 9是2种控制方法的机构输出运动轨迹q1、q2、q3的跟踪误差,从中可得该机构输出的运动轨迹虽然有抖振现象但并没有出现奇异性,因此证明自适应滑模控制器较常规滑模控制器的优越性。
如图 9所示,在t=1 s时刻左右,该机构实际输出曲线开始稳定跟踪期望轨迹,这说明该控制器的设计是合理正确的。
4 结论1) 基于正态分布、Flores接触力、Coulomb摩擦模型及非完整Lagrange方程实现了该机构间隙动力学建模与求解,并基于ADAMS软件进行了含间隙模型仿真,验证理论建模可行性。
2) 针对常规滑模变结构控制的抖振与无法准确抑制时变扰动问题,设计了该并联机构自适应滑模运动控制器,控制器省去了对不确定项上界的估计,对系统状态实时补偿,对比仿真计算结果显示提高了系统的鲁棒性。
本文从理论上对3-CPaRR并联机构进行了含间隙动力学建模及自适用滑模控制器的设计,在后续的研究工作中将对该机构的样机展开实验研究,同时考虑润滑、摩擦等因素对该系统相关特性产生的影响。
| [1] |
REIS V L, DANIEL G B, CAVALCA K L. Dynamic analysis of a lubricated planar slider-crank mechanism considering friction and Hertz contact effects[J]. Mechanism and machine theory, 2014, 74: 257-273. DOI:10.1016/j.mechmachtheory.2013.11.009 (  0) 0)
|
| [2] |
BOVET C, ZAMPONI L. An approach for predicting the internal behaviour of ball bearings under high moment load[J]. Mechanism and machine theory, 2016, 101: 1-22. DOI:10.1016/j.mechmachtheory.2016.03.002 (  0) 0)
|
| [3] |
QUENTAL C, FOLGADO J, AMBRÓSIO J, et al. A new shoulder model with a biologically inspired glenohumeral joint[J]. Medical engineering & physics, 2016, 38(9): 969-977. (  0) 0)
|
| [4] |
FRISOLI A, SOLAZZI M, PELLEGRINETTI D, et al. A new screw theory method for the estimation of position accuracy in spatial parallel manipulators with revolute joint clearances[J]. Mechanism and machine theory, 2011, 46(12): 1929-1949. DOI:10.1016/j.mechmachtheory.2011.07.004 (  0) 0)
|
| [5] |
CHEN Genliang, WANG Hao, LIN Zhongqin. A unified approach to the accuracy analysis of planar parallel manipulators both with input uncertainties and joint clearance[J]. Mechanism and machine theory, 2013, 64: 1-17. DOI:10.1016/j.mechmachtheory.2013.01.005 (  0) 0)
|
| [6] |
ZHAO Haiyang, XU Minqiang, WANG Jindong, et al. A parameters optimization method for planar joint clearance model and its application for dynamics simulation of reciprocating compressor[J]. Journal of sound and vibration, 2015, 344: 416-433. DOI:10.1016/j.jsv.2015.01.044 (  0) 0)
|
| [7] |
PEREIRA C, RAMALHO A, AMBROSIO J. Applicability domain of internal cylindrical contact force models[J]. Mechanism and machine theory, 2014, 78: 141-157. DOI:10.1016/j.mechmachtheory.2014.03.010 (  0) 0)
|
| [8] |
ERKAYA S. Prediction of vibration characteristics of a planar mechanism having imperfect joints using neural network[J]. Journal of mechanical science and technology, 2012, 26(5): 1419-1430. DOI:10.1007/s12206-012-0308-8 (  0) 0)
|
| [9] |
侯雨雷, 汪毅, 井国宁, 等. 含间隙RU-RPR解耦并联机构混沌与冲击现象[J]. 振动与冲击, 2017, 36(1): 215-222, 239. HOU Yulei, WANG Yi, JING Guoning, et al. Chaos and impact phenomena of a RU-RPR decoupled parallel mechanism containing clearance[J]. Journal of vibration and shock, 2017, 36(1): 215-222, 239. (  0) 0)
|
| [10] |
ZHAO Bo, ZHANG Zhinan, FANG Congcong, et al. Modeling and analysis of planar multibody system with mixed lubricated revolute joint[J]. Tribology international, 2016, 98: 229-241. DOI:10.1016/j.triboint.2016.02.024 (  0) 0)
|
| [11] |
ZHAO Bo, ZHOU Kun, XIE Youbai. A new numerical method for planar multibody system with mixed lubricated revolute joint[J]. International journal of mechanical sciences, 2016, 113: 105-119. DOI:10.1016/j.ijmecsci.2016.04.016 (  0) 0)
|
| [12] |
KOSHY C S, FLORES P, LANKARANI H M. Study of the effect of contact force model on the dynamic response of mechanical systems with dry clearance joints:computational and experimental approaches[J]. Nonlinear dynamics, 2013, 73(1/2): 325-338. (  0) 0)
|
| [13] |
BAI Zhengfeng, ZHAO Yang, CHEN Jun. Dynamics analysis of dual-axis positioning mechanism of satellite antenna with joint clearance[J]. Multidiscipline modeling in materials and structures, 2014, 10(1): 59-74. (  0) 0)
|
| [14] |
BAI Zhengfeng, LIU Yuqiang, SUN Yi. Investigation on dynamic responses of dual-axis positioning mechanism for satellite antenna considering joint clearance[J]. Journal of mechanical science and technology, 2015, 29(2): 453-460. DOI:10.1007/s12206-015-0105-2 (  0) 0)
|
| [15] |
MARQUES F, ISAAC F, DOURADO N, et al. An enhanced formulation to model spatial revolute joints with radial and axial clearances[J]. Mechanism and machine theory, 2017, 116: 123-144. DOI:10.1016/j.mechmachtheory.2017.05.020 (  0) 0)
|
| [16] |
SKRINJA L, SLAVIČ J, BOLTEŽAR M. A validated model for a pin-slot clearance joint[J]. Nonlinear dynamics, 2017, 88(1): 131-143. (  0) 0)
|
| [17] |
LI Y, WANG Yong. Sliding mode variable structure control of a redundantly actuated parallel robot[J]. Materials science forum, 2009, 626-627: 465-470. DOI:10.4028/www.scientific.net/MSF.626-627.465 (  0) 0)
|
| [18] |
MOHSEN J F, AKBARZADEH-T M R, AKBARZADEH A, et al. A dynamic-growing fuzzy-neuro controller, application to a 3PSP parallel robot[C]//Proceedings of 2012 IEEE International Conference on Fuzzy Systems. Brisbane, QLD, Australia, 2012: 1-6.
(  0) 0)
|
| [19] |
NIU Xuemei, GAO Guoqin, LIU Xinjun, et al. Dynamics and control of a novel 3-DOF parallel manipulator with actuation redundancy[J]. International journal of automation and computing, 2013, 10(6): 552-562. DOI:10.1007/s11633-013-0753-6 (  0) 0)
|
| [20] |
YU W S, WENG C C. H∞ tracking adaptive fuzzy integral sliding mode control for parallel manipulators[J]. Fuzzy sets and systems, 2014, 248: 1-38. DOI:10.1016/j.fss.2013.09.008 (  0) 0)
|
| [21] |
朱景原, 王见, 丁泽华, 等. 3-CPaRR并联机构的动力学分析及滑模控制[J]. 机械传动, 2018, 42(6): 68-75. ZHU Jingyuan, WANG Jian, DING Zehua, et al. Dynamics analysis and sliding mode control of 3-CPaRR parallel mechanism[J]. Journal of mechanical transmission, 2018, 42(6): 68-75. (  0) 0)
|
| [22] |
朱景原, 王见, 丁泽华, 等. 含关节间隙的3-CPaRR并联机构的运动学和动力学分析[J]. 振动与冲击, 2018, 37(18): 9-17, 29. ZHU Jingyuan, WANG Jian, DING Zehua, et al. Kinematics and dynamics analysis of a 3-CPaRR parallel mechanism with joint clearance[J]. Journal of vibration and shock, 2018, 37(18): 9-17, 29. (  0) 0)
|
| [23] |
王庚祥, 刘宏昭, 邓培生. 考虑球面副间隙的并联机构动力学模型[J]. 振动与冲击, 2014, 33(10): 43-49. WANG Gengxiang, LIU Hongzhao, DENG Peisheng. Dynamic modeling for a parallel mechanism considering spherical joint clearance[J]. Journal of vibration and shock, 2014, 33(10): 43-49. (  0) 0)
|
| [24] |
王庚祥, 刘宏昭. 考虑球面副间隙的4-SPS/CU并联机构动力学分析[J]. 机械工程学报, 2015, 51(1): 43-51. WANG Gengxiang, LIU Hongzhao. Dynamics analysis of 4-SPS/CU parallel mechanism with spherical joint clearance[J]. Journal of mechanical engineering, 2015, 51(1): 43-51. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


