2. 东北大学 航空动力装备振动及控制教育部重点实验室, 辽宁 沈阳 110819
2. Key Laboratory of Vibration and Control of Aero-Propulsion Systems Ministry of Education of China, Northeastern University, Shenyang 110819, China
带粘弹性层的纤维增强复合材料是近年来出现的一种新型复合材料,由粘弹性层和纤维树脂层交替粘接而成,具有重量轻、减振降噪能力强、抗冲击性能好等一系列优点[1]。目前,该类型复合材料制成的薄板结构件广泛应用于航空、航天、船舶、国防等领域[2-3]。
固有特性是深入研究结构系统振动特性的基础,掌握复合材料结构系统的固有特性对于动力学性能预测和动态优化设计都具有十分重要的作用[4]。近年,带粘弹性层的纤维增强复合材料薄板的固有特性有了很多进展。Johnson等[5]使用MSC/NASTRAN有限元软件,计算了三明治结构的固有频率,但求解缺少详实过程,也未进行实验验证。Fujimoto等[6]对粘弹性聚乙烯与碳纤维材料交替排布的复合材料梁的固有频率进行了计算和测试。Cupia等[7]计算了带粘弹性层的三层复合薄板在简支边界条件下的固有频率和损耗因子。Nayak等[8]应用高阶剪切变形理论计算了聚氯乙烯芯层的三明治复合薄板的固有特性但仅得到了无量纲固有频率。Wang等[9]应用哈密顿原理在四边简支边界条件下推导并计算获得了蜂窝芯夹层板的固有频率和振型。Araújo等[10]研究了具有频率依赖性的核心层为粘弹性材料的三明治薄板的固有特性问题,但仅在简支边界下计算获得了固有频率。胡明勇等[11]基于Reddy分层理论推导出四边简支边界条件下纤维/粘弹性层合板的动力学方程,并分析了固有频率的影响因素。Xiaohui等[12]提出了一种改进的zig-zag理论,该方法克服了软芯层(soft-core)三明治层合板应用高阶剪切变形理论预测固有频率过大的问题。杨坤等[13]利用Kelvin粘弹性本构模型,求解了四边简支边界条件下结构的固有频率等振动特性。赵晓春等[14]在简支边界条件下,使用ANSYS有限元软件求解了带有粘弹性橡胶芯层的三明治铝板的各阶固有频率及损耗因子。姜东等[15]提出了一种蜂窝夹层复合三明治薄板的等效模拟方法,并获得了自由边界条件下固有频率的数值计算结果。虽然人们对带粘弹性层的纤维增强复合薄板的固有特性问题开展了一定程度的研究,但上述研究绝大部分针对理想的边界条件,尚未发现在悬臂边界条件下开展研究的文献报道。为此,本文针对上述问题,基于正交多项式法[16]来表示振型函数,并通过Ritz法对带粘弹性层的纤维增强复合薄板的固有频率进行求解和计算,并通过实验验证了上述分析方法的正确性。
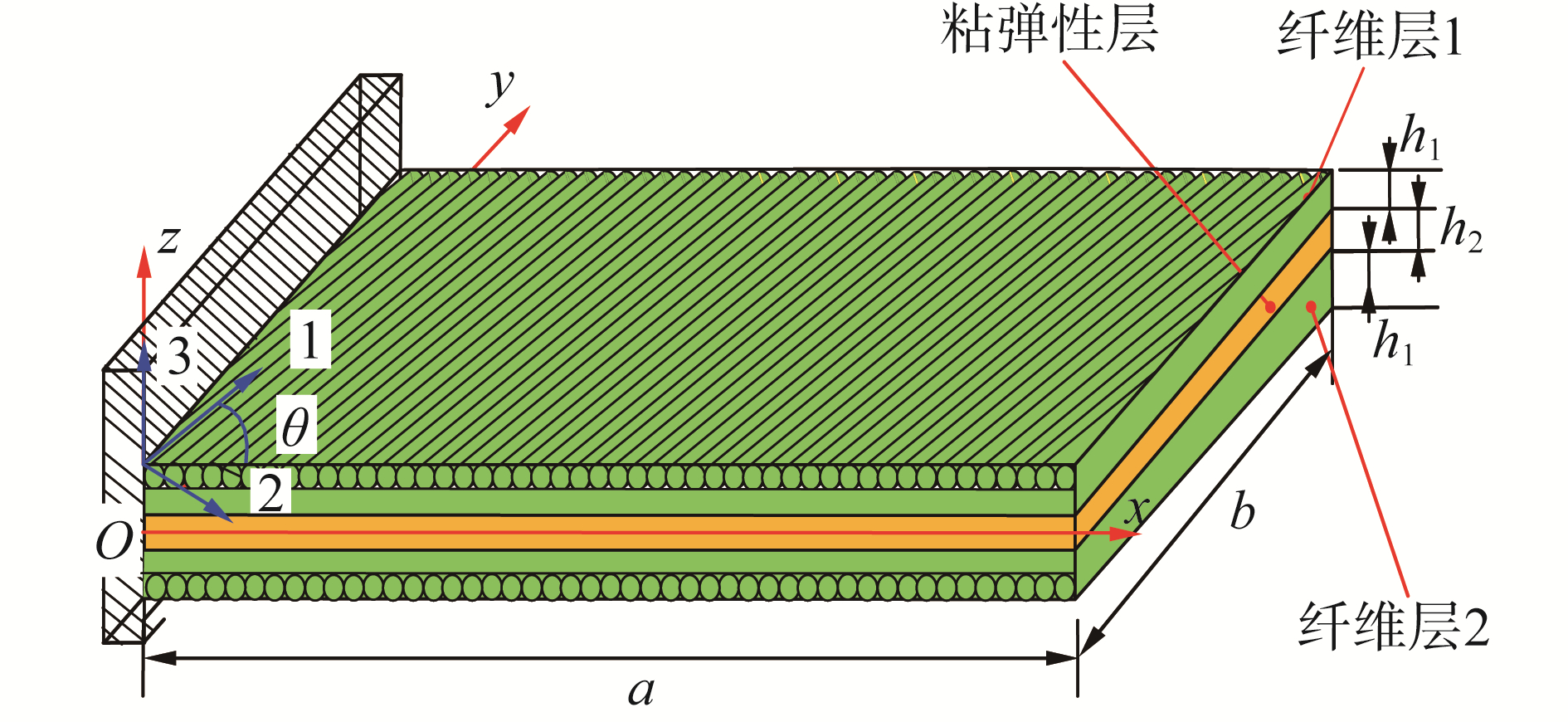
1 固有特性理论求解模型建立本文所研究的带粘弹性层的纤维增强复合薄板理论模型如图 1所示。其上、下两层是由n层具有正交各向异性的纤维与基体组合铺设而成,粘弹性层则处于其芯层位置。首先,将粘弹性层的中面设置为参考平面,并建立xoy坐标系,并假设复合板长度为a,宽度为b,纤维层厚度为h1,粘弹性层厚度为h2,总厚度h=2h1+h2。另外,假设其处于一端约束的悬臂边界条件下,且在纤维层中,总的铺层数为n,各铺层厚度均为h1/n,纤维纵向与x方向的夹角为θ。
|
Download:
|
| 图 1 带粘弹性层的纤维增强复合薄板的理论模型 Fig. 1 Theoretical model of fiber-reinforced composite thin plate with viscoelastic layer under cantilever boundary | |
由于所建立的模型为对称结构,故不存在弯曲和拉伸的耦合关系,根据小挠度薄板理论,其沿着x、y、z方向的位移分量u、v、w可表示为:
| $ \left\{ \begin{array}{l} u(x,y,z,t) = {u_0}(x,y,t) - z\frac{{\partial {w_0}(x,y,t)}}{{\partial x}}\\ v(x,y,z,t) = {v_0}(x,y,t) - z\frac{{\partial {w_0}(x,y,t)}}{{\partial y}}\\ w(x,y,z,t) = {w_0}(x,y,t) \end{array} \right. $ | (1) |
式中:u0、v0、w0分别表示薄板中面位移;t代表时间。
基于经典薄板理论,带粘弹性层的纤维增强复合薄板任意一点的应变可用位移表示为:
| $ \left\{ \begin{array}{l} {\varepsilon _x} = \frac{{\partial u}}{{\partial x}} = \frac{{\partial {u_0}}}{{\partial x}} - z\frac{{{\partial ^2}{w_0}}}{{\partial {x^2}}}\\ {\varepsilon _y} = \frac{{\partial v}}{{\partial y}} = \frac{{\partial {v_0}}}{{\partial y}} - z\frac{{{\partial ^2}{w_0}}}{{\partial {y^2}}}\\ {\gamma _{xy}} = \frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}} = \frac{{\partial {u_0}}}{{\partial y}} + \frac{{\partial {v_0}}}{{\partial x}} - 2z\frac{{{\partial ^2}{w_0}}}{{\partial x\partial y}}\\ {\varepsilon _z} = {\gamma _{yz}} = {\gamma _{xz}} = 0 \end{array} \right. $ | (2) |
式中:εx、εy、εz和γyz、γxz、γxy分别代表x、y和z方向的线应变与剪应变。εx、εy、εz代表x、y和z方向的线应变,γyz、γxz、γxy代表x、y和z方向的剪应变。
所以,其应力-应变关系的表达式为:
| $ \left[ {\begin{array}{*{20}{l}} {{\sigma _x}}\\ {{\sigma _y}}\\ {{\sigma _{xy}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{Q_{11}}}&{{Q_{12}}}&0\\ {{Q_{21}}}&{{Q_{22}}}&0\\ 0&0&{{Q_{66}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\varepsilon _x}}\\ {{\varepsilon _y}}\\ {{\gamma _{xy}}} \end{array}} \right] $ | (3) |
对于复合材料层,式中的各个元素见文献[2]。
对于粘弹性层,式中的各个元素可表示为:
| $ {Q_{11}} = {Q_{22}} = \frac{{{E_2}}}{{1 - v_2^2}},\;\;\;\;{Q_{12}} = {Q_{21}} = \frac{{{v_{12}}{E_2}}}{{1 - v_2^2}}, $ |
| $ {Q_{66}} = \frac{{{E_2}}}{{2\left( {1 + {v_2}} \right)}} $ |
式中:E2和υ1为粘弹性材料的弹性模量和泊松比;E11、E12和G12分别为纤维层中沿着纤维纵向、横向和剪切方向的弹性模量;υ12和υ21分别为相应的泊松比。
在纤维层中,如图 1所示,纤维方向与x轴的夹角为θ,利用转轴公式将应力-应变的关系推导为:
| $ {\left[ {\begin{array}{*{20}{l}} {{\sigma _x}}\\ {{\sigma _y}}\\ {{\sigma _{xy}}} \end{array}} \right]^{\left( k \right)}} = \left[ {\begin{array}{*{20}{c}} {{{\bar Q}_{11}}}&{{{\bar Q}_{12}}}&{{{\bar Q}_{16}}}\\ {{{\bar Q}_{21}}}&{{{\bar Q}_{22}}}&{{{\bar Q}_{26}}}\\ {{{\bar Q}_{16}}}&{{{\bar Q}_{26}}}&{{{\bar Q}_{66}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\varepsilon _x}}\\ {{\varepsilon _y}}\\ {{\gamma _{xy}}} \end{array}} \right] $ | (4) |
式中偏轴刚度矩阵元素见文献[2]。
在粘弹性层中,考虑剪切变形在xz和yz方向产生的应变能,将切应力τxz和τyz表示为:
| $ \frac{{\partial {\tau _{xz}}}}{{\partial z}} = - \frac{{\partial {\sigma _x}}}{{\partial x}} - \frac{{\partial {\tau _{xy}}}}{{\partial y}} $ | (5) |
| $ \frac{{\partial {\tau _{yz}}}}{{\partial z}} = - \frac{{\partial {\tau _{xy}}}}{{\partial x}} - \frac{{\partial {\sigma _y}}}{{\partial y}} $ | (6) |
其中:
| $ \left\{ \begin{array}{l} {\sigma _x} = - z\left( {{Q_{11}}\frac{{{\partial ^2}{w_0}}}{{\partial {x^2}}} + 2{Q_{12}}\frac{{{\partial ^2}{w_0}}}{{\partial {y^2}}}} \right)\\ {\sigma _y} = - z\left( {{Q_{12}}\frac{{{\partial ^2}{w_0}}}{{\partial {x^2}}} + 2{Q_{22}}\frac{{{\partial ^2}{w_0}}}{{\partial {y^2}}}} \right)\\ {\tau _{xy}} = - 2z{Q_{66}}\frac{{{\partial ^2}{w_0}}}{{\partial x\partial y}} \end{array} \right. $ | (7) |
将式(7)代入式(5)、(6),运用切应力边界条件:
| $ {\left. {{\tau _{xz}}} \right|_{z = \pm \frac{h}{2}}} = 0 $ | (8) |
| $ {\left. {{\tau _{yz}}} \right|_{z = \pm \frac{h}{2}}} = 0 $ | (9) |
可以求出切应力τxz和τyz:
| $ {\tau _{xz}} = \frac{1}{2}{A_{xz}}(x,y)\left( {{z^2} - \frac{{{h^2}}}{4}} \right), - \frac{h}{2} \le z \le \frac{h}{2} $ | (10) |
| $ {\tau _{yz}} = \frac{1}{2}{A_{yz}}(x,y)\left( {{z^2} - \frac{{{h^2}}}{4}} \right), - \frac{h}{2} \le z \le \frac{h}{2} $ | (11) |
其中:
| $ {A_{xz}}(x,y) = {Q_{11}}\frac{{{\partial ^3}{w_0}}}{{\partial {x^3}}} + \left( {{Q_{12}} + 2{Q_{66}}} \right)\frac{{{\partial ^2}{w_0}}}{{\partial x\partial {y^2}}} $ | (12) |
| $ {A_{yz}}(x,y) = \left( {{Q_{12}} + 2{Q_{66}}} \right)\frac{{{\partial ^2}{w_0}}}{{\partial {x^2}\partial y}} + {Q_{22}}\frac{{{\partial ^3}{w_0}}}{{\partial {y^3}}} $ | (13) |
在薄板的弯曲振动中,所建立模型的纤维层的动能和应变能可分别表示为:
| $ \left\{ \begin{array}{l} {E_{{\rm{k}}1}} = \frac{1}{2}\int_A {\int_{{h_2}/2}^{h/2} {{\rho _1}} } \left[ {{{\left( {\frac{{\partial u}}{{\partial t}}} \right)}^2} + {{\left( {\frac{{\partial v}}{{\partial t}}} \right)}^2} + {{\left( {\frac{{\partial w}}{{\partial t}}} \right)}^2}} \right]{\rm{d}}z{\rm{d}}A\\ {U_{{\rm{s1}}}} = \frac{1}{2}\int_A {\int_{{h_2}/2}^{h/2} {\left( {{\sigma _x}{\varepsilon _x} + {\sigma _y}{\varepsilon _y} + {\sigma _z}{\varepsilon _z}} \right){\rm{d}}z{\rm{d}}A} } \\ {E_{{\rm{k}}3}} = \frac{1}{2}\int_A {\int_{ - h/2}^{ - {h_2}/2} {{\rho _1}} } \left[ {{{\left( {\frac{{\partial u}}{{\partial t}}} \right)}^2} + {{\left( {\frac{{\partial v}}{{\partial t}}} \right)}^2} + {{\left( {\frac{{\partial w}}{{\partial t}}} \right)}^2}} \right]{\rm{d}}z{\rm{d}}A\\ {U_{{\rm{s}}3}} = \frac{1}{2}\int_A {\int_{ - h/2}^{ - {h_2}/2} {\left( {{\sigma _x}{\varepsilon _x} + {\sigma _y}{\varepsilon _y} + {\sigma _z}{\varepsilon _z}} \right){\rm{d}}z{\rm{d}}A} } \end{array} \right. $ | (14) |
粘弹性层的动能和应变能可分别表示为:
| $ \left\{ \begin{array}{l} {E_{{\rm{k}}2}} = \frac{1}{2}\int_A {\int_{ - {h_2}/2}^{{h_2}/2} {{\rho _2}} } \left[ {{{\left( {\frac{{\partial u}}{{\partial t}}} \right)}^2} + {{\left( {\frac{{\partial v}}{{\partial t}}} \right)}^2} + {{\left( {\frac{{\partial w}}{{\partial t}}} \right)}^2}} \right]{\rm{d}}z{\rm{d}}A\\ {U_{{\rm{s}}2}} = \frac{1}{2}\int_A {\mathop \smallint \nolimits_{ - {h_2}/2}^{{h_2}/2} } \cdot \\ \;\;\;\;\;\;\;\;\left( {{\sigma _x}{\varepsilon _x} + {\sigma _y}{\varepsilon _y} + {\sigma _z}{\varepsilon _z} + \frac{{{{\left( {{\tau _{xz}}} \right)}^2}}}{{2G}} + \frac{{{{\left( {{\tau _{yz}}} \right)}^2}}}{{2G}}} \right){\rm{d}}z{\rm{d}}A \end{array} \right. $ | (15) |
式中:ρ1和ρ2分别代表纤维层和粘弹性层的密度;A代表薄板的面积。
将式(1)、(2)代入式(14)、(15),再将式(4)代入式(14),并且将式(3)、(10)和(11)代入式(15)中,可获得纤维层和粘弹性层的动能和应变能通过中面位移w0的表达式:
| $ \begin{array}{l} {E_{{\rm{k}}1}} = \frac{1}{2}\int_A {\int_{{h_2}/2}^{h/2} {{\rho _1}} } \left[ {{z^2}{{\left( {\frac{{{\partial ^2}{w_0}}}{{\partial x\partial t}}} \right)}^2} + {z^2}{{\left( {\frac{{{\partial ^2}{w_0}}}{{\partial y\partial t}}} \right)}^2} + } \right.\\ \;\;\;\;\;\;\;\left. {{{\left( {\frac{{{\partial ^2}{w_0}}}{{\partial t}}} \right)}^2}} \right]{\rm{d}}z{\rm{d}}A \end{array} $ |
| $ \begin{array}{l} {E_{{\rm{k}}2}} = \frac{1}{2}\int_A {\int_{ - {h_2}/2}^{{h_2}/2} {{\rho _2}} } \left[ {{z^2}{{\left( {\frac{{{\partial ^2}{w_0}}}{{\partial x\partial t}}} \right)}^2} + {z^2}{{\left( {\frac{{{\partial ^2}{w_0}}}{{\partial y\partial t}}} \right)}^2} + } \right.\\ \;\;\;\;\;\;\;\left. {{{\left( {\frac{{{\partial ^2}{w_0}}}{{\partial t}}} \right)}^2}} \right]{\rm{d}}z{\rm{d}}A \end{array} $ |
| $ \begin{array}{l} {E_{{\rm{k}}3}} = \frac{1}{2}\int_A {\int_{ - h/2}^{ - {h_2}/2} {{\rho _1}} } \left[ {{z^2}{{\left( {\frac{{{\partial ^2}{w_0}}}{{\partial x\partial t}}} \right)}^2} + {z^2}{{\left( {\frac{{{\partial ^2}{w_0}}}{{\partial y\partial t}}} \right)}^2} + } \right.\\ \;\;\;\;\;\;\;\;\left. {{{\left( {\frac{{{\partial ^2}{w_0}}}{{\partial t}}} \right)}^2}} \right]{\rm{d}}z{\rm{d}}A \end{array} $ |
| $ \begin{array}{l} {U_{{\rm{s1}}}} = \frac{1}{2}\int_A {\int_{{h_2}/2}^{h/2} {{z^2}} } \left[ {{{\bar Q}_{11}}{{\left( {\frac{{{\partial ^2}{w_0}}}{{\partial {x^2}}}} \right)}^2} + 2{{\bar Q}_{12}}\frac{{{\partial ^2}{w_0}}}{{\partial {x^2}}}\frac{{{\partial ^2}{w_0}}}{{\partial {y^2}}} + } \right.\\ \;\;\;\;\;\;\;\;4{{\bar Q}_{16}}\frac{{{\partial ^2}{w_0}}}{{\partial {x^2}}}\frac{{{\partial ^2}{w_0}}}{{\partial x\partial y}} + {{\bar Q}_{22}}{\left( {\frac{{{\partial ^2}{w_0}}}{{\partial {y^2}}}} \right)^2} + \\ \left. {\;\;\;\;\;\;\;\;4{{\bar Q}_{26}}\frac{{{\partial ^2}{w_0}}}{{\partial {y^2}}}\frac{{{\partial ^2}{w_0}}}{{\partial x\partial y}} + 4{{\bar Q}_{66}}{{\left( {\frac{{{\partial ^2}{w_0}}}{{\partial x\partial y}}} \right)}^2}} \right]{\rm{d}}z{\rm{d}}A \end{array} $ |
| $ \begin{array}{l} {U_{{\rm{s}}2}} = \frac{1}{2}\int_A {\int_{ - {h_2}/2}^{h/2} {\left[ {{z^2}\left( {{Q_{11}}{{\left( {\frac{{{\partial ^2}{w_0}}}{{\partial {x^2}}}} \right)}^2} + 2{Q_{12}}\frac{{{\partial ^2}{w_0}}}{{\partial {x^2}}}\frac{{{\partial ^2}{w_0}}}{{\partial {y^2}}} + } \right.} \right.} } \\ \;\;\;\;\;\;\;\;4{Q_{16}}\frac{{{\partial ^2}{w_0}}}{{\partial {x^2}}}\frac{{{\partial ^2}{w_0}}}{{\partial x\partial y}} + {Q_{22}}{\left( {\frac{{{\partial ^2}{w_0}}}{{\partial {y^2}}}} \right)^2} + \\ \;\;\;\;\;\;\;\;\left. {4{Q_{26}}\frac{{{\partial ^2}{w_0}}}{{\partial {y^2}}}\frac{{{\partial ^2}{w_0}}}{{\partial x\partial y}} + 4{Q_{66}}{{\left( {\frac{{{\partial ^2}{w_0}}}{{\partial x\partial y}}} \right)}^2}} \right) + \\ \;\;\;\;\;\;\;\;\frac{1}{{4G}}\left( {\left( {{Q_{11}}\frac{{{\partial ^3}{w_0}}}{{\partial {x^3}}} + \left( {{Q_{12}} + 2{Q_{66}}} \right)\frac{{{\partial ^2}{w_0}}}{{\partial x\partial {y^2}}}} \right) \cdot } \right.\\ \;\;\;\;\;\;\;\;\;{\left. {\left( {{z^2} - \frac{{{h^2}}}{4}} \right)} \right)^2} + \left( {\left( {\left( {{Q_{12}} + 2{Q_{66}}} \right)\frac{{{\partial ^2}{w_0}}}{{\partial {x^2}\partial y}} + } \right.} \right.\\ \;\;\;\;\;\;\;\;\;\left. {{{\left. {\left. {{Q_{22}}\frac{{{\partial ^3}{w_0}}}{{\partial {y^3}}}} \right)\left( {{z^2} - \frac{{{h^2}}}{4}} \right)} \right)}^2}} \right]{\rm{d}}z{\rm{d}}A \end{array} $ |
| $ \begin{array}{l} {U_{{\rm{s}}3}} = \frac{1}{2}\int_A {\int_{ - h/2}^{ - {h_2}/2} {{z^2}} } \left[ {{{\bar Q}_{11}}{{\left( {\frac{{{\partial ^2}{w_0}}}{{\partial {x^2}}}} \right)}^2} + 2{{\bar Q}_{12}}\frac{{{\partial ^2}{w_0}}}{{\partial {x^2}}}\frac{{{\partial ^2}{w_0}}}{{\partial {y^2}}} + } \right.\\ \;\;\;\;\;\;\;\;\;4{{\bar Q}_{16}}\frac{{{\partial ^2}{w_0}}}{{\partial {x^2}}}\frac{{{\partial ^2}{w_0}}}{{\partial x\partial y}} + {{\bar Q}_{22}}{\left( {\frac{{{\partial ^2}{w_0}}}{{\partial {y^2}}}} \right)^2} + \\ \;\;\;\;\;\;\;\;\;\left. {4{{\bar Q}_{26}}\frac{{{\partial ^2}{w_0}}}{{\partial {y^2}}}\frac{{{\partial ^2}{w_0}}}{{\partial x\partial y}} + 4{{\bar Q}_{66}}{{\left( {\frac{{{\partial ^2}{w_0}}}{{\partial x\partial y}}} \right)}^2}} \right]{\rm{d}}z{\rm{d}}A \end{array} $ |
将各层的动能和应变能相加,可获得总的动能和应变能为:
| $ \left\{ {\begin{array}{*{20}{l}} {{E_k} = {E_{k1}} + {E_{k2}} + {E_{k3}}}\\ {{U_s} = {U_{s1}} + {U_{s2}} + {U_{s3}}} \end{array}} \right. $ | (16) |
根据正交多项式法,可将中面位移表示成为:
| $ {w_0} = \sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{A_{mn}}{P_m}(\xi ){P_n}(\eta )\sin (\omega t)} } $ | (17) |
式中:M和N为Ritz法求解时的截断系数;Amn为待定Ritz参数;ω为角固有频率;Pm(ξ)和Pn(η)为正交特征多项式。其具体的表达式为:
| $ \left\{ {\begin{array}{*{20}{l}} {{P_1}(\xi ) = \varphi (\xi ),{P_1}(\eta ) = \varphi (\eta )}\\ {{P_2}(\zeta ) = \left( {\zeta - {B_2}} \right){P_1}(\zeta ),\quad \zeta = \xi ,\eta ,k > 2}\\ {{P_k}(\zeta ) = \left( {\zeta - {B_k}} \right){P_{k - 1}}(\zeta ) - {C_k}{P_{k - 2}}(\zeta )} \end{array}} \right. $ | (18) |
式中:Bk和Ck为系数参数;ϕ(ξ)和φ(η)为确定边界条件的多项式函数,它们的表达式为:
| $ {B_k} = \frac{{\int_0^1 W (\zeta ){{\left[ {{P_{k - 1}}(\zeta )} \right]}^2}\zeta {\rm{d}}\zeta }}{{\int_0^1 W (\zeta ){{\left[ {{P_{k - 1}}(\zeta )} \right]}^2}{\rm{d}}\zeta }} $ |
| $ {C_k} = \frac{{\int_0^1 W (\zeta ){P_{k - 1}}(\zeta ){P_{k - 2}}(\zeta )\zeta {\rm{d}}\zeta }}{{\int_0^1 W (\zeta ){{\left[ {{P_{k - 2}}(\zeta )} \right]}^2}{\rm{d}}\zeta }} $ |
| $ \phi (\xi ) = {\xi ^p}{(1 - \xi )^q},\varphi (\eta ) = {\eta ^r}{(1 - \eta )^s} $ |
| $ \zeta = \xi ,\eta ;\xi = x/a,\eta = y/b $ |
式中:W(ζ)为正交化过程中使用的加权函数,通常取1;p、q、r、s根据自由、简支和固支不同的边界条件分别取值为0,1,2。
将式(17)代入式(16)中,分别令cos(ωt)=1和sin(ωt)=1即可得到含有待定Ritz参数的最大动能Ekmax和Usmax的表达式:
| $ U_k^{\max } = E_{k1}^{\max } + E_{k2}^{\max } + E_{k3}^{\max } $ | (19) |
| $ U_s^{\max } = U_{s1}^{\max } + U_{s2}^{\max } + U_{s3}^{\max } $ | (20) |
能量方程可表示为:
| $ L = E_k^{\max } - U_s^{\max } $ | (21) |
为了求解该类型复合薄板的固有特性,就要求解Ritz参数,令:
| $ \frac{{\partial L}}{{\partial {A_{mn}}}} = 0,m = 1,2, \cdots ,M,n = 1,2, \cdots ,N $ | (22) |
求解能量方程(21)的待定参数的广义特征值问题,可得:
| $ \left( {\mathit{\boldsymbol{K}} - {\omega ^2}\mathit{\boldsymbol{M}}} \right)\mathit{\boldsymbol{q}} = 0 $ | (23) |
式中:K为复合薄板的刚度矩阵,M为其质量矩阵,特征向量q=[A11, A12, …,Amn]T。若使式(23)有解,则特征向量q的系数矩阵行列式为0,即:
| $ {\rm{det}}\left( {\mathit{\boldsymbol{K}} - {\omega ^2}\mathit{\boldsymbol{M}}} \right) = 0 $ | (24) |
求解式(24)即可获得结构的各阶固有频率,其精度由M、N的值确定,M、N的值越大,所获得结果的精度越高。一般令M=8、N=8即可满足计算精度。最后,将所获得各阶固有频率代入式(23)中,可获得Amn的各待定参数,再代入式(17)中,即可获得各阶固有频率对应的模态振型。基于Matlab软件,编写了相应的程序,并给出了固有特性的分析流程图,如图 2所示。

|
Download:
|
| 图 2 固有特性分析流程图 Fig. 2 The analysis flow chart of the inherent characteristic | |
以由TC300碳纤维/YD127树脂基为外层,粘弹性材料ZN33为内层的复合薄板为研究对象。其长、宽、厚分别为270 mm×170 mm×3 mm,纤维层厚度为2 mm,铺层方式为正交铺设,即[(0/90) s],共有16层,上下各有8层,铺层具有相同的厚度和纤维体积分数,纤维纵向和横向弹性模量分别为136 GPa和7.92 GPa,泊松比0.32,密度1 618 kg/m3。粘弹性层的厚度为1 mm,剪切模量5 MPa,泊松比0.49,密度930 kg/m3。
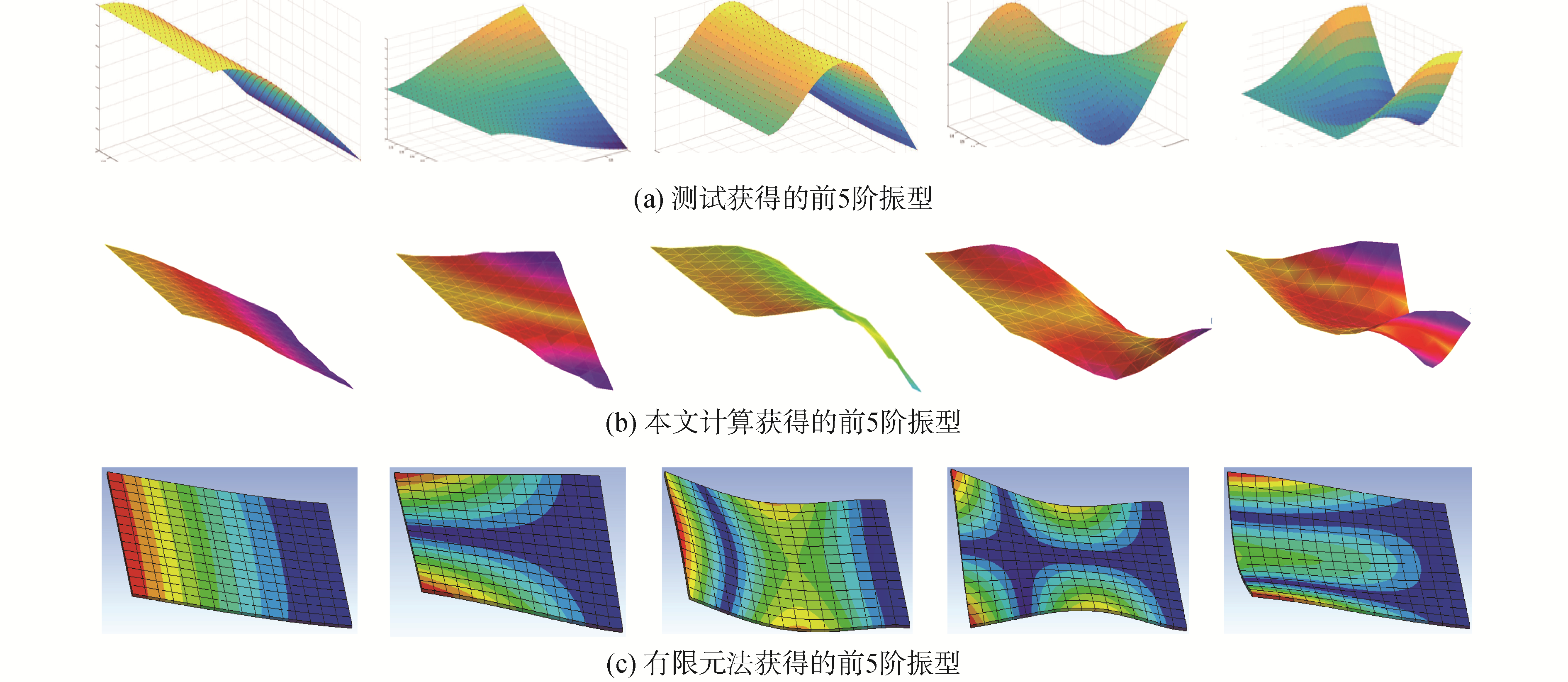
为了验证所提出的固有特性计算方法的正确性,搭建图 3所示的实验系统。首先,通过夹具将带粘弹性层的复合薄板的一边有效夹紧。然后,采用PCB086C01模态力锤对其进行激励,并通过BK-4517轻质加速度传感器来测试其振动响应。设定测试带宽为800 Hz,并在试验中将频率分辨率设定为0.125 Hz。为提高测试精度,分别对激励信号和响应信号添加力指数窗函数和指数窗函数。对激励信号和响应信号使用LMS采集仪进行实时采集,通过辨识实验获得的频响函数可获得前5阶固有频率结果,如表 1所示。然后建立15×7测点的线框模型,采用多点激励单点响应的方式,并通过LMS Testlab软件来辨识获得前5阶模态振型。同时,将通过Matlab程序计算获得的复合薄板固有频率与振型结果分别列入表 1和图 4中,为了便于证明该方法的准确性,将使用文献[5]的有限元方法计算获得复合薄板固有特性也分别列入表 1和图 4,并对两者误差进行了比较。

|
Download:
|
| 图 3 带粘弹性层的纤维增强复合薄板固有特性测试系统 Fig. 3 Test system of inherent characteristic of fiber-reinforced composite thin plate with viscoelastic layer | |
| 表 1 计算和测试获得的带粘弹性层的复合薄板前5阶固有频率和模态振型 Table 1 The first 5 inherent frequencies and modal shapes of composite thin plate with viscoelastic layer obtained by the calculation and experiment |
|
Download:
|
| 图 4 测试、计算和有限元法获得的带粘弹性层的复合薄板前5阶模态振型 Fig. 4 The first 5 modal shapes of composite thin plate with viscoelastic layer obtained by test, calculation and finite element method | |
通过与实验结果进行对比验证可知,利用本文所采用的理论方法,其获得的复合薄板前5阶模态振型,与实验及有限元法获得的模态振型相一致,且固有频率的计算误差处于2.9%~7.3%,与有限元法获得的计算结果也十分接近,进而验证了该计算方法的正确性。但仍有必要对上述误差原因进行分析,首先,在理论误差方面,建模时没有考虑粘弹性层与纤维层的层间应力,纤维层的横向剪切应力、以及复合材料参数分散性的影响;在实验误差方面,传感器附件质量和测试时边界条件也会对实验精度造成影响。
3 结论1) 在考虑粘弹性层剪切变形的基础上,推导了带有粘弹性层的纤维增强薄板的动力学方程,基于正交多项式法获得最大动能和应变能,并最终通过Ritz法计算获得了悬臂边界下的固有频率和振型。
2) 利用本文所采用的理论方法,其获得的复合薄板前5阶模态振型,与实验及有限元法获得的模态振型相一致,且固有频率的计算误差处于2.9%~7.3%,与有限元法获得的计算结果也十分接近,进而验证了该计算方法的正确性。
本文的研究方法可用于高性能飞机机翼的减振降噪预测,具有一定的工程应用前景。
| [1] |
孟光, 瞿叶高. 复合材料结构振动与声学[M]. 北京: 国防工业出版社, 2017: 1-7. MENG Guang, QU Yegao. Vibration and acoustics of composite structures[M]. Beijing: National Defense Industry Press, 2017: 1-7. (  0) 0)
|
| [2] |
沈观林, 胡更开. 复合材料力学[M]. 北京: 清华大学出版社, 2006. SHEN Guanlin, HU Gengkai. Mechanics of composite materials[M]. Beijing: Tsinghua University Press, 2006. (  0) 0)
|
| [3] |
齐红宇, 温卫东, 崔海涛. 含孔复合材料层合板疲劳寿命预测研究[J]. 航空动力学报, 2003, 18(5): 658-661. QI Hongyu, WEN Weidong, CUI Haitao. Fatigue life predication of notched composite material laminates[J]. Journal of aerospace power, 2003, 18(5): 658-661. DOI:10.3969/j.issn.1000-8055.2003.05.015 (  0) 0)
|
| [4] |
WEAVER JR W, TIMOSHENKO S P, YOUNG D H. Vibration problems in engineering[M]. 5th ed. Hoboken: Wiley, 1990.
(  0) 0)
|
| [5] |
JOHNSON C D, KIENHOLZ D A. Finite element prediction of damping in structures with constrained viscoelastic layers[J]. AIAA journal, 1982, 20(9): 1284-1290. DOI:10.2514/3.51190 (  0) 0)
|
| [6] |
FUJIMOTO J, TAMURA T, TODOME K, et al. Mechanical properties for CFRP/damping-material laminates[J]. Journal of reinforced plastics and composites, 1993, 12(7): 738-751. DOI:10.1177/073168449301200701 (  0) 0)
|
| [7] |
CUPIAŁ P, NIZIOŁ J. Vibration and damping analysis of a three-layered composite plate with a viscoelastic mid-layer[J]. Journal of sound and vibration, 1995, 183(1): 99-114. (  0) 0)
|
| [8] |
NAYAK A K, MOY S S J, SHENOI R A. Free vibration analysis of composite sandwich plates based on Reddy's higher-order theory[J]. Composites part B:engineering, 2002, 33(7): 505-519. DOI:10.1016/S1359-8368(02)00035-5 (  0) 0)
|
| [9] |
WANG Tongan, SOKOLINSKY V, RAJARAM S, et al. Consistent higher-order free vibration analysis of composite sandwich plates[J]. Composite structures, 2008, 82(4): 609-621. DOI:10.1016/j.compstruct.2007.02.009 (  0) 0)
|
| [10] |
ARAÚJO A L, SOARES C M M, SOARES C A M, et al. Optimal design and parameter estimation of frequency dependent viscoelastic laminated sandwich composite plates[J]. Composite structures, 2010, 92(9): 2321-2327. DOI:10.1016/j.compstruct.2009.07.006 (  0) 0)
|
| [11] |
胡明勇, 王安稳. 纤维增强粘弹性复合材料层合板的自由振动和应力分析[J]. 工程力学, 2010, 27(8): 10-14, 20. HU Mingyong, WANG Anwen. Free vibration and stresses analysis of fiber-reinforced viscoelastic composite laminated plates[J]. Engineering mechanics, 2010, 27(8): 10-14, 20. (  0) 0)
|
| [12] |
REN Xiaohui, CHEN Wanji. Free vibration analysis of laminated and sandwich plates using quadrilateral element based on an improved zig-zag theory[J]. Journal of composite materials, 2011, 45(21): 2173-2187. DOI:10.1177/0021998311401070 (  0) 0)
|
| [13] |
杨坤, 梅志远, 李华东. 粘弹性复合材料夹芯板稳态响应分析[J]. 振动与冲击, 2013, 32(7): 88-92. YANG Kun, MEI Zhiyuan, LI Huadong. Steady response analysis for a composite sandwich plate with viscoelastic core layer based on Kelvin model[J]. Journal of vibration and shock, 2013, 32(7): 88-92. DOI:10.3969/j.issn.1000-3835.2013.07.018 (  0) 0)
|
| [14] |
赵晓春, 李祥宁, 李凯, 等. 三明治夹层板振动特性与优化[J]. 中国舰船研究, 2013, 8(4): 46-51. ZHAO Xiaochun, LI Xiangning, LI Kai, et al. Analysis and optimization of the vibration characteristics of sandwich plates[J]. Chinese journal of ship research, 2013, 8(4): 46-51. DOI:10.3969/j.issn.1673-3185.2013.04.008 (  0) 0)
|
| [15] |
姜东, 江智远, 费庆国, 等. 考虑胶层的蜂窝夹层复合材料动态特性[J]. 东南大学学报(自然科学版), 2013, 43(5): 1068-1073. JIANG Dong, JIANG Zhiyuan, FEI Qingguo, et al. Dynamic characteristics of honeycomb sandwich composite considering effect of adhesive layer[J]. Journal of Southeast University (natural science edition), 2013, 43(5): 1068-1073. (  0) 0)
|
| [16] |
薛鹏程, 李晖, 常永乐, 等. 悬臂边界下纤维增强复合薄板固有频率计算及验证[J]. 航空动力学报, 2016, 31(7): 1754-1760. XUE Pengcheng, LI Hui, CHANG Yongle, et al. Natural frequency calculation and validation of fiber reinforced composite thin plate under cantilever boundary[J]. Journal of aerospace power, 2016, 31(7): 1754-1760. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


