2. 涝洲灌区管理站, 黑龙江 肇东 151100
2. Irrigation Station of Laozhou, Zhaodong 151100, China
闸门是用于关闭开放泄水通道的重要设施,水工建筑物的重要组成部分,可用于拦截水流、控制水位、调节流量以及排放泥沙和漂浮物等[1]。在寒冷地区结冰期内闸门还可能承受静冰挤压力的作用,静冰挤压力可能会导致闸门变形、破坏等,从而影响闸门的正常使用,静冰挤压力的作用也有可能非常微弱,对闸门安全不构成威胁。我国相关规范[2-3]不允许水工钢制泄洪闸门承受冰载荷的作用,仅建议使用冰盖开槽法、保温板法、电热法等以防止闸门附近结冰,这种规定保守、偏于安全。若冰载荷未对闸门安全造成威胁,则可以考虑允许闸门承受冰载荷作用以更大限度地发挥闸门的承载能力,从而节约运营成本,这就要求准确获取冰载荷分布,并在此基础上分析闸门强度。
寒冷地区结构物的实际冰载荷主要通过现场监测获取,Gong[4]通过应力计和应变计对加拿大七姐妹水电站的木质与钢制叠梁闸门的冰载荷进行了数年监测,给出了线冰载荷的变化规律。Brown[5-6]提出了一种间接方法,即通过倾斜计数据识别加拿大联邦大桥桥墩的冰载荷。载荷识别作为一种有效获取冰载荷的方法已经在海洋工程领域得到了广泛应用[7-10],但在寒冷地区水工钢闸门冰载荷识别方面研究不多,Zhang等[11-12]对弧形钢闸门进行了监测并通过多种反求算法计算出了冰载荷的近似分布。
本文在已有研究的基础上,提出了一种Tikhonov正则化方法(Tikhonov regularization method,TRM)与粒子群优化算法(particle swarm optimization,PSO)相结合的混合方法(TRM & PSO)用于载荷识别,以松花江流域哈尔滨段大顶子山水利枢纽泄洪闸门作为研究对象给出了冰载荷分布并在此基础上分析了闸门强度。
1 冰载荷分布识别冰层挤压力对闸门的作用是缓慢变化的过程,可认为冰挤压力为静态力,且结构的输入与输出呈线性关系。将闸门与冰的接触区域划分为若干个承载单元且假定每个承载单元上的冰载荷是均布的,所有监测点的监测应变与冰挤压力的线性关系为:
| $ \left[ {\begin{array}{*{20}{l}} {{\varepsilon _1}}\\ {{\varepsilon _2}}\\ {\; \vdots }\\ {{\varepsilon _n}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{K_{11}}}&{{K_{12}}}& \ldots &{{K_{1m}}}\\ {{K_{21}}}&{{K_{22}}}& \ldots &{{K_{2m}}}\\ {\;\; \vdots }&{\;\; \vdots }&{\;\; \vdots }&{\;\; \vdots }\\ {{K_{n1}}}&{{K_{n2}}}& \ldots &{{K_{nm}}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{l}} {{f_1}}\\ {{f_2}}\\ {\; \vdots }\\ {{f_m}} \end{array}} \right]{\rm{ }} $ | (1) |
式中:εi表示第i个传感器采集到的应变值;fj表示第j个承载单元上的均布力,MPa;Kij表示第j个承载单元上的单位均布力在第i个传感器位置处引起的应变值;m表示承载单元划分个数;n表示传感器个数。式(1)可简写为Kf=ε。
对于给定的传递矩阵K和一组应变数据ε, 载荷f可通过以下方法求出:
1) 若传递矩阵条件数很小,即非病态情况下,且m=n时:
| $ {\mathit{\pmb{f}}} = {{\mathit{\pmb{K}}}^{ - 1}}{\mathit{\pmb{\varepsilon}}} $ | (2) |
2) 若传递矩阵条件数较小,即非病态或病态情况非常弱,且m与n相差不大情况下,可通过求解传递矩阵M-P(Moore-Penrose)逆给出最小二乘解:
| $ {{\mathit{\pmb{f}}}_{{\rm{LSQ}}}} = {{\mathit{\pmb{K}}}^ + }{\mathit{\pmb{\varepsilon}}} $ | (3) |
3) 病态情况下,可采用截断奇异值分解法(truncated singular value decomposition, TSVD)、TRM或优化算法进行求解[11-14]。
1.1 有限元建模整个闸门结构采用shell281单元进行有限元建模,材料参数根据Q345D进行设置。有限元模型的边界条件根据闸门的实际工作状态进行设定:在支臂铰支座处约束全部线位移以及2向角位移,使有限元模型可绕铰支点上下转动;在闸门门板底部约束其垂向位移,如图 1所示。

|
Download:
|
| 图 1 寒区钢制闸门有限元模型 Fig. 1 Finite element model of a steel gate in a cold region | |
传递矩阵K表示结构输入与结构输出之间的线性映射关系,可在有限元模型中通过加载单位载荷模拟计算得出。计算传递矩阵分2步进行:
1) 把闸门冰载荷监测区划分为一定数量的承载单元,承载单元的数量应略少于应变传感器的数量。在本文中把闸门冰载荷监测区划分为20个承载单元,承载单元平均面积为0.81 m2,如图 2所示。

|
Download:
|
| 图 2 闸门承载单元划分 Fig. 2 Load bearing element division | |
2) 在某一承载单元对上加载单位均布力,计算出结构响应,通过传感器基座之间的间距变化量计算出平均应变,由此得到传递矩阵的其中一列。经过20次计算,可得到完整的传递矩阵K。闸门总计布置了22个应变传感器,K为22×20的矩阵。传递矩阵K的详细计算流程可参考文献[11-12]。
1.3 求解方法与精度验证 1.3.1 传统方法求解传递矩阵K的条件数为99.9,据此可认为冰载荷识别的数学模型的病态程度非常小或无病态,可用求解广义逆的方法给出最小二乘解,即式(3),也可用TRM或TSVD进行求解。TRM的正则化参数由L曲线法(L-curve method, L-curve)以及广义交叉验证法(generalized cross validation, GCV)计算得到,TSVD的截断参数同样由L-curve法和GCV法计算得到。因此,本文中的常规方法共有5种:M-P;TRM法(TRM & L-curve),其中正则化参数由L-curve法计算得到;TRM法(TRM & GCV),其中正则化参数由GCV法计算得到;TSVD法(TSVD & L-curve),其中正则化参数由L-curve法计算得到;TSVD法(TSVD & GCV),其中正则化参数由GCV法计算得到。
以上5种传统计算方法的精度通过以下步骤验证:1)假定3种分布载荷f,即均布、二次和三次载荷并通过ANSYS计算出监测位置处的结构应变ε;2)引入误差向量εw以模拟传感器的监测误差。假定传感器的监测数据误差小于±10 με,设εw为-10至10内的一组随机数。最终以ε+εw模拟监测应变;3)由5种常规算法反求冰载荷fm;4)把fm与f进行对比以验证反求计算的精度,如图 3所示。

|
Download:
|
| 图 3 常规方法计算结果 Fig. 3 Calculation results of conventional method | |
从图 3中可以发现:5种常规算法总体上不能给出令人满意的结果,误差偏大,最大误差约为0.05 MPa,但是在部分承载单元上,5种常规算法中有些方法能给出高精度的解。
1.3.2 混合算法TRM与TSVD的正则化参数与截断参数均可由L-curve与GCV法计算得到,然而这2种方法极有可能给出不同的正则化参数与截断参数,从而导致TRM与TSVD给出不同的计算结果。在计算正则化参数或截断参数的方法中,无法从原理上确认L-curve与GCV哪一种为最优方案。虽然常规的正则化方法存在不足,但是其计算结果在病态或弱病态情况下比较接近精确解。
PSO算法是一种基于群体的随机优化方法,从初始解开始逐步迭代寻优。在PSO中,每个潜在的解表示为一个粒子,每个粒子都有自己的位置和速度,以目标函数作为指引逐步接近最优解。虽然PSO算法容易应用,但是其存在“早熟”现象,以至于陷入局部最优解而降低计算精度。本文提出一种混合算法,以期在一定程度上克服PSO算法的缺点。
本文提的TRM与PSO的混合算法分为2个主要步骤:
1) 由TRM法计算得到大量初始解,其中TRM的正则化参数人为确定,涵盖一个非常大范围,即正则化参数定为:0、20、40、60、……、1 000。由此可以得到51组初始解;
2) 将计算得到的初始解代入PSO寻优迭代。如果单纯使用PSO求解多变量线性方程组,很可能会陷入局部最优解导致结果误差较大且收敛速度较慢。由TRM法计算得到的初始解在大部分位置比较接近最优解,进而加快PSO的收敛速度。
混合算法的精度验证步骤与传统算法相同,计算结果如图 4所示。对比传统方法(图 3)与混合方法(图 4)的求解结果可以看出在此算例中混合方法的计算精度要优于传统方法。故在本文中采用混合算法计算闸门冰载荷的近似分布。

|
Download:
|
| 图 4 混合算法反求结果 Fig. 4 Calculation results of hybrid algorithm | |
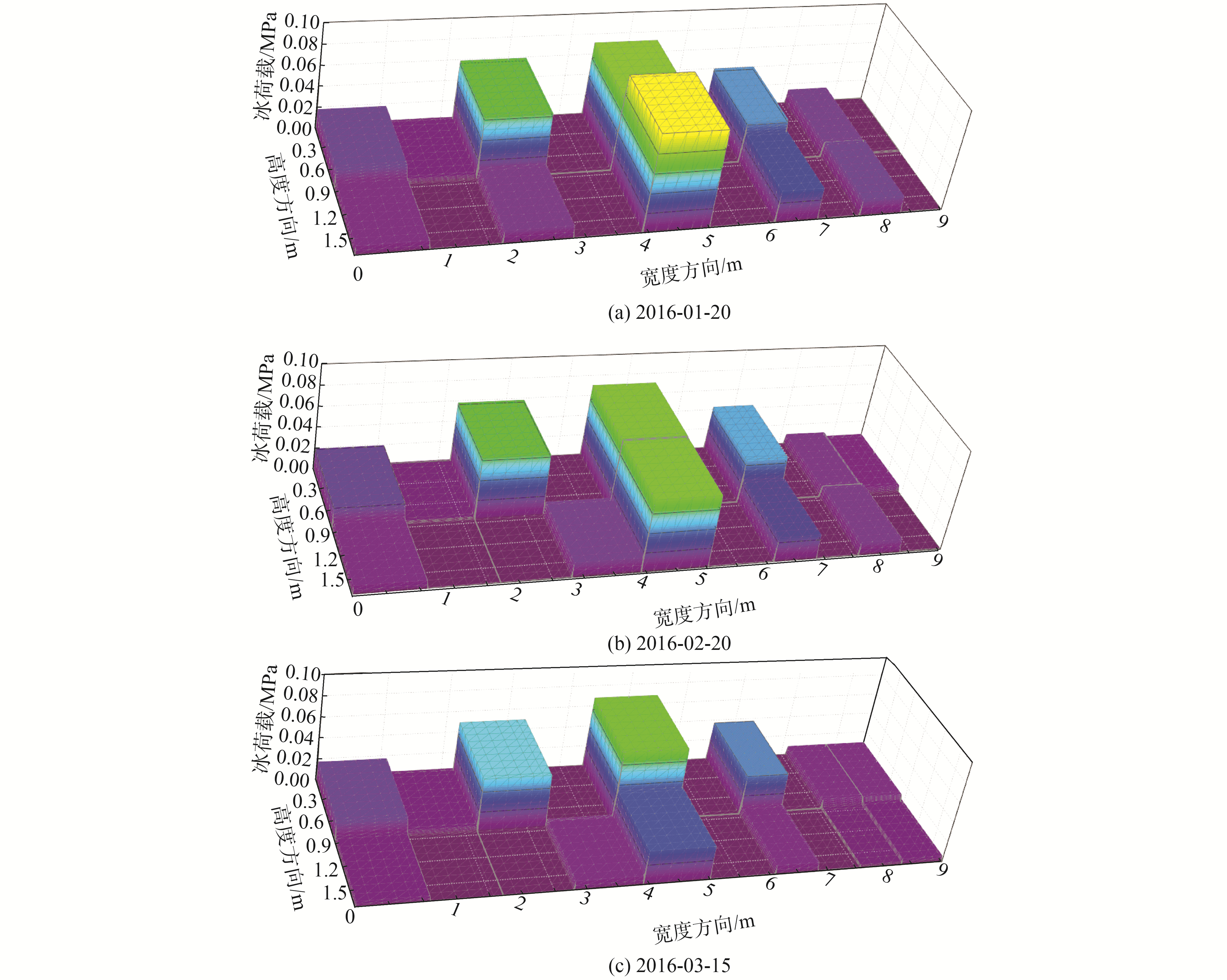
在闸门背面结构总计布置22个应变计以监测结构响应,监测系统每1 h采集一组应变和温度值。在2015-11-13至2016-3-20,监测系统每天采集24组应变与温度数据,共计得到约2 500组的有效数据。根据本文提出的混合算法结合闸门实际监测数据可计算出整个监测周期内的冰载荷近似分布,在此仅给给出2016-01-20、2016-02-20、2016-03-15最低温时刻的冰载荷,如图 5所示。
|
Download:
|
| 图 5 3个日期冰载荷近似分布 Fig. 5 Ice load approximate distribution of 3 days | |
从图 5中可以看到闸门冰载荷沿高度方向与宽度方向很不规律,最大冰载荷约为0.1 MPa。由冰载荷分布可计算出冰载荷合力,如图 6所示。冰载荷合力在结冰期内逐步波动上升。在12月底冰载荷达到最大,从3月中旬开始随冰层逐渐开化,冰载荷在短期内迅速下降至0附近。

|
Download:
|
| 图 6 闸门冰载荷合力 Fig. 6 Total ice force of steel gate | |
在整个监测周期内,取2015-11-13至2016-3-25内的有效监测数据并筛选出每天最低温时刻的应变数据识别出冰载荷分布。进而进行结构响应计算,结构响应计算计及冰载荷、闸门自重、静水压力以及动水压,其中动水压以20%的静水压计入到总载荷中。在所有计算模型中,第四强度等效应力均未超过200 MPa,其中2016-03-03的应力水平最高,为196.435 MPa,如图 7所示。

|
Download:
|
| 图 7 2016-03-03闸门结构响应 Fig. 7 Structural response of gate on 2016-03-03 | |
结构最大应力出现在闸门支臂与主横梁连接处,即应力集中点位置。闸门绝大部分位置的第四强度等效应力小于130 MPa。闸门支臂、主横梁以及垂梁均采用Q345D钢材。所以,结构应力水平均低于材料的屈服极限。
闸门结构的刚度分析主要通过主横梁的挠度进行,为防止闸门承载横梁的变形过大,SL74规范[3]中给出了许用挠度值,将其与计算挠度值(计及冰载荷的作用)进行对比。其中2016-03-03的主梁挠度值最大,为11.06 mm,小于挠度22 mm。冰载荷并未对闸门刚度产生过大影响,主梁的刚度足够。
特征值屈曲分析又称结构弹性稳定分析,指结构在外荷载作用下,在原来的平衡状态之外,出现了第2个平衡状态。在数学推导中解决的是一个求解特征值的问题,故而被称为特征值屈曲分析。本文在计及冰载荷作用的基础上通过ANSYS对闸门结构进行线性屈曲分析。其中2016-03-03的特征值最小,为2.88,表明结构并未失稳。
以上分析计算均基于1个假定,即每个承载单元内的冰载荷是均布的。实际作用于闸门的冰载荷不可能均匀分布,作用于每个承载单元内的并在可也不太可能是均布的。因此,承载单元均布载荷假定与实际情况有出入。结构实际的应力,主横梁的实际挠度可能大于计算值,结构线性屈曲的特征值可能会小于2.88。现取50%的安全系数,即认为结构最大应力为196.435×1.5=294.65 MPa,闸门绝大部分位置的第四强度等效应力小于130×1.5=195 MPa,主梁挠度值最大值为11.06×1.5=16.59 mm,结构线性屈曲最小特征值为2.88/1.5=1.92。在取50%的安全系数时,结构仍然是安全的。所以,可近似认为结构能够实现无防护越冬。
4 结论1) 在求解极弱病态(条件数接近100)的线性方程组(接近静定)时,常规的正则化方法或M-P逆法很难得到高精度的求解结果。
将正则化方法(正则化参数人为设定,涵盖较大范围)的计算结果作为粒子群优化算法的初始解能够加快其收敛速度且给出较高精度的求解结果。
2) 从结构应力水平计算结果可以看出,冰载荷会对闸门结构产生一定的影响,但并没有超出闸门的承载极限,而且冰载荷的影响仅仅局限于闸门上层直接与冰接触区域。
3) 中国相关规范规定寒冷地区结冰期水工钢闸门不允许承受静冰挤压力作用,这种规定有其不合理之处,若有类似于黑龙江大顶子山兼顾发电、泄洪和调节水位等诸多功能于一身的水利枢纽极有可能会因为发电站水轮机进水口处存在自由液面作为冰盖的内力释放区导致闸门所承受的静冰挤压力不大,同时闸门结构的强度足够,则可以考虑允许闸门承受静冰挤压力以更大限度发挥闸门的承载能力、节约运营成本。
| [1] |
徐乾清. 中国水利百科全书[M]. 2版. 北京: 中国水利水电出版社, 2006. XU Qianqing. Water conservancy encyclopedia China[M]. 2nd ed. Beijing: China Water Power Press, 2006. (  0) 0)
|
| [2] |
中华人民共和国水利部. SL 211-2006, 水工建筑物抗冰冻设计规范[S].北京: 中国水利水电出版社, 2006. Ministry of Water Resources of the PRC. SL 211-2006, Code for design of hydraulic structures against ice and freezing action[S]. Beijing: China Water Power Press, 2006. (  0) 0)
|
| [3] |
中华人民共和国电力工业部. DL/T 5039-1995, 水利水电工程钢闸门设计规范[S].北京: 中国电力出版社, 1995. Ministry of Power Industry of the PRC. DL/T 5039-1995, Design code for steel gate in water resources and hydropower projects[S]. Beijing: China Electric Power Press, 1995. (  0) 0)
|
| [4] |
GONG Y, PENNER R, COMFORT G, et al. Static ice loads on wooden and steel stoplogs at seven sisters[C]//Proceedings of the 10th Workshop on the Hydraulics of Ice Covered Rivers. Winnipeg, 1999.
(  0) 0)
|
| [5] |
BROWN T G. Analysis of ice event loads derived from structural response[J]. Cold regions science and technology, 2007(47): 224-232. (  0) 0)
|
| [6] |
BROWN T G, TIBBO J S, TRIPATHI D, et al. Extreme ice load events on the Confederation Bridge[J]. Cold regions science and technology, 2010, 60(1): 1-14. DOI:10.1016/j.coldregions.2009.08.004 (  0) 0)
|
| [7] |
RITCH R, FREDERKING R, JOHNSTON M, et al. Local ice pressures measured on a strain gauge panel during the CCGS terry fox bergy bit impact study[J]. Cold regions science and technology, 2008, 52(1): 29-49. DOI:10.1016/j.coldregions.2007.04.017 (  0) 0)
|
| [8] |
BARKER A, TIMCO G, GRAVESEN H, et al. Ice loading on Danish wind turbines: part 1: dynamic model tests[J]. Cold regions science and technology, 2005, 41(1): 1-23. DOI:10.1016/j.coldregions.2004.05.002 (  0) 0)
|
| [9] |
GRAVESEN H, SØRENSENS S L, VØLUND P, et al. Ice loading on Danish wind turbines: part 2. analyses of dynamic model test results[J]. Cold regions science and technology, 2005, 41(1): 25-47. DOI:10.1016/j.coldregions.2004.05.009 (  0) 0)
|
| [10] |
LEE T K, LEE J H, KIM H, et al. Field measurement of local ice pressures on the ARAON in the Beaufort Sea[J]. International journal of naval architecture and ocean engineering, 2014, 6(4): 788-799. DOI:10.2478/IJNAOE-2013-0213 (  0) 0)
|
| [11] |
ZHANG Meng, QU Xianqiang, KALHORI H, et al. Indirect monitoring of distributed ice loads on a steel gate in a cold region[J]. Cold regions science and technology, 2018, 151: 267-287. DOI:10.1016/j.coldregions.2018.04.001 (  0) 0)
|
| [12] |
ZHANG Meng, QIU Binbin, KALHORI H, et al. Hybrid reconstruction method for indirect monitoring of an ice load of a steel gate in a cold region[J]. Cold regions science and technology, 2019, 162: 19-34. DOI:10.1016/j.coldregions.2019.03.020 (  0) 0)
|
| [13] |
HANSEN P C. Regularization tools version 4.0 for Matlab 7.3[J]. Numerical algorithms, 2007, 46(2): 489-194. (  0) 0)
|
| [14] |
ZHANG Meng, QIU Binbin, ZHU Maoyu, et al. Novel computation method of reducing ill-posedness for structural static distributed load identification by optimising strain gauge location[J]. Mechanical systems and signal processing, 2019, 124: 83-110. DOI:10.1016/j.ymssp.2019.01.051 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


