低温环境中航行船舶的上层建筑在海浪飞溅作用下经常面临结冰问题,过冷水滴冻结累积形成的冰层将对设备造成危害。六角冰晶也称枝晶,是凝固过程中最常见的一种晶体生长形式,六角冰晶粒相互冻结在一起,最终形成表面光滑的冰壳[1-2]。在冰晶生长问题中,一大难题是对固液相变界面的处理,界面的移动往往很难追踪,而相场法通过引入一个宽度非常小的过渡层来代替跳跃间断或者尖锐界面,避免了复杂的界面追踪。相场法最先应用于金属模拟领域,而后经过发展,已广泛应用于材料科学、固体物理、电化学等领域。Kobayashi[3]数值求解了考虑各向异性的二维相场模型,并首次得到了过冷纯金属凝固的二维复杂枝晶生长形貌。Wheeler等[4]提出了模拟二元合金等温凝固的相场模型。Wheeler等[5]模拟计算了过冷镍的凝固过程。Kim等[6]建立了可用于合金模拟的相场模型,消除了WBM模型中界面厚度限制。Qin等[7]建立了多元合金凝固模型,与实验结果基本相符。
近年来,国内学者开始将相场模型运用到冰的凝固,陈梅英等[8-11]利用相场法在食品存储领域的冰晶生长有较多的研究;李方方等[12]实现了细胞尺度下的冰晶数值模拟;徐立等[13]讨论了无量纲过冷度对冰晶生长的影响;邹阳[14]对制冷剂中冰晶生长过程进行了数值模拟,结果与实验观察相一致。但都没有对Kobayashi模型的准确性及各主要参数意义进行讨论分析。
本文拟对水滴冻结第1阶段进行数值研究,采用Kobayashi相场模型来实现六角冰晶的数值模拟,验证结果,并讨论主要参数对冰晶生长的影响,从而深刻理解水滴冻结第1阶段即枝晶生长过程。
1 Kobayashi相场模型相场模型通过引入相变量P来描述固液状态,P为1时代表固态,P为0时代表液态,P在(0, 1)代表固液共存。同时引入温度变量T,则结冰问题数值由两个抛物线型偏微分方程组成:1)包含动量的运动相场方程;2)包含无量纲温度的热扩散方程[15]。
根据Kobayashi的假设[3],自由能函数采用金茨堡-朗道自由能形式,考虑自然界中的枝晶生长行为多具有各向异性,相场方程可表示为:
| $ \begin{array}{l} \tau \frac{{\partial P}}{{\partial t}} = - \nabla \left( {{{\left| {\nabla P} \right|}^2}\varepsilon \frac{{\partial \varepsilon }}{{\partial {\mathit{\pmb{n}}}}}} \right) + \nabla ({\varepsilon ^2})\nabla P + \\ \;\;\;\;\;\;\;\;\;\;{\varepsilon ^2}{\nabla ^2}P + {\rm{ }}P\left( {1 - P} \right)\left( {P - 0.5 + m\left( T \right)} \right) \end{array} $ | (1) |
根据焓守恒定律,温度场方程为:
| $ \frac{{\partial T}}{{\partial t}} = {\nabla ^2}T + {\rm{ }}K\frac{{\partial P}}{{\partial t}} $ | (2) |
式中:K∂P/∂t为源项,解释了界面处潜热的释放并且保持两相之间的能量平衡;K是潜热常值。
式(1)描述了界面层(扩散层)的形状、运动和位置,式(2)给出了界面层的温度。
2 数值求解过程 2.1 离散形式有限差分方法在均匀网格中进行离散求解,具有原理简单、方程便于建立和易于编程等优点,本文将采用有限差分法中的九点差分格式和中心差分格式分别求解相场及温度场控制方程。
以相场变量为例,时间离散采用一阶向前差分:
| $ \frac{{\partial P}}{{\partial t}} = \frac{{{P_{i, j, n + 1}} - {P_{i, j, n}}}}{{\Delta t}} + o(\Delta t) $ | (3) |
式中:Δt为时间步长,Pi, j, n+1和Pi, j, n分别是当前时刻和下一时刻的节点(i, j)处的相场变量。温度变量也采用相同差分形式。
空间离散基于均匀网格,由中心差分格式获得相场变量的一阶及二阶偏导离散形式,而针对相场控制方程中出现的拉普拉斯算子,本文通过九点差分格式进行离散:
| $ \begin{array}{l} {\nabla ^2}P = (2({P_{i + 1, j}} + {P_{i - 1, j}} + {P_{i, j + 1}} + {P_{i, j - 1}}) + \\ \;\;\;\;\;\;\;\;\;\;{P_{i + 1, j + 1}} + {P_{i + 1, j - 1}} + {P_{i - 1, j + 1}} + {P_{i - 1, j - 1}} - \\ \;\;\;\;\;\;\;\;\;\;12{P_{i, j}}){(^2}\Delta {x^2}) - 1 \end{array} $ | (4) |
九点差分格式可以满足本文模拟计算的稳定性[16],温度场方程离散形式与上述过程相似。
2.2 初始条件及边界条件迭代运算之前需要设定网格数、空间步长、时间步长等计算参数及驰豫时间、界面宽度、潜热常值、各向异性强度等物性参数。本文需设定划分网格区域Nx×Ny为300×300,网格间距Δx及Δy均为0.03,时间步长dt为0.0 001 s,驰豫时间τ为0.000 3,界面宽度平均值ε为0.01,潜热常值K为2.0,各向异性强度δ为0.02,各向异性模数j为6,无量纲融化温度TM为1,材料参数α为0.9,γ为10。
结晶温度总是低于融化温度,即液体开始结晶时需要一个冷却过程,同时液体中还必须有一定量的微小结晶核,结晶核的存在能够缩短过冷却过程,自然界中的冰核多由大气冰粒或降雪形成[2]。本文设置液体区域初始无量纲温度为0,而无量纲融化温度为1,从而形成过冷水区域,同时通过在计算区域中心设定固定半径的圆来引入晶核,见图 1,并设置初始条件:
| $ {x^2} + {y^2} \le {r^2}:P = 1, T = 1 $ | (5) |
| $ {x^2} + {y^2} > {r^2}:P = 0, T = 0 $ | (6) |

|
Download:
|
| 图 1 晶核设置示意 Fig. 1 A schematic diagram of nucleation | |
相场及温度场均采用zero-Neumann边界条件,即:∂P/∂n=∂T/∂n=0。
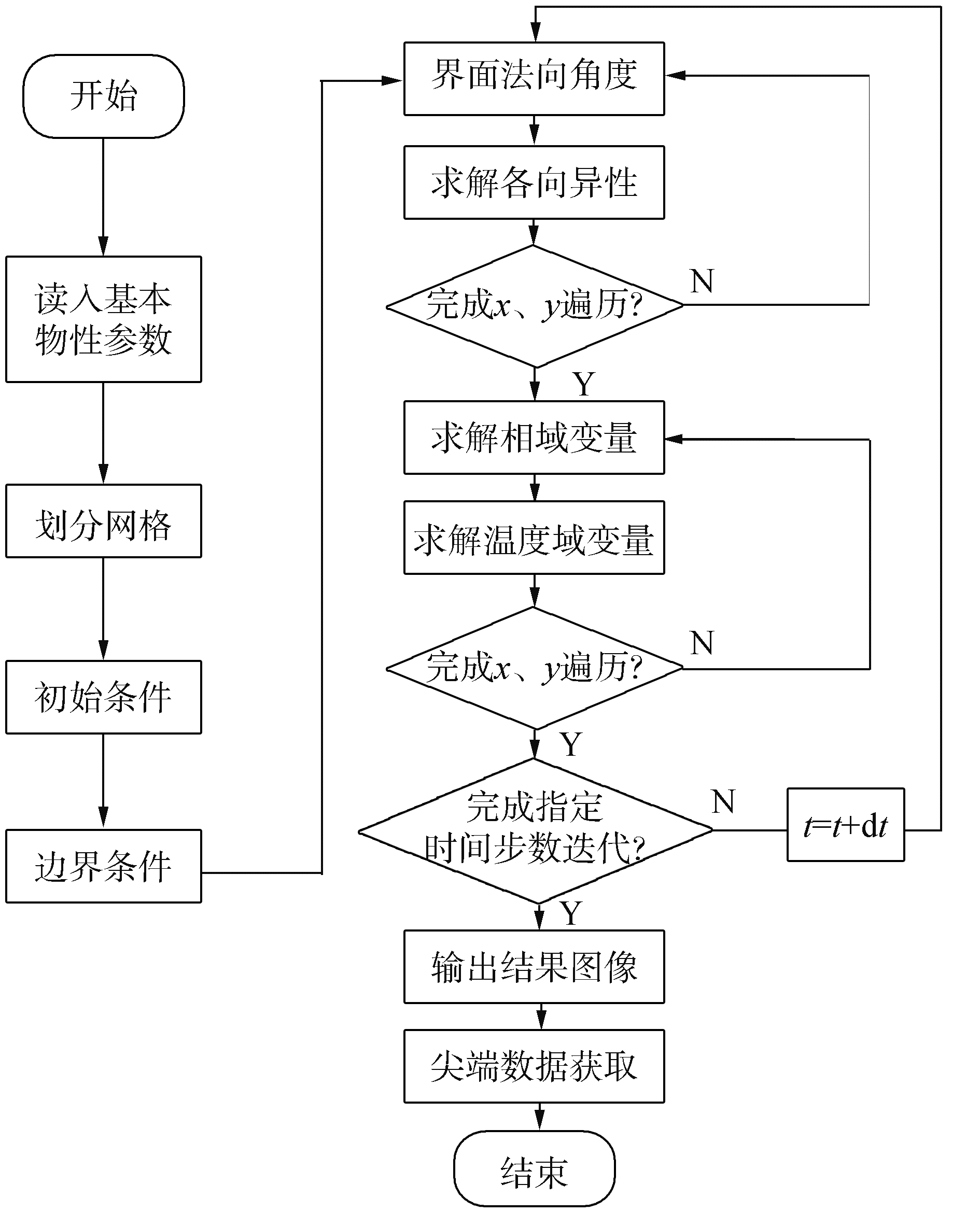
本文选用Python语言作为程序编写工具,具体流程如图 2所示。
|
Download:
|
| 图 2 冰晶计算程序基本流程 Fig. 2 Basic process of ice crystal calculation program | |
在没有外部扰动的冷水结冰时,冰晶粒与增长较快的水平轴平行,所以冰晶在水平方向上生长更快,冰晶生长时会由极小的冰球体发展到薄圆冰盘,冰盘会继续发展成六角星形[2],从圆盘到六角星形意味着冰快速生长的开始,六角冰晶彼此冻结在一起后会形成冰壳,厚度逐渐增加后便形成了一定体积的冰,完成整个结冰过程。冰晶生长过程见图 3。

|
Download:
|
| 图 3 冰晶生长过程 Fig. 3 The growth process of ice crystals | |
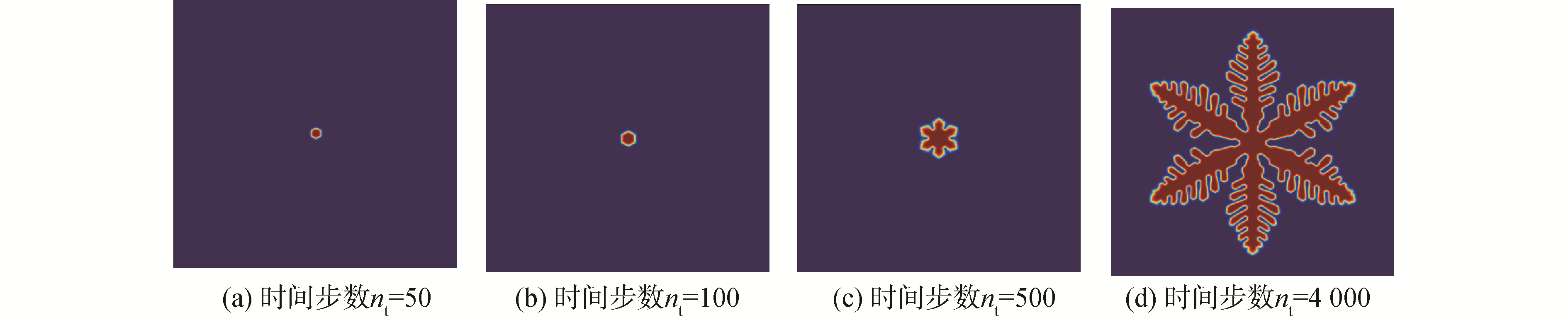
陶乐仁[17]利用低温显微镜观察了冰晶由晶核生长为类似雪花形状的过程,本文在给定上述基本参数基础上,分别设置时间迭代步数nt为50、100、500和4 000。由图 4可见,随着时间迭代步数的增加,初始晶核开始长大,首先由圆形生长为六边形,接着六边形的6个角开始突出生长,进而演化为6个分支,至此形成了六角冰晶的雏形。模拟结果与实验观察结果相一致。
|
Download:
|
| 图 4 模拟冰晶生长过程 Fig. 4 A schematic diagram for simulating the growth process of ice crystals | |
Libbrecht[18]展现了其团队拍摄到的形式多样的雪花照片,真实呈现了大自然界中广泛存在的雪花(见图 5(b)), 本文保持上述其他参数不变,划分网格区域为1 000×1 000,迭代1.0 s后获得了如图 5(a)所示的模拟结果,由图 5可见,本文模拟的六角冰晶形貌与大自然中真实存在的雪花是相似的,两图中各主支均生长出或长或短的侧分支,且生长较长的侧分支又生长出新的分支,有效说明了本文相场模型的真实性和准确性。

|
Download:
|
| 图 5 数值模拟结果与真实雪花对比 Fig. 5 Comparison between numerical simulation results and real snowflakes | |
Kobayashi相场模型中的弛豫时间、各向异性强度、潜热常值等物性参数会影响冰晶生长过程(包括尖端速度、尖端半径等)和冰晶形貌(侧枝大小、取向等)[19],本文将对模型中各主要参数进行敏感性分析,与真实冰晶形貌进行对比分析,进一步提高冰晶生长模拟的准确性。
3.1 弛豫时间τ弛豫时间τ与原子保持平衡位置并经历成核过程的快慢有关,τ值越小则原子保持平衡和成核的时间就越少,本文保持其他参数不变,依次设定τ为0.000 3、0.000 5、0.000 8,迭代时间均为0.20 s,由图 6可见,从左到右弛豫时间依次减小时,相同物理时间内冰晶生长速度依次增大,τ为0.008时,冰晶仅出现一次分支,且分支突出不明显,而τ为0.003时,冰晶已出现明显的二次分支,该现象与原子平衡时间的分析是一致的。弛豫时间对尖端生长速度及尖端半径也有直接的影响。考虑计算效率等因素,τ值不能无限减小,本文选择0.000 3为弛豫时间最优取值。

|
Download:
|
| 图 6 不同弛豫时间τ模拟结果 Fig. 6 Simulation results of different relaxation time | |
相场法中的界面宽度理论上应取真实值,但本文考虑计算可行性等因素,将界面宽度均值放大到可以计算的尺度,所以宽度均值对计算效率和模拟结果均有影响。保持其他参数不变,分别设定ε为0.009、0.01、0.011,迭代时间均为0.30 s,由图 7可见随着界宽均值的增加,枝晶生长尖端速度和尖端半径均增大。但为了保证计算准确度,ε应保持在尽可能小的范围内。

|
Download:
|
| 图 7 不同界面宽度均值ε模拟结果 Fig. 7 Simulation results of different mean interface width ε | |
本文相场模型中采用无量纲温度值T(r, t)=(Treal-TM)/(TM-T0),Treal为系统实时温度,TM为融化温度,T0为系统初始温度。由式可知,融化温度TM增加时,无量纲温度值会减小,从而加快生长过程,保持其他参数不变,依次设定融化温度TM为0.9、1.1、1.2,迭代时间均为0.20 s,由图 8可见,融化温度设定值从0.9增大到1.2时,枝晶生长速度加快,且侧枝的尖端速度也会增大,但尖端半径会响应减小,因此TM为1.2时,枝晶主干延伸的侧枝更长导致枝晶整体结构比较密集。可见融化温度对枝晶生长过程及最终形貌均有影响。

|
Download:
|
| 图 8 不同融化温度TM模拟结果 Fig. 8 Simulation results of different melting temperature TM | |
Kobayashi模型表述界面宽度关于角度的函数时引入了各项异性模数j,其能够影响晶体分支数目及最终形态。本文保持其他参数不变,依次设定j为4、6、8,迭代时间为0.30 s,由图 9可见,模数增加,侧枝的尖端速度及半径也会增加。

|
Download:
|
| 图 9 不同各向异性模数j模拟结果 Fig. 9 Simulation results of different anisotropic modulus j | |
各向异性强度δ是描述枝晶生长各向异性的重要参数,其会对冰晶形貌产生影响,当δ为0时,冰晶生长具有各向同性特点,本文保持其他参数不变,依次设定δ为0.005、0.03、0.05,迭代时间均为0.80 s,由图 10可见,δ为0.005时,冰晶生长具备各向同性和树枝形状特征。δ为0.03时,冰晶生长展现出树枝形状,且各主分支上出现的第二分支沿着各向异性生长,与真实雪花形貌相似。δ为0.06时,各分支出现明显不同,部分主分支仅有一侧存在第二分支,各向异性强度太大导致与真实雪花形状存在差异。本文选择0.03为最优各向异性强度。

|
Download:
|
| 图 10 不同各向异性强度δ模拟结果 Fig. 10 Simulation results of different anisotropic strength δ | |
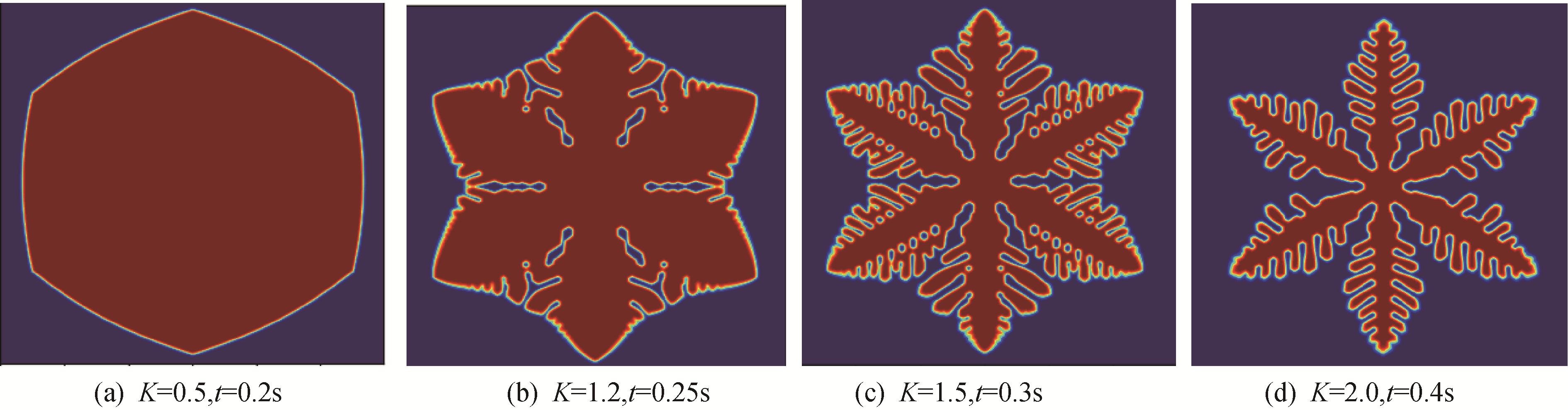
潜热常值K是相场模型最重要的物理参数,它解释了凝固前沿界面(即扩散层)的热量释放,对枝晶的整个生长过程均有影响。K值越大,说明从界面扩散层释放的热量越多。本文保持其他参数不变,依次设定K为0.5、1.0、1.5、2.0,计算网格区域均为300×300。由图 11可见,K为0.5时晶体生长为六边形且各边呈凸状,但随着K值增大,凸状逐渐消失,在K为1.2时,冰晶各边的中心出现凹陷,且凹痕内出现裂缝,裂缝内出现褶皱,展现出分支迹象,潜热常值为1.2时的冰晶形状实际上是六边形和六角分支的中间形式。K为1.5时,冰晶生长出现分支,且各主分支生出第二分支。K为2.0时,各主分支变得更细,相邻主分支的侧分支间距变大,冰晶生长成为类似雪花形状。
|
Download:
|
| 图 11 不同潜热常值K模拟结果 Fig. 11 Simulation results of different latent heat constants | |
1) 潜热常值作为影响冰晶生长的最主要参数,其象征着界面扩散层的热量释放,值越大,则能量释放越多,六角冰晶生长越明显,弛豫时间越小则冰晶生长越快,各向异性模数决定了冰晶生长的分支数目,广义上印证了凝固材料杂质的存在,各向异性强度影响冰晶侧分支生长,界面宽度均值则影响着冰晶生长尖端速度及半径。
2) 本文采用的相场模型不仅可以通过耦合相场与外场方程将微观与宏观结合起来,还能模拟分析晶体生长过程中的物性参数(如界面宽度、各向异性强度等)对冰晶生长的影响。
本文模拟了六角冰晶的生长,揭示了冰晶形成机理,为过冷水滴冻结第1阶段研究奠定了理论基础。后续研究将进一步引入更多水的物性参数,对模拟场与真实物理场进行有效结合,同时发展大尺度相场模拟技术,进而将微观尺度的枝晶生长和介观尺度的水滴冻结联系起来,使模拟结果更加真实。
| [1] |
白响恩, 王建忠, 肖英杰. 中国船舶首次穿越北极东北航道纪实[J]. 航海技术, 2013(1): 2-5. BAI Xiangen, WANG Jianzhong, XIAO Yingjie. Record of Chinese ships crossing the Arctic northeast passage for the first time[J]. Marine technology, 2013(1): 2-5. DOI:10.3969/j.issn.1006-1738.2013.01.001 (  0) 0)
|
| [2] |
丁德文. 工程海冰学概论[M]. 北京: 海洋出版社, 1999: 15-17. DING Dewen. An overview of engineering sea ice[M]. Beijing: China Ocean Press, 1999: 15-17. (  0) 0)
|
| [3] |
KOBAYASHI R. Modeling and numerical simulations of dendritic crystal growth[J]. Physica D: nonlinear phenomena, 1993, 63(3/4): 410-423. (  0) 0)
|
| [4] |
WHEELER A A, BOETTINGER W J, MCFADDEN G B. Phase-field model for isothermal phase transitions in binary alloys[J]. Physical review A, 1992, 45(10): 7424-7439. DOI:10.1103/PhysRevA.45.7424 (  0) 0)
|
| [5] |
WHEELER A A, MURRAY B T, SCHAEFER R J. Computation of dendrites using a phase field model[J]. Physica D: nonlinear phenomena, 1993, 66(1/2): 243-262. (  0) 0)
|
| [6] |
KIM S G, KIM W T, SUZUKI T. Phase-field model for binary alloys[J]. Physical review E, 1999, 60(6): 7186-7197. DOI:10.1103/PhysRevE.60.7186 (  0) 0)
|
| [7] |
QIN R S, WALLACH E R, THOMSON R C. A phase-field model for the solidification of multicomponent and multiphase alloys[J]. Journal of crystal growth, 2005, 279(1/2): 163-169. (  0) 0)
|
| [8] |
陈梅英, 欧忠辉, 卓艳云, 等. 相场法模拟冰晶生长的参数优化[J]. 南京大学学报(自然科学), 2014, 50(6): 873-882. CHEN Meiying, OU Zhonghui, ZHUO Yanyun, et al. Optimization of correlative parameters in numerical simulation of ice crystal growth by phase-field[J]. Journal of Nanjing University (natural science), 2014, 50(6): 873-882. (  0) 0)
|
| [9] |
陈梅英, 陈永雪, 王文成, 等. 冷冻浓缩过程冰晶生长的相场法模拟[J]. 福建农林大学学报(自然科学版), 2010, 39(5): 548-551. CHEN Meiying, CHEN Yongxue, WANG Wencheng, et al. Phase-field simulation of the growth mechanism of ice crystals in the process of freeze concentration[J]. Journal of Fujian Agriculture and Forestry University (natural science edition), 2010, 39(5): 548-551. (  0) 0)
|
| [10] |
陈梅英, 冯力, 欧忠辉, 等. 基于相场法的液态食品冷冻浓缩冰晶生长数值模拟[J]. 农业工程学报, 2014, 30(3): 231-237. CHEN Meiying, FENG Li, OU Zhonghui, et al. Numerical simulation of ice crystal growth of liquid food freeze concentration based on phase-field method[J]. Transactions of the Chinese society of agricultural engineering, 2014, 30(3): 231-237. (  0) 0)
|
| [11] |
卓艳云, 陈梅英, 陈锦权, 等. 各向异性系数对等温结晶冰晶生长相场法模拟的影响[J]. 低温物理学报, 2014, 36(3): 232-237. ZHUO Yanyun, CHEN Meiying, CHEN Jinquan, et al. Influence of anisotropy degree on isothermal crystallization process using phase-field[J]. Chinese journal of low temperature physics, 2014, 36(3): 232-237. (  0) 0)
|
| [12] |
李方方, 刘静, 乐凯. 细胞尺度冰晶生长行为的相场数值模拟[J]. 低温物理学报, 2008, 30(2): 172-175. LI Fangfang, LIU Jing, YUE Kai. Numerical simulation on lce crystal formulation in cellular level based on phase field theory[J]. Chinese journal of low temperature physics, 2008, 30(2): 172-175. (  0) 0)
|
| [13] |
徐立, 陈尚海, 江焕宝, 等. 极地船海水系统冰晶生长对换热器性能影响的相场模拟[J]. 中国修船, 2017, 30(2): 45-48. XU Li, CHEN Shanghai, JIANG Huanbao, et al. The phase field simulation of the influence of heat exchanger performance on ice crystals in sea water piping system of polar ship[J]. China shiprepair, 2017, 30(2): 45-48. (  0) 0)
|
| [14] |
邹阳, 钱华, 梁文清. 制冷剂中冰晶生长的数值模拟[J]. 制冷技术, 2017, 37(2): 64-69. ZOU Yang, QIAN Hua, LIANG Wenqing. Numerical simulation of ice crystal growth in refrigerant[J]. Chinese journal of refrigeration technology, 2017, 37(2): 64-69. DOI:10.3969/j.issn.2095-4468.2017.02.203 (  0) 0)
|
| [15] |
SHAH A, HAIDER A, SHAH S K. Numerical simulation of two-dimensional dendritic growth using phase-field model[J]. World journal of mechanics, 2014, 4(5): 128-136. DOI:10.4236/wjm.2014.45015 (  0) 0)
|
| [16] |
SANAL R. Numerical simulation of dendritic crystal growth using phase field method and investigating the effects of different physical parameter on the growth of the dendrite[J]. arXiv preprint arXiv: 1412.3197, 2014.
(  0) 0)
|
| [17] |
陶乐仁, 华泽钊. 低温保护剂溶液结晶过程的显微实验研究[J]. 工程热物理学报, 2001, 22(4): 481-484. TAO Leren, HUA Zezhao. A microscopic study of the crystallization in Cryoprotectent agents[J]. Journal of engineering thermophysics, 2001, 22(4): 481-484. DOI:10.3321/j.issn:0253-231X.2001.04.025 (  0) 0)
|
| [18] |
LIBBRECHT K G. Field guide to snowflakes[M]. Minnesota, USA: Voyageur Press, 2006: 53-63.
(  0) 0)
|
| [19] |
BIBEN T. Phase-field models for free-boundary problems[J]. European journal of physics, 2005, 26(5): S47-S55. DOI:10.1088/0143-0807/26/5/S06 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


