2. 天津大学 水利工程仿真与安全国家重点实验室, 天津 300072
2. State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China
深海输油管道是海洋油气开发系统的重要组成部分,长期受到极端荷载的作用,例如在原油输送过程中,为了保障原油的流动性,必须保证一定的输送温度,再考虑到原油本身的温度,深海的环境温度以及其他温度因素的作用,会导致管道热屈曲,引发管道破坏,导致严重的管道泄露事故,造成灾难性环境污染以及重大经济损失。本文所研究的深海双层管道[1]主要构造措施包括管道端部刚性连接的锚固件,沿管道长度分布的内外管间的对中环。
国内外学者对深海双层管道温度效应解析解进行了大量研究:Bokaian[2]的假设是在简化管道系统连接,基于各种工况荷载线性叠加的基础上,推导出双层管道系统末端温度应力的计算模型;余志兵等[3]对海底管道结构参考DNV2000规范进行了在位强度分析及极限状态校核,确定管道在工程中合理的钢管壁厚及钢管等级;陈志华等[4]对管道系统在稳态流动的非均匀温度场工况下进行有限元软件模拟,对模拟中的网格独立性进行重新分析,确定了合理的网格划分方式,得到了管道沿程温度曲线;黄俊等[5]通过ABAQUS软件对建立的管道有限元模型施加层流和紊流2种流态的非均匀温度荷载,考虑材料非线性,通过模态分析引入初始缺陷,针对不同温度工况和管土作用,进行管道系统非均匀温度效应下的参数化模拟分析;赵天奉[6]发表了新型计算解析模型,适用于研究刚性连接的双层管道系统温度应力,并给出了管道环向及轴向应力的显式表达公式;石云等[7]考虑双层管道内外管之间的相互作用,求出双层管结构在应变层面的过渡长度;刘晓霞等[8]在剪滞理论基础上提出了海底双层管道系统热膨胀分析的计算方法,得到埋置双层管线轴向力的分布状态,管线轴向力受土壤摩擦力的影响规律。
综上所述,目前缺乏符合实际深海环境和管道参数的深海双层管道的有限元模拟计算,尤其是在不均匀温度场作用下的双层管道的温度效应,因此,有必要对不均匀温度场作用下的海底双层管道进行研究。利用ITT单元以及非线性弹簧单元,优化深海双层管道模型,对深海双层管道进行ABAQUS有限元数值模拟,通过与解析解结果对比,得到了有效的有限元模型,最后对长短双层管道在均匀和不均匀温度场中的温度效应进行建模分析。
1 数值计算模型 1.1 单元选择有限元计算采用ABAQUS软件,在深海双层管道有限元分析过程中,由于管道模型很长,长度方向的尺寸远大于另外2个方向,所以双层管道利用PIPE31单元建立,见图 1~2。根据深海双层管道的构造形式,在双层管道的内外管之间存在centralizer[9](对中环)。在实际计算中,对中环对内外管的协同工作有重要作用,因此在建立模型的时候,必须考虑对中环的连接作用,由此利用ITT31单元,考虑双层管道中内外管连接的接触问题。通过命令流添加ITT31单元,单元包含2个节点,其中一个节点定义在内管内壁,另一个节点定义在外管内壁。

|
Download:
|
| 图 1 管道截面 Fig. 1 The cross section of the pipe-in-pipe | |

|
Download:
|
| 图 2 双层管道模型 Fig. 2 The pipe-in-pipe model | |
在边界条件模拟过程中[10],考虑到双层管道在温度荷载下发生轴向位移,管道与海床之间将会产生摩擦,采用二折线模型来模拟管土轴向相对作用。
在有限元分析计算过程中,文章使用非线性弹簧接触单元来模拟双层管道系统与刚性海床之间的摩擦连接,与刚性海床传统的硬接触不同,非线性弹簧接触单元包含2个节点,其一定义在双层管道系统外管外壁上,另一个节点设定在刚性海床上。通过定义弹簧单元变形量与受力之间的非线性关系,实现对管道系统与刚性海床间的非线性摩擦的有限元模拟[11-14]。
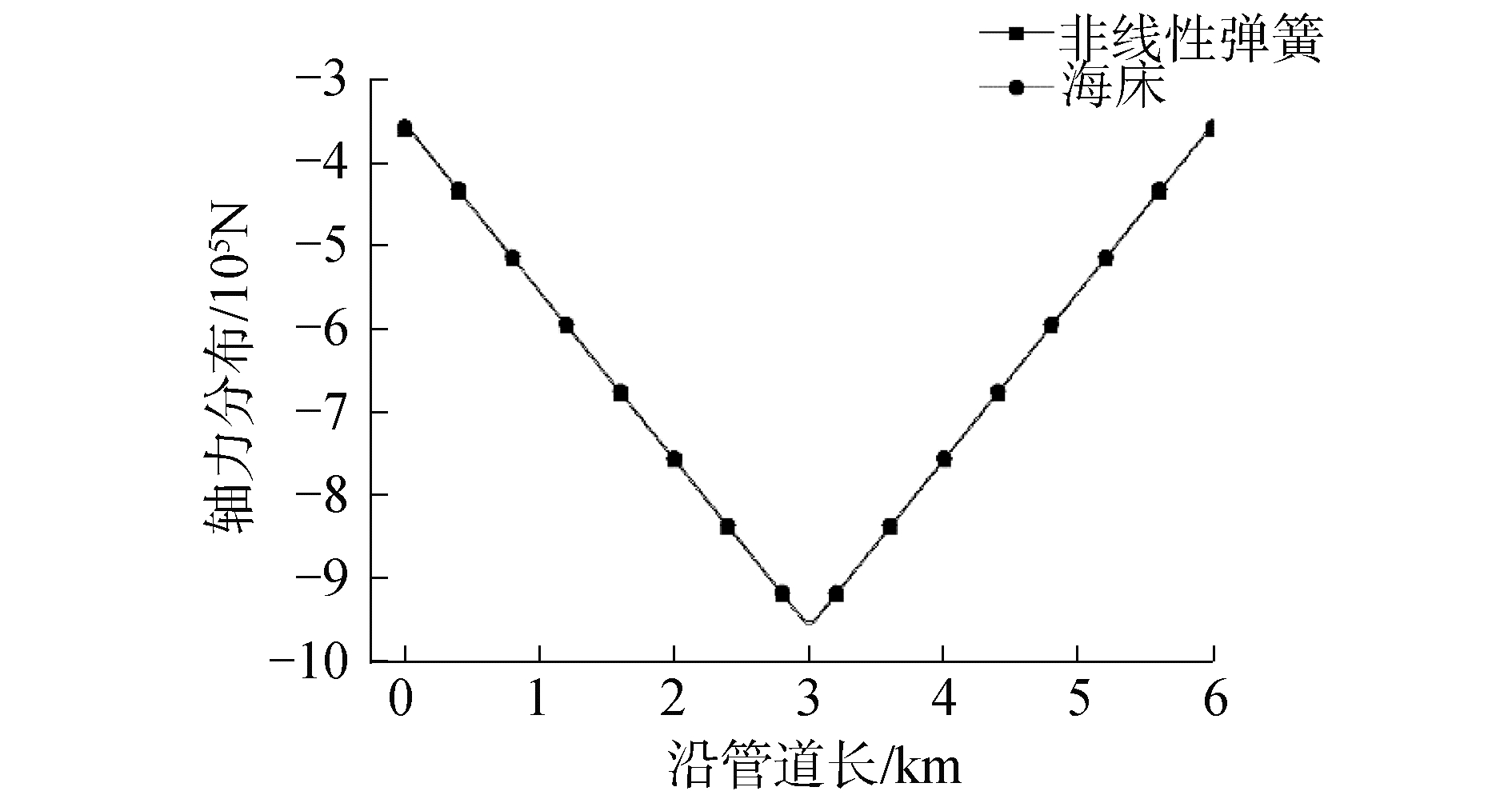
为验证非线性弹簧接触单元温度应力的计算准确性,利用6 000 m管道模型,将刚性海床摩擦的计算结果与弹簧接触单元计算结果沿全管道长度方向进行应力分布对比,验算单元选择的正确性。
在海床刚性摩擦接触下,沿管道全长分布的轴向力和轴向位移计算结果与非线性弹簧模拟摩擦的结果一致,是准确的,见图 3~4。

|
Download:
|
| 图 3 2种模型轴向位移计算结果对比 Fig. 3 The comparison of models′ axial displacement | |
|
Download:
|
| 图 4 温度应力对比 Fig. 4 The comparison of temperature stress | |
刚性海床模拟接触时管道最大轴向位移为1.105 9 m,非线性弹簧单元模拟时结果为1.105 6 m,结果基本一致。
通过验证,可以认为非线性弹簧单元很好地模拟了刚性海床与管道的摩擦接触,通过简化模型,省去了有限元计算过程中对seabed单元的建立,更方便地处理非均匀温度场的建模计算问题。
1.2 边界条件为了研究双层管道沿轴向的位移变化,水平对称轴选用轴边界条件;由于双层管道直接裸铺在海床上,深海水温保持恒定,外管外壁定义为恒温的温度边界条件。
1.3 载荷作用载荷作用[15]一共有4种:管道自重;在原油输送过程中,泵送原油流动的界面存在集中力;内管受到传送原油的管内压强;外管受到深海海底压强。
温度荷载采用预定义温度场来定义,根据Carr[10]给出的管道在流动开启和关闭过程中沿程温度时变曲线来定义每个单元受到的不同温度荷载。
2 深海双层管道均匀温度效应算例分析本节通过对比理论公式计算与ABAQUS数值模拟得到的轴向应力和轴向位移,来证明有限元分析模型的正确性,2种双层管道系统分别设定为11 000和6 000,因为深海管道由于长度过长,在沿管道长度方向会存在摩擦应变的积累,在特定点会出现应变为零现象,对于长短管道,会出现不同的锚固情况[7]。
2.1 模型参数双层管道模型内外管都采用API 5 L X60钢材,管道的弹性模量为2.071 N/m2, 材料密度为7 850 kg/m3, 管道材料热膨胀系数1.17×10-5/℃,泊松比0.3,主要参数见表 1。
| 表 1 双层管道计算参数 Table 1 The calculation parameters of the PIP |
Bokaian的解析公式[2]是通过大量简化计算模型,尤其是对管道系统内外管的连接构造简化,忽略不均匀温度场的工况分析以及内外管道的接触,很大程度上影响到解析公式的应用范围和计算准确性。双层管道系统温度应力主要受一些参数影响,包括内外管重量、管道的轴向刚度、管道长度、海床及内外管间摩擦和管道钢材的热膨胀特性等。
在本节使用的双层管道的温度应力计算公式中,内管和外管分别由小角标p和c代表。通过在管道两端的刚接的锚固件bulkhead受到以下的轴向平衡力:
| $ -N_{T, p}+N_{v, p}-N_{E}+F_{s}+N_{\delta}+N_{c}=0 $ |
式中:NT, p为受温度增加而导致的内管温度轴力;Nv, p为内管道所受的由泊松比产生的管道轴向作用力;NE为锚固件bulkhead处在内外管及深海水压力作用下产生的管道的端力;Nδ是因为内管轴向位移导致的管道轴向拉力;Nc为外管所受的拉力,公式表示此6种作用力在锚固件bulkhead处通过线性叠加取得平衡。
2.3 管道均匀温度效应数值计算结果对比通过ABAQUS有限元模拟,设置88 ℃均匀温度场,得到的长短管道的温度效应,包括轴向应力,轴向移动与理论计算公式得到的结果,如表 2所示,相对误差为均在1%左右。
| 表 2 双层管道有限元计算结果对比 Table 2 The finite element calculation result of the PIP |
利用经过验证的双层管道模型,根据Carr等[10]给出的管道在流动开启和关闭过程中沿程温度时变曲线,对管道施加入油口88 ℃的温度场,即入油口温度88 ℃,沿管道长度温度不均匀下降。
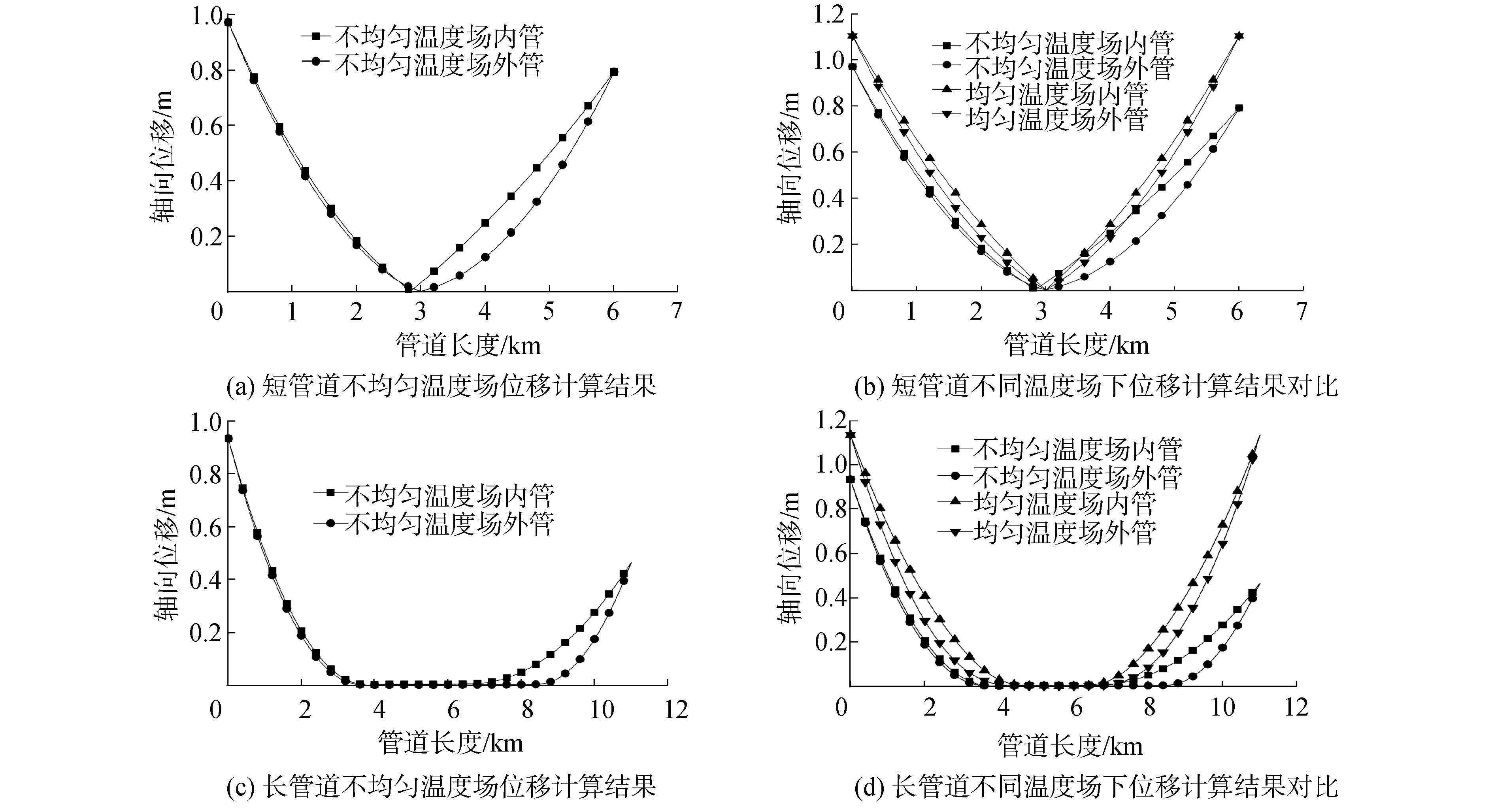
3.1 轴向位移从图 5(a)、(b)可以看出:在均匀温度场中,由于温度均匀对称,内外管轴向位移分布是对称的,并且在管道中部出现虚拟锚固点。在不均匀温度场中,受不均匀温度影响,管道出油口的位移小于入油口的位移,同时可以发现在不均匀温度场工况下,内外管道的虚拟锚固点并不重合,内管处的虚拟锚固点向左移动明显,外管的虚拟锚固点位于中部位置,管道系统整体运动趋势为外管在内管牵动作用下向出油口移动。在不均匀温度场工况下,内外管道间轴向位移差值在位于虚拟锚固点前的管道上游的入油口处明显小于管道下游。在不均匀温度场下管道的位移水平整体小于均匀温度场,并且在均匀温度场下内外管的虚拟锚固点重合在管道中央位置,位移差值较均匀。
|
Download:
|
| 图 5 不同管道不均匀温度场位移计算结果 Fig. 5 The displacement's results of the different pipeline under non-uniform temperature field | |
当双层管道长度比较长时,在管道端部锚固件bulkhead位置,外管的摩擦力累积,在温度作用下,当外管摩擦阻力数值等于的外管轴力值时,管道的轴向拉伸就会被抑制,锚固段就会出现在管道中央位置,此时锚固段的变形被完全抵消,轴向力停止变化,当管道长度足够长,管间的摩擦阻力在内管的积累也会出现锚固段,所以长管道系统的轴向位移在双层管会产生不同趋势。
从图 5(c)、(d)可以看出:在均匀温度场中,长管道位移和锚固段位置呈现对称的形式,长度为4 110 m;而在不均匀温度场中,长管道的轴向位移受影响较明显,管道入油口一侧的位移基本为出油口位移的2倍,锚固段出现在管道上游,内管锚固段长度为3 662 m,外管锚固段长度为5 459 m,入油口内外管的位移的差值远小于管道出油口的内外管位移值差值,由于外管的移动在内管的牵引下,在锚固段后,内外管的位移差值急剧加大。并且在不均匀温度场下,管道的整体位移能力下降,同时锚固段的长度增长显著,由于温度在出油口位置较低,导致管道锚固段向左移动,外管的左侧锚固点左移程度大于管道油入口处。
3.2 轴向应力从图 6(a)、(b)可以看出:在均匀温度场中,内外管轴力对称分布,外管的轴力变化较大;在不均匀温度场中,内管的轴向作用力左移现象显著,在内管虚拟锚固点之后,外管的轴向力急剧变化,出油口端外管的轴向拉力小于入油口端,同样内管出油口端的轴向压力也小于入油口端。内外管道在虚拟锚固点下游的位移在不均温度场下发生急剧变化,所以在不均匀温度场作用下产生的温度应力得以释放,相反,由于受到内管道的牵引且内外管上游的位移不均程度较低,所以管道的轴向位移和温度应力的不均匀变化趋势相同,温度作用力分布与均匀温度场温度应力分布接近。

|
Download:
|
| 图 6 不同管道不同温度场下位移计算结果对比 Fig. 6 The displacement's comparison of the different pipeline under different temperature fields | |
从图 6(c)、(d)可以看出:在均匀温度场中,由于管道与海床的接触摩擦力大于外管与对中环间的摩擦阻力,所以外管轴向拉力变化幅度较大,外管的位移在形成锚固段后趋于零,对中环的相对位移减小导致对内管的影响作用将增加,导致锚固段在内管产生后内管轴力变化幅度同时变大。在不均匀温度场中,管道受不均温度场影响,内外管轴向作用力上游入油口端要大于出油口端。2种温度场作用下,内管的轴力分布较位移情况较为不同,在内管形成锚固段过程中,由于管道的温度在锚固段位置处分布不均匀,因此在锚固段处管道所受的温度应力是不均匀的,在锚固段位置,内管的位移被限制并且随着温度场下降,管道的轴向压力在锚固段处随温度增加而减小。
4 结论1) 引入非线性弹簧(ITT)单元后,在温度应力的计算过程中,管道模型具有良好的精准度,与Bokaian的解析公式得到的结果差别小,很好地解决不均匀温度场的作用以及内外管间的摩擦接触等问题,同时可以计算多锚固件连接情况,通过软件模拟计算可以还原管道全长应力分布实际情况。
2) 通过建立非线性弹簧(ITT)单元,方便模拟位于刚性海床和管道之间的摩擦接触,方便相关管道模型的建立与计算。
3) 由于锚固件bulkhead的连接,双层管道(PIP)的温度效应受不均匀温度场工况影响显著,内管锚固点在不均匀温度场工况下向左移动,整体变化趋势为外管在内管牵引作用下向入油口端移动,内管锚固点先于外管出现,同时在锚固点前的游管道入油口处,内外管轴向位移差值显著小于管道下游。
4) 管道温度应力与轴向位移的变化趋势相似。在虚拟锚固点的下游,内外管的轴向位移在不均温度场工况中发生剧烈变化,温度应力与在均匀温度场工况下的值具有显著区别。在锚固段处,长管系统中的内管轴向压力并不是恒定的而是随着温度增加而减小。
| [1] |
WANG Zhe, CHEN Zhihua, LIU Hongbo, et al. Buckling response of pipe-in-pipe systems subjected to bending[J]. Transactions of Tianjin University, 2015, 21(6): 492-500. DOI:10.1007/s12209-015-2543-4 (  0) 0)
|
| [2] |
BOKAIAN A. Thermal expansion of pipe-in-pipe systems[J]. Marine Structures, 2004, 17(6): 475-500. DOI:10.1016/j.marstruc.2004.12.002 (  0) 0)
|
| [3] |
余志兵, 陈海龙.海底管道在位强度分析[C]//2007年度海洋工程学术会议论文集.贵阳, 2007: 8.
(  0) 0)
|
| [4] |
陈志华, 黄金超, 何永禹, 等. 深海管道稳态流动非均匀温度场研究[J]. 哈尔滨工程大学学报, 2017, 38(2): 189-194, 200. CHEN Zhihua, HUANG Jinchao, HE Yongyu, et al. Non-uniform temperature fields of a deep-sea pipeline in steady flow[J]. Journal of Harbin Engineering University, 2017, 38(2): 189-194, 200. (  0) 0)
|
| [5] |
黄俊, 黄金超, 刘红波, 等. 深海管道非均匀温度效应研究[J]. 工业建筑, 2016, 46(11): 40-48. HUANG Jun, HUANG Jinchao, LIU Hongbo, et al. Study of the non-uniform temperature effect of deep-sea pipelines[J]. Industrial construction, 2016, 46(11): 40-48. (  0) 0)
|
| [6] |
赵天奉.高温海底管道温度应力计算与屈曲模拟研究[D].大连: 大连理工大学, 2008. ZHAO Tianfeng. Research on thermal stress and buckling of HT submarine pipelines[D]. Dalian: Dalian University of Technology, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10141-2009041475.htm (  0) 0)
|
| [7] |
石云, 曹静.海底双层保温管热膨胀分析[C]//2009年度海洋工程学术会议论文集(上册).厦门, 2009: 6. SHI Yun, CAO Jing. Thermal expansion of subsea pipe-in-pipe systems[C]//Shipbuilding of China. Xiamen, 2009: 6. (  0) 0)
|
| [8] |
刘晓霞, 贾旭, 黄俊. 基于剪滞理论的海底双层管线热膨胀计算方法研究[J]. 中国海上油气, 2012, 24(2): 64-68. LIU Xiaoxia, JIA Xu, HUANG Jun. Study on thermal expansion calculation method for submarine pipe-in-pipe based on the shear lag theory[J]. China offshore oil and gas, 2012, 24(2): 64-68. DOI:10.3969/j.issn.1673-1506.2012.02.016 (  0) 0)
|
| [9] |
车小玉, 段梦兰, 曾霞光, 等.双层管和等效单层管隆起屈曲数值模拟[C]. Society for Underwater Technology Technical Conference, 2013. (  0) 0)
|
| [10] |
CARR M, SINCLAIR F, BRUTON D. Pipeline walking-understanding the field layout challenges, and analytical solutions developed for the SAFEBUCK JIP[C]//Offshore Technology Conference 2006.Houston, Texas, OTC-17945-MS.
(  0) 0)
|
| [11] |
Veritas D N. Offshore standard dnv-os-f101[J]. Submarine pipeline systems, 2000. (  0) 0)
|
| [12] |
陈志华, 黄金超, 赵思玥, 何永禹, 刘红波. 海底管道轴向移动数值模拟研究[J]. 哈尔滨工程大学学报, 2016, 37(9): 1197-1203. CHEN Zhihua, HUANG Jinchao, ZHAO Shiyue, et al. Numerical simulation of axial travel of submarine pipelines[J]. Journal of Harbin Engineering University, 2016, 37(9): 1197-1203. (  0) 0)
|
| [13] |
TORNES K, JURY J, OSE B. Axial creeping of high temperature flowlines caused by soil ratcheting[C]//Proceedings of the Conference on Offshore Mechanics and Arctic Engineering. ASME, (s.l.), 2000.
(  0) 0)
|
| [14] |
Maltby T.C., Calladine C.R., An investigation into upheaval buckling of buried pipelines-Ⅱ.Theory and analysis of experimental observations[J], International Journal of Meschanical Sciences, 1995, 37(9): 965-983.
(  0) 0)
|
| [15] |
黄金超.高温高压深海管道热力耦合效应研究[D].天津大学, 2017. Huang Jinchao.Analysis of the Thermal Coupling Effect for Deep-Sea Tunnel Under High Temperature and Pressure[J].Tianjin University. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


