2. 云洲智能科技有限公司, 广东 珠海 519000
2. Yunzhou Intelligent Technology Corporation, Zhuhai 519000, China
无人艇是典型的非线性、欠驱动控制系统,靠泊工作环境较为复杂,使其自主靠泊成为最困难、最复杂的难题之一;船舶的舵、桨通常是针对定常艏向和航速操纵设计,但无人艇靠泊时航速需要逐渐收敛且艏向需要不断调整,并受到低速导致的舵效差、岸壁效应带来的大扰动等显著影响,这使无人艇靠泊更加复杂和困难[1-2]。
张闯等[3]针对大型船舶的自主靠泊的过程中存在的航向稳定性差以及停船性能差等缺点,研究了航向控制以及航速控制对大型船舶自主靠泊过程的影响,同时进行了仿真,为大型船舶的实际自主靠泊提供了参考。Woo等[4]提出一种基于矢量场的制导方法,通过在靠泊过程的初始阶段减少与目标泊位的横向误差,来解决没有侧推的欠驱动无人艇的自主靠泊问题,并通过与传统制导方法的仿真对比试验,证明了所提方法的安全性和有效性,同时通过Monte-carlo模拟对所提方法的性能进行了测试。Mai等[5]提出一种基于PD控制器的无人艇自主靠泊方法,建立了无人艇在环境干扰下的控制模型,并基于其横向和纵向动力学模型设计出速度/艏向控制器,通过靠泊仿真试验验证了所提控制器具有良好抗干扰能力。
以上自主靠泊方法虽然在仿真试验中效果较好,但忽略了靠泊过程中障碍物的影响,也没有考虑靠泊过程中控制目标的变化,且缺乏外场试验验证,因此难以保证方法的实用性和有效性。轨迹规划是船舶完成自主靠泊的前提[1, 6],欠驱动船舶不具有跟踪任意轨迹的能力,因此在船舶自动靠泊中,要考虑欠驱动船舶自身运动的约束和水域受限影响,规划出可行轨迹[6-7]。目前常用的规划方法有:栅格法、可视图法、人工势场法和智能方法(如遗传算法、强化学习、神经网络等)。其中,人工势场法相对于其他方法存在局部极小值问题,易造成无人艇无法及时躲避障碍等问题,但是人工势场法凭借简单、计算量小、实时性强的优点,使其在路径规划领域得到了广泛应用[8-10],若充分考虑其缺陷、并结合无人艇特点改进算法,将使其优点得到更好应用。
本文针对无人艇靠泊轨迹规划问题,探索一种基于约束分析的改进人工势场法,将靠泊分成2个阶段进行研究:1)起始位置到码头附近某一过渡位置,称为“远端轨迹规划”;2)过渡位置到目标泊位的轨迹规划,称为“码头末端轨迹规划”。利用“海豚-Ⅰ”号小型无人艇开展自主靠泊外场试验,验证所提出方法的有效性和可行性。
1 面向无人艇自主靠泊的远端轨迹规划方法远端阶段指的是无人艇起始位置与期望泊位过渡位置之间的轨迹,过渡位置是指根据码头形状、大小、位置人为选定的一固定点,可以是进出港口必经之处或者无人艇专用通道,该阶段的主要任务是有效的避开障碍物。
基于人工势场法的路径规划方法因简单、高效得到了广泛的应用[8-10],但在实际的自主靠泊过程中包含诸多约束,如无人艇自身的运动约束、障碍物约束、码头末端约束等,而传统人工势场法中没有考虑这些约束问题,因而规划的路径并不一定能够满足实际需要。另外,针对无人艇靠泊规划而言,传统人工势场法主要面临局部极小点与弯角过大2种问题,为了解决这2个问题,本文提出障碍物补偿方法。
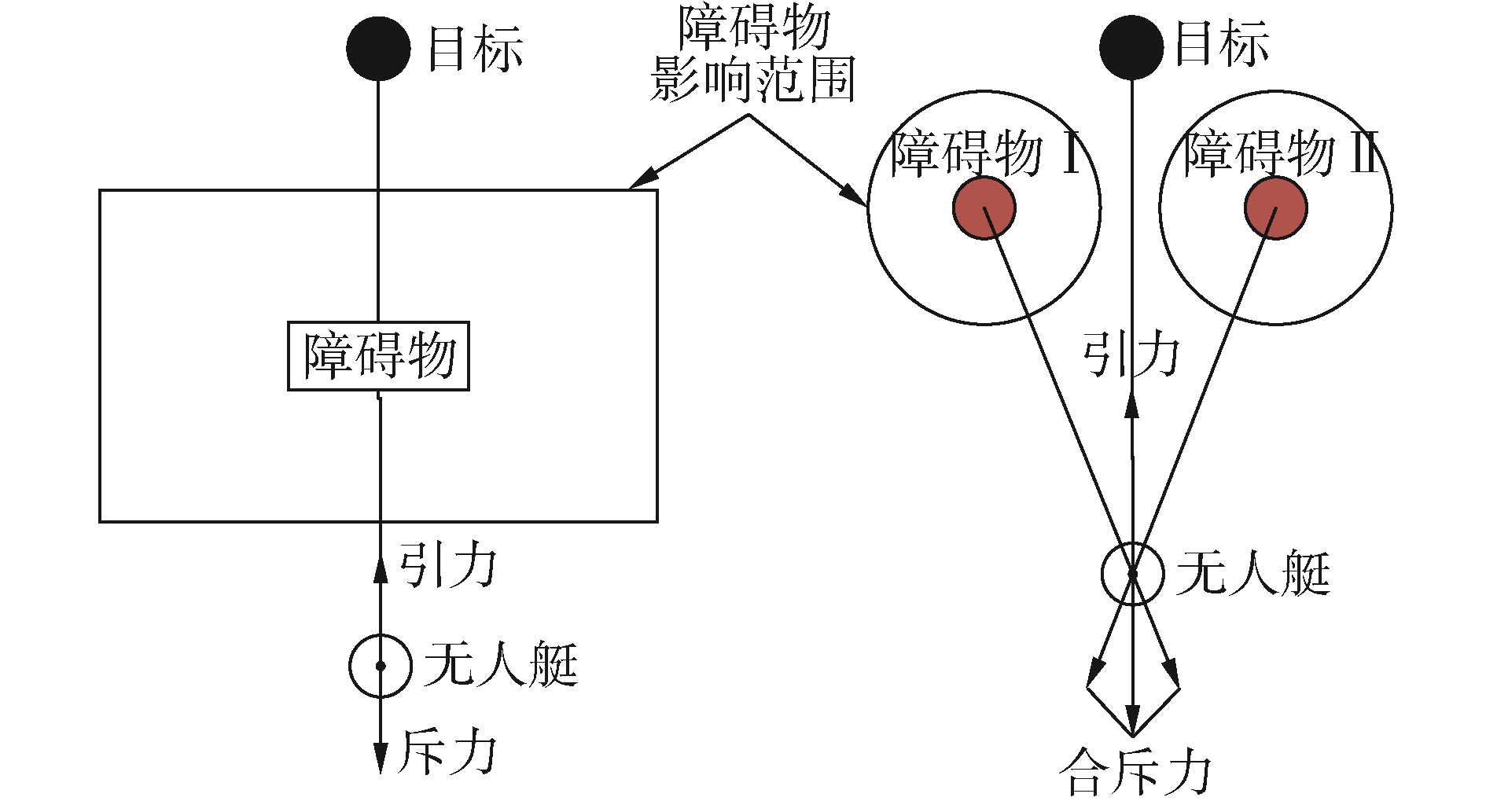
1.1 局部极小点当无人艇、障碍物以及目标点在同一条直线上,如图 1所示,无人艇在运动过程中,引力逐渐减小斥力逐渐增加且在同一条直线上,最终当引力与斥力相等时,无人艇陷入了局部极小点。
|
Download:
|
| 图 1 局部极小点示意 Fig. 1 Local minimum point schematic | |
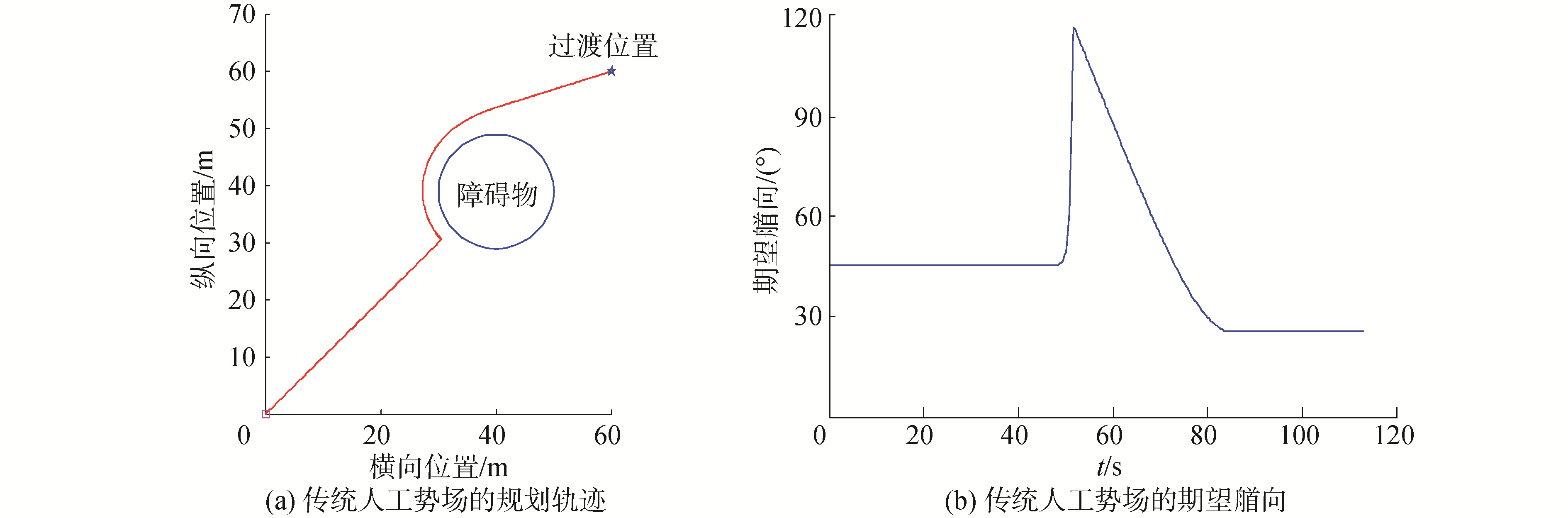
如图 2所示,当无人艇在绕过障碍时会因为斥力急剧增大,合力方向迅速变化,导致轨迹产生较大弯角,从而使艏向角急剧变化,由于无人艇受到自身运动约束,较难跟踪上该轨迹,且期望艏向的突变会导致无人艇很大程度上的超调,甚至与障碍物发生擦碰或者撞上障碍物。
|
Download:
|
| 图 2 大弯角示意 Fig. 2 Big bend angle diagram | |
通过上述分析,本文提出基于约束处理的改进人工势场法,在人工势场的基础上,当无人艇接近障碍物时,通过对艏向角做补偿,从而有效的避免上文所述局部极小点与弯角过大问题,影响艏向角补偿程度的因素主要包括以下几点:1)无人艇自身运动约束;2)障碍物的半径;3)障碍物影响半径;4)障碍物到无人艇与目标点连线的距离。
设ro为障碍物的半径;rz为障碍物的影响半径;d为障碍物到无人艇与目标点连线的距离;R为障碍补偿半径,其大小结合不同障碍物的d、ro、rz由经验设计得到;r为补偿角速度,与无人艇的几何尺度和机动能力有关,大小与R成正比,表示为r=k×R,其中k等于(0.05是最大补偿角速度,rad/s):
| $ k=\frac{0.05}{R_{2}-R_{1}} $ | (1) |
式中:R1, 2分别是R的最小值和最大值,这里令R2=2×rz,R1=rz/2,代入可得r=R/(30×rz),单位为rad/s。
障碍补偿过程示意图如图 3所示。

|
Download:
|
| 图 3 改进人工势场法流程 Fig. 3 Flow chart of the improved APF | |
障碍物补偿区域如图 4所示,首先判断障碍物位于起始点与目标点连线的哪一侧,确定补偿角速度的正负号;根据上述4个影响艏向角补偿程度的因素,确定障碍物补偿的范围R1≤R≤R2,确定补偿角速度r,如图障碍物影响半径为rz。
|
Download:
|
| 图 4 障碍物补偿示意 Fig. 4 Obstacle compensation diagram | |
设无人艇与障碍物实时距离为l:
1) 无人艇靠近障碍物。
当l>R2时,无人艇艏向只受到目标点的影响,方向为引力方向,补偿角速度,艏向角求解公式为:
| $ \psi=\theta_{1} $ | (2) |
式中:ψ表示无人艇艏向角;θ1表示引力方向。
当rz < l≤R2时,无人艇艏向受到目标点、补偿角速度的综合影响,补偿角速度为,艏向角求解公式为:
| $ \psi=\theta_{1}+r t $ | (3) |
式中t表示每步长所需的时间。
当R1 < l≤rz时,无人艇艏向受到目标点、障碍物、补偿角速度的综合影响,补偿角速度为,艏向角求解公式为:
| $ \psi=\theta_{0}+r t $ | (4) |
式中θ0表示引力与斥力的合力方向。
当l≤R1时,无人艇艏向受到目标点、障碍物综合影响,艏向角求解公式为:
| $ \psi=\theta_{0} $ | (5) |
2) 无人艇远离障碍物。
规定当无人艇第1次到达障碍物补偿区域最小边界(即l=R1)后,即便无人艇再次进入该区域,也不再针对该障碍做障碍物补偿。
当l≤rz时,无人艇艏向受到目标点、障碍物综合影响,艏向角求解公式为:
| $ \psi=\theta_{0} $ | (6) |
当l>rz时,无人艇艏向受到目标点引力的影响,艏向角求解公式为:
| $ \psi=\theta_{1} $ | (7) |
综上,无人艇下一步的更新位置表达式为:
| $ \left\{\begin{array}{l}{x_{k+1}=x_{k}+\cos \psi\left(U_{\mathrm{usv}} t\right)} \\ {y_{k+1}=y_{k}+\sin \psi\left(U_{\mathrm{usv}} t\right)}\end{array}\right. $ | (8) |
式中:Uusv是无人艇当前速度,t是步长。
1.4 仿真结果对比1) 传统人工势场法的规划结果。
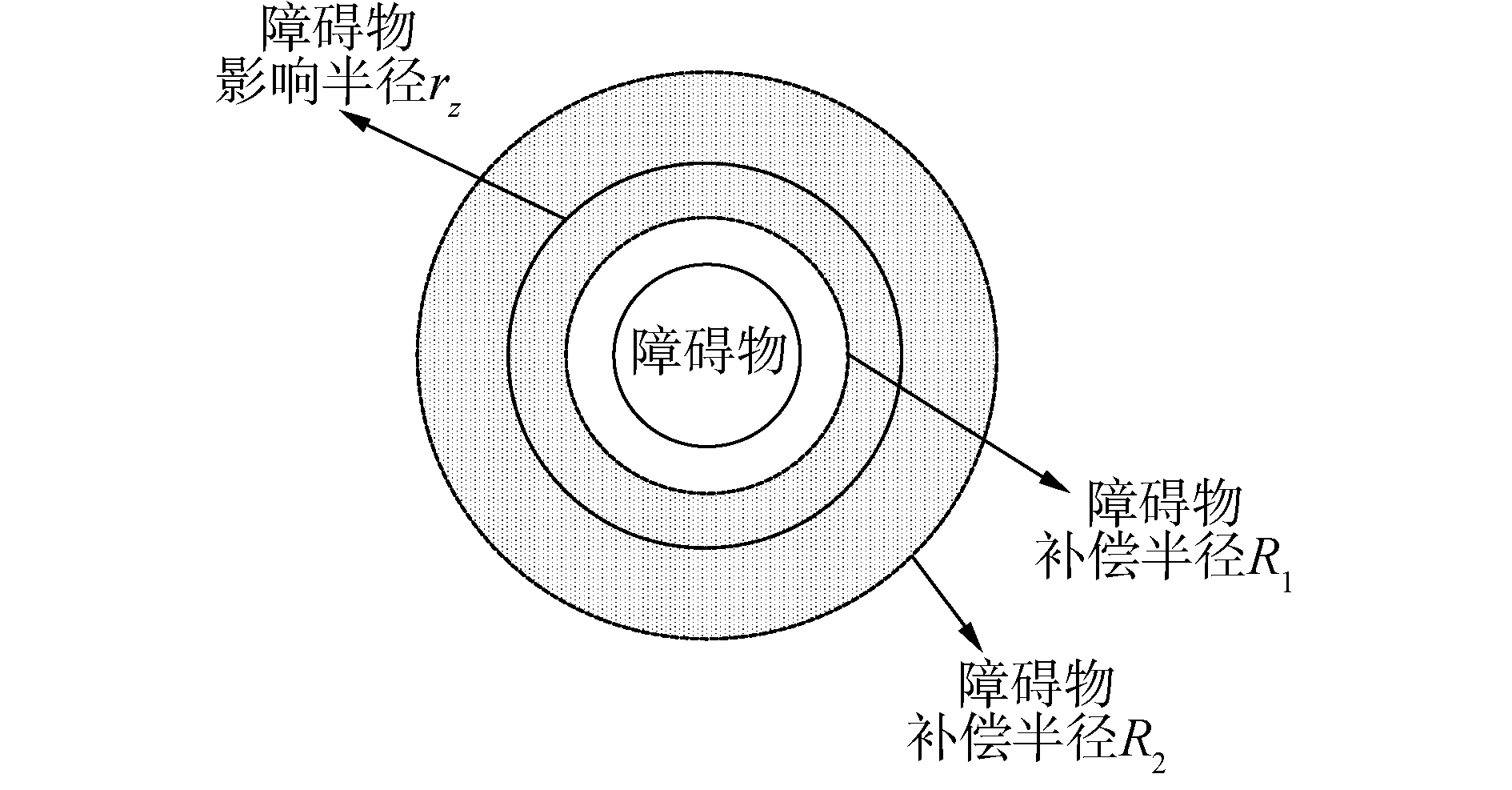
从图 5(a)可知,传统人工势场法所规划的轨迹,一是频繁存在较大弯角,二是最后陷入局部最小点,无法到达目标点。从图 5(b)可知,期望艏向角输出振荡明显,并最终陷入了死区。

|
Download:
|
| 图 5 基于传统方法规划的期望轨迹和艏向 Fig. 5 Expected trajectories and orientations based on traditional methods | |
2) 改进极小点人工势场法[11]的规划结果。
采用针对局部极小点而改进的人工势场法,仿真结果如图 6所示。

|
Download:
|
| 图 6 基于改进极小点规划的期望轨迹和艏向 Fig. 6 Expected trajectories and orientations based on the improved minimum point | |
从图 6可知,改进局部极小点后的规划轨迹虽然可以抵达目标点,但轨迹的期望艏向仍然存在振荡剧烈现象,受到艇体动力学特性等影响,在艏向控制中难以跟踪上剧烈振荡的期望艏向,从而无法实现对期望轨迹的跟踪;同时,存在诸多较大的弯角,也使无人艇很难跟踪上期望轨迹。
3) 障碍补偿人工势场法的规划结果。
加入障碍物补偿后,仿真结果如图 7所示,其中图 7(a)显示该轨迹可顺利到达目标点且轨迹中间没有出现较大弯角,图 7(b)所示期望艏向输出平缓、避免了振荡现象,这对于艏向控制极为有利。

|
Download:
|
| 图 7 基于障碍补偿规划的期望轨迹和艏向 Fig. 7 Expected trajectories and orientations based on obstacle compensation | |
码头末端轨迹规划考虑的是在码头区域内,距离目标泊位比较近的阶段,该阶段主要考虑的是码头终端约束,应用虚拟障碍物和虚拟目标点结合的人工势场法规划出从码头过渡位置到达泊位的满足无人艇和码头自身约束的轨迹,其中虚拟障碍物的位置、大小、个数信息根据经验设计得到,如图 8所示。

|
Download:
|
| 图 8 末端虚拟障碍物 Fig. 8 Terminal end virtual obstacle | |
远端轨迹规划与码头末端轨迹规划是分开来考虑的,由于远端轨迹末端无人艇艏向不确定,导致在过渡位置处与码头末端轨迹的衔接可能会出现较大拐点,所以需要规划出多条码头末端轨迹,根据远端轨迹过渡位置艏向角的不同选取不同的轨迹。
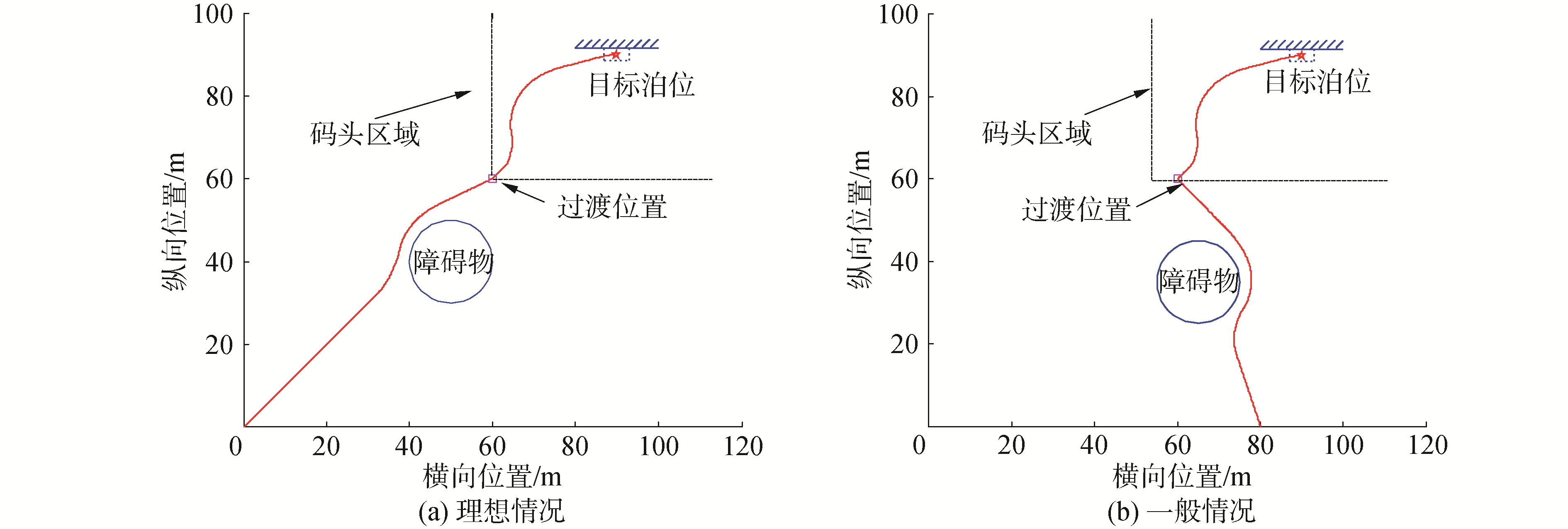
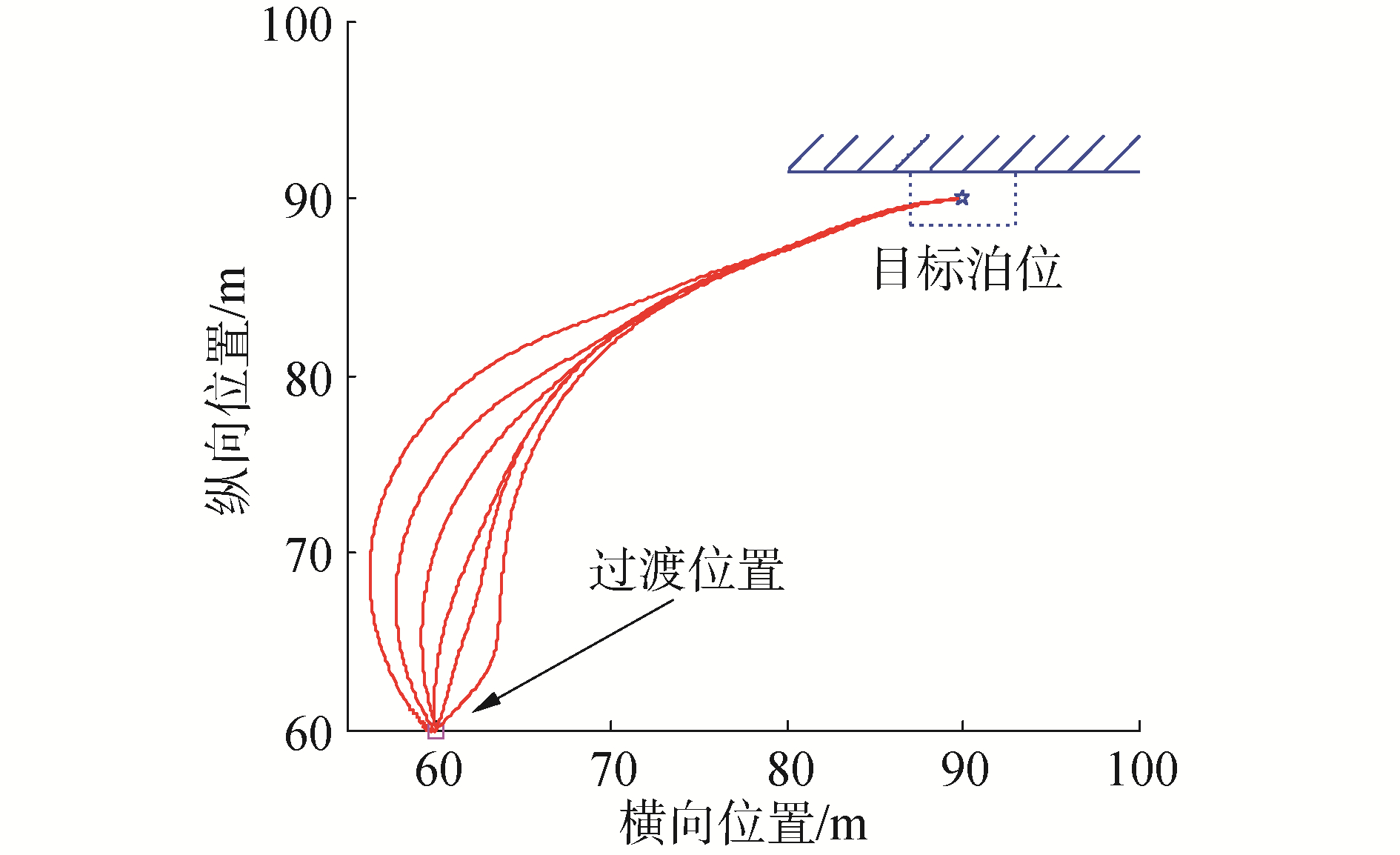
图 9(a)是期望的光顺轨迹,但大多数情况会如图 9(b)这样出现大的拐角。因此本文通过依次设置多个不同的虚拟障碍物,利用障碍补偿后的人工势场法规划出多条码头末端轨迹,如图 10所示,再根据无人艇到达过渡位置时不同的艏向角进行轨迹融合。
|
Download:
|
| 图 9 码头末端规划路径 Fig. 9 Terminal end planning path | |
|
Download:
|
| 图 10 码头末端轨迹库 Fig. 10 Terminal end trajectory library | |
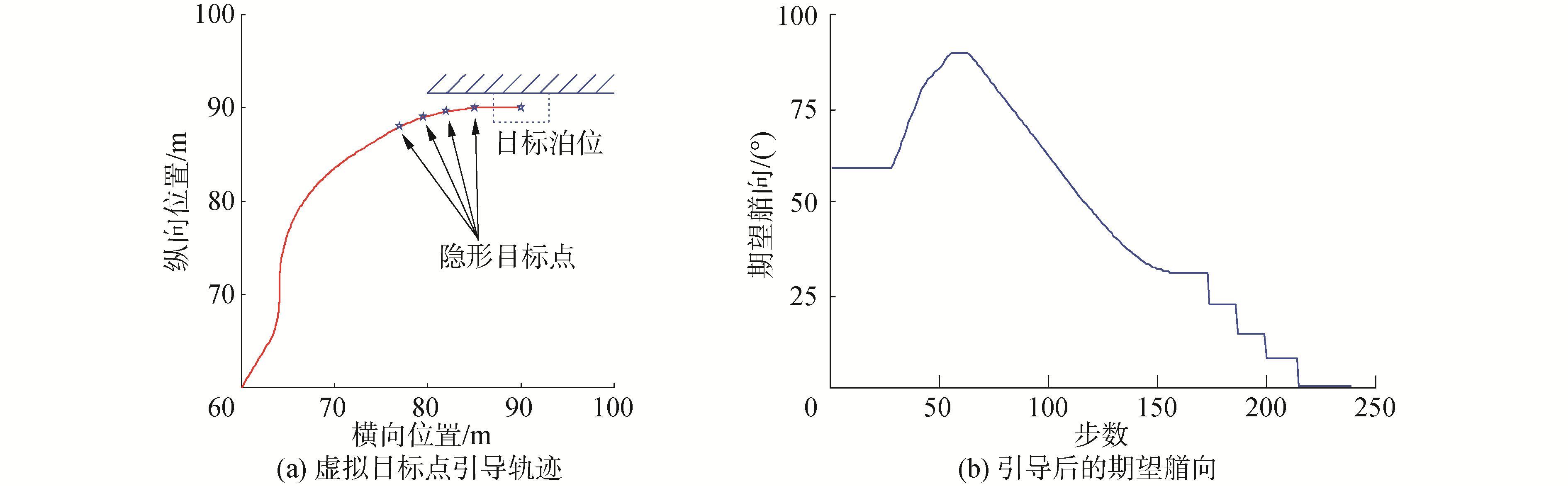
码头末端约束中要求无人艇最终姿态要与岸边平行,即艏向角等于0,由于无人艇进入码头区域之后速度大小受到一定的限制,当速度减小时无人艇舵效变差,艏向将不易调节,因此应尽早调节艏向,本文探索了虚拟目标点引导法,根据三次B样条曲线[12]添加4个虚拟目标点,如图 11(a)所示,艏向角的变化如图 11(b)。
|
Download:
|
| 图 11 基于虚拟目标的码头末端轨迹和期望艏向 Fig. 11 Terminal end trajectory and expected heading based on virtual targets | |
当无人艇通过过渡位置进入码头末端区域后,逐渐靠近目标泊位的过程中,在限制水域调节艇的姿态难度相对较大,最终还要停在目标泊位中心位置,因此其速度应缓慢减小至零。利用艇与轨迹中目标点的视线距离约束速度,其控制模型定义为:
| $ V_{t}=V_{\max } \frac{r}{r+\Delta r} $ | (9) |
式中:r表示无人艇到目标点的视线距离;Δr是用来调整无人艇航速的因数,如图 12为码头末端无人艇速度收敛图,Δr=5,即无人艇与目标点间的距离为5 m时,速度开始每步下降0.5 m。

|
Download:
|
| 图 12 基于视线法的码头末端期望速度 Fig. 12 Terminal end expected speed based on LOS | |
整合两阶段轨迹的关键在于过渡位置的衔接问题,根据不同的艏向位置选择不同的码头末端轨迹,远端轨迹规划阶段在过渡位置艏向为ψ,将轨迹从右至左依次命名为1~6号轨迹,基本选取规则为:
If 0°≤ψ < 30°,选取1号轨迹;
If 30°≤ψ < 60°,选取2号轨迹;
…
If 150°≤ψ < 180°,选取6号轨迹。
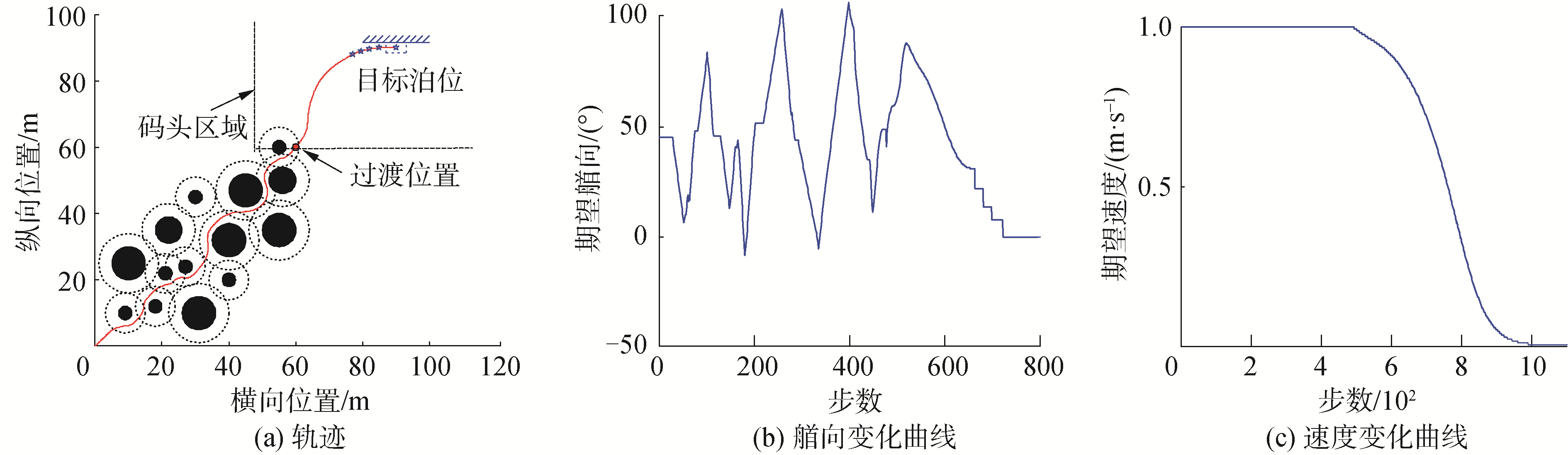
融合后的轨迹如图 13(a)所示,无人艇靠泊轨迹显示无人艇能够从障碍中安全通过,并最终到达目标泊位;从图 13(b)可知,无人艇自身运动约束也能满足艏向的变化要求;从图 13(c)可知速度曲线较为平滑,通过视线法(Line of Sight,LOS)解算期望速度的方法也很有效,最终规划出面向靠泊的可靠轨迹。
|
Download:
|
| 图 13 融合后的轨迹和期望艏向及速度 Fig. 13 Fusion trajectory and expected direction and speed | |
2017年5月,利用自研的“海豚-Ⅰ”号小型无人艇在松花江开展了无人艇自主靠泊试验。结合PD控制器[13-16]与传统人工势场轨迹规划方法进行对比试验,验证所提面向无人艇自主靠泊的分层轨迹规划方法的有效性,无人艇样机的长约2 m,宽约1 m,排水量约为55 kg,采用双推进器配置,整个无人艇控制系统基于嵌入式linux-OS搭建,软件运行环境为ARM Cortex-A5开发板,内核版本3.14.52。
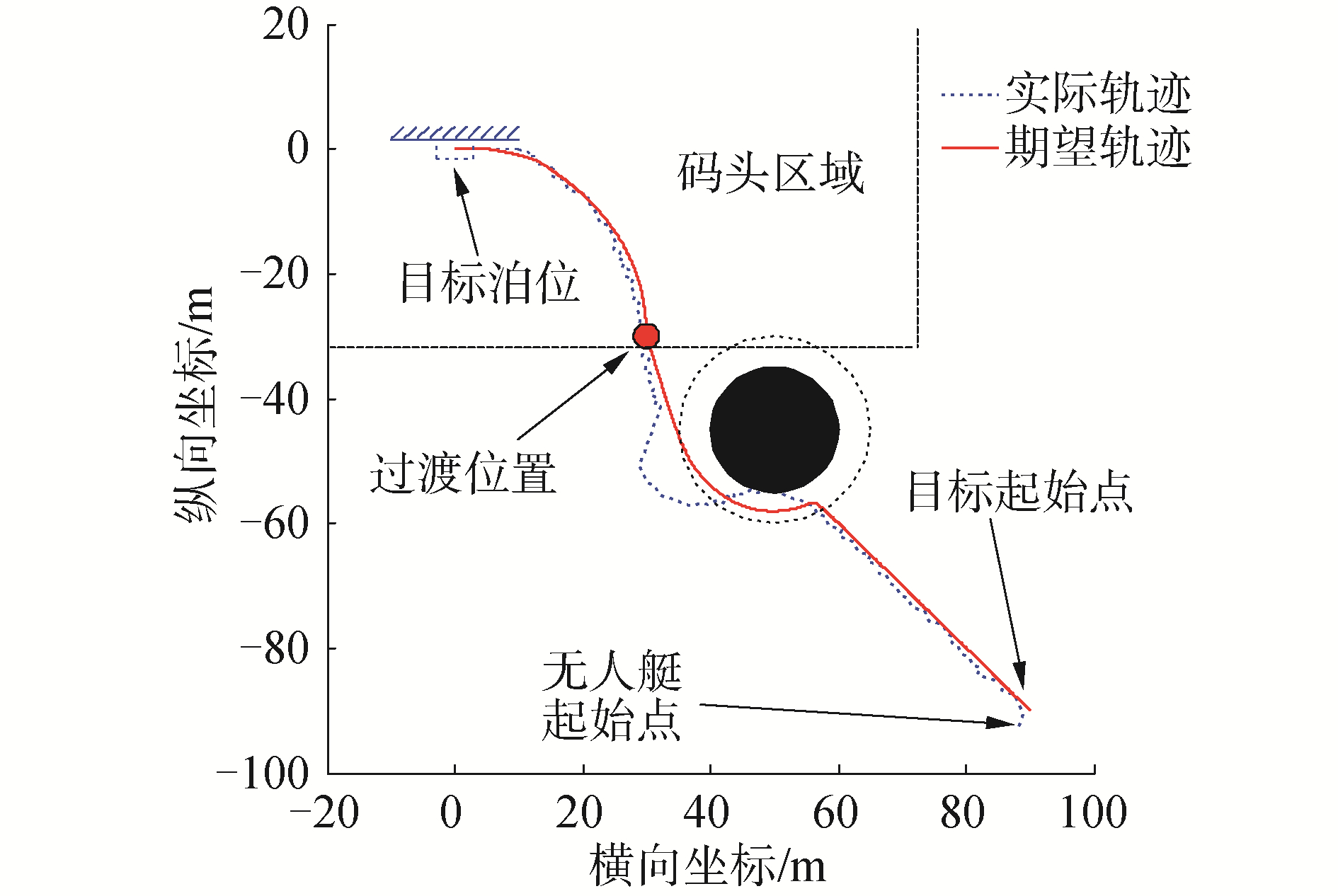
3.1 基于传统人工势场法的无人艇靠泊试验利用传统人工势场法规划出靠泊轨迹,再基于PD控制器对无人艇进行运动控制,完成靠泊试验(注:试验中发现,利用传统人工势场法在靠泊后期存在无人艇与岸壁发生碰撞的危险,基于安全性的考虑,防止无人艇在靠岸时发生碰撞造成设备损坏,本文仅在远端阶段采用传统人工势场法进行对比试验,而在码头末端阶段依然采用所提基于约束分析的改进人工势场法进行试验)。试验结果如图 15所示。

|
Download:
|
| 图 14 “海豚-Ⅰ”号无人艇样机 Fig. 14 "Dolphin-I" USV | |
|
Download:
|
| 图 15 基于传统人工势场法的无人艇靠泊试验 Fig. 15 USV berthing test based on traditional APF method | |
从图 15可知,无人艇在试图避开障碍的初始阶段,由于无人艇自身的惯性和低速下机动性较弱,无法及时规避障碍物而发生碰撞;同时由于期望艏向与当前艏向偏差较大,而留给无人艇调节的距离又很短,所以轨迹出现较大的超调。
如图 16所示为无人艇与目标点距离变化曲线,前期图中数据显示无人艇与目标点距离基本稳定在3 m(安全距离)左右,为了规避障碍物无人艇与目标点的距离增大到10 m左右,脱离障碍影响后距离重新收敛到3 m,进入码头末端轨迹阶段距离逐渐降到1 m以内。

|
Download:
|
| 图 16 无人艇与期望轨迹点之间的距离曲线 Fig. 16 The distance curve between USV and expected track points | |
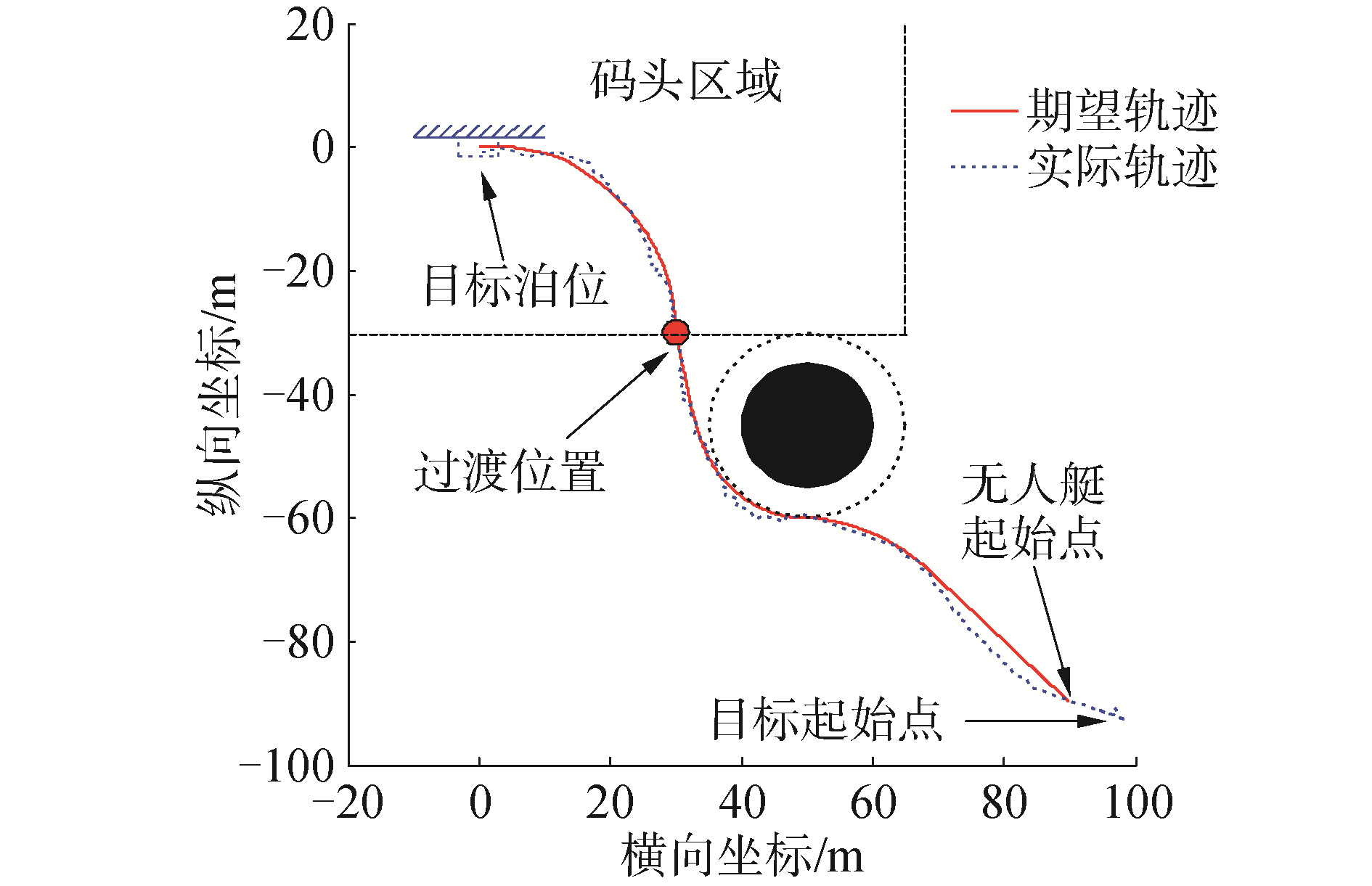
基于约束分析的改进人工势场法规划出无人艇靠泊轨迹,再借助相同的PD控制器进行无人艇靠泊试验,试验结果如图 17所示。
|
Download:
|
| 图 17 基于改进人工势场法的无人艇靠泊试验 Fig. 17 USV berthing test based on the improved APF method | |
如图 17所示,无人艇实际轨迹与目标轨迹基本重合,与图 15相比,既没有出现无人艇与障碍物相撞的情况,也没有出现轨迹超调的现象,表明该轨迹规划方法充分考虑了无人艇自身的惯性和低速下的弱机动状态,能使无人艇具有更好的跟踪性能。
从图 18可以看出,无人艇从静止开始加速追赶,无人艇与目标点的距离首先会增加,随后减小到与目标点相距3 m,最后到达目标泊位,靠泊过程没有出现大的超调现象。由靠泊试验对比可知,在控制器相同时,基于约束分析的改进人工势场法所规划轨迹具有更好的跟踪性能。

|
Download:
|
| 图 18 无人艇与期望轨迹点之间的距离曲线 Fig. 18 The distance curve between USV and expected track points | |
1) 提出面向无人艇自主靠泊的远端轨迹规划方法。解决了传统人工势场法中存在的期望艏向突变和振荡问题,所得到的轨迹光顺实用,有助于提升无人艇的跟踪控制性能;
2) 提出面向无人艇自主靠泊的码头末端轨迹规划方法。考虑靠泊后期码头泊位对无人艇艏向和速度的约束,使无人艇能够在不使用侧推的情况下自主、安全地完成靠泊任务;
3) 所提方法本身计算量相对较小,对无人艇自身硬件系统的要求较低,通过外场试验有效地验证其可行性和工程实用性。
| [1] |
张强, 张显库. 船舶自动靠泊控制研究综述[J]. 大连海事大学学报, 2015, 41(3): 1-9. ZHANG Qiang, ZHANG Xianku. Review on the research of ship automatic berthing control[J]. Journal of Dalian Maritime University, 2015, 41(3): 1-9. DOI:10.3969/j.issn.1671-7031.2015.03.001 (  0) 0)
|
| [2] |
AHMED Y A, HASEGAWA K. Implementation of automatic ship berthing using artificial neural network for free running experiment[C]//The 9th International Federation of Automatic Control (IFAC) Conference on Control Applications in Marine Systems (CAMS). Oxford, UK: IFAC-Elsevier Ltd, 2013: 25-30.
(  0) 0)
|
| [3] |
张闯, 范中洲. 大型船舶自主靠泊方法研究[J]. 中国水运, 2014, 14(8): 17-18, 20. ZHANG Chuang, FAN Zhongzhou. Study of self-berthing of the large vessel[J]. China water transport, 2014, 14(8): 17-18, 20. DOI:10.3969/j.issn.1006-7973.2014.08.006 (  0) 0)
|
| [4] |
WOO J, KIM N. Design of guidance law for docking of unmanned surface vehicle[J]. Journal of ocean engineering and technology, 2016, 30(3): 208-213. DOI:10.5574/KSOE.2016.30.3.208 (  0) 0)
|
| [5] |
VU M T, CHOI H S, OH J Y, et al. A study on automatic berthing control of an unmanned surface vehicle[J]. Journal of advanced research in ocean engineering, 2016, 2(4): 192-201. DOI:10.5574/JAROE.2016.2.4.192 (  0) 0)
|
| [6] |
AHMED Y A, HASEGAWA K. Automatic ship berthing using artificial neural network trained by consistent teaching data using nonlinear programming method[J]. Engineering applications of artificial intelligence, 2013, 26(10): 2287-2304. DOI:10.1016/j.engappai.2013.08.009 (  0) 0)
|
| [7] |
PARK J Y, KIM N. Design of an adaptive backstepping controller for auto-berthing a cruise ship under wind loads[J]. International journal of naval architecture and ocean engineering, 2014, 6(2): 347-360. DOI:10.2478/IJNAOE-2013-0184 (  0) 0)
|
| [8] |
MIZUNO N, KURODA M, OKAZAKI T, et al. Minimum time ship maneuvering method using neural network and nonlinear model predictive compensator[J]. Control engineering practice, 2007, 15(6): 757-765. DOI:10.1016/j.conengprac.2007.01.002 (  0) 0)
|
| [9] |
MIZUNO N, KAKAMI H, OKAZAKI T. Parallel simulation based predictive control scheme with application to approaching control for automatic berthing[J]. IFAC proceedings volumes, 2012, 45(27): 19-24. DOI:10.3182/20120919-3-IT-2046.00004 (  0) 0)
|
| [10] |
NAEEM W, HENRIQUE S C, HU Liang. A reactive COLREGs-compliant navigation strategy for autonomous maritime navigation[J]. IFAC-PapersOnLine, 2016, 49(23): 207-213. DOI:10.1016/j.ifacol.2016.10.344 (  0) 0)
|
| [11] |
江杰, 任恒靓. 基于改进人工势场法的移动机器人路径规划的研究[J]. 自动化应用, 2017(8): 80-81, 118. JIANG Jie, REN Hengliang. Research on mobile robot path planning based on improved artificial potential field[J]. Automation applications, 2017(8): 80-81, 118. DOI:10.3969/j.issn.1674-778X.2017.08.036 (  0) 0)
|
| [12] |
李晔, 姜言清, 张国成, 等. 考虑几何约束的AUV回收路径规划[J]. 机器人, 2015, 37(4): 478-485. LI Ye, JIANG Yanqing, ZHANG Guocheng, et al. AUV recovery path planning method considering geometrical constraints[J]. Robot, 2015, 37(4): 478-485. (  0) 0)
|
| [13] |
廖煜雷, 张铭钧, 董早鹏, 等. 无人艇运动控制方法的回顾与展望[J]. 中国造船, 2014, 55(4): 206-216. LIAO Yulei, ZHANG Mingjun, DONG Zaopeng, et al. Methods of motion control for unmanned surface vehicle:state of the art and perspective[J]. Shipbuilding of China, 2014, 55(4): 206-216. DOI:10.3969/j.issn.1000-4882.2014.04.025 (  0) 0)
|
| [14] |
LIAO Yulei, ZHANG Mingjun, WAN Lei. Serret-frenet frame based on path following control for underactuated unmanned surface vehicles with dynamic uncertainties[J]. Journal of Central South University, 2015, 22(1): 214-223. DOI:10.1007/s11771-015-2512-z (  0) 0)
|
| [15] |
LIAO Yulei, ZHANG Mingjun, WAN Lei, et al. Trajectory tracking control for underactuated unmanned surface vehicles with dynamic uncertainties[J]. Journal of central south university, 2016, 23(2): 370-378. DOI:10.1007/s11771-016-3082-4 (  0) 0)
|
| [16] |
LIAO Yulei, WANG Leifeng, LI Yiming, et al. The intelligent control system and experiments for an unmanned wave glider[J]. PLoS one, 2016, 11(12): e0168792. DOI:10.1371/journal.pone.0168792 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


