2. 中国船舶工业集团公司第七〇八研究所, 上海 200011
2. NO. 708 Research Institute of CSSC, Shanghai 200000, China
三体船由于其片体的存在使其获得了出色的水动力特性,但主体与片体之间的干扰效应增加了理论预报的难度。目前,基于无航速三维势流理论建立起来的数值算法被广泛地应用于船舶运动与波浪载荷数值预报。采用此类方法计算三体船运动与波浪载荷响应时,船体实际上没有前进速度,数值模型中一部分辐射波将在主船体与片体之间来回振荡而无法有效传播出去,当该区域上波浪的振荡频率与船体摇荡频率接近时便会出现共振现象。在发生共振的波浪频率附近,三体船的升沉与纵摇运动响应会急剧增大,船体梁所受的垂向载荷也会急剧增大。在理论计算中遇到的共振现象主要是由于采用无航速理论以及忽略水的粘性引起的,在真实的物理世界中并不会出现,所以这种仅仅在数值计算中出现的共振现象称为“伪共振”。通常伪共振对应的波浪频率处于海浪谱中主要波浪频率范围内,因此为了准确预报三体船的运动与波浪载荷,必须采取措施消除伪共振所带来的影响。
三体船作为一种高性能船型,有着十分突出的水动力性能,目前有大量针对三体船水动力性能的研究,包括三体船阻力特性[1-5]、耐波性[6-8]等方面。同时,由于船型特殊,学者们对三体船船体梁载荷以及连接桥载荷特点也开展了研究[9-11]。对于三体船运动与波浪载荷数值预报中的伪共振问题,相关的研究工作较少。Wu等[12]运用三维线性势流理论研究了浮体间距对水动力系数的影响;朱仁传[13]采用数值模拟方法分析了间隙对多浮体水动力性能的影响并且分析了在某些频率上的共振现象;繆国平等[14]针对运用切片理论计算双体船运动时遇到的伪共振问题,提出在两侧体之间的自由面上布置人工粘性阻尼来进行处理,并且取得了不错的效果。
本文基于三维势流理论,以一条三体船型为例对伪共振的成因及其相应的特性进行了系统的研究;给出了通过拓展的边界积分方程来解决伪共振问题的方法;最后给出了修正后的计算结果并与模型试验结果进行对比。
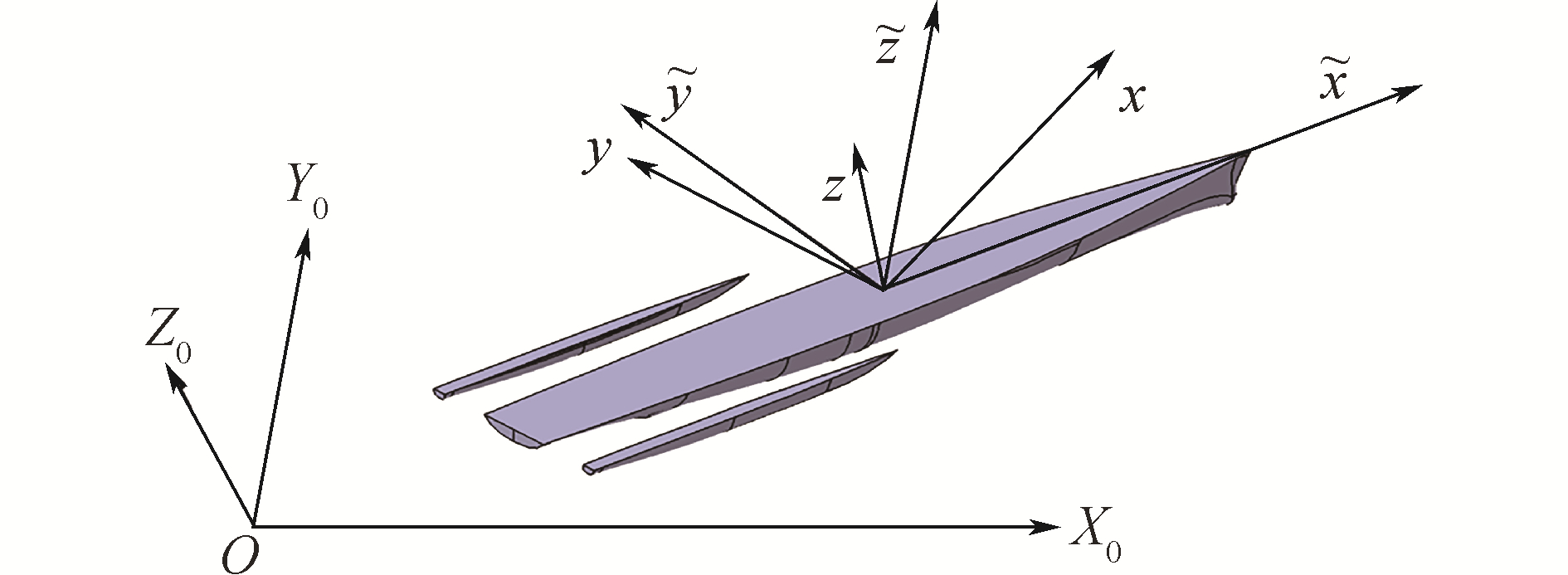
1 考虑粘性修正的三体船伪共振处理方法假设三体船以恒定速度U在规则波浪中运动,通过3个坐标系来描述整个船波系统:O-X0Y0Z0为固定坐标系,Z0轴竖直向上,OX0Y0平面与静水面重合;o-xyz是动坐标系,与船固结在一起;o-
|
Download:
|
| 图 1 坐标系示意 Fig. 1 Coordinate system | |
计算水域为无限水深,入射波的浪向角为β,则在参考坐标系中入射波速度势表示为:

|
(1) |
式中:A为入射波波幅;k为波数;g为重力加速度;ω0为波浪自然频率;ω为波浪遭遇频率。引入线性化假设条件,在规则波中流体总的非定常速度势可以表示为:
| $ \begin{aligned} \phi(x, y, z)=& \phi_{I}(x, y, z)+\phi_{D}(x, y, z)+\\ & \sum\limits_{j=1}^{6} \dot{\zeta}_{j} \phi_{j}(x, y, z) \end{aligned} $ | (2) |
式中:ϕI(x, y, z)为入射势;ϕD(x, y, z)为绕射势;ϕj(x, y, z)是船体单位模态运动下产生的辐射势;
对于求解非定常速度势的定解条件,本文对自由面条件进行如下修改:
| $ \begin{array}{l} [L]{\nabla ^2}{\phi _j}(x, y, z) = 0\\ [F]\left\{ {\begin{array}{*{20}{l}} { - {\omega ^2}{\phi _j} + g\frac{{\partial {\phi _j}}}{{\partial z}} = 0, }&{自由面{F_1}}\\ {g\frac{{\partial {\phi _j}}}{{\partial z}} - \left( {{\omega ^2} - i\upsilon \omega } \right){\phi _j} = 0, }&{自由面{F_2}} \end{array}} \right.\\ [S]\left\{ {\begin{array}{*{20}{l}} {{{\left. {\frac{{\partial {\phi _j}}}{{\partial n}}} \right|}_{S0}} = {n_j}}\\ {\frac{{\partial {\phi _7}}}{{\partial n}} = - \frac{{\partial {\phi _I}}}{{\partial n}}} \end{array}} \right.\\ [B]\mathop {\lim }\limits_{z \to - \infty } \nabla {\phi _j} = 0\\ [R]\mathop {\lim }\limits_{R \to \infty } \sqrt R \left( {\frac{{\partial {\phi _j}}}{{\partial R}} - ik{\phi _j}} \right) = 0 \end{array} $ | (3) |
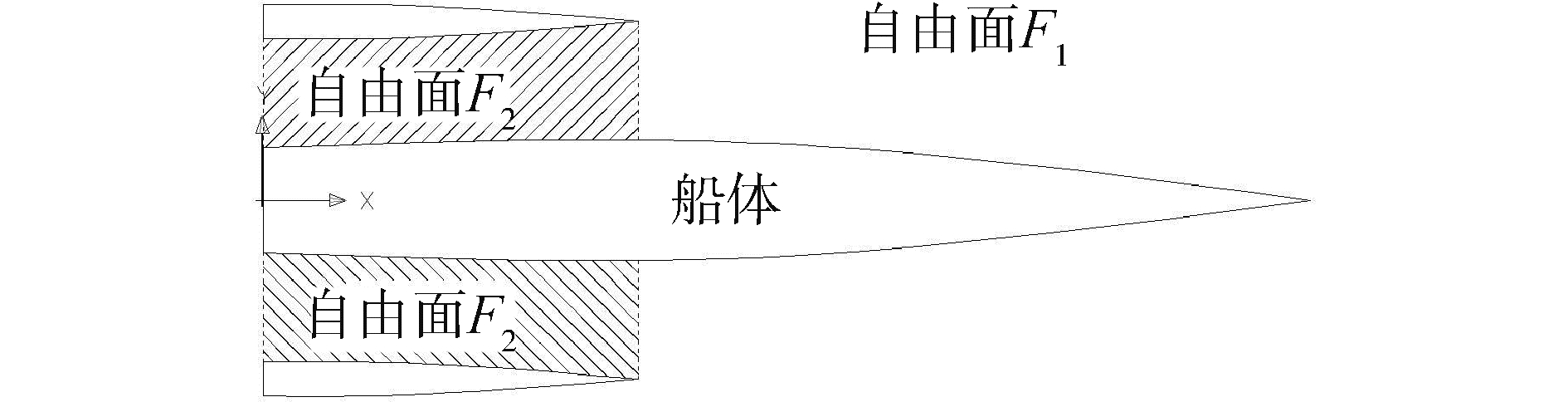
式中:j=1, 2, …, 6;ϕ7即为绕射势。定解条件中的自由面条件分为2部分:F2表示主船体与片体之间的自由面,为了消除伪共振现象,需要在此区域划分水动力网格,并在自由面条件中添加了粘性阻尼项;F1表示其他自由面,依然满足原自由面条件。选取的自由面格林函数无法满足物面条件以及经过修改的自由面条件。
|
Download:
|
| 图 2 自由面划分示意 Fig. 2 Division of the free surface | |
通过在船体内部虚构流场得到源汇分布模型[15-17],得到速度势的表达式为:
| $ \phi_{j}(P)=\iint\limits_{S_{+}+F_{2}} \sigma(Q) G(P, Q) \mathrm{d} s $ | (4) |
代入修改的自由面条件以及物面条件,得到扩展的分布源积分方程:
| $ \left\{ {\begin{array}{*{20}{l}} {2\pi \sigma (P) + \frac{{{\text{i}}\upsilon \omega }}{g}\iint\limits_{{F_2} + {S_0}} \sigma (Q)G(P, Q){\text{d}}s = 0, } \\ {\;\;\;P \in {F_2}} \\ {2\pi \sigma (P) + \iint\limits_{{F_2} + {S_0}} \sigma (Q)\frac{{\partial G(P, Q)}}{{\partial n}}{\text{d}}s = \frac{{\partial {\phi _j}(P)}}{{\partial n}}, } \\ {\;\;\;P \in {S_0}} \end{array}} \right. $ | (5) |
式中:j=1, 2, 3,…,7。源汇分布密度需要由物面条件和修改后的自由面条件共同确定,当粘性系数为0时与普通的分布源积分方程无异。
求解出速度势之后便可以求解波浪激励力、辐射力以及船体运动方程。
波浪激励力:
| $ F_{i}=\rho \iint\limits_{s}\left(\mathrm{i} \omega+U \frac{\partial}{\partial x}\right)\left(\phi_{I}(x, y, z)+\phi_{D}(x, y, z) n_{i}\right) \mathrm{d} S $ | (6) |
式中i=1, 2, …, 6。
辐射力:
| $ \begin{array}{c}{\sum\limits_{j=1}^{6} D_{i j} \zeta_{j}=-\rho \iint\limits_{s} \sum\limits_{j=1}^{6}\left(\mathrm{i} \omega+U \frac{\partial}{\partial x}\right) \zeta_{j} \phi_{j}(x, y, z) n_{j} \mathrm{d} S=} \\ {\sum\limits_{j=1}^{6}\left(\omega^{2} A_{i j}+\mathrm{i} \omega B_{i j}\right) \zeta_{j}}\end{array} $ | (7) |
船体运动方程:
| $ \sum\limits_{j = 1}^6 {\left[ { - {\omega ^2}\left( {M + {A_{ij}}} \right) - {\rm{i}}\omega {B_{ij}} + {C_{ij}}} \right]} {\zeta _j} = {F_i} $ | (8) |
式中:Aij为附加质量系数;Bij为阻尼系数;Cij为静水恢复系数;ζj为j方向的运动幅值。
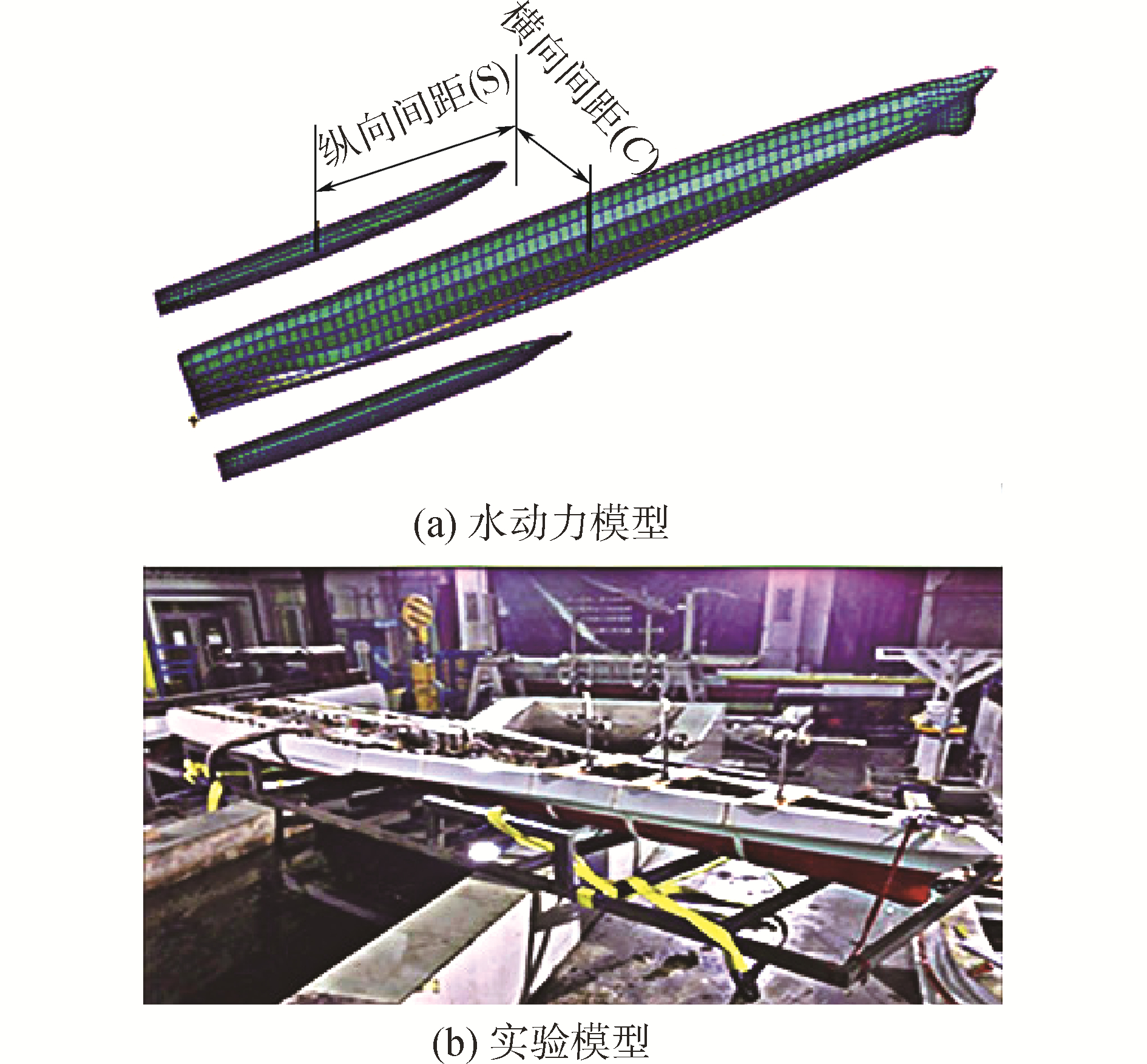
2 三体船伪共振特性分析本文基于上述理论方法对三体船伪共振问题进行了系统的计算分析。所有计算结果均以单位波幅下的响应形式给出。为了对数值计算方法进行验证,开展了模型试验研究。试验模型沿纵向划分为7分段,其中片体划分为2分段,实验中波长范围为0.4到1.5倍船长。其中垂向弯矩(VBM)采用无因次化表示:垂向弯矩My/(AρgL2B),L为设计水线长;B为型宽;My表示从船中剖面垂向弯矩。
| 表 1 三体船主尺度 Table 1 Main particulars of a trimaran |
图 4展示的是取不同面元数时的运动响应计算结果,计算工况取为有伪共振发生的迎浪工况。当面元数大于1 112个后,计算得到的运动响应结果趋于稳定。在伪共振发生的频率段内,随着面元数的增加,伪共振峰值大小逐渐减小,当面元数超过1 112个时,伪共振峰值也趋于稳定。以上计算表明当面元数达到1 112个时,计算得到的运动响应结果已经达到稳定,后续再增加面元数对计算结果的精度没有太大影响。在后续计算中使用的水动力模型对应的面元数均为1 112个。
|
Download:
|
| 图 3 三体船水动力模型与试验模型 Fig. 3 Hydrodynamic model and test modle of the trimaran | |

|
Download:
|
| 图 4 垂荡、纵摇运动随不同面元数变化 Fig. 4 Heave and pitch variation with different grids | |
图 5是数值模拟与模型试验的结果对比,可以看到理论结果与实验结果在低频段吻合较好,而在中高频率段内有很大差异,数值计算中存在伪共振问题,需要给予修正。

|
Download:
|
| 图 5 垂荡、纵摇运动和垂向弯矩理论与试验结果(12 kn) Fig. 5 Theoretical and experimental results of heave, pitch and VBM (12 kn) | |
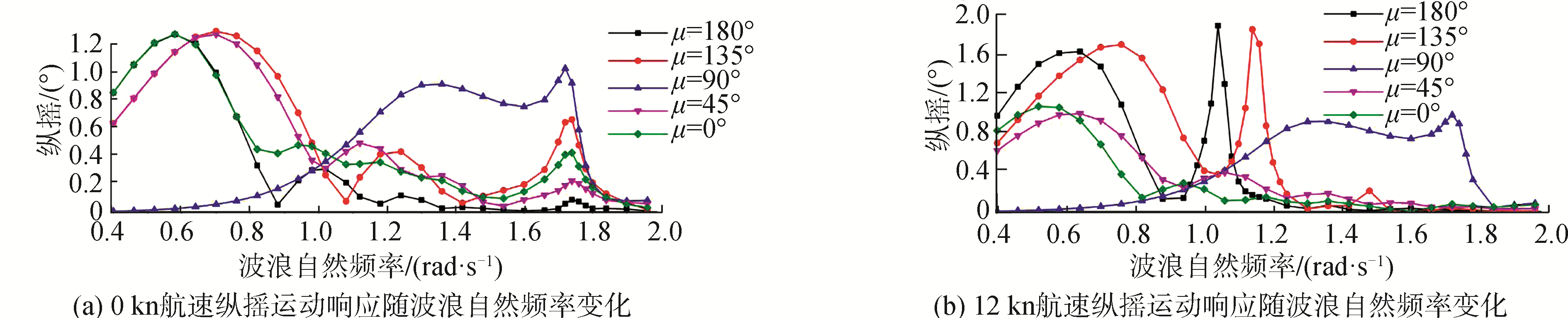
图 6~8展示的是三体船垂荡、纵摇、横摇运动响应随波浪频率的变化情况。可以看到,伪共振现象出现在垂荡与纵摇响应中,而横摇运动响应中并没有出现。对于垂荡与纵摇响应,当航速是0时,在波浪频率为1.74 rad/s处,各浪向下均有伪共振现象出现;而当航速是12 kn时,有伪共振出现的浪向则是迎浪、艏斜浪以及横浪。

|
Download:
|
| 图 6 0、12 kn航速时各浪向下垂荡运动 Fig. 6 Heave in different directions at 0 and 12 knots | |
|
Download:
|
| 图 7 0、12 kn航速时各浪向下纵摇运动 Fig. 7 Pitch in different directions at 0 and 12 knots | |

|
Download:
|
| 图 8 0、12 kn航速时各浪向下横摇运动 Fig. 8 Roll in different directions at 0 and 12 knots | |
在本文采用计算方法中,航速效应是通过将波浪自然频率转换为遭遇频率来体现。当波浪频率转换为遭遇频率是,不同航速及浪向下为伪共振峰值均对应1.74 rad/s。在本文采用的理论框架下,同一艘船型伪共振峰值遭遇频率与航速和浪向的关系不大。
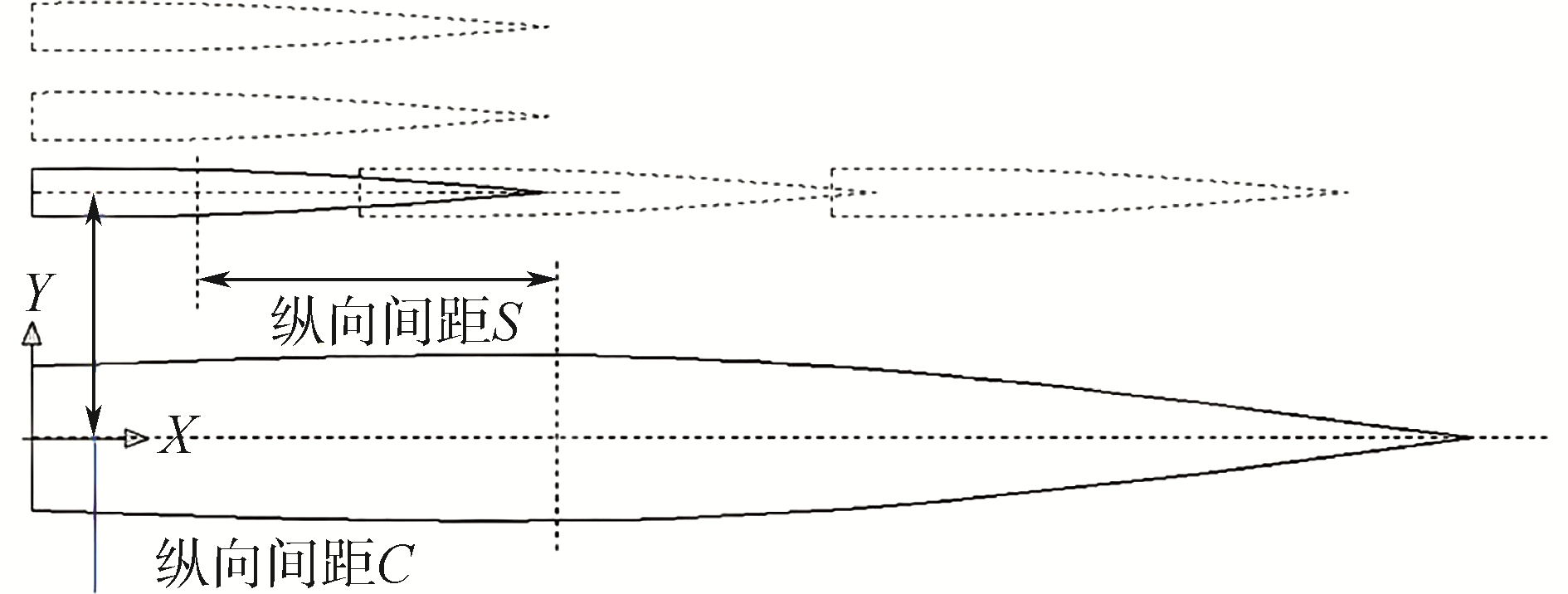
2.3 片体布置位置对伪共振的影响对片体与主船体横向间距C与纵向间距S无因次化,分别为:横向间距C/B;纵向间距S/L。其中B为型宽,L为设计水线长。
图 10展现的是主船体与片体的横向间距变化对伪共振的影响。随着横向间距的增大,伪共振的峰值频率在逐渐减小,峰值大小有先增大后减小的趋势。当横向间距增大到一定程度时在高频段出现了较小的二次共振。通过无限水深波长与频率的关系
|
Download:
|
| 图 9 三体船片体的不同布置位置 Fig. 9 Different layouts of side-hulls of the trimaran | |

|
Download:
|
| 图 10 垂荡和纵摇运动受片体横向位置的影响(12 kn) Fig. 10 Heave and pitch with different transversely position of side-hulls (12 kn) | |
图 11展现的是片体纵向位置的变化对伪共振的影响。片体从船艉移向船艏,伪共振峰值有先减小后增大的变化趋势,当片体位于船中部时没有发生伪共振。在片体远离船中时,自由面F2上波浪对船重心(接近于船体中部)产生的力矩较大,因而会使纵摇响应出现较大峰值;片体位于船中时,无法产生大的力矩,因而纵摇响应中没有出现伪共振。而垂荡响应中出现较大峰值则主要是由于纵摇与垂荡的耦合引起的,这在后续的计算中会加以证明。

|
Download:
|
| 图 11 垂荡和纵摇运动受片体纵向位置的影响(12 kn) Fig. 11 Heave and pitch with different longitudinally position of side-hulls (12 kn) | |
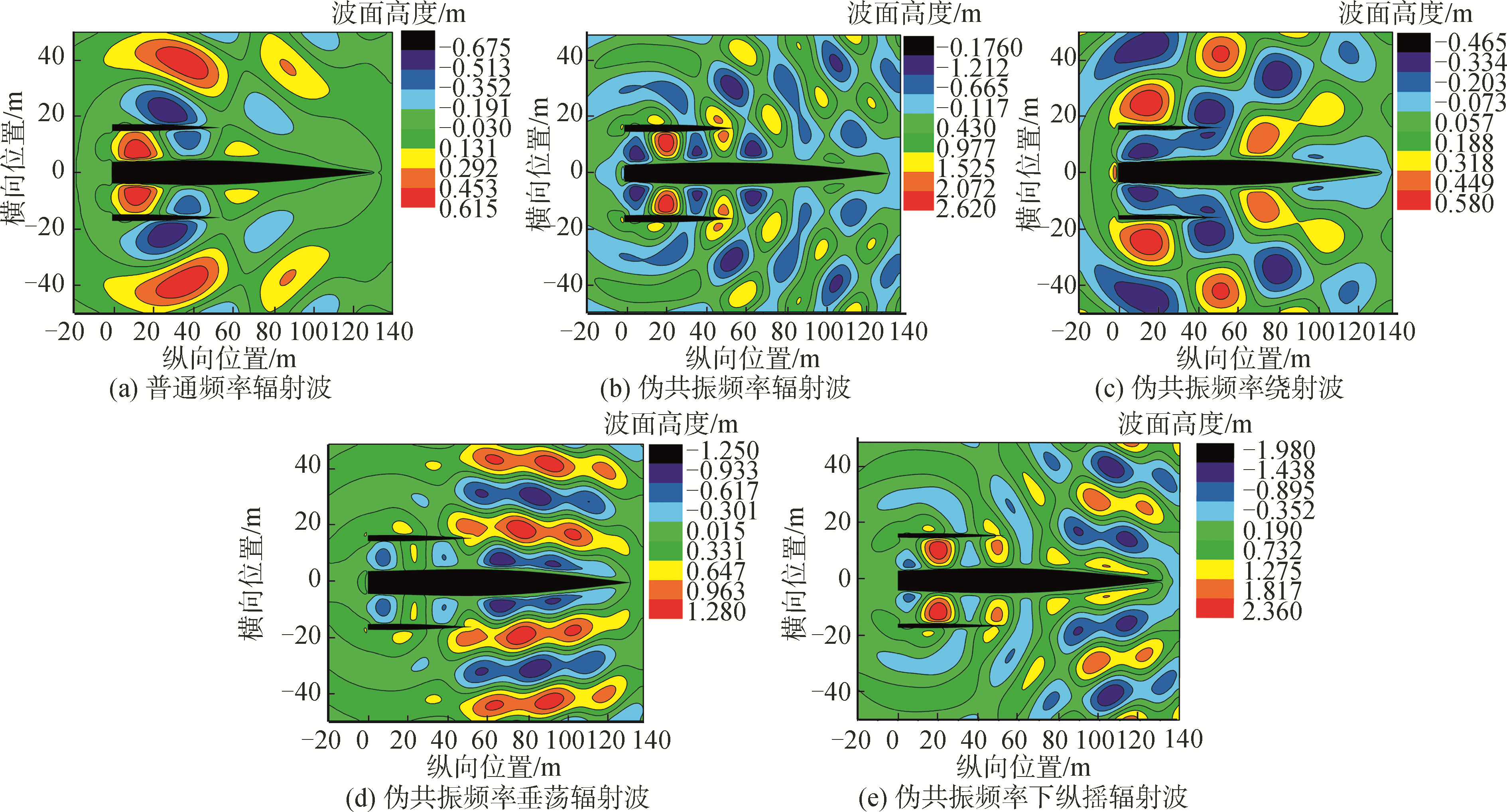
伪共振的出现实质是船波相互作用的影响,而对船舶摇荡兴波的波面高度分析能够反映不同成分的波浪能量在不同区域的变化特点。图 12为三体船摇荡兴波的波面高度的变化特点。
|
Download:
|
| 图 12 自由面上辐射波和绕射波波形 Fig. 12 Wave profile of radiation and diffraction wave on free surface of | |
图 12(a),当计算频率取为伪共振峰值频率时,在主船体与片体之间的自由面上出现了波幅异常巨大的辐射波浪,说明有相当大的能量聚集在该区域。图 12(b),当频率变为普通频率时,整个自由面上并未出现波幅异常巨大的辐射波。图 12(c),选取伪共振峰值频率计算,输出三体船的绕射波波面,整个自由面上并未出现波幅异常巨大的绕射波浪,表明辐射波的复杂传播是引起伪共振的关键所在,与绕射波的传播基本没有关系。
图 12(d)、(e)是伪共振峰值频率下三体船垂荡与纵摇运动产生的辐射波面图。在主船体与片体之间的自由面上,由纵摇运动产生的辐射波在该区域出现了波幅异常巨大的波浪,而垂荡运动产生的相对较大的辐射波并没有出现在主船体与片体之间的区域。上述计算说明伪共振发生时船与波能量的相互传递主要来自纵摇运动与辐射波的耦合,同时也表明纵摇运动似乎更有利于船体与波浪能量的相互传递。而垂荡运动响应上出现伪共振更多的是受到纵摇运动的影响。
3 三体船运动与载荷响应的伪共振修正以上计算表明,出现伪共振时有大量的波浪能量聚集在主船体与片体之间的自由面上。本文提出在主船体与片体之间的自由面上布置人工粘性阻尼,以此耗散掉在该区域来回振荡的部分辐射波的能量,从而达到消除伪共振的目的。
图 13(a)、(b)给出了选取不同粘性系数的数值计算结果与模型实验值的对比情况。在主船体与片体间的自由面(F2区域)上添加粘性阻尼后伪共振情况得到明显改善;并且在一定范围内,随着粘性阻尼系数增大,伪共振处的峰值在逐渐减小,符合客观事实;在其他频率段,修改自由面条件后对三体船运动响应并没有明显的影响;对比试验数据,当粘性阻尼系数取为0.4时,数值计算结果与试验数据能较好的吻合。

|
Download:
|
| 图 13 添加不同粘性阻尼后三体船运动响应以及兴波图 Fig. 13 Motion response and wave profile of trimaran after adding different viscous-coefficients | |
图 13(c)、(d)给出了选取不同粘性系数时对应的辐射波波面图,波幅最大的波浪依然出现在主船体与片体之间的自由面上,但是波幅的大小随着粘性系数的增大而逐渐减小;从能量的角度,波幅的减小说明该区域有部分波浪能量耗散出去,对于最终形成的船波稳态系统而言,意味着该区域的能量降低到了一定的程度。
从整个三体船的数值计算结果上来说,该方法对于伪共振有很好的处理效果。但是不同的片体布置方式或者同一艘船不同航速对粘性系数的选取有影响,根据本文的计算经验,粘性系数范围大致在0.1~0.5。
4 结论1) 对于本文所研究的伪共振问题,航速效应对伪共振的峰值大小有很大影响;在有航速情况下,伪共振的出现浪向角趋于迎浪到横浪之间;三体船的船型布置是影响伪共振的峰值频率变化的主要因素。
2) 伪共振的发生主要是来自纵摇运动与辐射波的耦合作用,而垂荡运动响应上出现伪共振更多的是受到纵摇运动的影响。
3) 拓展的积分方程方法能够有效的用于解决伪共振问题且对于其他频率段的计算结果影响不大,根据本文计算经验,最佳粘性系数一般取为0.1~0.5。
| [1] |
CHEN Jingpu, ZHU Dexiang, HE Shulong. Research on numerical prediction method for wavemaking resistance of catamaran/trimaran[J]. Journal of ship mechanics, 2006, 10(2): 23-29. (  0) 0)
|
| [2] |
李培勇, 裘泳铭, 顾敏童, 等. 超细长三体船阻力计算研究[J]. 船舶工程, 2002(2): 10-12. LI Peiyong, QIU Yongming, GU Minting, et al. Resistance analysis and calculation of trimaran with super-slender hulls[J]. Ship engineering, 2002(2): 10-12. DOI:10.3969/j.issn.1000-6982.2002.02.002 (  0) 0)
|
| [3] |
陈康, 黄德波. CFD技术在三体船阻力性能研究中的应用[J]. 哈尔滨工程大学学报, 2006, 27(3): 362-366. CHEN Kang, HUANG Debo. Application of CFD technology to the research of resistance performance of trimaran[J]. Journal of Harbin Engineering University, 2006, 27(3): 362-366. DOI:10.3969/j.issn.1006-7043.2006.03.010 (  0) 0)
|
| [4] |
ZHA Ruosi, YE Haixuan, SHEN Zhirong, et al. Numerical computations of resistance of high speed catamaran in calm water[J]. Journal of hydrodynamics, 2014, 26(6): 930-938. DOI:10.1016/S1001-6058(14)60102-5 (  0) 0)
|
| [5] |
WEI Yu, CHEN Xujun, WU Guanghuai, et al. A fast numerical method for trimaran wave resistance prediction[J]. Ocean engineering, 2015, 107: 70-84. DOI:10.1016/j.oceaneng.2015.07.008 (  0) 0)
|
| [6] |
李培勇, 冯铁城, 裘泳铭. 三体船横摇运动[J]. 中国造船, 2003, 44(1): 24-30. LI Peiyong, FENG Tiecheng, QIU Yongming. Investigation of trimaran roll motion characteristics[J]. Shipbuilding of China, 2003, 44(1): 24-30. DOI:10.3969/j.issn.1000-4882.2003.01.004 (  0) 0)
|
| [7] |
LEWANDOWSKI E M. Multi-vessel seakeeping computations with linear potential theory[J]. Ocean engineering, 2008, 35(11/12): 1121-1131. (  0) 0)
|
| [8] |
CASTIGLIONE T, STERN F, BOVA S, et al. Numerical investigation of the seakeeping behavior of a catamaran advancing in regular head waves[J]. Ocean engineering, 2011, 38(16): 1806-1822. DOI:10.1016/j.oceaneng.2011.09.003 (  0) 0)
|
| [9] |
FANG M C, CHEN T Y. A parametric study of wave loads on trimaran ships traveling in waves[J]. Ocean engineering, 2008, 35(8/9): 749-762. (  0) 0)
|
| [10] |
WANG Xueliang, HU Jiajun, GU Xuelian, et al. Comparative studies of the transverse structure design wave loads for a trimaran by model tests and rule calculations[J]. Journal of ship mechanics, 2011, 15(3): 269-275. (  0) 0)
|
| [11] |
XU Min, ZHANG Shilian. A numerical study on side hull optimization for trimaran[J]. Journal of hydrodynamics, 2011, 23(2): 265-272. DOI:10.1016/S1001-6058(10)60112-6 (  0) 0)
|
| [12] |
WU Guanghuai, SHEN Qing, CHEN Xujun, et al. Influence of the distance between floating bodies on hydrodynamic coefficients of floating multi-body system[J]. The ocean engineering, 2003, 21(4): 29-34. (  0) 0)
|
| [13] |
朱仁传, 朱海荣, 缪国平. 具有小间隙的多浮体系统水动力共振现象[J]. 上海交通大学学报, 2008, 42(8): 1238-1242. ZHU Renchuan, ZHU Hairong, LIAO Guopin. Influences on hydrodynamics of multiple floating structures with small gap in between[J]. Journal of Shanghai Jiao Tong University, 2008, 42(8): 1238-1242. DOI:10.3321/j.issn:1006-2467.2008.08.005 (  0) 0)
|
| [14] |
缪国平, 刘应中, 李谊乐, 等. 切片理论应用于双体船运动计算时的伪共振问题[J]. 中国造船, 1997(2): 32-38. LIAO Guopin, LIU Yingzhong, LI Yile, et al. On false resonance in application of strip theory to motion estimation for catamarans[J]. Shipbuilding of China, 1997(2): 32-38. (  0) 0)
|
| [15] |
NEWMAN J N. Double-precision evaluation of the oscillatory source potential[J]. Journal of ship research, 1984, 28(3): 151-154. (  0) 0)
|
| [16] |
缪国平, 刘应中. 关于不规则频率的注记[J]. 水动力学研究与进展, 1985(1): 71-81. LIAO Guoping, LIU Yingzhong. Notes on irregular frequencies[J]. Chinese journal of hydrodynamics, 1985(1): 71-81. (  0) 0)
|
| [17] |
OHMATSU S. On the irregular frequencies in the theory of oscillating bodies in a free surface[R]. Papers of Ship Research Institute, Tokyo, Japan: Ship Research Institute, 1975.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


