功能梯度材料是一种宏观材料特性在空间上呈连续梯度变化的多相复合材料,具有强度高、韧性好、耐高温、抗腐蚀等优良性能,已在船舶、核能、航空航天等领域得到广泛应用[1]。Praveen等[2]采用有限元法与von Karman板理论研究了功能梯度方板的静态、动态热弹性响应。Ferreira等[3]采用配点法与高阶剪切变形理论求解了功能梯度厚板自由振动的固有频率。Zhao等[4]基于无网格kp-Ritz法与一阶剪切变形理论研究了方板与斜板的振动特性。杨正光等[5]采用状态空间法获得了功能梯度板静力弯曲与自振基频的精确解。
为了减轻结构的重量、实现结构之间的连接、改变结构的共振频率,开孔板被广泛应用于工程中。Huang等[6]研究了带圆形、正方形、三角形等多种开孔形状的方板的振动特性;Kwak等[7]提出了不同坐标系统下的Rayleigh-Ritz法,并用其分析了带矩形或圆形开孔的矩形板的自由振动;Cho等[8]采用假设模态法研究了含多种开孔形状的矩形板的自由振动;文献[9-10]采用经典板理论计算了带矩形、圆形开孔的矩形板横向振动的固有频率;曹志远等[11]采用半解析梯度有限元法分析了复杂形状及开孔功能梯度板的三维振动;Lal等[12]研究了开孔对受机械与热载荷的功能梯度板后屈曲响应的影响。
等几何分析是由Hughes等提出的一种新型的有限元法[13-14]提出的有限元法,该方法采用CAD中的样条基函数统一表示几何模型与分析模型,从而将CAD与FEA有机地结合起来。与传统有限元相比,等几何分析有效地消除了网格划分引起的几何误差,能够轻易地提高样条基函数的阶次,近十几年来已应用于多个领域[15-18]。
本文首先介绍基于一阶剪切变形理论的功能梯度板自由振动的基本公式与等几何分析的基本原理,然后计算出各向同性孔板的固有频率,将其与现有文献中的结果进行比较,验证了本方法的有效性,最后分析了多种因素对功能梯度板自由振动的影响。
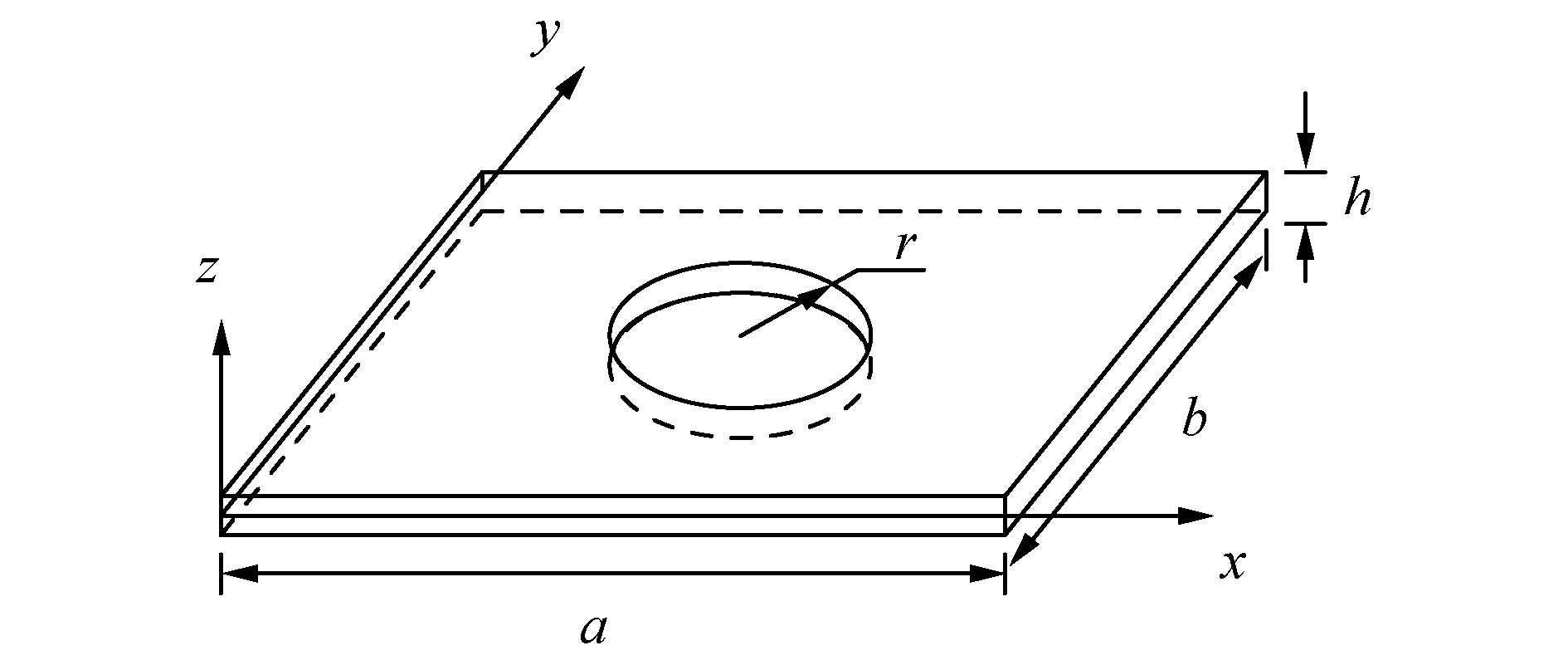
1 功能梯度Mindlin板的基本方程 1.1 带圆开孔的功能梯度矩形板图 1所示为金属-陶瓷两相功能梯度圆孔板,其几何尺寸如下:厚度h,长度a,宽度b,圆孔半径r。设从板的上表面到下表面,陶瓷的体积分数逐渐减小,金属的体积分数逐渐增大。等效材料属性沿厚度方向呈现功能梯度变化并遵循[17]:
|
Download:
|
| 图 1 带圆开孔的功能梯度矩形板 Fig. 1 Geometry of FG rectangle plate with a circular cutout | |
| $ {P_e} = {P_c}{V_c} + {P_m}\left( {1 - {V_c}} \right) $ | (1) |
| $ {V_c} = {\left( {1/2 + z/h} \right)^n} $ | (2) |
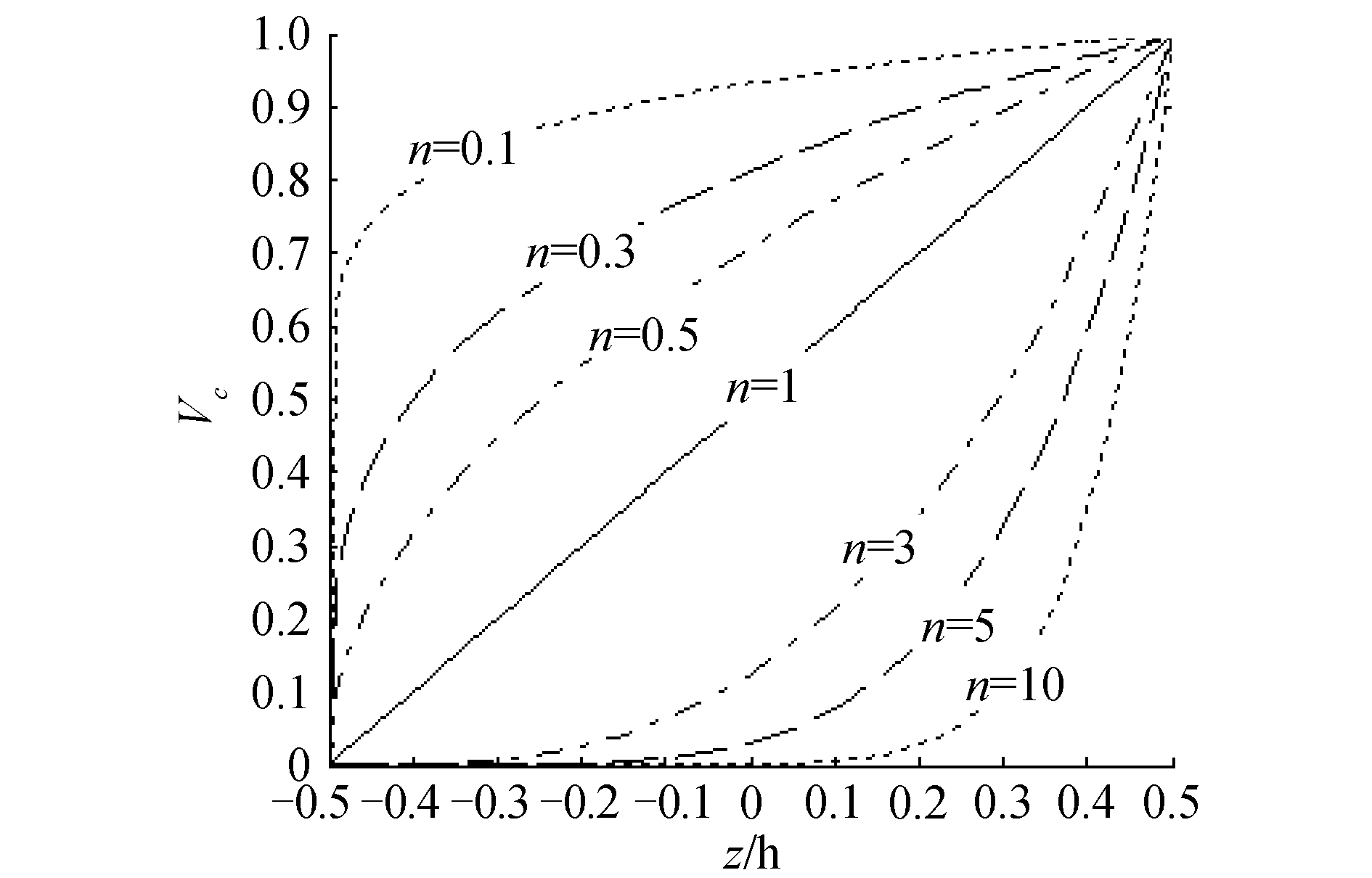
式中:Pc和Pm分别表示陶瓷与金属的物性参数(如泊松比ν、密度ρ、杨氏模量E),Vc为陶瓷的体积分数,n为梯度指数。图 2给出了体积分数随厚度方向的变化,当n=0或n→∞时,材料退化为各向同性。
|
Download:
|
| 图 2 体积分数随厚度的变化 Fig. 2 Variation of volume fraction Vc with the plate thickness | |
根据Mindlin板理论[4],板内任意一点的位移为:
| $ \left\{ \begin{array}{l} U\left( {x,y,z} \right) = {u_0}\left( {x,y} \right) + z{\theta _x}\left( {x,y} \right)\\ V\left( {x,y,z} \right) = {v_0}\left( {x,y} \right) + z{\theta _y}\left( {x,y} \right)\\ W\left( {x,y,z} \right) = {w_0}\left( {x,y} \right) \end{array} \right. $ | (3) |
式中:u0、v0、w0分别为板中面在x、y、z方向的位移;θx、θy分别为绕y轴和x轴的中面法线转角。
小变形条件下,应变-位移关系为:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\varepsilon }} = \left[ {\begin{array}{*{20}{c}} {{\varepsilon _x}}\\ {{\varepsilon _y}}\\ {{\gamma _{xy}}} \end{array}} \right] = {\mathit{\boldsymbol{\varepsilon }}_m} + z{\mathit{\boldsymbol{\varepsilon }}_b} = \left[ {\begin{array}{*{20}{c}} {{u_{0,x}}}\\ {{v_{0,y}}}\\ {{u_{0,y}} + {v_{0,x}}} \end{array}} \right] + z\left[ {\begin{array}{*{20}{c}} {{\theta _{x,x}}}\\ {{\theta _{y,y}}}\\ {{\theta _{x,y}} + {\theta _{y,x}}} \end{array}} \right]\\ \mathit{\boldsymbol{\gamma }} = \left[ {\begin{array}{*{20}{c}} {{\gamma _{xz}}}\\ {{\gamma _{yz}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\theta _x} + {w_{0,x}}}\\ {{\theta _y} + {w_{0,y}}} \end{array}} \right] \end{array} \right. $ | (5) |
式中下标“, ”代表变量对空间坐标的偏导数。
根据胡克定律,应力-应变关系为:
| $ \mathit{\boldsymbol{\sigma }} = \left[ {\begin{array}{*{20}{c}} {{\sigma _x}}\\ {{\sigma _y}}\\ {{\tau _{xy}}} \end{array}} \right] = \frac{{{E_e}}}{{1 - \nu _e^2}}\left[ {\begin{array}{*{20}{c}} 1&{{\nu _e}}&0\\ {{\nu _e}}&1&0\\ 0&0&{\frac{{1 - {\nu _e}}}{2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\varepsilon _x}}\\ {{\varepsilon _y}}\\ {{\gamma _{xy}}} \end{array}} \right] = \mathit{\boldsymbol{D\varepsilon }} $ | (6) |
| $ \mathit{\boldsymbol{\tau }} = \left[ {\begin{array}{*{20}{c}} {{\tau _{xz}}}\\ {{\tau _{yz}}} \end{array}} \right] = \frac{{k{E_e}}}{{2\left( {1 + {\nu _e}} \right)}}\left[ {\begin{array}{*{20}{c}} 1&0\\ 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\gamma _{xz}}}\\ {{\gamma _{yz}}} \end{array}} \right] = {\mathit{\boldsymbol{D}}_s}\mathit{\boldsymbol{\gamma }} $ | (7) |
式中k为剪切修正因子,本文取k=5/6。
2 Mindlin板自由振动的等几何分析 2.1 B样条基函数节点矢量E={ξ1, ξ2, …, ξn+p+1}由一组单调不递减的非负节点ξi(i=1, 2, …, n+p+1)组成,其中p为阶次,n为所构建基函数的个数。B样条基函数由Cox-de Boor递推公式定义为[19]
当p=0时,
| $ {N_{i,0}}\left( \xi \right) = \left\{ \begin{array}{l} 1,\;\;\;\;{\xi _i} \le \xi \le {\xi _{i + 1}}\\ 0,\;\;\;\;其他 \end{array} \right. $ | (8) |
当p>0时,
| $ {N_{i,p}}\left( \xi \right) = \frac{{\xi - {\xi _i}}}{{{\xi _{i + p}} - {\xi _i}}}{N_{i,p - 1}}\left( \xi \right) + \frac{{{\xi _{i + p + 1}} - \xi }}{{{\xi _{i + p + 1}} - {\xi _{i + 1}}}}{N_{i + 1,p - 1}}\left( \xi \right) $ | (9) |
NURBS基函数是B样条基函数的有理形式,其定义为[19]:
| $ R_i^p\left( {\xi ,\eta } \right) = \frac{{{w_i}{N_{i,p}}\left( \xi \right)}}{{\sum\limits_{i = 1}^n {{w_i}{N_{i,p}}\left( \xi \right)} }} $ | (10) |
式中wi为权重。
采用张量形式构建二维NURBS基函数如下[19]:
| $ R_{i,j}^{p,q}\left( {\xi ,\eta } \right) = \frac{{{w_{i,j}}{N_{i,p}}\left( \xi \right){M_{j,q}}\left( \eta \right)}}{{\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {{w_{i,j}}{N_{i,p}}\left( \xi \right){M_{j,q}}\left( \eta \right)} } }} $ | (11) |
式中:Ni, p与Mj, q分别为节点矢量E=[ξ1 ξ2…ξn+p+1]与H=[η1 η2…ηm+q+1]上定义的B样条基函数;wi, j为对应的二维权重。
NURBS曲面可由控制点Bi, j与NURBS基函数得[19]:
| $ S\left( {\xi ,\eta } \right) = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {R_{i,j}^{p,q}\left( {\xi ,\eta } \right){B_{i,j}}} } $ | (12) |
等几何分析采用NURBS基函数完成几何模型的建立及场变量的离散:
| $ {\mathit{\boldsymbol{x}}^h}\left( {\xi ,\eta } \right) = \sum\limits_{A = 1}^N {{R_A}\left( {\xi ,\eta } \right){\mathit{\boldsymbol{x}}_A}} $ | (13) |
| $ {\mathit{\boldsymbol{u}}^h}\left( {\xi ,\eta } \right) = \sum\limits_{A = 1}^N {{R_A}\left( {\xi ,\eta } \right){\mathit{\boldsymbol{u}}_A}} $ | (14) |
式中:RA(ξ, η)为NURBS基函数;xA=[xA yA]T为控制点;uA=[uA vA wA θxA θyA]T为其对应的位移自由度;N为控制点数目。这种方式使得精确几何的信息不会像传统有限元那样在网络划分时丢失,从而保证了后续分析的精确性。
由式(3)、(4)与(14)可得面内、弯曲及剪切应变为:
| $ {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\varepsilon }}_m^{\rm{T}}}&{\mathit{\boldsymbol{\varepsilon }}_b^{\rm{T}}}&{{\mathit{\boldsymbol{\gamma }}^{\rm{T}}}} \end{array}} \right]^{\rm{T}}} = \sum\limits_{A = 1}^N {\left[ {\begin{array}{*{20}{c}} {{{\left( {\mathit{\boldsymbol{B}}_A^m} \right)}^{\rm{T}}}}&{{{\left( {\mathit{\boldsymbol{B}}_A^b} \right)}^{\rm{T}}}}&{{{\left( {\mathit{\boldsymbol{B}}_A^s} \right)}^{\rm{T}}}} \end{array}} \right]{\mathit{\boldsymbol{u}}_A}} $ | (15) |
式中:
| $ \mathit{\boldsymbol{B}}_A^m = \left[ {\begin{array}{*{20}{c}} {{R_{A,x}}}&0&0&0&0\\ 0&{{R_{A,y}}}&0&0&0\\ {{R_{A,y}}}&{{R_{A,x}}}&0&0&0 \end{array}} \right] $ | (16) |
| $ \mathit{\boldsymbol{B}}_A^b = \left[ {\begin{array}{*{20}{c}} 0&0&0&{{R_{A,x}}}&0\\ 0&0&0&0&{{R_{A,y}}}\\ 0&0&0&{{R_{A,y}}}&{{R_{A,x}}} \end{array}} \right] $ | (17) |
| $ \mathit{\boldsymbol{B}}_A^s = \left[ {\begin{array}{*{20}{c}} 0&0&{{R_{A,x}}}&{{R_A}}&0\\ 0&0&{{R_{A,y}}}&0&{{R_A}} \end{array}} \right] $ | (18) |
自由振动问题的特征方程为:
| $ \left( {\mathit{\boldsymbol{K}} - {\omega ^2}\mathit{\boldsymbol{M}}} \right)\mathit{\boldsymbol{X}} = 0 $ | (19) |
式中:K与M为刚度和质量矩阵;ω为自振频率;X为振动模态。
刚度矩阵为:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{K}} = \int\limits_\Omega {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}^m}}&{{\mathit{\boldsymbol{B}}^b}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{D}}&{z\mathit{\boldsymbol{D}}}\\ {z\mathit{\boldsymbol{D}}}&{{z^2}\mathit{\boldsymbol{D}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}^m}}\\ {{\mathit{\boldsymbol{B}}^b}} \end{array}} \right]{\rm{d}}\mathit{\Omega }} + }\\ {\int\limits_\mathit{\Omega } {{{\left( {{\mathit{\boldsymbol{B}}^s}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{D}}_s}{\mathit{\boldsymbol{B}}^s}{\rm{d}}\mathit{\Omega }} } \end{array} $ | (20) |
质量矩阵为:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{M}} = \int\limits_\mathit{\Omega } {{\mathit{\boldsymbol{N}}^{\rm{T}}}\left[ {\begin{array}{*{20}{c}} {{\rho _e}}&0&0&{z{\rho _e}}&0\\ 0&{{\rho _e}}&0&0&{z{\rho _e}}\\ 0&0&{{\rho _e}}&0&0\\ {z{\rho _e}}&0&0&{{z^2}{\rho _e}}&0\\ 0&{z{\rho _e}}&0&0&{{z^2}{\rho _e}} \end{array}} \right]\mathit{\boldsymbol{N}}{\rm{d}}\mathit{\Omega }} }\\ {\mathit{\boldsymbol{N}} = \left[ {\begin{array}{*{20}{c}} {{R_{\rm{A}}}}&0&0&0&0\\ 0&{{R_{\rm{A}}}}&0&0&0\\ 0&0&{{R_{\rm{A}}}}&0&0\\ 0&0&0&{{R_{\rm{A}}}}&0\\ 0&0&0&0&{{R_{\rm{A}}}} \end{array}} \right]} \end{array} $ | (22) |
本节首先通过数值算例验证本文方法的有效性,然后对带圆开孔的功能梯度矩形板进行自由振动分析。算例中,圆孔为自由边界,矩形板四边施加3种边界如下[20]:
| $ \begin{array}{l} {\rm{SSSS}}:\\ \;\;\;\;\;\;\;\;x = 0\;与\;x = a:{v_0} = {w_0} = {\theta _y} = 0 \end{array} $ | (23) |
| $ y = 0\;与\;y = b:{u_0} = {w_0} = {\theta _x} = 0 $ | (24) |
| $ \begin{array}{l} {\rm{CSCS}}:\\ \;\;\;\;\;\;\;\;x = 0\;与\;x = a:{v_0} = {w_0} = {\theta _y} = 0 \end{array} $ | (25) |
| $ y = 0\;与\;y = b:{u_0} = {v_0} = {w_0} = {\theta _x} = {\theta _y} = 0 $ | (26) |
| $ \begin{array}{l} {\rm{CCCC:}}\\ \;\;\;\;\;\;\;\;四边:{u_0} = {v_0} = {w_0} = {\theta _x} = {\theta _y} = 0 \end{array} $ | (27) |
首先考虑各向同性的含圆孔矩形板,其几何及材料参数为:b=1 m,h=0.01 m,E=200 Gpa,ν=0.3,ρ=8 000 kg/m3。弯曲刚度D=Eh3/12(1-ν2),无量纲频率λ=ωa2(ρh/D)1/2。表 1给出了不同边界条件下带圆开孔矩形板的第一阶无量纲频率,并列出了假设模态法[8]的计算结果。显然,2种方法的结果吻合良好。
| 表 1 不同边界条件下带圆开孔板的第一阶无量纲频率 Table 1 The first non-dimensional frequency of rectangle plate with a cutout via different boundary conditions |
考虑带圆开孔Al/Al2O3矩形板,Al的材料参数为:Em=70 GPa,νm=0.3,ρm=2 707 kg/m3;Al2O3的材料参数为:Ec=380 GPa,νc=0.3,ρc=3 800 kg/m3。几何参数为:b=1 m,h=0.01 m,r=0.1 m;弯曲刚度Dc=Ech3/12(1-νc2),无量纲频率λ=ωa2(ρch/Dc)1/2。
不同边界条件及梯度指数下,带圆开孔矩形板的前六阶无量纲频率如表 2~4。从表格中可以看出:a)前六阶频率随着长宽比的增大而增大;b)随着梯度指数的增加,前六阶频率逐渐降低,原因是梯度指数的增加导致矩形板中陶瓷所占的体积分数减小,进而降低了板的整体刚度;此外,梯度在0~2固有频率的降幅大于梯度在2~10固有频率的降幅;c)边界条件对板的无量纲频率有明显影响,一般情况下,边界的约束越大,对应的频率越高;d)当长宽比a/b=1时(方板),第2阶与第3阶频率大小相等。图 3给出了四边固支时开孔板的前6阶模态振型,相关参数为a/b=1.5,n=1。
| 表 2 不同梯度指数下SSSS矩形板的前6阶无量纲频率 Table 2 The first six non-dimensional frequencies of SSSS rectangle plate with different gradient index n |
| 表 3 不同梯度指数下CSCS矩形板的前6阶无量纲频率 Table 3 The first six non-dimensional frequencies of CSCS rectangle plate with different gradient index n |
| 表 4 不同梯度指数下CCCC矩形板的前6阶无量纲频率 Table 4 The first six non-dimensional frequencies of CCCC rectangle plate with different gradient index n |

|
Download:
|
| 图 3 CCCC矩形板的前6阶模态振型 Fig. 3 The first six mode shapes of CCCC rectangle plate | |
带圆开孔功能梯度板的几何参数为:a=1.5 m,b=1 m,r=0.1 m,边界条件为四边固支,分析厚度对固有频率的影响。表 5给出了梯度指数n=1, 5的功能梯度板在不同厚度下的前6阶无量纲频率。由表 5可知,相同梯度指数时,频率随着板厚度的升高呈下降趋势;当厚度较小时,随着板厚度的增大,频率减小的幅度不大。
| 表 5 不同板厚度下CCCC矩形板的前6阶无量纲频率 Table 5 The first six non-dimensional frequencies of CCCC rectangle plate with different plate thickness h |
接下来分析圆孔半径对固有频率的影响,功能梯度板的几何尺寸为:a=2 m,b=1 m,h=0.01 m,边界条件为四边固支,不同梯度下前四阶无量纲频率随圆孔半径的变化如图 4所示。从图 4(a)可以看出,当梯度指数n=1时圆孔半径对矩形板的前四阶频率的影响是复杂的:a)当圆孔的半径相对于薄板的尺寸很小时,圆孔对板的固有频率的影响很小;b)当开孔尺寸增大到一定程度(0.1 m)后,第1阶与第3阶固有频率随着圆孔半径的增大而增加,第2阶与第4阶固有频率随着圆孔半径的增大先降低后升高;c)圆孔半径越大,薄板的第1阶与第2阶固有频率值越接近,此时,薄板的第3阶与第4阶固有频率值也越接近。从图 4(b)可以看出,当梯度指数n=5时矩形板的前四阶频率的影响随圆孔半径的变化规律与梯度指数n=1时相似,但对应频率值有所降低。

|
Download:
|
| 图 4 固支矩形板前四阶无量纲频率与圆孔半径r的关系 Fig. 4 The variation of the first four non-dimensional frequencies for clamped rectangle plate with radius r | |
1) 边界的约束越大,对应的频率越高;随着梯度指数的增加,前6阶固有频率逐渐降低;随着长宽比的增大,前6阶固有频率逐渐增大。
2) 前6阶固有频率随板厚度的升高而减小;开孔半径对前四阶频率的影响较为复杂。
3) 借助NURBS强大的几何建模能力,本方法适用于更加复杂的工程实际问题;此外,可以进一步研究力、热、电等多场耦合作用下的功能梯度板的动力学行为。
| [1] |
MIYAMOTO Y, KAYSSER W A, RABIN B H, et al. Functionally graded materials:design, processing and applications[M]. Berlin Heidelberg: Springer, 1999.
(  0) 0)
|
| [2] |
PRAVEEN G N, REDDY J N. Nonlinear transient thermoelastic analysis of functionally graded ceramic-metal plates[J]. International journal of solids and structures, 1998, 35(33): 4457-4476. DOI:10.1016/S0020-7683(97)00253-9 (  0) 0)
|
| [3] |
FERREIRA A J M, BATRA R C, ROQUE C M C, et al. Natural frequencies of functionally graded plates by a meshless method[J]. Composite structures, 2006, 75(1/2/3/4): 593-600. (  0) 0)
|
| [4] |
ZHAO X, LEE Y Y, LIEW K M. Free vibration analysis of functionally graded plates using the element-free kp -Ritz method[J]. Journal of sound and vibration, 2009, 319(3/4/5): 918-939. (  0) 0)
|
| [5] |
杨正光, 仲政, 戴瑛. 功能梯度矩形板的三维弹性分析[J]. 力学季刊, 2004, 25(1): 15-20. YANG Zhengguang, ZHONG Zheng, DAI Ying. Three dimensional elasticity analysis of a functionally graded rectangular plate[J]. Chinese quarterly of mechanics, 2004, 25(1): 15-20. DOI:10.3969/j.issn.0254-0053.2004.01.003 (  0) 0)
|
| [6] |
HUANG M, SAKIYAMA T. Free vibration analysis of rectangular plates with variously-shaped holes[J]. Journal of sound and vibration, 1999, 226(4): 769-786. DOI:10.1006/jsvi.1999.2313 (  0) 0)
|
| [7] |
KWAK M K, HAN Sangbo. Free vibration analysis of rectangular plate with a hole by means of independent coordinate coupling method[J]. Journal of sound and vibration, 2007, 306(1/2): 12-30. (  0) 0)
|
| [8] |
CHO D S, VLADIMIR N, CHOI T M. Approximate natural vibration analysis of rectangular plates with openings using assumed mode method[J]. International journal of naval architecture and ocean engineering, 2013, 5(3): 478-491. DOI:10.2478/IJNAOE-2013-0147 (  0) 0)
|
| [9] |
AVALOS D R, LARRONDO H A, LAURA P A A, et al. Transverse vibrations of simply supported rectangular plates with rectangular cutouts carrying an elastically mounted concentrated mass[J]. Journal of sound and vibration, 1997, 202(4): 585-592. DOI:10.1006/jsvi.1996.0811 (  0) 0)
|
| [10] |
LAURA P A A, ROSSI R E, AVALOS D R, et al. Transverse vibrations of a simply supported rectangular orthotropic plate with a circular perforation with a free edge[J]. Journal of sound and vibration, 1998, 212(4): 753-757. DOI:10.1006/jsvi.1997.1451 (  0) 0)
|
| [11] |
曹志远, 唐寿高, 程国华. 复杂形状及开孔功能梯度板的三维分析[J]. 应用数学和力学, 2009, 30(1): 15-20. CAO Zhiyuan, TANG Shougao, CHENG Guohua. 3D Analysis of the functionally graded material plates with complex shapes and various holes[J]. Applied mathematics and mechanics, 2009, 30(1): 15-20. (  0) 0)
|
| [12] |
LAL A, SINGH H N, SHEGOKAR N L. FEM model for stochastic mechanical and thermal postbuckling response of functionally graded material plates applied to panels with circular and square holes having material randomness[J]. International journal of mechanical sciences, 2012, 62(1): 18-33. DOI:10.1016/j.ijmecsci.2012.05.010 (  0) 0)
|
| [13] |
HUGHES T J R, COTTRELL J A, BAZILEVS Y. Isogeometric analysis:CAD, finite elements, NURBS, exact geometry and mesh refinement[J]. Computer methods in applied mechanics and engineering, 2005, 194(39/40/41): 4135-4195. (  0) 0)
|
| [14] |
COTTRELL J A, REALI A, BAZILEVS Y, et al. Isogeometric analysis of structural vibrations[J]. Computer methods in applied mechanics and engineering, 2006, 195(41/42/43): 5257-5296. (  0) 0)
|
| [15] |
WALL W A, FRENZEL M A, CYRON C. Isogeometric structural shape optimization[J]. Computer methods in applied mechanics and engineering, 2008, 197(33/34/35/36/37/38/39/40): 2976-2988. (  0) 0)
|
| [16] |
NGUYEN V P, ANITESCU C, BORDAS S P A, et al. Isogeometric analysis:An overview and computer implementation aspects[J]. Mathematics and computers in simulation, 2015, 117: 89-116. DOI:10.1016/j.matcom.2015.05.008 (  0) 0)
|
| [17] |
NGUYEN-XUAN H, TRAN L V, THAI C H, et al. Isogeometric analysis of functionally graded plates using a refined plate theory[J]. Composites part B:engineering, 2014, 64: 222-234. DOI:10.1016/j.compositesb.2014.04.001 (  0) 0)
|
| [18] |
DINACHANDRA M, RAJU S. Isogeometric analysis for acoustic fluid-structure interaction problems[J]. International journal of mechanical sciences, 2017, 131-132: 8-25. DOI:10.1016/j.ijmecsci.2017.06.041 (  0) 0)
|
| [19] |
PIEGL L, TILLER W. The NURBS book[M]. Berlin Heidelberg: Springer, 1997.
(  0) 0)
|
| [20] |
REDDY J N. Mechanics of laminated composite plates and shells:theory and analysis[M]. 2nd ed. New York: CRC Press, 2003.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


