利用控制图可以揭示系统潜在故障迹象,为设备维护策略提供参考信息,通过维护消除故障隐患,又使过程质量波动减少。因此,统计过程控制(statistics process control,SPC)与维护策略(maintenance strategy,MP)具有密切联系,综合考虑能提高生产系统经济效能,然而在实际研究中却常将二者独立分析[1-3]。文献[4-6]将SPC与MP运用至生产系统建模中。文献[7-8]建立了均值控制图和预防维护的联合模型。Zhong[9]等研究了二阶段生产系统中统计过程控制与维护的相关性。Divya等[10]提出了统计过程控制与预防维护的集成优化模型,并采用了CUSUM控制图来监控质量。Zhang等[11]提出的混合失效机制,研究了基于延迟监控策略的均值控制图与维修决策的集成优化模型。在设备之间设置缓冲区,在一定程度上能够应对因上游可修复设备发生故障而导致的生产停滞[12-13]。周炳海等[14]应用几何过程描述系统退化,以最小化成本为目标建立了考虑缓冲区的退化系统的维修更换模型。Ribeiro等[15]利用整数规划求解了最优缓冲区的大小。刘子龙等[16]研究了约束理论下的两设备一缓冲系统,同时考虑了产品的质量损失。
相比通过抽象的质量损失考虑生产过程中的质量变化,控制图能更好的实时监控质量过程。目前多数学者在联合优化控制图与维护策略时,研究对象多是单台设备,但实际情况需要考虑多台设备。本文研究了多设备生产系统下的控制图联合预防维护策略。同时,为了减少停机成本,在2台设备间设立缓冲区。针对该系统中不同设备的角色,确定不同的预防维护策略,在此基础上,以瓶颈设备的状态维护作为机会维护决策点,建立该生产系统的机会维护模型,实现成本的进一步降低。
1 串行生产系统维护问题 1.1 问题域描述与假设在图 1所示的以一台加工中心为核心的串行生产系中,上游为供应机,负责对毛坯进行打磨。加工中心完成加工成型,由于加工中心操作的复杂性和重要性,设置缓冲区以保证其可以持续运行。缓冲区的库存容量设为B,刚开始供应机M1以速率P生产零件,瓶颈机M2以需求率消耗,故缓冲区以速率P-D积累库存,当库存数量达到上限Bmax后,上游设备改以速率D进行生产,以维持库存平衡。

|
Download:
|
| 图 1 结合X-R控制图的两设备一缓冲生产系统 Fig. 1 Production system with buffers and X-R control chart | |
为了更好描述本文提出的维护建模方法,结合生产实际,补充如下假设:
1) 设备M2故障率服从二参数W2(m2, n2)的Weibull分布;设备M1故障率在受控与失控阶段分别服从W0(m0, n0)、W1(m1, n1)分布;
2) 当设备失控时,均值发生偏移:μ1=μ0+δσ0,其中δ为常数,且方差不变,产品均值控制限为:
| $ {C_{\rm{L}}} = {\mu _0} \pm k\frac{\sigma }{{\sqrt n }} $ | (1) |
3) M2在消耗完缓冲区库存再进行预防维护;
4) M1、M2的突发故障均采取小修的方式,且修复至故障前状态;
5) 设备的维修时间是随各自维修次数i增大而增大的函数:
| $ {T_{{\rm{pm}},t,i + 1}} = {T_{{\rm{pm}},t,i}}\left( {1 + {\lambda _n}} \right),\quad 0 < {\lambda _n} < 1 $ | (2) |
式中:λn是维修时间递增因子;n=1, 2分别代表M1、M2;
6) 设备在每次维护后都能从失控状态恢复为正常状态。
基于以上假设,本文在给定时长T内,为实现系统单位运行成本最小化,需要确定该系统的机会维护阈值R1*、瓶颈机的最优可靠性阈值R2*、对应的最佳缓冲区最大容量Bmax、最佳生产数量Q*和最佳控制限k*,即最优组合Ω=[R1*, R2*, Bmax, Q*, k*]。
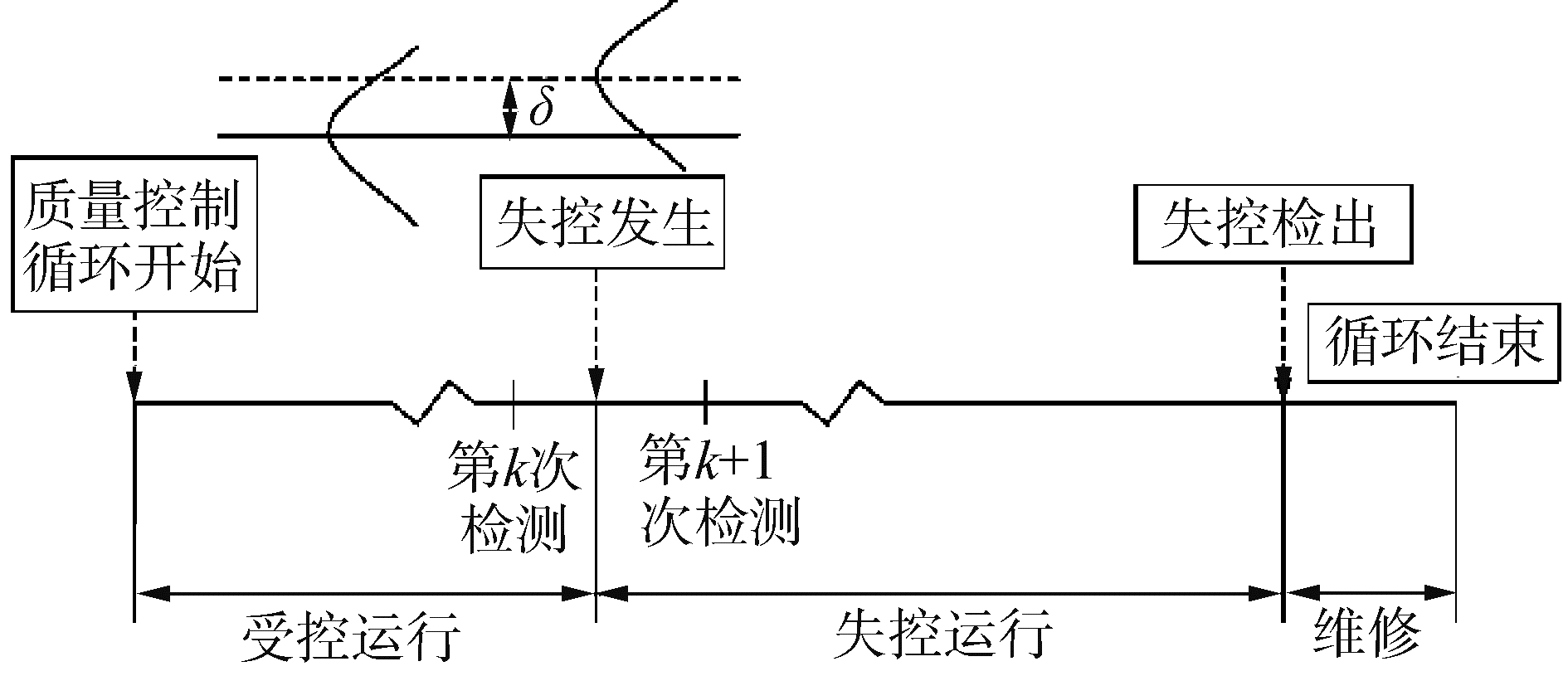
1.2 质量监控策略生产过程有失控状态和受控状态2种情形,如图 2所示。假设每一次质量控制循环开始时,生产系统均处于受控状态,在生产完一定批量的产品后,对所生产的产品进行质量检测。随着生产的进行,设备会因磨损和疲劳等因素发生退化,从而影响产品质量,表现在均值控制图的均值漂移。然而控制图并不能实时地将状态的转移检测出来,因为控制图的检验能力具有滞后性,而这种能力通常由平均失效运行链长来描述,在本文中以S表示在检测出失控状态之前所需要经历的生产运行时长。在实行维护后,生产过程回归受控状态,至此记为一次质量监控周期。
|
Download:
|
| 图 2 生产系统的质量控制策略 Fig. 2 Quality control policy for the production system | |
在生产系统的可靠性研究中,Weibull分布广泛用于模拟生产系统的失效。因此,本文假设该生产系统的质量偏移的产生时间t是一个服从二参数Weibull分布的随机变量,其概率密度函数为:
| $ f(t) = \frac{{{n_0}}}{{{m_0}}}{\left( {\frac{t}{{{m_0}}}} \right)^{{n_0} - 1}}\exp \left( { - {{\left( {\frac{t}{{{m_0}}}} \right)}^{{n_0}}}} \right) $ | (3) |
式中:m0为形状参数;n0为尺度参数;m0, n0, t>0。对此密度函数进行积分即可得到第h个质量监控周期的平均受控运行时间U:
| $ {\rm{E}}\left( {{U_h}} \right) = \int_0^\infty t f(t|h){\rm{d}}t $ | (4) |
平均失控运行时长S与控制限参数k、样本大小Q和均值偏移量δ相关:
| $ S = \frac{1}{{1 - (\mathit{\Phi }(K - \delta \sqrt Q ) - \mathit{\Phi }( - k - \delta \sqrt Q ))}} $ | (5) |
第h个质量控制周期的平均运行时长为:
| $ {\mathit{\Gamma }_h} = U + S $ | (6) |
在串行生产系统维护模型中,均值控制图一方面是对上游设备的产品过程质量进行控制;另一方面是为了从产品质量角度对设备状态进行预警,防止在生产中无明显异常迹象的情况下失效。当过程质量产生偏移,且控制图发出预警时,对上游设备实施预防维护,使过程质量恢复可控状态。瓶颈机采取状态维护,当其可靠度达到预定的阈值R2时需要对停机其进行机会维护。下游设备失效服从Weibull分布,其可靠性方程为:
| $ \left\{ {\begin{array}{*{20}{l}} {{R_2} = \exp \left( { - \int_0^{{T_{2,j}}} {{f_{2,j}}} (t){\rm{d}}t} \right)}\\ {{f_{2,j}}(t) = \frac{{{n_2}}}{{{m_2}}}{{\left( {\frac{t}{{{m_2}}}} \right)}^{{n_2} - 1}}\exp \left( { - {{\left( {\frac{t}{{{m_2}}}} \right)}^{{n_2}}}} \right)} \end{array}} \right. $ | (7) |
式中:T2, j表示设备M2第j次维护周期长度。
当下游设备进行状态维护时,预测上游设备的可靠度,若其低于机会维护阈值R1,则对上游设备同时进行机会维护。
实际生产中,设备故障率随着设备的役龄增加而随之上升;同时,设备无法通过预防性维护恢复至完好如初的状态,即预防维护是“修复非新”的。为了描述此类系统退化,通过引入故障率递增因子和役龄递减因子,那么上下游设备故障率模型为:
| $ \left\{ {\begin{array}{*{20}{l}} {{g_{1,i}}(t) = {b_1}{g_{1,i}}\left( {t + {a_1}{L_{1,i}}} \right)}\\ {{g_{2,i}}(t) = {b_2}{g_{2,i}}\left( {t + {a_2}{L_{2,i}}} \right)} \end{array}} \right. $ | (8) |
式中:i, j=1, 2, …, n表示设备M1或M2的第i或j次维护;b1、b2为故障率递增因子,a1、a2为役龄递减因子;L1, i、L2, j表示第i或j次维护周期时长。每次预防维护后,设备的初始故障率不为零值,且故障率变化率也随之增加。
2 维护策略数学模型构建记单位库存成本为cin,单次检测成本为cins,小修成本为ccm, n,预防维护成本为cpm, n,其中n=1, 2分别代表设备M1、M2,单位惩罚成本为cpen,M1在受控状态下的单位运行成本为c1, in,在失控状态下的单位运行成本为c1, out,M2的单位运行成本为c2, ope。那么第h个质量监控周期内的单位时间成本为库存成本、惩罚成本、运行成本、预防维护成本、小修成本、机会维护成本和检测成本之和除以周期长度:
| $ {C_h} = \frac{{{c_{{\rm{inv }}}} + {c_{{\rm{pen }}}} + {c_{{\rm{ope }}}} + {c_{{\rm{pm }}}} + {c_{{\rm{em }}}} + {c_{{\rm{on }}}} + {c_{{\rm{ins }}}}}}{{{\mathit{\Gamma }_h}}} $ | (9) |
根据状态维护的发生与否和状态维护的节点,生产过程中可能出现3种情形,即M2未进行状态维护(情形1)、状态维护发生在缓冲区建立时(情形2)和状态维护发生在缓冲区建立后(情形3)。
2.1 情形1若瓶颈机的状态维护节点未落在此次质量检测周期内,则不考虑机会维护。生产过程分为受控阶段与失控阶段,以生产Q数量产品所需的时间作为单位时间,受控、失控运行时长依据式(6)、式(7)可得。当检测出失控后,需要对M1实施预防维护,此时M2消耗缓冲区库存继续生产。由于只有在生产完Q数量产品后才能进行检测,记m为受控状态下历经的周期数,w为失控状态下历经的检测周期数,则情形1下的一次质量监控周期时长为:
| $ \left\{ {\begin{array}{*{20}{l}} {{T_h} = (m + w)\frac{Q}{D} + \max \left( {{T_{{\rm{pm}}1,i}},\frac{B}{D}} \right)}\\ {m = \left\lfloor {{\rm{E}}\left( {{U_h}} \right)} \right\rfloor }\\ {w = \left\lceil S \right\rceil } \end{array}} \right. $ | (10) |
记tms, p为第p次质量监控周期的开始时刻,te, p为第p次质量监控周期的结束时刻,则:
| $ \left\{ {\begin{array}{*{20}{l}} {{t_{{\rm{e}},p}} = {t_{{\rm{s}},p}} + {T_h}}\\ {{t_{{\rm{s}},p}} + 1 = {t_{{\rm{e}},p}}} \end{array}} \right. $ | (11) |
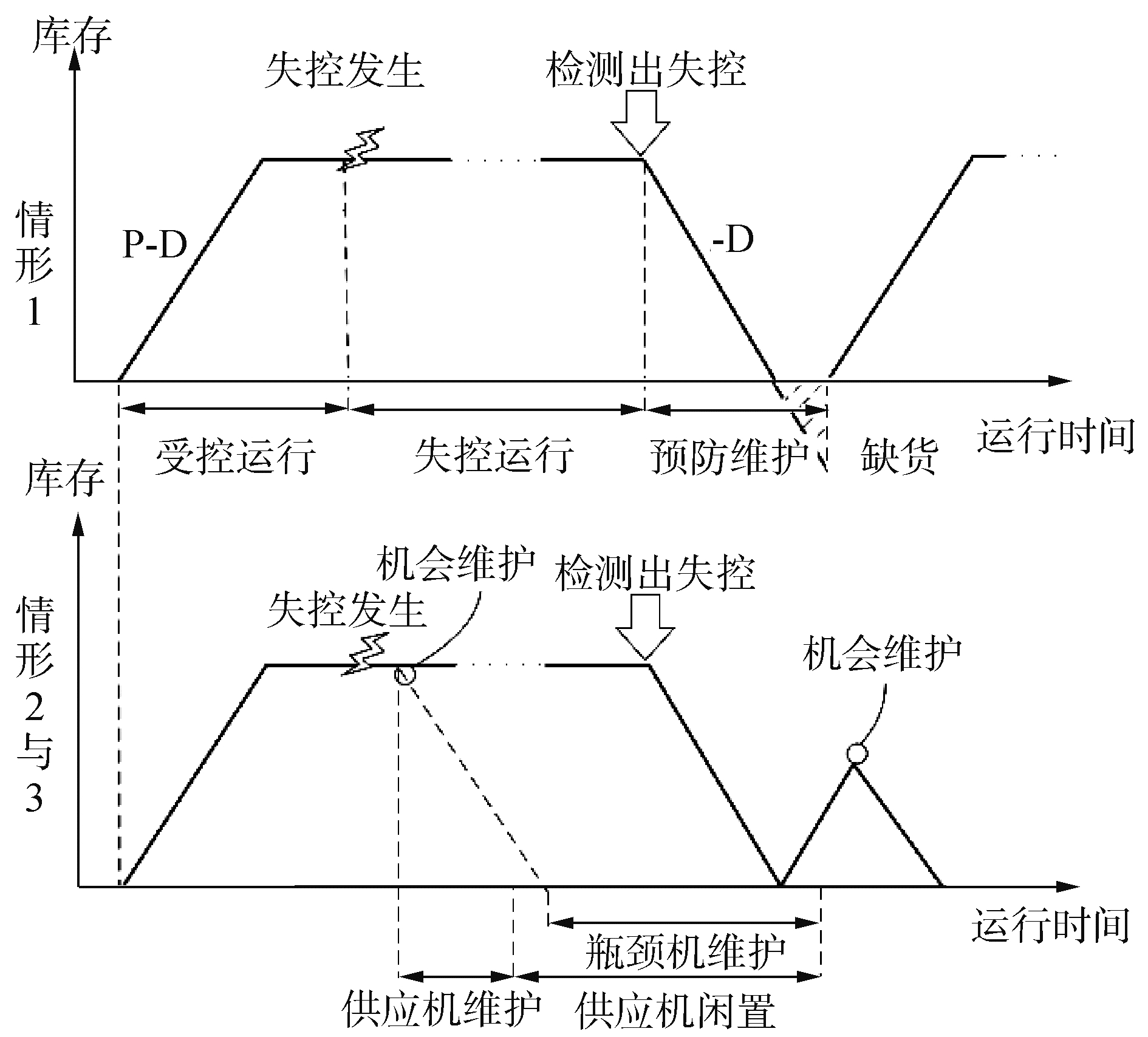
根据图 3可知情形1下缓冲区库存的变化情况,那么库存成本为:
|
Download:
|
| 图 3 3种情形下缓冲区库存变化 Fig. 3 Buffer position in three situations | |
| $ {C_{{\rm{inv}},h}} = \left( {B{T_h} - \frac{{{B^2}}}{{2(P - D)}} + \frac{{{B^2}}}{{2D}}} \right){c_{{\rm{inv}}}} $ | (12) |
由于M1在受控阶段与失控阶段的失效函数不同,因此在计算小修成本时,需分别估算受控阶段内平均故障次数与失控阶段内平均故障次数,则情形1下M1的小修成本为:
| $ {C_{{\rm{cm}},1}} = \left( {\int_0^{{\rm{E}}\left( {{U_h}} \right)} {{W_0}} (t){\rm{d}}t + \int_{{\rm{E}}\left( {{U_h}} \right)}^{{T_h}} {{W_1}} (t){\rm{d}}t} \right){c_{{\rm{cm}},1}} $ | (13) |
设备M2的小修成本为:
| $ {C_{{\rm{cm}},2}} = \left( {\int_0^{{T_h}} {{W_2}} (t){\rm{d}}t} \right){c_{{\rm{cm}},2}} $ | (14) |
若预防维护时间超出了缓冲库存的消耗时间,则M2处于饥饿状态,从而产生缺货成本;若预防维护时间小于缓冲库存的消耗时间,则M1处于闲置状态,从而产生闲置成本。因此,惩罚成本为:
| $ {C_{{\rm{pen}},h}} = \left| {{T_{{\rm{PMI}},i}} - \frac{B}{D}} \right|{c_{{\rm{pen}}}} $ | (15) |
M1在受控阶段与失控阶段的单位运行成本不同,因此情形1下总的运行成本为:
| $ {C_{{\rm{ope}},h}} = E\left( {{U_h}} \right){c_{1,{\rm{in}}}} + \left( {{T_h} - E\left( {{U_h}} \right)} \right){c_{1,{\rm{out}}}} + {T_h}{c_{2,{\rm{ope}}}} $ | (16) |
情形1下一次质量监控周期内的单位时间成本为库存成本、小修成本、惩罚成本、预防维护成本、检测成本和运行成本之和除以周期长度:
| $ \begin{array}{*{20}{c}} {{C_h} = \left( {{C_{{\rm{inv}},h}} + {C_{{\rm{pen}},h}} + {C_{{\rm{ope}},h}} + {c_{{\rm{pm}},1}} + } \right.}\\ {\left. {{C_{{\rm{cm}},h}} + {c_{{\rm{ins}}}}(m + w)} \right)/{T_h}} \end{array} $ | (17) |
若瓶颈机状态维护节点落在质量检测周期内,则需要判断当对M2进行状态维护时,M1是否进行机会维护。假设M2的第j次状态维护时刻为tpm2, j,此前系统已经历过h-1次质量监控周期,那么在状态维护时刻点处M1的可靠度为:
| $ {R_{1,p}} = \exp \left( { - \int_0^{{t_{{\rm{pm}}2,j}} - {t_{{\rm{s,h}}}}} {{f_{1,i}}} (t){\rm{d}}t} \right) $ | (18) |
式中:ts, h表示本次质量监控周期的开始时刻。若R1, p<R1,则对M1进行机会维护,否则不维护。
情形2下的第h个质量监控周期原计划时长T′h可依据式(10)进行计算,而其实际时长Th为:
| $ \begin{array}{*{20}{l}} {{T_h} = {t_{{\rm{pm2}},j}} - {t_{s,h}} + \max \left( {{\zeta _p}{T_{{\rm{pm1,}}i}},} \right.}\\ {\;\;\;\;\;\;\left. {\left( {\left( {{t_{{\rm{pm2}},j}} - {t_{s,h}}} \right)(P - D)/D + {T_{{\rm{pm}}2,j}}} \right)} \right)} \end{array} $ | (19) |
其中,ζp=(0, 1)分别表示M1不进行机会维护和进行机会维护。
情形2下一次质量监控周期内单位时间成本为库存成本、小修成本、惩罚成本、预防维护成本、机会维护成本和运行成本之和除以周期长度:
| $ \begin{array}{l} {C_h} = \left( {{C_{{\rm{inv }},h}} + {C_{{\rm{pen }},h}} + {C_{{\rm{ope }},h}} + {C_{{\rm{em }},h}} + } \right.\\ \;\;\;\;\;\;\;\left. {{C_{{\rm{om }},h}}{\zeta _p} + {c_{{\rm{pm }},2}}} \right)/{T_h} \end{array} $ | (20) |
其中:
| $ \begin{array}{l} {C_{{\rm{inv}},h}} = \left( {\left( {{t_{{\rm{pm}}2,j}} - {t_{s,h}}} \right)2(P - D)/2 + } \right.\\ \;\;\;\;\;\;\;\;\;\;\left. {\left( {\left( {{t_{{\rm{pm}}2,j}} - {t_{s,h}}} \right)(P - D)} \right)2/D} \right){c_{{\rm{inv}}}} \end{array} $ | (21) |
| $ {C_{{\rm{ope}},h}} = \left( {{t_{{\rm{pm}}2,j}} - {t_{s,h}}} \right){c_{1,{\rm{in}}}} + {T_h}{c_{2,{\rm{ope}}}} $ | (22) |
| $ {C_{{\rm{cm}},h}} = \left( {\int_0^{{T_h}} {{W_2}} (t){\rm{d}}t} \right){c_{{\rm{cm}},2}} + \left( {\int_0^{{T_h}} {{W_0}} (t){\rm{d}}t} \right){c_{{\rm{cm}},1}} $ | (23) |
| $ \begin{array}{l} {C_{{\rm{pen }},h}} = {c_{{\rm{pen }}}}\left( {{t_{{\rm{pm }}2,j}} - {t_{s,h}}} \right)(P - D)/D + \\ \;\;\;\;\;\;\;\;\;\;\left\{ {\begin{array}{*{20}{l}} {2{T_{{\rm{pm2}},j}}{c_{{\rm{pen }}}},{\zeta _p} = 0}\\ {\left| {{T_{{\rm{pm2 }},j}} - {T_{{\rm{pml }},i}}} \right|{c_{{\rm{pen }}}},{\zeta _p} = 1} \end{array}} \right. \end{array} $ | (24) |
| $ \begin{array}{l} {C_{{\rm{om}},h}} = {c_{{\rm{pen}}}}\left( {T_h^\prime - {T_h} - \min \left( {{T_{{\rm{pml}},i}}} \right.,} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\left. {\left( {\left( {{t_{{\rm{pm}}2,j}} - {t_{s,h}}} \right)(P - D)/D + {T_{{\rm{pm}}2,j}}} \right)} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;{c_{{\rm{cm}},1}}\left( {\int_{{T_h}}^{{\rm{E}}\left( {{U_h}} \right)} {{W_0}} (t){\rm{d}}t + } \right.\\ \left. {\left. {\;\;\;\;\;\;\;\;\;\;\;\;\int_{{\rm{E}}\left( {{U_h}} \right)}^{T_h^\prime } {{W_1}} (t){\rm{d}}t} \right)} \right) + {c_{{\rm{pm}},1}} \end{array} $ | (25) |
式(21)~(23)分别表示库存成本、运行成本和小修成本。式(24)中,当M1不需要机会维护即ζp=0时,为了避免阻塞现象,当达到M2状态维护节点时M1停工闲置,产生闲置成本。式(25)表示机会维护成本,由提前维护造成的生产损失成本、机会维护节省的停机成本、提前维护节省的小修成本和M1的预防维护成本构成。
2.3 情形3若瓶颈机的状态维护节点落在缓冲区建成完毕后,此时需判别维护节点处于受控还是失控区域,依次建立不同的成本模型。情形3下一次质量监控周期内的单位时间成本与情形2类似,不同之处在于当状态维护节点落在受控区域时,上游设备只产生受控运行成本,当维护节点落在失控区域时,同时产生受控与失控运行成本。同理,在计算维护节点落在失控区域情况下的小修成本和机会维护时,也应考虑受控与失控2种情况。
至此,3种情形下的成本模型建立完毕。对于给定的任务区间T,其各个质量监控周期内的单位时间成本的总和为:
| $ C = \sum\limits_{n = 1}^N {{C_h}} $ | (26) |
式中:N表示在给定T区间内生产系统所历经的质量检测周期数。通过探寻最优决策变量组合Ω=[R1*, R2*, Bmax, Q*, k*],使得总单位时间成本最小。
3 模型有效性算例分析本文通过数值算例来验证模型的有效性,模型参数为a1=0.2,a2=0.1,b1=b2=1.05,λ1=λ2=0.05,m0=200,n0=1.7,m1=100,n1=10,m2=2 000,n2=1.4,c1, in=50,c1, out=500,c2, ope=100,cin=5,cins=50,ccm, 1=2 000,ccm, 2=5 000,cpm, 1=200,cpm, 2=5 000,δ=0.2。由于优化模型较为复杂,难以通过一般解析法获取准确的最优解。因此,对于给定任务区间T=2 000,本文采用数值迭代的方法,通过控制变量,探究各个决策变量的最优性与变量之间的关联性。
3.1 状态维护阈值、机会维护阈值分析如图 4(a)所示,在给定条件下(Q=50、B=10、R1=0.97、k=3),当状态维护阈值较低时,预防维护周期长,瓶颈机可靠性低,且状态维护周期长意味着给定周期内机会维护次数少,综上导致成本升高。随着阈值增加,成本产生波动,因为随着可靠性要求的提高,维持可靠性所需的维护成本必然会增加,但较高的可靠性又能减少由于故障成本。当R2为0.85时,单位时间成本取得最小值Cmin为33 125.48。随着维护阈值继续提高至0.9,提高可靠性而过度维护将增加生产成本。

|
Download:
|
| 图 4 各个决策变量对单位时间成本的影响 Fig. 4 Impacts of diffirent decision parameters on cost | |
机会维护阈值的变化如图 4(b)所示。当阈值等于0时,即不采取机会维护而使用单一的反应性维护;当阈值等于1时,即采取群组维护策略。在阈值较低时,单位时间成本未发生变化,因为在质量检测周期结束时,上游设备的可靠度未降低至阈值以下,产生此现象的原因是设备衰退速度由模型参数决定。当阈值进一步提高时,上游设备的可靠度将低于阈值,此时需要进行机会维护。从图中可以看出,在采取机会维护后单位时间成本显著降低,当机会维护阈值达到0.97时,单位时间成本最低。随着阈值继续增加至1时,单位时间成本相较有所提高。这是因为机会维护次数增加的同时维护成本随之提高。
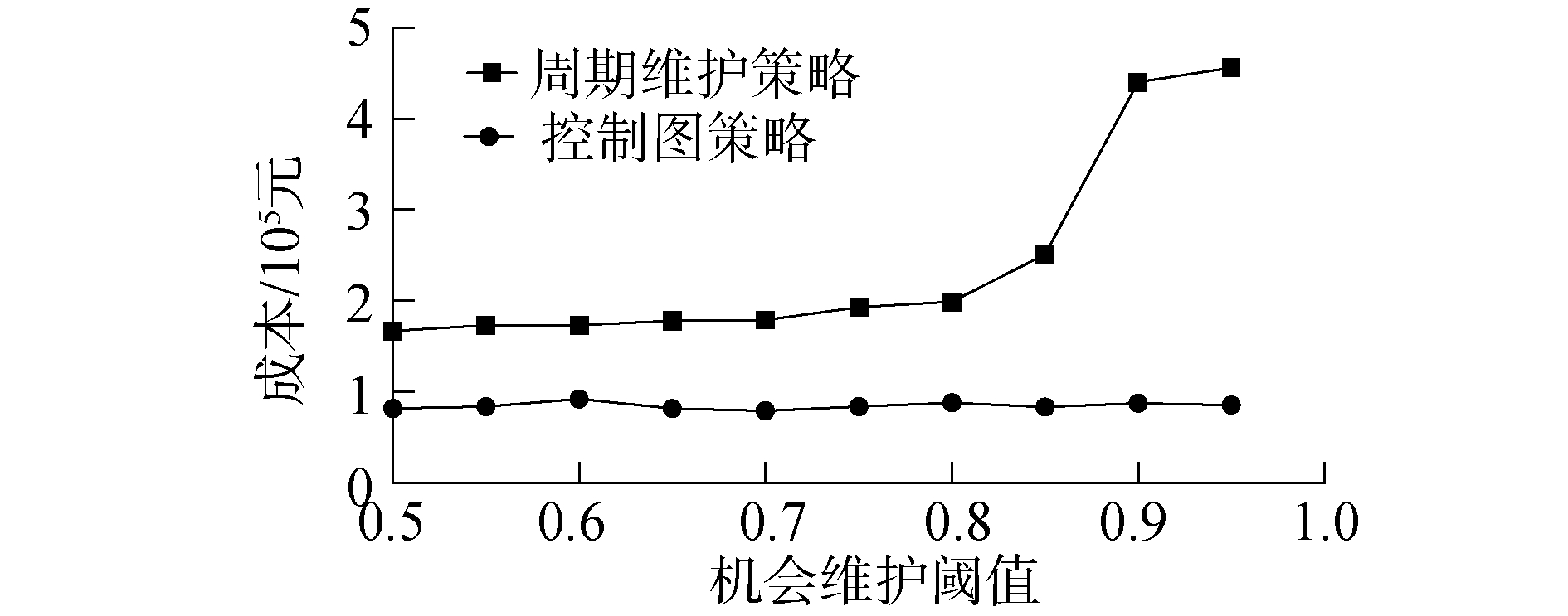
图 5则给出了基于控制图的维护策略和定周期维护策略下单位时间成本随R2的变化情况,前者能有效降低成本,提高经济效益。
|
Download:
|
| 图 5 控制图策略与周期维护策略下的单位时间成本 Fig. 5 Cost rate of control chart policy and periodic maintenance | |
如图 4(c)所示,在给定条件下(R1=0.97、R2=0.85、k=3、B=10),生产检测数量Q的变化会引起单位生产成本的变动。当生产检测数量Q较少时,单位生产成本较高,这是因为检测批量少意味着检测次数的增加,这就使得检测成本升高。随着生产检测批量的增加,单位运行成本逐渐下降,当Q=25时,单位生产成本取得最小值。此后,随着生产检测数量,单位运行成本有所增加,这是因为生产检测数量的增加意味着检测间隔变长,这将使失控运行时长进一步增加,设备的可靠性也有所降低,从而增加了成本。
缓冲区大小与单位时间成本的关系如图 4(d)所示。从图中可以看出,在图例前段部分单位时间成本逐渐降低,因为缓冲区在一定程度上可以减少因上游设备停机维护带来的损失。随着缓冲区的增加,单位时间成本随之增加,因为库存持有成本会随着缓冲区的增加而增加。当控制限参数为1、2、3、4、5、6时,单位时间成本分别为55 081、59 119、79 309、34 150、20 176、120 122。保持其他参数设置不变,控制限参数k取5时,成本最小。
综合上述分析,各决策变量对单位生产成本的影响符合实际生产过程中的现象。但最优决策除了决策变量之间的相互影响外,模型的输入参数也会影响最终的决策结果。因此,在实际应用中,仍然需要综合考虑系统的内部因素(如Weibull失效函数的参数)和外部环境的影响。
4 结论1) 以两设备一缓冲的串行生产系统作为研究对象,同时考虑将控制图触发上游设备维护决策,这一策略符合实际生产的需求,同时通过实验也表明,考虑控制图的联合维护模型比定周期维护模型更具经济效益。
2) 以直观而经济控制图监控产品质量,进而间接监控设备的状态,实际上也是一种状态维护的方式,通过优化控制图或选择效能更好的控制图可以更准确的反映生产状态,在减少成本的同时提高生产系统的稳定性。
3) 设立缓冲区能有效的减少停机损失,但缓冲区不宜过多,缓冲区越大意味着库存成本将增加,因此需要根据实际需求进行配置。
4) 控制图参数、维护阈值、缓冲区大小和生产检测批量对系统的性能影响是综合性的,因此需要权衡决策。
本文的模型对生产过程具有一定指导意义。今后的研究可以考虑时变型过程偏移量,以及通过仿真等技术动态模拟过程失控。
| [1] |
周炳海, 刘玉旺. 考虑设备劣化及随机需求的最优生产周期模型[J]. 哈尔滨工程大学学报, 2017, 38(6): 950-955. ZHOU Binghai, LIU Yuwang. An optimal production period model for a buffered system with machine deteriorating upstream and stochastic demand downstream[J]. Journal of Harbin Engineering University, 2017, 38(6): 950-955. (  0) 0)
|
| [2] |
TAMBE P P, KULKARNI M S. A superimposition based approach for maintenance and quality plan optimization with production schedule, availability, repair time and detection time constraints for a single machine[J]. Journal of manufacturing systems, 2015, 37: 17-32. DOI:10.1016/j.jmsy.2015.09.009 (  0) 0)
|
| [3] |
张晓文, 蒋祖华, 胡家文. 基于约束理论的多阶瓶颈串/并联系统的机会维护[J]. 哈尔滨工程大学学报, 2016, 37(9): 1275-1280, 1286. ZHANG Xiaowen, JIANG Zuhua, HU Jiawen. Opportunistic maintenance on series-parallel systems with multi-stage bottlenecks using the theory of constraints[J]. Journal of Harbin Engineering University, 2016, 37(9): 1275-1280, 1286. (  0) 0)
|
| [4] |
PANAGIOTIDOU S, TAGARAS G. Optimal integrated process control and maintenance under general deterioration[J]. Reliability engineering & system safety, 2012, 104: 58-70. (  0) 0)
|
| [5] |
BEN-DAYA M, RAHIM M A. Effect of maintenance on the economic design of x--control chart[J]. European journal of operational research, 2000, 120(1): 131-143. DOI:10.1016/S0377-2217(98)00379-8 (  0) 0)
|
| [6] |
BOUSLAH B, GHARBI A, PELLERIN R. Integrated production, sampling quality control and maintenance of deteriorating production systems with AOQL constraint[J]. Omega, 2016, 61: 110-126. DOI:10.1016/j.omega.2015.07.012 (  0) 0)
|
| [7] |
CASSADY C R, BOWDEN R O, LIEW L, et al. Combining preventive maintenance and statistical process control:a preliminary investigation[J]. IIE transactions, 2000, 32(6): 471-478. (  0) 0)
|
| [8] |
LINDERMAN K, MCKONE-SWEET K E, ANDERSON J C. An integrated systems approach to process control and maintenance[J]. European journal of operational research, 2005, 164(2): 324-340. DOI:10.1016/j.ejor.2003.11.026 (  0) 0)
|
| [9] |
ZHONG Jianlan, MA Yizhong. An integrated model based on statistical process control and maintenance for two-stage dependent processes[J]. Communications in statistics-simulation and computation, 2017, 46(1): 106-126. DOI:10.1080/03610918.2014.957841 (  0) 0)
|
| [10] |
SHRIVASTAVA D, KULKARNI M S, VRAT P. Integrated design of preventive maintenance and quality control policy parameters with CUSUM chart[J]. The international journal of advanced manufacturing technology, 2016, 82(9/10/11/12): 2101-2112. (  0) 0)
|
| [11] |
ZHANG Guojun, DENG Yuhao, ZHU Haiping, et al. Delayed maintenance policy optimisation based on X- control chart[J]. International journal of production research, 2015, 53(2): 341-353. DOI:10.1080/00207543.2014.923948 (  0) 0)
|
| [12] |
周炳海, 苏谊. 基于可变缓冲区存储量的串行生产线节能分析[J]. 哈尔滨工程大学学报, 2016, 37(6): 832-836. ZHOU Binghai, SU Yi. Energy-saving analysis of serial production lines based on the changeable buffers' storage[J]. Journal of Harbin Engineering University, 2016, 37(6): 832-836. (  0) 0)
|
| [13] |
PAVITSOS A, KYRIAKIDIS E G. Markov decision models for the optimal maintenance of a production unit with an upstream buffer[J]. Computers & operations research, 2009, 36(6): 1993-2006. (  0) 0)
|
| [14] |
成国庆, 周炳海, 李玲, 等. 考虑缓冲区库存的退化系统最优维修更换策略[J]. 计算机集成制造系统, 2015, 21(6): 1593-1600. CHENG Guoqing, ZHOU Binghai, LI Ling, et al. Optimal maintenance strategy for deteriorating systems with intermediate buffers[J]. Computer integrated manufacturing systems, 2015, 21(6): 1593-1600. (  0) 0)
|
| [15] |
RIBEIRO M A, SILVEIRA J L, QASSIM R Y. Joint optimisation of maintenance and buffer size in a manufacturing system[J]. European journal of operational research, 2007, 176(1): 405-413. DOI:10.1016/j.ejor.2005.08.007 (  0) 0)
|
| [16] |
周炳海, 刘子龙. 考虑质量损失的退化系统维护建模[J]. 浙江大学学报(工学版), 2016, 50(12): 2270-2276. ZHOU Binghai, LIU Zilong. Maintenance modeling for deteriorating system considering quality loss[J]. Journal of Zhejiang University (engineering science), 2016, 50(12): 2270-2276. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


