在先进反应堆的设计中,非能动安全技术对系统安全性的保障作用越来越突出。自然循环作为最重要的非能动技术,在核电及核供热部门中具有极大的应用前景。然而,在自然循环条件下发生的流动不稳定性却使系统设备面临机械疲劳、控制失效、热冲击等多种危害[1]。对该问题的研究,国内外学者多采用实验的手段,辅以理论分析或程序验证[2]。在数值模拟方面,RELAP5作为反应堆热工分析的著名系统程序,一直被用于核电站的系统热工水力特性分析和安全分析。该程序由美国Idaho实验室开发[3],在轻水堆核电厂的各种热工水力瞬态分析中,表现出极强的处理能力。
Hamidouche等[4]和William等[5]分别利用RELAP5程序对低压条件下的不稳定性起始点及相变模型进行了研究。然而,强迫循环高流速条件下得到的研究结果,不足以评估该程序对自然循环问题的分析能力。绝大多数的自然循环实验系统(如SIRIUS-N[6],CIRCUS等[7])都运行在中、低压条件下,两相自然循环在该条件下的模拟计算仍然是难点。程坤等[8]通过对动量方程的修改,对RELAP进行了二次开发,有效提高了该程序对摇摆条件下瞬态问题的分析能力。Kozmenkov[9]对低压自然循环下闪蒸引起的流动不稳定性进行了程序验证,数值计算结果与实验数据吻合较好,证明了RELAP5能够解决与闪蒸相关的不稳定性问题。
尽管许多学者利用RELAP5进行了数值计算,但是RELAP5在低压、低流量工况下,特别是自然循环情况工况下的适用性一直备受争议[9-11]。本文基于RELAP5/MOD3.3程序,结合自然循环系统流动不稳定性的实验数据,对RELAP5处理该问题的能力进行评估。针对流动不稳定性的起始点、类型、机理、系统动态特性等,比较程序与实验结果的差异性,分析评价了所建立的自然循环计算模型。
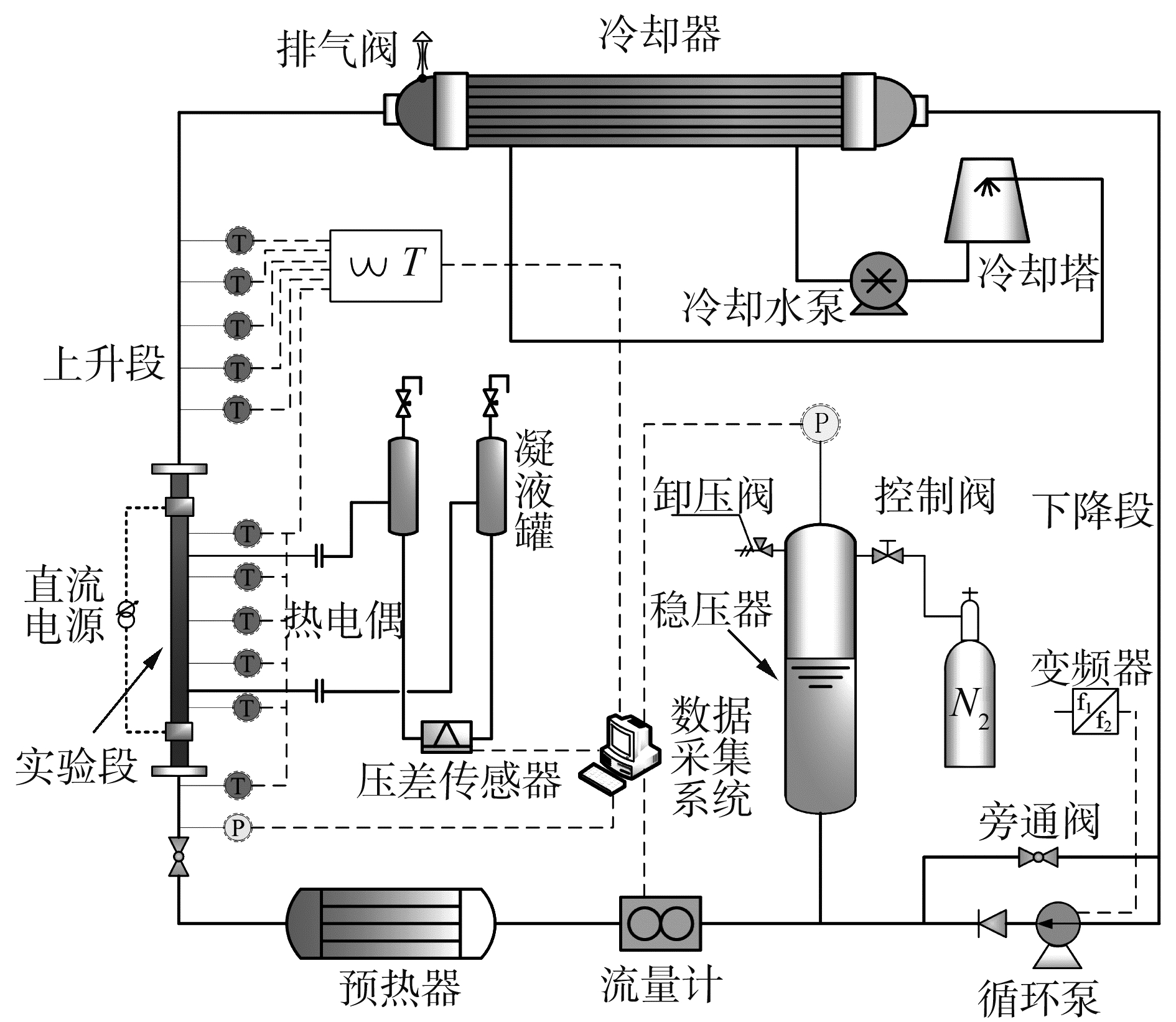
1 实验装置及实验过程图 1为低压自然循环实验装置示意图,主要由电加热实验段、绝热上升段、冷却器、循环泵、稳压器、预热器及相关测量仪表组成,回路内设备尺寸可见文献[12-13]。实验系统参照反应堆一回路的布置方式,加热段及冷却器热中心之间的高度差布置为3.4 m,可以开展自然循环流动不稳定性、强迫循环-自然循环过渡过程等多种实验研究。
|
Download:
|
| 图 1 实验装置示意 Fig. 1 Schematic of experimental apparatus | |
实验以水为工质,首先建立低功率下的强迫循环。然后,通过变频器调节泵转速并切换旁通阀门,将系统过渡到稳定的单相自然循环工况。过冷水在预热器中加热至设计工况后流入实验段加热,经绝热上升段后在管壳式换热器中冷却。工质温度降低后经下降段及旁通回路流回预热器,构成整个自然循环。数据采集终端利用NI系统,将温度、压力、压降、流量等信号实时传入采集系统,采样周期为0.1 s。
低压条件下,在上述稳态自然循环工况的基础上,开展了自然循环流动不稳定性实验。通过预热器及冷却器联合控制入口过冷度,进一步增加实验段加热功率,直至自然循环流动不稳定性出现。实验段进、出口及上升段共布置6个允差等级为I级的铠装热电偶,实验段外壁面设有21个N型热电偶;回路使用电磁流量计测量流量,测量范围0.14~1.4 m3/h,相对误差±0.3%;压差传感器测量精度为量程的±0.25%以内。自然循环实验系统压力p运行在0.2~0.5 MPa范围内,且入口过冷度ΔTsub, in维持在30~70 ℃,热流密度q″为28.4~355.4 kW/m2。
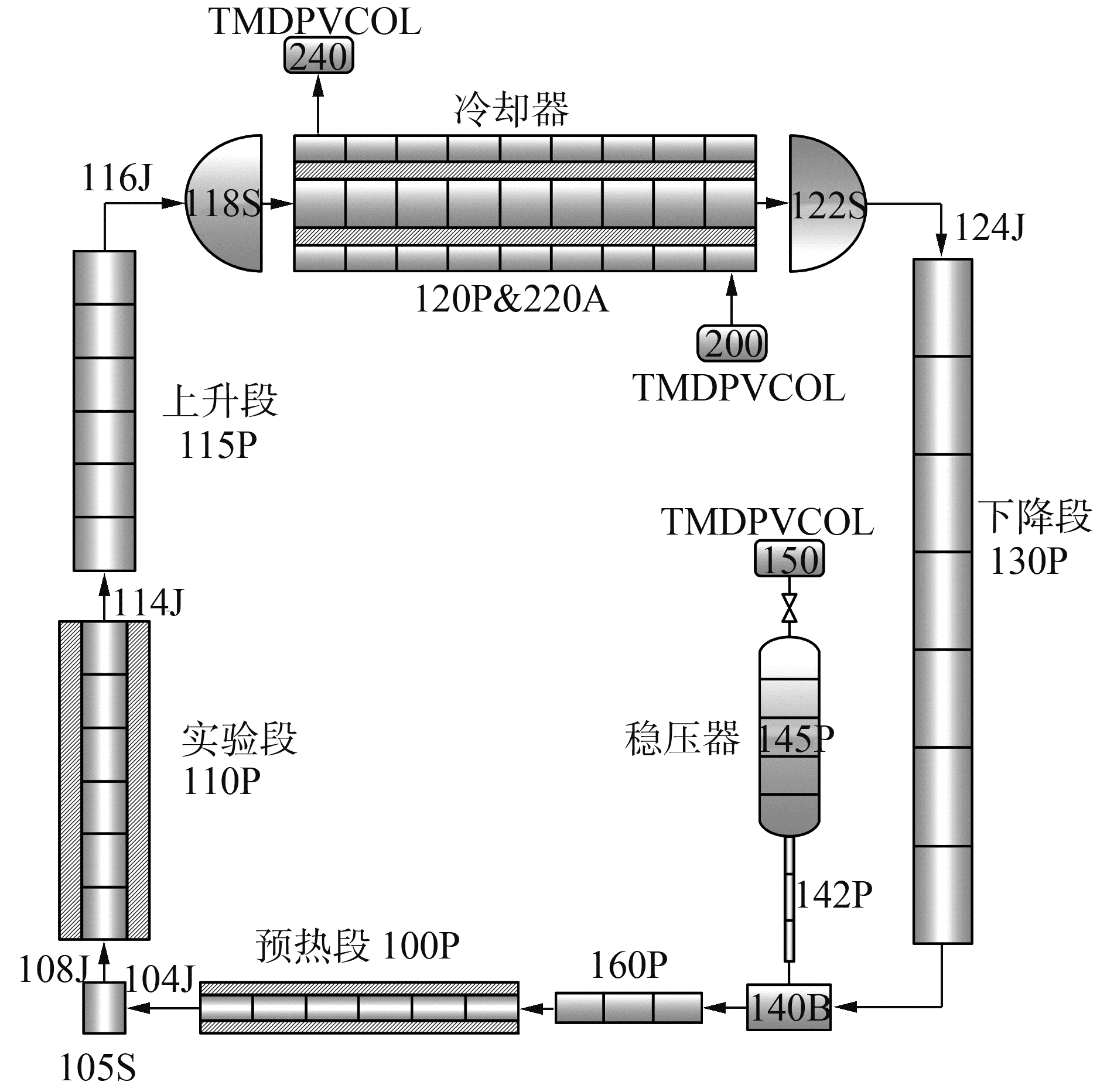
2 RELAP5计算模型简介 2.1 自然循环系统节点划分概述基于上述实验装置,建立了基于RELAP5的自然循环计算模型,并以实验中的稳态、瞬态以及流动不稳定性实验数据为基础,对RELAP5的模拟结果进行了评价。图 2为RELAP5节点图,其中100P为预热段,110P为电加热实验通道,加热功率由对应的热构件调节,115P为绝热上升段。120P为冷却器一次侧流体,220A为冷却器二次侧冷却水,利用冷、热流体的对流换热来带走回路中的热量。
|
Download:
|
| 图 2 自然循环系统RELAP5节点 Fig. 2 Layout of the RELAP5 nodalization for natural circulation system | |
计算过程中,通过时间相关控制体200 TMDPVOL给定二次侧的边界条件,结合预热段100P的功率投入比例来调节实验段入口过冷度ΔTsub, in。系统的压力边界则由稳压器145P及时间变量控制体150TMDPVOL设定。各部件的初始条件则根据实验数据初步给定,自然循环系统流量由冷、热段流体的密度差及回路阻力计算得出。
2.2 模型选择RELAP5/MOD3.3流体动力学模型采用一维、瞬态、两流体模型来解决两相混合物的流动问题。在数理模型的建立过程中,可以根据实际情况,利用自定义函数来修改RELAP5的模型。结合本实验系统,使用的主要模型为:
1) 壁面摩擦模型。
自然循环回路的阻力压降主要体现在摩擦阻力,需要指出的是在两相情况下,分相摩擦系数利用Chisholm[14]和Lockhart-Martinelli[15]模型计算,而其中摩阻系数λ的计算则根据流体流动状态来划分。层流及过渡区摩阻系数λL、λL,T分别为:
| $ {\lambda _{\rm{L}}} = 64/Re, \;\;\;\;\;0 \le Re < 2200 $ | (1) |
| $ \begin{array}{*{20}{c}} {{\lambda _{{\rm{L, T}}}} = (3.75 - 8250/{\rm{Re}})\left( {{\lambda _{T, 3000}} - {\lambda _{{\rm{L}}, 2200}}} \right) + }\\ {{\lambda _{{\rm{L, 2200}}}}, \quad 2200 \le Re < 3000} \end{array} $ | (2) |
紊流时,则利用Colebrook-White[16-17]修正关系式,紊流摩阻系数λL为:
| $ \begin{array}{l} \frac{1}{{\sqrt {{\lambda _{\rm{T}}}} }} = - 2\;{\rm{lg}}\left\{ {\frac{\varepsilon }{{3.7{D_{\rm{h}}}}} + \frac{{2.51}}{{Re}} \times } \right.\\ \;\;\;\;\;\;\;\;\;\left[ {1.14 - 2\;{\rm{lg}}\left( {\frac{\varepsilon }{{{D_{\rm{h}}}}} - \frac{{21.25}}{{R{e^{0.9}}}}} \right)} \right]\} \end{array} $ | (3) |
式中:ε为壁面粗糙度;Dh为圆管水力直径。
2) 两相传热模型。
对相变过程处理时,假设主流及壁面附近分别满足各自的界面能量平衡方程。同时利用相比焓及界面传质两者结合的方式描述相变过程[18-19],该方法能较好地解决过冷沸腾及蒸汽冷凝问题。经整理后,主流处相界面质量交换率Γig为:
沸腾过程:
| $ {\mathit{\Gamma }_{{\rm{ig}}}} = - \frac{{{H_{{\rm{ig}}}}\left( {{T_s} - {T_{\rm{g}}}} \right) + {H_{{\rm{if}}}}\left( {{T_{\rm{s}}} - {T_{\rm{f}}}} \right)}}{{h_{\rm{g}}^s - {h_{\rm{f}}}}}, {\mathit{\Gamma }_{{\rm{ig}}}} \ge 0 $ | (4) |
冷凝过程:
| $ {\mathit{\Gamma }_{{\rm{ig}}}} = - \frac{{{H_{{\rm{ig}}}}\left( {{T_s} - {T_{\rm{g}}}} \right) + {H_{{\rm{if}}}}\left( {{T_{\rm{s}}} - {T_{\rm{f}}}} \right)}}{{{h_{\rm{g}}} - h_{\rm{f}}^s}}, {\mathit{\Gamma }_{{\rm{ig}}}} \ge 0 $ | (5) |
式中:Hig为蒸汽界面传热系数; Hif为液体界面传热系数; Ts为饱和温度; Tg为气相温度; Tf为液相温度; hs为饱和相比焓; hg为气相比焓; hf为液相比焓。
壁面热边界层内的质量交换,即单位体积壁面附近的产气率Γwg为:
| $ {\mathit{\Gamma }_{{\rm{wg}}}} = \frac{{q{A_{\rm{w}}}}}{{V\left( {h_{\rm{g}}^s - {h_{\rm{f}}}} \right)}} \times \frac{{{\rm{min}}\left( {{h_{\rm{f}}}, h_{\rm{f}}^s} \right) - {h_{{\rm{er}}}}}}{{\left( {h_{\rm{s}}^f - {h_{{\rm{cr}}}}} \right)(1 + \varepsilon )}} $ | (6) |
式中:q为热流密度; Aw为内表面积; V为控制体体积; hcr为根据斯坦东数St和努塞尔数Nu计算得到的临界比焓; ε为折算系数。
3 参数敏感性分析 3.1 空间步长敏感性利用RELAP5进行反应堆瞬态热工水力计算时,必须保证数值计算的收敛性、稳定性及准确性。夏庚磊等[20]根据不同节点下极限热负荷计算结果,对节点无关性进行评估。结果表明:节点划分的合理性对流动不稳定性起始点的预测有较大影响。彭天骥等[21]则通过人为构造一瞬态过程来划分节点,但这类验证缺乏足够的实验数据来支撑。
合理的网格划分能有效地保证计算的准确性,RELAP5给出了网格的基本划分原则[22],即网格尺寸与水力直径的比值ζ满足式(7),而满足该条件后,计算的稳定性也会增强:
| $ \zeta = \frac{{\Delta L}}{{{D_h}}} \ge 0.5 $ | (7) |
式中:L为网格尺寸。
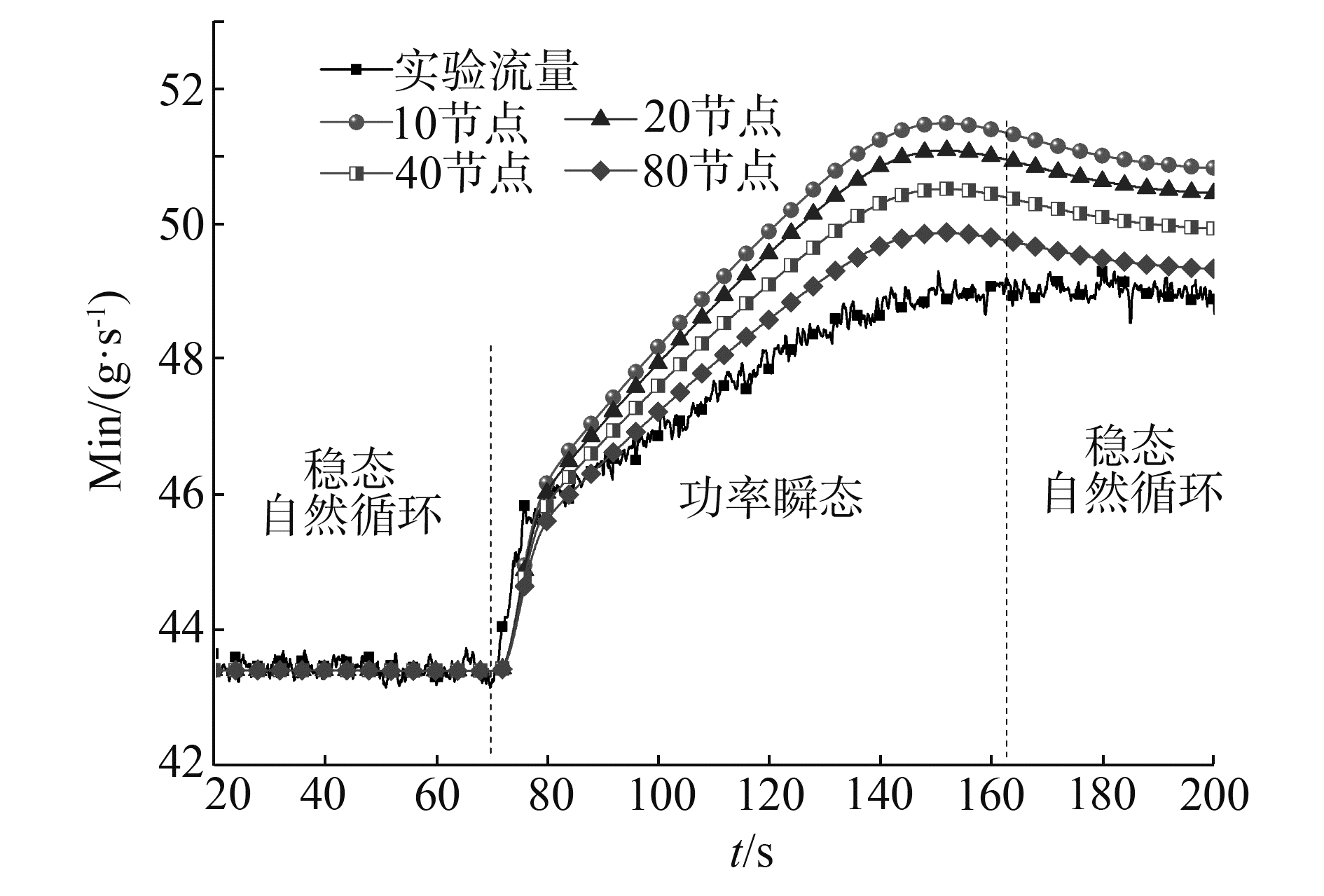
本文依据该原则,结合自然循环瞬态实验数据,讨论了不同节点方案对计算结果的影响。当实验回路建立了稳态自然循环后,令加热功率由6.25 kW阶跃增加至9.6 kW,比较自然循环流量的变化过程对节点的敏感性。如图 3所示,以实验段110P为例,随着节点数量的增加,流量的变化过程与实验更加接近。
|
Download:
|
| 图 3 节点划分对自然循环瞬态特性的影响 Fig. 3 The impact of nodalization on natural circulation transient character | |
另外,从图 3不难看出,自然循环瞬态受节点数量的影响更大,流量会出现超调,而稳态流量受节点数量影响不大。自然循环回路驱动力主要由冷、热段流体密度差决定,节点划分更细致会使各个控制体的流体密度变化计算更准确。
3.2 时间步长敏感性在RELAP5开发过程中,Ransom曾指出时间步长对两相瞬态有较大影响,如果选取不合适,不仅模拟结果与实验偏差很大,计算过程的收敛性也会受到影响。Krishnamurthy的研究则表明出口附近空泡份额对时间步长依赖性明显,受空间步长影响较小[23]。本文发现,仅对空间步长进行无关性检验,不能完全保证自然循环瞬态分析的正确性。
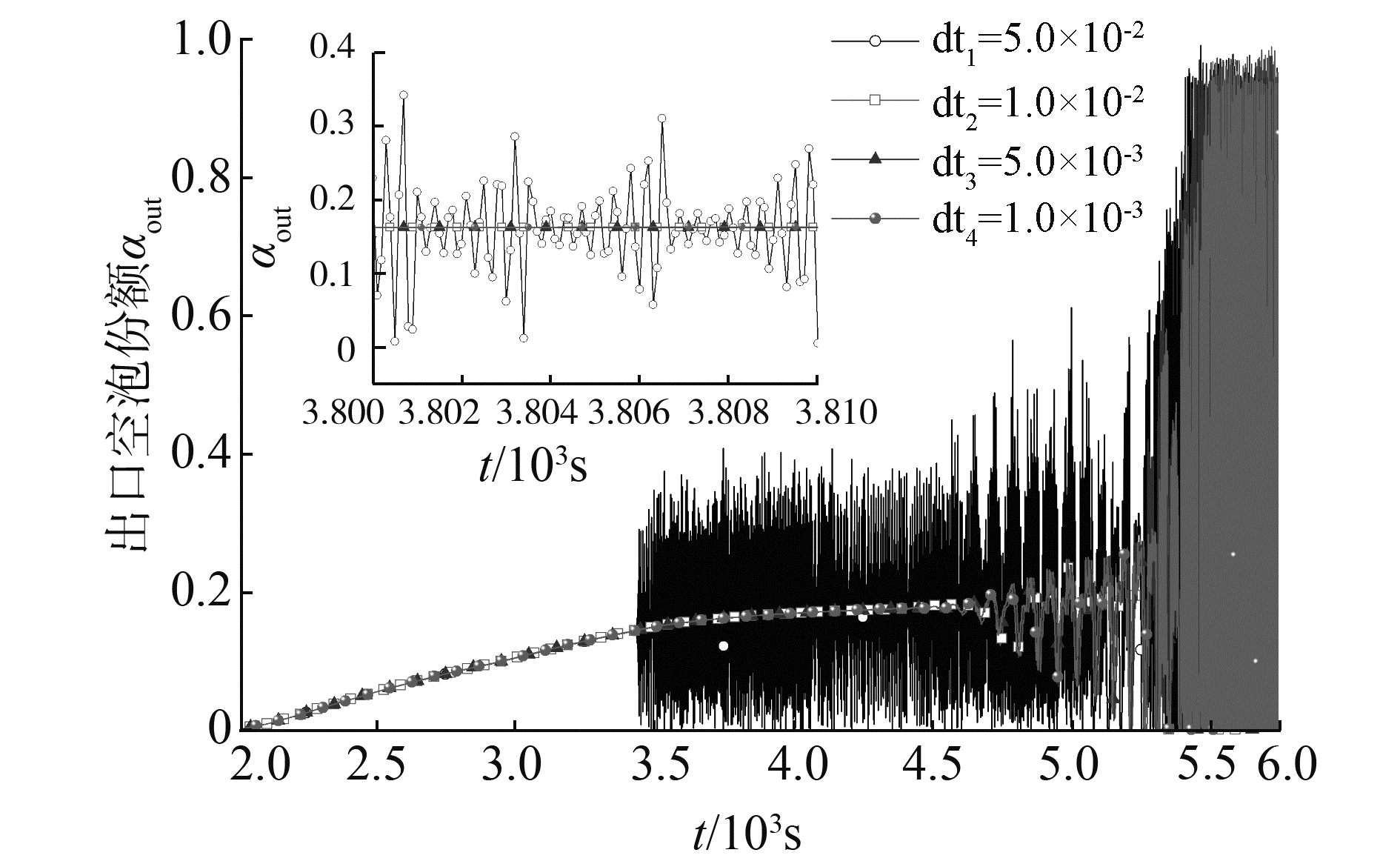
如图 4所示,针对相同的节点划分方案,通过步进增加加热功率,使自然循环由单相过渡到两相直至流动不稳定性出现。当时间步长取值较大时,加热段出口空泡份额αout计算不收敛。显然,利用RELAP5模拟低压自然循环系统前,需要对时间步长进行讨论。
|
Download:
|
| 图 4 时间步长对两相自然循环的影响 Fig. 4 The influence of time step on two-phase natural circulation | |
瞬态问题计算中,减小库郎数(Courant number),如降低时间步长Δt,可以有效增强计算稳定性,这点对自然循环流动不稳定性问题尤为重要。因为在自然循环系统参数周期性振荡期间,回路多处都处于非平衡状态。流体热工参数之间的相互耦合使振荡过程得以维持,而实验段、上升段内的换热直接受到空泡分布的影响。
因此,利用RELAP5进行瞬态模拟前,必须消除时间步长产生的干扰。本文从数值计算的角度,对上述工况的库郎数进行分析。一维网格的库郎数Ci可以定义为:
| $ C_{i}=\frac{u \Delta t}{\Delta z}=\frac{\overline{M} \Delta t}{\rho_{i} A_{i} \Delta z} $ | (8) |
式中:u为流体速度;Δt为时间步长;Δz为网格尺寸;M为回路质量流量;ρ为流体密度;A为流动截面积。它可以有效反映单位时间步长内流体通过的网格数量。同一节点方案,同一时间步长,回路不同位置的库郎数不尽相同。选取典型工况对库郎数的讨论结果如表 1所示,各工况均保持特征比ζ为1.42。
| 表 1 不同库郎数时收敛性验证 Table 1 Validation of convergence for courant number |
当库郎数Ci≤1时,计算结果收敛性较好。由于两相流动问题中相间拖曳系数κi大于单相,隐式算法中时间步长受库郎数限制更为明显。因此,两相自然循环应结合库郎数来合理选取空间及时间步长。
在图 1所示的自然循环系统中,两相流动主要出现在实验段、上升段、冷却器。显然,这些部件由于受到最大库郎数限制,需要更小的时间步长才能保证计算的准确性。但是这也不可避免地会降低单相段的计算效率。
4 流动不稳定性分析在低压条件下,开展了自然循环流动不稳定性实验。通过调整预热器功率及二次侧冷却水流量,保持加热段入口过冷度不变。逐渐增加实验段功率,发现在较高热流密度下,自然循环系统各参数发生大幅度的自持振荡。
图 5为RELAP5程序计算结果与实验数据在不稳定性发生期间主要参数的对比情况。流量的振荡形式相似,振荡周期的计算值比实验值偏大7.4%,幅值偏大17.35%。时均流量的计算结果明显高于实验值,会导致流动不稳定性起始点预测偏于保守,即极限热负荷计算值偏高。

|
Download:
|
| 图 5 实验结果与计算结果对比 Fig. 5 Comparison between experimental data and calculation results | |
在低压高热流密度下,加热段出口产气率比低热流密度工况更快。当出口发生饱和沸腾后,自然循环流量随驱动力增大而迅速变大。此时,在较高的系统流量下,加热段出口变为过冷流体,驱动力开始下降。同时,在加热段出口产生的大量气泡被带到绝热上升段内。由于冷凝不充分,上升段仍可以提供一定的驱动力,因此流量下降比上升过程更缓慢。
通过建立恰当的模型及参数敏感性验证,RELAP5能够模拟这种振荡幅值较大的流动不稳定性。如图 6所示,气、液两相流体交替通过加热段出口和上升段,结合脉动期间有效驱动压头的变化,可以较好地揭示自然循环系统的参数变化规律。

|
Download:
|
| 图 6 流动不稳定期间主要参数变化规律 Fig. 6 Variation of main parameters during flow instability | |
图 5和图 6为同一工况,由图 6的计算结果可知,流量下降过程中,沸腾产生的两相流体进入上升段后,由于气泡的不断被冷凝,上升段流体平均温度升高,流体平均温度更接近当地压力下的饱和温度。上升段出口会出现一定程度的闪蒸并向上游发展,同时部分气泡由于冷凝不充分而在上升段内积累。上升段内流体平均密度降低,弥补了加热段的驱动压头,从而延缓自然循环流量的下降。自然循环系统中出现的流动不稳定性往往是多个参数耦合作用的结果。本文采用快速傅里叶变换对低压高热流密度下出现的不稳定性衍化规律进行分析,结果如图 7所示。其中,热流密度q″为334.1 kW·m2,系统压力为0.48 MPa,入口过冷度ΔTsub, in为49.8 ℃。

|
Download:
|
| 图 7 复合动态流动不稳定性幅度谱图 Fig. 7 The amplitude spectrum of compound dynamic instability | |
研究中出现的流量周期性振荡,可以分解为一个基波和若干谐波。根据输运时间及基波频率f1,将该流动不稳定性归为由密度波主导的复合动态流动不稳定性[12]。实验值和计算值均有一个奇次谐波f3(三次谐波),根据上述讨论并结合流量及各参数的时域规律,该过程对应的非线性负载为上升段内的相变(冷凝与闪蒸)。
5 结论1) 针对低压自然循环实验系统,利用RELAP5建立了能够计算自然循环系统特性的数理模型。能够较准确地模拟自然循环系统的各瞬态特性。
2) 对低压两相自然循环问题,模化过程必须细致,尤其对于有相变存在的部件。两相自然循环瞬态过程对时间步长有一定的依赖性,仅对空间步长进行无关性检验,不能完全保证自然循环瞬态分析的正确性。无关性验证时应保证库郎数不大于1。
3) RELAP5能够实现对高热流密度下的自然循环流动不稳定现象的模拟,不稳定性起始点预测值偏低。
| [1] |
徐济鋆. 沸腾传热和气液两相流[M]. 2版. 北京: 原子能出版社, 2001: 183-188.
(  0) 0)
|
| [2] |
谭思超, 高璞珍, 苏光辉. 摇摆运动条件下自然循环流动的实验和理论研究[J]. 哈尔滨工程大学学报, 2007, 28(11): 1213-1217. TAN Sichao, GAO Puzhen, SU Guanghui. Experimental and theoretical study on natural circulation flow under rolling motion condition[J]. Journal of Harbin Engineering University, 2007, 28(11): 1213-1217. DOI:10.3969/j.issn.1006-7043.2007.11.005 (  0) 0)
|
| [3] |
Nuclear Safety Analysis Division. RELAP5/MOD3.3 code manual volume Ⅰ:code structure, system models, and solution methods[M]. US: Nuclear Regulatory Commission, 2001.
(  0) 0)
|
| [4] |
HAMIDOUCHE T, BOUSBIA-SALAH A. RELAP5/3.2 assessment against low pressure onset of flow instability in parallel heated channels[J]. Annals of nuclear energy, 2006, 33(6): 510-520. DOI:10.1016/j.anucene.2006.01.004 (  0) 0)
|
| [5] |
FULLMER W D, KUMAR V, BROOKS C S. Validation of RELAP5/MOD3.3 for subcooled boiling, flashing and condensation in a vertical annulus[J]. Progress in nuclear energy, 2016, 93: 205-217. DOI:10.1016/j.pnucene.2016.08.013 (  0) 0)
|
| [6] |
FURUYA M, INADA F, VAN DER HAGEN T H J J. Flashing-induced density wave oscillations in a natural circulation BWR-mechanism of instability and stability map[J]. Nuclear engineering and design, 2005, 235(15): 1557-1569. DOI:10.1016/j.nucengdes.2005.01.006 (  0) 0)
|
| [7] |
MARCEL C P, ROHDE M, VAN DER HAGEN T H J J. Experimental and numerical investigations on flashing induced instabilities in a single channel[J]. Experimental thermal and fluid science, 2009, 33(8): 1197-1208. DOI:10.1016/j.expthermflusci.2009.08.001 (  0) 0)
|
| [8] |
程坤, 谭思超, 陈莹莹, 等. 海洋条件反应堆热工水力系统分析程序开发及验证[J]. 哈尔滨工程大学学报, 2017, 38(8): 1223-1230. CHENG Kun, TAN Sichao, CHEN Yingying, et al. Development and validation of nuclear reactor thermal-hydraulic system analysis code under ocean conditions[J]. Journal of Harbin Engineering University, 2017, 38(8): 1223-1230. (  0) 0)
|
| [9] |
KOZMENKOV Y, ROHDE U, MANERA A. Validation of the RELAP5 code for the modeling of flashing-induced instabilities under natural-circulation conditions using experimental data from the CIRCUS test facility[J]. Nuclear engineering and design, 2012, 243: 168-175. DOI:10.1016/j.nucengdes.2011.10.053 (  0) 0)
|
| [10] |
TISELJ I, ERNE G. Some comments on the behavior of the RELAP5 numerical scheme at very small time steps[J]. Nuclear science and engineering, 2000, 134(3): 306-311. DOI:10.13182/NSE134-306 (  0) 0)
|
| [11] |
LAKSHMANAN S P, PANDEY M. Numerical investigations on power ramping procedure for a natural circulation boiling water reactor[J]. Nuclear engineering and design, 2010, 240(4): 860-867. (  0) 0)
|
| [12] |
王强, 高璞珍, 王忠乙, 等. 低压高过冷度下自然循环流动不稳定性实验研究[J]. 原子能科学技术, 2018, 52(5): 822-828. WANG Qiang, GAO Puzhen, WANG Zhongyi, et al. Experimental investigation on flow instability under low pressure and high subcooling natural circulation conditions[J]. Atomic energy science and technology, 2018, 52(5): 822-828. (  0) 0)
|
| [13] |
WANG Qiang, GAO Puzhen, CHEN Xianbing, et al. An investigation on flashing-induced natural circulation instabilities based on RELAP5 code[J]. Annals of nuclear energy, 2018, 121: 210-222. DOI:10.1016/j.anucene.2018.07.035 (  0) 0)
|
| [14] |
CHISHOLM D. A theoretical basis for the lockhart-martinelli correlation for two-phase flow[J]. International journal of heat and mass transfer, 1967, 10(12): 1767-1778. DOI:10.1016/0017-9310(67)90047-6 (  0) 0)
|
| [15] |
LOCKHART R W, MARTINELLI R C. Proposed correlation of data for isothermal two-phase, two-component flow in pipes[J]. Chemical engineering progress, 1949, 45(1): 39-48. (  0) 0)
|
| [16] |
COLEBROOK C F. Turbulent flow in pipes, with particular reference to the transition region between the smooth and rough pipe laws[J]. Journal of the Institution of civil engineers, 1939, 11(4): 133-156. DOI:10.1680/ijoti.1939.13150 (  0) 0)
|
| [17] |
ZIGRANG D J, SYLVESTER N D. A review of explicit friction factor equations[J]. Journal of energy resources technology, 1985, 107(2): 280-283. (  0) 0)
|
| [18] |
Nuclear Safety Analysis Division. RELAP5/MOD3.3 code manual volume Ⅳ:models and correlations[M]. Rockville: Information Systems Laboratories, Inc., 2001.
(  0) 0)
|
| [19] |
SAHA P, ZUBER N. Point of net vapor generation and vapor void fraction in subcooled boiling[C]//Proceedings of the 5th International Heat Transfer Conference. Tokyo, Japan, 1974: 175-179.
(  0) 0)
|
| [20] |
夏庚磊, 郭赟, 彭敏俊. 基于RELAP5的两管平行通道流动不稳定性研究[J]. 原子能科学技术, 2010, 44(6): 694-700. XIA Genglei, GUO Yun, PENG Minjun. Investigation on two-phase flow instability in parallel channels based on RELAP5 code[J]. Atomic energy science and technology, 2010, 44(6): 694-700. (  0) 0)
|
| [21] |
彭天骥, 邱金荣, 郭赟, 等. 欠热沸腾诱发自然循环不稳定性的研究[J]. 原子能科学技术, 2013, 47(3): 381-390. PENG Tianji, QIU Jinrong, GUO Yun, et al. Study on instability of natural circulation induced by subcooled boiling[J]. Atomic energy science and technology, 2013, 47(3): 381-390. (  0) 0)
|
| [22] |
Nuclear Safety Analysis Division. RELAP5/MOD3.3 code manual volume Ⅴ: user's Guidelines[Z]. US: Nuclear Regulatory Commission, 2001.
(  0) 0)
|
| [23] |
Nuclear Safety Analysis Division. RELAP5/MOD3 code manual volume Ⅵ: validation of numerical techniques in RELAP5/Mod3.0[Z]. US: Nuclear Regulatory Commission, 2001.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


