2. 湖南大学 土木工程学院, 湖南 长沙 410082;
3. 西南交通大学 土木工程学院, 四川 成都 610031
2. College of Civil Engineering, Hu'nan University, Changsha 410082, China;
3. School of Civil Engineering, Southwest JiaoTong University, Chengdu 610031, China
钢管构件被广泛应用于各种建筑结构和海洋工程结构,偏心相贯连接节点为钢管之间连接的一种形式,对比弦杆(主管)轴线与腹杆(支管)轴线相交于一点的常规钢管相贯节点,支、主管轴线并不相交而是产生偏心距的偏心相贯连接节点具有一些优点:更好的美学效果、便于高空焊接施工(节点连接处支管不完全断开从而可以直接叠放在主管上)等。无加劲构造导致钢管相贯节点在工程常见几何参数范围内表现出明显的半刚性连接特性[1-2],节点的刚度对于整体结构的安全性、受力性能等产生影响[3-6]。然而,目前关于钢管相贯节点在支管轴力作用下的刚度的研究相对较多[6-13],关于平面外弯矩作用下钢管相贯节点刚度的研究相对较少[14-15],关于钢管偏心相贯节点的平面外抗弯刚度的研究则几乎没有。
本文对一种十字形矩形钢管偏心相贯节点的平面外抗弯刚度进行研究。首先介绍节点构造特点,进行一个节点试验用于观察节点局部变形特点及校验有限元模型。根据试验及有限元所得节点变形特点,借鉴文献[7]将T形矩形钢管相贯节点的承载力计算模型(塑性铰线模型)移植改进后用于建立节点在支管轴力作用下的刚度模型的方法,在此基础上建立关于十字形矩形钢管偏心相贯节点的平面外抗弯刚度计算的3梁系模型。通过有限元参数化分析所得的大量节点刚度数据,对节点刚度理论模型进行修正,结合多元非线性回归分析,获得节点的平面外抗弯刚度参数化计算式,为矩形钢管偏心相贯节点用于工程设计提供参考。
1 节点的构造与有限元模型本文研究的十字形矩形钢管偏心相贯节点的构造特点如下,支管的上翼缘连通、但中间部分的下翼缘与腹板切割后形成槽口,然后将其插入主管,主管两侧支管的下翼缘及腹板与相邻主管腹板表面通过角焊缝连接,搭在主管上的支管上翼缘与主管上翼缘亦用角焊缝焊接起来。此类节点在扁平网壳结构中具有便于高空施工等优点。竖向荷载作用下,平面外弯矩Mo将成为此类节点的主要内力,节点构造及其受力简图如图 1所示。Mo可简化为沿着支管轴线方向且作用于支管上、下翼缘的一对力偶F。在F的作用下,支管上翼缘以轴向拉伸变形为主,支管下翼缘则以相邻主管腹板的局部凹陷变形为主,这种局部凹陷变形致使支管(视为杆系)产生了近似刚体的转动,即节点的转角ψ,这种转动产生了支管相对主管的转动,即节点半刚性。

|
Download:
|
| 图 1 十字形矩形钢管偏心相贯节点构造及其受力简图 Fig. 1 Eccentric RHS cross-type joints and its force diagram | |
进行一个节点试验用来考察节点局部变形特征及校验有限元模型,其构造同图 1,但在支、主管端部增加端板等附加装置。此外,在支管上翼缘加一块厚为8 mm的盖板以确保不出现支管上翼缘拉断破坏,盖板在两端通过角焊缝与支管上翼缘连接。试件的尺寸与加载装置照片见图 2,试件支、主管的材料性能试验见表 1。

|
Download:
|
| 图 2 试件尺寸和加载装置照片 Fig. 2 Test specimen and setup | |
| 表 1 材料性能试验结果(平均值) Table 1 Measured material properties (average value) |
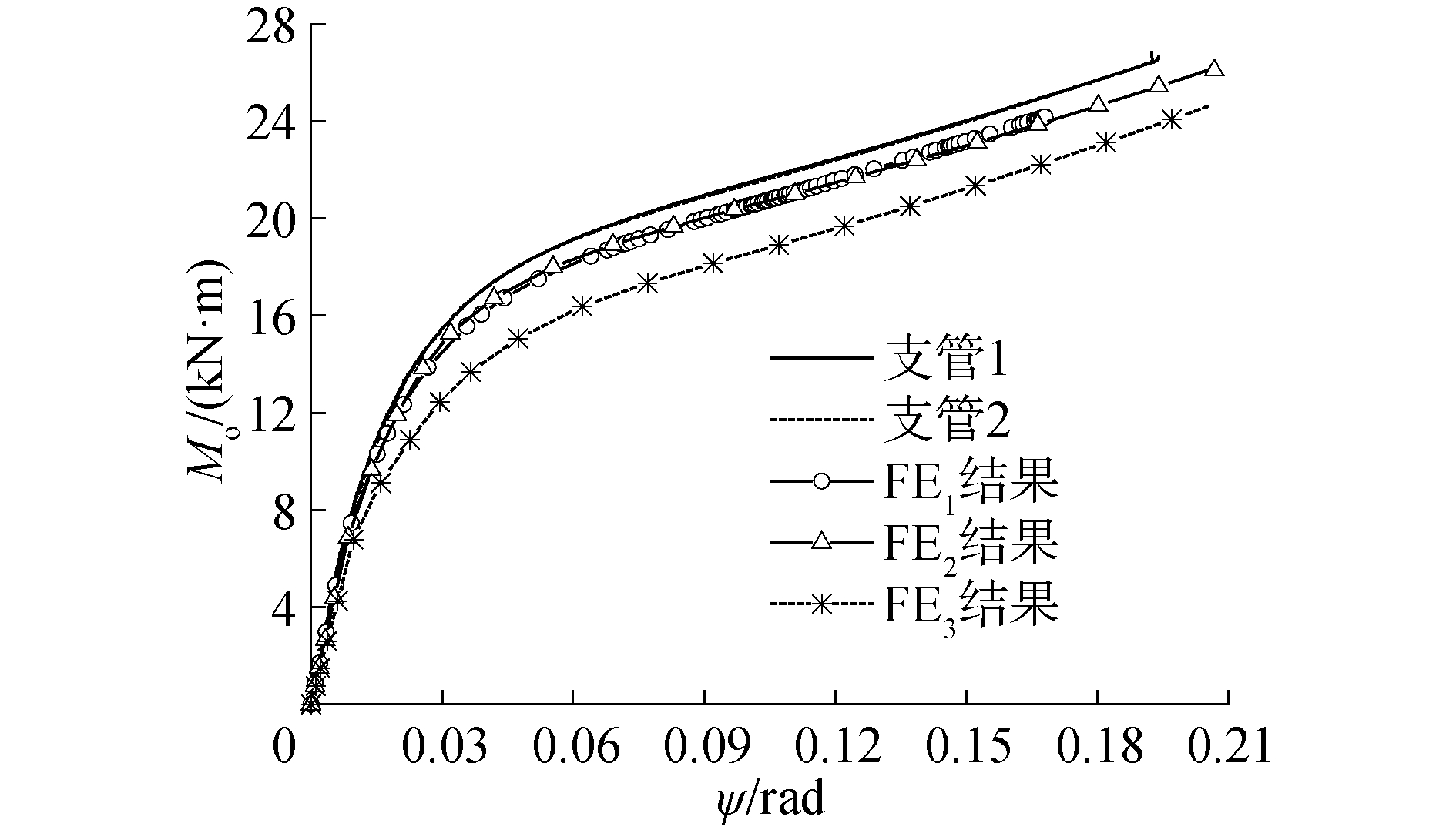
试验过程在另文节点承载力的研究中详述[16],这里给出节点平面外弯矩-转角(Mo-ψ)曲线用于研究节点弹性平面外抗弯刚度,见图 3。图中的支管1、2分别为主管两侧的支管所得Mo-ψ曲线, 图中的FE1~FE3为模拟试件的3种有限元模型计算所得结果。3种有限元模型均采用在对称面处施加对称约束的半结构模型;在主管的端板上施加模拟试验的铰接支座,在支管端施加垂直于支、主管平面的集中力,模拟千斤顶作用;采用ABAQUS的六面体单元C3D8R[17],网格划分时,主管管壁、支管翼缘、支管腹板的厚度方向分别为5、4、2层,中间3H内的主管、根部h内的支管的单元接近正方体,向外逐渐过渡到长、短边之比为5的长方体单元。材料本构关系采用双线型强化模型,弹性模量E见表 1,强化阶段切线模量Et=(fut-fyt)/(εut-εyt),其中fyt、εyt、fut、εut分别为真实的屈服强度、屈服应变、极限强度、极限应变,由表 1的名义应力和应变按照文献[17]的方法换算得到。3个有限元模型区别在细部构造方面:FE1模型中主管、带有槽口的支管、盖板、角焊缝各为独立的part[17],角焊缝的侧面和与之相接触的主管腹板的面、支管腹板及下翼缘的面、盖板的端面之间通过tie约束[17];FE2不考虑角焊缝,直接将主管、支管、盖板merge[17]成一个整体;FE3为FE2去掉盖板。
|
Download:
|
| 图 3 节点的平面外弯矩-转角曲线(Mo-ψ曲线) Fig. 3 Out-of-plane bending moment-rotation curves of the joints | |
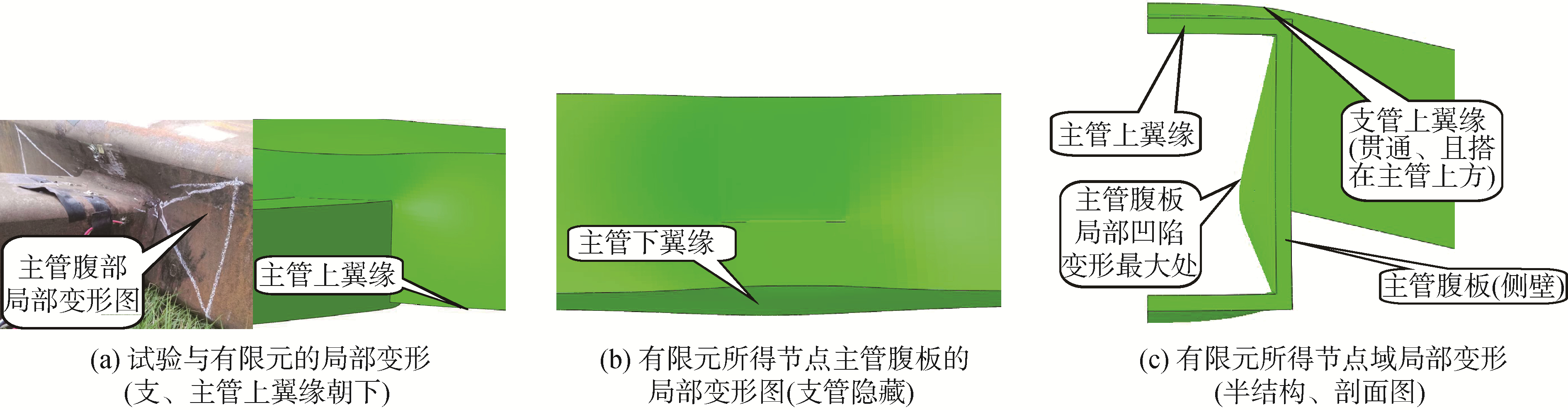
由图 3可知,FE1~FE3所得的Mo-ψ曲线在总体趋势与试验结果一致,FE1与FE2的Mo-ψ曲线与试验结果非常接近,FE3所得曲线比前三者低约10%。取Mo-ψ曲线中前3步的弯矩与转角比值的平均值(3个比值很接近)作为节点的平面外抗弯弹性(初始)刚度,可得试验、FE1、FE2、FE3的刚度值依次为866、860、822、709 kN ·m,模拟了试件盖板的FE1和FE2与试验结果很接近,表明有限元模型可用于后续参数化分析。对比3个有限元所得刚度值,表明盖板使得节点刚度增加约14%,但焊缝仅使节点刚度增加约4%,文献[18]的研究亦表明焊缝仅略提高节点刚度,故后续有限元分析不再考虑焊缝影响。图 4给出试验和FE3所得节点变形的对比,表明有限元较好地反映了试验结果。
|
Download:
|
| 图 4 试验与有限元所得节点平面外弯矩作用下的局部变形 Fig. 4 Local deformation for Eccentric RHS cross-type joints under out-of-plane moment from test and FEA result | |
由图 4可知,连接支管的主管侧壁在平面外弯矩作用下的局部变形特征具有以下特点:1)主管侧壁(腹板)的局部凹陷变形大致分为近似刚体转动区域、抵抗支管传来压力F的支撑区域;2)支撑区域又大致分为1个中央区和2个边区。图 5给出这些区域的分布和大致形状:近似刚体转动区域cdef、1个中央区abfe、2个边区ade和bcf,其中凹陷变形最显著的位置为ef。借鉴文献[7]将塑性铰线模型移植用于建立T形钢管节点轴向刚度计算的方法,将本文的支撑区域简化为3根截面宽度变化的梁来等效主管腹板对支管的约束作用。其中,截面高度为T而宽度呈梯形变化的梁用来等效中央区abfe、截面高度为T而宽度呈三角形变化的梁用来等效边区ade和bcf,将近似刚体转动区域cdef视为与支管相连接的刚片,如此形成可用于计算十字形矩形钢管偏心相贯节点在平面外弯矩作用下的局部变形(节点刚度)的3梁系模型,见图 6。

|
Download:
|
| 图 5 平面外弯矩作用下的节点局部变形区域分类 Fig. 5 Regions classification of the joint local deformation under out-of-plane bending moment | |

|
Download:
|
| 图 6 节点平面外抗弯刚度计算的3杆系模型 Fig. 6 Three-beam model for rigidity computation of eccentric RHS cross-type joint under out-of-plane moment | |
每一类梁的边界条件假定如下:beam1(代表区域abfe)的近端和远端(与主管下翼缘连接)均假定为固定约束;beam2(代表区域ade和bcf)的近端假定为转动约束为零的点连接(点e和f),考虑到水平方向约束对小变形问题无影响,最终假定为仅竖向约束;beam2的远端受主管管壁约束,简化为转动刚度为λET3的弹性约束,λ为一常数。关于beam1与beam2的跨度值,忽略钢管壁厚的影响,由几何关系(见图 5)可得l1=H-h、l2=(H-h)/tanα。关于α的取值,采用最小势能原理[19]来确定。外力(平面外弯矩)所做功Moψ等于所有塑性绞线转动产生内能En的总和;塑性铰线共6类,依次为ab、ef、ad与bc、ae与bf、de与cf、cd(见图 5),每一条塑性铰线的内能为φilimp,其中mp=fyT2/4为单位宽度屈服弯矩,通过几何关系将每一条塑性铰线的长度li、相对转角φi分别表示为关于tanα和关于最大凹陷变形Δp(见图 5)的函数;再利用平截面假定得ψ=Δp/h,将外力功等于内能的式子进行简化得到Mo关于α、β等的表达式;最后利用最小势能原理(令Mo对α的求导为零)可得α:
| $ \alpha = \arctan \sqrt {(1 - \beta )/\beta } $ | (1) |
利用结构力学,得到3梁系模型中beam1、beam2在远端不动而近端下沉Δ时相应的剪力V1、V2,再根据Mo=F(h-t)=(V1+2V2)(h-t),经简化后最终得节点平面外抗弯弹性刚度Koe:
| $ \begin{array}{l} {K_{{\rm{oe}}}} = {M_{\rm{o}}}/\psi = F(h - t)/(\Delta /h) \approx F{h^2}/\Delta = \\ E{T^3}\left[ {\frac{{{\beta _1}{\beta ^2}}}{{3{{(1 - \beta )}^3}}} + {{\left( {\frac{\beta }{{1 - \beta }}} \right)}^{2.5}} + } \right.\\ \frac{{2\lambda \beta }}{{(1 - \beta )\left( {1 + 6\lambda \sqrt {\beta - {\beta ^2}} } \right)}}] \end{array} $ | (2) |
β、β1、μ、γ、τ、T(意义见图 1)构成确定十字形矩形钢管偏心相贯节点的几何参数,这些参数均有可能影响节点平面外抗弯刚度Koe。理论式(2)反映了Koe与ET3成正比、与β1呈线性关系,亦给出了Koe与β之间的函数形式,但无法反映参数γ、μ、τ的影响。以有限元为手段进行参数分析,研究各参数对Koe的影响。参数化分析的节点有限元模型类同第1节的FE3模型,但删除连接头等附加装置,主管两端施加固定约束,支管端的集中力改为集中弯矩,模型中主管长度、带槽口的支管总长度分别为10H、8h+B,钢管弹性模量E为206 GPa。
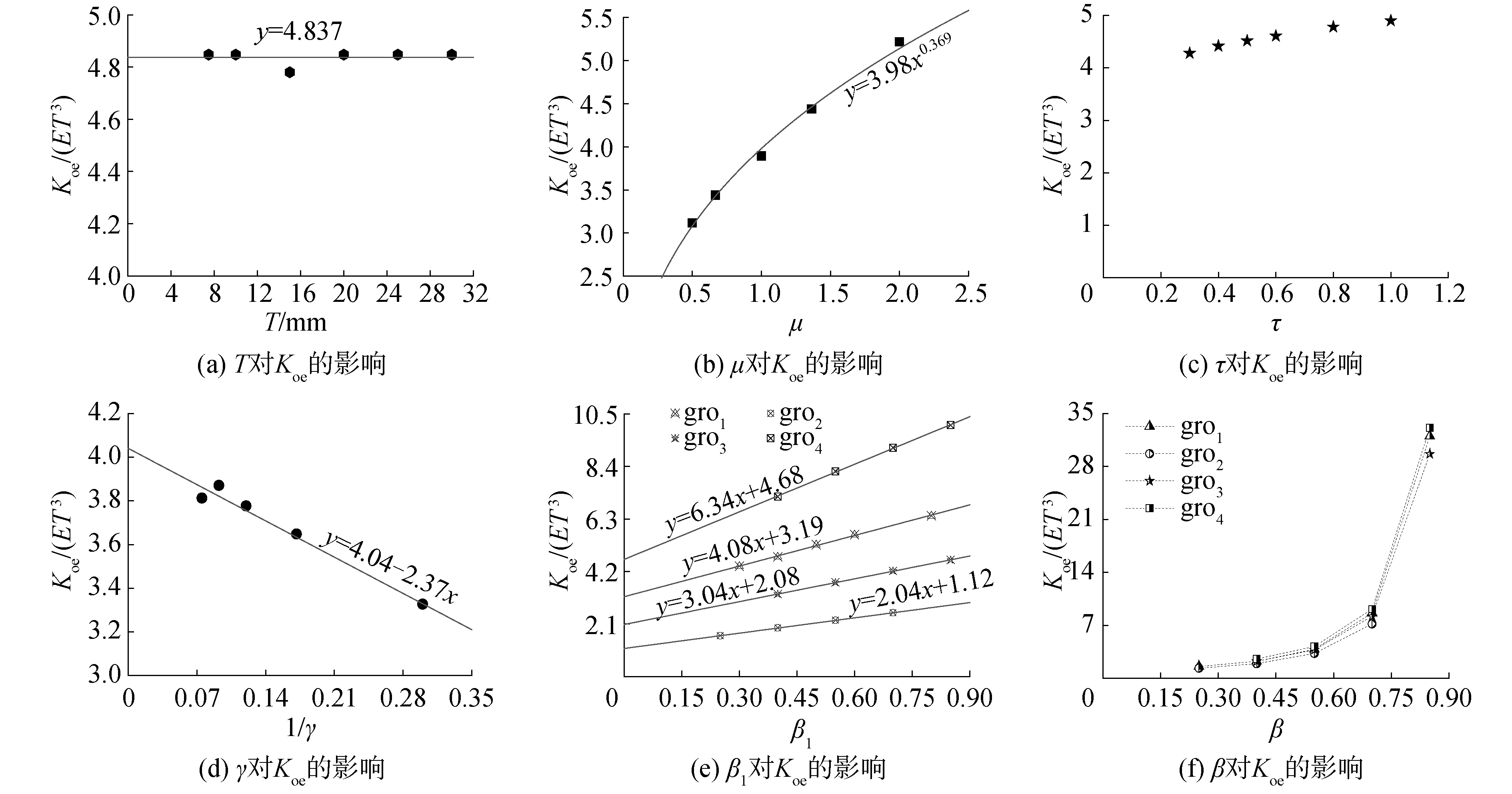
图 7给出了Koe关于T等的单参数分析结果,图中纵坐标为KoeE-1T-3,散点为有限元所得数据,水平线为各散点的平均值,斜直线或曲线为根据各散点拟合而来。固定β=0.6、β1=0.4、μ=1.5、τ=0.8、γ=10变化T(7.5~30 mm)时,由图 7(a)可知,KoeE-1T-3的范围为4.78~4.85,差异在3%以内,认为Koe与T 3成正比。变化E亦得到类似结论,不再赘述,验证了理论式(2)的Koe与ET3成正比的关系。其他参数不变(H=300 mm、T=15 mm、β=0.6、β1=0.4、τ=0.8)变化μ(0.5~2)时,由图 7(b)可知幂函数可近似反映Koe与μ的关系;Koe随着μ的增加而略有增加的原因如下:当H与T不变而μ增加则意味着主管翼缘的宽厚比降低,其对腹板的约束加强,增强了节点刚度。其他参数不变(β=0.6、β1=0.4、H×B×T=300× 200×15 mm)变化τ(0.3~1)时,由图 7c可知Koe随着τ的增加而略有增加,最大值与最小值差异约13%;当τ在工程中常用的范围内(0.4~0.8)时,最大值与最小值的差异约8%,故忽略τ对Koe的影响。其他参数不变(β=0.55、β1=0.4、μ=1.5、τ=0.8、T=15 mm)变化γ(3.33~13.33)时,由图 7(c)可知,线性函数即可反映Koe与1/γ之间的关系。
|
Download:
|
| 图 7 参数T、μ、γ、τ、β1、β对节点平面外抗弯刚度Koe的影响 Fig. 7 Effect of parameters T, μ, γ, τ, β1 and β on Koe | |
式(2)表明参数β与β1对Koe存在相互影响效应,故对β、β1进行较全面的单参数分析。考虑到矩形管截面高宽比适用范围为0.5~2、屈服线模型适用0.25≤β≤0.85[19],设计了4组参数进行分析。第1组固定H×B×T=300 mm×200 mm×15 mm、τ=0.8、β=0.6 (β1=0.4)变化0.3≤β1≤0.8 (0.25≤β≤0.85);第2~4组均固定H×B×T=360 mm×300 mm×15 mm、τ=0.8,依次固定β(β1)取0.4、0.55、0.7而变化β1(β)取0.25~0.7、0.4~ 0.85、0.4~0.85。图 7(e)、(f)分别给出Koe (KoeE-1T-3)随着β1、β的变化,图中gro1~gro4为第1~4组的结果。由图 7(e)可知,Koe与β1间呈线性函数关系且斜率和截距随着β变化而变化,式(2)亦证明了这点。对比图 7(e)和图 7(f)可知,β对Koe的影响比β1大得多、且β与Koe之间近似指数函数关系,考虑到根号函数可通过泰勒展开为多项式,多项式又是指数函数的级数展开,故式(2)的中括号的后2项可简化为一个关于β的指数函数,与中括号的第1项一起形成关于β的复杂函数。经过多次尝试,exp(c0+c1β+c2β2)比简单的指数函数exp(cβ)能更准确地反映β与Koe之间的关系。
3.2 节点平面外抗弯刚度的参数化计算式通过单参数分析,十字形矩形钢管偏心相贯节点的平面外抗弯弹性刚度Koe的最终形式如下:
| $ {K_{{\rm{oe}}}} = E{T^3}{\mu ^{{c_0}}}\left( {{C_1} + \frac{{{C_2}}}{\gamma }} \right)\left( {\frac{{{\beta _1}{\beta ^2}}}{{3{{(1 - \beta )}^3}}} + {{\rm{e}}^{{C_3} + {C_4}\beta + {C_5}{\beta ^2}}}} \right) $ | (3) |
式中:C0~C5为常系数。采用全参数有限元计算获得足够多的数据并结合回归分析确定这些常系数,固定E=206 GPa、B=300 mm、T=15 mm、τ=0.8,考虑到屈服线模型前提为β≤0.85[19],β(β1)选取如下:0.25(相应的β1取0.25、0.4、0.55),0.4(β1取0.25、0.4、0.55、0.7),0.55(β1取0.4、0.55、0.7、085),0.7(β1取0.4、0.55、0.7、0.85)、0.85(β1取0.55、0.7、0.85);如此形成β、β1变化的18个数据。在此基础上取γ为5、8、12、16、20,相应参数μ为0.5、0.8、1.2、1.6、2,结合前面单参数分析所得数据,得到120个节点刚度数据,通过置信度为95%的多元非线性回归分析确定常系数C0~C5,最终得到关于Koe的参数化计算式:
| $ {K_{\rm{i}}} = E{T^3}{\mu ^{0.61}}\left( {0.29 - \frac{{0.31}}{\gamma }} \right)\left( {\frac{{{\beta _1}{\beta ^2}}}{{3{{(1 - \beta )}^3}}} + {{\rm{e}}^{1.31 - 0.19\beta + 4.11{\beta ^2}}}} \right) $ | (4) |
利用有限元计算所得数据来校验参数化计算式(4)的合理性,参数范围为β(0.25~0.85)、β1(0.25~ 0.85)、γ(3.33~20)、μ(0.5~2.0)、τ(0.3~1.0)、T(7.5~30 mm),基本覆盖了工程常用范围。图 8给出了有限元所得Koe与式(4)计算值的比较,图中的纵坐标为计算值和有限元所得值之间的相对误差。由图 8可知,大多数误差在15%以内,极少数误差超过25%且大部分位于工程中应用较少的β≤0.4,误差最大值约32%,所有误差的绝对值的平均值为9.5%。文献[6, 18]的研究表明,15%的误差对于钢管节点的初始(弹性)刚度而言属于相当小。因此,由3梁系模型发展而来的十字形矩形钢管偏心相贯节点在两侧支管同向相等平面外弯矩作用下(工程中最常见荷载工况)的刚度的参数化计算式总体上较好地反映了节点的平面外抗弯半刚性特性。

|
Download:
|
| 图 8 式(4)计算值与有限元结果的误差 Fig. 8 Error of stiffness values between FEA and Eq (4) | |
将表 1和图 2中所给的节点试验的相关节点参数(主管壁厚T取实测值8.2 mm)代入式(4)可算得节点抗弯刚度值为690 kN ·m,其比试验和有限元(FE3)所得值866 kN ·m、709 kN ·m分别低了约20%、3%,考虑到式(4)是基于无盖板加强的节点有限元参数化分析回归拟合而来,而第1节结果表明盖板能使节点刚度增加约14%,故式(4)较好地反映了实际结果。
4 结论1) 试验和有限元结果表明,节点域在平面外弯矩作用下的局部变形大致分为近似刚体转动区域和抵抗支管传来力的支撑区域,支撑区域可进一步简化为三根梁。
2) 通过理论模型和数值分析表明,节点平面外抗弯刚度与主管壁厚T的三次方成正比、与支管截面宽度与主管截面高度之比β1呈线性关系、与主管截面高厚比的倒数γ-1呈线性关系、与主管截面高宽比μ呈幂函数关系、与支主管截面高度比β近似指数函数关系,
3) 节点抗弯刚度受支主管壁厚比τ的影响小、但受的β影响大,且参数β与β1对节点抗弯刚度存在相互影响效应,
4) 试验和有限元结果验证了节点平面外抗弯刚度参数化计算式的合理性。
基于三梁系模型建立的矩形钢管偏心相贯节点平面外抗弯刚度参数化计算式,具有表达式较简洁、物理意义明确等优点,同时也为此类节点应用于工程设计提供理论参考和技术支持。
| [1] |
OCHI K. Rotational stiffness of rectangular tubular joints-flexural rigidity equation and classification of unstiffened connections[C]//Proceedings of the 4th Pacific Structural Steel Conference. New York, 1995: 65-72.
(  0) 0)
|
| [2] |
SILVA L A P, NEVES L F N, GOMES F C T. Rotational stiffness of rectangular hollow sections composite joint[J]. Journal of structural engineering, 2003, 129(4): 487-494. DOI:10.1061/(ASCE)0733-9445(2003)129:4(487) (  0) 0)
|
| [3] |
WANG Jingfeng, LI Guoqiang. A practical design method for semi-rigid composite frames under vertical loads[J]. Journal of constructional steel research, 2008, 64(2): 176-189. DOI:10.1016/j.jcsr.2007.05.005 (  0) 0)
|
| [4] |
范峰, 曹正罡, 崔美艳. 半刚性节点单层球面网壳的弹塑性稳定性分析[J]. 哈尔滨工业大学学报, 2009, 41(4): 1-6. FAN Feng, CAO Zhenggang, CUI Meiyan. Elasto-plastic stability of semi-rigidity joint single-layer reticulated domes[J]. Journal of Harbin Institute of Technology, 2009, 41(4): 1-6. DOI:10.3321/j.issn:0367-6234.2009.04.001 (  0) 0)
|
| [5] |
MA Huihuan, FAN Feng, WEN Peng, et al. Experimental and numerical studies on a single-layer cylindrical reticulated shell with semi-rigid joints[J]. Thin-walled structures, 2015, 86: 1-9. DOI:10.1016/j.tws.2014.08.006 (  0) 0)
|
| [6] |
JIA L J, CHEN Y Y. Elastic axial rigidity formula for multiplanar CHS X-joint and its effect on performance of single-layered ribbed domes[C]//Proceedings of the 13th International Symposium on Tubular Structures. Hong Kong, China, 2010: 85-93.
(  0) 0)
|
| [7] |
武振宇, 谭慧光, 张耀春. 不等宽T型方钢管节点的刚度计算[J]. 哈尔滨建筑大学学报, 2002, 35(5): 13-16, 27. WU Zhenyu, TAN Huiguang, ZHANG Yaochun. Stiffness of stepped T-type RHS joints subjected to axial loading[J]. Journal of Harbin University of Civil Engineering and Architecture, 2002, 35(5): 13-16, 27. (  0) 0)
|
| [8] |
梁战场.直接焊接K型间隙矩形管节点轴向刚度研究[D].哈尔滨: 哈尔滨工业大学, 2008. LIANG Zhanchang. Research on axial stiffness of directly welded k-type gapped RHS-Joints[D]. Harbin: Harbin Institute of Technology, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10213-2009291251.htm (  0) 0)
|
| [9] |
AHMADI H, NEJAD A Z. Local joint flexibility of two-planar tubular DK-joints in OWTs subjected to axial loading:parametric study of geometrical effects and design formulation[J]. Ocean engineering, 2017, 136: 1-10. DOI:10.1016/j.oceaneng.2017.03.011 (  0) 0)
|
| [10] |
赵必大, 刘成清, 章圣冶, 等. Y型圆钢管相贯节点轴向刚度计算模型[J]. 西南交通大学学报, 2015, 50(5): 872-878. ZHAO Bida, LIU Chengqing, ZHANG Shengye, et al. Calculation model for axial rigidity of CHS Y-type joints[J]. Journal of Southwest JiaoTong University, 2015, 50(5): 872-878. DOI:10.3969/j.issn.0258-2724.2015.05.016 (  0) 0)
|
| [11] |
刘成清, 倪向勇, 赵世春. 高层斜交网格结构斜交柱节点抗震性能研究[J]. 铁道科学与工程学报, 2015, 12(3): 600-608. LIU Chengqing, NI Xiangyong, ZHAO Shichun. Research on seismic performance of the joint in high-rise non- perpendicular grid structure[J]. Journal of railway science and engineering, 2015, 12(3): 600-608. DOI:10.3969/j.issn.1672-7029.2015.03.023 (  0) 0)
|
| [12] |
赵必大, 刘成清, 余丛迪, 等. 圆钢管-横向板相贯连接节点轴向刚度研究[J]. 西南交通大学学报, 2017, 52(5): 977-984. ZHAO Bida, LIU Chengqing, YU Congdi, et al. Axial rigidity of unstiffened transverse plate-to-circular hollow section (CHS) joints[J]. Journal of Southwest JiaoTong University, 2017, 52(5): 977-984. DOI:10.3969/j.issn.0258-2724.2017.05.019 (  0) 0)
|
| [13] |
LIU Chengqing, MA Kaiqiang. Calculation model of the lateral stiffness of high-rise diagrid tube structures based on the modular method[J]. The structural design of tall and special buildings, 2017, 26(4): e1333. DOI:10.1002/tal.1333 (  0) 0)
|
| [14] |
邱国志, 赵金城. X型圆钢管相贯节点刚度试验[J]. 上海交通大学学报, 2008, 42(6): 966-970. QIU Guozhi, ZHAO Jincheng. Experimental research on rigidity of circular tubular X-joints[J]. Journal of Shanghai Jiao Tong University, 2008, 42(6): 966-970. DOI:10.3321/j.issn:1006-2467.2008.06.024 (  0) 0)
|
| [15] |
赵必大, 赵滇生, 申屠倩芸, 等. 平面X形矩形钢管相贯节点平面外抗弯刚度[J]. 建筑结构学报, 2016, 37(S1): 399-405. ZHAO Bida, ZHAO Diansheng, SHENTU Qianyun, et al. Rigidity of unstiffened X-type RHS joints subjected to out-of-plane bending[J]. Journal of building structures, 2016, 37(S1): 399-405. (  0) 0)
|
| [16] |
赵必大, 柯柯, 姜文澜, 等. 矩形钢管偏心相贯节点的平面外抗弯性能研究[J]. 华中科技大学学报(自然科学版), 2018, 46(7): 29-35. ZHAO Bida, KE Ke, JIANG Wenlan, et al. Research on out-plane flexural performance of unstiffened eccentric RHS joints[J]. Journal of Huazhong University of Science and Technology (nature science edition), 2018, 46(7): 29-35. (  0) 0)
|
| [17] |
庄茁, 由小川, 廖剑晖, 等. 基于ABAQUS的有限元分析和应用[M]. 北京: 清华大学出版社, 2009. ZHUANG Zhuo, YOU Xiaochuan, LIAO Jianhui, et al. Finite element analysis and application based on ABAQUS[M]. Beijing: Tsinghua University Press, 2009. (  0) 0)
|
| [18] |
JIA L J, CHEN Y Y. Evaluation of elastic in-plane flexural rigidity of unstiffened multiplanar CHS X-joints[J]. International journal of steel structures, 2014, 14(1): 23-30. (  0) 0)
|
| [19] |
WARDENIER J.钢管截面的结构应用[M].张其林, 刘大康, 译.上海: 同济大学出版社, 2004. WARDENIER J. Hollow sections in structural applications[M]. ZHANG Qiling, LIU Dakang, trans. Shanghai: Tongji University Press, 2004 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


