液体耦合式换热器[1]是现有燃气轮机使用的间冷器形式之一,凭借其节省机上空间、易于维护和清洗等优势已在WR-21等船用燃气轮机上获得了成功应用[2-4]。近年来许多学者致力于船用燃机液体耦合式间冷器的优化设计。文献[5]借助板翅式换热器换热和压降计算方法设计了船用燃机模块化间冷器并优化了结构参数。文献[6]应用效率—传热单元数法建立了板翅式间冷器的数学模型,并应用改进Alopex算法优化了间冷器的结构尺寸。文献[7]应用模拟退火算法实施了对船用燃机间冷器的结构优化。上述间冷器的优化设计过程均以简单循环燃机运行工况下的低压压气机出口参数作为间冷器空气侧入口参数,且将间冷器乙二醇侧的流量、海水侧的流量和入口温度视为常数。另外,在对间冷燃机变工况性能的仿真研究中,间冷器入口条件或出口条件也常被视作常值处理,难以在间冷燃机全工况范围内保证间冷器运行的优化。如文献[8]在假定进口水温和进口水流量不变的前提下,分别实施了间冷循环燃气轮机推进模式和发电模式的稳态及动态仿真。文献[9]在研究冷却液流量和温度等参数对间冷器性能影响的基础上,提到确定合理的液侧流量的意义,但在具体优化过程中需要人工输入液侧环境参数。因此,为了充分发挥间冷器潜力和挖掘间冷燃机的性能,有必要研究间冷器装机后的优化运行。本文建立了一种基于等效间冷度的液体耦合式间冷器稳态变工况计算模型,在变工况特性分析的基础上建立了间冷器稳态运行的多目标优化模型,并提出一种基于变步长搜索的分层序列法求得该多目标优化问题的有效解。
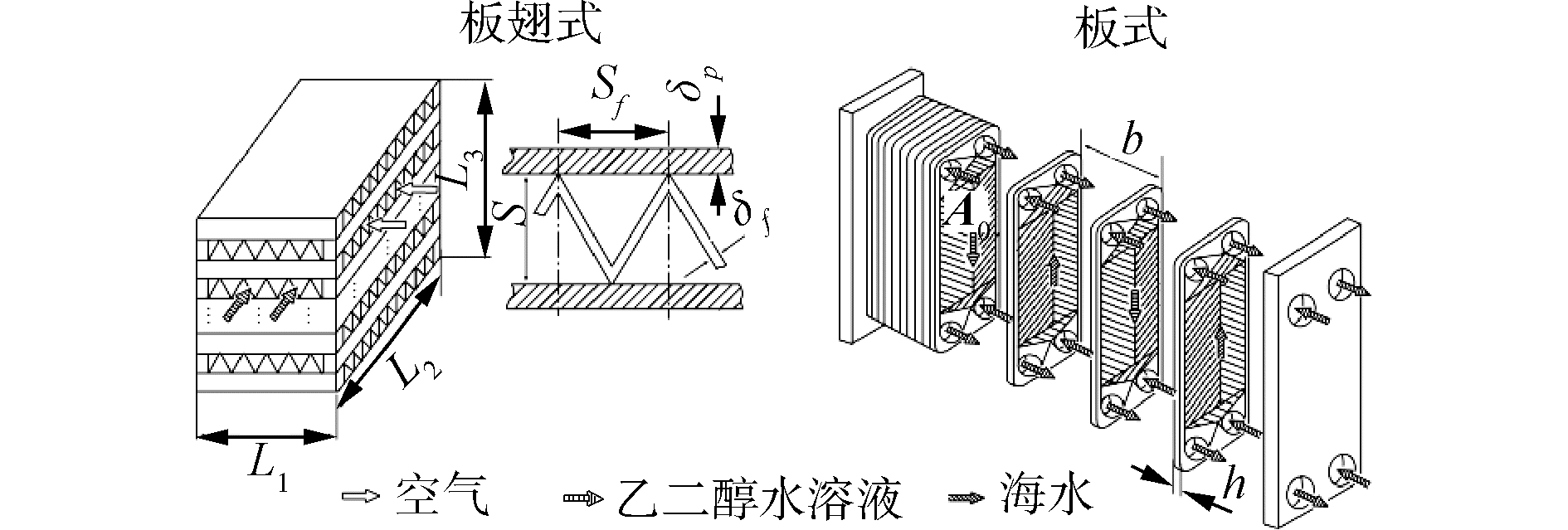
1 液体耦合式间冷器物理模型本文选择锯齿型板翅式换热器和具有人字形波纹板的对称型板式换热器,分别作为机上和机外换热器,结构如图 1所示。机上换热器取文献[8]中经Aspen Muse软件优化后的结构参数,见表 1。机外换热器取北京京海换热设备制造有限公司BRS06型逆流板式换热器产品[10]的结构参数,见表 2。
|
Download:
|
| 图 1 液体耦合式间冷器物理模型 Fig. 1 Physical model of fluid coupling type intercooler | |
| 表 2 机外间冷器结构参数 Table 2 Structure parameters of off-engine intercooler |
图 2为液体耦合式间冷器装机示意图。间冷燃机工作时,间冷器分两级完成海水对燃机低压压气机出口空气的冷却,从而减小高压压气机功耗,提高燃机性能。

|
Download:
|
| 图 2 间冷器装机示意 Fig. 2 Schematic of intercooler installed on gas turbine | |
机上换热器和机外换热器由乙二醇流体耦合在一起,有:
| $ {T_{{\rm{EG}}{\rm{.on}}{\rm{.in}}}} = {T_{{\rm{EG}}{\rm{.off}}{\rm{.out}}}} $ | (1) |
| $ {T_{{\rm{EG}}{\rm{.on}}{\rm{.out}}}} = {T_{{\rm{EG}}{\rm{.off}}{\rm{.in}}}} $ | (2) |
式中:T为温度;下标a、EG和s分别表示空气、乙二醇溶液和海水;on和off分别表示机上换热器和机外换热器;in和out分别代表入口和出口。
为简化间冷器的数学建模,本文作如下假设:
1) 忽略管路中的换热和压力损失,认为系统的换热和压力损失全部由换热器芯体产生;
2) 忽略海面的海—气温差,认为机上间冷器空气侧入口温度与海水表面温度相等[11-13]。
3) 忽略间冷器冷凝,将环境大气简化为干空气处理。
2 稳态变工况计算 2.1 等效间冷度定义及可行性分析由换热器基本原理,机上换热器和机外换热器的换热效率σon、σoff分别表示为:
| $ {\sigma _{{\rm{on}}}} = \frac{{{T_{{\rm{a}}{\rm{.in}}}} - {T_{{\rm{a}}{\rm{.out}}}}}}{{{T_{{\rm{a}}{\rm{.in}}}} - {T_{{\rm{EG}}{\rm{.on}}{\rm{.in}}}}}} $ | (3) |
| $ {\sigma _{{\rm{off}}}} = \frac{{{T_{{\rm{EG}}{\rm{.off}}{\rm{.in}}}} - {T_{{\rm{EG}}{\rm{.off}}{\rm{.out}}}}}}{{{T_{{\rm{EG}}{\rm{.off}}{\rm{.in}}}} - {T_{{\rm{s}}{\rm{.in}}}}}} $ | (4) |
将机上、机外换热器等效成一个换热器,模仿式(3)、(4)的表达方法定义等效后的换热器的换热效率σeq,不妨称之为等效间冷度,表达式为:
| $ {\sigma _{{\rm{eq}}}} = \frac{{{T_{{\rm{a,in}}}} - {T_{{\rm{a,out}}}}}}{{{T_{{\rm{a,in}}}} - {T_{{\rm{s,in}}}}}} $ | (5) |
联立式(1)~(5),化简得σon、σoff、σeq三者之间的等式关系为:
| $ \begin{array}{*{20}{c}} {\frac{1}{{{\sigma _{{\rm{eq}}}}}} = \frac{1}{{{\sigma _{{\rm{on}}}} \cdot {\sigma _{{\rm{off}}}}}} + }\\ {\frac{{{T_{{\rm{a}}{\rm{.in}}}} - {T_{{\rm{EG}}{\rm{.off}}{\rm{.in}}}}}}{{{\sigma _{{\rm{on}}}}\left( {{T_{{\rm{a}}{\rm{.in}}}} - {T_{{\rm{EG}}{\rm{.off}}{\rm{.in}}}}} \right) + {\sigma _{{\rm{on}}}} \cdot {\sigma _{{\rm{off}}}}\left( {{T_{{\rm{EG}}{\rm{.off}}{\rm{.in}}}} - {T_{{\rm{s}}{\rm{.in}}}}} \right)}} \cdot }\\ {\left( {1 - \frac{1}{{{\sigma _{{\rm{off}}}}}}} \right)} \end{array} $ | (6) |
因为Ta, in-TEG.off.in>0,TEG.off.in-Ts.in>0,1-1/σoff<0,显然有
| $ \frac{1}{{{\sigma _{{\rm{eq}}}}}} < \frac{1}{{{\sigma _{{\rm{on}}}} \cdot {\sigma _{{\rm{off}}}}}}且\frac{1}{{{\sigma _{{\rm{eq}}}}}} > \frac{1}{{{\sigma _{{\rm{on}}}} \cdot {\sigma _{{\rm{off}}}}}} + \frac{1}{{{\sigma _{{\rm{on}}}}}}\left( {1 - \frac{1}{{{\sigma _{{\rm{off}}}}}}} \right)。$ |
则σon、σoff、σeq三者之间的不等式关系为:
| $ {\sigma _{{\rm{on}}}} \cdot {\sigma _{{\rm{off}}}} < {\sigma _{{\rm{eq}}}} < {\sigma _{{\rm{on}}}} $ | (7) |
即等效间冷度大于机上、机外换热器换热效率的乘积,而小于机上换热器的换热效率。
间冷燃机在某一工况下运行时,大气温度为Ta.0,低压压气机的压比和效率分别为πCL和ηCL,则间冷器空气侧入口(燃机低压压气机出口)温度为:
| $ {T_{{\rm{a}}{\rm{.in}}}} = {T_{a.0}}\left[ {1 + \frac{{{\pi _{{\rm{CL}}}}^{\frac{{k - 1}}{k}} - 1}}{{{n_{{\rm{CL}}}}}}} \right] $ | (8) |
由上述第2条假设知:
| $ {T_{{\rm{s}}{\rm{.in}}}} = {T_{{\rm{a}}.0}} $ | (9) |
设低压压气机出口与燃机进口气流的温比为:
| $ a\left( {{\pi _{{\rm{CL}}}},{n_{{\rm{CL}}}}} \right) = 1 + \frac{{{\pi _{{\rm{CL}}}}^{\frac{{k - 1}}{k}} - 1}}{{{n_{{\rm{CL}}}}}} $ | (10) |
设间冷器出口与燃机进口气流的温比为:
| $ \beta = \frac{{{T_{{\rm{a}}.{\rm{out}}}}}}{{{T_{{\rm{a}}.0}}}} $ | (11) |
联立式(5)、(8)~(11)并化简得:
| $ {\sigma _{{\rm{eq}}}} = \frac{{\alpha - \beta }}{{\alpha - 1}} $ | (12) |
于是,等效间冷度σeq不仅建立起与σon和σoff的联系,而且当燃机工作在某一状态(α一定)时,σeq与参数β一一对应,若再固定大气条件,则σeq与间冷器空气侧出口温度Ta.out一一对应。另外,由机上换热器结构参数和进、出口温度不难求得气流经过机上换热器的压力损失[6]。因此,在间冷器—燃机的耦合系统中,等效间冷度σeq可作为表征间冷器对燃机影响的单一参数。
2.2 稳态变工况耦合换热模型液体耦合式间冷器装机运行时,在某一大气条件下,对应燃机某一工作状态,只要给定σon、σoff、σeq,就可以通过机上、机外换热器的计算得到该状态下间冷器的全部工作参数。改变σon、σoff、σeq,则可获得间冷器的稳态变工况数据。
2.2.1 机上换热器计算燃机工作点已知则空气侧质量流量qa已知。给定σon、σoff、σeq,则由式(1)~(5)可求得Ta.in、Ta.out、TEG.on.in和TEG.on.out,再根据机上换热器的结构参数,可以求出给空气和乙二醇水溶液的比定压热容Cpa和CpEG.on。
由热平衡方程
| $ \begin{array}{*{20}{c}} {{q_{{\rm{EG}}{\rm{.on}}}}{C_{{\rm{pEG}}{\rm{.on}}}}\left( {{T_{{\rm{EG}}{\rm{.on}}{\rm{.out}}}} - {T_{{\rm{EG}}{\rm{.on}}{\rm{.in}}}}} \right) = }\\ {{q_{\rm{a}}}C{q_{\rm{a}}}\left( {{T_{{\rm{a}}{\rm{.in}}}} - {T_{{\rm{a}}{\rm{.out}}}}} \right)} \end{array} $ | (13) |
可以求得乙二醇水溶液的质量流量qEG.on。进而求出空气和乙二醇水溶液的其他物性参数。
于是空气侧压降为:
| $ \Delta {P_{\rm{a}}} = g_{{\rm{m}}{\rm{.a}}}^2 \cdot {\mathit{\boldsymbol{v}}_{{\rm{a}}{\rm{.in}}}}\left[ {\left( {\frac{{{\mathit{\boldsymbol{v}}_{{\rm{a}}{\rm{.out}}}}}}{{{\mathit{\boldsymbol{v}}_{{\rm{a}}{\rm{.in}}}}}} - 1} \right) + 2\frac{{{f_a} \cdot {L_1} \cdot {\mathit{\boldsymbol{v}}_{{\rm{a}}{\rm{.m}}}}}}{{{d_{{\rm{ea}}}} \cdot {\mathit{\boldsymbol{v}}_{{\rm{a}}{\rm{.in}}}}}}} \right] $ | (14) |
式中:g和ν分别表示流体的质量流速和动力粘度;L1、L2和de分别表示间冷器芯体的长度、宽度和当量直径;f表示范宁系数。
乙二醇流经换热器芯体的压降为:
| $ \begin{array}{*{20}{c}} {\Delta {p_{{\rm{EG}}{\rm{.on}}}} = g_{{\rm{m}}{\rm{.EG}}{\rm{.on}}}^2 \cdot {\mathit{\boldsymbol{v}}_{{\rm{EG}}{\rm{.on}}{\rm{.in}}}}\left[ {\left( {\frac{{{\mathit{\boldsymbol{v}}_{{\rm{EG}}{\rm{.on}}{\rm{.out}}}}}}{{{\mathit{\boldsymbol{v}}_{{\rm{EG}}{\rm{.on}}{\rm{.in}}}}}} - 1} \right) + } \right.}\\ {\left. {2\frac{{{f_{{\rm{EG}}{\rm{.on}}}} \cdot {L_2} \cdot {\mathit{\boldsymbol{v}}_{{\rm{EG}}{\rm{.on}}{\rm{.m}}}}}}{{{d_{{\rm{e}}{\rm{.EG}}{\rm{.on}}}} \cdot {\mathit{\boldsymbol{v}}_{{\rm{EG}}{\rm{.on}}{\rm{.in}}}}}}} \right]} \end{array} $ | (15) |
与机上换热器不同,在海水侧出口温度Ts.out未知条件下,机外换热器需假设Ts.out初值后进行迭代计算。
由乙二醇循环回路的流量平衡可知机外换热器乙二醇的质量流量为:
| $ {q_{{\rm{EG}}{\rm{.off}}}} = {q_{{\rm{EG}}{\rm{.on}}}} $ | (16) |
由热平衡方程:
| $ \begin{array}{*{20}{c}} {{q_{\rm{s}}}{C_{{\rm{ps}}}}\left( {{T_{{\rm{s}}{\rm{.out}}}} - {T_{{\rm{s}}{\rm{.in}}}}} \right) = }\\ {{q_{{\rm{EG}}{\rm{.off}}}}{C_{{\rm{pEG}}{\rm{.off}}}}\left( {{T_{{\rm{EG}}{\rm{.off}}{\rm{.in}}}} - {T_{{\rm{EG}}{\rm{.off}}{\rm{.out}}}}} \right)} \end{array} $ | (17) |
可求得对应的海水质量流量qs。
根据机外换热器进、出口温度和结构参数,可以求出乙二醇和海水的各物性参数。
则乙二醇侧板间流速为:
| $ {V_s} = \frac{{{q_{{\rm{EG}}{\rm{.off}}}}}}{{{\rho _{{\rm{EG}}}} \cdot {n_1} \cdot {A_{{\rm{s}}{\rm{.EG}}}}}} $ | (18) |
式中n和A分别为流道数和单通道流动横截面积。
海水侧板间流速为:
| $ {K_{{\rm{off}}}} = \frac{{{q_{\rm{s}}}}}{{{\rho _{\rm{s}}} \cdot {n_2} \cdot {A_{\rm{s}}}}} $ | (19) |
机外换热器的总传热系数为:
| $ {K_{{\rm{off}}}} = {\left( {\frac{1}{{{\alpha _{{\rm{EG}}}}}} + \frac{1}{{{\alpha _{\rm{s}}}}} + {R_0}} \right)^{ - 1}} $ | (20) |
式中:R0为考虑板片及污垢系数后的热阻,可根据具体情况取某一常数;αEG.off和αs分别为乙二醇和海水的对流传热系数,表达分别为:
| $ {\alpha _{{\rm{EG}}{\rm{.off}}}} = \frac{{{N_{{\rm{u}}{\rm{.EG}}{\rm{.off}}}} \cdot {\lambda _{{\rm{EG}}{\rm{.off}}}}}}{{d{e_{{\rm{EG}}{\rm{.off}}}}}} $ | (21) |
| $ {\alpha _{\rm{s}}} = \frac{{{N_{{\rm{u}}{\rm{.s}}}} \cdot {\lambda _{\rm{s}}}}}{{{d_{{\rm{es}}}}}} $ | (22) |
式中Nu和λ分别为努谢尔特数和导热系数。
另外,由传热速率方程式,也可得到机外换热器总传热系数为:
| $ {{K'}_{{\rm{off}}}} = \frac{\phi }{{{A_{{\rm{off}}}} \cdot \Delta {t_{{\rm{m}}{\rm{.off}}}}}} $ | (23) |
式中:Δtm平均对数温差;ϕ为传热量,可由式(13)左侧求出。将式(20)和式(23)的计算结果进行比较,如果|K′off-Koff|不满足迭代精度要求,则改变海水侧出口温度Ts.out的设定值,重新上述机外换热器的计算,直至两者相等。此时乙二醇流经机外换热器的压降为:
| $ \Delta {P_{{\rm{EG}}{\rm{.off}}}} = {N_{{\rm{u}}{\rm{.EG}}{\rm{.off}}}} \cdot {\rho _{{\rm{EG}}{\rm{.off}}}} \cdot V_{{\rm{EG}}{\rm{.off}}}^2 $ | (24) |
式中Eu和ρ分别为欧拉数和密度。
海水流经机外间冷器的压降为:
| $ \Delta {P_{\rm{s}}} = {E_{{\rm{u}}{\rm{.s}}}} \cdot {\rho _{\rm{s}}} \cdot V_{\rm{s}}^2 $ | (25) |
乙二醇在机上、机外换热器中总的压降为:
| $ \Delta {P_{{\rm{EG}}}} = {P_{{\rm{EG}}{\rm{.on}}}} + {P_{{\rm{EG}}{\rm{.off}}}} $ | (26) |
可得乙二醇循环泵功耗为:
| $ {P_{{\rm{b}}{\rm{.EG}}}} = \frac{{{q_{{\rm{EC}}}} \cdot \Delta {P_{{\rm{EG}}}}}}{{{\rho _{{\rm{EG}}}}}} $ | (27) |
海水泵功耗为:
| $ {P_{{\rm{b}}{\rm{.s}}}} = \frac{{{q_{\rm{s}}} \cdot \Delta {P_{\rm{s}}}}}{{{\rho _{\rm{s}}}}} $ | (28) |
不失一般性,任取海平面标准大气条件下某型燃气轮机低压压气机工作点(πCL = 4.6,ηCL = 0.87,qa = 86 kg/s)作为入口条件,取表 1和表 2为间冷器结构参数,运行上述稳态变工况耦合换热模型可获得该条件下间冷器的全部工况,并做如下分析:
由全工况计算结果得到间冷器空气侧出口温度和压降随等效间冷度的变化曲线,如图 3所示。由图 3可以看出,间冷器空气侧出口温度和压降均随等效间冷度的增加呈线性降低趋势。从提高间冷燃机功率的角度考虑,等效间冷度越大越好。理想情况是使间冷器空气侧出口温度降至环境温度[14],但此时要求等效间冷度等于1(式(5)),这和式(7)中等效间冷度的取值范围相悖。等效间冷度的提高受到机上换热器换热效率的限制,因此应尽量让机上间冷器以最大设计换热效率(σon.d)运行。

|
Download:
|
| 图 3 空气侧出口参数随等效间冷度的变化曲线 Fig. 3 Airside parameters versus equivalent intercooler effectiveness | |
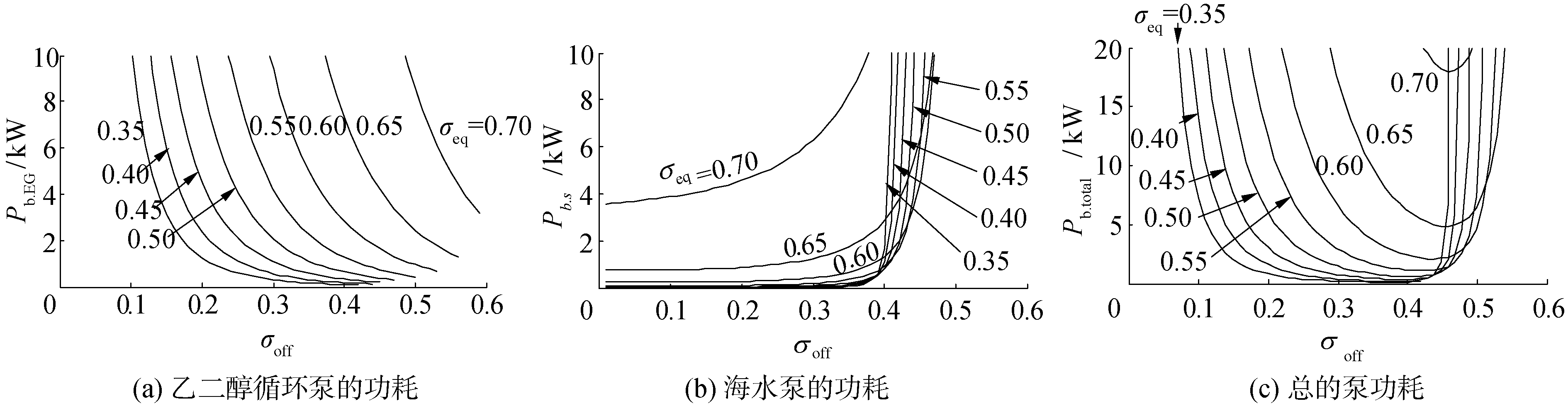
由全工况计算结果得到乙二醇循环泵功耗、海水循环泵功耗以及总的泵功耗(Pb.total = Pb.EG+Pb.s)随等效间冷度和机外换热效率的变化曲线,如图 4所示。
|
Download:
|
| 图 4 泵功耗随机外换热效率的变化曲线 Fig. 4 Pump power versus off-engine intercooler effectiveness | |
由图 4(a)和(b)可以看出,保持机外间冷器换热效率不变时,乙二醇循环泵的功耗和海水循环泵的功耗均随着等效间冷度的增加而增加。保持等效间冷度不变时,乙二醇循环泵的功耗随着机外间冷器换热效率的增加而单调减小,而海水循环泵的功耗随着机外间冷器换热效率的增加而单调增加。
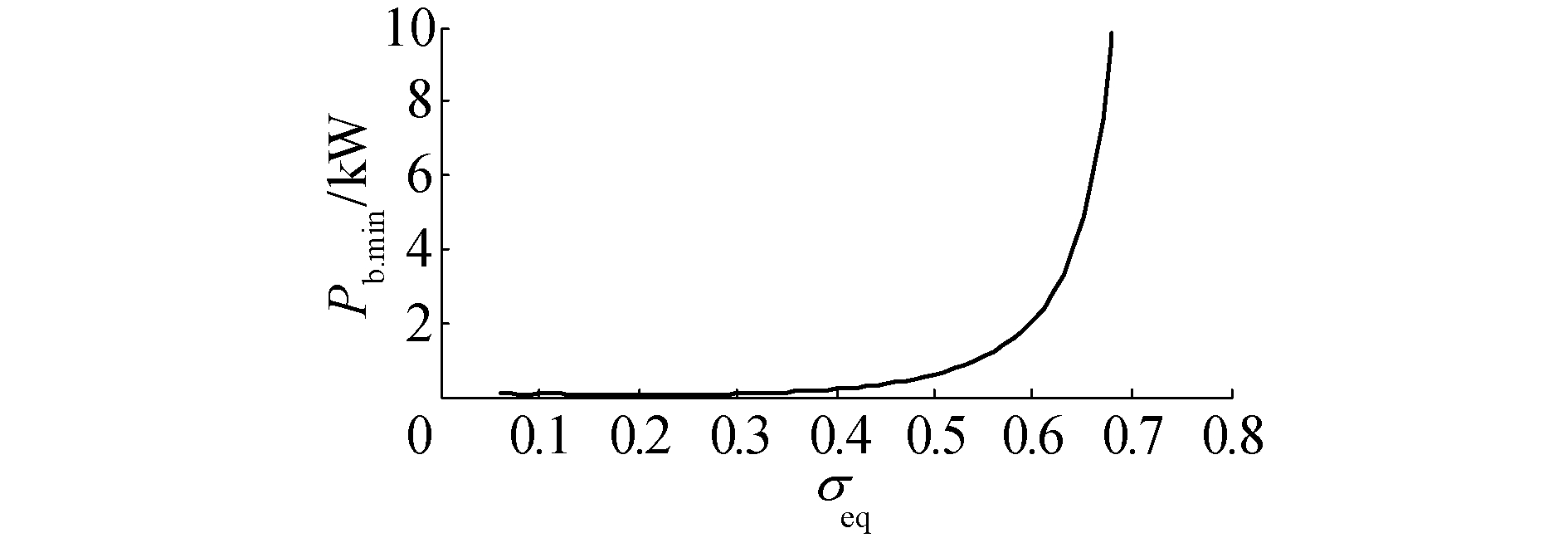
从图 4(c)中可以看出,对应某一固定的等效间冷度,间冷器总的泵耗功率随着机外换热器换热效率呈先减小后增大的趋势,机外换热器存在一个最佳换热效率,使总的泵耗功率获得极小值。并且该极小值点随着等效间冷度的增加而向右移动。进一步可画出等效间冷度与对应总的最小泵耗功率Pb.min的变化关系曲线,如图 5所示。
|
Download:
|
| 图 5 Pb.min随σeq的变化曲线 Fig. 5 Minimum total pump power versus equivalent intercooler effectiveness | |
从图 5中可以看出,间冷器最小功耗Pb.min随着等效间冷度的增加而增加:在等效间冷度小于0.6的区间内Pb.min变化较为缓慢;等效间冷度在0.6~0.65时Pb.min增加较快(从1 984 W增加到4 177 W);当等效间冷度大于0.65后,Pb.min急剧增加,直至进入饱和区。由式(6)也可以看出,只有当TEG.off.in无限接近于Ts.in时,等效间冷度才会无限接近于机上换热器的换热效率,而此时由于温差很小,只能无限提高换热介质的流量,必然导致总的泵功耗无限大,因此在工程上是无法实现的。
综上,间冷器运行时除需考虑其对提高燃机性能的贡献外,自身的运行功耗不容忽略。由于降低间冷器空气侧出口温度、压降与减小间冷器运行功耗是矛盾的,所以间冷器装机后的运行优化问题本质上是二者之间的权衡。
3 稳态运行优化 3.1 多目标优化问题描述船用燃机间冷器的稳态运行应在对燃机性能贡献尽量大(空气侧出口温度和压降尽量小)的前提下,运行能耗尽量小。其稳态运行优化可视为一个多目标优化问题,描述如下:
| $ \left\{ \begin{array}{l} \max \;\;\;{\sigma _{{\rm{eq}}}} = {f_1}\left( \mathit{\boldsymbol{x}} \right)\\ \min \;\;\;{P_{{\rm{b}}{\rm{.total}}}} = {f_2}\left( \mathit{\boldsymbol{x}} \right)\\ {\rm{s}}.\;{\rm{t}}.\;\;\;\;{g_i}\left( \mathit{\boldsymbol{x}} \right) \le 0,i = 1,2, \cdots ,\mathit{\boldsymbol{m}}\\ \;\;\;\;\;\;\;\;{P_{{\rm{b}}{\rm{.EG}}}}\left( \mathit{\boldsymbol{x}} \right) \le {P_{{\rm{b}}{\rm{.EG}}{\rm{.d}}}}\\ \;\;\;\;\;\;\;\;{P_{{\rm{b}}{\rm{.s}}}}\left( \mathit{\boldsymbol{x}} \right) \le {P_{{\rm{b}}{\rm{.s}}{\rm{.d}}}} \end{array} \right. $ | (29) |
式中:x = (σeq, σoff)T∈R2为决策向量;σoff.d为设计值;σeq取值范围符合式(7)。σeq和Pb.total为2个相互矛盾的优化目标函数。σeq同时又是决策变量,取最大值时可使空气侧出口温度最低(图 3(a))且压降(图 3(b))最小,此时间冷器对燃机性能的贡献最大;Pb.total由间冷器耦合换热计算获得,取最小值时可使间冷器的运行能耗最小。gi(x)≤0为来自燃机的m个约束条件,诸如最大转速限制、最高燃气初温限制等。Pb.EG(x)≤Pb.EG.d和Pb.s(x)≤Pb.s.d为间冷器自身的约束条件,表示乙二醇循环泵和海水泵的运行功率分别不超过其最大设计功率。为简化间冷器运行优化问题的求解,做2点假设:1)若乙二醇循环泵和海水循环泵满足最大功率约束,则认为自然满足换热通道内的压力和流速限制;2)忽略来自燃机的最大转速、最高燃气温度等限制。
3.2 基于变步长搜索的分层序列法求解分层序列法[15]是将多目标优化问题的各目标函数按其重要程度逐一排序,然后依次对各目标函数在约束条件下求解,特点是后一目标应在前一目标最优解域内进行优化。在式(29)所描述的优化问题中,显然应选择max{σeq}作为主要目标,而max{Pb.total}为次要目标。为了提高求解精度并保证全局优化能力,本文将变步长搜索与分层序列法相结合,求解液体耦合式间冷器的运行优化问题。优化流程如图 6所示,搜索区域如图 7所示,具体步骤如下:

|
Download:
|
| 图 6 优化流程 Fig. 6 Optimization flow chart | |

|
Download:
|
| 图 7 优化算法的解域 Fig. 7 Solving domain of optimization algorithm | |
1) 置迭代计数器i = 1, 由决策向量x的取值范围确定初始搜索空间D1i(图 7中为一梯形),记
2) 针对空间D1i中以步长λi离散后的各点实施间冷器耦合换热计算,获得优化目标函数(σeq和Pb.total)值以及约束条件(Pb.EG和Pb.s)值,与决策变量(σeq和σoff)一起构成间冷器全工况运行数据M1i。
3) 由约束条件Pb.EG(x)≤Pb.EG.d和Pb.s(x)≤Pb.s.d截断M1i,确定满足约束条件的解空间D2i(图 7中为一梯形),记
4) 在空间D2i中搜索主要目标σeq的最大值σeq.max,获得主要目标函数最优值集合D3i,记D3i = {x|σeq = σeq.max}∩ D2i。
判断D3i若为一条直线(图 7中梯形D2i的边),则执行5);否则D3i必为一点,令D4i = D3i,执行6)。
5) 在D3i中搜索次要目标Pb.total的最小值Pb.min,获得次要目标函数最优值集合D4i(图 7中为一点),记D4i = {x|Pb.total = Pb.min}∩ D3i。
6) 若Ta.outi-1-Ta.outi>0.1 K,则以D4i为中心,以2λi为边长重设搜索空间D1i+1(正方形),并重设搜索步长λi+1 = λi/n,n为步长收缩因子。置迭代计数器i = i+1, 转2)。
若Ta.outi-1-Ta.outi>0.1 K,则输出D 4i。
3.3 稳态运行优化算例及分析表 3为文献[8]中某型间冷燃机推进模式下100%、70%、35% 3种典型工况的低压压气机参数。以表 3中的数据作为入口条件,应用基于变步长搜索的分层序列法对上述液体耦合式间冷器实施稳态运行优化。循环泵最大功率功率限制取Pb.EG.d = Pb.s.d = 5 kW,初始步长取λ1 = 0.1,步长收缩因子取n = 10。
优化过程中发现,对于燃机的3种典型工况,上述优化方法均可使间冷器运行参数快速收敛。以间冷燃机100%工况为例,表 4给出了每次搜索得到的间冷器主要运行参数。可以看出仅经历4次搜索即可获得间冷器运行优化问题在分层优化意义下的解,验证了本文提出的基于变步长搜索的分层序列法求解液体耦合式间冷器多目标优化问题的有效性。
| 表 4 间冷器运行优化结果 Table 4 Optimization results of intercooler operation |
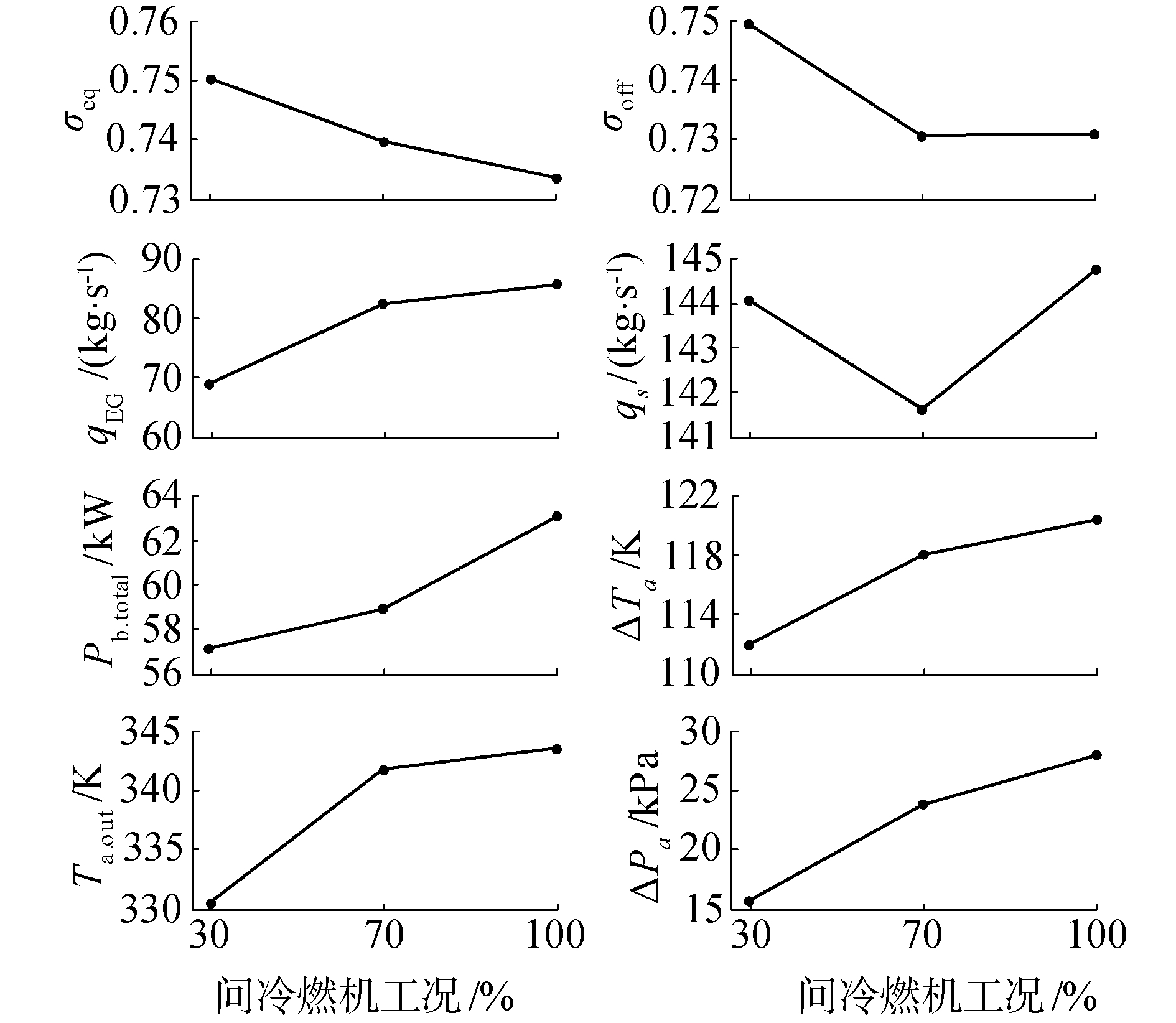
根据燃机3种典型工况下的间冷器稳态运行优化结果,画出间冷器参数随燃机3种典型工况的变化曲线如图 8所示。
|
Download:
|
| 图 8 间冷器参数随燃机工况的变化曲线 Fig. 8 Operating parameters of intercooler versus working conditions of gas turbine | |
图 8说明为了兼顾燃机性能和间冷器能耗,应合理调节间冷器运行。具体是:海水侧应保持较大流量运行,伴随着燃机工况从35%提高到100%,海水流量变化幅度很小,约3 kg/s。乙二醇流量增加较为明显,从68.92 kg/s提高至85.94 kg/s,导致总的泵耗功率从5 715.81 kW增加至6 302.16 kW。随着燃机工况的增加,间冷器出口温降和压降均增加,但趋势越来越缓慢。
4 结论1) 等效间冷度可作为表征间冷器对燃机性能影响的单一参数,其定义可在仿真中弱化间冷器内部及间冷器与燃机之间的耦合。
2) 推导机上、机外换热器换热效率和等效间冷度三者间的关系,并建立液体耦合式间冷器的稳态变工况计算模型。该模型迭代变量少,循环次数少,计算效率高。仿真结果揭示了间冷器运行状态对提高燃机性能和降低间冷器能耗的矛盾性。
3) 建立了液体耦合式间冷器稳态运行的多目标优化模型,并为此设计了一种基于变步长搜索的分层序列求解方法。仿真结果表明该方法收敛快,精度高。
4) 间冷器运行优化的建模及求解方法,可为进一步开展间冷器燃机整体性能优化以及间冷燃机控制策略的选择提供一定参考。
| [1] |
余建祖. 换热器原理与设计[M]. 北京: 北京航空航天大学出版社, 2006: 1-7.
(  0) 0)
|
| [2] |
SHEPARD S B, BOWEN T L, CHIPRICH J M. Design and development of the WR-21 intercooled recuperated (ICR) marine gas turbine[J]. Journal of engineering for gas turbines and power, 1995, 117(3): 557-562. DOI:10.1115/1.2814131 (  0) 0)
|
| [3] |
孙爱军, 肖娜新, 马力. WR-21舰船用燃气轮机的设计特点[J]. 航空发动机, 2010, 36(4): 49-52, 31. SUN Aijun, XIAO Naxin, MA Li. Design characteristics of WR-21 marine gas turbine[J]. Aeroengine, 2010, 36(4): 49-52, 31. DOI:10.3969/j.issn.1672-3147.2010.04.013 (  0) 0)
|
| [4] |
MCCARTHY S J, SCOTT I. The WR-21 intercooled recuperated gas turbine engine: operation and integration into the royal navy type 45 destroyer power system[C]//ASME Turbo Expo 2002: Power for Land, Sea, and Air. Amsterdam, The Netherlands, 2002: 977-984.
(  0) 0)
|
| [5] |
董威, 高鹏, 郑培英, 等. 舰船燃气轮机间冷器优化设计与性能分析[J]. 航空发动机, 2011, 37(3): 22-25. DONG Wei, GAO Peng, ZHENG Peiying, et al. Optimal design and performance analysis of marine gas turbine intercooler[J]. Aeroengine, 2011, 37(3): 22-25. DOI:10.3969/j.issn.1672-3147.2011.03.008 (  0) 0)
|
| [6] |
肖鑫, 屈卫东. 基于改进Alopex算法的燃机中冷器优化设计[J]. 计算机仿真, 2013, 30(9): 318-321. XIAO Xin, QU Weidong. Improved Alopex algorithm on the optimization design of gas turbine intercooler[J]. Computer simulation, 2013, 30(9): 318-321. DOI:10.3969/j.issn.1006-9348.2013.09.074 (  0) 0)
|
| [7] |
ZHAO N B, WEN X Y, LI S Y. Dynamic time-delay characteristics and structural optimization design of marine gas turbine intercooler[J]. Mathematical problems in engineering, 2014, 2014: 701843. (  0) 0)
|
| [8] |
张善科.船用间冷循环燃气轮机性能仿真研究[D].北京: 中国舰船研究院, 2012: 24-36. ZHANG Shanke. Simulation research on performance of marine intercooled cycle gas turbine[D]. Beijing: China Ship Research Institute, 2012: 24-36. http://cdmd.cnki.com.cn/Article/CDMD-10217-1011020556.htm (  0) 0)
|
| [9] |
张杨.燃气轮机间冷器性能分析及优化设计[D].哈尔滨: 哈尔滨工程大学, 2014: 43-57. ZHANG Yang. Optimal design and performance analysis of heat transfer for gas turbine intercooler[D]. Harbin: Harbin Engineering University, 2014: 43-57. http://cdmd.cnki.com.cn/Article/CDMD-10217-1017244894.htm (  0) 0)
|
| [10] |
程宝华, 李先瑞. 板式换热器及换热装置技术应用手册[M]. 北京: 中国建筑工业出版社, 2005.
(  0) 0)
|
| [11] |
LIN Ailian, LIANG Jianyin, GU Dejun, et al. On the relationship between convection intensity of south china sea summer monsoon and air-sea temperature difference in the tropical oceans[J]. Acta oceanologica sinica, 2004, 23(2): 267-278. (  0) 0)
|
| [12] |
熊学军. 中国近海海洋-物理海洋与海洋气象[M]. 北京: 海洋出版社, 2012.
(  0) 0)
|
| [13] |
CHOI H, ZHANG Yuanhang. Monthly variation of sea-air temperature differences in the Korean coast[J]. Journal of oceanography, 2004, 61(5): 359-367. (  0) 0)
|
| [14] |
赵士杭. 燃气轮机循环与变工况性能[M]. 北京: 清华大学出版社, 1993: 19-23.
(  0) 0)
|
| [15] |
张秀利, 梁迎春, 董申. 多目标结构模糊优化的分层序列法[J]. 机械设计与制造, 1999(5): 44-45. ZHANG Xiuli, LIANG Yingchun, DONG Shen. Lexicographic method for fuzzy multiobjective optimization of structures[J]. Machinery design & manufacture, 1999(5): 44-45. DOI:10.3969/j.issn.1001-3997.1999.05.019 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


