欠驱动船舶没有侧推,而且存在模型参数不确定和海洋环境干扰等问题,单一的控制方法已不能很好的满足跟踪控制性能要求,因此探寻新的非线性路径跟踪控制器更富有挑战性和实际工程意义。文献[1-4]在Lyapunov直接法的基础上,分别加入了Backstepping方法、微分同胚等效变换、神经网络和投影算法,设计了路径跟踪控制器,并仿真验证了控制策略的有效性。文献[5]将Nussbaum增益与反步法相结合,提出一种新的自适应控制方法,实现船舶直线路径的保持。文献[6]为得到可进行控制器演绎的船舶模型,将欠驱动船舶运动数学模型进行转换,并提出了鲁棒自适应方案,通过仿真验证欠驱动船舶能够跟踪上虚拟航迹。为改善控制效果,引入对系统参数变化和外界干扰具有不变性的滑模控制方法。文献[7]采用改进的LOS制导律将欠驱动系统的控制问题转化为全驱动系统的控制问题,设计滑模控制器消除航向误差,仿真实验表明该方法的有效性。文献[8]提出一种自适应非线性二阶滑模控制器,与PID二阶滑模控制器相比,该控制器具有更快的收敛和更小的超调。文献[9-10]采用模糊、反步思想和滑模控制方法提出一种自适应鲁棒控制系统,仿真结果表明控制器具有良好的适应性和鲁棒性。文献[11-13]提出一种非线性迭代滑模控制方法,分别以欠驱动水面船舶、AUV、UUV为控制对象,进行了航迹跟踪控制,仿真结果表明该算法对外界干扰具有一定的鲁棒性。为提高控制器的自适应性,文献[14]设计了一种带有模糊优化的自适应非线性迭代滑模控制器,并应用于风帆助航船舶的航向控制,仿真验证了控制器具有强鲁棒性。
滑模控制往往存在抖振问题,利用神经网络的高度学习能力可减小滑模抖振作用。文献[15]提出一种基于强化学习的欠驱动船舶路径跟踪神经网络自适应迭代滑模控制方法,仿真结果表明舵角抖振量明显减小,但该控制方法在设计过程中只证明了系统稳定时参数的存在性,实际应用中存在一定局限。文献[16]利用神经网络在线学习的特点,优化由Lyapunov稳定性条件所得的误差函数,设计出一种神经元滑模控制器,并通过实验对该方法进行了验证。文献[17]利用可视距离思想,结合神经网络和滑模方法,设计了一种神经滑模鲁棒控制器,能够较好地抑制抖振问题,但该控制器得到的控制量是力和力矩,与实际工程应用有一定差距。
本文借鉴文献[13-15]的非线性迭代滑模设计方法,结合文献[16]的Lyapunov稳定性条件构造思想,采用Adaline单神经元和最小二乘法,提出一种神经元自适应迭代滑模控制器,并应用于欠驱动船舶路径跟踪控制中,在风浪流等干扰下对文献[15]中5446TEU集装箱船模型进行路径跟踪控制仿真,并将仿真结果与文献[13]中迭代滑模控制器进行对比分析。
1 路径跟踪问题描述 1.1 欠驱动船舶运动模型为便于船舶路径跟踪控制器的设计,根据文献[6],可将单桨单舵欠驱动船舶运动模型变换为关于控制舵角和螺旋桨转速的仿射非线性系统,并表示为:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{u}}\cos \mathit{\boldsymbol{\psi }} - \mathit{\boldsymbol{v}}\sin \mathit{\boldsymbol{\psi }} + {\mathit{\boldsymbol{u}}_{\rm{c}}}\cos {\mathit{\boldsymbol{\psi }}_{\rm{c}}}\\ \mathit{\boldsymbol{\dot y}} = \mathit{\boldsymbol{v}}\cos \mathit{\boldsymbol{\psi }} + \mathit{\boldsymbol{u}}\sin \mathit{\boldsymbol{\psi }} + {\mathit{\boldsymbol{u}}_{\rm{c}}}\sin {\mathit{\boldsymbol{\psi }}_{\rm{c}}}\\ \mathit{\boldsymbol{\dot \psi }} = \mathit{\boldsymbol{r}}\\ \mathit{\boldsymbol{\dot u}} = \frac{{{m_{22}}}}{{{m_{11}}}}\mathit{\boldsymbol{vr}} - \frac{{{\mathit{\boldsymbol{f}}_u}\left( \mathit{\boldsymbol{u}} \right)}}{{{m_{11}}}} + \frac{{T\left( \cdot \right)}}{{{m_{11}}}}\mathit{\boldsymbol{n}} + {d_{{\rm{wu}}}}\\ \mathit{\boldsymbol{\dot v}} = - \frac{{{m_{11}}}}{{{m_{22}}}}\mathit{\boldsymbol{ur}} - \frac{{{\mathit{\boldsymbol{f}}_v}\left( \mathit{\boldsymbol{v}} \right)}}{{{m_{22}}}} + {d_{{\rm{wv}}}}\\ \mathit{\boldsymbol{\dot r}} = - \frac{{{Y_{\rm{H}}}{x_{\rm{C}}}}}{{{m_{33}}}} - \frac{{{f_r}\left( r \right)}}{{{m_{33}}}} + \frac{{F\left( \cdot \right)}}{{{m_{33}}}}\delta + {d_{{\rm{wr}}}} \end{array} \right. $ | (1) |
式中: u、v、r分别表示附体坐标系下船舶的纵荡速度、横荡速度、艏摇角速度; uc是水流速度;x、y是船舶重心在固定坐标系的位置;ψ是航向角;ψc是水流的方向;fu(u)、fv(v)和fr(r)为高阶流体动力项;n为螺旋桨转速;δ为舵机舵角;m11、m22、m33表示包括附加质量在内的惯性参数;T(·)为螺旋桨增益;F(·)为控制舵增益;dwu、dwv、dwr主要用于表示不可测的外界干扰力与力矩以及对船舶运动影响较小的其它自由度运动的作用力,本文使用文献[15]中的风浪流干扰力模型。在实际工程中,螺旋桨和控制舵的增益是有限的。其中螺旋桨增益T(·)和控制舵增益F(·)的表达式为:
| $ \left\{ \begin{array}{l} T\left( \cdot \right) = \left( {1 - {t_{\rm{p}}}} \right)\left| n \right|\rho D_{\rm{p}}^4{k_{\rm{T}}}\left( {{J_{\rm{p}}}} \right)\\ F\left( \cdot \right) = - 0.5\left( {{x_{\rm{R}}} + {a_{\rm{H}}}{x_{\rm{H}}}} \right)\rho {A_{\rm{R}}}{f_\alpha }U_{\rm{r}}^2\cos \delta \end{array} \right. $ | (2) |
式中:tp、ρ、Dp分别为螺旋桨的推力减额分数、海水密度、直径;kT(Jp)、Jp分别为螺旋桨推力系数和推进系数;xR为舵上横向作用点的纵向坐标,一般可取xR=-0.5;aH为操舵诱导船体横向力的修正因子,一般在0~1变化;xH为操舵诱导船体横向力作用中心到船舶重心的距离,实际上约为-0.4~-0.5;AR为舵面积;fα为升力系数在冲角α=0时的斜率;Ur为舵处来流的有效流速,根据船舶操纵舵的约束条件δ∈(-35, 35),故cosδ是恒正的,因此F(·)也是恒正的。
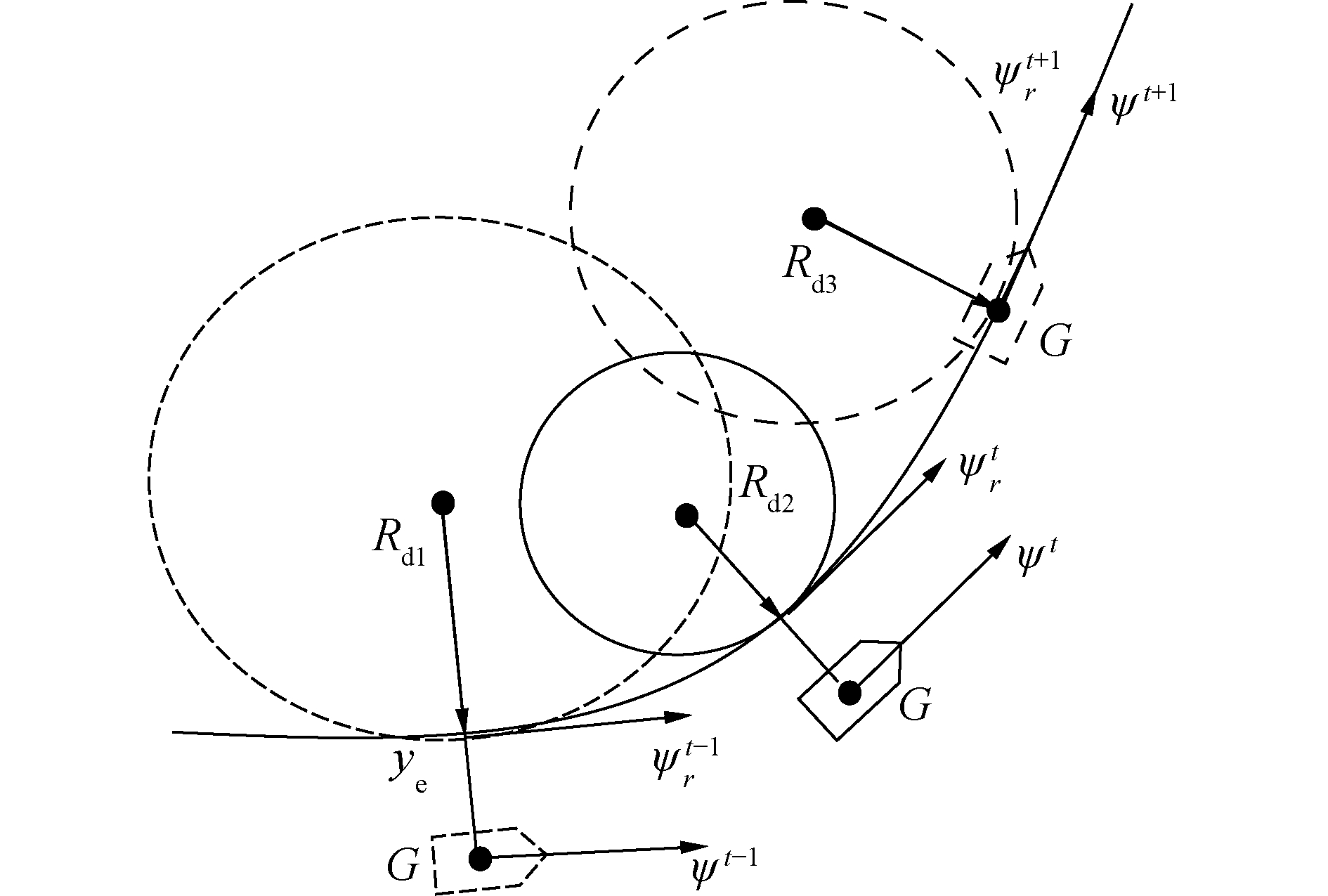
1.2 路径跟踪偏差计算当船舶要跟踪某个光滑的期望路径时,路径曲线上任意一点都可以表示成某个半径为R的圆与该曲线的切点,其切线即为该点的期望航向,该点到船舶重心G的距离为船舶的航迹偏差,该距离为法向距离,通常情况下指最近的距离,因此只要当航迹偏差趋向于零,船舶就能跟踪上圆路径,进而可以近似认为船舶可以跟踪任何光滑曲线路径,如图 1所示为船舶的路径跟踪偏差。其中ψt-1、ψt和ψt+1分别为船舶前一时刻、目前时刻和后一时刻的航向角,ψrt-1、ψrt和ψrt+1分别为对应位置下的期望航向角,Rd1、Rd2和Rd3分别为对应位置下相切圆的半径,ye表示航迹偏差。则船舶航迹偏差和船舶航向可以表示为:
| $ \left\{ \begin{array}{l} {y_{\rm{e}}} = {\left[ {{{\left( {x - {x_0}} \right)}^2} + {{\left( {y - {y_0}} \right)}^2}} \right]^{1/2}} - R\\ {\psi _{\rm{r}}} = \arctan \left( {\frac{{y - {y_0}}}{{x - {x_0}}}} \right) \pm {\rm{ \mathit{ π} }}/2 \end{array} \right. $ | (3) |
|
Download:
|
| 图 1 路径跟踪偏差示意图 Fig. 1 Diagram of tracking error in path following | |
式中:(x0,y0)为圆心坐标;R为半径。定义航向偏差为ψe=ψ-ψr,另外因为航迹跟踪需要确定正方向,顺时针时ψr取正号,逆时针时ψr取负号。
实际工程上,在外界干扰有界的情况下,欠驱动船舶路径跟踪控制系统是可控的,为实现更好的路径跟踪控制效果,做出如下假设:
假设1:船舶的速度、加速度以及外界干扰在t∈R+是光滑有界的;
假设2:船舶的纵向速度u为正,且大于流速uc远大于横向速度v, 即u>uc>>|v|;
假设3:纵向速度u(t)满足李普希兹条件,存在常数L满足以下不等式:
| $ \left| {u\left( {{t_2}} \right) - u\left( {{t_1}} \right)} \right| \le L\Delta t $ | (4) |
式中:t2=t1+Δt。
控制目标:在假设1、2、3的条件下,设计欠驱动船舶路径跟踪控制器,实现路径跟踪控制,并且保证系统内所有信号一致最终有界。
2 路径跟踪控制器设计 2.1 非线性迭代滑动模态设计滑动模态决定了变结构控制系统的性能和滑动阶段控制品质。根据船舶操纵舵的约束条件可知,当船舶在航迹偏差较大时,为避免舵机转向饱和,控制增益应适当减小;而当航迹偏差较小时,为使船舶尽快稳定在期望航迹上,控制增益应适当加大。线性滑模不能满足上述要求,故本文引入非线性双曲正切函数进行滑模设计。双曲正切函数表示为:
| $ \tanh x = \frac{{{{\rm{e}}^x} - {{\rm{e}}^{ - x}}}}{{{{\rm{e}}^x} + {{\rm{e}}^{ - x}}}} $ | (5) |
由式(5)可以看出当x→0时,该函数斜率较大,x逐渐增大时,其斜率成非线性变小,直至趋近零,该函数可满足控制目标要求以及船舶操纵舵的约束条件。
根据路径跟踪偏差计算得到的航迹偏差ye和航向偏差ψe,为构造出最高阶滑模面与舵角之间的函数关系,需要设计四阶非线性迭代滑动模态,具体步骤分以下3步进行。
第1步,设计航迹偏差ye的非线性滑动模态为:
| $ {\sigma _1}\left( {{y_{\rm{e}}}} \right) = {k_1}\tanh \left( {{k_0}{y_{\rm{e}}}} \right) + {{\dot y}_{\rm{e}}}\left( {{k_0}, {k_1} \in {{\bf{R}}^ + }} \right) $ | (6) |
由上式可知,当σ1→0时,
第2步,根据船舶操纵舵的约束条件,为了限制船舶转艏的最大速率,设计带积分的时变滑动模态为:
| $ {\sigma _2}\left( {{\sigma _1}, {\psi _{\rm{e}}}} \right) = {\psi _{\rm{e}}} + {k_2}\int_0^t {\tanh {\sigma _1}{\rm{d}}s\left( {{k_2} \in {{\bf{R}}^ + }} \right)} $ | (7) |
由式(7)可以看出,当σ2→0时,ψe→-k2×∫0ttanhσ1ds以及
以下将证明当σ2→0时,可得σ1→0。
证明:根据σ1定义及系统连续性可知,对所有t∈[t1, t2],若σ1(t2)≤0,则一定存在0<ξ<1,满足σ1(t1+ξΔt)=0,且对所有t∈[t1, t1+ξΔt],有σ1>0,则在t1=t2时, 有:
| $ \begin{array}{*{20}{c}} {\Delta {\psi _{\rm{e}}} = {\psi _{\rm{e}}}\left( {{t_2}} \right) - {\psi _{\rm{e}}}\left( {{t_1}} \right) = {{\dot \psi }_{\rm{e}}}\left( {{t_1} + \xi \Delta t} \right)\Delta t}\\ { = - {k_2}\tanh \left[ {{\sigma _1}\left( {{t_1} + \xi \Delta t} \right)} \right]\Delta t} \end{array} $ | (8) |
| $ \begin{array}{*{20}{c}} {\sin \left[ {{\psi _{\rm{e}}}\left( {{t_2}} \right)} \right] - \sin \left[ {{\psi _{\rm{e}}}\left( {{t_1}} \right)} \right] = }\\ {\cos \left[ {{\psi _{\rm{e}}}\left( {{t_1} + \xi \Delta t} \right)} \right]\Delta {\psi _{\rm{e}}}} \end{array} $ | (9) |
由假设1可知,可忽略横向速度v与流速uc,则Δσ1可近似表示为:
| $ \begin{array}{*{20}{c}} {\Delta {\sigma _1} \approx {k_1}\tanh \left[ {{k_0}{y_{\rm{e}}}\left( {{t_2}} \right)} \right] - {k_1}\tanh \left[ {{k_0}{y_{\rm{e}}}\left( {{t_1}} \right)} \right] - }\\ {\mathit{\boldsymbol{u}}\left( {{t_2}} \right)\left\{ {\sin \left[ {{\psi _{\rm{e}}}\left( {{t_2}} \right)} \right] - \sin \left[ {{\psi _{\rm{e}}}\left( {{t_1}} \right)} \right]} \right\} + }\\ {\sin \left[ {{\psi _{\rm{e}}}\left( {{t_1}} \right)} \right]\left[ {u\left( {{t_2}} \right) - \mathit{\boldsymbol{u}}\left( {{t_1}} \right)} \right]} \end{array} $ | (10) |
将式(8)、(9)代入式(10)可得:
| $ \begin{array}{*{20}{c}} {\Delta {\sigma _1} = {k_1}\tanh \left[ {{k_0}{y_{\rm{e}}}\left( {{t_2}} \right)} \right] - {k_1}\tanh \left[ {{k_0}{y_{\rm{e}}}\left( {{t_1}} \right)} \right] - }\\ {u\left( {{t_2}} \right)\left\{ {\cos \left[ {{\psi _{\rm{e}}}\left( {{t_1} + \xi \Delta t} \right)} \right]{k_2}\tanh \left[ {{\sigma _1}\left( {{t_1} + } \right.} \right.} \right.}\\ {\left. {\left. {\left. {\xi \Delta t} \right)} \right]\Delta t} \right\} + \sin \left[ {{\psi _{\rm{e}}}\left( {{t_1}} \right)} \right]\left[ {\mathit{\boldsymbol{u}}\left( {{t_2}} \right) - \mathit{\boldsymbol{u}}\left( {{t_1}} \right)} \right]} \end{array} $ | (11) |
由假设3得:
| $ \begin{array}{*{20}{c}} {\Delta {\sigma _1} \le 2{k_1} + L\Delta t - }\\ {\mathit{\boldsymbol{u}}\left( {{t_2}} \right)\cos \left[ {{\psi _{\rm{e}}}\left( {{t_1} + \xi \Delta t} \right)} \right]{k_2}\tanh \left[ {{\sigma _1}\left( {{t_1} + \xi \Delta t} \right)} \right]\Delta t} \end{array} $ | (12) |
因为u>0以及cos(ψe(t1+ξΔt))>0,故存在σ1>0,k2∈ R+,使Δσ1≤0。同理,当t=t1,存在σ1 < 0,k2∈R+,使Δσ1≥0。可以看出最终σ1在趋于0的一定宽度边界层内滑动,系统处于近似滑动模态。故得当σ2→0时,有σ1→0。证毕。
第3步,为了构造出最高阶滑模面与控制舵角δ之间的一阶函数关系,结合双曲正切函数的严格有界,设计滑动模态为:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\sigma }}_3}\left( {{\sigma _2}} \right) = {k_3}\tanh \left( {{\sigma _2}} \right) + {{\dot \sigma }_2}\\ {\mathit{\boldsymbol{\sigma }}_4}\left( {{\sigma _3}} \right) = {k_4}\tanh \left( {{\sigma _3}} \right) + {{\dot \sigma }_3} \end{array} \right. $ | (13) |
k3、k4∈R+则控制目标进一步转化为对σ4的控制。将式(13)中的σ4全部展开得:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\sigma }}_4} = {k_4}\tanh {\sigma _3} + }\\ {{k_3}\left[ {r + {k_2}\tanh {\sigma _1}} \right]/{{\left[ {\cosh {\sigma _2}} \right]}^2} + }\\ {{k_2}\left\{ {{k_0}{k_1}{{\dot y}_{\rm{e}}}/{{\left[ {\cosh \left( {{k_0}{y_{\rm{e}}}} \right)} \right]}^2} + {{\ddot y}_{\rm{e}}}} \right\}/{{\left[ {\cosh {\sigma _1}} \right]}^2} - }\\ {{Y_{\rm{H}}}{x_{\rm{C}}}/{m_{33}} - {f_r}\left( r \right)/{m_{33}} + \left[ {F\left( \cdot \right)/{m_{33}}} \right]\delta + {d_{{\rm{wr}}}}} \end{array} $ | (14) |
式(14)构造出了最高阶滑模面σ4与控制舵角δ之间的函数关系。因此只要实现σ4→0,即有σ3→0,σ2→0,σ1→0,就能确保航迹偏差ye稳定收敛。
2.2 神经元自适应控制器设计为实现σ4→0,需要对舵角δ进行控制器设计。选取李雅谱诺夫函数:
| $ V = \frac{1}{2}\mathit{\boldsymbol{\sigma }}_4^{\rm{T}}{\mathit{\boldsymbol{\sigma }}_4} $ | (15) |
对上式求导可得:
| $ \dot V = \mathit{\boldsymbol{\sigma }}_4^{\rm{T}}{{\mathit{\boldsymbol{\dot \sigma }}}_4} $ | (16) |
若能使
| $ \dot V = - \mathit{\boldsymbol{\sigma }}_4^{\rm{T}}\mathit{\boldsymbol{D}}{\mathit{\boldsymbol{\sigma }}_4} $ | (17) |
式中:D为设计的正定矩阵。
将式(16)和(17)联立,可得系统稳定的条件为
| $ \left( {{{\mathit{\boldsymbol{\dot \sigma }}}_4} + \mathit{\boldsymbol{D}}{\mathit{\boldsymbol{\sigma }}_4}} \right) = 0 $ | (18) |
将式(14)代入(18)中,可得控制舵角δ为:
| $ \begin{array}{*{20}{c}} {\delta = - {d_{{\rm{wr}}}}\frac{{{m_{33}}}}{{F\left( \cdot \right)}} + \frac{{{m_{33}}}}{{F\left( \cdot \right)}}\left[ {\frac{{{Y_{\rm{H}}}{x_{\rm{C}}}}}{{{m_{33}}}} + \frac{{{f_r}r}}{{{m_{33}}}}} \right] + }\\ {\frac{{{m_{33}}}}{{F\left( \cdot \right)}}\left[ { - \frac{1}{D}{{\dot \sigma }_4} - {k_4}\tanh {\sigma _3}} \right.}\\ {\left. { - {k_3}{{\left( {{\rm{sech}}{\sigma _2}} \right)}^2}{{\dot \sigma }_2} - {k_2}{{\left( {{\rm{sech}}{\sigma _1}} \right)}^2}{{\dot \sigma }_1}} \right]} \end{array} $ | (19) |
式(19)中含有相关船舶模型参数以及外界干扰等信号,在实际工程中存在模型参数不确定和干扰时变等问题,故由式(19)直接计算出控制舵角δ比较困难。为此,本文根据稳定性条件
| $ \left\{ \begin{array}{l} \tau = \mathit{\boldsymbol{Wx}}\\ \delta = \beta \tau \end{array} \right. $ | (20) |
式中:x为神经元自适应控制的输入层;
为了满足稳定性条件
| $ \mathit{\boldsymbol{E}} = \frac{1}{2}{\left( {{{\mathit{\boldsymbol{\dot \sigma }}}_4} + \mathit{\boldsymbol{D}}{\sigma _4}} \right)^2} $ | (21) |
通过调整权重W使E→0,满足系统稳定性条件
设计权重变化方程如下:
| $ \mathit{\boldsymbol{\dot W}} = - \eta \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \mathit{\boldsymbol{W}}}} $ | (22) |
式中:η>0为学习常数。式(21)可以写成:
| $ \mathit{\boldsymbol{\dot W}} = - \eta \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \delta }}\frac{{\partial \delta }}{{\partial \tau }}\frac{{\partial \tau }}{{\partial \mathit{\boldsymbol{W}}}} = - \eta \beta \frac{{\partial \mathit{\boldsymbol{E}}}}{{\partial \delta }}\mathit{\boldsymbol{x}} $ | (23) |
将式(21)代入到式(23)中得:
| $ \mathit{\boldsymbol{\dot W}} = - \eta \beta \left( {{{\mathit{\boldsymbol{\dot \sigma }}}_4} + \mathit{\boldsymbol{D}}{\mathit{\boldsymbol{\sigma }}_4}} \right)\left( {\frac{{\partial {{\mathit{\boldsymbol{\dot \sigma }}}_4}}}{{\partial \delta }} + \mathit{\boldsymbol{D}}\frac{{\partial {\mathit{\boldsymbol{\sigma }}_4}}}{{\partial \delta }}} \right)\mathit{\boldsymbol{x}} $ | (24) |
式(24)中,对δ求偏导得
| $ \frac{{\partial {\mathit{\boldsymbol{\sigma }}_4}}}{{\partial \delta }} = F\left( \cdot \right)/{m_{33}} $ | (25) |
将式(14)中σ4求导得:
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot \sigma }}}_4} = {k_4}{{\left( {{\text{sech}}{\sigma _3}} \right)}^2}\left[ {{k_3}{{\dot \sigma }_2}{{\left( {{\text{sech}}{\sigma _2}} \right)}^2} + {{\ddot \psi }_e} + } \right.} \\ {\left. {{k_2}{{\left( {{\text{sech}}{\sigma _1}} \right)}^2}{{\dot \sigma }_1}} \right] - 2{k_3}{{\left( {{{\dot \sigma }_2}} \right)}^2}{{\left( {{\text{sech}}{\sigma _2}} \right)}^2}\tanh {\sigma _2} + } \\ {{k_3}{{\left( {{\text{sech}}{\sigma _1}} \right)}^2}\left[ {{{\ddot \psi }_e} + {k_1}{{\left( {{\text{sech}}{\sigma _1}} \right)}^2}{{\dot \sigma }_1}} \right] + {{\dddot \sigma }_2}} \end{array} $ | (26) |
式(26)对δ求偏导得:
| $ \frac{{\partial {{\mathit{\boldsymbol{\dot \sigma }}}_4}}}{{\partial \delta }} = \left[ {{k_4}{{\left( {{\rm{sech}}{\sigma _3}} \right)}^2} + {k_3}{{\left( {{\rm{sech}}{\sigma _2}} \right)}^2}} \right]F\left( \cdot \right)/{m_{33}} $ | (27) |
将式(25)和(27)代入式(24)中,可得
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot W}} = - \eta \beta \left( {{{\mathit{\boldsymbol{\dot \sigma }}}_4} + \mathit{\boldsymbol{D}}{\mathit{\boldsymbol{\sigma }}_4}} \right)F\left( \cdot \right)\mathit{\boldsymbol{x}} \times }\\ {\left[ {{k_4}{{\left( {{\rm{sech}}{\sigma _3}} \right)}^2} + {k_3}{{\left( {{\rm{sech}}{\sigma _2}} \right)}^2} + \mathit{\boldsymbol{D}}} \right]/{m_{33}}} \end{array} $ | (28) |
式中:由于F(·)/m33与船舶模型有关,而且都是恒正的船舶固有参数,因此可以将其近似为一个标量值,与学习常数η合并为一个神经元调节参数,设为η′。则式(28)可以表示为:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot W}} = - \eta '\beta \left( {{{\mathit{\boldsymbol{\dot \sigma }}}_4} + \mathit{\boldsymbol{D}}{\mathit{\boldsymbol{\sigma }}_4}} \right)\mathit{\boldsymbol{x}} \times }\\ {\left[ {{k_4}{{\left( {{\rm{sech}}{\sigma _3}} \right)}^2} + {k_3}{{\left( {{\rm{sech}}{\sigma _2}} \right)}^2} + \mathit{\boldsymbol{D}}} \right]} \end{array} $ | (29) |
由式(29)可以看出,该神经元自适应控制不需要模型参数以及外界干扰的相关数据。如果系统不满足条件
为验证上述所设计的神经元自适应迭代滑模路径跟踪控制器的有效性,本文引用文献[15]中5446TEU集装箱船为对象进行路径跟踪控制仿真,并与文献[13]设计的迭代滑模控制方法进行比较。
在仿真中,船舶所选取的期望轨迹为以(2 000, 2 000)为圆心,2 000为半径的圆轨迹。船初始位置在(0, 0)点,初始船速27 kn。外界海洋环境干扰设置为风速10 m/s、流速2 m/s,方向均为110°,浪的波高为3 m,遭遇频率为0.75 Hz。神经元自适应迭代滑模路径跟踪控制器的参数设定为:k0、k2、k3、k4分别取0.8、1.0×10-3、1.0×10-4、1.0×10-7和0.04,D值取10 000,β取0.1,η′是0.1。
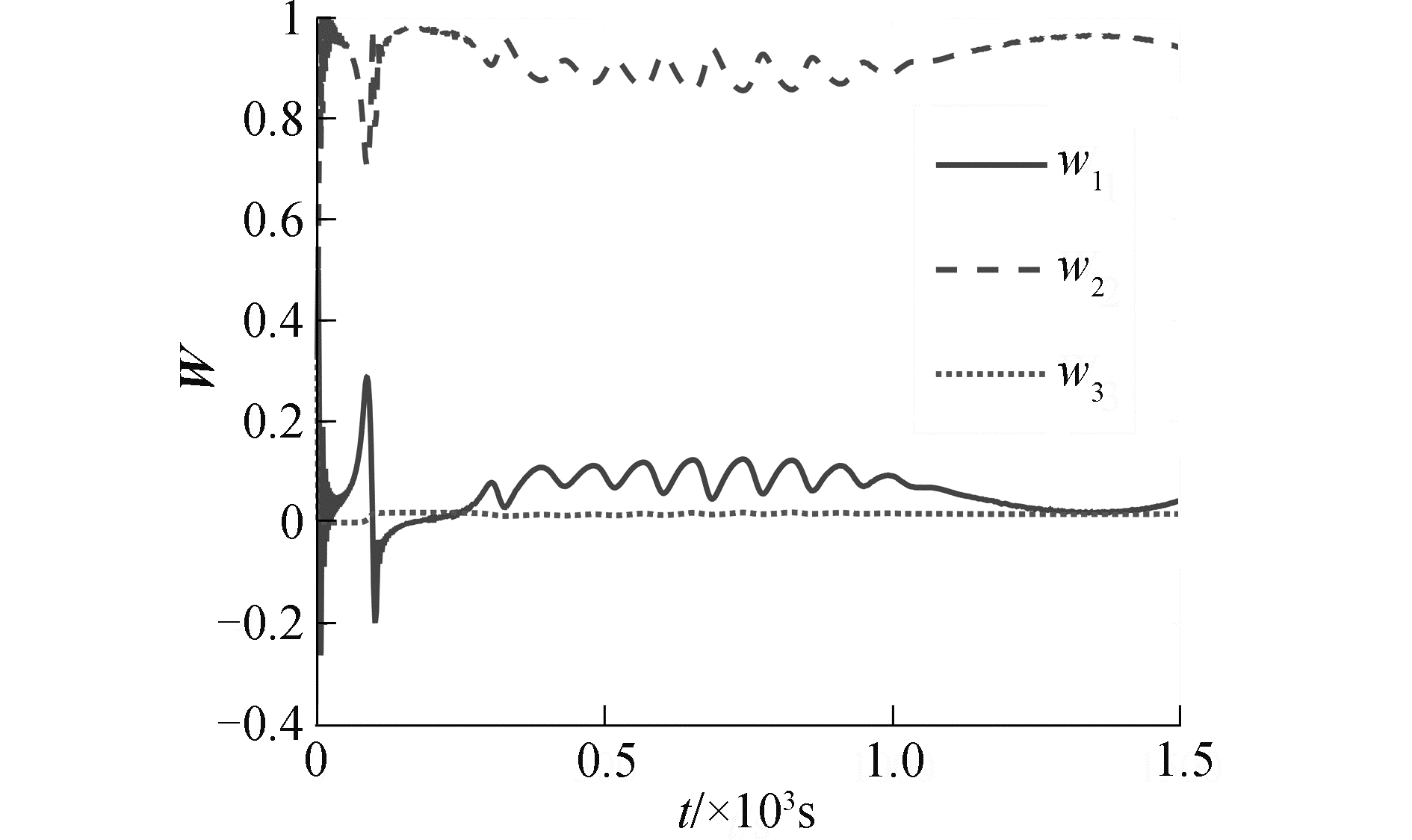
仿真结果如图 2~6所示。图 2为欠驱动船舶实际运行的路径曲线和参考路径曲线,图 3为船舶在2种控制算法下跟踪期望路径的误差曲线。结合图 2和图 3可以看出,神经元自适应迭代滑模控制算法跟踪误差更小,稳定性增强,更符合实际工程要求。图 4所示,迭代滑模控制输出的舵角一直存在着较大的抖动,而神经元自适应迭代滑模控制输出的舵角较为平滑,抖动明显减小。通过图 5,可以发现迭代滑模控制方法滑模面宽度较大,而神经元自适应迭代滑模控制方法滑模面宽度较小,更稳定。图 6为神经元自适应迭代滑模控制方法的权重变化曲线,可以看出起初权重一直在调节,直到跟踪上圆路径之后,权重学习变化率很小,稳定在某个范围内,并且在600~1 000 s,所受到的风浪流干扰最大时,权重进行微调,其中可以看出w1极大时w2极小,w1极小时w2极大,体现出通过参数的微调控制系统能够补偿外界干扰。

|
Download:
|
| 图 2 圆路径跟踪图 Fig. 2 The graph of circular path tracking | |

|
Download:
|
| 图 3 圆路径误差曲线图 Fig. 3 The graph of circular path error | |

|
Download:
|
| 图 4 圆路径舵角曲线图 Fig. 4 The graph of circular path rudder angle | |

|
Download:
|
| 图 5 圆路径σ4曲线图 Fig. 5 The graph of circular path σ4 | |
|
Download:
|
| 图 6 圆路径权重W曲线图 Fig. 6 The graph of circular path weights W | |
1) 所提出的神经元自适应迭代滑模控制方法能够在线学习,避免对模型参数不确定项和外界干扰进行估计,增强了控制器的自适应性。
2) 相比较于迭代滑模控制器,神经元自适应迭代滑模控制器的路径跟踪更准确,舵机控制效果更平滑有效,在保证了跟踪效果的同时,延长了舵机的使用寿命,更加符合实际工程需求。
| [1] |
DO K D. Global robust adaptive path-tracking control of underactuated ships under stochastic disturbances[J]. Ocean engineering, 2016, 111: 267-278. DOI:10.1016/j.oceaneng.2015.10.038 (  0) 0)
|
| [2] |
MENG Wei, GUO Chen, CHEN Rong. Adaptive output feedback control for path following of underactuated ships with uncertain dynamics[C]//Proceedings of the 27th Chinese Control and Decision Conference. Qingdao, China, 2015: 5383-5386. https://www.researchgate.net/publication/283659536_Adaptive_output_feedback_control_for_path_following_of_underactuated_ships_with_uncertain_dynamics
(  0) 0)
|
| [3] |
刘杨, 郭晨, 沈智鹏, 等. 欠驱动船舶路径跟踪的神经网络稳定自适应控制[J]. 控制理论与应用, 2010, 27(2): 169-174. LIU Yang, GUO Chen, SHEN Zhipeng, et al. Stable adaptive neural network control of path following for underactuated ships[J]. Control theory & applications, 2010, 27(2): 169-174. (  0) 0)
|
| [4] |
DO K D. Global path-following control of stochastic underactuated ships:a level curve approach[J]. Journal of dynamic systems, measurement, and control, 2015, 137(7): 071010. DOI:10.1115/1.4029885 (  0) 0)
|
| [5] |
YAN Xuehua, SONG Xinmin, LI Yueyang. Global straight-path tracking control design for underactuated ships with unknown control direction[C]//Proceedings of the 34th Chinese Control Conference. Hangzhou, China, 2015: 4449-4452. https://www.researchgate.net/publication/301387349_Global_straight-path_tracking_control_design_for_underactuated_ships_with_unknown_control_direction
(  0) 0)
|
| [6] |
ZHANG Guoqing, ZHANG Xianku. A novel DVS guidance principle and robust adaptive path-following control for underactuated ships using low frequency gain-learning[J]. ISA transactions, 2015, 56: 75-85. DOI:10.1016/j.isatra.2014.12.002 (  0) 0)
|
| [7] |
QIN Z H, LIN Z, SUN H B, et al. Sliding-mode control of path following for underactuated ships based on high gain observer[J]. Journal of central south university, 2016, 23(12): 3356-3364. DOI:10.1007/s11771-016-3401-9 (  0) 0)
|
| [8] |
ZHANG G C, HUANG H, QIN H D, et al. A novel adaptive second order sliding mode path following control for a portable AUV[J]. Ocean engineering, 2018, 151: 82-92. DOI:10.1016/j.oceaneng.2017.12.054 (  0) 0)
|
| [9] |
LIANG X, QU X, WAN L, et al. Three-dimensional path following of an underactuated AUV based on fuzzy backstepping sliding mode control[J]. International journal of fuzzy systems, 2018, 20(2): 640-649. DOI:10.1007/s40815-017-0386-y (  0) 0)
|
| [10] |
LIANG X, WAN L, BLAKE J I R, et al. Path following of an underactuated AUV based on fuzzy backstepping sliding mode control[J]. International journal of advanced robotic systems, 2016, 13: 122-129. DOI:10.5772/64065 (  0) 0)
|
| [11] |
卜仁祥, 刘正江, 李铁山. 迭代滑模增量反馈及在船舶航向控制中的应用[J]. 哈尔滨工程大学学报, 2007, 28(3): 268-272. BU Renxiang, LIU Zhengjiang, LI Tieshan. Iterative sliding mode based increment feedback control and its application to ship autopilot[J]. Journal of Harbin Engineering University, 2007, 28(3): 268-272. DOI:10.3969/j.issn.1006-7043.2007.03.005 (  0) 0)
|
| [12] |
边信黔, 程相勤, 贾鹤鸣, 等. 基于迭代滑模增量反馈的欠驱动AUV地形跟踪控制[J]. 控制与决策, 2011, 26(2): 289-292, 296. BIAN Xinqian, CHENG Xiangqin, JIA Heming, et al. A bottom-following controller for underactuated AUV based on iterative sliding and increment feedback[J]. Control and decision, 2011, 26(2): 289-292, 296. (  0) 0)
|
| [13] |
贾鹤鸣, 张利军, 程相勤, 等. 基于非线性迭代滑模的欠驱动UUV三维航迹跟踪控制[J]. 自动化学报, 2012, 38(2): 308-314. JIA Heming, ZHANG Lijun, CHENG Xiangqin, et al. Three-dimensional path following control for an underactuated UUV based on nonlinear iterative sliding mode[J]. Acta automatica sinica, 2012, 38(2): 308-314. (  0) 0)
|
| [14] |
沈智鹏, 姜仲昊, 王国峰, 等. 风帆助航船舶运动的模糊自适应迭代滑模控制[J]. 哈尔滨工程大学学报, 2016, 37(5): 634-639. SHEN Zhipeng, JIANG Zhonghao, WANG Guofeng, et al. Fuzzy-adaptive iterative sliding-mode control for sail-assisted ship motion[J]. Journal of Harbin Engineering University, 2016, 37(5): 634-639. (  0) 0)
|
| [15] |
沈智鹏, 代昌盛. 欠驱动船舶路径跟踪的强化学习迭代滑模控制[J]. 哈尔滨工程大学学报, 2017, 38(5): 697-704. SHEN Zhipeng, DAI Changsheng. Iterative sliding mode control based on reinforced learning and used for path tracking of under-actuated ship[J]. Journal of Harbin Engineering University, 2017, 38(5): 697-704. (  0) 0)
|
| [16] |
YILDIZ Y, SABANOVIC A, ABIDI K. Sliding-mode neuro-controller for uncertain systems[J]. IEEE transactions on industrial electronics, 2007, 54(3): 1676-1685. DOI:10.1109/TIE.2007.894719 (  0) 0)
|
| [17] |
杨震, 刘繁明, 王岩. 欠驱动船舶路径跟踪的神经滑模控制[J]. 中国造船, 2015, 56(2): 45-55. YANG Zhen, LIU Fanming, WANG Yan. Path following of underactuated surface vessels based on neural sliding mode[J]. Shipbuilding of China, 2015, 56(2): 45-55. DOI:10.3969/j.issn.1000-4882.2015.02.006 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


