2. 天津理工大学 天津市先进机电系统设计与智能控制重点实验室, 天津 300384;
3. 天津理工大学 机电工程国家级实验教学示范中心, 天津 300384
2. Tianjin Key Laboratory of the Design and Intelligent Control of the Advanced Mechatronical System, Tianjin University of Technology, Tianjin 300384, China;
3. National Demonstration Center for Experimental Mechanical and Electrical Engineering Education, Tianjin University of Technology, Tianjin 300384, China
非线性能量阱(nonlinear energy sink, NES)的概念提出于2000年左右,它是在动力吸振器的基础上发展出来的[1]。线性动力吸振器需要与主结构发生共振以实现减振,这导致其只能应用于振动频率变化较小的设备。弱非线性动力吸振器能够在一定程度上拓宽减振频带,然而它仍然只能从某一特定频带吸收振动能量。半主动式、主动式和混合式吸振器设计,使动力吸振器具有频率跟踪或/和多频带减振能力,然而这些方案需要额外的能源装置和控制器,因此其应用存在很大局限性。非线性能量阱是一种具有纯非线性刚度的吸振器,由于具有宽频吸振、轻质等优点,吸引了大量研究者的关注。研究表明,非线性能量阱的吸振效能要明显高于传统被动式吸振器[2-3]。近年来,非线性能量阱被用于抑制多种结构的振动,例如:抑制圆柱筒的涡激振动[4]、建筑结构振动[5-7]、转子在临界速度时的回转振动[8]、气动载荷下复合材料板的振动[9]、机翼的气动失稳[10]、卫星结构的整体振动[11]等。
通过对常规非线性能量阱(仅包含单个纯非线性刚度元件、单个线性阻尼元件和单个质量元件)的结构进行改进,可以提升非线性能量阱的吸振能力。并联和串联式非线性能量阱是其中两种简单有效的改进方案。Vaurigaud等[12]研究了连接并联非线性能量阱的多自由度主振子在冲击载荷和简谐载荷作用下的振动响应。Savadkoohi等[13]实验研究了连接并联非线性能量阱的四自由度主振子的响应,能量阱取得了较好的减振效果。Nguyen等[14]对常规和并联非线性能量阱进行了优化设计。Zhang等[15]对比了连接于轴向运动梁的常规和并联非线性能量阱的吸振效能,研究证明并联非线性能量阱能够取得较好的减振效果。Tsakirtzis等[16]研究了连接串联非线性能量阱的两自由度线性主系统的复杂动力学响应。Gendelman等[17]研究了串联非线性能量阱参数对其吸振效能的影响,肯定了串联非线性能量阱比具有相同质量的常规非线性能量阱具有更强的吸振效能。Grinberg等[18]分析了连接串联非线性能量阱的线性主振子的周期、准周期和混沌响应,同样肯定了串联非线性能量阱吸振效能。
目前,已经展开的一些关于并联和串联非线性能量阱吸振效能的研究,在同一研究条件下对两种能量阱效能的对比研究非常缺乏。并且,未见有在考虑主振系统受温度等移频效应的影响下,对两种能量阱减振能力的研究。本文在对简支梁附加相同质量的前提下,研究了并联和串联非线性能量阱参数对其吸振效能的影响规律,分析了两种能量阱吸振效能随冲击幅值和温度的变化情况。此外,从能量阱自身参数和系统外部影响因素两个方面,对两种能量阱的减振能力进行了对比分析。
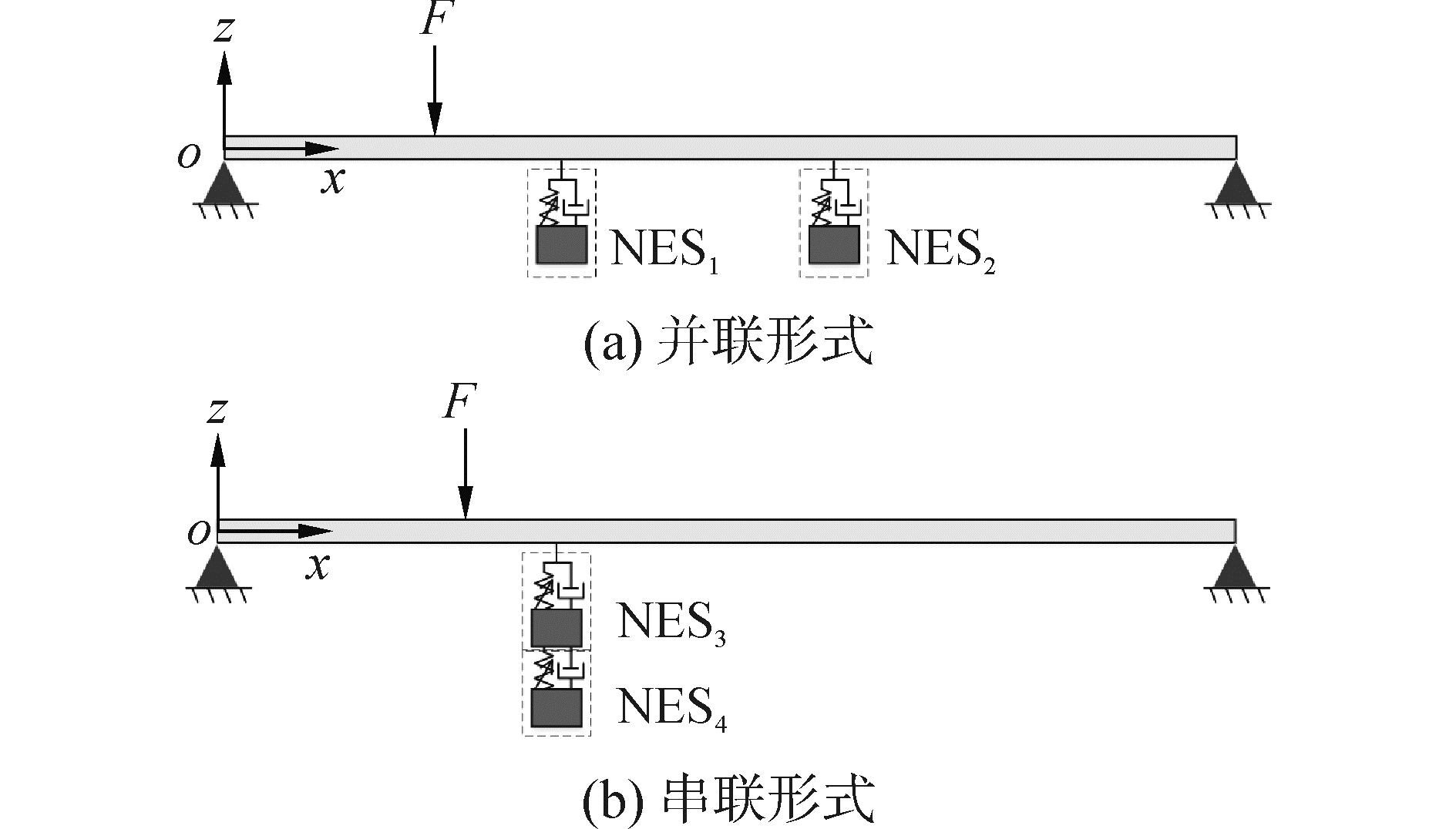
1 动力学方程连接并联和串联NES的简支梁,如图 1所示。坐标系oxz置于简支梁的中面上,梁厚度和长度分别表示为h和l,梁的弹性模量、密度和阻尼系数分别为E、ρ和μ0。每个NES均具有纯非线性刚度和线性阻尼,其质量系数、刚度系数和阻尼系数分别表示为mi、ki和μi。简支梁承受作用于b点冲击载荷F。并联NES的两个子装置分别安装于a1和a2两个位置,串联NES安装于a3点。
|
Download:
|
| 图 1 非线性能量阱 Fig. 1 Nonlinear energy sinks | |
简支梁的位移场可表述为中面横向位移w0的函数:
| $ u\left( {x, z, t} \right) = - z\frac{{\partial {w_0}\left( {x, t} \right)}}{{\partial x}}, w\left( {x, z, t} \right) = {w_0}\left( {x, t} \right) $ | (1) |
式中u和w分别表示梁内任一点的面内位移和横向位移。应变和应力可分别表示为
| $ {\varepsilon _x} = - z\frac{{{\partial ^2}{w_0}}}{{\partial {x^2}}}, {\sigma _x} = E({\varepsilon _x} - \alpha \Delta T) $ | (2) |
式中:E为梁的弹性模量;α为热膨胀系数;ΔT表示温差,且ΔT=T-Tref,Tref=22 ℃。
利用哈密顿原理,可以得到两个系统的动力学方程。连接并联NES的简支梁的动力学方程为
| $ \begin{array}{*{20}{c}} {I\frac{{{\partial ^2}{w_0}}}{{\partial {t^2}}} + {\mu _0}\frac{{\partial {w_0}}}{{\partial t}} + D\frac{{{\partial ^4}{w_0}}}{{\partial {x^4}}} + {N^T}\frac{{{\partial ^2}{w_0}}}{{\partial {x^2}}} + }\\ {[{k_1}{{({u_1} - {v_1})}^3} + {\mu _1}({{\dot u}_1} - {{\dot v}_1})]\delta (x - {a_1}) + }\\ {[{k_2}{{({u_2} - {v_2})}^3} + {\mu _2}({{\dot u}_2} - {{\dot v}_2})]\delta (x - {a_2}) = F\delta \left( {x - b} \right), }\\ {{m_1}{{\ddot v}_1} + {k_1}{{({v_1} - {u_1})}^3} + {\mu _1}({{\dot v}_1} - {{\dot u}_1}) = 0, }\\ {{m_2}{{\ddot v}_2} + {k_2}{{({v_2} - {u_2})}^3} + {\mu _2}({{\dot v}_2} - {{\dot u}_2}) = 0} \end{array} $ | (3) |
连接串联NES的简支梁的动力学方程为
| $ \begin{array}{*{20}{c}} {I\frac{{{\partial ^2}{w_0}}}{{\partial {t^2}}} + {\mu _0}\frac{{\partial {w_0}}}{{\partial t}} + D\frac{{{\partial ^4}{w_0}}}{{\partial {x^4}}} + {N^T}\frac{{{\partial ^2}{w_0}}}{{\partial {x^2}}} + }\\ {[{k_3}{{({u_3} - {v_3})}^3} + {\mu _3}({{\dot u}_3} - {{\dot v}_3})]\delta (x - {a_3}) = F\delta \left( {x - b} \right), }\\ {{m_3}{{\ddot v}_3} + {k_3}{{({v_3} - {u_3})}^3} + {\mu _3}({{\dot v}_3} - {{\dot u}_3}) + }\\ {{k_4}{{({v_3} - {v_4})}^3} + {\mu _4}({{\dot v}_3} - {{\dot v}_4}) = 0, }\\ {{m_4}{{\ddot v}_4} + {k_4}{{({v_4} - {v_3})}^3} + {\mu _4}({{\dot v}_4} - {{\dot v}_3}) = 0} \end{array} $ | (4) |
其中,u1=w0(a1, t), u2=w0(a2, t), u3=w0(a3, t), vi表示各NES的位移。弯曲刚度D、惯性矩I和热应力NT分别为
| $ D = \smallint _{ - h/2}^{h/2}\mathit{\boldsymbol{E}}{z^2}{\rm{d}}z, \mathit{\boldsymbol{I}} = \smallint _{ - h/2}^{h/2}\rho {\rm{d}}z, {\mathit{\boldsymbol{N}}^{\rm{T}}} = \smallint _{ - h/2}^{h/2}E\alpha T{\rm{d}}z, $ | (5) |
引入无量纲参数:
| $ \left\{ \begin{array}{l} {{\bar w}_0} = \frac{{{w_0}}}{h}, {{\bar v}_i} = \frac{{{v_i}}}{h}, \bar x = \frac{x}{l}, \bar F = \frac{{{l^4}}}{{E{h^4}}}F, {{\bar k}_i} = \frac{{{l^4}}}{{Eh}}{k_i}, \\ \bar t = \frac{h}{{{l^2}}}{\left( {\frac{E}{\rho }} \right)^{1/2}}t, {{\bar \mu }_i} = \frac{l}{h}{\left( {\frac{1}{{\rho E}}} \right)^{1/2}}{\mu _i}, {{\bar a}_i} = \frac{{{a_i}}}{l}, \\ \bar b = \frac{b}{l} \end{array} \right. $ | (6) |
简支梁的横向位移w0可表示为
| $ {w_0}\left( {x, t} \right) = \mathop \sum \limits_{n = 1}^N {w_n}\left( t \right){q_n}\left( x \right) $ | (7) |
对于简支边界条件,
连接并联NES的简支梁的动力学方程为
| $ \begin{array}{*{20}{c}} {{{\ddot w}_m} + {\gamma _0}{{\dot w}_m} + \omega _m^2{w_m} + \{ {k_1}{{[\mathop \sum \limits_{n = 1}^N {w_n}{q_n}({a_1}) - {v_1}]^3}} + }\\ {\gamma [\mathop \sum \limits_{n = 1}^N {{\dot w}_n}{q_n}({a_1}) - {{\dot v}_1}]\} {q_m}({a_1}) + }\\ {\{ {k_2}{{[\mathop \sum \limits_{n = 1}^N {w_n}{q_n}({a_2}) - {v_2}]^3}} + }\\ {{\gamma _2}[\mathop \sum \limits_{n = 1}^N {{\dot w}_n}{q_n}({a_2}) - {{\dot v}_2}]\} {q_m}({a_2}) = F{q_m}\left( b \right), }\\ {{\varepsilon _1}{{\ddot v}_1} + {k_1}{{[{v_1} - \mathop \sum \limits_{n = 1}^N {w_n}\left( t \right){q_n}({a_1})]^3}} + }\\ {{\gamma _1}[{{\dot v}_1} - \mathop \sum \limits_{n = 1}^N {{\dot w}_n}\left( t \right){q_n}({a_1})] = 0, }\\ {{\varepsilon _2}{{\ddot v}_2} + {k_2}{{[{v_2} - \mathop \sum \limits_{n = 1}^N {w_n}\left( t \right){q_n}({a_2})]^3}} + }\\ {{\gamma _2}[{{\dot v}_2} - \mathop \sum \limits_{n = 1}^N {{\dot w}_n}\left( t \right){q_n}({a_2})] = 0} \end{array} $ | (8) |
其中,
连接串联NES的简支梁的动力学方程为
| $ \begin{array}{*{20}{c}} {{{\ddot w}_m} + {\gamma _0}{{\dot w}_m} + \omega _m^2{w_m} + \{ {k_3}{{[\mathop \sum \limits_{n = 1}^N {w_n}{q_n}({a_3}) - {v_3}]^3}} + }\\ {{\gamma _3}[\mathop \sum \limits_{n = 1}^N {{\dot w}_n}{q_n}({a_3}) - {{\dot v}_3}]\} {q_m}({a_3}) = F{q_m}\left( b \right), }\\ {{\varepsilon _3}{{\ddot v}_3} + {k_3}{{[{v_3} - \mathop \sum \limits_{n = 1}^N {w_n}\left( t \right){q_n}({a_3})]^3}} + }\\ {{\gamma _3}[{{\dot v}_3} - \mathop \sum \limits_{n = 1}^N {{\dot w}_n}\left( t \right){q_n}({a_3})] + }\\ {{k_4}{{({v_3} - {v_4})}^3} + {\gamma _4}({{\dot v}_3} - {{\dot v}_4}) = 0, }\\ {{\varepsilon _4}{{\ddot v}_4} + {k_4}{{({v_4} - {v_3})}^3} + {\gamma _4}({{\dot v}_4} - {{\dot v}_3}) = 0} \end{array} $ | (9) |
利用Matlab程序研究并联和串联非线性能量阱的吸振效能。梁选用不锈钢材料,其材料和结构参数分别为:弹性模量E=1.93×1011 Pa,密度ρ=7 750 kg/m3,热膨胀系数α=1.7×10-5,梁长l=0.5 m,梁厚h=0.02 m。在分析过程中,兼顾计算的收敛性和效率,简支梁取前五阶模态[19]。此外,并联和串联非线性能量阱中各子装置的质量系数均取0.05,冲击载荷F表述为半波形式:
| $ F = \left\{ {\begin{array}{*{20}{l}} {A\sin \left( {2{\rm{ \mathsf{ π} }}t/T} \right)}&{0 \le t \le T/2}\\ {0, }&{t > T/2} \end{array}} \right. $ | (10) |
且始终作用于b=0.35。其中T=0.4/π。
通常以能量耗散率表征冲击载荷作用下非线性能量阱的吸振效能。并联非线性能量阱的能量耗散率计算公式为
| $ \begin{array}{*{20}{c}} {{\eta _1} = }\\ {\frac{{\smallint _0^t({\gamma _1}{{[\mathop \sum \limits_{n = 1}^N {{\dot w}_n}{q_n}({a_1}) - {{\dot v}_1}]^2}} + {\gamma _2}{{[\mathop \sum \limits_{n = 1}^N {{\dot w}_n}{q_n}({a_2}) - {{\dot v}_2}]^2}}){\rm{d}}\tau }}{{\smallint _0^TF\mathop \sum \limits_{n = 1}^N {{\dot w}_n}{q_n}\left( b \right){\rm{d}}t}}}\\ \end{array} $ |
串联非线性能量阱的能量耗散率计算公式为
| $ \begin{array}{*{20}{c}} {{\eta _2} = }\\ {\frac{{\smallint _0^t({\gamma _3}{{[\mathop \sum \limits_{n = 1}^N {{\dot w}_n}{q_n}({a_3}) - {{\dot v}_3}]^2}} + {\gamma _4}{{({{\dot v}_3} - {{\dot v}_4})}^2}){\rm{d}}\tau }}{{\smallint _0^TF\mathop \sum \limits_{n = 1}^N {{\dot w}_n}{q_n}\left( b \right){\rm{d}}t}}} \end{array} $ |
图 2为并联非线性能量阱的能量耗散率随其参数的变化情况。图中红色区域内能量阱的能量耗散率具有较大值。由图 2(a)和2(b)可知,能量耗散率与刚度系数、阻尼系数的关系,均非单调变化,而是在两个系数取值于某一范围时得到较高的值。其中,两个子能量阱的刚度系数的取值均应较小一些,两个阻尼系数中,阻尼系数γ1的取值较小即可,γ2的取值相对灵活。在上述分析过程中,两个子能量阱安装位置分别为0.35和0.6。此外,图 2(a)中,γ1=γ2=0.2,图 2(b)中,k1=k2=60,冲击载荷幅值A=10。图 2(c)中,令γ1=γ2=0.2、k1=k2=60,该图为两个子能量阱的安装位置对能量耗散率的影响,安装位置从梁端点变化到梁中点的过程中,能量耗散率并非单调变化,这与前五阶模态的形函数有关。需注意的是,同一颜色在不同图中表示的能量耗散率的取值区间是不同的,应参照每幅图中的图例进行分析。

|
Download:
|
| 图 2 并联非线性能量阱的吸振效能 Fig. 2 Vibration absorption efficiency of the parallel NES | |
图 3为串联非线性能量阱的能量耗散率随其参数的变化情况。刚度和阻尼系数的取值原则与并联非线性能量阱的差别较大。与梁直接连接的能量阱的刚度和阻尼系数应取较大值,而另一能量阱的刚度和阻尼系数应取较小值。其中,k4的取值过大会较大地影响串联非线性能量阱的吸振效能,而两个子能量阱的阻尼系数的取值相对自由,为获得较高的吸振效能,γ3的取值应较大一些,γ4的取值应较小一些。图 3(a)中,γ3=γ4=0.2,图 3(b)中,k3=400、k4=40,安装位置均为0.35。图 3(c)中,令γ3=γ4=0.2、k3=400、k4=40,该图为串联非线性能量阱的安装位置对能量耗散系数的影响,其规律与并联非线性能量阱的规律类似,安装位置不合理会较大影响能量阱的作用。综合分析图 2和图 3可知,并联和串联非线性能量阱均可以对冲击载荷起到较好的吸振作用,但吸振效能的高低与其参数的选取关系较大,且两者的参数设置原则差异较大。

|
Download:
|
| 图 3 串联非线性能量阱的吸振效能 Fig. 3 Vibration absorption efficiency of the series NES | |
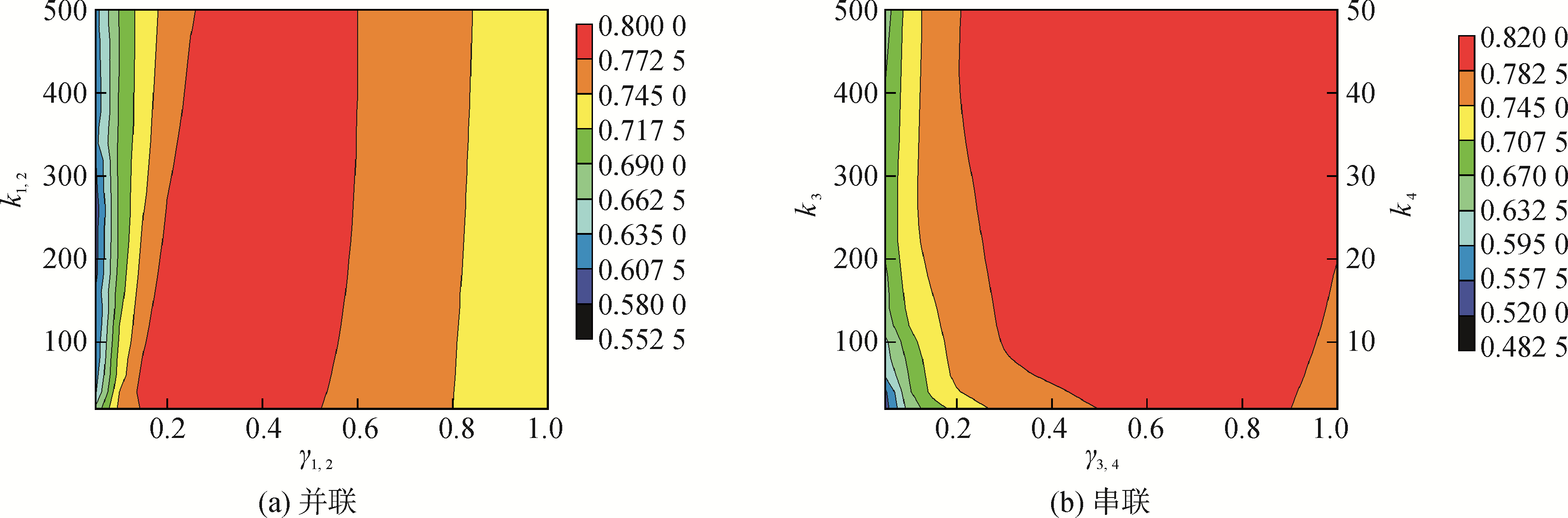
图 4(a)中,令两个子能量阱的刚度和阻尼系数保持同步变化,分析能量耗散率的变化规律。在阻尼系数较小时,刚度系数对能量耗散率的影响较大,在γ1, 2=0.4附近的区间内,可以获得较高的能量耗散率。保持刚度系数不变,随着阻尼系数的增大,能量耗散率均具有先增大后减小的变化规律。图 4(b)中,令两个子能量阱的阻尼系数保持同步变化,k3从20变化至500,k4从2变化至50,当阻尼系数取值较小时,随刚度的变化,能量耗散率的变化幅度较大。反之,能量耗散率随刚度的变化幅度较小。图 3和图 4中,冲击幅值与图 2中相同。图 4中,能量阱的安装位置分别与图 2(a)和图 3(a)相同。
|
Download:
|
| 图 4 非线性能量阱吸振效能与刚度系数、阻尼系数的关系 Fig. 4 The relation between vibration absorption efficiency of NESs and stiffness coefficient, damping coefficient | |
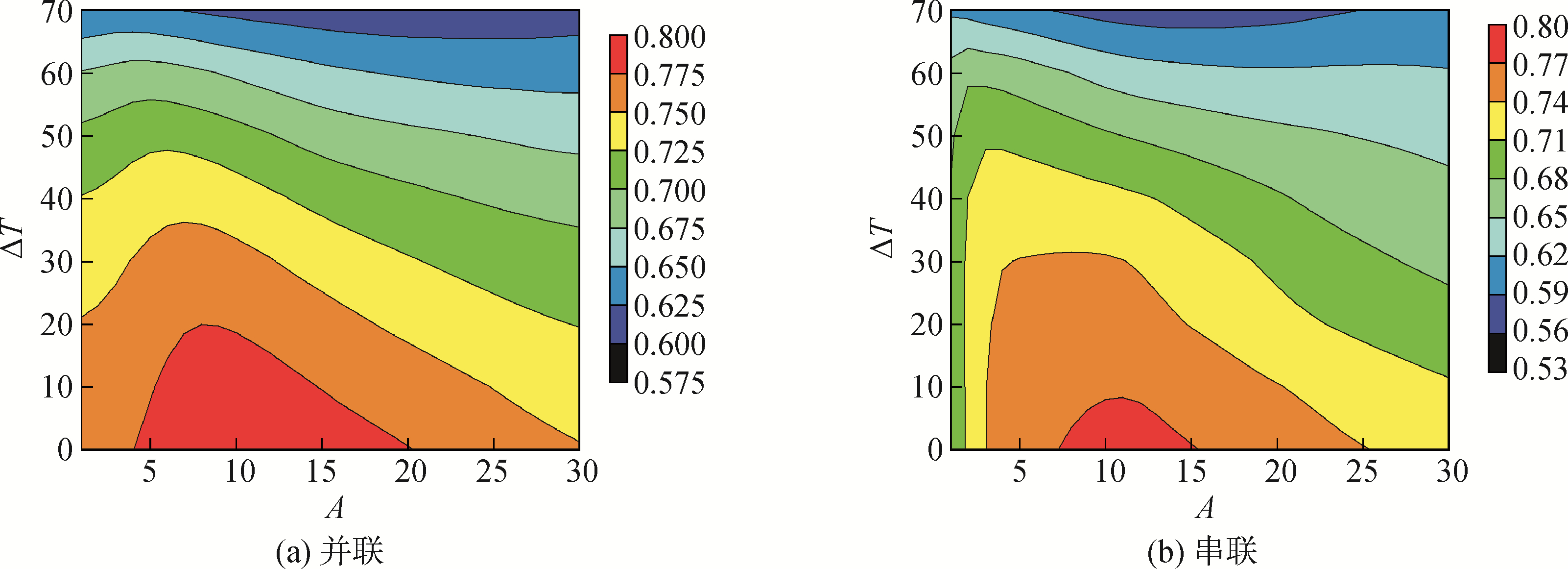
图 5为并联和串联非线性能量阱吸振效能随冲击幅值和温差的变化情况,并联能量阱的参数选取为:k1=60,k2=60,γ1=0.2,γ2=0.2,a1=0.35,a2=0.6。串联非线性能量阱的参数选取为:k3=400,k4=40,γ1=0.2,γ2=0.2,a3=0.35。在任意温度下,随着冲击幅值的增加,并联与串联非线性能量阱的吸振效能的变化规律均为先增大后减小,达到最高能量耗散率时对应的冲击幅值随着温度的增加而减小。在同一冲击幅值下,随着温度的增加,并联和串联非线性能量阱的吸振效能均逐渐降低。与并联非线性能量阱相比,串联非线性能量阱在较低和较高冲击载荷下的能量耗散率较低,随外部因素变化,串联非线性能量阱的吸振效能变化幅度较大,即其鲁棒性相对较差。
|
Download:
|
| 图 5 非线性能量阱吸振效能随冲击幅值和温差的变化 Fig. 5 The variation of vibration absorption efficiency of NESs with shock amplitude and temperature difference | |
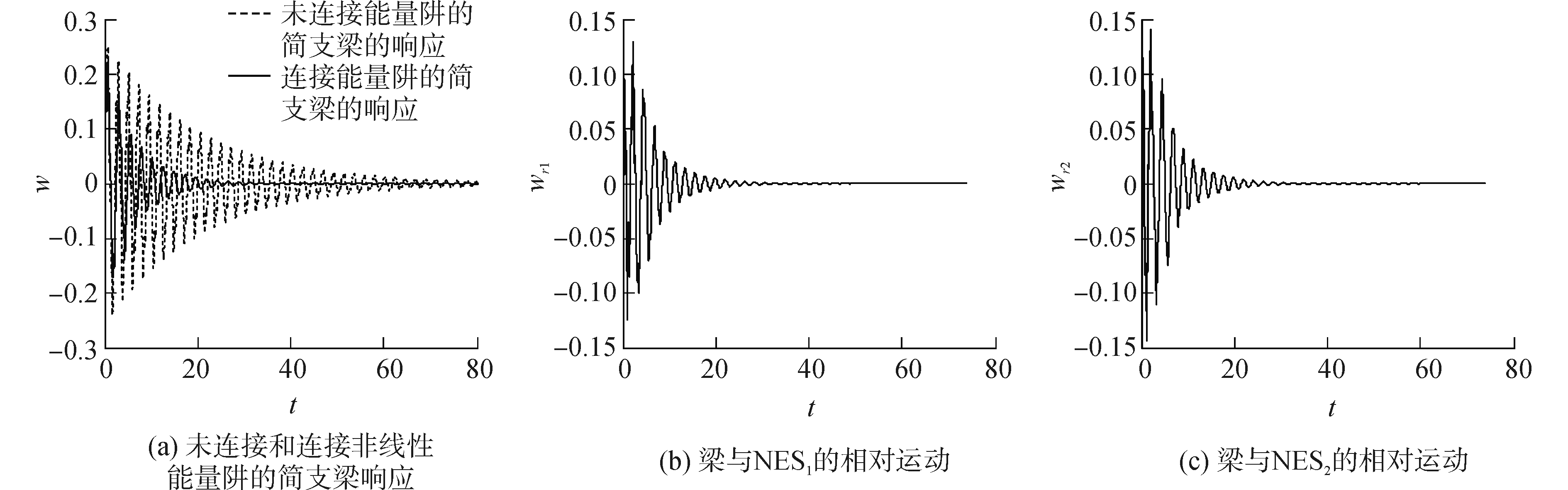
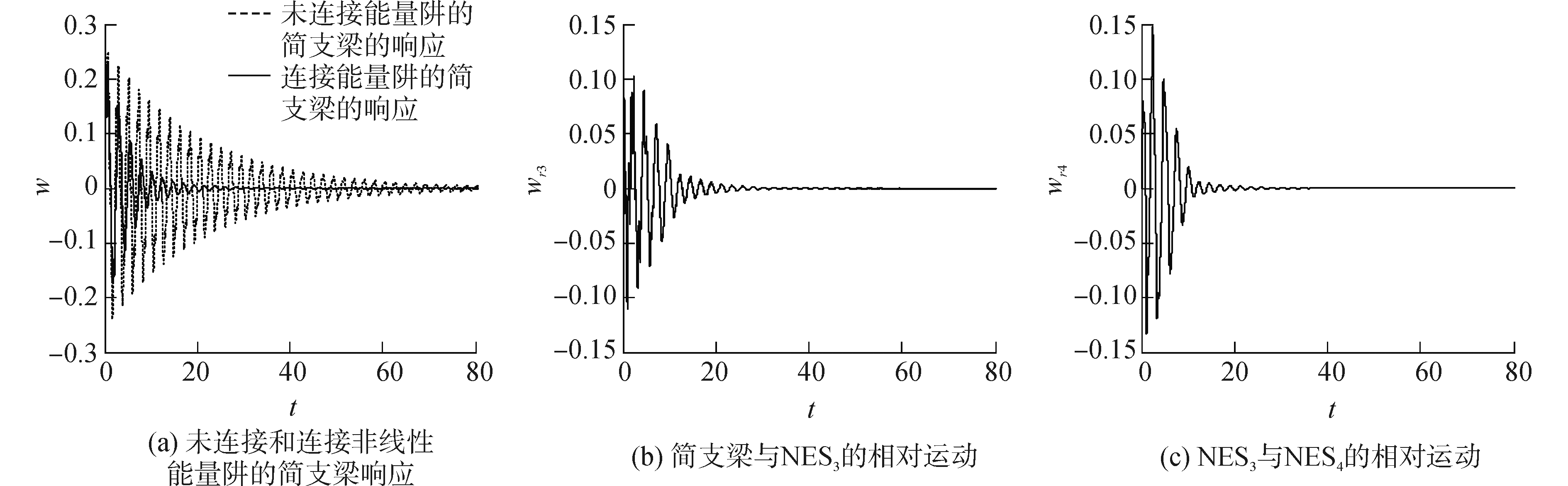
为进一步分析两种非线性能量阱振动响应的差异,图 6和图 7分别给出了含并联和串联非线性能量阱系统的瞬态波形图。两图中,两个能量阱的参数选取与图 5相同。图 6(a)和7(a)中,未连接能量阱的简支梁的响应和连接了能量阱的简支梁的响应,均取得了较好的减振效果。由图 6可知,并联非线性能量阱的两个子装置与简支梁之间的相对位移较为接近。图 7表明,串联非线性能量阱中,两个子装置之间的最大相对位移明显大于简支梁和与其连接的子装置之间的最大相对位移,两者呈1.5倍的关系。
|
Download:
|
| 图 6 含并联非线性能量阱系统的位移响应 Fig. 6 The displacements of the system with parallel NES | |
|
Download:
|
| 图 7 含串联非线性能量阱系统的位移响应 Fig. 7 The displacements of the system with series NES | |
1) 两种非线性能量阱的参数设置原则差异较大。并联非线性能量阱中的两个子装置的参数可设置的较为接近。串联非线性能量阱中,直接连接于主振结构的子能量阱的刚度系数应数倍于另一个子能量阱的刚度系数。
2) 随着冲击幅值的增加,并联与串联非线性能量阱吸振效能的变化规律均为先增大后减小,随着温度的增加,两种非线性能量阱的吸振效能均逐渐降低。相对而言,串联非线性能量阱的吸振效能容易受到外部因素的影响,并联非线性能量阱显示了相对较好的鲁棒性。
由于强非线性因素的引入,使得加入非线性能量阱后的系统的动力学行为变得更加复杂。能量阱参数设置的误差以及外部影响因素的大幅变化都会导致非线性能量阱吸振效能的降低,而非线性能量阱宽频被动吸振和轻质的特点是其他类型的吸振器难以实现的,如何在非线性能量阱设计和改进过程中扬长避短,最大程度地发挥该类吸振器的优点,是值得研究的课题。
| [1] |
GENDELMAN V. Transition of energy to a nonlinear localized mode in a highly asymmetric system of two oscillators[J]. Nonlinear dynamics, 2001, 25(1-3): 237-253. (  0) 0)
|
| [2] |
GOURDON F, LAMARQUE C H, PERNOT S. Contribution to efficiency of irreversible passive energy pumping with a strong nonlinear attachment[J]. Nonlinear dynamics, 2007, 50(4): 793-808. DOI:10.1007/s11071-007-9229-y (  0) 0)
|
| [3] |
SAMANI F S, PELLICANO F. Vibration reduction on beams subjected to moving loads using linear and nonlinear dynamic absorbers[J]. Journal of sound and vibration, 2009, 325(4): 742-754. (  0) 0)
|
| [4] |
TUMKUR R K R, DOMANY E, GENDELMAN O V, MASUD A, et al. Reduced-order model for laminar vortex-induced vibration of a rigid circular cylinder with an internal nonlinear absorber[J]. Communications in nonlinear science and numerical simulation, 2013, 18(7): 1916-1930. DOI:10.1016/j.cnsns.2012.11.028 (  0) 0)
|
| [5] |
LUO J, WIERSCHEM N E, FAHNESTOCK L A, et al. Realization of a strongly nonlinear vibration-mitigation device using elastomeric bumpers[J]. Journal of engineering mechanics, 2014, 140(5): 04014009. DOI:10.1061/(ASCE)EM.1943-7889.0000692 (  0) 0)
|
| [6] |
陈勇, 徐羿. 基于非线性能量吸振器的高耸结构减振分析[J]. 振动与冲击, 2014, 33(9): 27-32. CHEN Yong, XU Yi. Vibration suppression analysis for a tall structure attached with a nonlinear energy sink absorber[J]. Journal of vibration and shock, 2014, 33(9): 27-32. (  0) 0)
|
| [7] |
刘中坡, 乌建中, 王菁菁, 等. 轨道型非线性能量阱对高层结构脉动风振的控制仿真[J]. 振动工程学报, 2016, 29(6): 1088-1096. LIU Zhongpo, Wu Jianzhong, Wang Jingjing, et al. Simulation of truck nonlinear energy sink for wind-induced vibration control in high-rise building[J]. Journal of vibration engineering, 2016, 29(6): 1088-1096. (  0) 0)
|
| [8] |
GUO C Z, AL-SHUDEIFAT M A, VAKAKIS A F, et al. Vibration reduction in unbalanced hollow rotor systems with nonlinear energy sinks[J]. Nonlinear dynamics, 2015, 79(1): 527-538. (  0) 0)
|
| [9] |
ZHANG Y W, ZHANG H, HOU S, et al. Vibration suppression of composite laminated plate with nonlinear energy sink[J]. Acta astronautica, 2016, 123: 109-115. DOI:10.1016/j.actaastro.2016.02.021 (  0) 0)
|
| [10] |
LEE Y S, VAKAKIS A F, BERGMAN L A, et al. Suppression of aeroelastic instability using broadband passive targeted energy transfers, part 1:theory[J]. AIAA journal, 2007, 45(3): 693-711. DOI:10.2514/1.24062 (  0) 0)
|
| [11] |
YANG K, ZHANG Y W, DING H, et al. Nonlinear energy sink for whole-spacecraft vbration reduction[J]. Journal of vibration and acoustics, 2017, 139(2): 021011. DOI:10.1115/1.4035377 (  0) 0)
|
| [12] |
VAURIGAUD B, SAVADKOOHI A T, LAMARQUE C H. Targeted energy transfer with parallel nonlinear energy sinks. Part Ⅰ:Design theory and numerical results[J]. Nonlinear dynamics, 2011, 66(4): 763-780. DOI:10.1007/s11071-011-9949-x (  0) 0)
|
| [13] |
SAVADKOOHI A T, VAURIGAUD B, LAMARQUE C H. Targeted energy transfer with parallel nonlinear energy sinks. Part Ⅱ:theory and experiments[J]. Nonlinear dynamics, 2012, 67(1): 37-46. (  0) 0)
|
| [14] |
NGUYEN T A, PERNOT S. Design criteria for optimally tuned nonlinear energy sinks-part 1:transient regime[J]. Nonlinear dynamics, 2012, 69(1/2): 1-19. (  0) 0)
|
| [15] |
ZHANG Y W, ZHANG Z, CHEN L Q, et al. Impulse-induced Vibration Suppression of an Axially Moving Beam with Parallel Nonlinear Energy Sinks[J]. Nonlinear dynamics, 2015, 82(1/2): 61-71. (  0) 0)
|
| [16] |
TSAKIRTZIS S, PANAGOPOULOS P N, KERSCHEN G, et al. Complex dynamics and targeted energy transfer in linear oscillators coupled to multi-degree-of-freedom essentially nonlinear attachments[J]. Nonlinear dynamics, 2007, 48(3): 285-318. DOI:10.1007/s11071-006-9089-x (  0) 0)
|
| [17] |
GENDELMAN O V, SAPSIS T, VAKAKIS A F. Enhance passive targeted energy transfer in strongly nonlinear mechanical oscillators[J]. Journal of sound and vibration, 2011, 330(1): 1-8. DOI:10.1016/j.jsv.2010.08.014 (  0) 0)
|
| [18] |
GRINBERG I, LANTON V, GENDELMAN O V. Response regimes in linear oscillator with 2DOF nonlinear energy sink under periodic forcing[J]. Nonlinear dynamics, 2012, 69(4): 1889-1902. DOI:10.1007/s11071-012-0394-2 (  0) 0)
|
| [19] |
GEORGIADES F, VAKAIS A F. Dynamics of a linear beam with an attached local nonlinear energy sink[J]. Communications in nonlinear science and numerical simulation, 2007, 12(5): 643-651. DOI:10.1016/j.cnsns.2005.07.003 (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


