2. 哈尔滨工程大学 动力与能源工程学院, 黑龙江 哈尔滨 150001
2. College of Power and Energy Engineering, Harbin Engineering University, Harbin 150001, China
目前油膜厚度测量方法有多种[1-2],其中超声波测量技术具有不破坏测试环境、使用方便和安全性好等优点,开始应用于低速柴油机气缸油膜厚度的测量。Tattersall通过超声脉冲法进行粘结测试,发现嵌入介质Ⅰ内的介质Ⅱ与Ⅰ相比是薄层时,介质Ⅱ可由轻质弹簧替换[3]。Park等[4]研究介质厚度、超声波频率和介质声阻抗对利用超声波脉冲回波方法测量液体膜厚度的影响。Dwyer-Joyce等[5]分析了润滑油膜不同厚度范围适用的测量理论方法,并设计了静、动态油膜厚度测量装置。Zhang等[6]针对超声波技术缺乏校准程序的缺点,探讨润滑油膜厚度超声测量的校准技术。并对超声波传感器线性阵列进行研究,将垂直入射扩展到任何角度的斜入射超声波测量,对厚度为2~9 μm的油膜进行了实验[6-7]。Hunter等[8]研究了无损检测中自动聚焦问题,并利用超声阵列对复杂的几何形状进行了评估。Gasni等[9]研究了弹簧模型中粗糙表面接触时反射率与刚度关系,得出反射率不是直接与实际接触的面积有关,而是取决于表面接触微凸体的个数、形状和分布。Dwyer[10]研究了弹性流体动力润滑中边界润滑或混合润滑时超声膜厚测量机理,且通过实验对其进行验证。文献[11-15]对超声波测量油膜厚度的方法也进行了研究,并在理论和应用方面得到大量的成果。
油膜测量位置往往处于高温高压的状态,而超声波在介质中的声阻等特性受到介质密度、温度和压力的影响,因此会造成超声波测量油膜厚度的计算误差。此外,利用等效弹簧模型计算油膜厚度时,反射率的误差也会对油膜厚度计算造成影响,这些分析对确定超声波测量油膜厚度的计算精度非常重要。本文将针对上述问题,开展理论分析。
1 基本原理和数学模型当超声波入射在两个不同介质的边界时,一些能量被反射,一些被透射。能量反射的多少可以用反射率Rm来表示:
| $ {R_m} = \frac{{{Z_2} - {Z_1}}}{{{Z_2} + {Z_1}}} $ | (1) |
式中:Z2和Z1分别表示边界两边的介质声阻;Z=ρc, ρ是介质的密度;c是声波在介质中的传播速度(表 1是常见介质的密度和声速)。
| 表 1 常见介质的性质 Table 1 The properties of common materials |
当超声波入射在多层不同介质的边界时,每个边界上的反射波和入射波会相互叠加。对于金属-液体-金属三层介质结构,如果中间层液体介质厚度很小,与入射超声波的波长一致,则可以采用谐振模型理论计算该液体介质厚度[3],即中间层介质厚度:
| $ H = \frac{{cm}}{{2{f_m}}} $ | (2) |
式中:m是谐振的阶数;fm是m阶谐振频率。
同时,对于金属-液体-金属的三层介质结构,入射超声波的反射率表示为:
| $ \begin{array}{*{20}{c}} {{R_m} = }\\ {\frac{{{{\rm{e}}^{\frac{{2j\omega h}}{{{c_2}}}}}\left( {{Z_2} - {Z_3}} \right)\left( {{Z_1} + {Z_2}} \right) + \left( {{Z_1} - {Z_2}} \right)\left( {{Z_2} + {Z_3}} \right)}}{{{{\rm{e}}^{\frac{{2j\omega h}}{{{c_2}}}}}\left( {{Z_2} - {Z_3}} \right)\left( {{Z_1} - {Z_2}} \right) + \left( {{Z_1} + {Z_2}} \right)\left( {{Z_2} + {Z_3}} \right)}}} \end{array} $ | (3) |
式中:ω是声波的角频率;c2是声波在中间Ⅱ层介质的声速。Z1、Z2和Z3分别表示第Ⅰ层、中间Ⅱ层和第Ⅲ层介质声阻。
如果ω是谐振频率,此时的反射率为:
| $ {R_m} = \frac{{{Z_1} - {Z_3}}}{{{Z_1} + {Z_3}}} $ | (4) |
如果Z1=Z3,此时的反射率为Rm=0。
利用式(3),取不锈钢-油-不锈钢三层介质结构,可得到超声波反射率和入射频率间的关系曲线,如图 1所示。该图反应了不同油膜厚度下,不同声波频率及其反射率变化关系,当反射率等于0时,对应其谐振频率。油膜厚度越小,其谐振频率越高。

|
Download:
|
| 图 1 不锈钢-油-不锈钢三层介质的超声波反射率和入射频率关系曲线 Fig. 1 Relationship between reflection coefficient and incident frequency of the ultrasound transmitting on stainless-steel-oil-stainless-steel medium | |
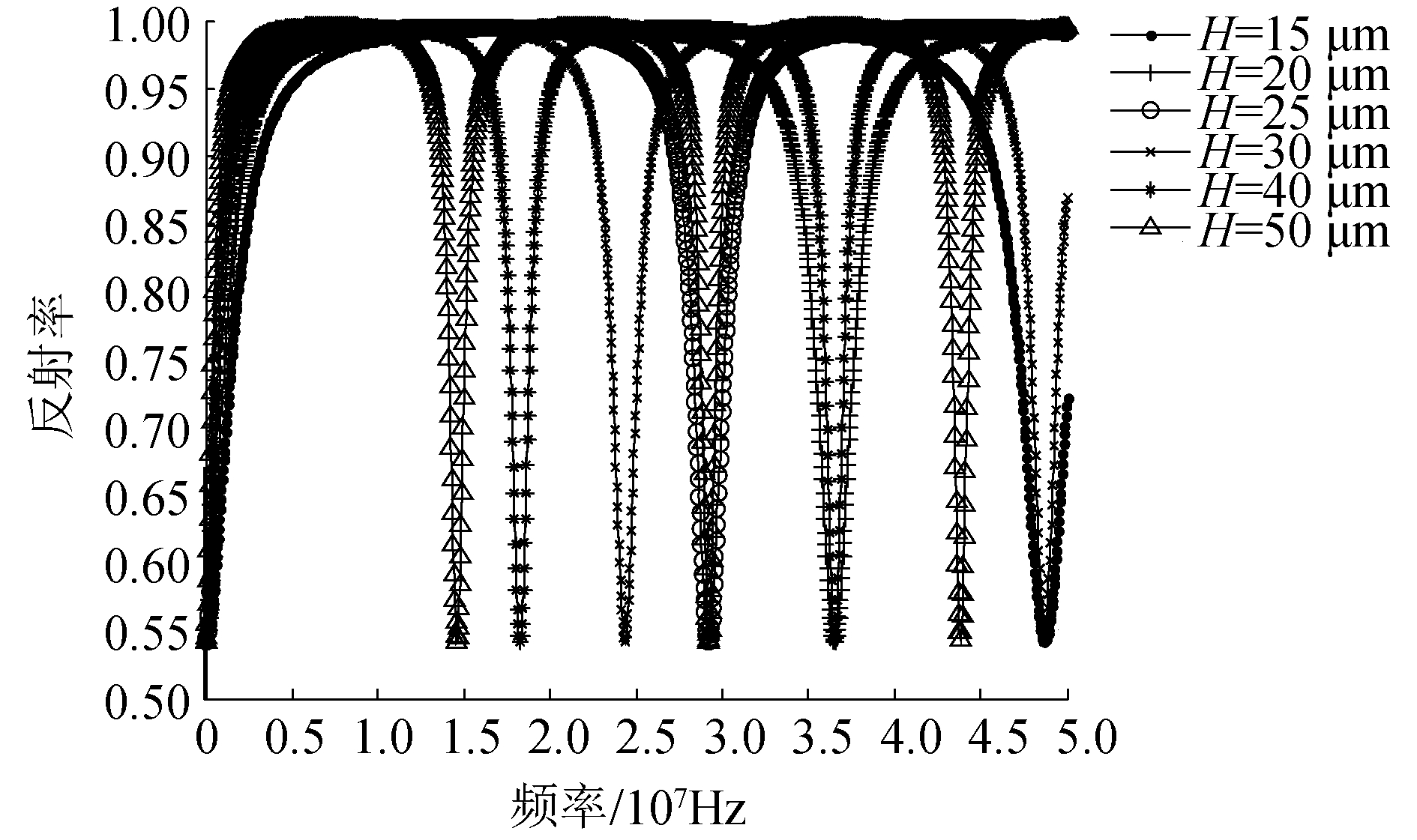
如取不锈钢-油-铝三层介质结构,超声波反射率和入射频率之间的关系曲线和不锈钢-油-不锈钢三层介质相似,如图 2所示,但由于Z1≠Z3,此时的最小反射率为Rm=0.541 8。
|
Download:
|
| 图 2 不锈钢-油-铝三层介质的超声波反射率和入射频率关系曲线 Fig. 2 Relationship between reflection coefficient and incident frequency of the ultrasound transmitting on stainless-steel-oil-aluminum medium | |
由于超声波换能器的制造频率限制,谐振模型一般只适于10~200 μm的油膜厚度测量。
1.2 等效弹簧模型对于金属-液体-金属3层介质结构,如果中间层液体介质厚度小于入射超声波的波长,超声波在边界的反射率可以用液体层等效弹簧的刚度来确定[3],即:
| $ R\left( f \right) = \sqrt {\frac{{{{\left( {\omega {z_1}{z_3}} \right)}^2} + {k^2}{{\left( {{z_1} - {z_3}} \right)}^2}}}{{{{\left( {\omega {z_1}{z_3}} \right)}^2} + {k^2}{{\left( {{z_1} + {z_3}} \right)}^2}}}} $ | (5) |
式中:R(f)是反射率;k是液体层等效弹簧刚度;ω是超声波的角频率(ω=2πf)。
液体层的刚度可以表示为:
| $ k = B/H $ | (6) |
式中:B是液体层的体积模量;H是油膜层的厚度。
由式(5)和(6),可以得到液体层介质厚度和反射率的关系:
| $ H = \frac{{\rho {c^2}}}{{\omega {z_1}{z_3}}}\sqrt {\left( {\frac{{{{\left| {R\left( f \right)} \right|}^2}{{\left( {{z_1} + {z_3}} \right)}^2} - {{\left( {{z_1} - {z_3}} \right)}^2}}}{{1 - {{\left| {R\left( f \right)} \right|}^2}}}} \right)} $ | (7) |
式中:ρ是液体层介质的密度,c是液体层介质的声速。
如果z1=z3=z,式(7)可以简化为:
| $ H = \frac{{\rho {c^2}}}{{{\rm{ \mathsf{ π} }}fz}}\sqrt {\left( {\frac{{{{\left| {R\left( f \right)} \right|}^2}}}{{1 - {{\left| {R\left( f \right)} \right|}^2}}}} \right)} $ | (8) |
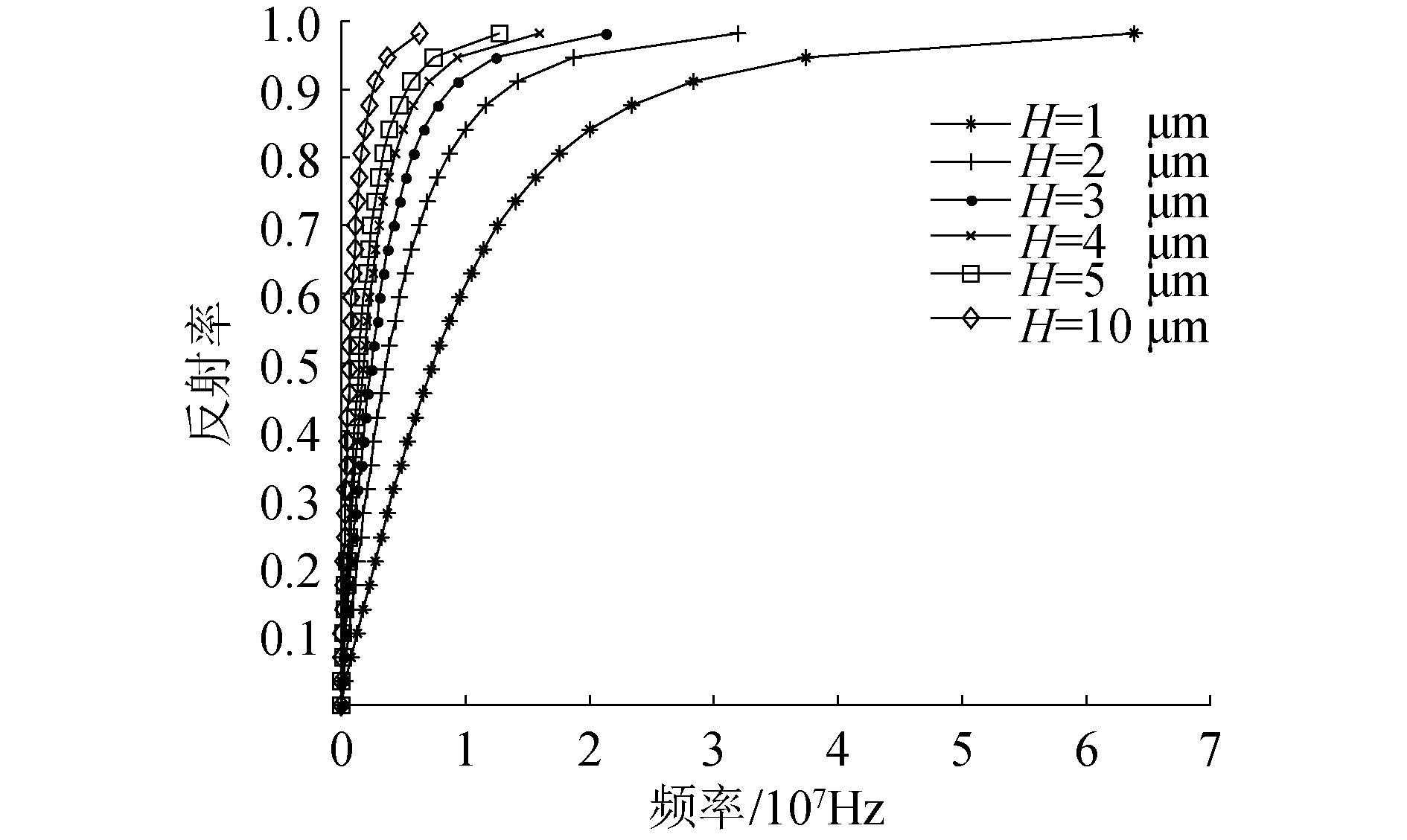
利用式(8),取不锈钢-油-不锈钢3层介质结构,可得到超声波反射率(系数)和入射频率之间的关系曲线,如图 3所示。该图反映出不同油膜厚度下,不同声波频率和反射率变化规律。反之,对应不同的频率和反射率,可以得到不同的油膜厚度。值得注意的是,对于某一厚度油膜,随着频率增加,反射率趋于1,再无明显增加,这表示此时已无法通过频率和反射率计算得到油膜厚度。越厚的油膜需要越小的超声波频率测量;越薄的油膜需要越大的超声波频率测量;对于某一超声波频率,只能测量一定范围内的油膜厚度。
|
Download:
|
| 图 3 不锈钢-油-不锈钢3层介质的超声波反射率和入射频率关系曲线 Fig. 3 Relationship between reflection coefficient and incident frequency of the ultrasound transmitting on stainless-steel-oil-stainless-steel medium | |
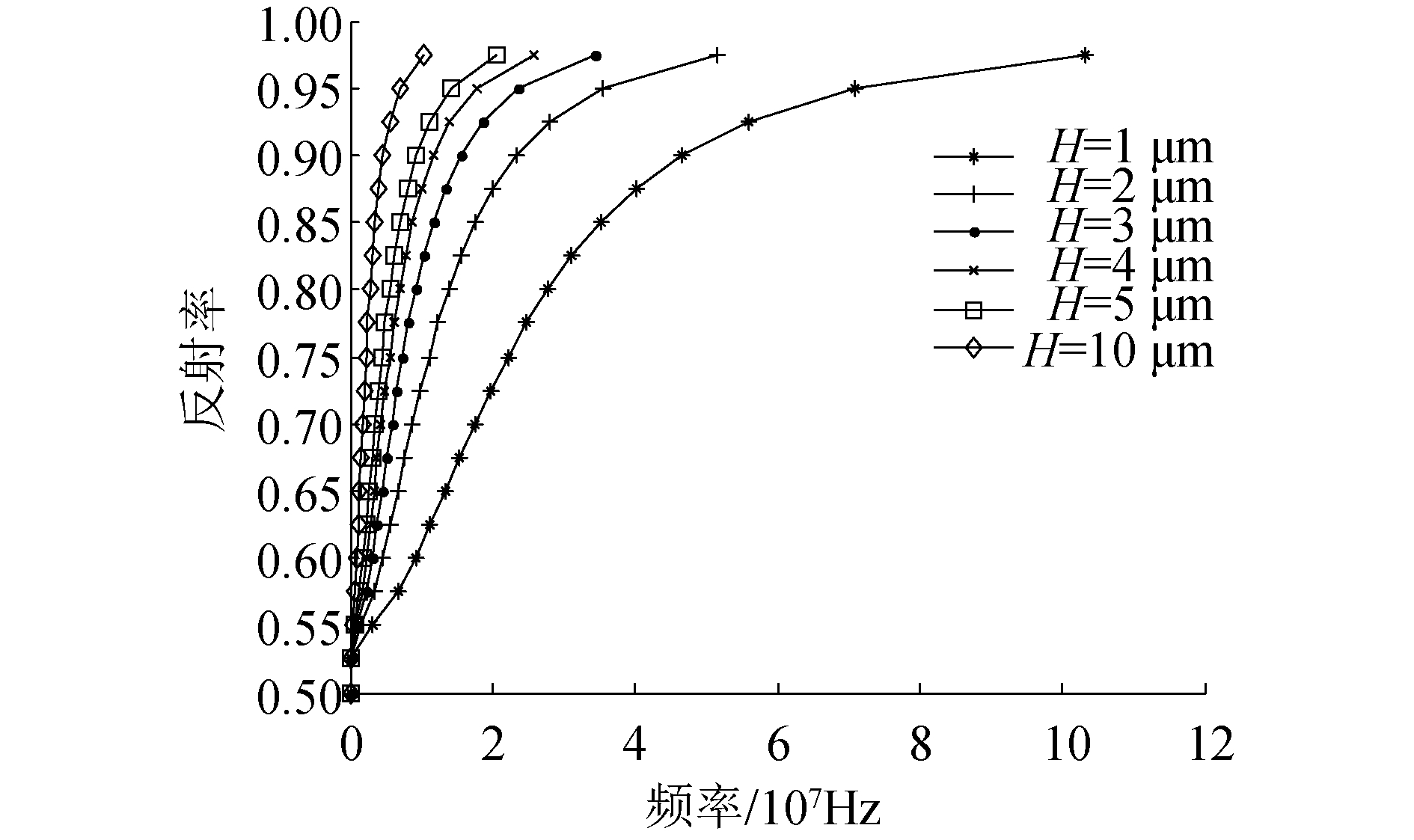
如取不锈钢-油-铝3层介质结构,超声波反射率和入射频率之间的关系曲线和不锈钢-油-不锈钢3层介质结构相似,如图 4所示,不同之处在于反射率最小为0.541 8。
|
Download:
|
| 图 4 不锈钢-油-铝3层介质的超声波反射率和入射频率关系曲线 Fig. 4 Relationship between reflection coefficient and incident frequency of the ultrasound transmitting on stainless-steel-oil-aluminum medium | |
如果以反射率为输入变量,对式(7)进行泰勒展开,去掉二次项以上部分,则得到:
| $ \begin{array}{*{20}{c}} {\Delta H = H\left( {R + \Delta R} \right) - H\left( R \right)}\\ {\Delta H = \frac{{\rho {c^2}}}{{\omega {z_1}{z_3}}} \cdot }\\ {\frac{{\left| {\Delta R} \right|\left( {{{\left( {{z_1} + {z_3}} \right)}^2} - {{\left( {{z_1} - {z_3}} \right)}^2}} \right)}}{{\sqrt {\left( {\frac{{{{\left| {\Delta R} \right|}^2}{{\left( {{z_1} + {z_3}} \right)}^2} - {{\left( {{z_1} - {z_3}} \right)}^2}}}{{1 - {{\left| {\Delta R} \right|}^2}}}} \right){{\left( {1 - {{\left| {\Delta R} \right|}^2}} \right)}^2}} }}} \end{array} $ | (9) |
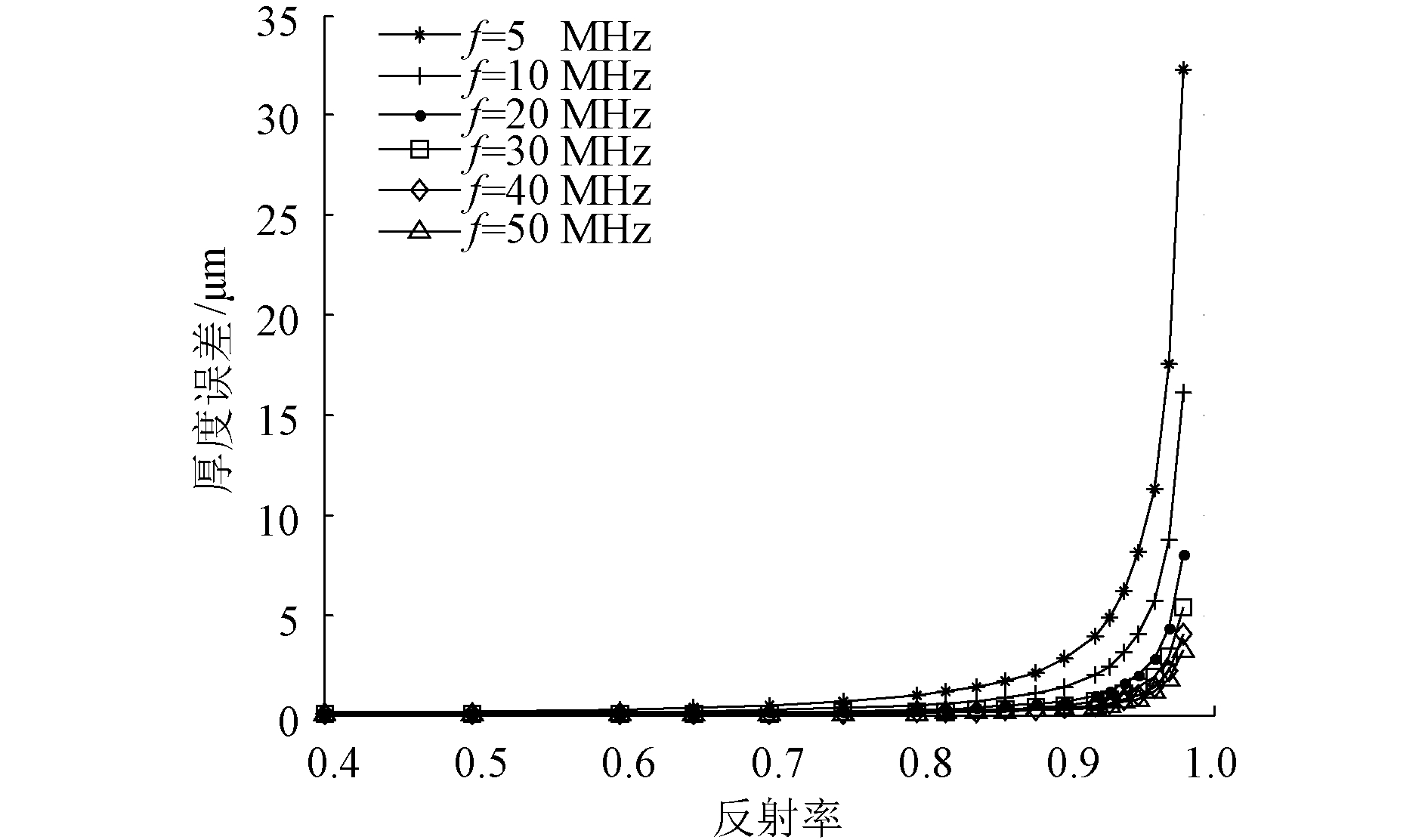
若取不锈钢-油-不锈钢3层介质结构,ΔR取0.1R,式(8)的计算结果如图 5所示。结果显示在反射率误差为10%时,随着反射率的增加,计算得到的油膜厚度误差增加,当反射率趋近1时,误差无限大。同时,超声波频率越高,误差越小。
|
Download:
|
| 图 5 不锈钢-油-不锈钢3层介质的超声波反射率误差影响曲线 Fig. 5 Reflection coefficient error of the ultrasound transmitting on stainless-steel-oil-stainless-steel medium | |
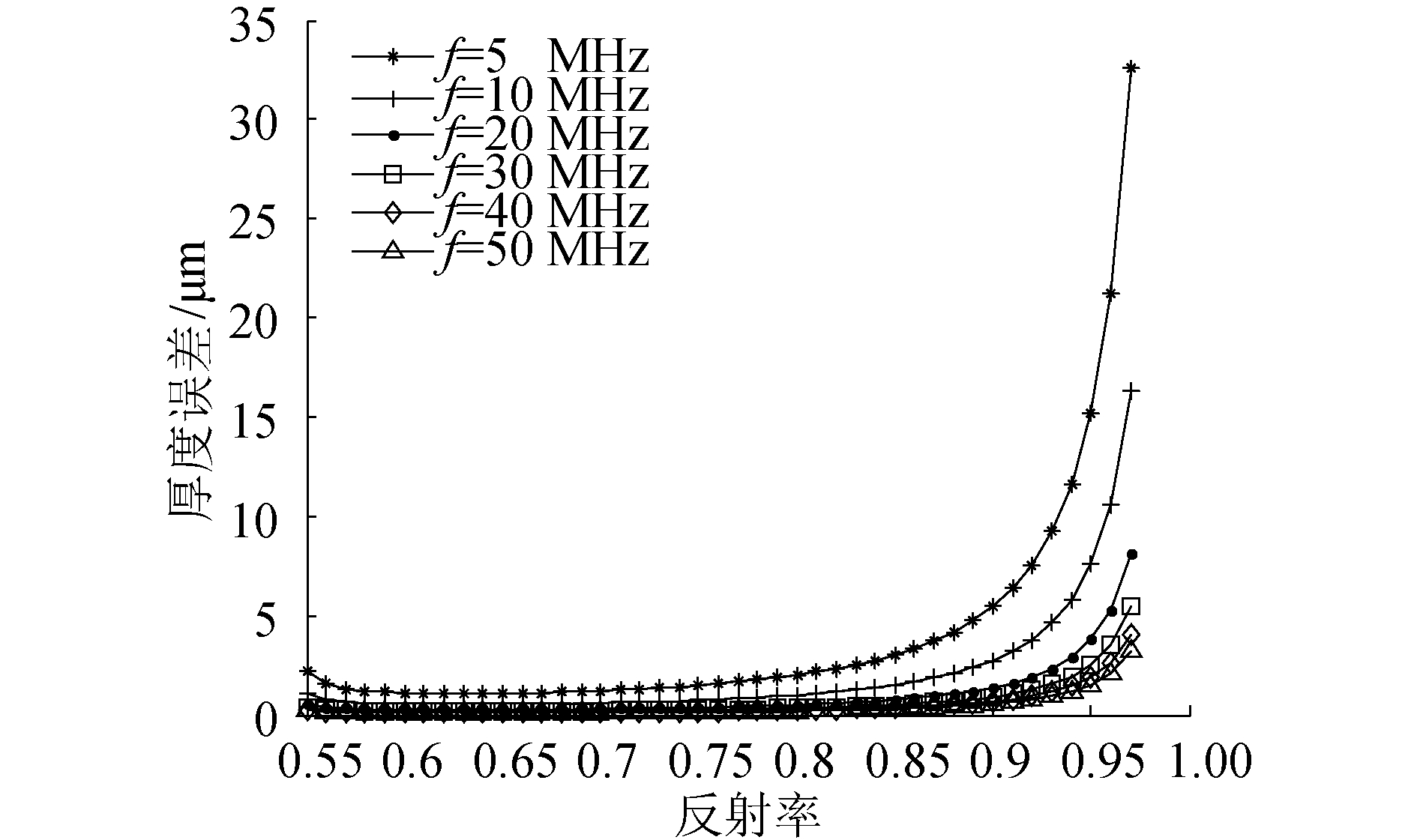
若取不锈钢-油-铝3层介质结构,ΔR取0.1R,则得到图 6所示结果。除了上面的结论外,还可以得到在接近最小反射率0.541 8时,油膜厚度误差也增加。此外,在相同反射率下,不锈钢-油-铝3层介质结构的计算误差大于不锈钢-油-不锈钢3层介质结构的计算误差。
|
Download:
|
| 图 6 不锈钢-油-铝3层介质的超声波反射率误差影响曲线 Fig. 6 Reflection coefficient error of the ultrasound transmitting on stainless-steel-oil-aluminum medium | |
图 5、图 6显示的绝对误差不易看出误差的相对大小。按照相对误差计算公式:
| $ \frac{{H\left( {R + \Delta R} \right) - H\left( R \right)}}{{H\left( R \right)}} $ | (10) |
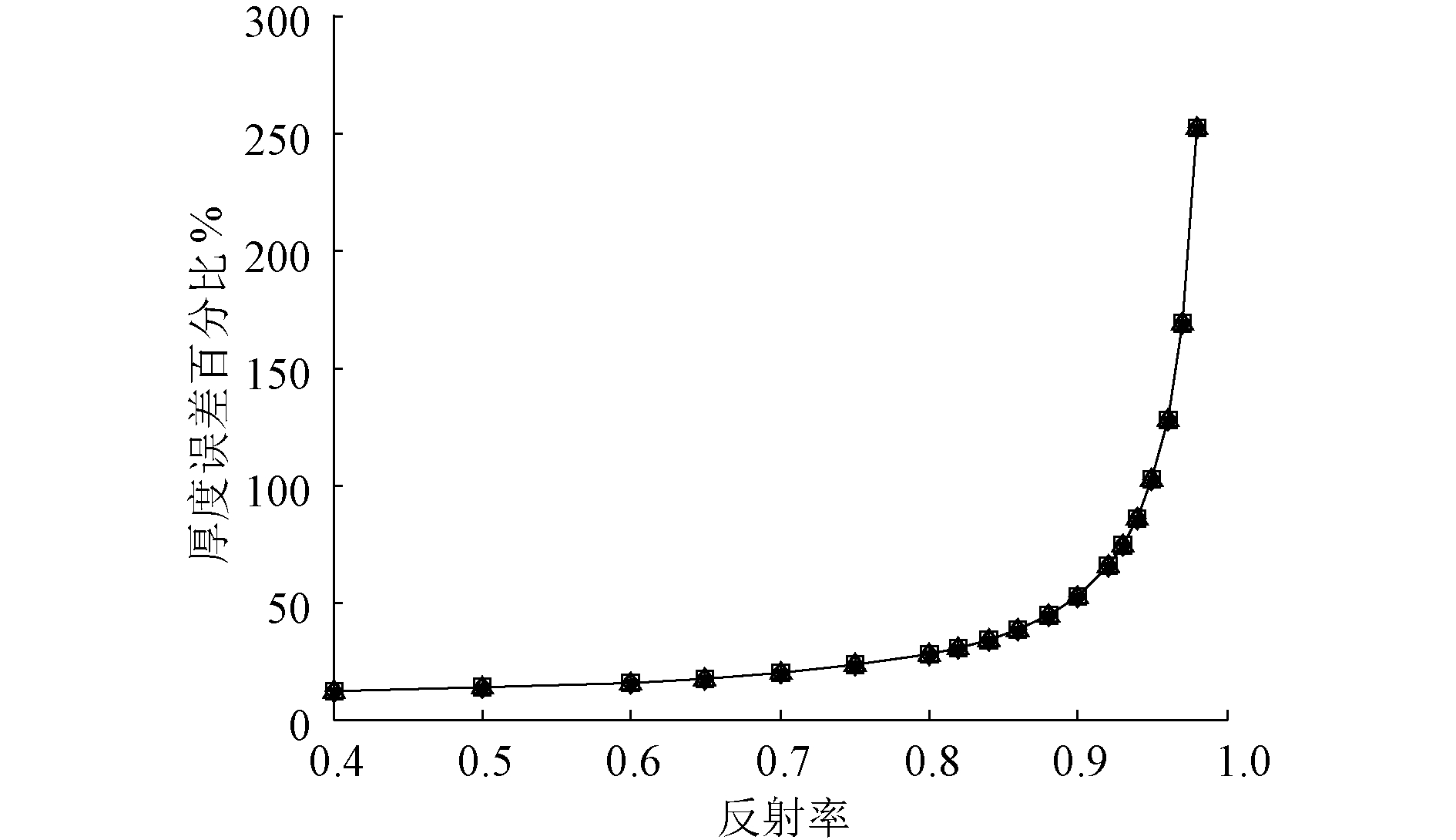
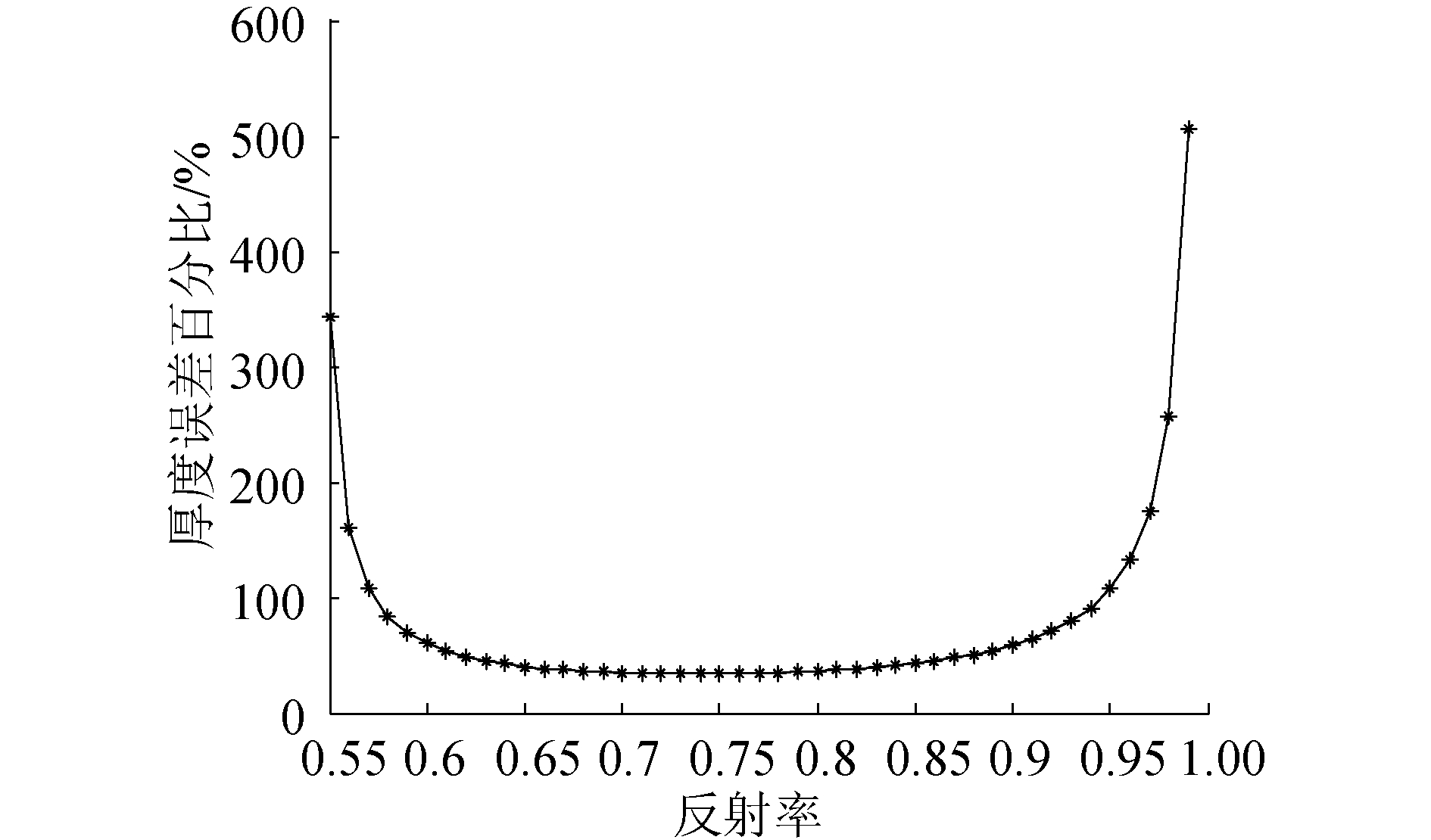
并取ΔR=0.1R。不锈钢-油-不锈钢3层介质结构的相对误差曲线如图 7所示。不锈钢-油-铝3层介质结构的相对误差曲线如图 8所示。此2图可以清楚看出上面误差规律。
|
Download:
|
| 图 7 不锈钢-油-不锈钢3层介质的超声波反射率相对误差影响曲线 Fig. 7 Relative reflection coefficient error of the ultrasound transmitting on stainless-steel-oil-stainless-steel medium | |
|
Download:
|
| 图 8 不锈钢-油-铝3层介质的超声波反射率误差相对影响曲线 Fig. 8 Relative reflection coefficient error of the ultrasound transmitting on stainless-steel-oil-aluminum medium | |
因此,当采用等效弹簧模型计算油膜厚度时,为保证测量精度,宜取:
| $ 1.1\left( {\frac{{{Z_2} - {Z_1}}}{{{Z_2} + {Z_1}}}} \right) < R\left( f \right) < 0.95 $ | (11) |
如果R(f)→1或者
采用谐振模型或者等效弹簧刚度模型在计算油膜厚度时,需要用到滑油的密度和声速等数据,而这些数据与温度和压强有关,因此温度和压力对测量精度至关重要。Chorazewski等[16]试验研究了温度从0 ℃到150 ℃,压强从标准大气压到200 MPa的范围内,ISO 4113标准试验油的体积、体积弹性模量、压缩性系数、粘度和比热容等各项物理性质。利用其试验结果,进行数据处理得到下面ISO 4113标准试验油的密度和声速曲线,分别如图 9和10所示。

|
Download:
|
| 图 9 ISO 4113标准试验油的温度、压强和密度关系曲线 Fig. 9 Relationship between temperature, pressure and density of ISO 4113 oil | |

|
Download:
|
| 图 10 ISO 4113标准试验油的温度、压强和声速关系曲线 Fig. 10 Relationship between temperature, pressure and acoustic velocity of ISO 4113 oil | |
通过曲面拟合,可以得到ISO 4113标准试验油的温度、压强和密度的关系函数如下:
| $ \begin{array}{l} \rho = \left[ {835.798 - 1.473\;43T + 3.92P - 0.007{P^2} - } \right.\\ \;\;\;\;\;\;\left. {1 \times {{10}^{ - 6}}{P^2}} \right]/\left[ {1 - 0.000\;866T - 8.5 \times {{10}^{ - 7}}{T^2} + } \right.\\ \;\;\;\;\;\;\left. {0.004\;01P - 8.4 \times {{10}^{ - 6}}{P^2}} \right] \end{array} $ | (12) |
式中:T单位是°;P的单位是Pa。
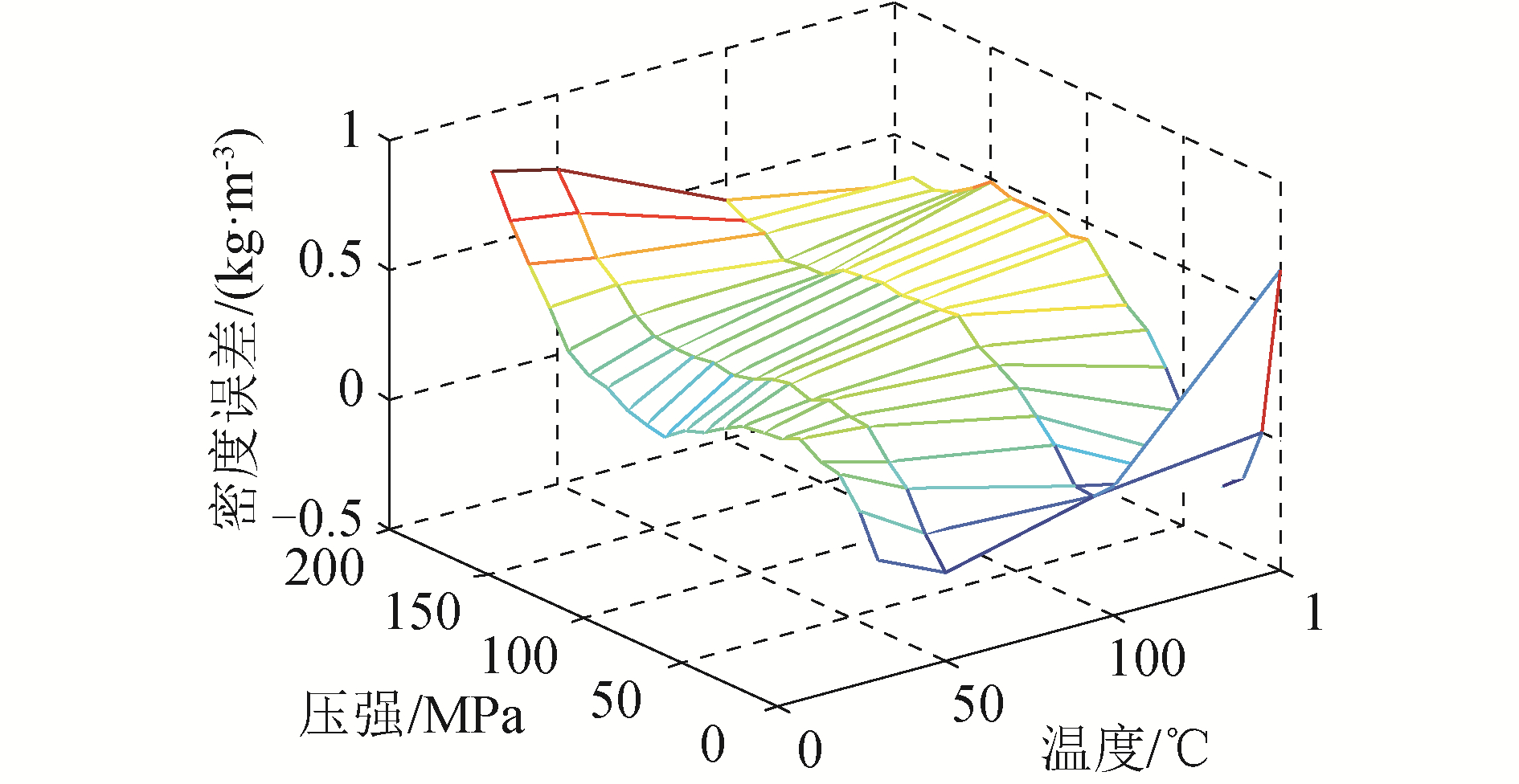
式(12)的拟合最大误差点在30 ℃,200 MPa处,误差为0.774 kg/m3,最大相对误差0.008 66%。式(12)拟合数据和试验数据的均方差为0.289 8 kg/m3。图 11显示了拟合密度和试验数据的误差。
|
Download:
|
| 图 11 拟合ISO 4113标准试验油密度和试验数据的误差 Fig. 11 Density error between experimental data and fitting data of ISO 4113 oil | |
通过曲面拟合还可以得到ISO 4113标准试验油的温度、压强和声速的关系函数如下:
| $ \begin{array}{l} c = \left[ {1\;501.164 - 2.9T + 13.65P - 0.009\;17{P^2} - } \right.\\ \;\;\;\;\;\left. {4 \times {{10}^{ - 5}}{P^2}} \right]/\left[ {1 + 0.001\;41T - 3.8 \times {{10}^{ - 6}}{T^2} + } \right.\\ \;\;\;\;\;\left. {0.006P - 1.4 \times {{10}^{ - 5}}{P^2}} \right] \end{array} $ | (13) |
式中:T单位℃;P单位Pa。
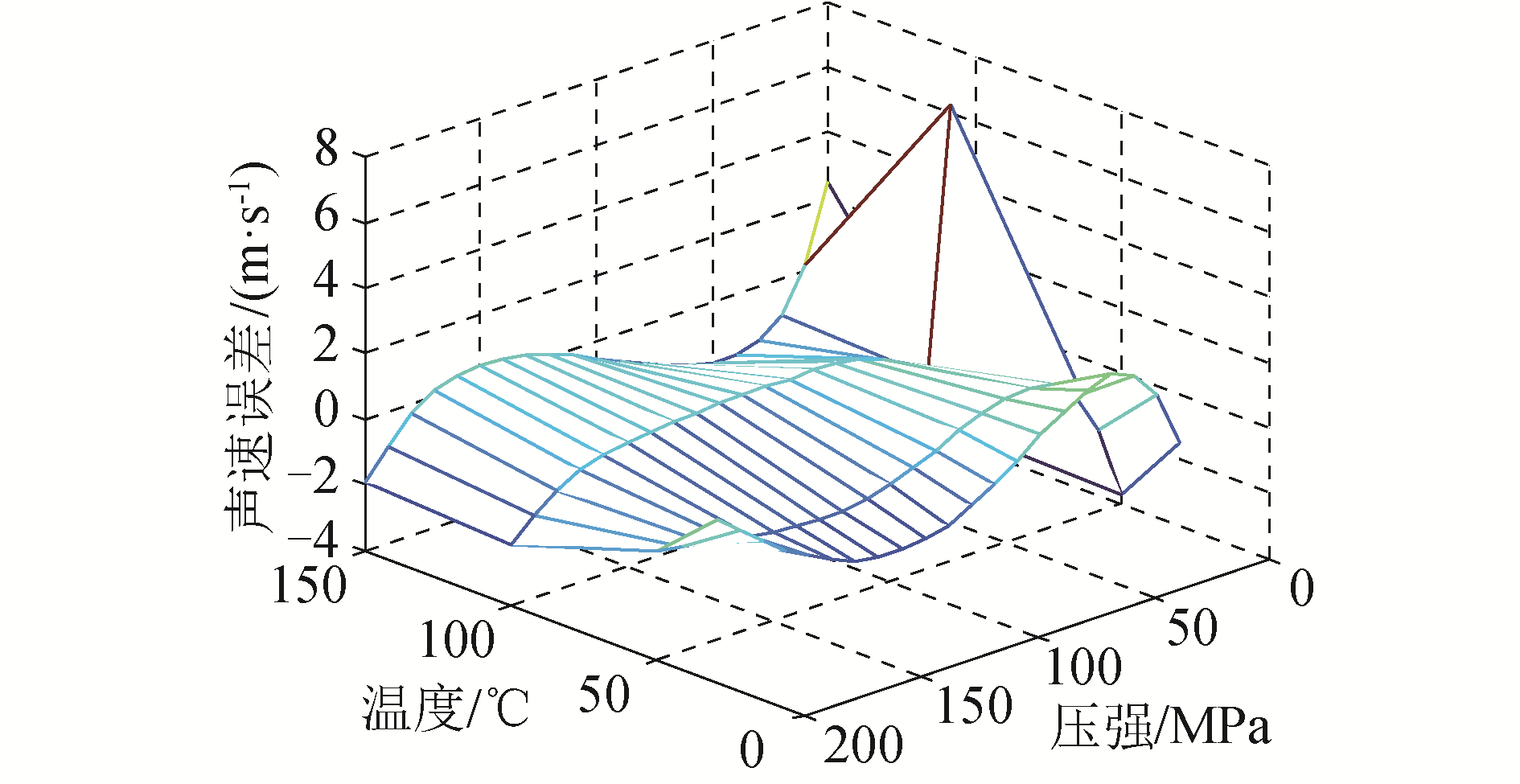
式(13)的拟合最大误差点在100 ℃,10 MPa处,误差为6.761 8 m/s,最大相对误差0.59%。式(13)拟合数据和试验数据的均方差为0.936 3 m/s。图 12显示了拟合声速和试验数据的误差。
|
Download:
|
| 图 12 拟合ISO 4113标准试验油声速和试验数据的误差 Fig. 12 Acoustic velocity error between experimental data and fitting data of ISO 4113 oil | |
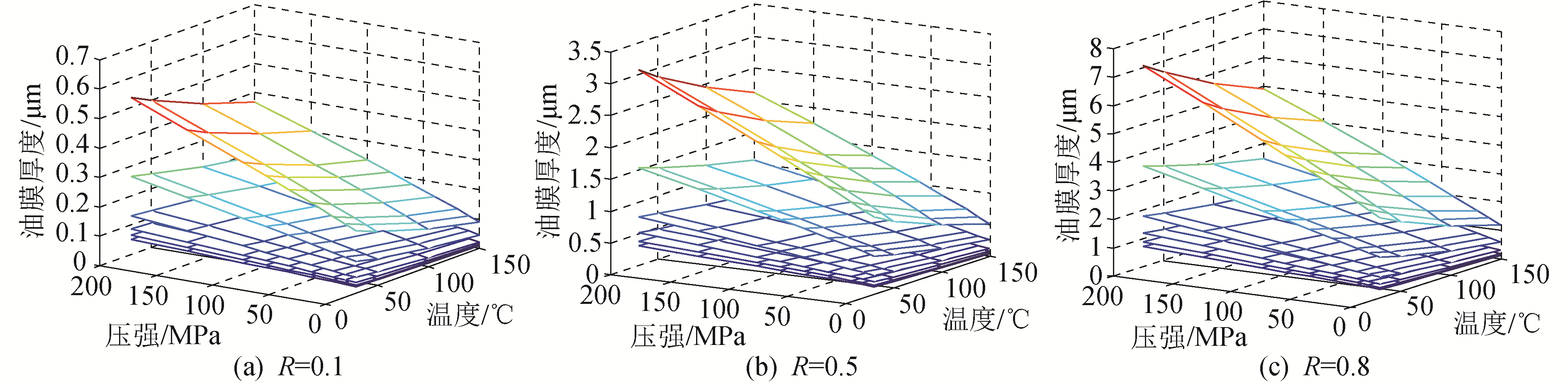
如果取不锈钢-油-不锈钢3层介质结构,并且不考虑温度压强对金属的物理特性影响,仅考虑温度压强对油膜的影响。采用谐振模型理论时,按照式(2),可知温度压强对油膜厚度计算结果的影响和图 10基本一致。采用等效弹簧模型时,利用ISO 4113标准试验油在不同温度和压强下的密度和声速数据,得到温度和压强对油膜厚度的计算结果影响如图 13所示。
|
Download:
|
| 图 13 温度和压力对不锈钢-油-不锈钢3层介质的超声波测量油膜厚度的影响 Fig. 13 The effect of temperature and pressure on the measuring thickness of oil film with an ultrasound transmitting on stainless-steel-oil-stainless-steel medium | |
图 13分别表示不同反射率下温度和压强对计算结果的影响。首先,图 13显示,当反射率小时,温度和压强对计算结果的绝对影响也小,而反射率大时,温度和压强对计算结果的绝对影响也大;其次,温度对结果的影响远小于压强对结果的影响。
图 13的子图各有5条曲线,从上到下分别是超声波频率为5、10、20、30和40 MHz时的计算结果。从图 13可以得到,随着温度的升高,油膜厚度计算值减少;随着压强的提高,油膜厚度计算值增加;超声波频率越低,温度和压强的绝对影响越大。
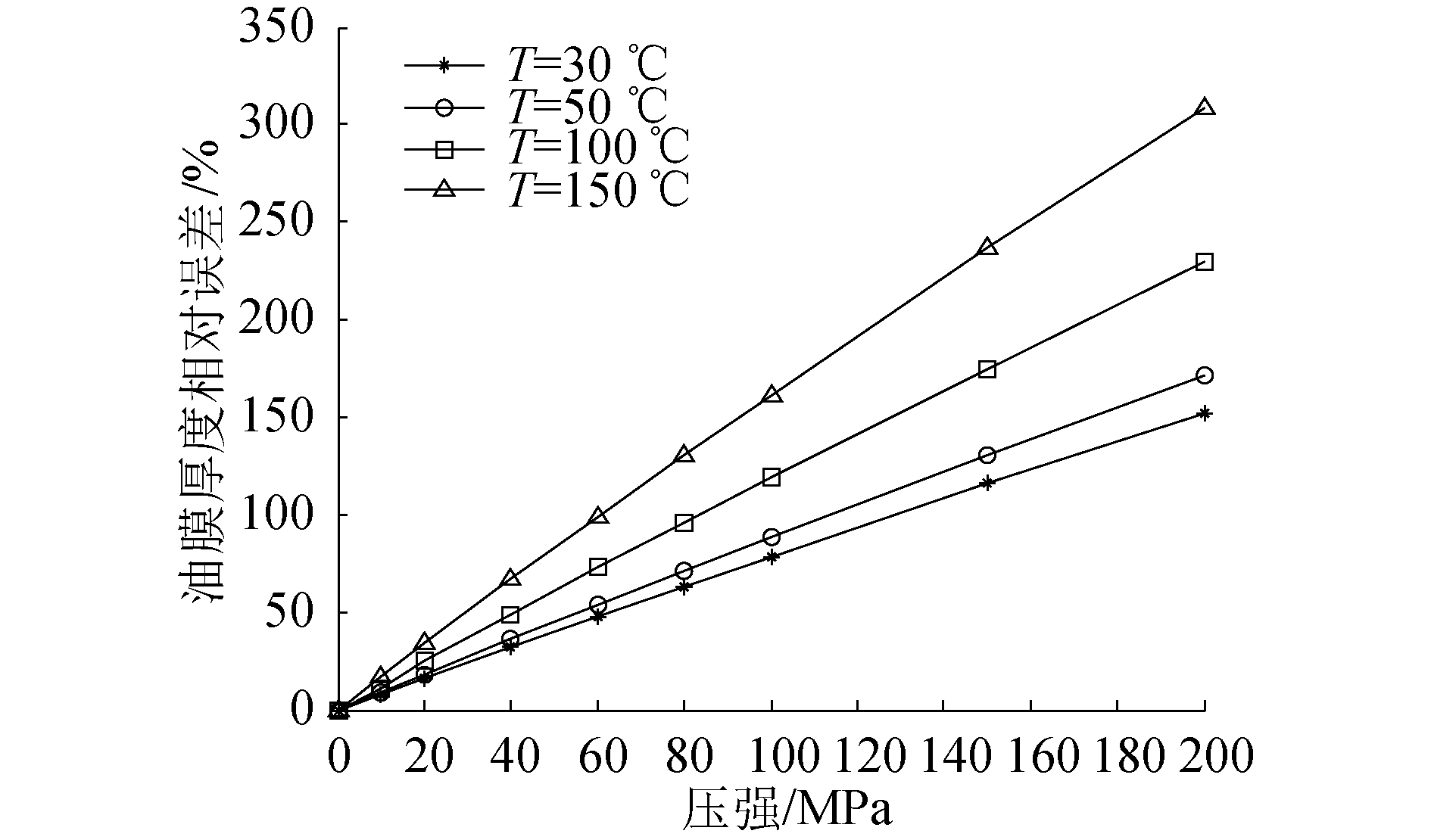
如果分别以30、50、100和150 ℃,以及标准大气压为基准,研究压强对计算结果的相对误差,可得图 14。结果显示温度和压力越大,相对误差越大。但反射率和超声波频率对相对误差没有影响。
|
Download:
|
| 图 14 温度和压强对不锈钢-油-不锈钢3层介质的超声波测量油膜厚度的相对误差影响 Fig. 14 The relative error effect of temperature and pressure on the measuring thickness of oil film with an ultrasound transmitting on stainless-steel-oil-stainless-steel medium | |
1) 由于现有超声波换能器的制造频率限制,谐振模型一般只适于10~200 μm的油膜厚度测量,测量的油膜厚度越小,要求换能器频率越高;等效弹簧模型一般适于小于10 μm油膜厚度测量,测量的油膜厚度越小,要求换能器频率越高;对于某一超声波频率,只能测量一定范围内油膜厚度。
2) 采用等效弹簧模型时,随着反射率的增加,计算得到的油膜厚度误差变大,当反射率接近1时,误差无限大;油膜两侧的介质不同时,反射率接近最小值Rmin,计算误差增大;同时,超声波频率越高,误差越小;为了保证测量精度,反射率宜取[1.1Rmin,0.95]内。在相同反射率下,油膜两侧的介质不同时的计算误差大于介质相同时。
3) 相对于温度,压强对测量值有较大影响。随着温度的升高,油膜厚度值减少;随着压强的提高,油膜厚度计算值增加;超声波频率越低,温度和压强的绝对影响越大;反射率越小,油膜厚度计算值越小。因此,在高温高压下,需要考虑声阻特性的影响。
本研究没有考虑温度和压强对金属的影响,温度和压强对金属的声速会有较大影响,因此在后续需要开展研究分析。
| [1] |
TING L L. Development of a laser fluorescence technique for measuring piston ring oil film thickness[J]. Journal of tribology, 1980, 102(2): 165-170. (  0) 0)
|
| [2] |
PARKS Ⅱ J E, ARMFIELD J S, BARBER T E, et al. In situ measurement of fuel in the cylinder wall oil film of a combustion engine by LIF spectroscopy[J]. Applied spectroscopy, 1998, 52(1): 112-118. DOI:10.1366/0003702981942410 (  0) 0)
|
| [3] |
TATTERSALL H G. The ultrasonic pulse-echo technique as applied to adhesion testing[J]. Journal of physics D:applied physics, 2002, 6(7): 819-832. (  0) 0)
|
| [4] |
PARK J R, LEE S K. Liquid film thickness measurement by an ultrasonic pulse echo method[J]. Nuclear engineering and technology, 1985, 17(1): 25-33. (  0) 0)
|
| [5] |
DWYER-JOYCE R S, DRINKWATER B W, DONOHOE C J. The measurement of lubricant-film thickness using ultrasound[J]. Proceedings of the royal society A, 2003, 459(2032): 957-976. DOI:10.1098/rspa.2002.1018 (  0) 0)
|
| [6] |
ZHANG Jie, DRINKWATER B W, DWYER-JOYCE R S. Calibration of the ultrasonic lubricant-film thickness measurement technique[J]. Measurement science and echnology, 2005, 16(9): 1784-1791. DOI:10.1088/0957-0233/16/9/010 (  0) 0)
|
| [7] |
ZHANG Jie, DRINKWATER B W. Thin oil-film thickness distribution measurement using ultrasonic arrays[J]. NDT & E international, 2008, 41(8): 596-601. (  0) 0)
|
| [8] |
HUNTER A J, DRINKWATER B W, WILCOX P D. Autofocusing ultrasonic imagery for non-destructive testing and evaluation of specimens with complicated geometries[J]. NDT & E international, 2010, 43(2): 78-85. (  0) 0)
|
| [9] |
GASNI, D, WAN IBRAHIM, M K, DWYER-JOYCE, R S. Measurement of lubricant film thickness in the Iso-Viscous elastohydrodynamic regime[J]. Tribology international, 2011, 44(7-8): 933-944. DOI:10.1016/j.triboint.2011.03.010 (  0) 0)
|
| [10] |
DWYER-JOYCE R S, REDDYHOFF T, ZHU J. Ultrasonic measurement for film thickness and solid contact in elastohydrodynamic lubrication[J]. Journal of tribology, 2011, 133(3): 031501. DOI:10.1115/1.4004105 (  0) 0)
|
| [11] |
张锐, 万明习, 陈晓, 等. 超薄弹性层超声反射纵波频域定征方法[J]. 仪器仪表学报, 2001, 22(4): 376-379. ZHANG Rui, WAN Mingxi, CHEN Xiao, et al. Characterization of the ultra-thin elastic layer by ultrasonic longitudinal reflection wave in the frequency domain[J]. Chinese journal of scientific instrument, 2001, 22(4): 376-379. DOI:10.3321/j.issn:0254-3087.2001.04.012 (  0) 0)
|
| [12] |
卢黎明. 基于超声波的液体滑动轴承润滑油厚度的测定[J]. 润滑与密封, 2007, 32(5): 165-168. LU Liming. The measurement of shaft locus of liquid sliding bearing[J]. Lubrication engineering, 2007, 32(5): 165-168. DOI:10.3969/j.issn.0254-0150.2007.05.049 (  0) 0)
|
| [13] |
焦敬品, 张强, 吴斌, 等. 机械结构流体层厚度超声测量方法理论研究[J]. 声学技术, 2009, 28(3): 240-244. JIAO Jingpin, ZHANG Qiang, WU Bin, et al. Theoretical research on thickness measurement of fluid layer in mechanical structure by using ultrasonic technique[J]. Technical acoustics, 2009, 28(3): 240-244. DOI:10.3969/j.issn1000-3630.2009.03.009 (  0) 0)
|
| [14] |
唐伟坤, 马希直. 利用反射系数测量油膜厚度的研究[J]. 润滑与密封, 2010, 35(12): 44-47. TANG Weikun, MA Xizhi. The research on measuring oil film thickness by reflection coefficients[J]. Lubrication engineering, 2010, 35(12): 44-47. DOI:10.3969/j.issn.0254-0150.2010.12.010 (  0) 0)
|
| [15] |
申洪苗, 马希直. 薄油膜厚度分布超声测量机制研究[J]. 润滑与密封, 2013, 38(5): 46-50. SHEN Hongmiao, MA Xizhi. Research on the mechanism for ultrasonic measurement of thin oil-film thickness distribution[J]. Lubrication engineering, 2013, 38(5): 46-50. (  0) 0)
|
| [16] |
CHORAZEWSKI M, DERGAL F, SAWAYA T, et al. Thermophysical properties of normafluid (ISO 4113) over wide pressure and temperature ranges[J]. Fuel, 2013, 105: 440-450. DOI:10.1016/j.fuel.2012.05.059 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


