水下航行器是人类探索和开发海洋的重要装备之一,随着科技发展和海洋开发步伐的加快,人们对于包括续航力、航速等在内的水下航行器性能提出了更高的要求。良好的水动力外形可使水下航行器在航行过程中产生较小的阻力,使其具有更大的续航力和更高的航速。可见,外形的设计是水下航行设计的重要内容,是提高其综合性能的重要途径之一。多年来,水下航行器的外形优化已受到众多学者的关注[1-3]。杨卓懿等[4]根据系列回转体数值计算结果,建立了潜水器阻力近似模型,采用模型试验进行了验证,实现了艇型能源一体化设计,为潜水器设计提供了参考。罗蔚林等[5]基于iSIGHT软件,利用协同优化方法,构建了自动化集成设计平台,确定了水下航行器壳体流线形式。庞永杰等[6]应用CFD数值方法以二维模型代替三维模型,提出一种近壁面y+函数模型,最后对比了多岛遗传算法和粒子群法的优劣,使计算效率得到了明显的提高。
然而,水下航行器在设计、制造和使用等阶段存在的随机性和不确定因素是不可避免的,这些因素必然导致设计结果与实际产生偏离,从而对其性能产生不利影响。针对水下航行器水动力、结构设计中的不确定性,人们已开展了研究。刘方[7]以Petrel Ⅱ样机为例,建立了考虑安装阶段螺旋桨偏角不确定性情况下的运动和动力学模型,分析了艇体长度和直径不确定性等对航行轨迹影响。刘峰等[8]针对耐压壳体进行了极限载荷灵敏度分析,利用第二代非支配排序遗传算法进行优化求解,对比了不同稳健性要求下的优化结果。
本文以某型水下航行器外形为研究对象,基于二次开发的Java文件驱动STAR-CCM+,实现了水下航行器直航阻力的参数化分析,获得了定水深、高雷诺数条件下水下航行器直航阻力的计算结果,拟合得到相应的近似模型。通过对NSGA-Ⅲ算法和稳健性方法的研究,建立了考虑不确定性因素的水下航行器外形多目标优化模型,进行了稳健性优化求解,并与确定性优化结果进行了比较。
1 外形参数化建模及直航阻力计算 1.1 水下航行器外形及设计参数回转体可通过数学表达式进行表达,具有便于分析计算、适用性广等优点[9],已成为大多数水下航行器的外形形式。本文所研究的水下航行器外形设计为鱼雷型回转体[10],设计工作水深400 m,目标航速30 m/s。将其外形进行适当简化,见图 1。图 1中,设置3个设计变量分别为艇体半径Lr、平行中体长度Lm和艉部去流段长度Lt。设计变量的可行域范围列于表 1。

|
Download:
|
| 图 1 水下航行器外形 Fig. 1 Shape of autonomous underwater vehicle | |
| 表 1 设计变量可行域范围 Tab.1 Feasible region of design variables |
外形优化目标是艇体直航阻力Fx最小,且Fx应小于18 000 N;同时为增加航行器能源等设备的空间,艇身包络体积V应尽量最大。因此,确定Fx、V为外形设计的优化目标。
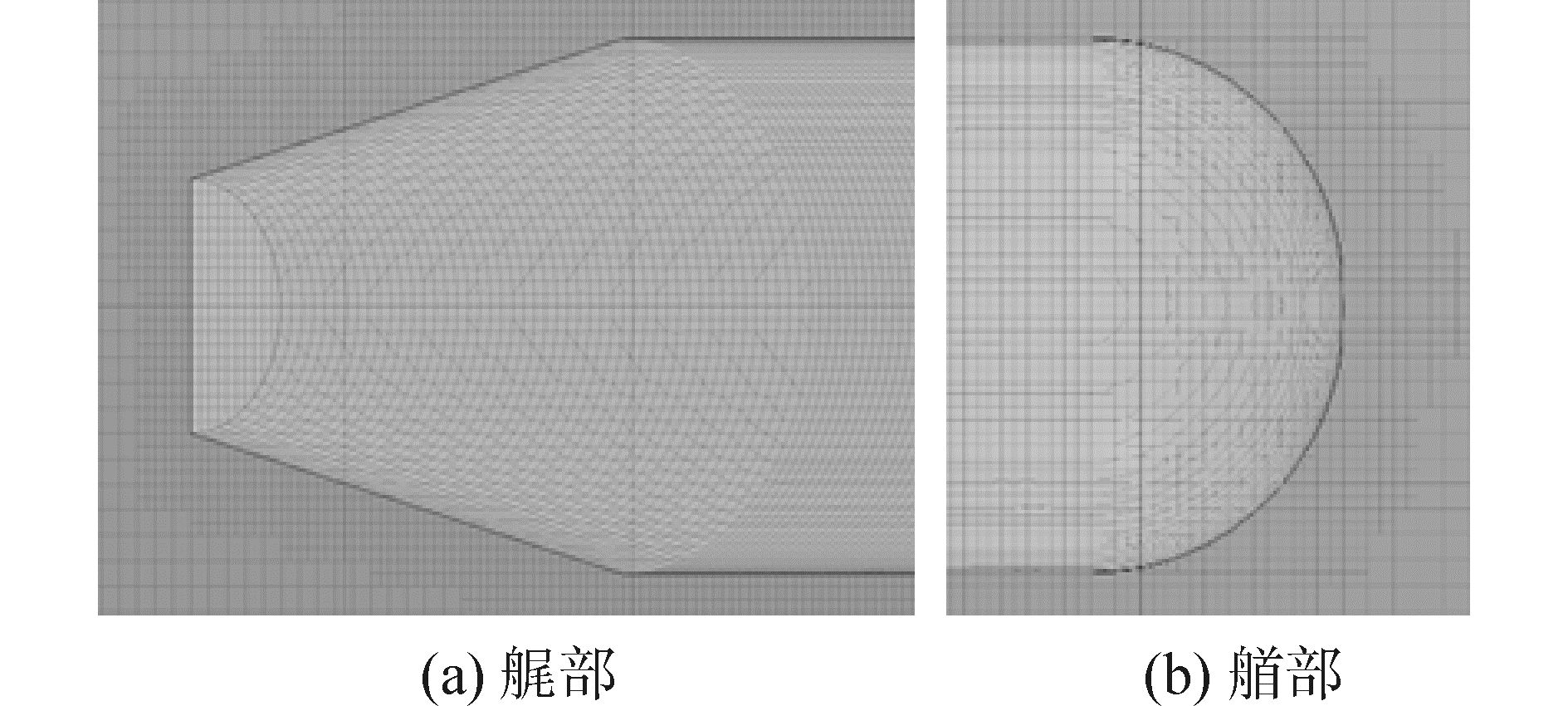
1.2 基于参数化的外形阻力计算利用STAR-CCM+软件对于水下航行器直航阻力进行计算,将物理条件与网格条件分离,以实现参数驱动,网格仅用来定义拓扑结构,而不参与区域之间的信息传递,可使网格加密的选择更为自由。以模型末端横剖面中心点为原点,设计模型处于前20 m,后20 m,上下各5 m,侧方5 m的长方体计算域内。计算域内设置前、侧、上、下平面均为速度进口,模型中纵剖面所在平面为对称平面,计算域后平面为压力出口。艉部和艏部网格划分见图 2,计算域与加密域尺度设置见表 2。
|
Download:
|
| 图 2 艉部和艏部网格 Fig. 2 Grid of stern and stem | |
| 表 2 计算域与加密域尺度设置 Tab.2 Dimension of calculate region |
利用RANS方法(雷诺时均化的N-S方法)求解不可压缩流体。其方程如下
| $ \begin{array}{l} \frac{{\partial (\rho {u_i})}}{{\partial t}} + \frac{\partial }{{{x_j}}}(\rho {u_i}{u_j}) = \frac{{-\partial p}}{{\partial {x_i}}} + \\ \frac{\partial }{{{x_j}}}\left( {\mu \frac{{\partial {u_i}}}{{\partial {x_j}}}-\rho u{\prime _i}u{\prime _j}} \right) + {S_i}\;\;\;\;\;i, j = 1, 2, 3 \end{array} $ | (1) |
式中:t为流场中计算时间, ρ为流体密度, ui为i方向速度, uj为j方向速度, xi为i方向坐标, xj为j方向坐, μ为湍动黏度, p为压力, u′i为i方向脉动速度, u′j为j方向脉动速度, Si为源项。
选择标准k-ε模型作为湍流模型,湍动能k、湍动耗散率ε分别定义为
| $ \begin{array}{l} k = \frac{{\overline {u{\prime _i}u{\prime _j}} }}{2} = \frac{1}{2}(\overline {u{\prime _i}^2} + \overline {u{\prime _j}^2} + \overline {u{\prime _k}^2} )\\ \;\;\;\;\;\;\varepsilon = \frac{\mu }{\rho }\overline {\left( {\frac{{\partial u{\prime _i}}}{{\partial {x_k}}}} \right)\left( {\frac{{\partial u{\prime _i}}}{{\partial {x_k}}}} \right)} \end{array} $ | (2) |
式中:uk为k方向速度, xk为k方向坐标。
此时与之相对应的输运方程为[12]
| $ \begin{array}{l} \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial (\rho k{u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[{\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + \\ \;\;\;\;\;\;{G_k} + {G_b} - \rho \varepsilon - {Y_M} + {S_k}\\ \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial (\rho \varepsilon {u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[{\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \\ \;\;\;\;{C_{1\varepsilon }}\frac{\varepsilon }{k}({G_k} + {C_{3\varepsilon }}{G_b}) -{C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} + {S_\varepsilon } \end{array} $ | (3) |
式中:Gk、Gb为湍动能k的产生项,分别由平均速度梯度Gb浮力引起;YM为代表可压湍流中脉动扩张的贡献;σk、σε为Prandtl数,分别与湍动能k和耗散率ε对应;C1ε、C2ε、C3ε为经验常数;Sk、Sε是用户定义的源项。
由STAR-CCM+软件计算得到初始设计模型半模航行阻力为6 873.02 N,由对称性原则可得设计水下航行器整体阻力Fx为13 746.04 N。与文献[10]相比,相同外形参数、同等初始条件下,本文计算值与其误差在5.2%,说明计算结果具有一定准确性。
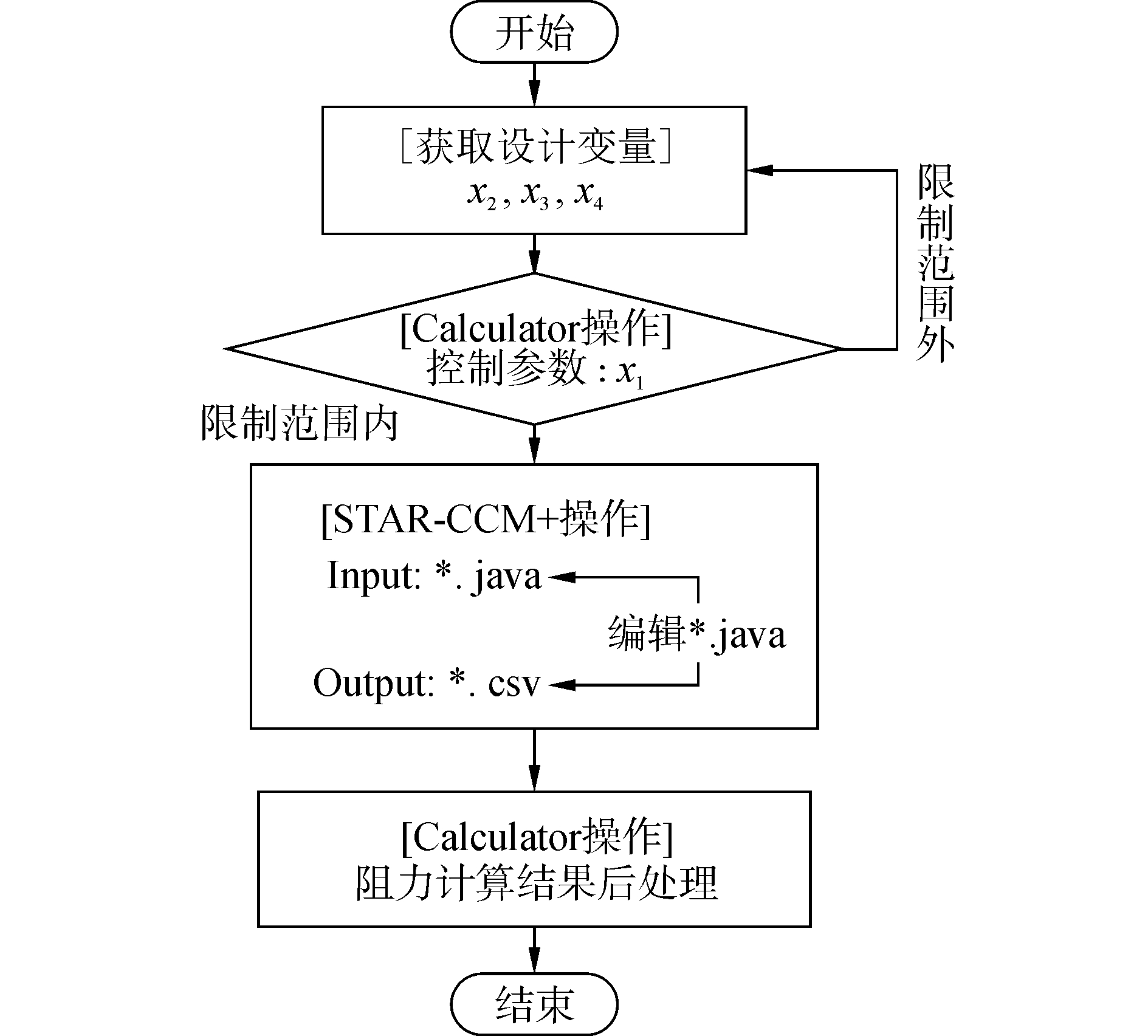
在外形优化设计中,需要对众多方案进行计算和选择,普通建模方法需要反复建模,存在计算效率低、建模精度可能不高等缺陷。参数化建模通过建立图形约束和几何关系与参数尺寸的对应关系,由尺寸参数值的变化直接控制实体模型的变化[12]。在STAR-CCM+软件运行过程中,通过对*.java文件中代码的二次开发实现参数化模型建立、计算域生成、边界条件与物理条件设置、网格划分、求解器与迭代停止标准的设置、计算分析、数据读取和寻优输出,进一步通过iSIGHT多学科优化软件调用批处理文件*.bat进行批量操作。参数化分析流程见图 3。
|
Download:
|
| 图 3 参数化分析流程 Fig. 3 Flow chart of parametric analysis process | |
最优拉丁超立方法(optimal Latin hypercube method, Opt LHD)是一种基于贝叶斯和频率理论的试验设计方法,其通过重新构造和改进了拉丁矩阵中的构建列相关系数矩阵Tij和改进列相关系数ρmax[13],使所有试验点尽量均匀的分布在设计空间,具有非常好的空间填充性和均衡性。本文采用Opt LHD进行试验设计样本点的采样。
2.2 响应面模型响应面模型(response surface method,RSM)将试验设计与数理统计学分析相结合,是一种构建设计变量与相应之间映射关系的方法[14]。其本质是进行多项式求解,具有透明性高、简单、高效等优点。按照阶数RSM可分为一阶、二阶、三阶和四阶。其中,四阶RSM的表达式为
| $ \begin{array}{l} \hat F(x) = a_0 + \sum\limits_{i = 1}^N {{b_i}{x_i}} + \sum\limits_{i = 1}^N {{c_{ii}}x_i^2} + \sum\limits_{i = 1}^N {{d_i}x_i^3} + \\ \;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^N {{e_i}x_i^4} + \sum\limits_{1 \le i \le j \le N}^N {{f_{ij}}{x_i}{x_j}} \end{array} $ | (4) |
式中:
四阶响应面的初始化过程不考虑二阶以上交叉项,至少需要[(M+1)(M+2)]/(2+2M)个样本点,M为因子个数,即至少需要16组样本点。综合考虑计算效率和优化过程可行性限制,每个因子在设计空间内均分为81份,即81个水平,每个水平位置采用0~2次,最终得到81组试验方案,得到的试验设计响应值如表 3所示。
| 表 3 阻力试验设计响应值 Tab.3 Response value of AUV drag |
对于图 4的样本点进行参数化分析,采用四阶响应面模型进行拟合,得到的设计变量与阻力值Fx的四阶响应面近似模型为
| $ \begin{array}{l} {F_x} = 5\;685\;942-575{L_m}-80\;603\;801{L_r}-\\ 416\;473{L_t} + 979L_m^2 + 432\;955\;832L_r^2 + \\ \;1\;043\;632L_t^2 + 2\;276{L_m}{L_r} + 773{L_m}{L_t} - \\ \;115\;226{L_r}{L_t} - 214L_m^3 - 1\;031\;474\;381L_r^3 - \\ \;1\;078\;519L_t^3 + 14L_m^4 + 920\;889\;566L_r^4 + 414\;974L_t^4 \end{array} $ | (5) |

|
Download:
|
| 图 4 最优拉丁超立方法选点 Fig. 4 Distribution of Opt-LHD sample points | |
艇身包络体体积V为
| $ \begin{array}{l} V = 2.094\;304\;835\;9L_r^3 + 3.141\;592\;653\;8L_r^2{L_m} + \\ 1.047\;197\;551{L_t}(0.015\;625 + L_r^2 + 0.125{L_r}) \end{array} $ | (6) |
衡量近似模型拟合精度的方法有多种,其中可以表征变量与相应线性相关关系的复相关系数法最为常用。复相关系数法的R2值表示为
| $ {R^2} = 1- \left[{\sum\limits_{i = 1}^n {{{({y_i}-{{\hat y}_i})}^2}} \sum\limits_{i = 1}^n {{{({y_i}-{{\bar y}_i})}^2}} } \right] $ | (7) |
式中:n为样本数, yi为真实响应,
R2是介于0~1实数,越接近1说明拟合效果越好,工程上要求其数值在0.9以上即可初步满足拟合要求。根据响应面模型,选择评估校核的验证样本为20组,其阻力值R2为0.969 32,满足工程需要。
3 多目标确定性优化 3.1 NSGA-Ⅲ算法多目标优化的实质是采用优化算法进行求解,求解得到的结果为Pareto解集。NSGA-Ⅲ是Kalyanmoy等[15]提出的新一代非支配遗传算法,其主体运算框架与NSGA-Ⅱ基本一致。NSGA-Ⅲ在小生境技术中引入参考点代替拥挤度进行种群在pt+1=∪i=1l-1Fi,St=∪i=1lF,且St>N,其中pt+1个体已经被选中;Fi为第i非支配层级;N为种群总数;条件下的子代选择。具体选择方法:对于M个优化目标问题,利用式(8)选取份数为p,计算参考点个数H使其与种群数量N大体一致,应用系统方法确定点在标准超平面上位置[15]。
| $ H = \left( {\begin{array}{*{20}{c}} {M - p{\rm{ }} + {\rm{ }}1}\\ p \end{array}} \right)$ | (8) |
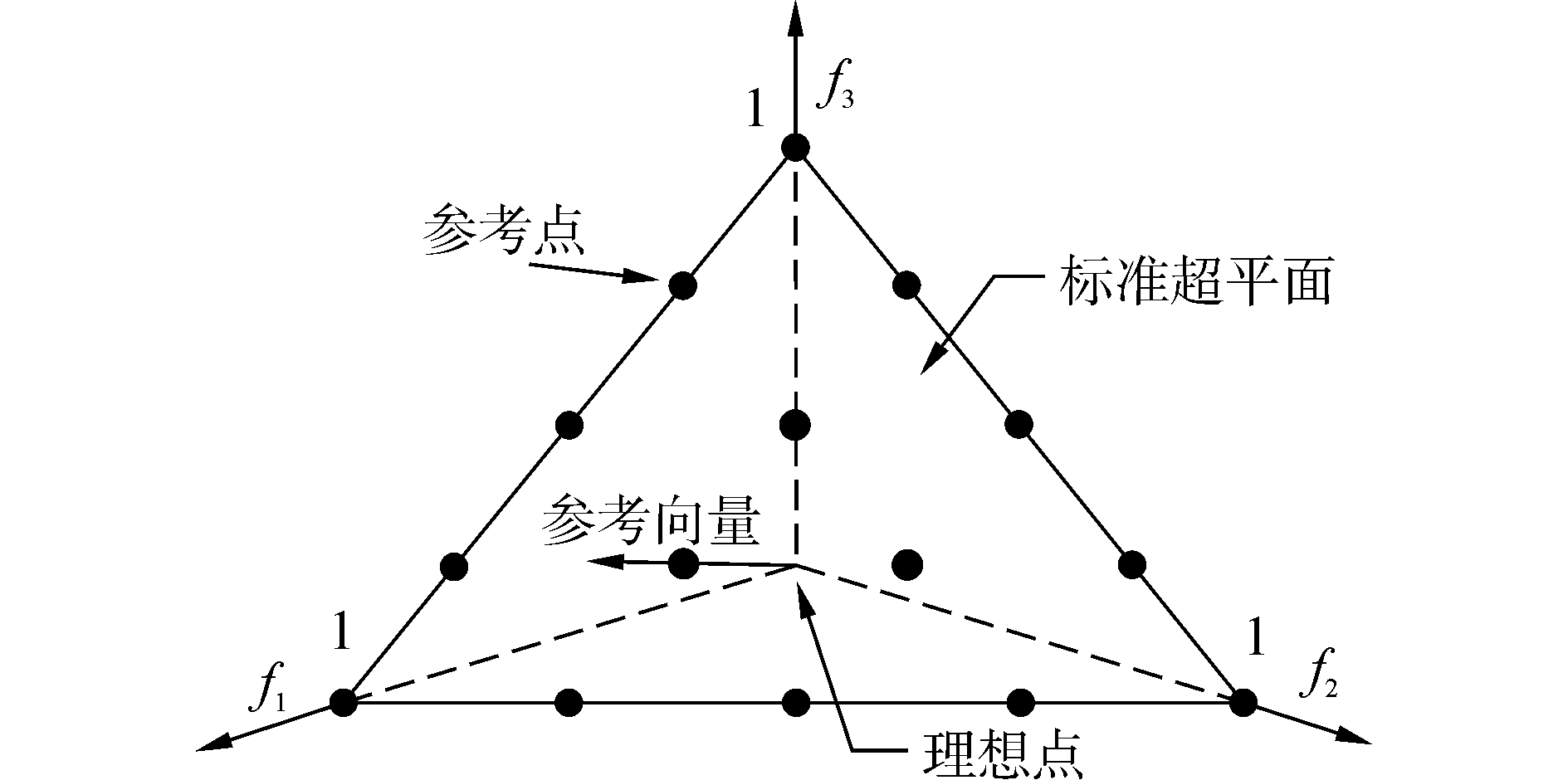
图 5为p=4时三维空间中参考点选取图。再通过ASF函数对参考点与坐标原点构成的参考向量进行标准化和归一化[16]:
| $ {\rm{ASF}}\left( {X, W} \right) = {\rm{MA}}{{\rm{X}}_{i = 1:m}}\frac{{f{\prime _i}\left( x \right)}}{{{W_i}}}, f_i^n\left( x \right) = \frac{{f{\prime _i}\left( x \right)}}{{{a_i}}} $ | (9) |
|
Download:
|
| 图 5 参考点选择示意图 Fig. 5 Schematic diagram of reference points selecting | |
最后根据支配层中个体与参考向量的距离关系将其与各参考点关联,记参考点在pt+1中关联个体个数pj。pj=0时在Fi中搜寻该参考点关联个体,若有则从中选择距离最小个体移入pt+1,反之则删除该参考点。

|
Download:
|
| 图 6 参考点关联个体示意图 Fig. 6 Schematic diagram of reference points correlate individuals | |
pj>0时选择距离最小个体进入pt+1,相比于上一代算法,NSGA-Ⅲ算法在选择子代时对标准超平面进行了有效分割的方法,代替了上一代算法中基于排挤机制的小生境技术,使子代更加均匀地分布在可能的寻优可行域空间内,提升了子代样本的多样性,并防止早熟。因此,更加适应于求解优化目标较多的多目标优化问题。
3.2 水下航行器外形多目标优化求解多目标优化问题可表述为
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{min}}:{{\{ {f_1}\left( x \right), {f_2}\left( x \right), \ldots {f_k}\left( x \right)\} }^{\rm{T}}}}\\ {{\rm{s}}.{\rm{t}}.}\\ {{g_j}\left( x \right) \le 0, j = 1, 2, \ldots, J}\\ {{x_L} \le x \le {x_U}} \end{array}} \right. $ | (10) |
式中:f1(x)、f2(x)、…、fk(x)是k组目标函数,gj(x)是第j个约束条件,J为总约束个数,xL、xU分别为设计变量上下约束边界。
根据水下航行器外形设计参数、所得到的近似模型等,建立的外形多目标优化模型为
| $ \left\{ \begin{array}{l} {\rm{min}}:{F_x};{\rm{max}}:V\\ {\rm{s}}.{\rm{t}}.\\ {F_x} \le 18\;000\\ {\rm{D}}.{\rm{v}}:{L_r};{L_m};{L_t} \end{array} \right. $ | (11) |
设置种群数量为60,进化代数为80,交叉概率为0.9,交叉分布指数为10,变异分布指数为20。得到的Pareto解集见图 7。

|
Download:
|
| 图 7 艇体阻力与设计变量Pareto解集 Fig. 7 Pareto solution set of hull resistance and design variable | |
图 7结合式(6)分析可以看出,在艇体阻力尽量最小前提下,若增加艇身包络体艇体体积,应首先同时增加艉部去流段Lt和艇体半径Lr,且去流段长度Lm增速应大于艇体半径增加速度,使艉部长度首先达到可行域上限,然后继续增加艇体半径长度,最后增大平行中体长度到最大尺寸。
4 多目标稳健性优化方法 4.1 稳健性优化尽管确定性优化已经得到了广泛应用,但在考虑设计变量的摄动和环境噪音影响时,其有效性和可靠性可能大幅度下降,甚至不可信[17]。稳健性优化又称鲁棒性设计,其是在追求优化目标平均效能的基础上,将其概率分布的标准差作为考虑因素,使平均效能变化相对于外界影响因素不敏感。图 8为确定性优化与稳健性优化的比较,x轴代表包含设计变量和噪声因素在内的变量,y轴代表被搜寻最小值的目标效能。

|
Download:
|
| 图 8 确定性优化与稳健性优化比较 Fig. 8 Deterministic optimization compared with robust optimization | |
图 8中,点1是确定性优化选择的最优点,是整个系统的最小值,但其对外界变化在±Δx范围内非常敏感;点2是可靠性优化点,在±Δx范围内均未超过限制条件,但其对外界变化也比较敏感;点3是稳健性优化点,虽在取值上不如点1、点2,但在可变范围±Δx内部变化较平缓,具有更好的稳健性。考虑稳健性的优化目标评价函数:
| $ \begin{array}{l} {\rm{E}}\left( {L\left( y \right)} \right) = {\rm{E}}\{ {(y-{y_0})^2}\} = {\rm{E}}\{ {\left( {y-\bar y} \right)^2} + \;\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(\bar y-{y_0})2\} = Y_\mu ^2 + Y_\sigma ^2 \end{array} $ | (11) |
式中:y为优化目标特征值, y0为目标值, y为优化目标期望值, Yμ2为优化目标特征值的方差, Yσ2为优化目标均值。
目前比较常用的稳健性方法是6σ稳健性设计,σ指概率分布的标准差,6σ稳健性设计指设计变量μ在±6σ范围内波动时,仍能保证优化目标平均效能在可接受范围内。多目标优化的稳健性设计问题可表述为[18]
| $ \begin{array}{l} {\rm{min}}:[{f_1}({Y_{\mu 1}}\left( x \right), {Y_{\sigma 1}}\left( x \right)), {f_2}({Y_{\mu 2}}\left( x \right), {Y_{\sigma 2}}\left( x \right)), \ldots \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{f_k}({Y_{\mu k}}\left( x \right), {Y_{\sigma k}}\left( x \right)){]^{\rm{T}}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{s}}.{\rm{t}}.\\ {g_{\mu j}}\left( x \right) + \eta {g_{\sigma j}}\left( x \right) \le 0, j = 1, 2, \ldots, J\\ \;\;\;\;\;\;\;\;{x_L} + \eta {x_\sigma } \le {x_\mu } \le {x_U} -\eta {x_\sigma } \end{array} $ | (12) |
式中:gμj(x)及gσj(x)分别为第j个约束条件的均值和标准差:xμ、xσ则是设计变量的均值和标准差;η代表波动范围,常用的6σ稳健性设计中,η取值为6。在水下航行器外形优化设计中主要考虑工业制造过程中不确定性因素,取设计变量制造误差的方差变异系数0.01。多目标稳健性优化模型确定为
| $ \begin{array}{l} {\rm{min}}:\{ {F_{x\mu }};{F_{x\sigma }}\} ;{\rm{max}}:\{ {V_\mu };{V_\sigma }\} \\ {\rm{s}}.{\rm{t}}.\\ {F_{x\mu }} \le 16\;920\\ {\rm{D}}.{\rm{v}}:{L_r};{L_m};{L_t} \end{array} $ | (13) |
优化目标均值和方差的计算采用蒙特卡洛描述性抽样方法结合响应面模型计算,取抽样组数为100。
4.2 水下航行器外形多目标稳健性优化求解通过多目标方法求解的稳健性优化关于艇体阻力和艇身包络体体积平均值与确定性优化结果对比的Pareto解集如图 9。

|
Download:
|
| 图 9 确定性优化与稳健性优化Pareto解集对比 Fig. 9 Pareto solution set′s comparison between of deterministic optimization and robustness optimization | |
可以看出稳健性优化结果在优化目标数值上较确定性优化结果差,但差距并不显著。考虑加工制造误差条件下优化目标标准差分布情况,稳健性优化后Vσ和Fxσ平均值分别下降12.18%和31.21%;中位数分别下降了7.69%和34.77%。使艇身包络体体积和艇体阻力性能稳健性显著提升。采用最小距离法确定图 9中两个解集的设计方案如表 4。
| 表 4 设计方案对比 Tab.4 Comparison of design schemes |
相比于初始方案,确定性优化结果虽然艇体阻力上升了11.99%,但总包络体体积增加了54.66%,提升效果显著。稳健性方案则在艇体阻力上升12.34%的条件下,总包络体体积增加了51.98%,说明方案具有一定的稳健性,更具实际应用价值。
5 结论1) 参数分析的实现、响应面近似模型的建立,在保证计算精度的前提下,大幅减低了计算代价,提高了设计效率。
2) 在进行多个优化目标的全局Pareto解集求解过程中,相对于前一代非支配算法,NSGA-Ⅲ可提高计算效率,可有效避免早熟现象,适合作为稳健性优化的寻优方法。
3) 相比于初始方案,优化方案在提升艇体包络体积方面效果显著,虽然稳健性方案相对于确定性方案的降阻和增容效果稍差,但在一定程度上降低了外界因素对水下航行器性能的影响,更加满足工程需要。
| [1] |
舒乐时, 周奇, 蒋平, 等. 基于序贯Kriging模型的潜器型线优化设计[J]. 船舶工程, 2016, 38(9): 43-46. SHU Leshi, ZHOU Qi, JIANG Ping, et al. Shape optimization design of submersible based on sequential Kriging model[J]. Ship engineering, 2016, 38(9): 43-46. (  0) 0)
|
| [2] |
李龙, 张宏伟, 王延辉. 无人自治水下航行器外形及推进系统优化设计[J]. 机械设计, 2017, 34(5): 23-29. LI Long, ZHANG Hongwei, WANG Yanhui. Autonomous underwater vehicle appearance and propulsion system optimization design[J]. Journal of machine design, 2017, 34(5): 23-29. (  0) 0)
|
| [3] |
王小庆, 潘子英, 陈鲁愚. 非回转型水下航行器操纵运动特性研究[C]//Proceedings of 2013 the Society for Underwater Technology Technical Conference. 上海: 水下技术协会中国分会, 中国石油大学, 2013. WANG Xiaoqing, PAN Ziying, CHEN Luyu. A study on maneuvering characteristics for the non-body-of-revolution underwater vehicle[C]//Proceedings of 2013 the Society for Underwater Technology Technical Conference. Shanghai: China Branch of the Underwater Technology Association, China University of Petroleum, 2013. (  0) 0)
|
| [4] |
杨卓懿. 无人潜器总体方案设计的多学科优化方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2012. YANG Zhuoyi. A Study on multidisciplinary design optimization method for scheme design of autonomous underwater vehicle[D]. Harbin: Harbin Engineering University, 2012. (  0) 0)
|
| [5] |
LUO Weilin, LYU Weijing. An application of multidisciplinary design optimization to the hydrodynamic performances of underwater robots[J]. Ocean engineering, 2015, 104: 686-697. DOI:10.1016/j.oceaneng.2015.06.011 (  0) 0)
|
| [6] |
GAO Ting, WANG Yaxing, PANG Yongjie, et al. Hull shape optimization for autonomous underwater vehicles using CFD[J]. Engineering applications of computational fluid mechanics, 2016, 10(1): 599-607. DOI:10.1080/19942060.2016.1224735 (  0) 0)
|
| [7] |
刘方. 混合驱动水下滑翔机系统设计与运动行为研究[D]. 天津: 天津大学, 2014. LIU Fang. System design and motion behaviors analysis of the hybrid underwater glider[D]. Tianjin: Tianjin University, 2014. (  0) 0)
|
| [8] |
刘峰, 韩端峰, 姚军. 有开孔加强结构耐压球壳稳健性优化[J]. 哈尔滨工程大学学报, 2016, 37(12): 1613-1618, 1637. LIU Feng, HAN Duanfeng, YAO Jun. Robust optimization of a pressure spherical shell with a strengthened opening[J]. Journal of Harbin engineering university, 2016, 37(12): 1613-1618, 1637. (  0) 0)
|
| [9] |
LI Xiaodong, TANG Wenyong, QU Xue. Structural reliability of membrane LNG hull accidentally damaged considering cargo leakage cryogenic impacts[C]//Proceedings of the 6th International ASRA Net Conference, 2012.
(  0) 0)
|
| [10] |
李学斌, 甘霖. AUV总体概念设计中的多学科和多目标优化研究[J]. 海洋技术学报, 2008, 27(2): 77-82. LI Xuebin, GAN Lin. Study on multi-disciplinary design and multi-objective problem in conceptual design of AUV[J]. Ocean technology, 2008, 27(2): 77-82. (  0) 0)
|
| [11] |
VERROUST A, SCHONEK F, ROLLER D. Rule-oriented method for parameterized computer-aided design[J]. Computer-aided design, 1992, 24(10): 531-540. DOI:10.1016/0010-4485(92)90040-H (  0) 0)
|
| [12] |
杨卓懿, 于宪钊, 庞永杰, 等. 基于多目标遗传算法的潜器外形优化设计[J]. 船舶力学, 2011, 15(8): 874-880. YANG Zhuoyi, YU Xianzhao, PANG Yongjie, et al. Optimization of submersible shape based on multi-objective genetic algorithm[J]. Journal of ship mechanics, 2011, 15(8): 874-880. (  0) 0)
|
| [13] |
THOMAS M C. Efficient nearly orthogonal and space-filling experimental designs for high-dimensional complex models[D]. Monterey, California: Naval Postgraduate School, 2002.
(  0) 0)
|
| [14] |
SIMPSON T W, BOOKER A J, GHOSH D, et al. Approximation methods in multidisciplinary analysis and optimization:a panel discussion[J]. Structural and multidisciplinary optimization, 2004, 27(5): 302-313. (  0) 0)
|
| [15] |
DAS I, DENNIS J E. Normal-boundary intersection:a new method for generating the Pareto surface in nonlinear multicriteria optimization problems[J]. Society for industrial and applied mathematics, 1998, 8(3): 631-657. (  0) 0)
|
| [16] |
DEB K, JAIN H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part i:solving problems with box constraints[J]. IEEE transactions on evolutionary computation, 2013, 18(4): 577-601. (  0) 0)
|
| [17] |
陈小前, 姚雯, 欧阳琦. 飞行器不确定性多学科设计优化理论与应用[M]. 北京: 科学出版社, 2013. CHEN Xiaoqian, YAO Wen, OUYANG Qi. Theory and application of uncertainty-based multidisciplinary design optimization for flight vehicles[M]. Beijing: Science Press, 2013. (  0) 0)
|
| [18] |
SUN Guangyong, LI Guangyao, ZHOU Shiwei, et al. Crashworthiness design of vehicle by using multiobjective robust optimization[J]. Structural and multidisciplinary optimization, 2011, 44(1): 99-110. DOI:10.1007/s00158-010-0601-z (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


