2. 中国核动力研究设计院 核反应堆系统设计技术重点实验室, 四川 成都 610213
2. Science and Technology on Reactor System Design Technology Laboratory, Nuclear Power Institute of China, Chengdu 610213, China
核电厂发生LOCA事故时,大量高温蒸汽会喷放进入安全壳大气空间,导致其内部温度与压力的升高[1-3]。若安全壳内压力超过其设计限值,则安全壳的完整性可能会遭到破坏,使大量放射性物质释放进入外界环境,危害公众安全。为解决这一问题,目前三代核电站中设置了非能动安全壳冷却系统,通过冷凝安全壳大气空间的蒸汽以实现降温降压的目的,进而保证安全壳内压力处于安全限值以内。需要注意的是,事故条件下安全壳大气空间为蒸汽和空气的混合气体,即蒸汽冷凝时伴有大量不凝性气体。相比于纯蒸汽冷凝,含不凝性气体蒸汽冷凝具有换热系数低、所处热工环境复杂等特点[4]。
针对上述问题,研究人员对含不凝性气体蒸汽冷凝换热特性开展了一些实验研究[5],并得到若干冷凝换热系数实验关联式[6-10]。但由于与冷凝换热相耦合的参量较多,实验过程中严格控制单一变量不易实现。此外,现有实验关联式中各参量的作用主要通过以往经验或实验数据拟合得到,这导致不同关联式中某些参量的影响程度存在一定的差异。比如,不同实验研究中壁面过冷度与冷凝换热系数之间的关系持有不同的结论。文献[7, 11]发现冷凝换热系数与壁面过冷度成正相关关系,而文献[8, 12-13]得到相反结论。
相比于实验研究,数值模拟具有单一变量易于控制、效率高等特点。此外,通过数值模拟的方法可以得到局部、连续的空间场分布。对计算域内局部细节现象的分析有助于对含不凝性气体蒸汽冷凝特性的深入了解。为此,本文使用CFD计算软件STAR-CCM+进行了含空气蒸汽冷凝的数值模拟分析,以期对主流流速、壁面过冷度、压力、换热面长度等参量对冷凝换热特性的影响有进一步的认识。
1 冷凝数值计算模型 1.1 基本控制方程计算中所使用的基本控制方程描述如下。
连续性方程:
| $ \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho w} \right) = {S_m} $ | (1) |
动量方程:
| $ \frac{{\partial \left( {\rho w} \right)}}{{\partial t}} + \nabla \cdot \left( {\rho ww} \right) = \nabla \cdot P + \rho f + {S_{\rho v}} $ | (2) |
能量方程:
| $ \begin{array}{*{20}{c}} {\frac{{\partial \left( {\rho E} \right)}}{{\partial t}} + \nabla \cdot \left( {\rho wE} \right) = \rho f \cdot w + \nabla \cdot \left( {P \cdot w} \right) + }\\ {\nabla \cdot \left( {{k_{{\rm{eff}}}}\nabla T} \right) + {S_h}} \end{array} $ | (3) |
组分方程:
| $ \frac{{\partial \left( {\rho {\omega _j}} \right)}}{{\partial t}} + \nabla \cdot \left( {\rho w{\omega _j}} \right) = \nabla \cdot \left( {\rho {D_j}\nabla {\omega _j}} \right) + {m_j} $ | (4) |
式中:ρ为密度;w表示速度;Sm为质量源项;P表示表面力;f为体积力;Sρv是动量源项;E为能量;keff表示等效导热系数;Sh为能量源项;下标j表示气体组分。
计算中采用隐式耦合求解器对三维离散网格进行瞬态求解。湍流模型使用软件默认的可实现的k-ε两层模型。该模型可以应用低Y+壁面处理,同时对旋转、有大反压力梯度的边界层、分离、回流等现象有更好的预测结果。其适用于自然对流条件下含空气蒸汽冷凝研究。
1.2 冷凝模型数值模拟中采用基于扩散理论的冷凝模型。该模型从分子扩散传质层面考虑了含不凝性气体蒸汽冷凝过程,且能够体现蒸汽在气-液交界面冷凝后在近壁面区形成的一层含空气浓度很高的气膜。冷凝过程中,主流区域的蒸汽需穿过这层气膜到气-液交界面冷凝。此外,在含空气蒸汽冷凝传热过程中,主要热阻存在于壁面附近的空气膜层,液膜层的热阻可以忽略不计。文献[5]表明,即便蒸汽质量份额在98%的条件下,液膜热阻也仅占总热阻的5%。因此,在本文中忽略液膜层的影响。
本文以空气和蒸汽的混合气体为例讨论所使用的冷凝模型。这两种气体的传质方程可表示为:
对于蒸汽有:
| $ {m_v} = \rho w{\omega _v} - \rho D\frac{{\partial {\omega _v}}}{{\partial n}}\left| {_i} \right. $ | (5) |
对于空气有:
| $ {m_{{\rm{air}}}} = \rho w{\omega _{{\rm{air}}}} - \rho D\frac{{\partial {\omega _{{\rm{air}}}}}}{{\partial n}}\left| {_i} \right. $ | (6) |
式中:m为质量通量;ω表示质量份额;D是质扩散系数;n表示冷凝壁面法向距离;下标v、air和i分别表示蒸汽、空气和气-液交界面。
基于以上两式,气-液交界面处,两种组分气体传质的总和可以表示为:
| $ \begin{array}{*{20}{c}} {{m_{{\rm{cond}}}} = {m_v} + {m_{{\rm{air}}}} = }\\ {\rho w\left( {{\omega _v} + {\omega _{{\rm{air}}}}} \right) - \rho D{{\left| {\frac{{\partial \left( {{\omega _v} + {\omega _{{\rm{air}}}}} \right)}}{{\partial n}}} \right|}_i}} \end{array} $ | (7) |
式中下标cond表示冷凝。
考虑到混合气体中只有蒸汽在气-液交界面发生冷凝,且蒸汽与空气的质量份额总和为1,则有:
| $ {m_{{\rm{cond}}}} = {m_v} = \rho w $ | (8) |
将式(8)代入式(5),得到蒸汽冷凝率表达式:
| $ {m_{{\rm{cond}}}} = - {\left| {\left( {\frac{{\rho D}}{{1 - {\omega _v}}}} \right)\frac{{\partial {\omega _v}}}{{\partial n}}} \right|_i} $ | (9) |
其中,两组份混合气体的扩散系数D由下式计算[14]:
| $ D = {D_0}{\left( {\frac{T}{{{T_0}}}} \right)^{1.75}}{\left( {\frac{P}{{{P_0}}}} \right)^{ - 1}} $ | (10) |
式中:T为绝对温度; P表示压力;下标0表示标准状态。
计算求解时,通过比较壁面温度是否小于近壁面区蒸汽分压所对应的饱和温度来判断蒸汽是否发生冷凝。若发生冷凝,蒸汽及其所携带的动量与能量从近壁面第一层网格(代表气-液交界面)内移除。蒸汽的饱和温度与饱和压力的对应关系用安托因方程描述:
| $ \ln \left( {\frac{{{P_{{\rm{sat}}}}}}{{{P_0}}}} \right) = 11.949 - \frac{{3\;978.205}}{{T - 39.801}} $ | (11) |
式中下标sat表示蒸汽饱和状态。
由基本控制方程可知,冷凝模型中最重要的是在近壁面区关于质量源项Sm、动量源项Sρv以及能量源项Sh的处理。
蒸汽在近壁面网格中移除的过程可通过在相应控制体内添加合适的质量、动量和能量源项方程来实现。这些方程具体表示为:
质量源项:
| $ {S_m} = - \left( {\frac{{\rho D}}{{1 - {\omega _v}}}} \right)\frac{{\partial {\omega _v}}}{{\partial n}}\left| {_i} \right. $ | (12) |
动量源项:
| $ {\mathit{\boldsymbol{S}}_{\rho v}} = {S_m}w $ | (13) |
能量源项:
| $ {S_h} = {S_m}\dot h $ | (14) |
式中
为验证基于扩散理论的含不凝性气体蒸汽冷凝模型对局部冷凝换热特性的模拟效果,本文对COPAIN实验进行了计算分析。该实验装置的长、宽、高分别为0.5、0.6、2.0 m。冷凝换热面位于装置的一个侧壁面,其宽和高分为0.6 m和2 m。数值计算模型的几何与网格结构简图如图 1所示。计算中,选取COPAIN[15]实验的6个典型工况(如表 1所示)来设置初始和边界条件。这些工况涵盖了不同的压力、壁面过冷度、空气质量份额及主流流速。计算模型设置顶部为速度入口、底部为压力出口、冷凝壁面为恒温、其他壁面为绝热边界。

|
Download:
|
| 图 1 COPAIN实验装置计算模型几何与网格简图 Fig. 1 Structure and mesh diagram of COPAIN model | |
| 表 1 COPAIN实验计算工况 Table 1 Calculation conditions of COPAIN experiment |
网格无关性验证中,选取基本网格尺寸0.02~0.06 m、边界层层数2~15层、Y+值范围1~190。结果发现,基本网格尺寸的变化对局部热流密度的影响仅为3%,而边界层层数和Y+值对冷凝换热特性的影响较大。当边界层层数为2层、Y+>5时,无法有效模拟壁面热流密度分布。因而,数值模拟中选取基本网格尺寸0.04 m、边界层网格15层,并通过调整第一层网格厚度保证Y+<5。
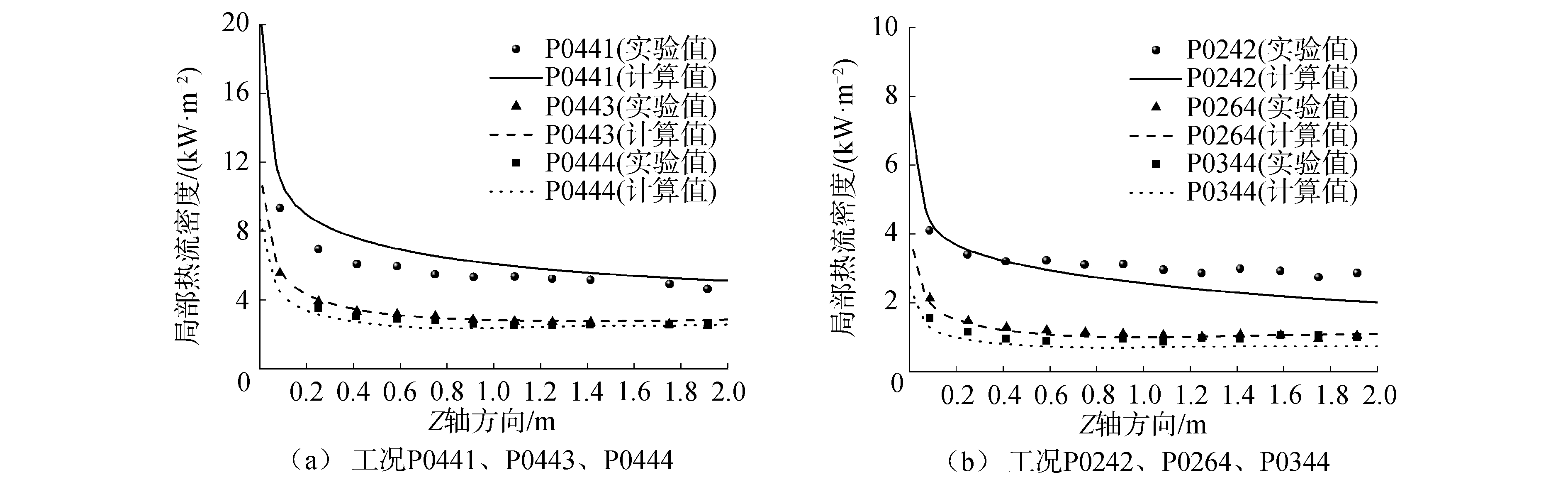
在COPAIN实验中,蒸汽冷凝换热受强迫对流和自然对流的共同作用。其中,强迫对流源于实验段进出口压差;自然对流源于冷凝面和主流气体的温度差以及蒸汽冷凝导致的局部混合气体密度的增加。COPAIN实验结果发现[15]:当主流流速在1 m/s以下时,自然对流起主导作用(本文称之为自然对流主导区);当主流流速在1 m/s以上时,强迫对流起主导作用(本文称之为强迫对流主导区)。主流流速接近1 m/s时,自然对流与强迫对流的作用相当(本文称之为强迫-自然对流共同作用区)。图 2示出了不同流动状态和空气质量份额条件下,数值模拟结果和实验值的对比。可以看出,沿Z轴方向(如图 1所示),计算所得局部热流密度变化趋势与实验结果基本一致。通过对比各实验测点位置处的实验值和数值计算结果发现,93%的数值计算结果与实验值的偏差在25%以内。可见,所用冷凝模型可以较好地模拟不同流动状态下含不凝性气体蒸汽冷凝的局部换热特性。
|
Download:
|
| 图 2 不同实验工况下局部热流密度对比 Fig. 2 Comparison of local heat flux at different conditions | |
为考察蒸汽冷凝换热特性从强迫对流主导区逐渐过渡到自然对流主导区时的变化情况,计算中参照COPAIN实验工况,选取主流流速范围为0.1~3 m/s。为在较广的参数范围内进行讨论,主流空气质量份额范围取为0.1~0.9、气体压力取0.2~0.6 MPa、壁面过冷度取6 ℃~50 ℃。
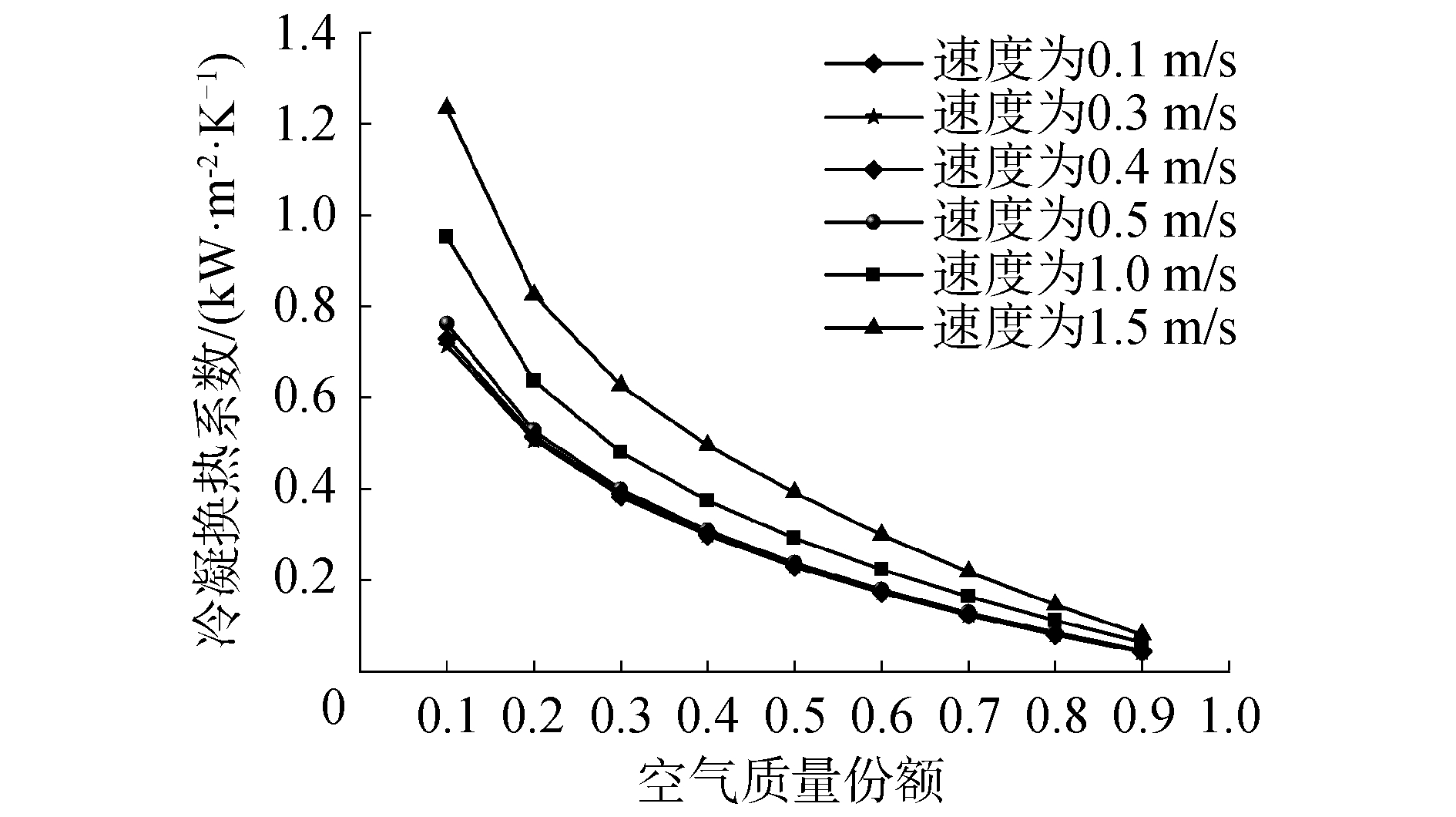
典型结果如图 3所示。其给出了不同主流流速条件下,冷凝换热系数随空气质量份额的变化关系。可以看出,当主流流速高于0.5 m/s时,冷凝换热系数随流速的增加有明显的提高。当主流流速从0.5 m/s增加到1 m/s时,冷凝换热系数的最大增幅为25%。而当主流流速在0.5 m/s以下时,冷凝换热系数之间的偏差仅为6.7%。
|
Download:
|
| 图 3 主流流速对冷凝换热系数的影响 Fig. 3 The effect of mainstream velocity on condensation heat transfer coefficient | |
这主要是由于冷凝过程中,在低温冷凝换热面和蒸汽冷凝的共同作用下,会使冷凝壁面附近混合气体密度增加,重力的驱动导致近壁面气体的流速高于主流气体流速。由图 4(a)可知,近壁面气体的流速随主流流速的降低有明显的增加。当主流流速在0.1~0.5 m/s范围内时,自然对流的作用使近壁面气体流速达到主流流速的1.6倍以上。结合图 3给出的流速与冷凝换热特性的关系可知,当主流流速低于0.5 m/s时,主流流速对冷凝换热系数的影响可以忽略不计。

|
Download:
|
| 图 4 不同主流条件下的出口速度场分布 Fig. 4 Velocity distribution under different mainstream conditions | |
对比图 4中不同压力和壁面过冷度下的模拟结果发现:压力的变化对近壁面气体流动特性的影响较小;壁面过冷度对近壁面气体流动特性的影响较大。当壁面过冷度为6 ℃时,近壁面区气体速度的增幅变小。这主要是由于过冷度和冷凝量降低,近壁面区与主流区气体的密度差减小,导致自然对流的驱动力不足。该壁面过冷度下,主流流速小于0.5 m/s时,冷凝换热系数变化了20%。当壁面过冷度高于10 ℃时,冷凝换热系数的变化均小于10%。
上述计算结果表明,主流流速在0.5 m/s以下时可以认为是冷凝换热的自然对流主导区,0.5~1.5 m/s时为自然-强迫对流共同作用区,大于1.5 m/s时为强迫对流主导区。
基于这一结论,后续各计算工况中选取主流流速为0.5 m/s以考察自然对流起主导作用时,其他热工参量对冷凝换热特性的影响。
3.2 壁面过冷度的影响为进一步讨论壁面过冷度对冷凝换热特性的影响,本文采用冷凝计算模型在压力0.2 MPa,不同空气质量份额的条件下展开了数值模拟研究。计算所得壁面过冷度与冷凝换热系数之间的关系汇总于图 5。

|
Download:
|
| 图 5 壁面过冷度对冷凝换热系数的影响 Fig. 5 The effect of wall sub-cooling on condensation heat transfer coefficient | |
可看出,冷凝换热系数随壁面过冷度的升高而降低。在不同的空气质量份额条件下,冷凝换热系数随壁面过冷度呈负幂次方关系。由图 5可知,过冷度的幂指数不是一个常数,其与空气质量份额和壁面过冷度有关。当空气质量份额从0.9降低到0.1时,幂指数的绝对值明显增大。在相同空气质量份额条件下,壁面过冷度小于30 ℃时,幂指数可近似认为是一常数。壁面过冷度大于30 ℃时,幂指数绝对值随过冷度的升高而明显增大。通过数据拟合得到:
| $ f\left( h \right) = a\Delta {T^{ - 0.002\;18\Delta T - 0.604\;02W_a^2 + 0.927\;34{W_a} - 0.344\;97}} $ | (15) |
在计算参数范围内,过冷度的幂指数在-0.008 3~-0.367。
3.3 换热面高度的影响为考察换热面高度对冷凝换热特性的影响,本文对比分析了换热面高度分别为0.5、1、2、4和6 m时的局部热流密度和平均冷凝换热系数。此外,在换热面高度同为6 m的条件下,还对比了不同的主流空气质量份额对换热面热流密度分布的影响。计算结果如图 6和图 7所示。由图 6可知,换热面局部热流密度沿气体流动方向可以分为两个区域,即下降区和缓慢上升区。由图 8可知,在下降区(小于0.72 m),换热面附近空气浓度边界层很薄且处于发展增厚阶段。这一高度范围内,蒸汽扩散传质能力较强,局部热流密度的变化主要取决于空气浓度边界层的发展情况。浓度边界层厚度的定义式为:

|
Download:
|
| 图 6 不同换热面高度下的局部热流密度 Fig. 6 Local heat flux under different condensation wall height conditions | |

|
Download:
|
| 图 7 不同换热面高度下平均冷凝换热系数 Fig. 7 Average heat transfer coefficient under different condensation wall height conditions | |

|
Download:
|
| 图 8 空气浓度边界层与单位面积蒸汽冷凝率 Fig. 8 Concentration boundary layer and condensation rate | |
| $ {\omega _{\delta ,{\rm{air}}}} - {\omega _{i,{\rm{air}}}} = 0.99\left( {{\omega _{{\rm{main}},{\rm{air}}}} - {\omega _{{\rm{i}},{\rm{air}}}}} \right) $ | (16) |
式中:下标δ为边界层厚度,main表示主流。
在缓慢上升区(大于0.72 m),局部热流密度沿气体流动方向呈现缓慢增加的趋势。这主要是由于近壁面气体的密度高于主流气体,重力的作用使近壁面气体的流速沿流动方向不断增大(如图 4所示),这会有助于局部热流密度的增加。
图 7给出了平均冷凝换热系数随换热面高度的变化关系。可见,平均冷凝换热系数随换热面高度的变化相对平缓。其具体分布形式与空气质量份额有关。当空气质量份额不小于0.5时,冷凝换热系数随换热面高度的增加具有先降低后增加的趋势。换热系数的最小值出现在2.0~2.5 m。当空气质量份额为0.1时,冷凝换热系数随换热面高度的增加先降低后基本保持不变。总体上,当换热面高度大于1 m时,平均冷凝换热系数基本保持不变。
3.4 压力的影响压力对含不凝性气体蒸汽冷凝特性的影响可通过式(9)和式(10)给出的冷凝模型求解方程进行分析。可知,压力的变化会通过改变扩散系数和混合气体密度的大小来影响冷凝换热性能。其具体体现在以下3个方面:1)随着压力的升高,气体扩散系数降低,蒸汽冷凝量随扩散系数的降低而减小;2)在空气质量份额不变的条件下,压力的增加会使主流气体饱和温度升高,扩散系数随温度的升高而增大。这一过程中,扩散系数的增大会促进蒸汽冷凝;3)蒸汽密度随压力的升高而增大,浓度梯度相同的条件下,蒸汽冷凝率随密度的增加而增大。
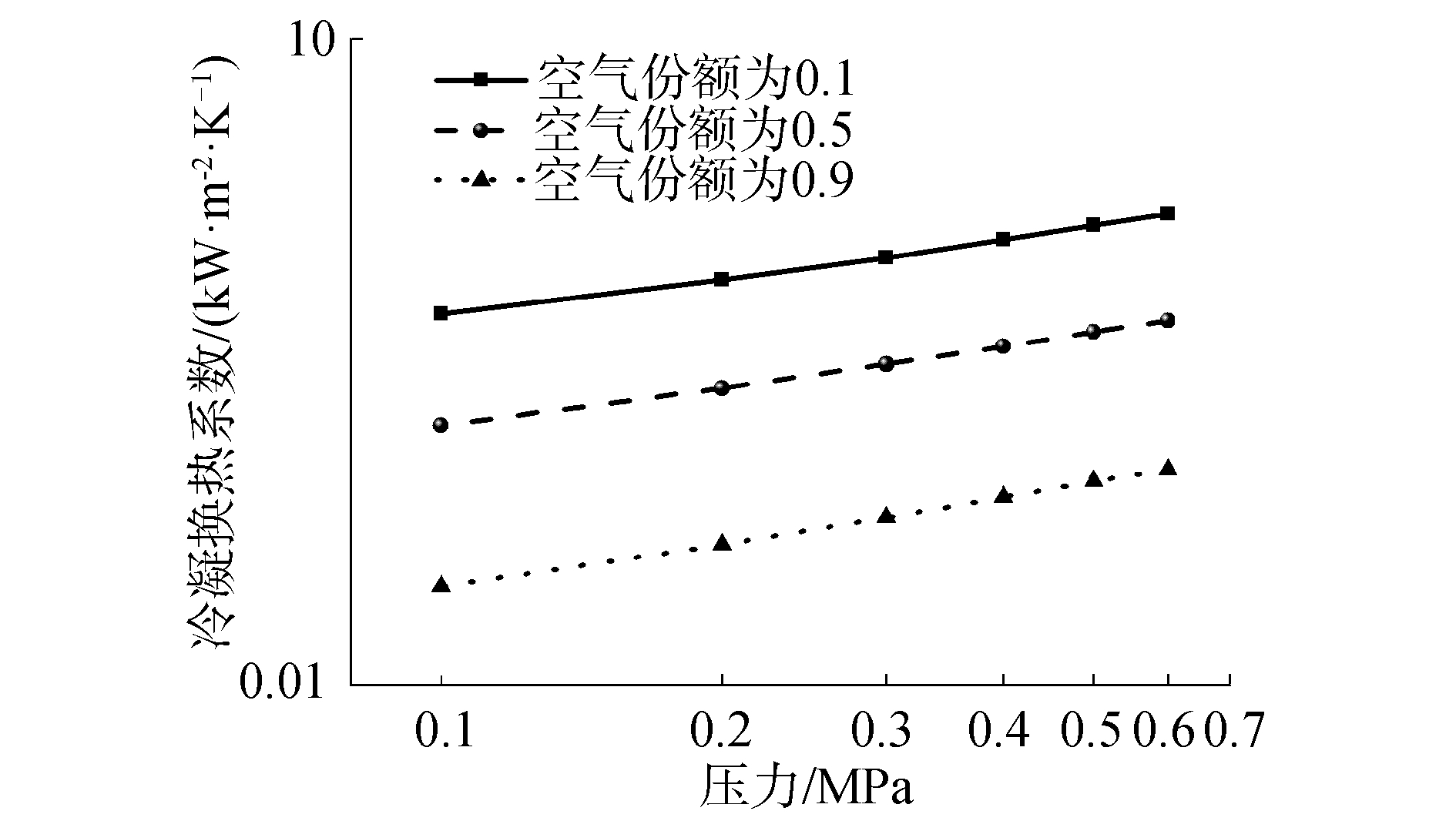
对图 9所示的计算结果进行分析发现,在不同空气质量份额(10%~90%)条件下,冷凝换热系数随压力的升高而增大。这说明上述3个影响因素中,后两种因素的影响程度要大于前者。图中,冷凝换热系数与压力之间具有斜率约为0.64的线性关系,即在上述3个因素的共同作用下,蒸汽冷凝换热系数与压力的0.64次方成正比。
|
Download:
|
| 图 9 不同压力条件下的冷凝换热系数(ΔT=40 ℃) Fig. 9 Condensation heat transfer coefficient at different pressure conditions (ΔT=40 ℃) | |
1) 蒸汽冷凝换热特性在强迫对流主导区受主流流速影响明显。当主流流速从0.5 m/s增加到1 m/s时,冷凝换热系数最大增加了25%。在自然对流主导区,冷凝传热性能受主流流速的影响可以忽略不计。主流流速在0.5 m/s以下时,冷凝换热系数之间的偏差仅为6.7%。
2) 冷凝换热系数随壁面过冷度的增加而降低。两者在不同质量份额条件下呈幂次方关系。过冷度的幂指数不为恒定值,其与壁面过冷度和空气质量份额有关。在计算参数范围内(0.1<ωa<0.9,4<ΔT<50),过冷度的幂指数在-0.008 3~-0.367,Dehbi和Green拟合得到的幂指数在这一范围内。
3) 局部热流密度沿气体流动方向(Z轴方向)可分下降区和缓慢上升区。下降区的形成与空气浓度边界层的形成与发展有关。缓慢上升区的形成与近壁面气体流动特性有关。2个区域的转折点在0.68~1.24 m。平均冷凝换热系数随冷凝换热面高度的变化相对平缓,其具体分布形式受空气质量份额影响较大。当空气质量份额不小于0.5时,冷凝换热系数随高度的增加具有较为明显的先降低后增加的趋势。最小值位于2.0~2.5 m。当空气质量份额接近0.1时,冷凝换热系数随高度的增加先降低后几乎保持不变。
4) 凝换热系数随气体压力的升高而增大且两者呈幂次方关系。在不同的空气质量份额条件下(0.1<ωa<0.9),冷凝换热系数为压力的0.645次方。
| [1] |
宿吉强, 王辉, 孙中宁, 等. 含空气蒸汽冷凝传热特性数值模拟[J]. 化工学报, 2014, 65(9): 3425-3433. SU Jiqiang, WANG Hui, SUN Zhongning, et al. Numerical simulations for steam condensation in presence of air[J]. CIESC journal, 2014, 65(9): 3425-3433. DOI:10.3969/j.issn.0438-1157.2014.09.016 (  0) 0)
|
| [2] |
宿吉强, 范黎, 高力. 安全壳冷却系统蒸汽冷凝传热研究综述[J]. 原子能科学技术, 2016, 50(11): 1956-1966. SU Jiqiang, FAN Li, GAO Li. Review of steam condensation heat transfer under containment cooling system condition[J]. Atomic energy science and technology, 2016, 50(11): 1956-1966. (  0) 0)
|
| [3] |
潘丽强, 宿吉强, 范广铭, 等. 含空气的蒸汽冷凝传热模型研究[J]. 核动力工程, 2015, 36(6): 45-50. PAN Liqiang, SU Jiqiang, FAN Guangming, et al. Study on steam/air condensation heat transfer model[J]. Nuclear power engineering, 2015, 36(6): 45-50. (  0) 0)
|
| [4] |
李军, 刘长亮, 李晓明. 非能动安全壳冷却系统设计研究[J]. 核科学与工程, 2018, 38(04): 632-639. LI Jun, LIU Changliang, LI Xiaoming. Study on the design of passive containment cooling system[J]. Nuclear science and engineering, 2018, 38(04): 632-639. DOI:10.3969/j.issn.0258-0918.2018.04.016 (  0) 0)
|
| [5] |
李军, 李晓明, 喻新利, 等. 非能动安全壳热量导出系统设计方案及评价[J]. 原子能科学技术, 2018, 52(6): 1021-1027. LI Jun, LI Xiaoming, YU Xinli, et al. Design and evaluation of passive containment heat removal system[J]. Atomic energy science and technology, 2018, 52(6): 1021-1027. (  0) 0)
|
| [6] |
白晋华, 赵博. 基于Relap5的非能动安全壳热量导出系统优化[J]. 核动力工程, 2017, 38(6): 14-17. BAI Jihua, ZHAO Bo. Optimization of design on passive containment cooling system by using relap5 code[J]. Nuclear power engineering, 2017, 38(6): 14-17. (  0) 0)
|
| [7] |
TONG Pan, FAN Guangming, SUN Zhongning, et al. An experimental investigation of pure steam and steam-air mixtures condensation outside a vertical pin-fin tube[J]. Experimental thermal and fluid science, 2015, 69: 141-148. DOI:10.1016/j.expthermflusci.2015.08.009 (  0) 0)
|
| [8] |
DE LA ROSA J, ESCRIVÁ A, HERRANZ L, et al. Review on condensation on the containment structures[J]. Progress in nuclear energy, 2009, 51(1): 32-66. DOI:10.1016/j.pnucene.2008.01.003 (  0) 0)
|
| [9] |
宿吉强, 孙中宁, 范广铭, 等. 含不凝性气体的蒸汽冷凝传热实验研究[J]. 核动力工程, 2014, 35(1): 36-41. SU Jiqiang, SUN Zhongning, FAN Guangming, et al. Analysis of experiments for vertical out-tube steam condensation in presence of non-condensable gases[J]. Nuclear power engineering, 2014, 35(1): 36-41. (  0) 0)
|
| [10] |
DEHBI A. A unified correlation for steam condensation rates in the presence of air-helium mixtures under naturally driven flows[J]. Nuclear engineering and design, 2016, 300: 601-609. DOI:10.1016/j.nucengdes.2016.02.009 (  0) 0)
|
| [11] |
LIU H, TODREAS N E, DRISCOLL M J. An experimental investigation of a passive cooling unit for nuclear plant containment[J]. Nuclear engineering and design, 2000, 199(3): 243-255. DOI:10.1016/S0029-5493(00)00229-6 (  0) 0)
|
| [12] |
SU Jiqiang, SUN Zhongning, FAN Guangming, et al. Experimental study of the effect of non-condensable gases on steam condensation over a vertical tube external surface[J]. Nuclear engineering and design, 2013, 262: 201-208. DOI:10.1016/j.nucengdes.2013.05.002 (  0) 0)
|
| [13] |
LEE Y, JANG Y, CHOI D. An experimental study of air-steam condensation on the exterior surface of a vertical tube under natural convection conditions[J]. International journal of heat and mass transfer, 2017, 104: 1034-1047. DOI:10.1016/j.ijheatmasstransfer.2016.09.016 (  0) 0)
|
| [14] |
UCHIDA H, OYAMA A, TOGO Y. Evaluation of post-incident cooling systems of light-water power reactors[C]//Proceedings of the Third International Conference on the Peaceful Uses of Atomic Energy. Geneva. 1965: 93-104.
(  0) 0)
|
| [15] |
KAWAKUBO M, ARITOMI M, KIKURA H, et al. An experimental study on the cooling characteristics of passive containment cooling systems[J]. Journal of nuclear science and technology, 2009, 46(4): 339-345. DOI:10.1080/18811248.2007.9711539 (  0) 0)
|
| [16] |
DEHBI A. The effects of non-condensable gases on steam condensation under turbulence natural convection conditions[D]. Cambridge: Massachusetts Institute of Technology, 1990.
(  0) 0)
|
| [17] |
GREEN J, ALMENAS K. An overview of the primary parameters and methods for determining condensation heat transfer to containment structures[J]. Nuclear safety, 1996, 37: 26-48. (  0) 0)
|
| [18] |
BEJAN A. Convection heat transfer[M]. 4th ed. Hoboken: John Wiley & Sons, 2013.
(  0) 0)
|
| [19] |
CHENG X, BAZIN P, CORNET P, et al. Experimental data base for containment thermal hydraulic analysis[J]. Nuclear engineering and design, 2001, 204(1/3): 267-284. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


