2. 四川大学 水力学与山区河流开发保护国家重点实验室, 四川 成都 610065
2. State Key Laboratory of Hydraulics and Mountain River Engineering, Sichuan University, Chengdu 610065, China
大型渠系经常遇到提水泵站与节制闸联合工作的情况,由于泵站和节制闸的布置情况不同,造成互相影响下的流场难以捉摸,这种影响一方面容易造成节制闸流动不对称而影响泄流稳定,抗冲护砌范围难以确定,另一方面泵站引渠流动也容易产生旋涡、流速不均匀等现象。
对于提水泵站与节制闸联合工作的设计及模拟研究,目前还没有详细明确的规范和计算方法,王雷等[1]、谢省宗等[2]采用三维紊流数值模拟对南水北调中线惠南庄泵站压力前池布置方案进行了分析研究,王芳芳等[3]、陈松山等[4]对泵站前池及部分引水明渠水流流场进行三维数值模拟得到整流优化改进方案,高传昌等[5]采用非连续底坎、非连续挑流坎与压水板3种整流措施相结合使渠道进站水流流态得到良好的改善。虞鸿等[6]通过对杭州三堡排涝工程的泵站数值模拟得到导流墩的外形、位置和尺寸改变会对引渠流态有比较显著的影响。Constantinescu等[7-8]用湍流模型数值模拟了泵站集水池水流及漩涡,并分析了紊流模型在对水池漩涡进行预测方面的作用,证明了采用高雷诺数k-w模型进行数值模拟可使旋涡强度降低;Aldama等[9]采用数值模拟结合线性规划的方法对单相流的泵站进行了优化;Antonio等[10]对具有特殊结构的Socorridos泵站将实物模拟,实验与数值模拟结合进行了深入研究。他们的研究仅仅针对泵站前的压力前池或导流墩的流场,并没有分析相互影响的因素。本文针对青龙河1#节制闸和提水泵站的联合工作,进行数值模拟分析,得到了闸站之间的相互影响,提出4种优化方案,对流场进行了优化。
1 青龙山灌区数学模型青龙山灌区建造了一条长约50 km的大型渠系,天然渠底起伏变化,平均坡度基本为零,节制闸桩号为22+000,提水泵站的桩号为21+950。
按照工程设计要求,青龙河干渠设计分为一期设计和终期设计,一期上游设计流量为181.98 m3/s,提水泵站设计流量为36.52 m3/s;终期上游设计流量为330.96 m3/s,提水泵站设计流量为39.39 m3/s。
1.1 控制方程Mike21 FM水动力模型是基于三向不可压缩和Reynolds值均布的Navier-Stokes方程,并服从于Boussinesq假定和静水压力的假定,模型考虑了科氏力、涡黏性等方面[11-14]。
连续方程:
| $ \frac{{\partial h}}{{\partial t}} + \frac{{\partial h\bar u}}{{\partial x}} + \frac{{\partial h\bar v}}{{\partial y}} = hS $ | (1) |
X方向水平动量方程为:
| $ \begin{array}{l} \frac{{\partial h\bar u}}{{\partial t}} + \frac{{\partial h\;{{\bar u}^2}}}{{\partial x}} + \frac{{\partial h\;\bar u\bar v}}{{\partial y}} = f\bar vh - gh\frac{{\partial \eta }}{{\partial x}} - \\ \frac{h}{{{\rho _0}}}\frac{{\partial {p_a}}}{{\partial x}} - \frac{{g{h^2}}}{{2{\rho _0}}}\frac{{\partial \rho }}{{\partial x}} + \frac{{{\tau _{sx}}}}{{{\rho _0}}} - \frac{{{\tau _{bx}}}}{{{\rho _0}}} - \frac{1}{{{\rho _0}}}\left( {\frac{{\partial {s_{xx}}}}{{\partial x}} + \frac{{\partial {s_{xy}}}}{{\partial y}}} \right) + \\ \frac{\partial }{{\partial x}}\left( {h{T_{xx}}} \right) + \frac{\partial }{{\partial y}}\left( {h{T_{xy}}} \right) + h{u_s}S \end{array} $ | (2) |
Y方向水平动量方程为:
| $ \begin{array}{l} \frac{{\partial h\bar v}}{{\partial t}} + \frac{{\partial h\;\bar u\bar v}}{{\partial x}} + \frac{{\partial h\;{{\bar v}^2}}}{{\partial y}} = - f\bar uh - gh\frac{{\partial \eta }}{{\partial y}} - \\ \frac{h}{{{\rho _0}}}\frac{{\partial {p_a}}}{{\partial y}} - \frac{{g{h^2}}}{{2{\rho _0}}}\frac{{\partial \rho }}{{\partial y}} + \frac{{{\tau _{sy}}}}{{{\rho _0}}} - \frac{{{\tau _{by}}}}{{{\rho _0}}} - \frac{1}{{{\rho _0}}}\left( {\frac{{\partial {s_{yx}}}}{{\partial x}} + \frac{{\partial {s_{yy}}}}{{\partial y}}} \right) + \\ \frac{\partial }{{\partial x}}\left( {h{T_{xy}}} \right) + \frac{\partial }{{\partial y}}\left( {h{T_{yy}}} \right) + h{v_s}S \end{array} $ | (3) |
采用基于单元中心的有限体积法对二维浅水控制方程进行离散求解。
1.2 边界条件和网格划分 1.2.1 模拟工况的确定为更好地对节制闸与泵站联合工作的相互关系进行研究,选择青龙河段18+300至24+600段进行数值模拟,灌区位置如图 1所示,其中节制闸与提水泵站距离入口3 700 m,距离出口2 600 m。根据工程设计,分别对灌溉终期设计和一期设计的节制闸和提水泵站的联合进行数值模拟,模拟工况如下:

|
Download:
|
| 图 1 青龙山灌区 Fig. 1 Qinglong irrigation district | |
模拟工况1:渠道上游流量181.98 m3/s,泵站提水流量36.52 m3/s;
模拟工况2:渠道上游流量330.96 m3/s,泵站提水流量39.39 m3/s。
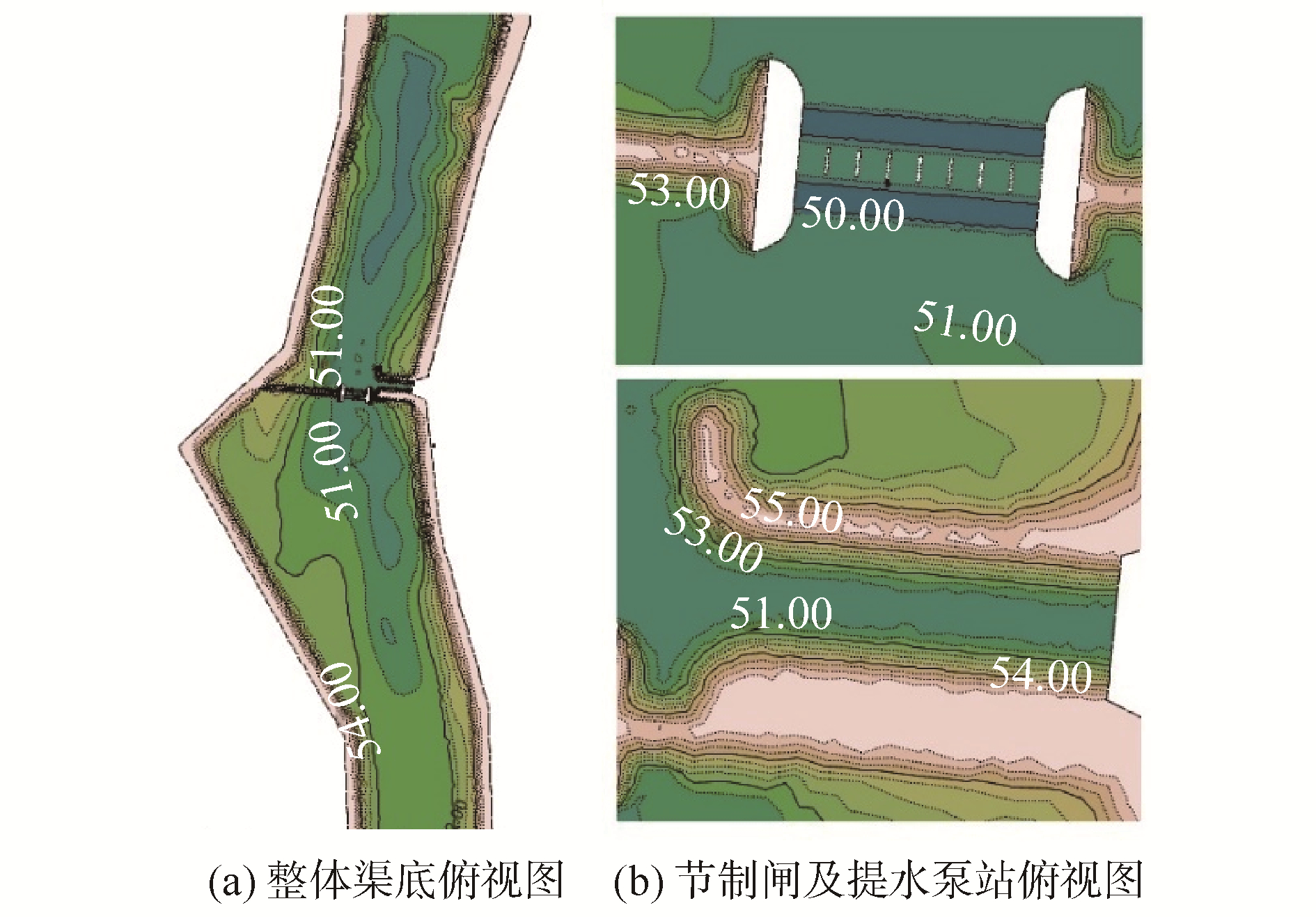
1.2.2 几何模型和网格划分根据上游边界18+300至下游边界24+600之间的青龙河实测大断面数据,以及渠道两侧提防工程、节制闸、提水泵站的工程设计图,建立该河段、节制闸及提水泵站的几何模型,如图 2所示,其中堤防和人工渠精细至坡脚线和相关线。
|
Download:
|
| 图 2 几何模型 Fig. 2 The geometric model | |
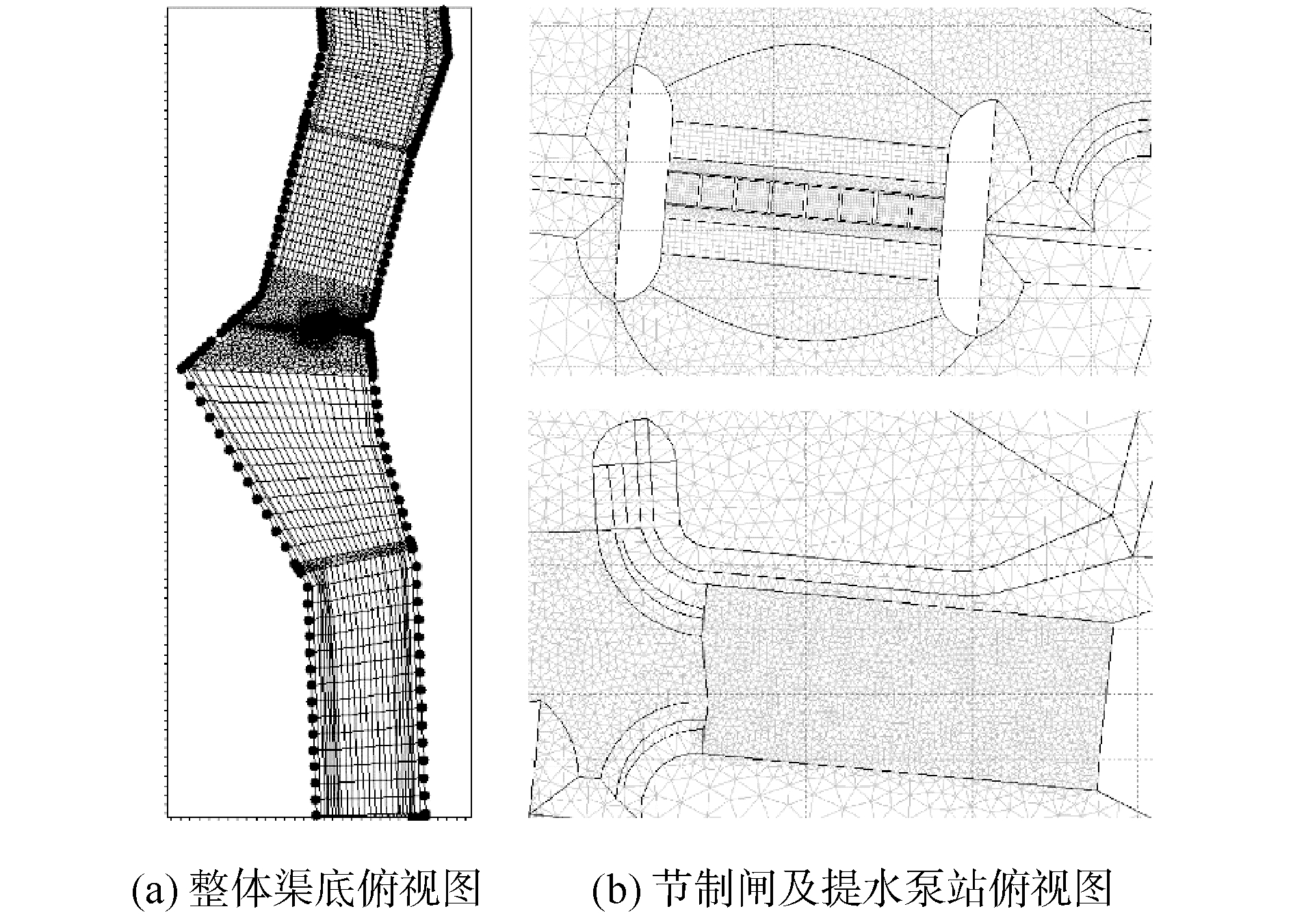
在原工程设计的基础上,改变尺寸划分了4种不同数量的网格,分别针对一期设计和终期设计工况进行了数值模拟计算,结果表明在网格数在2.0万(19 468)为最优,模拟计算网格如图 3所示。
|
Download:
|
| 图 3 网格划分 Fig. 3 Simulated mesh map | |
青龙河提水泵站和节制闸模拟计算工况共2个,其边界类型和设定标准如表 1所示。其中闸墩采用无滑移壁面条件,堤防采用滑移壁面条件。
| 表 1 模拟工况边界条件表 Table 1 Boundary conditions of simulation mode |
实测模拟干渠段平均流速为0.4 m/s左右,流过整段时间约4.5 h,为使本次模拟流场充分达到稳定,模拟时段长取6 h,时间步长为30 s。
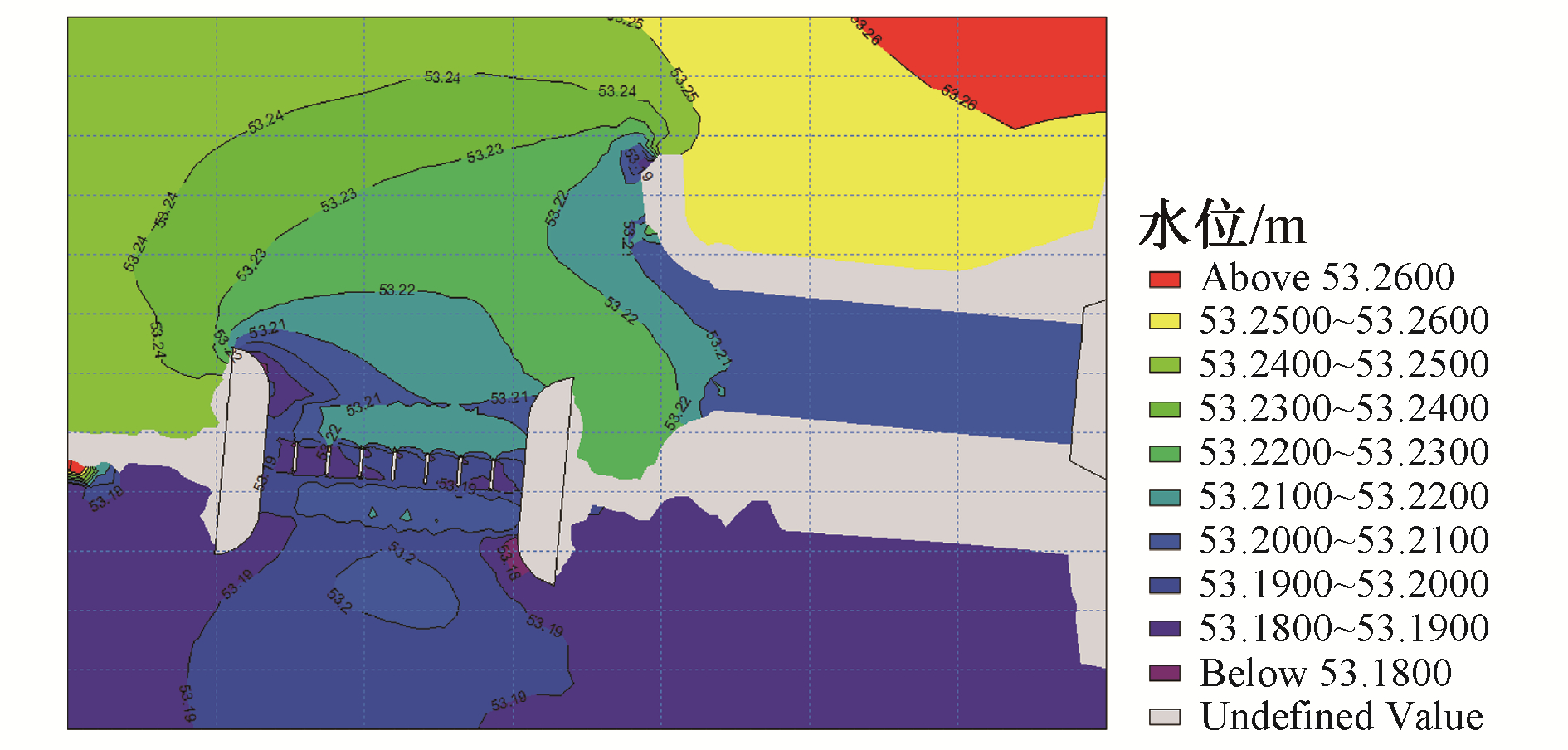
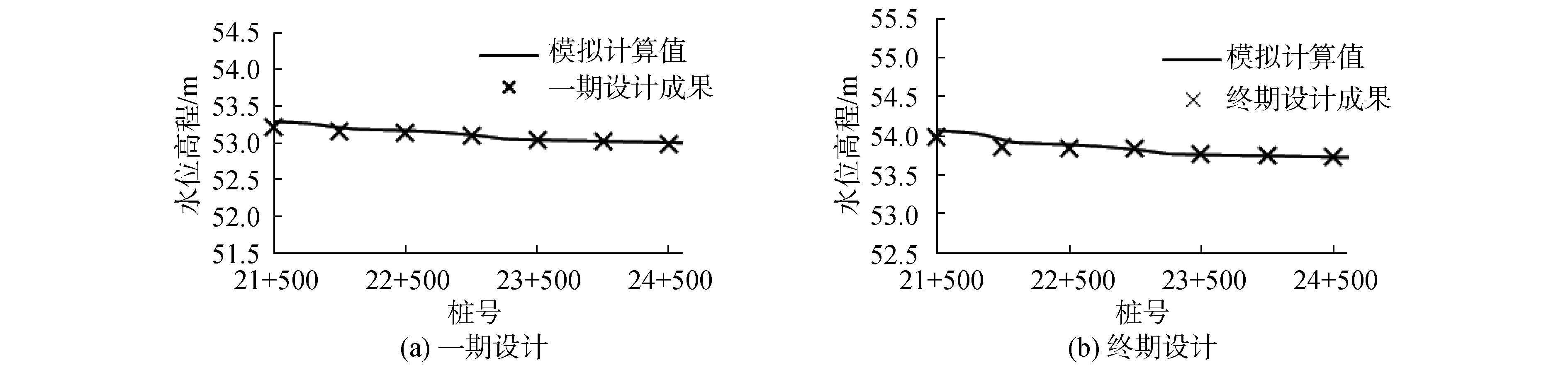
2 数值模型的率定由于工程尚处于设计阶段,因此无实测资料进行率定,经分析确定以桩号21+500~桩号24+600之间的设计成果[15]和模拟计算成果对比,来判断数值模型的可行性。对比如图 5所示。
|
Download:
|
| 图 5 一期设计水位等值线 Fig. 5 Water level contour map of the first design | |
通过图 4水面线对比分析,模拟值与设计值吻合度良好。因此,数值计算模型在网格划分,渠底糙率,边界条件,计算控制条件等的设置是合理的,数值模型结果可信。
|
Download:
|
| 图 4 纵向水面线对比 Fig. 4 Comparison of longitudinal water surface profile | |
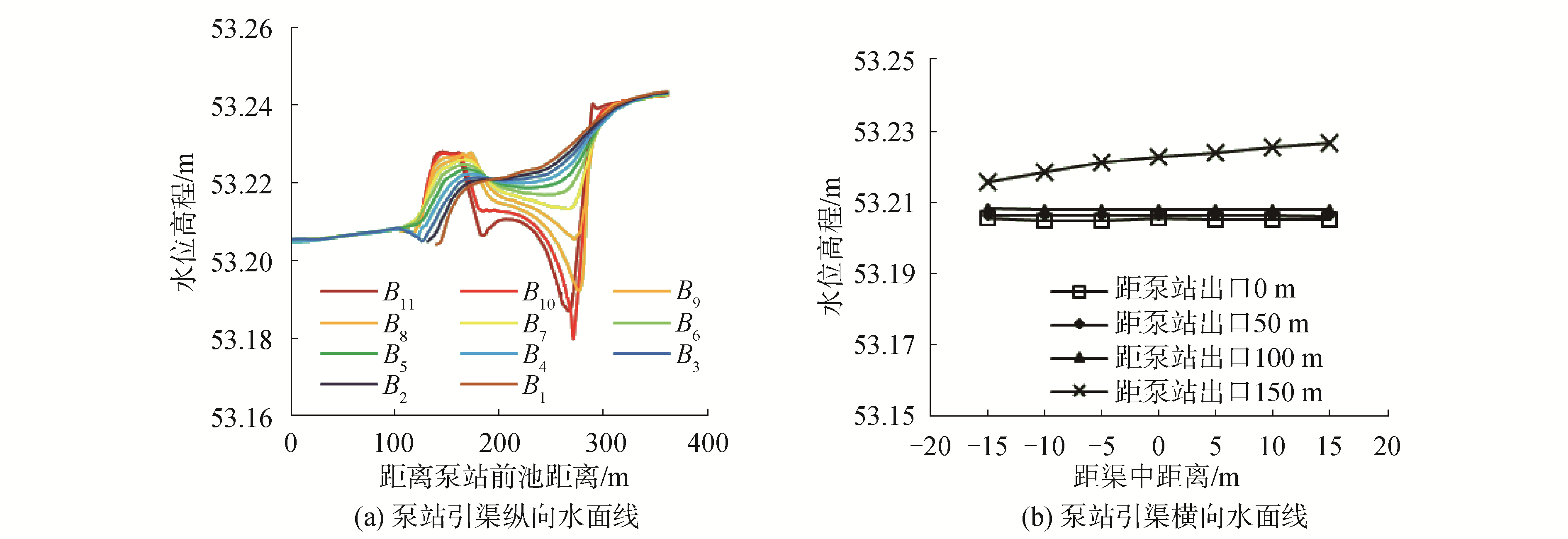
为了更加详细地研究节制闸与泵站附近的水面线与流场,选取泵站前池入口位置为坐标原点,X轴指向上游。以引渠中线为标准,两侧每隔5 m取一个典型纵向断面。泵站引渠共取11个典型纵断面,以Bi(i=1, 2,…,11)表示。横断面按照平行于出口断面向上游,每50 m取一个,泵站引渠共4个典型横断面。
3.2 一期设计模拟结果 3.2.1 水面线分析图 5中,Qtotal=181.98 m3/s,Qpum=36.52 m3/s,由图 5一期设计的节制闸与提水泵站附近的水面等值线图分析可知,泵站引渠内水面平稳,平均比降约为0.15‰,最高水位53.21 m;由于分流的原因,在引渠左导墙前侧出现约为3.5‰的水面比降。
在1#节制闸的前方,节制闸左边墩处水面比右边墩处水面高0.03 m,在闸墩内,右侧水面普遍比左侧水面高0.02 m,节制闸前方水面比降为0.17‰。经过节制闸闸墩后,闸墩后侧水面关于节制闸较为对称,后侧最高水位为53.22 m。
典型横、纵断面水面线如图 6所示。由图 6(a),可以明显看出水流通过1#节制闸时形成的局部水面变化,泵站出口与节制闸前水位相比降低了0.02 m左右。由图 6(b),泵站引渠横向水面线有轻微波动,其中距离泵站出口150 m的横向水面线受到节制闸泄流的影响变化较大,其他横向水面线基本对称。
|
Download:
|
| 图 6 一期设计水面线 Fig. 6 The longitudinal water surface line of the first design | |
流场模拟数据如图 7所示,在泵站前方的引渠内,流速比较均匀,最大流速为0.60 m/s,没有出现漩涡等不良流态;在引渠左岸导墙前端,流速比较集中,最大流速均达到0.90 m/s。

|
Download:
|
| 图 7 一期设计泵站及1#节制闸流场图 Fig. 7 The flow field diagram of the Pumping Station and 1# check gate e of the first design | |
在1#节制闸前方100 m范围内,流动不对称情况较为突出,在节制闸右边墩前端,最大流速达到0.91 m/s,左边墩前端的流速为0.62 m/s,均在上游护砌范围之内。由图 7(b)可知,主流从上游右岸偏向下游左岸,下游最大流速为0.81 m/s,也在下游护砌范围内。
由于泵站引水影响,导致节制闸附近流动不对称情况明显,从而影响节制闸的正常工作;同时由于节制闸泄流影响,导致引水渠道入口左导墙有流速集中现象,不利于引水。节制闸与泵站的相互影响较为明显,需要进行适当优化。
3.3 终期设计模拟结果 3.3.1 水面线分析图 8中,Qtotal′=330.96 m3/s,Qpum′=39.39 m3/s。由图 8终期设计的节制闸与提水泵站附近的水面等值线图分析可知,较一期设计结果,泵站引渠的水面高程变化不大,水面比降为0.08‰,最高水位为53.98 m;由于分流原因,在引渠左导墙前侧出现约为6‰的水面比降。在引渠右岸入口附近因为分流形成一个较大面积壅水,最高壅高达54.01 m。

|
Download:
|
| 图 8 终期设计水位等值线 Fig. 8 Water level contour map of the last design | |
在1#节制闸前方,节制闸左边墩处水面比右边墩处的水面高0.03 m,在闸墩内,左右两侧水面大致相同,节制闸前方水面比降为0.59‰。经过节制闸闸墩后,闸墩后侧水面关于节制闸对称,后侧最高水位为53.93 m。
终期设计典型断面的水面线如图 9所示。由图 10(a)可知,水流通过1#节制闸时形成了明显的局部水面变化,由于泵站引用流量较小,泵站出口与节制闸前水位几乎持平。由图 10(b)可知,受到节制闸泄流的影响,距离泵站出口150 m的横向水面线比一期设计变化更大,泵站取水口附近横向水面线的左岸水位稍微高于右岸,进入取水口平直段后,水面比较平稳,横向水面线基本对称。

|
Download:
|
| 图 9 终期设计水面线 Fig. 9 The longitudinal water surface line of the last design | |

|
Download:
|
| 图 10 泵站及1#节制闸流场图 Fig. 10 The flow field diagram of the Pumping Station and 1# check gate of the last design | |
流场数据如图 10所示。在泵站前方的引渠内,流速不太均匀,在引渠右前侧的最高流速为0.66 m/s,而渠道其他地方的流速为0.45 m/s,但渠道内没有出现漩涡等不良流态;在引渠左岸导墙前端,流速比较集中,最大流速均达到1.05 m/s。
在1#节制闸前方50 m范围内流动不对称情况较突出,在节制闸右边墩前端,流速达到1.38 m/s,左边墩前端的流速为1.18 m/s,均超过了上游护砌范围。由图 10(b)可知,同一期设计情况一样,水流流速方向从上游右岸偏向下游左岸。在节制闸后方,经过整流后的流动比较对称,下游最大流速为1.12 m/s,也超过下游护砌范围。
由于终期设计泵站引水较多,导致节制闸附近流动不对称情况更加明显,从而影响节制闸正常工作;同时由于节制闸泄流影响,导致引水渠道入口左导墙有流速集中现象,不利于引水。节制闸与泵站的相互影响较一期更明显,故需要进行优化。
3.4 综合分析由数值模拟结果分析可知:1#节制闸前方都出现了流动不对称现象,其中终期设计更为显著,这对节制闸的泄水和闸墩冲刷是非常不利的。泵站引渠入口处的流速波动都比较大,且在终期设计时,引渠内产生不均匀的流速,影响泵站正常工作。同时,在节制闸边墩和引渠导墙多处出现限制流速范围超过护砌设计范围。因此无论一期设计还是终期设计,都需要对节制闸与泵站的联合工作进行优化。
4 优化方案及流场分析 4.1 优化方案的确定根据上述数模结果分析和实际工程经验得知,优化方案应从减小闸墩上方壅水、增大过水断面面积和减小泵站引水的局部水头损失2个方面出发。现确定4个优化方案,具体优化措施如表 2所示。
| 表 2 优化方案 Table 2 Optimization schemes |
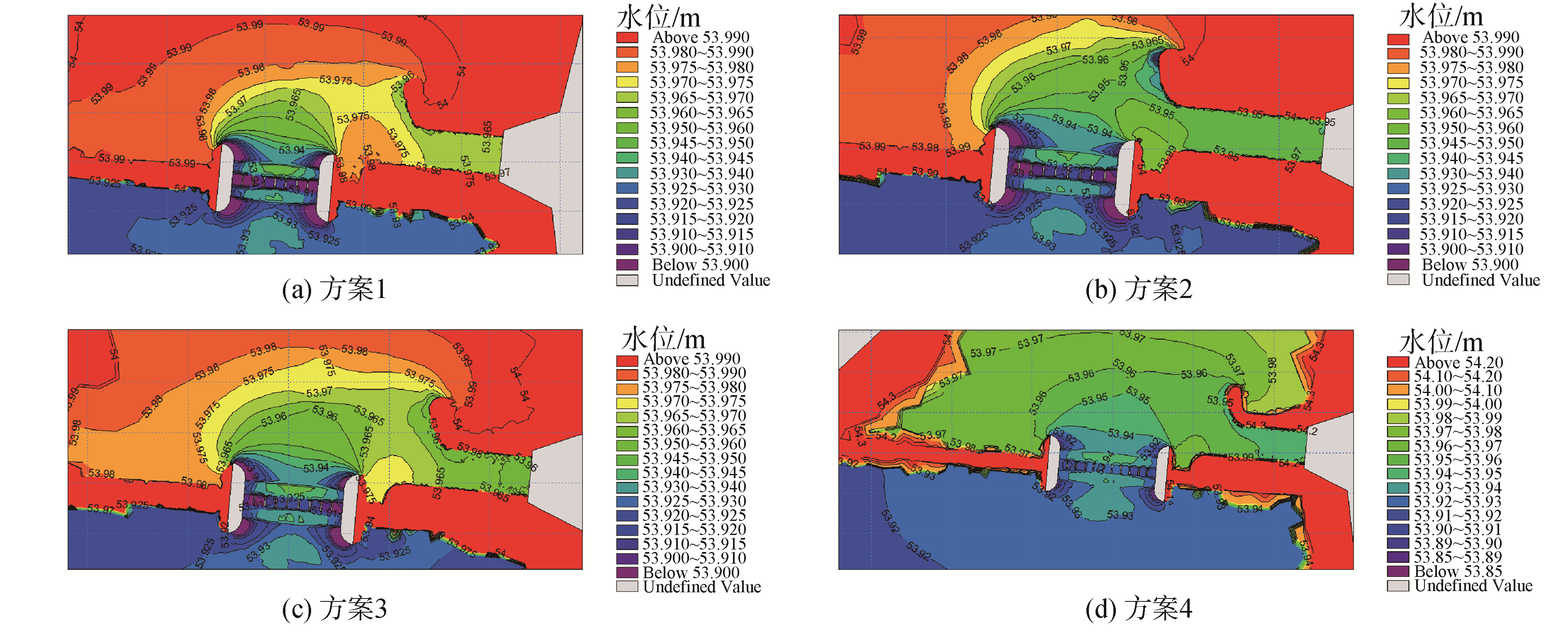
由图 11中的4种优化方案的水位等值线分析可知:方案2单扩一孔无法使泵站的水位等值线对称;方案1、3、4通过移动引水渠导墙,水位大致基于节制闸中心线对称,对于方案2、3、4来说,引水渠前池的水位变化不是很大,这样更利于引水,其中方案4的节制闸下方水位比较稳定。
|
Download:
|
| 图 11 优化方案水位等值线图 Fig. 11 The water-level contour line map of optimization schemes | |
根据4种优化方案的流场数据,方案1改善了节制闸前方的流动不对称性,但节制闸上、下游边墩附近超出0.8 m/s流速的范围比较大。方案2节制闸后方超过0.8 m/s流速的范围有了减小,但是节制闸前方流动依然不对称,且引渠左导墙前流速较大,达到0.9 m/s,不满足要求。
方案3、4通过扩孔与后移导墙的联合布置,有效地降低了引渠左导墙前侧流速,同时可以明显改善节制闸流动对称性,而且节制闸上下游超过0.8 m/s的范围继续减小。较好地改善了节制闸的流场的流动对称性,优化结果基本达到设计要求。
5 结论1) 结合MIKE21 FM水动力模块对泵站和节制闸联合工作情况下的流场进行了数值模拟,分析了水面线和流场数据,获得了泵站和节制闸联合工作的相互影响关系。
2) 针对泵站和1#节制闸流场不对称及流速过大的问题,提出了4个优化方案,由各方案模拟结果对比分析,确定方案4对于改善节制闸流动对称性、降低过闸最大流速、降低引渠左导墙处最大流速是最有利的。
| [1] |
王雷, 史文彪, 杨开林, 等. 南水北调中线惠南庄泵站进水前池布置方案的分析研究[J]. 南水北调与水利科技, 2008, 6(1): 185-193. WANG Lei, SHI Wenbiao, YANG Kailin, et al. Analyses of the layout the forebay of Hui-Nan-Zhuang pump station[J]. South-to-North water transfers and water science and technology, 2008, 6(1): 185-193. DOI:10.3969/j.issn.1672-1683.2008.01.049 (  0) 0)
|
| [2] |
谢省宗, 王雷, 冯宾春, 等. 惠南庄泵站前池流道模型试验研究[J]. 南水北调与水利科技, 2005, 3(4): 4-7. XIE Shengzong, WANG Lei, FENG Binchun, et al. Flow channel hydraulics test for forebay of the Huinanzhuang pumping station[J]. South-to-North water transfers and water science & technology, 2005, 3(4): 4-7. DOI:10.3969/j.issn.1672-1683.2005.04.002 (  0) 0)
|
| [3] |
王芳芳, 吴时强, 肖潇, 等. 三维数值模拟在泵站侧向进水前池的应用[J]. 水利水运工程学报, 2014(2): 54-59. WANG Fangfang, WU Shiqiang, XIAO Xiao, et al. 3-D numerical simulation for side-inlet forebay of a pumping station[J]. Hydro-science and engineering, 2014(2): 54-59. DOI:10.3969/j.issn.1009-640X.2014.02.009 (  0) 0)
|
| [4] |
陈松山, 屈磊飞, 葛强, 等. 泵站枢纽三维湍流数值模拟研究[J]. 扬州大学学报(自然科学版), 2005, 8(2): 70-73. CHEN Songshan, QU Leifei, GE Qiang, et al. Numerical simulation of three-dimension turbulent flow in pumping station projects[J]. Journal of Yangzhou university (natural science edition), 2005, 8(2): 70-73. (  0) 0)
|
| [5] |
高传昌, 刘新阳, 石礼文, 等. 泵站前池与进水池整流方案数值模拟[J]. 水力发电学报, 2011, 30(2): 54-59. GAO Chuanchang, LIU Xinyang, SHI Liwen, et al. Numerical simulation of flow pattern modification schemes for the forebay and suction sump of pumping station[J]. Journal of hydroelectric engineering, 2011, 30(2): 54-59. (  0) 0)
|
| [6] |
虞鸿, 张永进, 刘海泉. 大型泵站前池复杂流场的数值模拟及优化设计[J]. 水电自动化与大坝监测, 2013, 37(4): 66-70. YU Hong, ZHANG Yongjin, LIU Haiquan. Numeric simulation and optimum design for large pump station with complicated flow distribution[J]. Hydropower automation and dam monitoring, 2013, 37(4): 66-70. DOI:10.3969/j.issn.1671-3893.2013.04.017 (  0) 0)
|
| [7] |
CONSTANTINESCU G S, PATEL V C. Numerical model for simulation of pump-intake flow and vortices[J]. Journal of hydraulic engineering, 1998, 124(2): 123-134. DOI:10.1061/(ASCE)0733-9429(1998)124:2(123) (  0) 0)
|
| [8] |
CONSTANTINESCU G S, PATEL V C. Role of turbulence model in prediction of pump-bay vortices[J]. Journal of hydraulic engineering, 2000, 126(5): 387-391. DOI:10.1061/(ASCE)0733-9429(2000)126:5(387) (  0) 0)
|
| [9] |
ALDAMA A A. Pupping rate optimization in a storm drainage system through the combined use of numerical simulation and linear programming[J]. Advances in water resources, 1991, 14(4): 192-202. DOI:10.1016/0309-1708(91)90015-G (  0) 0)
|
| [10] |
ANTONIO P, ALMEIDA S J, ANTONIO A, et al. Socorridos pumping station-numerical modelling[M]//SCHWEIGER H F. Numerical Methods in Geotechnical Engineering: Sixth European Conference on Numerical Methods in Geotechnical Engineering. London: CRC Press, 2006: 367-372.
(  0) 0)
|
| [11] |
耿敬, 张洋, 李明伟, 等. 洪水数值模拟的三维动态可视化方法[J]. 哈尔滨工程大学学报, 2018, 39(7): 1179-1185. GENG Jing, ZHANG Yang, LI Mingwei, et al. Research on 3D dynamic visualization based on flood numerical simulation[J]. Journal of Harbin Engineering University, 2018, 39(7): 1179-1185. (  0) 0)
|
| [12] |
CAMASSA R, HOLM D D. An integrable shallow water equation with peaked solitons[J]. Physical review letters, 1993, 71(11): 1661. DOI:10.1103/PhysRevLett.71.1661 (  0) 0)
|
| [13] |
CONSTANTIN A, ESCHER J. Wave breaking for nonlinear nonlocal shallow water equations[J]. Acta mathematica, 1998, 181(2): 229-243. DOI:10.1007/BF02392586 (  0) 0)
|
| [14] |
IVERSON R M. Landslide triggering by rain infiltration[J]. Water resources research, 2000, 36(7): 1897-1910. DOI:10.1029/2000WR900090 (  0) 0)
|
| [15] |
张洪雨, 李葛飞, 李刚.青龙河总干渠灌溉及泄洪能力数模实验研究[R].黑龙江: 黑龙江农垦勘测设计研究院, 2015.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


