21世纪,各制造强国先后提出了一系列研究计划或战略规划,以确保本国制造业未来竞争力,例如德国的“Industry 4.0”(工业4.0)[1]、“中国制造2025”规划等[2]。无论是工业4.0,还是我国的制造2025,其实质是自动化向数字化、信息化和智能化的进一步发展。作为其重要支撑的仿真技术将得到进一步发展、完善和应用。仿真环境不仅将更真实地模拟制造过程,还将被逐渐用于人机交互以提高制造过程监控的共融性[2-4]。
Wang等[5]针对制造系统提出了网络化的监控系统结构,在该系统中不仅能对工业机器人进行仿真,而且还能以三维可视化环境为基础监控工业机器人的工作过程。Tilbury等[6-7]以三维的虚拟环境为基础,逐步加入物理仿真和通信接口,以实现制造系统仿真和监控相融合的虚拟环境。Abrate等[8]以六自由度的COMAU NS 12工业机器人为研究对象,开发了一个在线的机器人虚拟监控平台。Novák-marcinčin等[9]利用虚拟现实建模语言VRML构建了机器人ROANS的计算机辅助控制系统,可实现三维可视化的机器人操控。Vick等[10]为了分析工业机器人雕刻石雕的工艺过程,设计了通过上层计算机控制机器人的人机交互系统,并通过仿真进行了验证。Sanfilippo等[11]针对KUKA工业机器人的控制系统,利用Java开发了开源的跨平台的监控通信接口JOpenShowVar,以实现机器人的网络化监控。Maly等[12]针对工业4.0描绘的人机交互界面,利用增强现实的数据可视化技术和人机交互技术,构建了工业机器人的监控界面。王宏民等[13]研究了遥操作骨科手术机器人在Internet环境下主从控制的相关问题。
综合上述文献可以看出,机器人作为智能化系统中重要设备,其相关的仿真和监控得到了广泛研究,促进了形象直观的三维可视化交互环境逐渐成为仿真和监控的主要方式。但由于工业机器人开放性较差,加上研究起步较晚,相关理论和技术尚不成熟。鉴于此,本文在前人研究基础上,结合文献[14]和实验条件,以6R工业机器人为研究对象构建仿真系统,并以仿真的三维可视化环境为基础,开源的JOpenShowVar为通信接口实现网络化的、实时的、具有三维可交互人机界面的6R工业机器人监控系统。
1 6R工业机器人的运动学模型 1.1 机器人的正运动学6R工业机器人的基本结构如图 1所示,根据该结构和D-H参数法[15]可为机器人各杆件建立局部坐标系如图 1所示。

|
Download:
|
| 图 1 机器人的三维模型和局部坐标系 Fig. 1 3D models and local coordinate systems of a robot | |
图 1中,坐标系xbybzb是机器人的世界坐标系;坐标系x0y0z0是根据关节1的转动方向为机器人基座建立的局部坐标系;坐标系xfyfzf为机器人的法兰坐标系;其余坐标系分别为各杆件的局部坐标系。根据图中的几何关系和尺寸,可整理得到机器人的D-H参数,如表 1所示。
| 表 1 D-H参数表 Table 1 D-H parameters |
表 1中θ1,θ2,…,θ6为机器人的实际关节角度值。根据表 1的D-H参数,可直接写出机器人的正运动学模型为
| $ {}_6^0\mathit{\boldsymbol{T = }}\left[ {\begin{array}{*{20}{c}} {{T_{11}}}&{{T_{12}}}&{{T_{13}}}&{{T_{14}}}\\ {{T_{21}}}&{{T_{22}}}&{{T_{23}}}&{{T_{24}}}\\ {{T_{31}}}&{{T_{32}}}&{{T_{33}}}&{{T_{34}}}\\ 0&0&0&1 \end{array}} \right] $ | (1) |
为了简化表达,将sin θi记为Si,cos θi记为Ci,则式(1)中T11,T21,…, T34分别为:
| $ \begin{array}{*{20}{c}} {{T_{11}} = {C_1}{C_2}{S_3}{S_4}{S_6} - {C_5}{C_6}{S_1}{S_4} - {C_1}{C_2}{C_3}{C_6}{S_5} - }\\ {{C_4}{S_1}{S_6} + {C_1}{C_3}{S_2}{S_4}{S_6} + {C_1}{C_6}{S_2}{S_3}{S_5} - }\\ {{C_1}{C_2}{C_4}{C_5}{C_6}{S_3} - {C_1}{C_3}{C_4}{C_5}{C_6}{S_2}} \end{array} $ | (2) |
| $ \begin{array}{*{20}{c}} {{T_{21}} = {C_2}{C_3}{C_6}{S_1}{S_5} - {C_1}{C_5}{C_6}{S_4} - {C_1}{C_4}{S_6} - }\\ {{C_2}{S_1}{S_3}{S_4}{S_6} - {C_3}{S_1}{S_2}{S_4}{S_6} - }\\ {{C_6}{S_1}{S_2}{S_3}{S_5} + {C_2}{C_4}{C_5}{C_6}{S_1}{S_3} + }\\ {{C_3}{C_4}{C_5}{C_6}{S_1}{S_2}} \end{array} $ | (3) |
| $ \begin{array}{*{20}{c}} {{T_{31}} = {C_2}{C_3}{S_4}{S_6} + {C_2}{C_6}{S_3}{S_5} + {C_3}{C_6}{S_2}{S_5} - }\\ {{S_2}{S_3}{S_4}{S_6} - {C_2}{C_3}{C_4}{C_5}{C_6} + {C_4}{C_5}{C_6}{S_2}{S_3}} \end{array} $ | (4) |
| $ \begin{array}{*{20}{c}} {{T_{12}} = {C_4}{C_6}{S_1} - {C_5}{S_1}{S_4}{S_6} - {C_1}{C_2}{C_6}{S_3}{S_4} - }\\ {{C_1}{C_3}{C_6}{S_2}{S_4} - {C_1}{C_2}{C_3}{S_5}{S_6} + {C_1}{S_2}{S_3}{S_5}{S_6} - }\\ {{C_1}{C_2}{C_4}{C_5}{S_3}{S_6} - {C_1}{C_3}{C_4}{C_5}{S_2}{S_6}} \end{array} $ | (5) |
| $ \begin{array}{*{20}{c}} {{T_{22}} = {C_1}{C_4}{C_6} - {C_1}{C_5}{S_4}{S_6} + {C_2}{C_6}{S_1}{S_3}{S_4} + }\\ {{C_3}{C_6}{S_1}{S_2}{S_4} + {C_2}{C_3}{S_1}{S_5}{S_6} - {S_1}{S_2}{S_3}{S_5}{S_6} + }\\ {{C_2}{C_4}{C_5}{S_1}{S_3}{S_6} + {C_3}{C_4}{C_5}{S_1}{S_2}{S_6}} \end{array} $ | (6) |
| $ \begin{array}{*{20}{c}} {{T_{32}} = {C_6}{S_2}{S_3}{S_4} - {C_2}{C_3}{C_6}{S_4} + {C_2}{S_3}{S_5}{S_6} + }\\ {{C_3}{S_2}{S_5}{S_6} - {C_2}{C_3}{C_4}{C_5}{S_6} + {C_4}{C_5}{S_2}{S_3}{S_6}} \end{array} $ | (7) |
| $ \begin{array}{*{20}{c}} {{T_{13}} = {C_1}{C_2}{C_3}{C_5} - {S_1}{S_4}{S_5} - {C_1}{C_5}{S_2}{S_3} - }\\ {{C_1}{C_2}{C_4}{S_3}{S_5} - {C_1}{C_3}{C_4}{S_2}{S_5}} \end{array} $ | (8) |
| $ \begin{array}{*{20}{c}} {{T_{23}} = {C_5}{S_1}{S_2}{S_3} - {C_2}{C_3}{C_5}{S_1} - {C_1}{S_4}{S_5} + }\\ {{C_2}{C_4}{S_1}{S_2}{S_5} + {C_3}{C_4}{S_1}{S_2}{S_5}} \end{array} $ | (9) |
| $ {T_{33}} = {C_4}{S_2}{S_3}{S_5} - {C_3}{C_5}{S_2} - {C_2}{C_3}{C_4}{S_5} - {C_2}{C_5}{S_3} $ | (10) |
| $ \begin{array}{*{20}{c}} {{T_{14}} = 260{C_1} + 680{C_1}{C_2} - 670{C_1}{S_2}{S_3} + }\\ {670{C_1}{C_2}{C_3} - 35{C_1}{C_2}{S_3} - 35{C_1}{C_3}{S_2}} \end{array} $ | (11) |
| $ \begin{array}{*{20}{c}} {{T_{24}} = 260{S_1} + 680{C_2}{S_1} - 35{C_2}{S_1}{S_3} - }\\ {35{C_3}{S_1}{S_2} - 670{S_1}{S_2}{S_3} + 670{C_2}{C_3}{S_1}} \end{array} $ | (12) |
| $ \begin{array}{*{20}{c}} {{T_{34}} = 35{C_2}{C_3} - 35{S_2}{S_3} + 670{C_2}{S_3} + }\\ {670{C_3}{S_2} + 680{S_2}} \end{array} $ | (13) |
根据式(1)可进一步得到机器人世界坐标系xbybzb和法兰坐标系xfyfzf之间的变换矩阵为:
| $ {}_f^b\mathit{\boldsymbol{T = }}\left[ {\begin{array}{*{20}{c}} {{T_{11}}}&{{T_{12}}}&{{T_{13}}}&{158{T_{13}} + {T_{14}}}\\ { - {T_{21}}}&{ - {T_{22}}}&{ - {T_{23}}}&{ - 158{T_{23}} - {T_{24}}}\\ { - {T_{31}}}&{ - {T_{32}}}&{ - {T_{33}}}&{675 - {T_{34}} - 158{T_{33}}}\\ 0&0&0&1 \end{array}} \right] $ | (14) |
机器人逆运动学的求解方法主要有数值法和解析法两大类,数值法可省去推导逆解模型的复杂过程,但需要进行迭代计算,而且每次迭代只能求解得到一组结果。解析法在推导得到复杂的逆解模型后,就能高效地计算得到逆解的所有结果。本文中,实时的计算效果是保证实时仿真的前提,因此利用解析法求解机器人逆运动学的所有逆解更适用于本文的研究。
1) 求解θ1。
由式(11)和式(12)可解得:
| $ {\theta _1} = \arctan \left( {\frac{{{T_{24}}}}{{{T_{14}}}}} \right) + k{\rm{ \mathsf{ π} }} $ | (15) |
式中:在保证θ1处于工作区间[-185, 185]的前提下k的取值可能为-1、0或1。此外,当T14=0时,θ1=±π/2;当T14和T24同时为0时,机器人处于奇异位置,无封闭逆解。
2) 求解θ2。
与θ1不同,θ2难以从式(2)~(13)中直接变换得到,为此可根据机器人正运动学模型构造为:
| $ {}_2^1{\mathit{\boldsymbol{T}}^{ - 1}} \cdot {}_1^0{\mathit{\boldsymbol{T}}^{ - 1}} \cdot {}_6^0\mathit{\boldsymbol{T}} = {}_3^2\mathit{\boldsymbol{T}} \cdot {}_4^3\mathit{\boldsymbol{T}} \cdot {}_5^4\mathit{\boldsymbol{T}} \cdot {}_6^5\mathit{\boldsymbol{T}} $ | (16) |
由式(16)中的矩阵元素相等,可解得:
| $ {\theta _2} = \arcsin \left( {\frac{c}{{\sqrt {{a^2} + {b^2}} }}} \right) - \gamma + 2k{\rm{ \mathsf{ π} }} $ |
或
| $ {\rm{ \mathsf{ π} }} - \arcsin \left( {\frac{c}{{\sqrt {{a^2} + {b^2}} }}} \right) - \gamma + 2k{\rm{ \mathsf{ π} }} $ | (17) |
式中:γ=arctan2(a, b),k为整数,但k取值需保证θ2处于工作区间[-155, 35],a、b、c分别为:
| $ \left\{ \begin{array}{l} a = 353\;600 - 1\;360{T_{14}}{C_1} - 1\;360{T_{24}}{S_1}\\ b = - 1\;360{T_{34}}\\ c = 520{T_{14}}{C_1} + 520{T_{24}}{S_1} - {\left( {{C_1}} \right)^2}\left( {{{\left( {{T_{14}}} \right)}^2} - } \right.\\ \;\;\;\;\;\left. {{{\left( {{T_{24}}} \right)}^2}} \right) - {\left( {{T_{24}}} \right)^2} - {\left( {{T_{34}}} \right)^2} - \\ \;\;\;\;\;{T_{14}}{T_{24}}\sin \left( {2{\theta _1}} \right) - 79\;875 \end{array} \right. $ | (18) |
3) 求解θ3。
与θ2的求解类似,可解得θ3为
| $ \begin{array}{*{20}{c}} {{\theta _3} = \pm \arcsin \left( {\frac{{260{S_2} + {T_{34}}{C_2} - {T_{14}}{C_1}{S_2} - {T_{24}}{S_1}{S_2}}}{{\sqrt {450125} }}} \right) - }\\ {\arctan 2\left( {35,670} \right) + k{\rm{ \mathsf{ π} }}} \end{array} $ | (19) |
式中:k为整数,但k的取值需保证θ3处于工作区间[-130, 154]。
4) 求解θ5。
| $ \begin{array}{*{20}{c}} {{\theta _5} = 2k{\rm{ \mathsf{ π} }} \pm {\rm{arccos}}\left( {{T_{33}}{C_2}{S_3} + {T_{33}}{C_3}{S_2} + {T_{13}}{C_1}{C_2}{C_3} + } \right.}\\ {\left. {{T_{23}}{C_2}{C_3}{S_1} - {T_{13}}{C_1}{S_2}{S_3} - {T_{23}}{S_1}{S_2}{S_3}} \right)} \end{array} $ | (20) |
式中:k为整数,但k的取值需保证θ5处于工作区间[-130, 130]。
5) 求解θ4。
| $ \begin{array}{*{20}{c}} {{\theta _5} = 2k{\rm{ \mathsf{ π} }} \pm {\rm{arccos}}\left( {\left( {{T_{33}}{C_2}{C_3} - {T_{33}}{S_2}{S_3} - {T_{13}}{C_1}{C_2}{S_3} - } \right.} \right.}\\ {\left. {\left. {{T_{13}}{C_1}{C_3}{S_2} - {T_{23}}{C_2}{S_1}{S_3} - {T_{23}}{C_3}{S_1}{S_2}} \right)/{S_5}} \right)} \end{array} $ | (21) |
式中:k为整数,但k的取值需保证θ4处于工作区间[-350, 350]。此外,由式(21)可求解得到θ4的充分条件为S5≠0。然而根据机器人的结构简图可以看出S5=0时,即第4个关节和第5个关节的轴线共线,机器人则处于奇异位置,无封闭逆解。
6) 求解θ6。
| $ \begin{array}{*{20}{c}} {{\theta _6} = k{\rm{ \mathsf{ π} }} \pm \arcsin \left( {\left( {{T_{12}}{C_1}{S_2}{S_3} - {T_{32}}{C_3}{S_2} - {T_{12}}{C_1}{C_2}{C_3} - } \right.} \right.}\\ {\left. {\left. {{T_{22}}{C_2}{C_3}{S_1} - {T_{32}}{C_2}{S_3} - {T_{22}}{S_1}{S_2}{S_3}} \right)/{S_5}} \right)} \end{array} $ | (22) |
式中:k为整数,但k的取值需保证θ6处于工作区间[-350, 350]。
至此,已得到所有关节角的解析解,即运动学逆解。但求解θ2时采用了平方的形式,为避免增根,在逆解得到所有解后,需代入式(14)中进行验根。
1.3 机器人的雅克比矩阵雅克比矩阵是指描述机器人关节角速度和执行端速度的线性变换关系。由其构成的关节空间到笛卡尔空间的速度变换关系可表示为:
| $ \mathit{\boldsymbol{V}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{v}}\\ \mathit{\boldsymbol{w}} \end{array}} \right] = \mathit{\boldsymbol{J\dot \theta }} $ | (23) |
式中:V为机器人执行端在笛卡尔空间的广义速度;J即为与关节角度值有关的雅克比矩阵;v为机器人执行端的线速度;
雅克比矩阵J的求解可直接利用正运动模型求导得到,但只能直接得到整体的雅克比矩阵。另一种求解雅克比矩阵的矢量积方法[16],不仅可得到整体的雅克比矩阵,而且还可获得机器人每个杆件的线速度和角速度。因此,本文选择后一种方法为机器人建立雅克比矩阵。
根据图 1建立的局部参考坐标系可直接写出坐标系xi+1yi+1zi+1原点(杆件i+1)的旋转角速度为
| $ \left\{ \begin{array}{l} {}^0{\mathit{\boldsymbol{\omega }}_1} = {{\dot \theta }_1} \cdot {\left[ {\begin{array}{*{20}{c}} 0&0&1 \end{array}} \right]^{\rm{T}}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 0\\ {}^{i - 1}{\mathit{\boldsymbol{\omega }}_{i + 1}} = {}^{i - 1}{\mathit{\boldsymbol{\omega }}_i} + _i^{i - 1}\mathit{\boldsymbol{R}} \cdot \left[ {{{\dot \theta }_{I + 1}} \cdot \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 1 \end{array}} \right]} \right],\;\;\;\;i = 1,2, \cdots ,5 \end{array} \right. $ | (24) |
式中:i-1ωi+1为旋转角速度在坐标系xi-1yi-1zi-1下的矢量形式;
同样地,可直接写出坐标系xi+1yi+1zi+1原点(杆件i+1)的线速度为:
| $ \left\{ \begin{array}{l} {}^0{\mathit{\boldsymbol{v}}_0} = 0,\;\;\;i = 0\\ {}^i{\mathit{\boldsymbol{v}}_{i + 1}} = {}^i{\mathit{\boldsymbol{v}}_i} + {}^i{\mathit{\boldsymbol{\omega }}_{i + 1}} \times {}^i{\mathit{\boldsymbol{P}}_{i + 1}},\;\;\;\;\;i = 1,2, \cdots ,5 \end{array} \right. $ | (25) |
式中:ivi+1为线速度在坐标系xiyizi下的矢量形式;iPi+1为坐标系xi+1yi+1zi+1的原点在坐标系xiyizi下的位置坐标。
根据式(24)和式(25)可整理得到机器人执行端的旋转角速度ω和线速度v分别为:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\omega }} = \left( {{}_5^0\mathit{\boldsymbol{R}} \cdot {{\dot \theta }_6} + {}_4^0\mathit{\boldsymbol{R}} \cdot {{\dot \theta }_5} + {}_3^0\mathit{\boldsymbol{R}} \cdot {{\dot \theta }_4} + {}_2^0\mathit{\boldsymbol{R}} \cdot {{\dot \theta }_3} + } \right.}\\ {\left. {{}_1^0\mathit{\boldsymbol{R}} \cdot {{\dot \theta }_2} + {{\dot \theta }_1}} \right) \cdot {{\left[ {\begin{array}{*{20}{c}} 0&0&1 \end{array}} \right]}^{\rm{T}}}} \end{array} $ | (26) |
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{v}} = {}_5^0\mathit{\boldsymbol{R}} \cdot \left( {{}^5{\mathit{\boldsymbol{\omega }}_6} \times {}^5{\mathit{\boldsymbol{P}}_6}} \right) + {}_4^0\mathit{\boldsymbol{R}} \cdot \left( {{}^4{\mathit{\boldsymbol{\omega }}_5} \times {}^4{\mathit{\boldsymbol{P}}_5}} \right) + }\\ {{}_3^0\mathit{\boldsymbol{R}} \cdot \left( {{}^3{\mathit{\boldsymbol{\omega }}_4} \times {}^3{\mathit{\boldsymbol{P}}_4}} \right) + {}_2^0\mathit{\boldsymbol{R}} \cdot \left( {{}^2{\mathit{\boldsymbol{\omega }}_3} \times {}^2{\mathit{\boldsymbol{P}}_3}} \right) + }\\ {{}_1^0\mathit{\boldsymbol{R}} \cdot \left( {{}^1{\mathit{\boldsymbol{\omega }}_2} \times {}^1{\mathit{\boldsymbol{P}}_2}} \right) + {}^0{\mathit{\boldsymbol{\omega }}_1} \times {}^0{\mathit{\boldsymbol{P}}_1}} \end{array} $ | (27) |
由此,可进一步整理得到机器人雅克比矩阵J中的i+1列为:
| $ {\mathit{\boldsymbol{J}}_{i + 1}} = \left[ {\begin{array}{*{20}{c}} {{}_i^0\mathit{\boldsymbol{R}} \cdot \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 1 \end{array}} \right] \times {}^0\mathit{\boldsymbol{P}}_6^i}\\ {{}_i^0\mathit{\boldsymbol{R}} \cdot \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ 1 \end{array}} \right]} \end{array}} \right] $ | (28) |
式中:0P6i=50R·5P6+…+i0R·iPi+1,i=0, 1, …, 5。
2 仿真和监控平台的搭建机器人的仿真和监控平台可分为具备人机交互的可视化环境、控制指令编译和运行、以及监控通信接口三大模块。为此,分别对3部分的实现方法进行阐述。
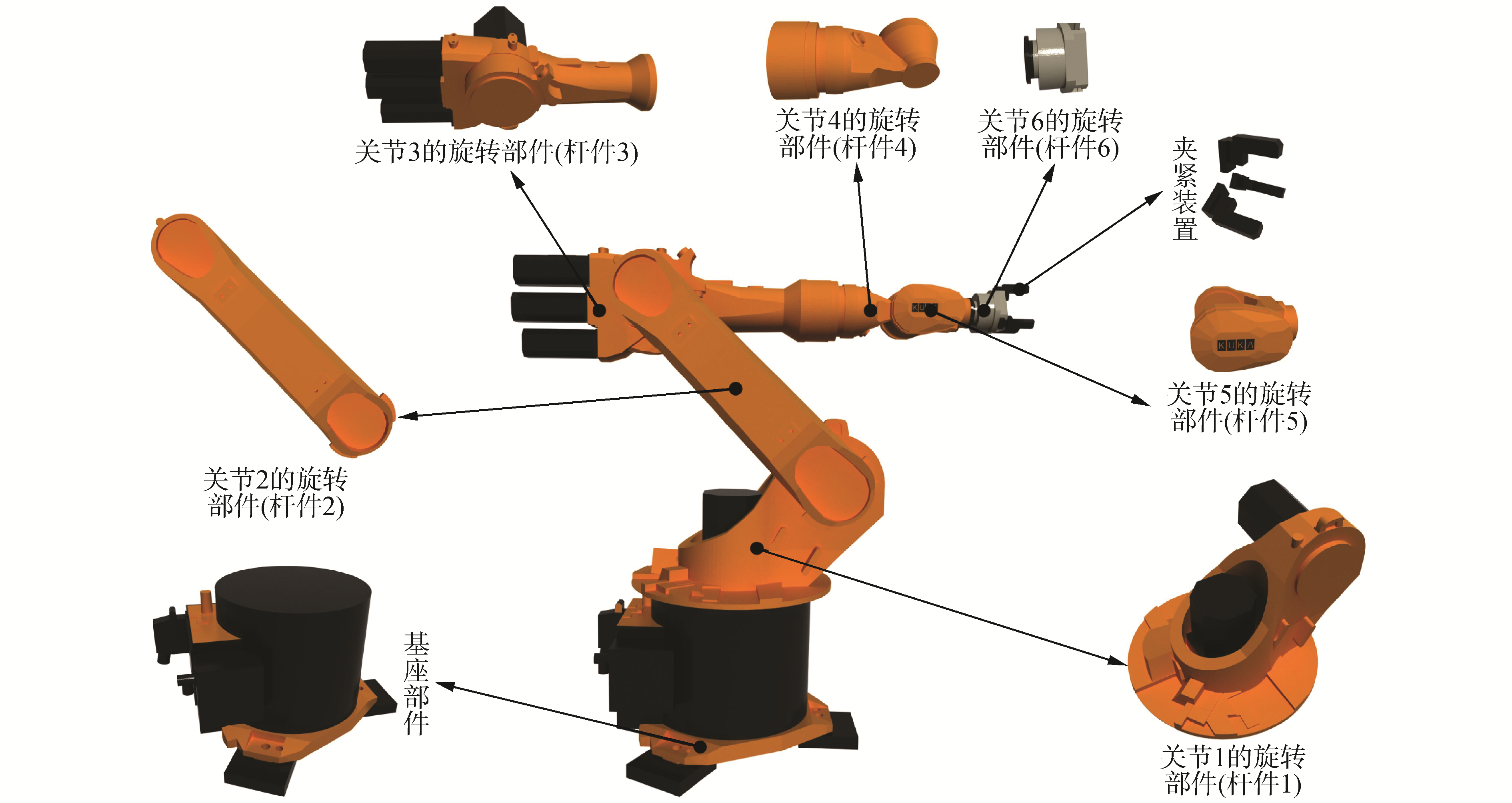
2.1 仿真和监控的可视化环境借助建模软件为机器人建立1:1的三维模型。显然,机器人是由众多零件组成的综合系统,其内部具有复杂的零件结构和装配关系。但对于本文的仿真和监控而言,可视化环境是对机器人空间位置和运动状态的直观描述,并不涉及其内部零件的具体细节,因此建模时可按照独立原则和运动关系将机器人分为不同的运动部件,建立对应的部件模型,如图 2所示。
|
Download:
|
| 图 2 机器人的部件模型分类 Fig. 2 Classification of component models of a robot | |
根据图 2中的部件分类和运动关系可进一步建立机器人各部件模型的逻辑从属关系,如图 3所示。图 3采用了3层次结构树来描述机器人各部件模型的从属关系,分别为机器人树、运动树和部件树。固定不动的机器人部件模型,在可视化环境中只需要给定位置和方向属性即可;而对于处于运动关系下的部件模型,除了给定位置和方向属性外,还需要根据其从属关系设定相应的运动属性,以便在可视化环境中实现相应的运动效果。

|
Download:
|
| 图 3 机器人部件模型的逻辑从属关系 Fig. 3 Inter-dependent relationships between the component models of a robot | |
控制指令编译和运行是机器人仿真的核心功能。对于本文的KUKA机器人控制系统,其控制指令是由SRC程序源文件和DAT数据文件组成。SRC程序源文件中具有变量使用、函数调用、条件判断等详细的程序语句。在SRC文件中所使用的变量,其定义和赋值则来自于DAT文件。因此,可根据控制指令文件的形式设计机器人的控制指令编译和运行流程,如图 4所示。

|
Download:
|
| 图 4 机器人的控制指令编译和运行流程 Fig. 4 Process diagram of compiling a robot program | |
图 4中将机器人控制指令的编译和运行流程分为了仿真前的初始化和仿真过程中的数据处理。仿真前初始化的实质是将控制指令中的信息提取到结构体数组中,以便于进一步处理和应用。而对于代码遍历(信息提取)过程,则是以机器人控制指令规定的折合标识符作为循环提取标识。从机器人控制指令中提取到的控制信息,即为期望的关节位置或执行端工具运动状态。为了将控制信息用于驱动可视化环境中机器人模型,以实现机器人仿真。在控制机器人模型运行阶段则采用PID控制作为设计仿真平台中控制器的基本形式。
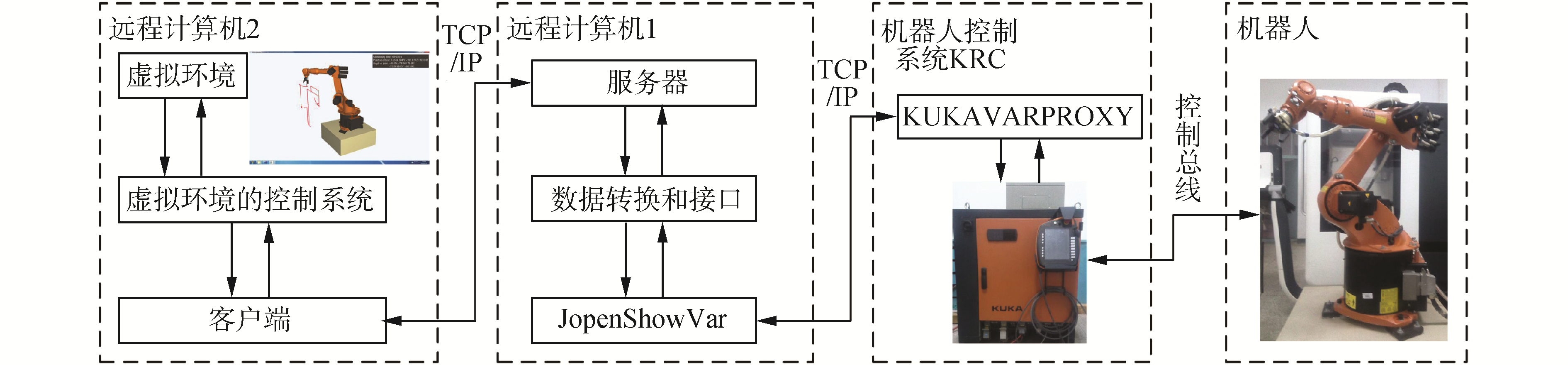
2.3 监控的通信结构和接口针对KUKA机器人控制系统,利用免费开源的网络通信开发包JOpenShowVar[11]设计监控的通信结构,如图 5所示。
|
Download:
|
| 图 5 机器人监控的通信结构 Fig. 5 Communication architecture of monitoring a robot | |
图 5中,KUKAVARPROXY为网络通信开发包的服务器,负责完成与机器人的读写操作,以及与上级客户端的通信。JopenShowVar则为开发包的通信类,通过调用该类中的函数可实现与服务器KUKAVARPROXY的通信。此外,由于开发包的通信类是通过Java语言来实现的,而Java语言相比于C++语言在处理数据方面其计算能力较差。然而机器人的虚拟监控正需要实时地处理大量数据,并需要实现渲染显示机器人的运行状态和轨迹。正因如此,为了保证虚拟监控的实时性,在机器人的虚拟监控系统中拟使用2台计算机实现监控过程。其中远程计算机1主要完成数据转化,由Java语言开发实现。而远程计算机2则是虚拟监控的主要程序,包括实时渲染显示监控结果(机器人的可视化环境),由C++语言和OpenGL图形接口实现。
3 实验验证为了验证前述内容正确性,利用C+ +语言、Java语言、OpenGL图形接口[17]、以及矩阵运算软件包Eigen 3.2.5[18]开发实现机器人仿真和监控系统。
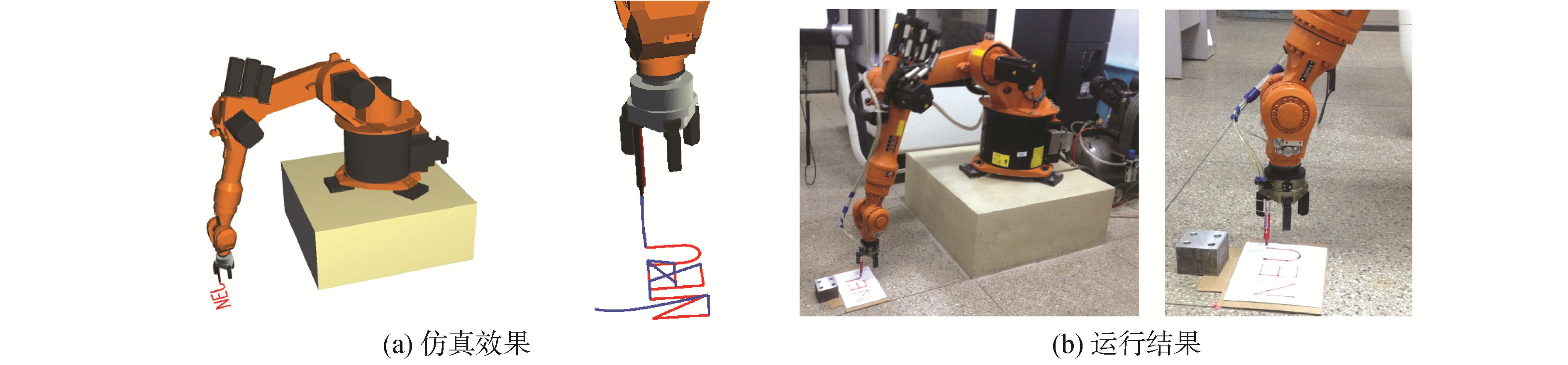
3.1 仿真和运行实例对比图 6为一段典型控制指令在仿真平台上的仿真效果和机器人实际运行结果对比。
|
Download:
|
| 图 6 机器人仿真和运行实例 Fig. 6 Examples of simulation and operation of a robot | |
该段控制指令是控制机器人书写“NEU”字符的工作过程。在仿真效果图中轨迹为书写“NEU”字符的过渡轨迹,为了便于对比观察仿真效果和运行结果,在仿真过程中过渡轨迹的绘制功能可随时关闭和打开,仿真的观察视角也可任意变换和缩放。对比图 6中同一段控制指令的仿真效果和运行结果可以看出,仿真和实际运行轨迹相同,由此可验证文中运动学模型、雅克比矩阵和程序模块的正确性和可靠性。
3.2 监控测试根据图 5描述的监控通信结构,连接机器人网络化的监控硬件平台,如图 7所示。其中,各远程计算机的主要硬件参数如表 2所示。

|
Download:
|
| 图 7 监控机器人的硬件平台 Fig. 7 Hardware platform of monitoring a robot | |
| 表 2 远程计算机的硬件参数 Table 2 Hardware parameters of remote computers |
为了保证网络通信的稳定性,设置机器人为固定IP,且通信端口为7 000。为此,可通过机器人的控制面板设置固定IP和端口,同时还需要将机器人的网络通信协议设置为TCP/IP,具体的设置过程如图 8所示。相应的设置远程计算机为固定IP,以保证IP地址与机器人的IP地址处于同一子网,具体设置如图 9所示。

|
Download:
|
| 图 8 机器人的网络配置 Fig. 8 Network configuration of a robot | |
|
Download:
|
| 图 9 远程计算机的IP设置 Fig. 9 IP configuration of remote computers | |
在图 7的硬件平台上运行系统的各监控模块,可得到机器人监控效果和数据如图 10所示。图 10为控制机器人做任意运动时的监控效果。远程计算机2上虚拟监控的可视化环境可形象直观地实时显示机器人的位置姿态,同时绘制了机器人执行端的运行轨迹。而远程计算机1则实现了监控数据在机器人和虚拟监控端的传输,且监控数据读取耗时基本在5 ms左右,而其最大耗时在20 ms以内。由此可以说明实现的监控系统不仅具有形象直观的人机界面,还具有良好的实时性。
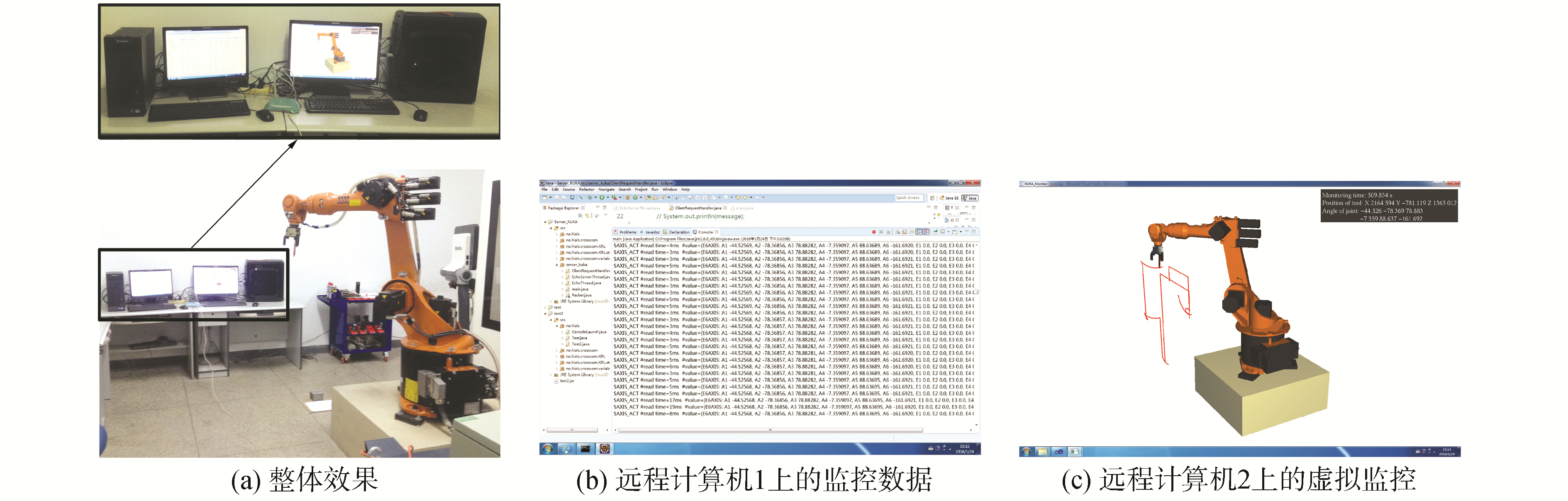
|
Download:
|
| 图 10 机器人的虚拟监控效果 Fig. 10 Virtual monitoring of a robot | |
1) 该仿真系统符合工业机器人的实际控制结构,更接近机器人的实际运行过程,并且完全利用C++语言和OpenGL图形接口从底层开发实现,因此其仿真模块能够得到灵活的改进、完善和应用,具有良好的科研和应用价值。
2) 仿真和监控系统初步实现了以虚拟环境作为人机交互界面的工业机器人监控,通过实验测试其最大延迟在20 ms以内,具有良好的实时性。
此外,该系统采用了多机协作的网络化监控,为进一步补充和完善机器人的智能化监控功能预留了充足的硬件计算资源。因此,可在此系统基础上展开工业机器人监控的后续研究和开发,促进工业机器人从自动化向智能化转变,以顺应工业4.0或制造2025所倡导的智能制造发展趋势。
| [1] |
张曙. 工业4.0和智能制造[J]. 机械设计与制造工程, 2014, 43(8): 1-5. ZHANG Shu. The industry 4.0 and intelligent manufacturing[J]. Machine design and manufacturing engineering, 2014, 43(8): 1-5. DOI:10.3969/j.issn.2095-509X.2014.08.001 (  0) 0)
|
| [2] |
贺正楚, 潘红玉. 德国"工业4.0"与"中国制造2025"[J]. 长沙理工大学学报(社会科学版), 2015, 30(3): 103-110. HE Zhengchu, PAN Hongyu. Germany "industry 4.0" and "Made in China 2025"[J]. Journal of Changsha University of Science & Technology (social science), 2015, 30(3): 103-110. DOI:10.3969/j.issn.1672-934X.2015.03.014 (  0) 0)
|
| [3] |
RVßMANN M, LORENZ M, GERBERT P, et al. Industry 4.0:The future of productivity and growth in manufacturing industries[M]. Boston: The Boston consulting group, 2015: 1-14.
(  0) 0)
|
| [4] |
喜崇彬. 工业4.0下机器人行业的发展机遇——访IHS工业自动化-亚太研究组研究总监张键[J]. 物流技术与应用, 2015, 20(6): 103-106. XI Chongbin. Development opportunity of industrial robot with Industry 4.0——interviewing Zhang Jian, majordomo of IHS industrial automation Asia-pacific research group[J]. Logistics & material handling, 2015, 20(6): 103-106. (  0) 0)
|
| [5] |
WANG Lihui. Planning towards enhanced adaptability in digital manufacturing[J]. International journal of computer integrated manufacturing, 2011, 24(5): 378-390. DOI:10.1080/0951192X.2010.506657 (  0) 0)
|
| [6] |
HARRISON S H. Virtual fusion: the integration and analysis of simulation and real process for manufacturing process deployment[D]. Michigan: University of Michigan, 2011: 20-106.
(  0) 0)
|
| [7] |
MOYNE J, HARRISON Ⅲ W S. Virtual fusion: the complete integration of simulation for reduced ramp-up and reconfiguration cost[EB/OL]. Ann Arbor: NSF Engineering Research Center for Reconfigurable Manufacturing Systems, 2009.[2017-06-15]. https://erc.engin.umich.edu/wp-content/uploads/sites/50/2013/08/VirtualFusion.pdf.
(  0) 0)
|
| [8] |
ABRATE F, INDRI M, LAZZERO I, et al. Efficient solutions for programming and safe monitoring of an industrial robot via a virtual cell[C]//Proceedings of 2011 IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Budapest, Hungary, 2011: 434-439. https://ieeexplore.ieee.org/document/6026994
(  0) 0)
|
| [9] |
NOVÁK-MARCINČIN J, DOLIAK M, HLOCH S, et al. Application of the virtual reality modelling language to computer aided robot control system ROANS[J]. Strojarstvo, 2010, 52(2): 227-232. (  0) 0)
|
| [10] |
VICK A, SURDILOVIC D, DRÄGER A K, et al. The industrial robot as intelligent tool carrier for human-robot interactive artwork[C]//Proceedings of the 23rd IEEE International Symposium on Robot and Human Interactive Communication. Edinburgh, UK, 2014: 880-885. https://ieeexplore.ieee.org/document/6926364
(  0) 0)
|
| [11] |
SANFILIPPO F, HATLEDAL L I, ZHANG Houxiang, et al. Controlling Kuka industrial robots:flexible communication interface JOpenShowVar[J]. IEEE robotics & automation magazine, 2015, 22(4): 96-109. (  0) 0)
|
| [12] |
MALÝ I, SEDLÁČEK D, LEITÃO P. Augmented reality experiments with industrial robot in industry 4.0 environment[C]//Proceedings of 2016 IEEE International Conference on Industrial Informatics. Poitiers, France, 2016: 176-181. https://ieeexplore.ieee.org/document/7819154
(  0) 0)
|
| [13] |
王宏民, 杜志江, 闫志远, 等. 遥操作骨科复位手术网络时延控制研究[J]. 哈尔滨工程大学学报, 2016, 37(6): 860-866. WANG Hongmin, DU Zhijiang, YAN Zhiyuan, et al. Research on controlling network time delay in teleoperation orthopedic restoration surgery[J]. Journal of Harbin Engineering university, 2016, 37(6): 860-866. (  0) 0)
|
| [14] |
黎柏春, 杨建宇, 耿磊, 等. 基于实时逆运动学算法的6R机器人三维仿真[J]. 组合机床与自动化加工技术, 2014(3): 45-48. LI Baichun, YANG Jianyu, GENG Lei, et al. Three-dimensional simulation of 6R robot based on real time inverse kinematic algorithm[J]. Modular machine tool & automatic manufacturing technique, 2014(3): 45-48. (  0) 0)
|
| [15] |
蔡自兴, 谢斌. 机器人学[M]. 3版. 北京: 清华大学出版社, 2015: 35-74. CAI Zixing, XIE Bin. Robotics[M]. 3rd ed. Beijing: Tsinghua University Press, 2015: 35-74. (  0) 0)
|
| [16] |
PIRES J N. Industrial robots programming:building applications for the factories of the future[M]. New York: Springer, 2007: 47-57.
(  0) 0)
|
| [17] |
SHREINER D, SELLERS G, KESSENICH J, et al. OpenGL programming guide:the official guide to learning OpenGL, version 4.3[M]. 8th ed. Reading, MA: Addison-Wesley Professional, 2013: 25-189.
(  0) 0)
|
| [18] |
JACOB B, GUENNEBAUD G. Eigen is a C++ template library for linear algebra: matrices, vectors, numerical solvers, and related algorithms[EB/OL]. 2017.[2017-06-15]. http://eigen.tuxfamily.org/index.php?title=Main_Page.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


