机器人技术最基本、广泛的应用是机械臂的操作任务。而其基本功能之一即为末端执行器的目标抓取功能[1-3]。受机械臂性能、多任务操作等因素的影响,机械臂不可能对目标进行精确无偏差的捕获,需要有一定的容差性能。末端执行器也不能保证每次捕获时处于相同初始位置。基于此,对目标位姿进行在线估计有其必要性。各种位姿估计的相关研究分为非接触式估计和接触式估计。
非接触式估计在末端执行器与目标发生接触之前,通过视觉、距离等传感器,结合目标几何特征进行目标位姿估计。Font等[4]通过安装在末端执行器上的双目视觉传感器检测水果采集过程中的目标体积、距离、位置等信息。Mehta等[5]通过安装在固定基座上的视觉传感器,估计目标位置,实现机械臂的闭环控制。在空间机器人捕获非合作目标时,徐文福等[6]提出立体视觉的目标测量方法。胡杰等[7]通过激光扫描测距仪实现攀爬机器人对杆件的位姿检测。张禹等[8-9]采用激光测距传感器实现卫星喷管位姿估计过程。
接触式估计根据末端执行器与目标之间发生接触时的触觉、力、位置等信息进行估计。此处估计的结果不限于二者之间的相对位姿,还可能是接触状态、接触面局部特征等信息,再结合已知的物体特征信息可以进行物体位姿估计过程。接触固定物体时,Tsujimura等[10]提出通过点接触时已知触点几何特征和接触力/矩信息判断接触点坐标和法向向量。当接触非固定物体时,Haidacher等[11]提出只使用灵巧手位置传感器和指尖几何特征,判断接触点位置和法向向量的方法。在得到接触信息的基础上,可以进行物体形状、位姿重构。Phung等[12]提出通过相近区域内的最少的4个接触点计算2个主曲率,最后实现局部三维重构。Yu等[13]通过多次触点操作判断二次曲面位置和几何参数。Moll等[14]通过多点触觉信息,提出同时估计未知凸状物体形状和运动状态的方法。部分学者也针对特定目标捕获任务的目标位姿估计进行了研究,Lam等[15]仅使用触觉传感器完成攀爬机器人的目标杆件建模。Yoon等[16]在夹爪内壁安装4个接触开关,根据接触时的通断信号提示抓取过程是否对齐。
非接触式估计对环境要求较高,有时需要引入其他传感器和视觉靶标,使系统更加复杂。而在系统集成六维力/矩传感器时,进行接触式估计不会增加硬件复杂度。文献中的接触式估计方法一般针对常规几何构型进行位姿估计,考虑特定复杂几何构型的应用较少。此外,大部分研究是基于固定不变的触点信息,忽略了可能出现的触点变化过程。为了解决研制的同步三指式末端执行器捕获过程中的目标位姿估计问题,本文提出基于接触力信息的位姿估计方法,在系统具有两次或冗余接触信息时,分别采用空间平面相交的方法和最小二乘法进行位姿估计,以期为主动规划运动奠定基础。
1 三指式末端执行器 1.1 机械系统吴军等[17-18]已研制了一种同步三指式末端执行器,其结构如图 1所示。3个捕获手指轴对称分布,在同一个驱动器作用下实现同步运动。楔型的对接接口可将捕获手指引导到中心区域。

|
Download:
|
| 图 1 末端执行器及对接接口 Fig. 1 End-effector and grapple interface | |
通过对运动链进行分析,能够在末端执行器坐标系OXeYeZe中表达某个指尖点j坐标为:
| $ {}^e{\mathit{\boldsymbol{T}}_j} = \left[ {\begin{array}{*{20}{c}} {{}^e{T_{jx}}}\\ {{}^e{T_{jy}}}\\ {{}^e{T_{jz}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{f_{{e_{{T_{jx}}}}}}\left( \varphi \right)}\\ {{f_{{e_{{T_{jy}}}}}}\left( \varphi \right)}\\ {{f_{{e_{{T_{jz}}}}}}\left( \varphi \right)} \end{array}} \right],\left( {j = {\rm{I}},{\rm{II}},{\rm{III}}} \right) $ | (1) |
式中φ是作为输入参数的主动连杆角度。
1.2 位姿估计任务假设因捕获过程的复杂性,仅对主要典型因素进行分析,对系统做出如下假设:
1) 碰撞过程中只考虑单点接触的情况;
2) 忽略点接触情况下的摩擦力影响;
3) 忽略末端执行器传动系统中的间隙、柔性等非线性因素的影响;
4) 只分析具有相对较大位姿偏差的初始包络阶段;
5) 对接接口大致向上安装,如图 1所示。
2 位姿估计方法 2.1 接触手指识别方法将对接接口三叶型外壳向其OXiYi平面投影如图 2所示。当末端执行器与对接接口发生接触时,必为某捕获指尖与对应约束面发生接触。无摩擦力的假设使对接接口对末端执行器的作用力必垂直于接触面,以图 2中所示手指Ⅰ与约束面a发生接触为例,垂直接触面的作用力F与Xi轴正向夹角θ为{θ}={50°, 130°, -70°, 10°, 170°, -110°}中元素。因此通过夹角θ=arctan(iFy/iFz)即可判断约束面。在实际接触时,接触力通过末端执行器腕部的六维力/矩传感器进行测量,并转换到坐标系OXeYeZe中表示为eF=iReT·iF。机械臂系统的控制精度可使末端执行器与对接接口之间的姿态偏差保持在较小的范围内,所有可通过eθ=arctan(eFy/eFz)判断约束面,从而判断接触手指。

|
Download:
|
| 图 2 对接接口投影平面 Fig. 2 Projection plane of the grapple interface | |
通过接触手指识别方法和末端执行器运动学分析,可根据当前接触的力/矩信息得到当前接触指尖中心点T在坐标系OXeYeZe中的坐标为eT。经过接触点C并与接触力F共线的直线被称为外力向量线[10]。由于无摩擦力的假设及指尖球面特征,指尖接触力必通过接触点C及其球面中心,即指尖中心点T。因此可得接触点C坐标为:
| $ {}^e\mathit{\boldsymbol{C}} = {}^e\mathit{\boldsymbol{T}} - r{}^e\mathit{\boldsymbol{F}}/\left\| {{}^e\mathit{\boldsymbol{F}}} \right\| $ | (2) |
式中r为指尖球面半径。
接触力F应与对接接口的对应约束面垂直,因而约束面的的单位法向向量n可选为与F同向,在坐标系OXeYeZe中表达为:
| $ {}^e\mathit{\boldsymbol{n}} = {}^e\mathit{\boldsymbol{F}}/\left\| {{}^e\mathit{\boldsymbol{F}}} \right\| $ | (3) |
将坐标系OXeYeZe中表达的接触点坐标eC和单位向量en转换到坐标系OXoYoZo中,得到oC和on。
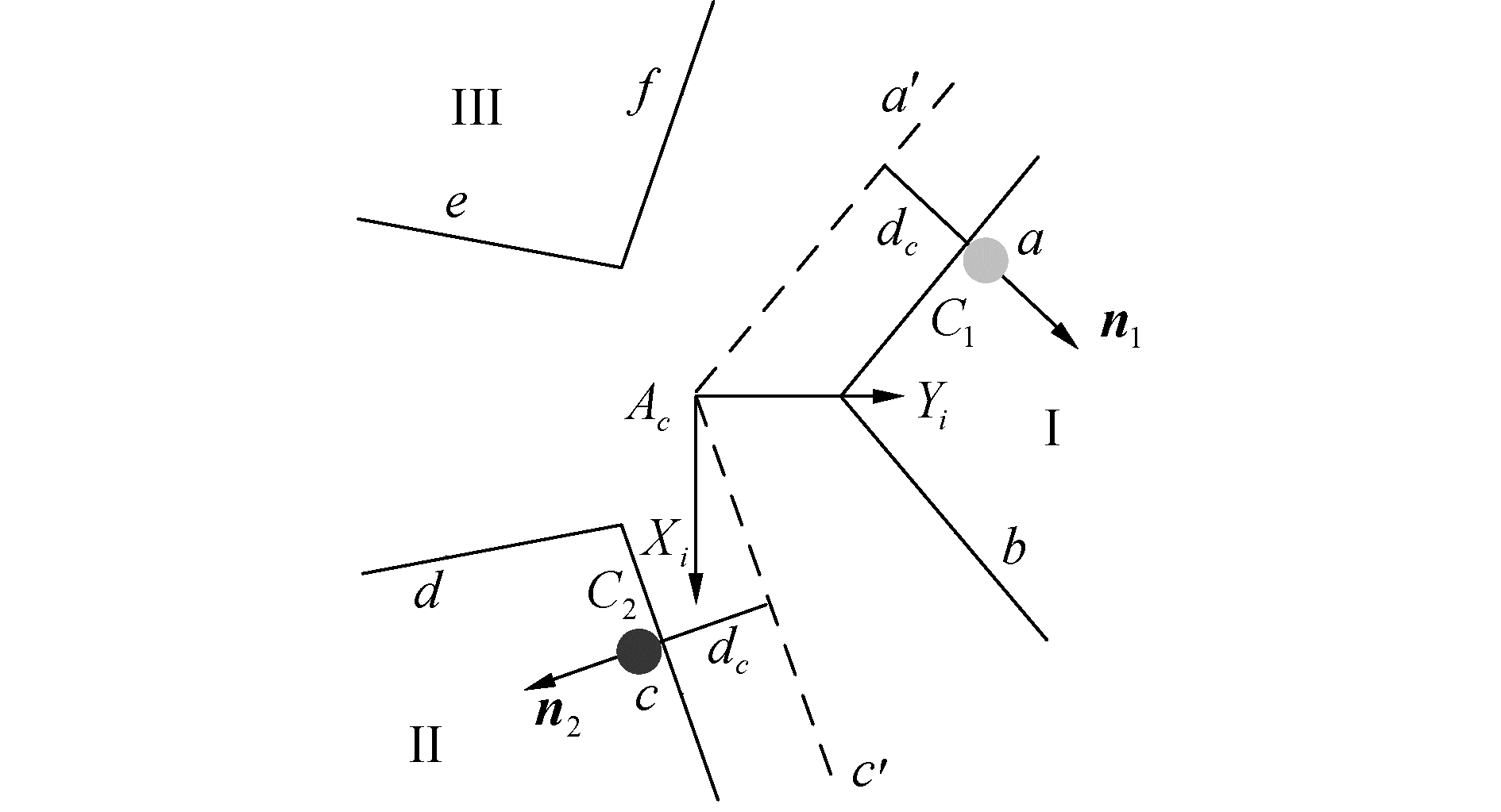
2.3 基于最少接触信息的位姿估计两次接触信息示意图如图 3所示,假设两次接触分别发生在约束面a和c以作说明。单位向量n1可为约束面a的单位法线向量,将约束面a沿-n1方向平移dc距离得到平面a′,其中dc为对接接口中心轴线与各约束面之间的距离,则平面a′必过对接接口中心轴线。平面a′的一般方程为:
| $ {}^o{n_{1x}}{}^ox + {}^o{n_{1y}}{}^oy + {}^o{n_{1z}}{}^oz + {p_1} + {d_c} = 0 $ | (4) |
|
Download:
|
| 图 3 两次接触信息示意 Fig. 3 Diagram of two contact information | |
式中p1=-(on1xC1x+on1yoC1y+on1zoC1z)。
同理,根据第二次接触信息可得过中心轴线的另一平面c′一般方程为:
| $ {}^o{n_{2x}}{}^ox + {}^o{n_{2y}}{}^oy + {}^o{n_{2z}}{}^oz + {p_2} + {d_c} = 0 $ | (5) |
式中p2=-(on2xoC2x+on2yoC2y+on2zoC2z)。
因两次接触发生在不同的约束面,则n1×n2≠ 0,平面a′与平面c′有且仅有一条交线。设交线方向向量为s,应满足与平面a′与平面c′的法线向量同时垂直,并根据接触面组合保证从对接接口指向外部,所以在接触面为a、c的情况下,s在坐标系OXoYoZo中表达为
| $ {}^o\mathit{\boldsymbol{s}} = \left( {{}^o{\mathit{\boldsymbol{n}}_2} \times {}^o{\mathit{\boldsymbol{n}}_1}} \right)/\left\| {{}^o{\mathit{\boldsymbol{n}}_2} \times {}^o{\mathit{\boldsymbol{n}}_1}} \right\| $ | (6) |
坐标系OXiYiZi原点用I表示,位于坐标系OXeYeZe原点E与各指尖几何中心点Ct之间的区域,设其在坐标系OXoYoZo中坐标为oI=[oIx oIy oIz]T。
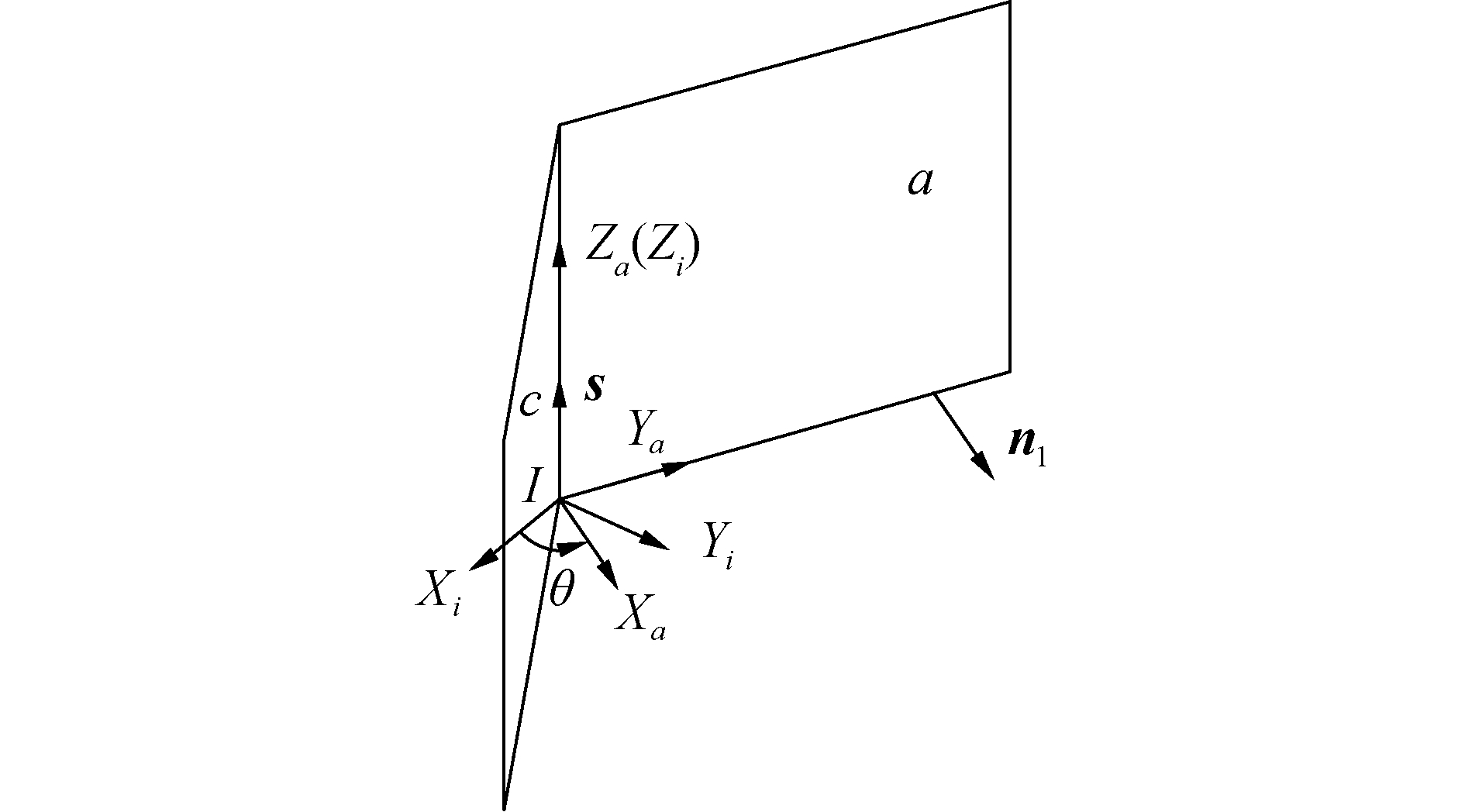
建立接触面a坐标系OXaYaZa和对接接口坐标系OXiYiZi如图 4所示,二者原点重合,Za轴与s同向,Xa轴与n1同向。由图 4可得,坐标系OXaYaZa绕Za轴旋转对应的-θ可得坐标系OXiYiZi。为区分不同接触面信息所得结果,此处-θ记为-θa,所得坐标系估计结果记为OXiaYiaZia,它相对于坐标系OXoYoZo的转换矩阵为:
| $ {}^o{\mathit{\boldsymbol{T}}_{ia}} = {}^o{\mathit{\boldsymbol{T}}_a}{\rm{Rot}}\left( {z, - {\theta _a}} \right) = \left[ {\begin{array}{*{20}{c}} {{}^o{\mathit{\boldsymbol{x}}_{ia}}}&{{}^o{\mathit{\boldsymbol{y}}_{ia}}}&{{}^o{\mathit{\boldsymbol{z}}_{ia}}}&{{}^o\mathit{\boldsymbol{I}}}\\ 0&0&0&1 \end{array}} \right] $ | (7) |
|
Download:
|
| 图 4 对接接口坐标系示意 Fig. 4 Diagram of grapple interface frame | |
式中[oxia oyia ozia]T为坐标系OXiaYiaZia各轴单位向量在坐标系OXoYoZo中的坐标。
同理,通过接触面c的接触信息可得另一个对接接口坐标系估计结果OXicYicZic相对于坐标系OXoYoZo的转换矩阵为:
| $ {}^o{\mathit{\boldsymbol{T}}_{ic}} = \left[ {\begin{array}{*{20}{c}} {{}^o{\mathit{\boldsymbol{x}}_{ic}}}&{{}^o{\mathit{\boldsymbol{y}}_{ic}}}&{{}^o{\mathit{\boldsymbol{z}}_{ic}}}&{{}^o\mathit{\boldsymbol{I}}}\\ 0&0&0&1 \end{array}} \right] $ | (8) |
估计坐标系OXiaYiaZia、OXicYicZic的Zic轴同向,则取新的Zi轴方向单位矢量ozi=ozia=ozic。而oyia与oyic之间可能存在较小偏差,将两个估计结果结合起来,取新的Yi轴方向单位矢量为:
| $ {}^o{\mathit{\boldsymbol{y}}_i} = \left( {{}^o{\mathit{\boldsymbol{y}}_{ia}} + {}^o{\mathit{\boldsymbol{y}}_{ic}}} \right)/\left\| {{}^o{\mathit{\boldsymbol{y}}_{ia}} + {}^o{\mathit{\boldsymbol{y}}_{ic}}} \right\| $ | (9) |
根据两次接触力信息所得的坐标系OXiYiZi相对于坐标系OXoYoZo的坐标转换矩阵估计为:
| $ {}^o{\mathit{\boldsymbol{T}}_i} = \left[ {\begin{array}{*{20}{c}} {{}^o{\mathit{\boldsymbol{x}}_i}}&{{}^o{\mathit{\boldsymbol{y}}_i}}&{{}^o{\mathit{\boldsymbol{z}}_i}}&{{}^o\mathit{\boldsymbol{I}}}\\ 0&0&0&1 \end{array}} \right] $ | (10) |
通过求取RPY变换解的方法可以求得绕固定轴转角Ψ、θ、ϕ。所以位姿估计向量为Pest=[oIx oIy oIz ψ θ ϕ]T。
3 冗余接触估计更新方法当捕获手指与对接接口发生N次接触时(N≥3),仅使用其中两次接触信息即可判断对接接口与末端执行器之间的相对位姿,如何使用冗余的接触信息更新估计结果将是本节研究的重点。
3.1 中心轴线估计更新N次接触中,各接触面ck(k=1, 2, …, N)沿-nk方向平移dc距离得到平面c′k应交于一条公共直线。但由于结构加工误差、力/矩传感器误差等因素的影响,各平面c′k间的交线存在差异。我们通过求得对接接口有效区域内的两个点,使每点到各平面c′k间的距离和最小,由两点确定的直线即为对接接口中心轴线估计结果。
中心轴线上2个有效点坐标分别为oA1=[oA1x oA1y oA1z]T、oA2=[oA2x oA2y oA2z]T。对接接口的有效部分大致在eIe1=[0 0 eCtz/2]T与eIe2=[0 0 2eCtz]T之间。假设A1与Ie1,A2与Ie2分别在Zo轴上具有相同的坐标,即oA1z=oIe1z,oA2z=oIe2z。至此,每个有效作用点还有2个未知变量。
由于nk为单位向量,点A1到平面c′k的距离为:
| $ {D_{1k}} = \left| {{}^o{n_{kx}}{}^o{A_{1x}} + {}^o{n_{ky}}{}^o{A_{1y}} + {}^o{n_{kz}}{}^o{A_{1z}} + {p_k} + {d_k}} \right| $ | (11) |
式中pk=-(onkxoCkx+onkyoCky+onkzoCkz)。
采用最小二乘法求取点A1坐标。当点A1到各平面c′k的距离平方和取得最小时,如下函数取得最小:
| $ {\mathit{\boldsymbol{j}}_1} = \left[ {\begin{array}{*{20}{c}} {{}^o{A_{1x}}}\\ {{}^o{A_{1y}}}\\ {{}^o{A_{1z}}}\\ 1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{A_{11}}}&{{A_{12}}}&{{A_{31}}}&{{A_{14}}}\\ {{A_{12}}}&{{A_{22}}}&{{A_{23}}}&{{A_{24}}}\\ {{A_{31}}}&{{A_{23}}}&{{A_{33}}}&{{A_{34}}}\\ {{A_{14}}}&{{A_{24}}}&{{A_{34}}}&{{A_{44}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{}^o{A_{1x}}}\\ {{}^o{A_{1y}}}\\ {{}^o{A_{1z}}}\\ 0 \end{array}} \right] $ | (12) |
式中:
| $ \left\{ \begin{array}{l} {A_{11}} = \sum\limits_{k = 1}^N {{}^on_{kx}^2} ,{A_{22}} = \sum\limits_{k = 1}^N {{}^on_{ky}^2} ,{A_{33}} = \sum\limits_{k = 1}^N {{}^on_{kz}^2} ,\\ {A_{44}} = \sum\limits_{k = 1}^N {{{\left( {{p_k} + {d_c}} \right)}^2}} ,{A_{12}} = \sum\limits_{k = 1}^N {{}^o{n_{kx}}{}^o{n_{ky}}} ,\\ {A_{23}} = \sum\limits_{k = 1}^N {{}^o{n_{ky}}{}^o{n_{kz}}} ,{A_{31}} = \sum\limits_{k = 1}^N {{}^o{n_{kz}}{}^o{n_{kx}}} ,\\ {A_{14}} = \sum\limits_{k = 1}^N {{}^o{n_{kx}}\left( {{p_k} + {d_c}} \right)} ,\\ {A_{24}} = \sum\limits_{k = 1}^N {{}^o{n_{ky}}\left( {{p_k} + {d_c}} \right)} ,\\ {A_{34}} = \sum\limits_{k = 1}^N {{}^o{n_{kz}}\left( {{p_k} + {d_c}} \right)} 。\end{array} \right. $ |
定义J1中oA1xy=[oA1x oA1y]T。当J1取得最小值时,∂J1/∂oA1xy= 0,可得:
| $ {}^o{\mathit{\boldsymbol{A}}_{1xy}} = \left[ {\begin{array}{*{20}{c}} {{}^o{A_{1x}}}\\ {{}^o{A_{1y}}} \end{array}} \right] = - {\left[ {\begin{array}{*{20}{c}} {{A_{11}}}&{{A_{12}}}\\ {{A_{12}}}&{{A_{22}}} \end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{A_{31}}}&{{A_{14}}}\\ {{A_{23}}}&{{A_{24}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{}^o{A_{1z}}}\\ 1 \end{array}} \right] $ | (13) |
通过冗余接触信息已得到估计点A1坐标,同理可得估计点A2坐标。中心轴线的单位向量s被更新为s=
设第k次接触点为Ck,位于约束面ck上。将点Ck沿-nk方向平移dc距离得到点C′k。如图 4所示,Pk是点C′k在更新后中心轴线上的垂足,则其坐标满足。

|
Download:
|
| 图 5 第k次接触的更新结果 Fig. 5 Estimation update from the kth contact | |
坐标系oXkYkZk绕Za轴旋转φk得到坐标系OXikYikZik,所以坐标系OXikYikZik相对于坐标系OXoYoZo的转换矩阵为
| $ \begin{array}{*{20}{c}} {{}^o{\mathit{\boldsymbol{T}}_{ik}} = {}^o{\mathit{\boldsymbol{T}}_k}{\rm{Rot}}\left( {z,{\varphi _k}} \right) = }\\ {\left[ {\begin{array}{*{20}{c}} {{}^o{\mathit{\boldsymbol{y}}_k} \times {}^o\mathit{\boldsymbol{s}}}&{{}^o{\mathit{\boldsymbol{y}}_k}}&{{}^o\mathit{\boldsymbol{s}}}&{{}^o\mathit{\boldsymbol{I}}}\\ {\bf{0}}&{\bf{0}}&{\bf{0}}&1 \end{array}} \right]{\rm{Rot}}\left( {z,{\varphi _k}} \right) = }\\ {\left[ {\begin{array}{*{20}{c}} {{}^o{\mathit{\boldsymbol{x}}_{ik}}}&{{}^o{\mathit{\boldsymbol{y}}_{ik}}}&{{}^o{\mathit{\boldsymbol{z}}_{ik}}}&{{}^o\mathit{\boldsymbol{I}}}\\ {\bf{0}}&{\bf{0}}&{\bf{0}}&1 \end{array}} \right]} \end{array} $ | (14) |
式中:oyk为
通过所有接触信息可以得到N个坐标系OXikYikZik(k=1, 2, …, N)估计结果,其中所有Zik轴相同,所以Zi轴单位向量估计结果更新为ozi=ozik。但是对于不同的k,oyik可能存在微小变化,Yi轴单位向量估计结果更新为:
| $ {}^o{\mathit{\boldsymbol{y}}_i} = \sum\limits_{k = 1}^N {{}^o{\mathit{\boldsymbol{y}}_{ik}}} /\left\| {\sum\limits_{k = 1}^N {{}^o{\mathit{\boldsymbol{y}}_{ik}}} } \right\| $ | (15) |
所有oyik具有相同的原点I且与同一向量ozi垂直,则所有oyik与计算得到的oyi在同一个垂直于ozi的平面内。至此,已更新考虑所有接触信息的坐标系OXiYiZi估计结果。
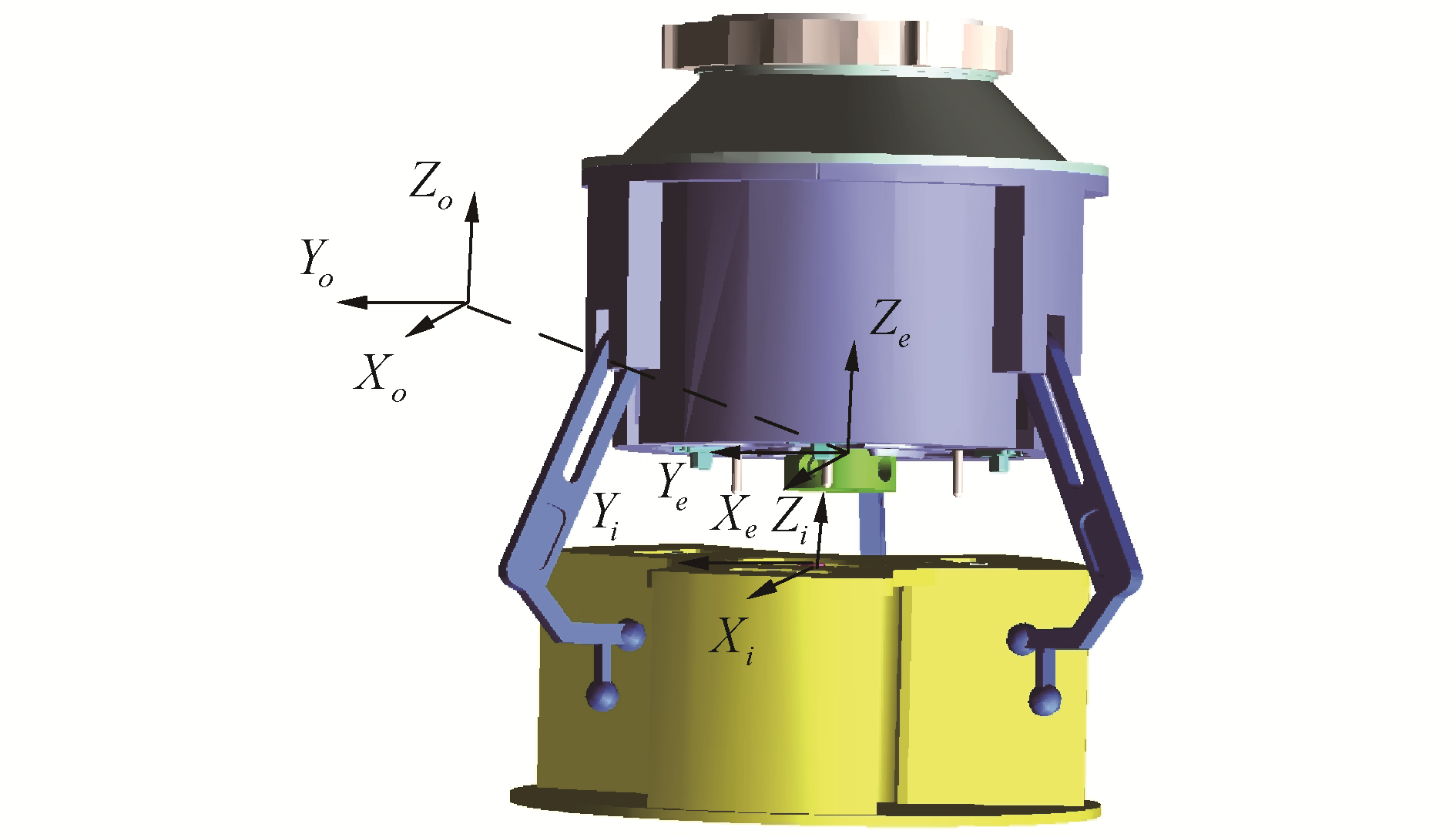
4 位姿估计仿真 4.1 仿真设计仿真模型设计如图 6所示,由于未对机械臂进行建模,假设末端执行器初始时刻位于坐标系OXoYoZo原点,对接接口与其存在一定的初始位姿偏差。仿真过程中,为了保证与实际情况一致,对接接口保持不动,末端执行器根据位置指令运动,以完成对接接口位姿估计及矫正过程。
|
Download:
|
| 图 6 仿真模型设计 Fig. 6 Simulation setup | |
为了避免接触信息的单一性,末端执行器在某次接触后,沿其法向加入随机水平转角的方向上运动。任务开始时,末端执行器收缩手指。当发生第1次接触后,末端执行器张开手指并按规划运动。当发生第2次接触后,末端执行器再次进行抓取,并按规划运动。在发生第3次接触后,末端执行器停止抓取以获得更丰富的接触信息。
位置和姿态向量分别采用笛卡尔距离d和通用旋转变换的旋转角Θ两个变量进行表示。设定冗余接触估计的终止条件为相邻两次估计结果变化低于一定阈值或总接触次数达到上限,即:
| $ \left| {{d_k} - {d_{k - 1}}} \right| < {d_{{\rm{th}}}}\;{\rm{or}}\;\left| {{\mathit{\Theta }_k} - {\mathit{\Theta }_{k - 1}}} \right| < {\mathit{\Theta }_{{\rm{th}}}}\;{\rm{or}}\;k > {k_{{\rm{th}}}} $ | (16) |
式中:dth为位置估计终止阈值,仿真中取0.3 mm;kth为姿态估计终止阈值,仿真中取0.3°;kth为接触次数上限,仿真中取10;
根据这些仿真条件,本文在不同初始位姿情况下进行了3类仿真实验:
1) 只有位置偏差
2) 只有姿态偏差
3) 位置和姿态偏差同时存在
多次仿真中的典型仿真结果如表 1所示,从中可以看出最少姿态估计能够得到与实际位姿存在一定误差的结果,然后通过冗余信息估计能够大幅减小误差,证明的冗余信息估计的有效性。
| 表 1 位姿估计结果 Table 1 Pose estimation results |
取多次仿真中一例以作说明,对接接口相对于系统坐标系的位姿偏差为:
| $ {\mathit{\boldsymbol{P}}_i} = {\left[ {\begin{array}{*{20}{c}} {5.5\;\;{\rm{mm}}}&{10\;{\rm{mm}}}&{ - 15\;{\rm{mm}}}&{{2^ \circ }}&{{4^ \circ }}&{{3^ \circ }} \end{array}} \right]^{\rm{T}}} $ |
位置和姿态估计误差分别通过估计结果与实际位姿之间的笛卡尔距离Δd和相对旋转角ΔΘ进行表示,多次接触过程中的估计误差如图 7所示,最后的残余误差为。其中A区域表示初始的两次接触过程,经过两次接触后,使用最少接触信息估计方法得到B区域内的估计误差,此时位置、姿态误差都较大。然后经过C区域内的多次接触,使用冗余信息估计更新方法,位姿偏差逐步缩小,最后的残余误差能够通过阻抗控制进行补偿,并在后续平行约束阶段逐步消除。位置残余误差主要来源于坐标系OXiYiZi原点的在Zi方向的坐标假设,原点位置估计误差因此影响姿态估计误差,主要体现在绕Zi方向的旋转角度估计结果。

|
Download:
|
| 图 7 位姿估计误差 Fig. 7 Error in pose estimation | |
1) 本文采用接触力信息提出了针对一种同步三指式末端执行器的目标位姿估计方法。通过ADAMS/MATLAB联合仿真证明:所提出的估计方法能够有效估计目标位姿,估计误差随接触信息增加而逐步提高。初步验证了该方法的有效性。
2) 本文在不引入其他传感器的前提下实现了末端执行器捕获过程中的目标位姿估计。所提出的方法不仅适用于本文所述同步三指式末端执行器,也适用于类似爪式末端执行器,具有一定的通用性。
目前正在建设基于轻型机械臂的捕获控制实验平台,后续研究工作将主要在于估计精度的提高和样机实验验证。
| [1] |
吕辛, 夏艳, 刘荣强. 欠驱动自适应式捕获装置设计[J]. 哈尔滨工程大学学报, 2016, 37(12): 1709-1715. LYU Xin, XIA Yan, LIU Rongqiang. Design of an under-actuated self-adaptive capture device[J]. Journal of Harbin Engineering University, 2016, 37(12): 1709-1715. (  0) 0)
|
| [2] |
FENG Fei, LIU Yiwei, LIU Hong, et al. Design schemes and comparison research of the end-effector of large space manipulator[J]. Chinese journal of mechanical engineering, 2012, 25(4): 674-687. DOI:10.3901/CJME.2012.04.674 (  0) 0)
|
| [3] |
CIOCARLIE M, HICKS F M, HOLMBERG R, et al. The velo gripper:A versatile single-actuator design for enveloping, parallel and fingertip grasps[J]. The international journal of robotics research, 2014, 33(5): 753-767. DOI:10.1177/0278364913519148 (  0) 0)
|
| [4] |
FONT D, PALLEJ T, TRESANCHEZ M, et al. A proposal for automatic fruit harvesting by combining a low cost stereovision camera and a robotic arm[J]. Sensors, 2014, 14(7): 11557-11579. DOI:10.3390/s140711557 (  0) 0)
|
| [5] |
MEHTA S S, BURKS T F. Vision-based control of robotic manipulator for citrus harvesting[J]. Computers and electronics in agriculture, 2014, 102: 146-158. DOI:10.1016/j.compag.2014.01.003 (  0) 0)
|
| [6] |
徐文福, 梁斌, 李成, 等. 空间机器人捕获非合作目标的测量与规划方法[J]. 机器人, 2010, 32(1): 61-69. XU Wenfu, LIANG Bin, LI Cheng, et al. Measurement and planning approach of space robot for capturing non-cooperative target[J]. Robot, 2010, 32(1): 61-69. (  0) 0)
|
| [7] |
胡杰, 管贻生, 吴品弘, 等. 双手爪爬杆机器人对杆件的位姿检测与自主抓夹[J]. 机器人, 2014, 36(5): 569-575. HU Jie, GUAN Yisheng, WU Pinhong, et al. Pole pose measurement and autonomous grasping with a biped climbing robot[J]. Robot, 2014, 36(5): 569-575. (  0) 0)
|
| [8] |
ZHANG Yu, SUN Kui, LIU Hong, et al. Pose measurement of nozzle based on laser range finders for capturing satellite[J]. Proceedings of the institution of mechanical engineers, Part G:journal of aerospace engineering, 2016, 230(8): 1385-1396. DOI:10.1177/0954410015611150 (  0) 0)
|
| [9] |
张禹, 孙奎, 张元飞, 等. 用于机械臂末端感知的激光测距传感器设计[J]. 机器人, 2014, 36(5): 519-526, 534. ZHANG Yu, SUN Kui, ZHANG Yuanfei, et al. Design of a laser range finder for end perception of robot arm[J]. Robot, 2014, 36(5): 519-526, 534. (  0) 0)
|
| [10] |
TSUJIMURA T, YABUTA T. Object detection by tactile sensing method employing force/torque information[J]. IEEE transactions on robotics and automation, 1989, 5(4): 444-450. DOI:10.1109/70.88059 (  0) 0)
|
| [11] |
HAIDACHER S, HIRZINGER G. Contact point identification in multi-fingered grasps exploiting kinematic constraints[C]//Proceedings of 2002 IEEE International Conference on Robotics and Automation. Washington, DC, USA, 2002: 1597-1603. https://www.mendeley.com/catalogue/contact-point-identification-multifingered-grasps-exploiting-kinematic-constraints/
(  0) 0)
|
| [12] |
PHUNG T C, KIM M J, MOON H, et al. Exploration of local surface geometry with minimum number of contact points and surface normal information[J]. International journal of control, automation and systems, 2012, 10(2): 383-395. DOI:10.1007/s12555-012-0218-7 (  0) 0)
|
| [13] |
YU Yong, KAMO Y, KAWAKOE H, et al. Estimation of contact shape of quadric environment with object probing operation[C]//2005 IEEE/RSJ International Conference on Intelligent Robots and Systems. Edmonton, Alta, Canada, 2005: 2351-2356. https://www.mendeley.com/catalogue/estimation-contact-shape-quadric-environment-object-probing-operation/
(  0) 0)
|
| [14] |
MOLL M, ERDMANN M A. Dynamic shape reconstruction using tactile sensors[C]//Proceedings of 2002 IEEE International Conference on Robotics and Automation. Washington, DC, USA, 2002: 1636-1641. https://www.mendeley.com/catalogue/dynamic-shape-reconstruction-using-tactile-sensors/
(  0) 0)
|
| [15] |
LAM T L, XU Yangsheng. Treebot: autonomous tree climbing by tactile sensing[C]//2011 IEEE International Conference on Robotics and Automation. Shanghai, China, 2011: 789-794. https://www.mendeley.com/catalogue/treebot-autonomous-tree-climbing-tactile-sensing/
(  0) 0)
|
| [16] |
YOON Y, RUS D. Shady3D: a robot that climbs 3D trusses[C]//Proceedings of 2007 IEEE International Conference on Robotics and Automation. Roma, Italy, 2007: 4071-4076. https://ieeexplore.ieee.org/document/4209722
(  0) 0)
|
| [17] |
WU Jun, FAN Shaowei, JIN Minghe, et al. Design and experiment of a universal space-saving end-effector for multi-task operations[J]. Industrial robot:an international journal, 2016, 43(2): 193-203. DOI:10.1108/IR-07-2015-0132 (  0) 0)
|
| [18] |
WU Jun, FAN Shaowei, NI Fenglei, et al. A space-saving end-effector with capture and actuation transmission capabilities[C]//2014 IEEE International Conference on Robotics and Biomimetics. Bali, Indonesia, 2014: 2203-2208. https://ieeexplore.ieee.org/document/7090664
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


