2. 同济大学 岩土及地下工程教育部重点实验室, 上海 200092;
3. 山东科技大学 土木建筑学院 山东省土木工程防灾减灾重点实验室, 山东 青岛 266590
2. Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education, Tongji University, Shanghai 200092, China;
3. Shandong Key Laboratory of Civil Engineering Disaster Prevention & Mitigation, College of Civil Engineering and Architecture, Shandong Univ. of Sci. & Tech., Qingdao 266590, China
边界元法最终形成的线性方程组系数矩阵是一个非对称满系数矩阵,采用直接法(高斯消去)求解时,计算量随问题自由度呈o(N3)增长,这极大限制了边界元法的解题速度和解题规模。因此,在问题规模较大时,采用适合的迭代法求解边界元法方程是必要的[1]。由Saad等发展的广义极小残值算法(generalized minimum residual algorithm, GMRES)是一种专门用于求解系数矩阵为大型非对称阵的高效Krylov子空间迭代法[2],非常适合于求解边界元法所形成的线性方程组,提高了边界元法的解题规模和解题速度[3]。
为追求更优的数值特性,GMRES算法发展了多种变体,包括原理型GMRES,重开始的GMRES算法(记为GMRES(m))和预条件的GMRES算法(记为PGMRES)。
原理型GMRES有两点不足:1)不能无限收敛。极限收敛精度接近κ(A)ε[4],其中ε为机器精度,κ(A)为待分解矩阵A的条件数;Leung[5]和王人鹏[6]均从数值算例中观察到该现象。2)只具有长迭代格式。随迭代次数的增加,需要的内存不断增大。重开始型GMRES(m)算法的提出克服了原理性算法以上两点不足,但该算法在m取值足够小时可能导致算法停滞[7]。只有在系数矩阵满足特殊要求时,算法可以保证收敛[8];而边界元法形成的方程组是无法满足这些要求的,因此GMRES(m)的停滞对于其在边界元法中的应用仍是一个较大问题。仅通过经验选择合适的m具有一定盲目性,有例子表明GMRES(m)对于任何m<n都不收敛,只有m=n时收敛到最终精度。虽有学者对免停滞GMRES(m)进行研究,如徐明华[9]提出一种具有适当参数再开始的GMRES算法,该算法虽可避免算法停滞,但同时又带来m取值大时占存储空间大的问题。
预条件技术通过对原系数方程左乘或右乘一个矩阵来得到一个新的等价方程,新方程与原方程有相同的解,但具有更好的谱性质,收敛更快[10-11]。当预条件选取非常有效时,甚至不用诉诸于重开始(PGMRES(m))来提高算法精度减小运算内存,原理型的算法(PGMRES)就能很快地收敛到较高精度。既保存了原理型GMRES收敛性上的优势,又克服了其收敛精度和占内存大的缺点,因此在工程问题的边界元法求解中得到应用。段文洋等[12]将采用不完全LU分解预条件的GMRES(m)用于大型浮体水动力边界元分析中,取得了较高计算效率。张健飞等[13]通过大量算例对GMRES在三维弹性静力问题边界元分析中的实用化和并行化技术进行了深入研究,研究表明右预条件比左预条件效果好。陈泽军等[14]以弹性立方体受压为例,对预条件的GMRES(m)在求解边界元方程时的特性进行了研究,发现块Jacobi预条件对边界元问题有尤其好的效果。尽管上述成果通过不同算例证实了右预条件和块Jacobi预条件对三维弹性静力问题边界分析有效,但对于为什么这种预条件形式对边界元分析形成的方程尤其有效没有做出解释。
基于此,本文以不同约束条件的薄板弯曲问题为例,进一步讨论了Jacobi、块Jacobi和对称Gauss-Sediel迭代作为预条件的三种预条件形式对原理型GMRES算法收敛性的影响;并探讨其与约束条件的关系,尝试对为什么某种预条件形式对边界元法形成方程尤其有效做出解释。
1 三维弹性力学问题基本理论弹性静力学问题的控制微分方程为纳维叶-拉密方程[3]:
| $ \begin{array}{*{20}{c}} {\left( {\lambda + G} \right){u_{i,ij}} + G{u_{j,ii}} + {b_j} = 0,}&{{x_j} \in \mathit{\Omega }} \end{array} $ | (1) |
定解边界条件如下
| $ \begin{array}{*{20}{c}} {{u_j} = {{\bar u}_j},}&{x \in {\mathit{\Gamma }_1}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{p_j} = {n_i}{\sigma _{ij}} = {{\bar p}_j},}&{x \in {\mathit{\Gamma }_2}} \end{array} $ |
式中:位移分量uj及应力分量σij是场点Q的位置坐标(x1Q, x2Q, x3Q)的函数,λ和G为拉梅常数,Ω为所求问题的区域,pj和pj分别为边界Γ1和Γ2上已知的位移和面力,ni为边界的外法线方向余弦;下标i, j取值集合为(1, 2, 3)。
利用加权余量法或功的互等定理,并进行边界上的延拓,得到边界积分方程:
| $ c_{lk}^Pu_k^P = \iint_\mathit{\Gamma } {{p_k}u_{lk}^ * {\text{d}}\mathit{\Gamma }} - \iint_\mathit{\Gamma } {{p_k}u_{lk}^ * {\text{d}}\mathit{\Gamma l}},k = 1,2,3 $ | (2) |
式中:clkP为方程系数,随P点位置取不同值;ulk*和plk*是弹性力学空间问题的基本解,又称Kelvin基本解。
对式(2)进行离散得边界元法控制方程:
| $ \mathit{\boldsymbol{HU}} = \mathit{\boldsymbol{GP}} $ | (3) |
式中:U和P是结点位移和结点面力3N阶列阵,N是结点数。系数矩阵H和G都是3N阶方阵,其子块可记为HlkPQ和GlkPQ,每个子块为一3×3阶的方阵。子块中各元素的计算公式为
| $ h_{lk}^{\left( {P,Q,J} \right)} = \int_{ - 1}^1 {\int_{ - 1}^1 {p_{lk}^ * {\varphi _J}\left| {{J_{\xi \eta }}} \right|{\rm{d}}\xi {\rm{d}}\eta } } $ | (4) |
| $ g_{lk}^{\left( {P,Q,J} \right)} = \int_{ - 1}^1 {\int_{ - 1}^1 {u_{lk}^ * {\varphi _J}\left| {{J_{\xi \eta }}} \right|{\rm{d}}\xi {\rm{d}}\eta } } $ | (5) |
当P≠Q时,式(4)直接采用高斯数值积分求解;当P=Q时,对应系数矩阵的对角线子块,式(4)和式(5)分别具有1/r2和1/r阶奇异性。后者通过退化单元的方法解决,前者通过刚体位移法求解,即
| $ \mathit{\boldsymbol{H}}_{lk}^{PP} = - \sum\limits_n {\mathit{\boldsymbol{H}}_{lk}^{PQ}} $ | (6) |
可见,H矩阵具有一定的弱对角占优性。
根据边界条件,将U中已知元素与P中对应元素交换,同时系数矩阵中对应元素对调得
| $ \mathit{\boldsymbol{H'U'}} = \mathit{\boldsymbol{G'P'}} $ | (7) |
此时,矩阵P'中全部为已知元素,U'中全部为未知元素,系数矩阵H'和G'都为已知。记H'为A,U'为x,将式(7)等号右边两项相乘后记为列阵b。这样,得到边界元法求解的线性方程组标准形式
| $ \mathit{\boldsymbol{Ax}} = \mathit{\boldsymbol{b}} $ | (8) |
求解方程(6)的GMRES原理总结如图 1所示,具体推导见相关文献[7-8, 11]。首先通过变量代换将线性方程组化成等价方程,从而构造余量和Krylov子空间;再通过Galerkin原理将求其绝对解的问题转化成求其最小二乘解的问题;然后,用Arnoldi过程和Givens旋转将该系数矩阵为非对称满阵的最小二乘问题转化成系数矩阵为一上三角矩阵加一行0的最小二乘问题;最终只通过回代求得该上三角方程绝对解,即为该最小二乘问题解。

|
Download:
|
| 图 1 GMRES算法整体流程 Fig. 1 Overall flow of GMRES algorithm | |
原理型算法的自然语言描述如下,具体执行见文献[15]附录D算法2.1。算法中采用基于修正Gram-Schmidt(MGS)正交化方法的Arnoldi过程。
GMRES算法:
1) 开始:选取x0并计算r0=b-Ax0及v1=r0/‖r0‖;
2) 迭代:对j=1, 2, …直至收敛,计算
| $ {h_{i,j}} = \left( {\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{v}}_j},{\mathit{\boldsymbol{v}}_i}} \right),i = 1,2, \cdots ,j $ |
| $ {\mathit{\boldsymbol{v}}_{j + 1}} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{v}}_j} - \sum\limits_{i = 1}^j {{h_{i,j}}{\mathit{\boldsymbol{v}}_i}} $ |
| $ {h_{i + 1,j}} = \left\| {{\mathit{\boldsymbol{v}}_{j + 1}}} \right\|\;且\;{\mathit{\boldsymbol{v}}_{j + 1}} = {\mathit{\boldsymbol{v}}_{j + 1}}/{h_{j + 1,j}} $ |
3) 形成近似解:xj=x0+Vjyj,其中yj∈Rj使‖βe1-Hjyj‖极小。
2.2 预条件矩阵对原方程(8)施加预条件的格式为
| $ \left( {M_{\rm{L}}^{ - 1}AM_{\bf{R}}^{ - 1}} \right)\left( {{M_{\rm{R}}}x} \right) = M_{\rm{L}}^{ - 1}b $ |
新方程记为
| $ \tilde A\tilde x = \tilde b $ | (9) |
其中,
式(8)为最全面形式的一种预条件,通常只有左预条件或右预条件。左右预条件的算法见文献[15]附录D算法3.1和算法3.2,附录矩形框标识部分为与非预条件算法的区别;对于分裂预条件则需要两者综合。
本文实现了Jacobi预条件(JacP)、块Jacobi预条件(BJacP)和对称的Gauss-Sediel迭代作为预条件(SGSP)。记系数矩阵A=EA+DA+FA。其中,EA、DA、FA分别为A的纯下三角部分、对角元素部分和纯上三角部分组成的矩阵。则Jacobi预条件和对称的Gauss-Sediel迭代作为预条件的预条件矩阵可表示为
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{M}}_{{\rm{Jac}}}} = {\mathit{\boldsymbol{D}}_A}\\ {\mathit{\boldsymbol{M}}_{{\rm{SGS}}}} = \mathit{\boldsymbol{LU}} = \left( {{\mathit{\boldsymbol{D}}_A} + {E_A}} \right){\left( {{\mathit{\boldsymbol{D}}_A}} \right)^{ - 1}}\left( {{\mathit{\boldsymbol{D}}_A} + {\mathit{\boldsymbol{F}}_A}} \right) \end{array} \right. $ | (10) |
对于三维弹性力学问题形成的3N×3N系数矩阵A,矩阵中的每个元素记为ai, j, 下标i、j取自集合{1, 2, 3, …, 3N},将该集合3个元素为一组分为N个子集:{1, 2, 3}, {4, 5, 6}, …,{3N-2, 3N-1, 3N}。组成块Jacobi预条件矩阵的元素定义为[10]
| $ {m_{i,j}} = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {a_{i,j}},\\ 0, \end{array}&\begin{array}{l} i、j\;属于同一下标子集\\ 其他 \end{array} \end{array}} \right. $ | (11) |
可见,块Jacobi预条件矩阵是一个块对角矩阵,对于三维问题子块大小为3×3。
Jacobi和块Jacoib预条件分别按左、右预条件的形式施加(L-JacP, R-JacP, L-BJacP和R-BJacP);式(11)采用分裂预条件的形式施加(记为SGSP),取L=(DA+EA)(DA)-1, U=(DA+FA)。
3 不同约束条件的薄板弯曲问题三维边界元分析以均布荷载下不同约束条件的薄板弯曲问题为例,研究Jacobi、块Jacobi和对称Gauss-Sediel迭代作为预条件的三种预条件形式对GMRES算法收敛性的影响,并探讨了其与约束条件的关系;在此基础上,选择效果较好的预条件形式,对比随问题自由度的增加Gauss消去与采用该预条件形式的GMRES算法计算效率上的差距。
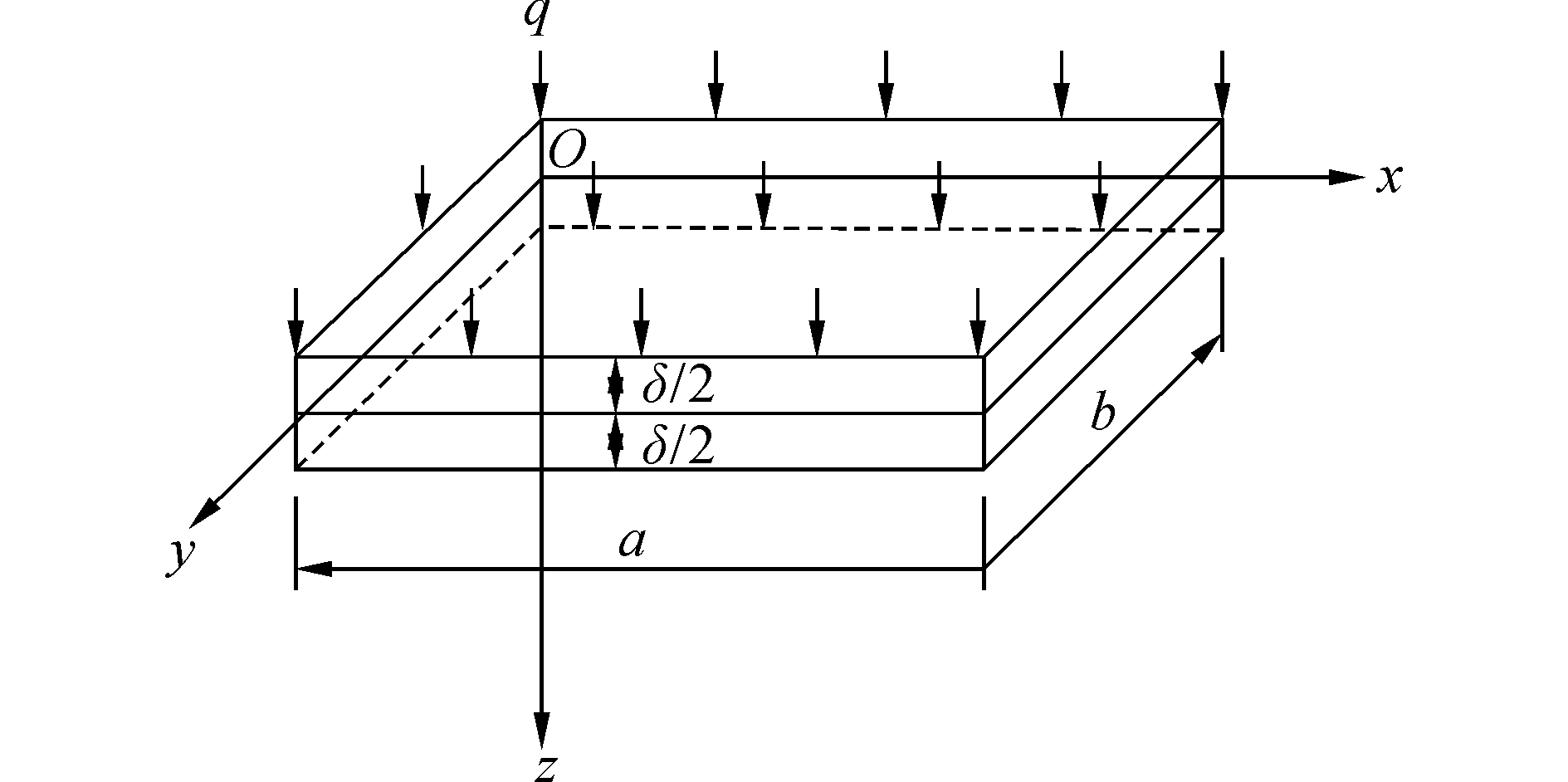
均布荷载薄板弯曲问题如图 2所示。图中,取a=b=14 m, δ=2 m, q=100 N/m2,材料弹性参数E=2.1×106 Pa, μ=0.3。
|
Download:
|
| 图 2 均布荷载下薄板弯曲问题 Fig. 2 Thin-plate bending under uniform loading | |
对于薄板弯曲问题形成的线性方程组,算例1探讨不同预条件形式GMRES算法加速收敛的效果,并研究其与约束条件的关系。
共讨论Case1-1~Case 1-4 4种工况,4种工况依次对应的边界条件为:左右两对边(x=0和x=a)边界受固定约束和简支约束;四侧边(x=0, x=a, y=0和y=b)均受固定约束和简支约束。四种工况均按八结点四边形单元划分网格,网格尺寸为1 m;共划分504个单元,1 514个节点,自由度为4 542。
3.1.1 采用GMRES的BEM解与FEM解对比进行不同预条件下GMRES算法收敛性分析之前,首先确认所编写PGMRES程序的正确性。可直接将求得的解与Gauss消去对比,但为使对比更直观且具有一定物理意义,本文对比采用PGMRES的BEM解和采用大型成熟有限元计算软件ANSYS计算的FEM解;以此间接证明所编PGMRES程序的正确性,并确认所选控制精度的可行性。
对Case 1-1~Case 1-4 4种工况,进行ANSYS有限元计算。FEM计算采用8结点立方体单元,划分两套网格:FEM1和FEM2。FEM1网格尺寸为0.5 m, 该网格密度近似等价于BEM 8结点4边形单元尺寸1 m的网格(表 1中Case1所示网格),共计3 136个单元,4 205个结点;FEM2网格尺寸加密为0.25 m, 共25 088个单元,29 241个结点。
| 表 1 不同数值方法所得板面中心点处z向位移 Tab.1 Displacement along z direction on center point of the plate surfaces caculated in varied methods |
考察不同计算方法板上下面中心点处z方向的位移,如表 1所示。由表 1可见,采用所编写PGMRES程序的BEM法求得的位移解与采用ANSYS软件计算的FEM解吻合良好。并且,FEM解随网格密度的增大有向BEM解靠近的趋势。同时,这也显示了BEM方法的优越性,能大大减小计算问题的规模,相同网格密度比FEM计算精度高。证实了所编写PGMRES程序的正确性,及控制精度εtol=1×10-6的可行性。
3.1.2 预条件加速收敛效果与约束条件的关系从两个角度对不同预条件的PGMRES收敛特性进行分析:1)对同一约束条件的物理问题,分析不同预条件类型对该问题求解的收敛特性;2)采用同一类型预条件形式,讨论不同约束条件对该预条件形式加速收敛效果的影响。
1) 不同预条件类型求解同一约束条件问题的收敛特性。
对Case1形成的N=4 542的线性方程组,控制精度取εtol=1×10-6时,采用不同预条件形式的PGMRES算法计算,得到相对余量随迭代次数的变化如图 3所示。

|
Download:
|
| 图 3 不同预条件类型的原理型PGMRES收敛特性 Fig. 3 Convergence behavior of rational GMRES with different preconditioning techniques | |
可见,不同约束条件下,所采用的预条件的算法均起到了加速收敛的效果,均能比不采用预条件的算法更快收敛到目标精度。其中,SGSP在m较小时,收敛效果不如没有施加预条件(UNP)的算法;但m增大到一定程度后,收敛速度明显提高。Jacobi预条件和块Jacobi预条件均表现出较好的收敛效果,但两者效果并无明显差异;左右预条件有明显差异,右预条件明显比左预条件效果好,这与文献[13]中得到的结论一致。
对比图 3四个子图可知,不同预条件形式对加速GMRES解方程组收敛性的效果受所研究问题约束条件的影响。尽管如此,R-BJacP和R-JacP总能取得最好的收敛效果。
2) 同一预条件类型求解不同约束条件问题的收敛特性。
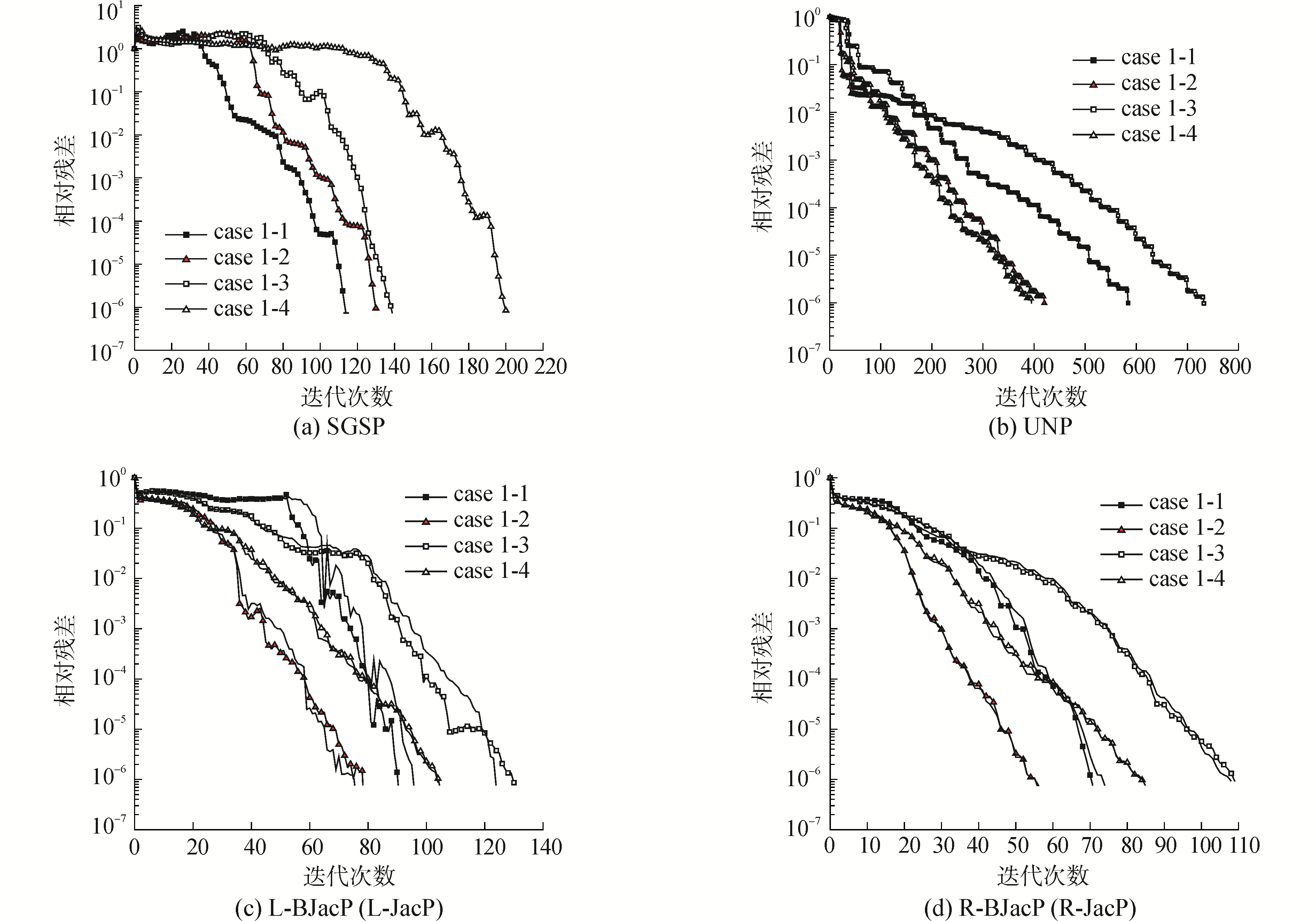
同一预条件类型对不同约束条件下的物理问题加速收敛效果如图 4所示。其中,由于块Jacobi预条件和Jacobi预条件收敛效果差别不大,图 4(c)和图 4(d)均有两种预条件形式。
|
Download:
|
| 图 4 不同约束条件下原理型PGMRES收敛特性 Fig. 4 Convergence behavior of PGMRES in solving problems with different boundary conditions | |
由图 4可见,不采用预条件的算法图 4(b)对Case1-4四边固支的收敛最快,其次是Case1-2四边简支,对Case1-1对边简支收敛相对较慢,Case1-3对边固支收敛最慢。预条件以后的算法均能改变这种收敛快慢排序。SGSP对四种约束条件按收敛效果从好到坏排序为Case1-1, 1-2, 1-3和1-4,即位移约束越少,SGSP收敛效果越好。L-JacP和L-BJacP对各边界条件的物理问题收敛效果排序为Case 1-2, 1-1, 1-4, 1-3,其中对Case1-1的收敛效果在m取值较小时也不明显,m增大到50以后才有加速收敛效果。对各类约束问题总有最好加速收敛效果的R-JacP和R-BJacP,收敛效果较好,一直呈加速收敛状态。在控制精度小于10-4之前,对不同边界条件加速收敛的效果排序为Case 1-2, 1-4, 1-1和1-3;在控制精度大于该值以后,按收敛快慢排序为Case 1-2, 1-1, 1-4和1-3。
采用R-BJacP的PGMRES算法,尽管控制精度不同时,不同约束条件的问题收敛效果不同;但有一规律是不变的,即同类型的边界条件(Case 1-1和Case 1-3, Case 1-2和Case1-4)简支的比固支的收敛快。这与边界元法系数矩阵计算中的刚体位移原理(式(5))有关。由式(5)可知,边界元法生成的H矩阵具有一定对角占优的特点,占优元素的位置正好跟块Jacobi预条件矩阵非零元素位置相同。而在形成边界元法最终系数矩阵A时,并非全由H的元素组成,还有对调来的G的元素。而G没有类似上式的关系存在,这会破坏对角占优性。因此,当位移边界条件少时,收敛特性更好;表现为图 4 (d)同类型边界条件简支比固支收敛快。该规律对JacP和SGSP也适用。
综上,R-BJacP与R-JacP对边界元法形成方程具有较好加速收敛效果,且同类型边界条件简支比固支收敛快。
3.2 算例2:采用R-JacP的PGMRES算法与Gauss消去计算时间对比根据Case1数值试验的结果,R-BJacP和R-JacP预条件均取得较好的收敛效果,且两者效果无明显差别。Case2采用R-BJacP预条件形式,对比随问题规模的增加,采用该预条件形式的PGMRES算法与Gauss消去直接解法计算效率的差异。
取Case1中的一种情况(Case 1-4, 四边固支)划分不同密度的网格进行计算。Case2-1网格尺寸为2 m, Case2-2网格同Case1-4,Case 2-3沿厚度方向网格尺寸为0.5 m, 其余方向1 m,Case2-4网格尺寸沿厚度方向为0.5 m, 其余方向0.7 m。各工况节点信息列于表 2。
| 表 2 算例2所分析各工况 Tab.2 Cases to be analyzed in Case 2 |
取控制精度εtol=1×10-6, 随问题自由度的增大,采用R-BJacP的PGMRES算法与采用Gauss消去直接法求解的计算时间如表 3所示。
| 表 3 算例2所分析各工况 Tab.3 Cases to be analyzed in Case 2 |
可见,随问题自由度的增大,全主元高斯消去计算时间大幅增加,预条件的GMRES算法优势更明显。当自由度超过1万时,前者求解时间达6 h,而采用R-BJacP的PGMRES算法却仅用6 min;计算时间相差60倍,求解效率显著提高。
4 结论1) 采用PGMRES算法的边界元解比相同网格密度的有限元解取得了更高的计算精度。
2) 左右预条件有明显差异,右预条件普遍较好;右块Jacobi预条件与右Jacobi预条件对边界元法形成方程具有尤其好的加速收敛效果,且同类型边界条件简支比固支收敛快,这与边界元法线性方程组形成过程中式(5)的刚体位移原理有关。
3) 随问题自由度的增加,采用右块Jacobi预条件的GMRES算法比Gauss消去求解三维边界元静力分析所形成线性方程组效率显著提高;当问题自由度上万时,后者计算时间为前者60倍。
| [1] |
戴华. 求解大规模矩阵问题的Krylov子空间方法[J]. 南京航空航天大学学报, 2001, 33(2): 139-145. DAI Hua. Krylov subspace methods for solving large scale matrix problems[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2001, 33(2): 139-145. DOI:10.3969/j.issn.1005-2615.2001.02.009 (  0) 0)
|
| [2] |
SAAD Y, SCHULTZ M H. GMRES:a generalized minimal residual algorithm for solving nonsymmetric linear systems[J]. SIAM journal on scientific and statistical computing, 1986, 7(3): 856-869. DOI:10.1137/0907058 (  0) 0)
|
| [3] |
姜弘道. 弹性力学问题的边界元法[M]. 北京: 中国水利水电出版社, 2008: 180-187. JIANG Hongdao. Boundary element method for elastic problems[M]. Beijing: China Water Power Press, 2008: 180-187. (  0) 0)
|
| [4] |
GREENBAUM A, ROZLOŽNIÍK M, STRAKOŠ Z. Numerical behaviour of the modified Gram-Schmidt GMRES implementation[J]. BIT numerical mathematics, 1997, 37(3): 706-719. DOI:10.1007/BF02510248 (  0) 0)
|
| [5] |
LEUNG C Y, WALKER S P. Iterative solution of large three-dimensional BEM elastostatic analyses using the GMRES technique[J]. International journal for numerical methods in engineering, 1997, 40(12): 2227-2236. DOI:10.1002/(ISSN)1097-0207 (  0) 0)
|
| [6] |
王人鹏, 沈祖炎, 钱若军. 应用Krylov子空间方法求解边界元方程组[J]. 同济大学学报, 1997, 25(2): 212-217. WANG Renpeng, SHEN Zuyan, QIAN Ruojun. Solutions of BEM equations with Krylov subspace method[J]. Journal of Tongji University, 1997, 25(2): 212-217. (  0) 0)
|
| [7] |
蔡大用, 白峰杉. 高等数值分析[M]. 北京: 清华大学出版社, 1997: 71-93. CAI Dayong, BAI Fengshan. Advanced numerical analysis[M]. Beijing: Tsinghua University Press, 1997: 71-93. (  0) 0)
|
| [8] |
李乃成, 梅立泉. 数值分析[M]. 北京: 科学出版社, 2011: 100-111. LI Naicheng, MEI Liquan. Numerical analysis[M]. Beijing: Science Press, 2011: 100-111. (  0) 0)
|
| [9] |
徐明华. 具有适当参数的再开始的GMRES算法[J]. 江苏石油化工学院学报, 1999, 11(3): 52-55. XU Minghua. A restarted GMRES method with adaptive parameter[J]. Journal of Jiangsu Institute of Petrochemical Technology, 1999, 11(3): 52-55. (  0) 0)
|
| [10] |
BARRETT R, BERRY M, CHAN T F, et al. Templates for the solution of linear systems:building blocks for iterative methods[M]. Philadelphia: SIAM, 2006: 35-41.
(  0) 0)
|
| [11] |
SAAD Y. Iterative methods for sparse linear systems[M]. Philadelphia, USA: Society for Industrial and Applied Mathematics, 2003: 171-180.
(  0) 0)
|
| [12] |
段文洋, 刁峰, 陈纪康. 预条件GMRES(m)算法在大型浮体水动力边界元分析中的应用[J]. 哈尔滨工程大学学报, 2013, 34(11): 1363-1368. DUAN Wenyang, DIAO Feng, CHEN Jikang. Application of preconditioned and restarted GMRES to the boundary element analysis of large floating structures[J]. Journal of Harbin Engineering University, 2013, 34(11): 1363-1368. (  0) 0)
|
| [13] |
张健飞, 姜弘道. 适合于求解边界元方程组的GMRES算法的实用化和并行化研究[J]. 计算力学学报, 2004, 21(5): 620-624. ZHANG Jianfei, JIANG Hongdao. Study on the utilization and parallelization of the GMRES algorithm for BEM systems solution[J]. Chinese journal of computational mechanics, 2004, 21(5): 620-624. DOI:10.3969/j.issn.1007-4708.2004.05.019 (  0) 0)
|
| [14] |
陈泽军, 肖宏. 预条件GMRES(m)法迭代求解大规模边界元弹性问题[J]. 固体力学学报, 2006, 27(S1): 50-55. CHEN Zejun, XIAO Hong. Iterative solution of large-scale BEM elasticity problems using the preconditioned GMRES(m) technique[J]. Acta mechnica solida sinica, 2006, 27(S1): 50-55. (  0) 0)
|
| [15] |
陈娟.梯度材料弹性力学问题的解析解和数值解研究[D].青岛: 山东科技大学, 2014: 83-85. CHEN Juan. Study on analytical and numerical solutions of elastic problems in FGMs[D]. Qingdao: Shandong University of Science and Technology, 2014: 83-85. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


