由于舰载机着舰环境十分恶劣^[1]，飞行员操作稍有不慎就会造成机毁人亡。尤其是海况比较恶劣时，对舰载机的控制精度和收敛速度要求就会更高，因此设计一种控制精度高，收敛速度快的控制器，对舰载机安全着舰尤为重要。

非线性动态逆控制方法由于其物理概念清晰，在许多领域已经取得了较好的控制效果^[2-4]。但舰载机着舰过程存在建模误差和很大的外部扰动，使得一般的动态逆方法很难达到期望的控制效果^[5-6]。朱齐丹等^[7]针对舰载机着舰非线性问题，考虑舰艉流扰动影响，提出了一种基于动态逆的滑模控制方法，具有较强的鲁棒性，但没有考虑建模误差引起的逆误差对系统造成的影响。韩英华等^[8]针对无人机的着陆问题，采用了非线性动态逆的控制方法，提出如果建模过程中存在建模误差，需要通过其他方法来消除误差。Crassidis等^[9]考虑舰艉气流对舰载机着舰的影响，利用鲁棒控制技术，提高舰载机着舰进度以及抑制舰艉气流的能力。鲁可等^[10]针对无人战斗机着舰问题，采用PID方法对层叠结构的动态逆控制器进行校正，这种方法结构简单，鲁棒性较强，但同样没有考虑到系统的建模误差。Lungu等^[11]考虑气流干扰和传感器误差对飞机着陆影响，将动态逆控制方法和H_∞方法结合提高着陆的轨迹跟踪能力，但是采用的是线性模型，具有一定的局限性。Abaspour^[12]在动态逆控制方法中使用模糊控制的方法调节动态逆内外环增益，提高系统对不确定环境的鲁棒性，但这种方法会降低控制效果和轨迹跟踪能力。

本文针对舰载机着舰过程中的建模和干扰问题，提出了一种非线性动态逆与神经网络结合的方法。利用神经网络能精确逼近任意非线性函数的能力^[13]，在非线性动态逆控制回路中引入在线神经网络，对由于建模误差和其他因素引起的逆误差进行动态补偿，改善动态逆的控制精度。同时由于舰载机要求在很短的时间内就要完成着舰，本文引入自适应学习率算子，通过自适应地改变神经网络的学习率，提高神经网络的收敛速度，从而提高控制器控制速度。

1 舰载机着舰问题描述 1.1 舰载机着舰运动模型

舰载机着舰过程是一个短暂、低速、低空的情况，舰载机力的方程组如下

$ \left\{ \begin{array}{l} \dot u = vr - wq - g\sin \theta + \frac{{{F_x}}}{m}\\ \dot v = - ur + wp + g\cos \theta \sin \phi + \frac{{{F_y}}}{m}\\ \dot w = uq - vp + g\cos \theta \cos \phi + \frac{{{F_z}}}{m} \end{array} \right. $

(1)

式中：m为舰载机质量, g为重力加速度，舰载机速度V按机体轴坐标系的三个轴做投影，u、v和w为表示沿x、y和z轴的速度分量，R_Σ为总空气动力，T为发动机推力，F_x、F_y和F_z为沿x、y和z轴的分力。

将舰载机受到的合外力矩向机体坐标系进行分解，分别得到三个坐标轴的力矩分量L、M和N，舰载机力矩方程组如下

$ \left\{ \begin{array}{l} \dot p = \left( {{c_1}r + {c_2}p} \right)q + {c_3}\bar L + {c_4}N\\ \dot q = {c_5}pr - {c_6}\left( {{p^2} - {r^2}} \right) + {c_7}M\\ \dot r = \left( {{c_8}p - {c_2}r} \right)q + {c_4}L + {c_9}N \end{array} \right. $

(2)

其中${c_1} = \frac{{({I_y} - {I_z}){I_z} - I_{xz}^2}}{{{I_x}{I_z} - I_{xz}^2}}, {c_2} = \frac{{({I_x} - {I_y} + {I_z}){I_{xz}}}}{{{I_x}{I_z} - I_{xz}^2}}, {\rm{ }} $ ${c_3} = \frac{{{I_z}}}{{{I_x}{I_z} - I_{xz}^2}}, {\rm{ }}{c_4} = \frac{{{I_{xz}}}}{{{I_x}{I_z} - I_{xz}^2}}, {\rm{ }}{c_5} = \frac{{({I_z} - {I_x})}}{{{I_y}}}, $ $ {c_6} = \frac{{{I_{xz}}}}{{{I_y}}}, {\rm{ }}{c_7} = \frac{1}{{{I_y}}}, {c_8} = \frac{{{I_x}({I_x} - {I_y}) + I_{xz}^2}}{{{I_x}{I_z} - I_{xz}^2}}, {\rm{ }}{c_9} = \frac{{{I_x}}}{{{I_x}{I_z} - I_{xz}^2}}$

根据角速度和姿态角的关系就可得到舰载机的运动学方程组：

$ \left\{ \begin{array}{l} \dot \phi = p + \left( {r\cos \phi + q\sin \phi } \right)\tan \theta \\ \dot \theta = q\cos \phi - r\sin \phi \\ \dot \psi = \frac{1}{{\cos \theta }}\left( {r\cos \phi + q\sin \phi } \right) \end{array} \right. $

(3)

联立式(1)~(3)，可得到舰载机着舰非线性模型^[14]。

1.2 舰艉气流模型

舰载机着舰过程最大的干扰便是舰艉流，舰艉气流主要由四部分组成：随机自由大气紊流分量、稳态分量、周期分量、随机分量。这四种分量在美军标MIL-HDBK-1797^[15]中有具体的建模表达式和仿真。

本文通过选取3级海况下的舰艉流仿真分析舰艉流在舰载机着舰过程中对着舰影响。考虑到着舰前12.5 s才受到舰艉流的影响，所以不考虑43.8 s前的着舰过程，仿真将直接从43.8 s开始，如图 1所示。从图中可以看出，舰艉气流对舰载机着舰有着显著的影响，最大能造成5 m/s的速度变化，所以不能忽视舰艉流对舰载机着舰的影响。因此设计的控制器需要具有抑制舰艉流干扰的能力。

2 控制器设计 2.1 非线性动态逆舰载机着舰控制器设计

动态逆方法是建立在逆系统理论基础上的，实质上是将一个系统的非线性部分通过引入一个适当的非线性输入来加以抵消，并用一个期望的动态模型(通常为线性的)来代替。同时由于舰载机的控制量少于系统的状态量，所以不能得到控制系统的全逆。为解决这一问题，将非线性动态逆方法与奇异摄动理论结合, 将系统分为快慢不同的子系统进行近似求解^[16]。

根据文中舰载机的六自由度非线性模型可知，舰载机有九个状态变量，即

$ \mathit{\boldsymbol{x}} = {\left[ {\begin{array}{*{20}{c}} p&q&r&f&q&y&u&v&w \end{array}} \right]^{\rm{T}}} $

根据时标分离的原理，结合工程实际，可将这九个状态变量划分成为快、较快和慢三组。${\mathit{\boldsymbol{x}}_1} = {\left[ {p\;\;q\;\;r} \right]^{\rm{T}}} $为快变化量，$ {\mathit{\boldsymbol{x}}_2} = {\left[ {\varphi \;\;\theta \;\;\psi } \right]^{\rm{T}}}$为较快变化量，${\mathit{\boldsymbol{x}}_3} = {\left[ {u\;\;v\;\;w} \right]^{\rm{T}}} $为较慢变化量。

分析舰载机模型，舰载机的控制量为$\mathit{\boldsymbol{u}} = [{\delta _{\rm{e}}}\;\;{\delta _{\rm{a}}}\;\;{\delta _{\rm{r}}}\;\;{\delta _{\rm{T}}}] $，分为两组：${\mathit{\boldsymbol{\delta }}_1} = [{\delta _{\rm{e}}}\;\;{\delta _{\rm{a}}}\;\;{\delta _{\rm{r}}}] $为舵面控制量；${\mathit{\boldsymbol{\delta }}_2} = {\mathit{\boldsymbol{\delta }}_{\rm{T}}} $为油门控制量, 控制变量隐含在六自由度模型中。

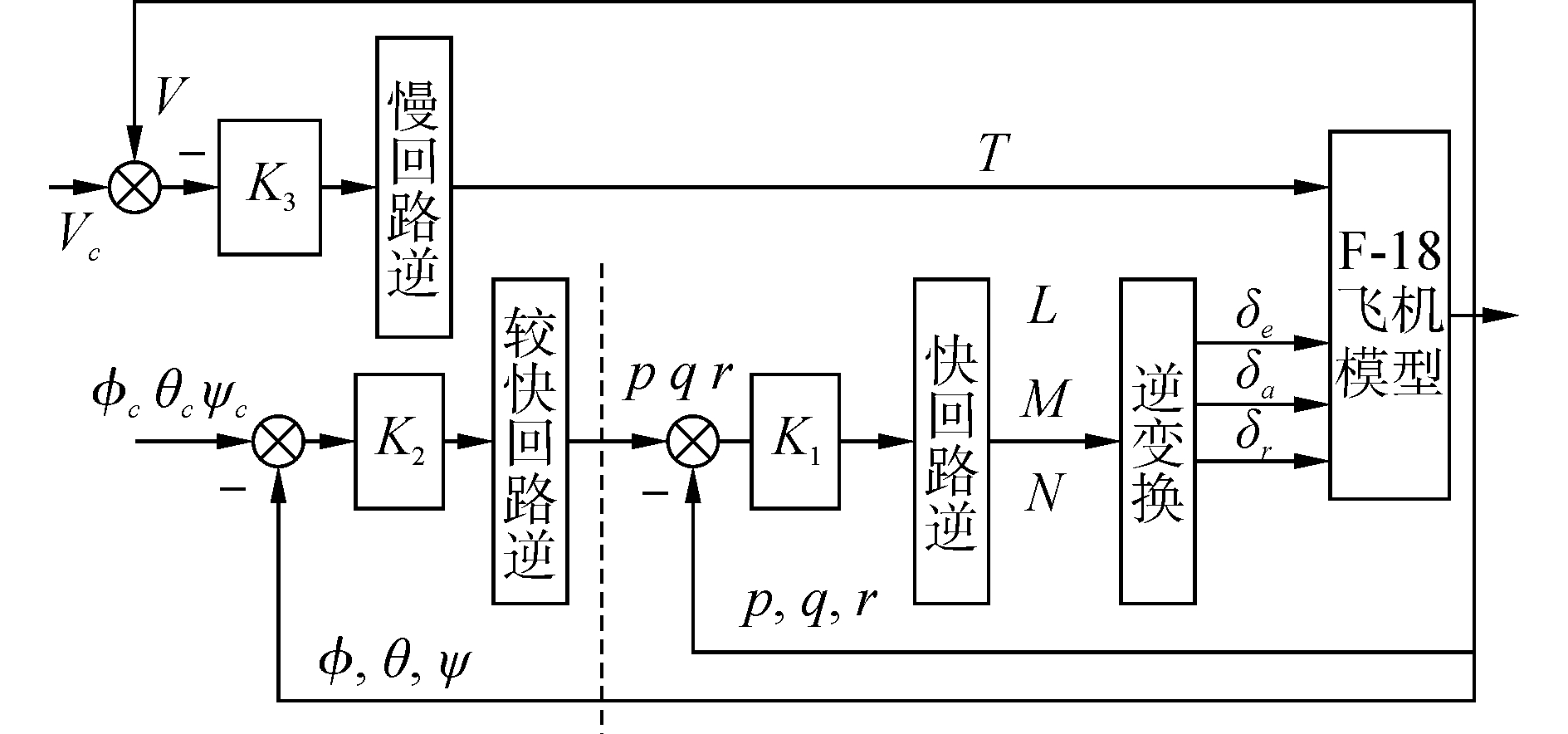
分析模型发现，系统状态变量在时间上有明显的差别，首先变化的是姿态角速度，随后是姿态角的变化，最后是速度，根据这一特性将文中所确定的飞机数学模型进行合理的划分，从而将飞机数学模型分成有着内在联系的三个子系统，如图 2所示。

时标分离后的子系统可表示为

$ {{\mathit{\boldsymbol{\dot x}}}_{\rm{f}}} = {F_{\rm{f}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{f}}}} \right) + {G_{\rm{f}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{f}}}} \right)\mathit{\boldsymbol{u}} $

(4)

$ {{\mathit{\boldsymbol{\dot x}}}_{\rm{s}}} = {F_{\rm{s}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) + {G_{\rm{s}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right){\mathit{\boldsymbol{x}}_{\rm{f}}} $

(5)

其中: $ {\mathit{\boldsymbol{x}}_{\rm{f}}} = {\left[ {p\;\;q\;\;r} \right]^{\rm{T}}}, {\rm{ }}{\mathit{\boldsymbol{x}}_{\rm{s}}} = {\left[ {\varphi \;\;\theta \;\;\psi } \right]^{\rm{T}}}, \mathit{\boldsymbol{u}} = {[{\delta _{\rm{e}}}\;\;{\delta _{\rm{a}}}\;\;{\delta _{\rm{r}}}]^{\rm{T}}}$。

设慢回路状态变量的动态期望值为

$ {{\mathit{\boldsymbol{\dot x}}}_{{\rm{sd}}}} = {\left[ {\begin{array}{*{20}{c}} {\dot \varphi }&{\dot \theta }&{\dot \psi } \end{array}} \right]^{\rm{T}}} $

由式(5)可以解出快回路的输入指令为

$ {\mathit{\boldsymbol{x}}_{{\rm{fc}}}} = \mathit{\boldsymbol{G}}_{\rm{s}}^{ - 1}\left( {{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)\left[ {{{\mathit{\boldsymbol{\dot x}}}_{{\rm{sd}}}} - {F_{\rm{s}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)} \right] $

(6)

在此基础上，设与x_fc相应的快回路状态期望$ {{\mathit{\boldsymbol{\dot x}}}_{{\rm{fd}}}} = {\rm{ }}{[\dot p\;\;\dot q\;\;\dot r]^{\rm{T}}}$，由式(4)可以解得舰载机理想控制输入为

$ u = \mathit{\boldsymbol{G}}_{\rm{f}}^{ - 1}\left( {{\mathit{\boldsymbol{x}}_{\rm{f}}}} \right)\left[ {{{\mathit{\boldsymbol{\dot x}}}_{{\rm{fd}}}} - {F_{\rm{f}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{f}}}} \right)} \right] $

(7)

但动态逆控制方法并非适用一切情况，它要求系统的非线性部分为解析的，或是某种程度上是连续的，只有这样的系统，才能求逆。因此动态逆方法对模型要求很高，因此需要对动态逆加以改进。

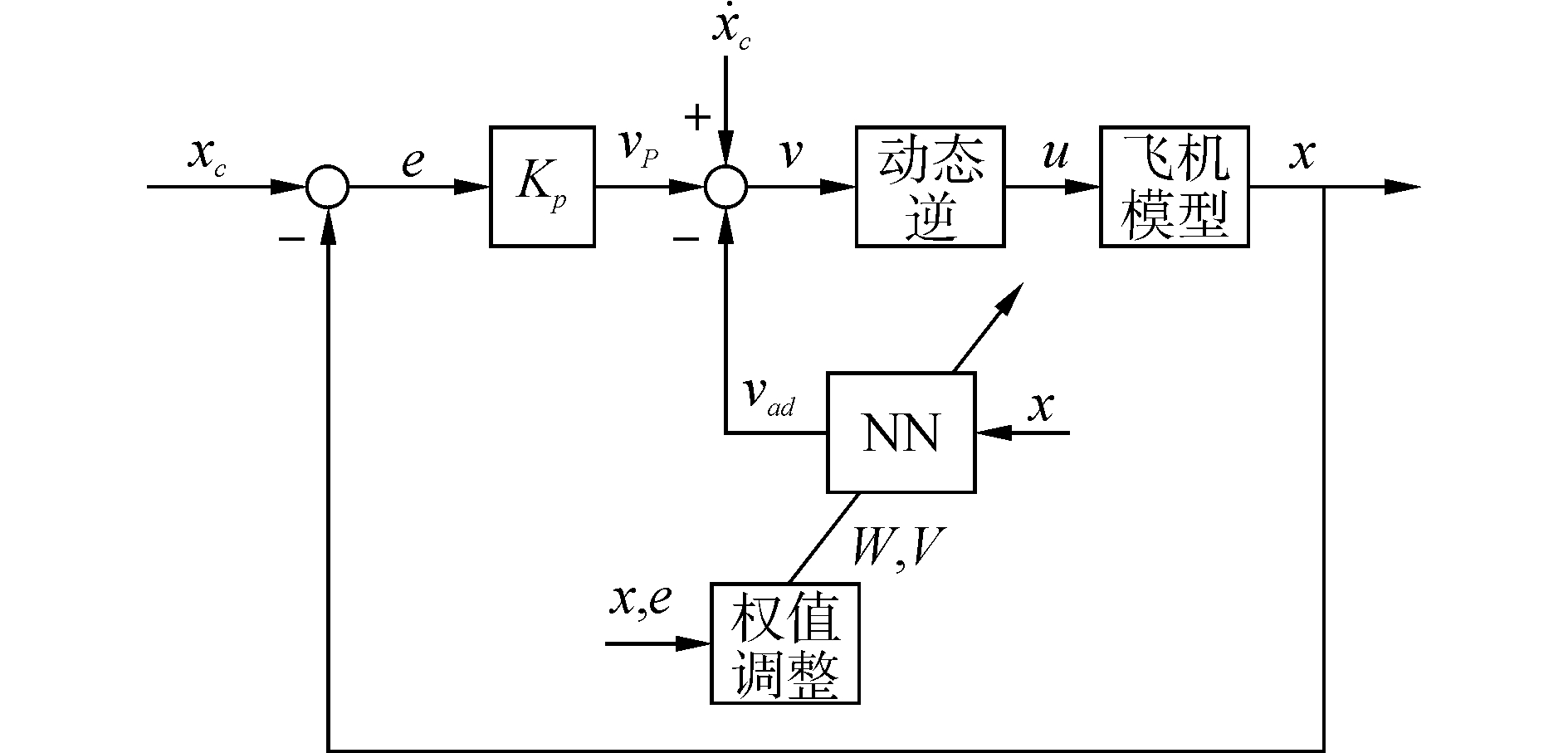
2.2 神经网络动态逆舰载机着舰控制器设计

建模不准确、求逆计算、外界干扰都可能引起系统状态误差从而影响控制器的效果，因此，本文在控制器中加入在线神经网络，对舰载机着舰过程中建模误差和干扰进行动态补偿，从而提高控制器效果。控制系统结构图如图 3所示。

由图 3可知，飞机的模型为存在系统误差的非线性模型:

$ \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{f}} + g\mathit{\boldsymbol{u}} + \Delta $

(8)

动态逆控制器输出可以表示为

$ \mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{g}}^{ - 1}}\left( { - \mathit{\boldsymbol{f}} + \mathit{\boldsymbol{v}}} \right) $

(9)

将式(9)代入式(8)中可以得到采用动态逆控制器后的系统模型:

$ \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{v}} + \Delta $

(10)

式中：v表示系统的伪控制信号，Δ表示由建模不准确、求逆计算以及外界干扰等因素引起的动态逆误差。

由图 3知，动态逆控制器的伪控制信号v由三部分组成：期望状态的积分信号$ {{\mathit{\boldsymbol{\dot x}}}_{\rm{c}}}$、期望状态的比例信号v_P及神经网络自适应补偿信号v_ad。

$ \mathit{\boldsymbol{v}} = {\mathit{\boldsymbol{v}}_{\rm{p}}} + {{\mathit{\boldsymbol{\dot x}}}_{\rm{c}}} - {\mathit{\boldsymbol{v}}_{{\rm{ad}}}} $

(11)

输入与输出之间的误差关系为

$ \left\{ \begin{array}{l} \mathit{\boldsymbol{e}} = {\mathit{\boldsymbol{x}}_{\rm{c}}} - \mathit{\boldsymbol{x}}\\ \mathit{\boldsymbol{\dot e}} = {{\mathit{\boldsymbol{\dot x}}}_{\rm{c}}} - \mathit{\boldsymbol{\dot x}} \end{array} \right. $

(12)

将式(10)和(11)代入式(12)，整理为

$ \mathit{\boldsymbol{\dot e}} = - {k_{\rm{p}}}\mathit{\boldsymbol{e}} + \left( {{\mathit{\boldsymbol{v}}_{{\rm{ad}}}} - \Delta } \right) $

(13)

由式(13)可知，理想情况下，v_ad能够完全重构逆误差，文献[2]介绍了推导过程，本文不再详述。

2.3 神经网络的构造

考虑到舰载机着舰对时间和精度的要求，本文采用改进的BP神经网络，用以提高网络的收敛速度和训练精度。BP神经网络的输入输出映射关系可以表示为

$ {y_i} = \sum\limits_{j = 1}^{{N_2}} {\left[ {{\mathit{\boldsymbol{w}}_{ij}}\sigma \left( {\sum\limits_{k = 1}^{{N_1}} {{v_{j{\rm{k}}}}{{\bar x}_{\rm{k}}}} + {\theta _{{\rm{v}}j}}} \right) + {\theta _{{\rm{w}}i}}} \right]} $

(14)

式中：i=1, 2, …, N₃，v_jk表示输入层到隐含层之间的连接权值，w_ij表示隐含层到输出层之间的连接权值，θ_vj、θ_wi表示阈值，N₁、N₂、N₃表示输入层、隐层、输出层神经元个数。σ(·)表示隐层激励函数，本文选取S型激励函数如下

$ \sigma \left( z \right) = \frac{1}{{1 + {\mathit{\boldsymbol{e}}^{ - az}}}} $

式中：z∈R，a为激励系数，e为系统误差。

输入、输出和激励矩阵如下

$ \mathit{\boldsymbol{x}} = {\left[ {1,{x_1},{x_2}, \cdots ,{x_{{N_1}}}} \right]^{\rm{T}}} $

(15)

$ \mathit{\boldsymbol{y}} = {\left[ {1,{y_1},{y_2}, \cdots ,{y_{{N_3}}}} \right]^{\rm{T}}} $

(16)

$ \mathit{\boldsymbol{\sigma }}\left( z \right) = {\left[ {1,\sigma \left( {{z_1}} \right),\sigma \left( {{z_2}} \right), \cdots ,\sigma \left( {{z_{{N_2}}}} \right)} \right]^{\rm{T}}} $

(17)

重新定义神经网络权值矩阵，将阈值包含在权值矩阵中，即

$ {\mathit{\boldsymbol{W}}^{\rm{T}}} = \left[ {{\theta _{{\rm{w}}i}}\left| {{\mathit{\boldsymbol{w}}_{ij}}} \right.} \right],{\mathit{\boldsymbol{V}}^{\rm{T}}} = \left[ {{\theta _{{\rm{v}}i}}\left| {{\mathit{\boldsymbol{v}}_{ij}}} \right.} \right] $

(18)

这样神经网络的映射关系就可以表示为

$ \mathit{\boldsymbol{y}} = {\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{\sigma }}\left( {{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{x}}} \right) $

(19)

本文的神经网络不需要离线训练，网络的权值调整通过李雅普诺夫稳定性定理得到。网络的渐进收敛性，可以通过选取适当的李雅普诺夫函数进行证明^[17]。网络的权值调整规则如下

$ \mathit{\boldsymbol{\dot W}} = - \left\{ {\left( {\mathit{\boldsymbol{\sigma }} - {{\sigma '}_z}{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{x}}} \right)\mathit{\boldsymbol{e}} + \lambda \left\| \mathit{\boldsymbol{e}} \right\|\mathit{\boldsymbol{W}}} \right\}{\mathit{\Gamma }_W} $

(20)

$ \mathit{\boldsymbol{\dot V}} = - \left\{ {\mathit{\boldsymbol{xeW}}{{\sigma '}_z} + \lambda \left\| \mathit{\boldsymbol{e}} \right\|\mathit{\boldsymbol{V}}} \right\}{\mathit{\Gamma }_V} $

(21)

式中：$\mathit{\boldsymbol{\sigma }} = \mathit{\boldsymbol{\sigma }}({\mathit{\boldsymbol{V}}^{\rm{T}}}x),{{\sigma '}_z} = \frac{{{\rm{d}}\sigma \left( z \right)}}{{{\rm{d}}z}},{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_W},{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_V} $为学习率。

由式(20)、(21)可知，学习率Г的大小直接影响权值矩阵的取值，从而影响网络的收敛速度。若学习率Г过小，网络收敛速度则会变慢；若学习率Г过大，则会引起权值调整在收敛处的上下摆动，影响系统的精度。为了解决学习率Г取值矛盾，提高网络的收敛速度。本文对学习率Г进行自适应调整。调整规则如下：

$ \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\left( k \right) = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} {k_1}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\left( {k - 1} \right),\\ \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\left( {k - 1} \right),\\ {k_2}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\left( {k - 1} \right), \end{array}&\begin{array}{l} E\left( {k - 1} \right) > E\left( k \right)\\ E\left( {k - 1} \right) = E\left( k \right)\\ E\left( {k - 1} \right) < E\left( k \right) \end{array} \end{array}} \right. $

(22)

式中：k₁>1，0 < k₂ < 1，由式(19)可知，对于不同的误差变化，每一步学习都会影响学习率的调整。

根据式(19)~(22)即可求出神经网络动态补偿输出。

3 着舰仿真

为了验证控制器的效果，验证控制器指令跟踪性能。分别对一般动态逆、神经网络动态逆和改进神经网络动态逆进行仿真。仿真所采用的舰载机模型存在建模误差，以俯仰角为例，初始俯仰角为0°，起初俯仰角指令为5°，5 s后指令变为3°。仿真图如图 4所示。

图 4可以看出一般动态逆控制器无法精确跟踪控制指令。因此需要将神经网络动态补偿引入控制器中。加了神经网络后，系统能够很好地抑制系统的建模误差，但是从图中也可以发现，系统的收敛速度不是很快，并不能满足舰载机着舰对控制速度的要求，所以需要对神经网络进行改进，提高控制器的响应速度。点划线为增加了自适应学习率的改进神经网络动态逆俯仰角响应曲线图，从图中可以看出，俯仰角大概在2 s时就能达到收敛，且能够精确跟踪俯仰角指令，说明改进的神经网络能有效的提高收敛速度和控制精度。

为了更好地验证控制器效果，将控制器用于舰载机着舰仿真中，考虑系统的建模误差和外部舰艉气流的干扰。给定-3.5°的期望下滑高度指令，舰载机的初始速度为69.3 m/s，迎角为8.5°，俯仰角为5°，初始高度为250 m。选取本文所得到的3级海况下的舰艉流进行仿真，考虑到着舰前12.5 s才受到舰艉流的影响，所以在43.8 s时加入舰艉气流干扰，图(5)是一般动态逆控制器高度曲线和高度误差曲线，H_c为给定的控制指令，h为实际状态。从图中可以看出，在未加扰动前，建模误差起主导影响，一般动态逆虽然有跟踪误差但还是满足着舰要求的，但是当舰艉流加入时，一般的动态逆控制器明显不能满足着舰要求。因此需要加入神经网络对对建模误差和外部干扰进行补偿。

如图 6为加入改进神经网络的动态逆控制高度曲线和高度误差曲线，H_c为给定的控制指令，H为实际状态。从图中可以看出，加入改进的神经网络后，在建模误差占主导时，能够快速跟踪高度指令，当舰艉流扰动加入时，高度误差虽有波动，但是波动很小，满足舰载机着舰高度误差的要求。通过仿真验证证明，所设计的改进神经网络动态逆控制器，能够满足舰载机着舰对时间和精度的要求。

4 结论

1) 动态逆控制方法能有效解决舰载机着舰非线性控制问题，同时采用快慢子系统分别求逆方法很好地解决了输入输出变量不相等不能求全逆问题。

2) 神经网络动态逆控制方法对建模误差以及舰艉气流干扰具有很好的抑制作用，能有效控制舰载机着舰轨迹，保证安全着舰。

3) 通过引入自适应学习率，使学习率随误差的改变而改变，从而有效提高神经网络的收敛速度，满足舰载机着舰对速度和精度的要求。

4) 对于恶劣海况，神经网络动态逆控制方法比一般控制方法能更加有效保证舰载机着舰安全。

另外，本文未考虑甲板运运动对舰载机着舰的影响，这将是下一步研究的方向。