2. 重庆市高新工程勘察设计院有限公司, 重庆 400047
2. Chongqing Hi-new Geotechnical Investigation and Design Institute Co., Ltd., Chongqing 400047, China
现有基础类型主要为钢筋混凝土基础与无筋扩展基础。无筋扩展基础抗压性能较好,抗拉、抗弯性能差;钢筋混凝土基础不仅具备良好的抗压性能,在抗拉、抗弯性能上也明显优于无筋扩展基础。国内外对土质地基中钢筋混凝土基础与无筋扩展基础的应力分布规律通过长期研究已经得到了明确的结论并在实际工程中广泛应用。岩质地基基础的研究则相对滞后,现有研究成果还未取得统一的结论。本文主要针对岩质地基中的钢筋混凝土独立基础的应力分布规律进行研究,以期对岩质地基中钢筋混凝土独立基础的研究提供一些有益的成果。
Fox[1]对双层系统接触面受竖向均布荷载下的基底应力进行了试验,得到了不同地基强度比值和不同荷载宽度与埋深比值下的应力比。Whiteman等[2]通过试验得到了半无限体上矩形刚性基础的竖向位移近似解。Muki[3]给出了轴对称圆形弹性地基在半无限空间下的应力分布计算方法。Schiffman等[4]给出了轴对称椭圆形弹性地基在半无限空间下的应力分布。云天铨[5]运用线载荷积分法求解了水平刚性岩基上在受垂直集中力作用下的Fredholm第一类积分方程,并进行了数值验证。文丕华[6]提出的求解方法是在Southwell对称问题基本方程基础上应用Hankle变换对受圆形均布荷载的基底应力求解。在模型试验方面,阴可等[7]对岩石地基上扩展基础的基底反力试验数据进行了分析;艾智勇等[8]对分层地基上矩形刚性基础的基底反力、沉降和倾斜进行了计算;阴可等[9]对岩石地基上扩展基础的受力特性进行了分析。上述方法未对嵌固于岩体中的矩形基础应力分布规律和计算方法进行研究,也未考虑斜向荷载情况。
本文在结合前人研究基础上,采用斜向受荷下的岩质地基基础模型试验与模型三维有限元分析对斜向受荷下岩质地基基础应力分布规律与破坏模式进行研究。对基础压应力集中核心区边界与接触面参数法向刚度、切向刚度解进行推导与验证。
2 斜向荷载作用下基础模型试验在前人研究基础上本文设计了斜向受荷下的岩质地基基础模型试验,试验参数详见图 1。

|
Download:
|
| 图 1 试验模型几何尺寸图 Fig. 1 The foundation design plan figure | |
根据J1~J4卸载后试件裂纹分布图分析,试件在受荷过程中初始裂纹呈十字分布于基底(图 2中圈区为裂纹初始发育区)。基底裂纹从柱头倾斜角度45°延长线在底部投影区开始向试件上部扩展,随着荷载的持续增加,裂纹扩展直至试件面侧。

|
Download:
|
| 图 2 试件破坏后基底裂纹分布图 Fig. 2 Test specimen damage graphs | |
试件底部预埋钢筋应变片的数据采集分析能较好的反应基础底部应力分布特点。试验中试件J1~J4基底应变片数据统计如图 3所示。

|
Download:
|
| 图 3 应变片数据统计图 Fig. 3 Strain gauge data statistical figures | |
试件J1应变极值出现在S4与S7号应变片,J2极值出现在S10与S11号应变片,并以其为中心向四周扩展形成类圆形区域。试件J3应变极值出现在S11、S12、S13、S14号应变片,J4极值出现在S15、S16、S17、S20号应变片。J1~J4应变分布以极值区为中心向四周扩展形成边界类圆形的应变较大值区域(图 4)。较大值区与基底混凝土开裂初始区位置分布基础一致。基底应变与裂纹扩展规律表明,基底混凝土破坏是由应变较大值区受拉形成。

|
Download:
|
| 图 4 应变片大值分布区域图 Fig. 4 Large strain gauge value distribution area figures | |
从图 4所示分布规律可知,随着试件高度增大,应变较大值区向基底中部偏移,受荷载入射角度影响逐渐减小,影响面积逐渐增大。综上所述,基础破坏程度与基础高宽比(h/b)存在直接关系。高宽比(h/b)较小时,岩质地基中的钢筋混凝土基础基底呈现剪切破坏特征;随着高宽比(h/b)增大,基础受弯拉破坏的特征逐渐明显。在高宽比较小时应增加基础高度,防止基础发生剪切破坏;在高宽比较大时应增加基底钢筋,防止基础发生弯拉破坏。
3 基础三维有限元分析本文对不同基础高宽比(h/b)的岩质地基基础进行三维有限元分析,模型采用D-P准则作为岩体材料[10],其余参数同模型试验,采用接触单元模拟岩体与基础的接触。
选取模型J2、J3、J4进行数值模拟,得到中轴剖面与基底横截面的第一主应力云图(图 5)。

|
Download:
|
| 图 5 第一主应力分布云图 Fig. 5 First principal stress distribution figures | |
通过竖向与横向应力云图剖面可得,斜向受荷条件下基础内压应力核心区呈椭圆球体。由于岩体弹性模量大于混凝土弹性模量,使基础四周与底面岩体成为强约束区,压应力核心区在边界条件影响下导致拉应力区的形成与扩展。
压应力核心区在高宽比(h/b)较小时,核心区边界距离基础边界距离小,拉应力难以扩展,在基底集中形成拉应力集中区;随着高宽比(h/b)增大,承受拉应力的混凝土体增加,拉应力扩展但应力值减小。横截面应力图(图 5)反映基底拉应力区范围随高宽比增大向基底中心明显偏移。上述结论验证了模型试验得到的结论(图 4),其破坏模式是基础混凝土在荷载与岩体边界强约束共同作用下在混凝土内形成压应力核心体,核心体边界与基础边界间混凝土出现受拉破坏,简称混凝土压胀-受拉破坏。
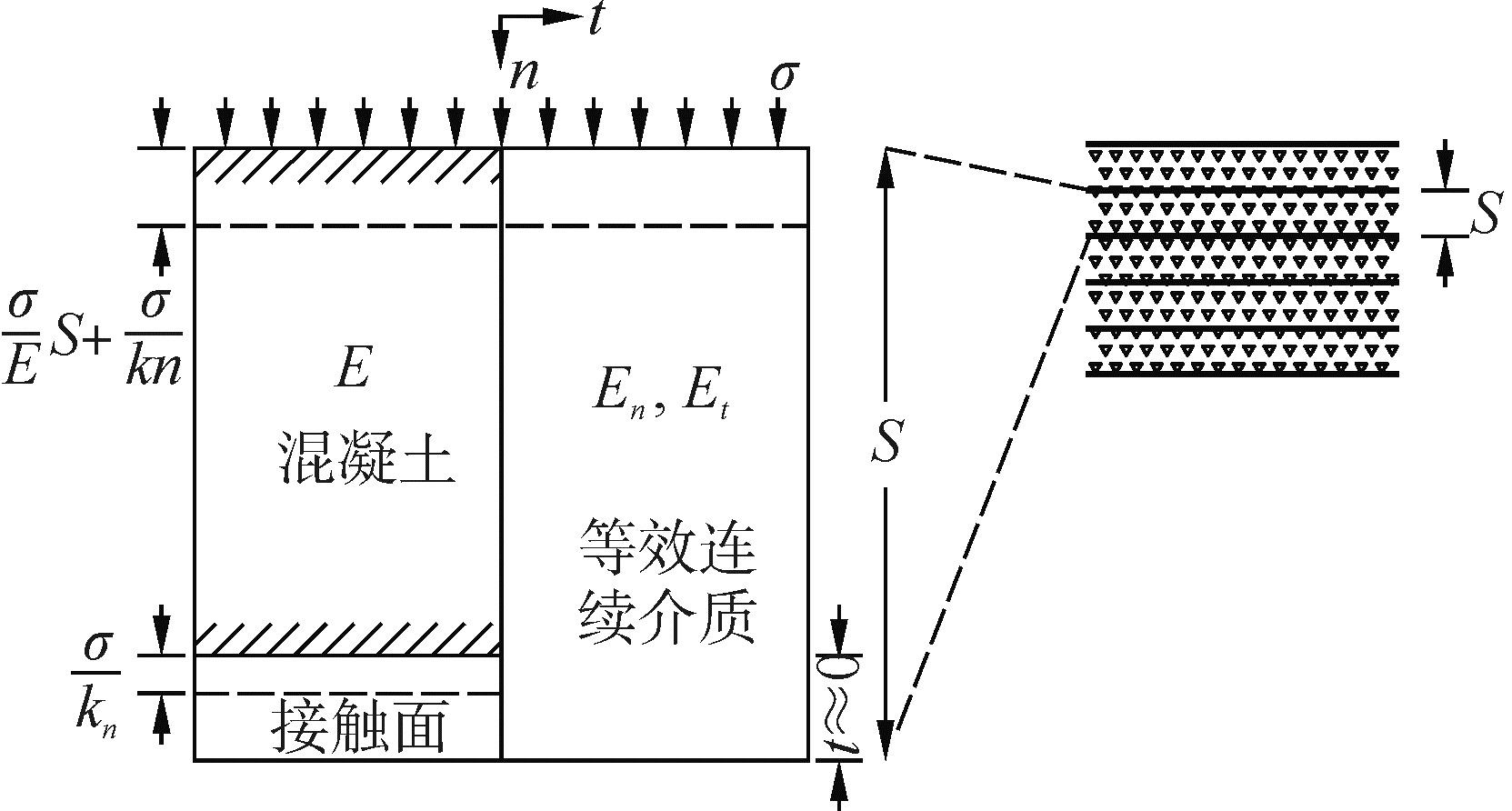
4 基础压应力核心区的理论计算分析基础内应力分布特征过程中,压应力核心集中区边界的求解是问题的关键。本文在模型试验与三维有限元分析基础上,引入Goodman[11]层状岩体内应力求解中的等效各向同性介质理论对基础压应力核心体边界进行求解。等效各向同性介质是将含有接触面的材料在荷载作用下的模量进行等效(图 6)。
|
Download:
|
| 图 6 等效连续介质原理图 Fig. 6 Equivalent continuum Schematic diagrams | |
求解过程中将混凝土基础与岩体的接触面等效视作不同岩体相互接触的闭合面。混凝土材料特性采用弹性模量E、剪切模量G与泊松比μ表征,Ent为弹性模量t分量。通过位移等效原理将混凝土体与底部接触面等效为等效各向同性介质,等效各向同性介质通过弹性模量En与剪切模量Gnt表征。其中接触面的特征采用法向刚度kn与切向刚度ks进行描述。等效原理的表达式为
| $ \frac{\sigma }{E}S + \frac{\sigma }{{{k_n}}} = \frac{\sigma }{{{E_{nt}}}}S $ | (1) |
| $ \frac{1}{E} + \frac{1}{{{k_n}S}} = \frac{1}{{{E_n}}} $ | (2) |
| $ \frac{\tau }{G}S + \frac{\tau }{{{k_s}}} = \frac{\tau }{{{G_{nt}}}}S $ | (3) |
| $ \frac{1}{G} + \frac{1}{{{k_s}S}} = \frac{1}{{{G_{nt}}}} $ | (4) |
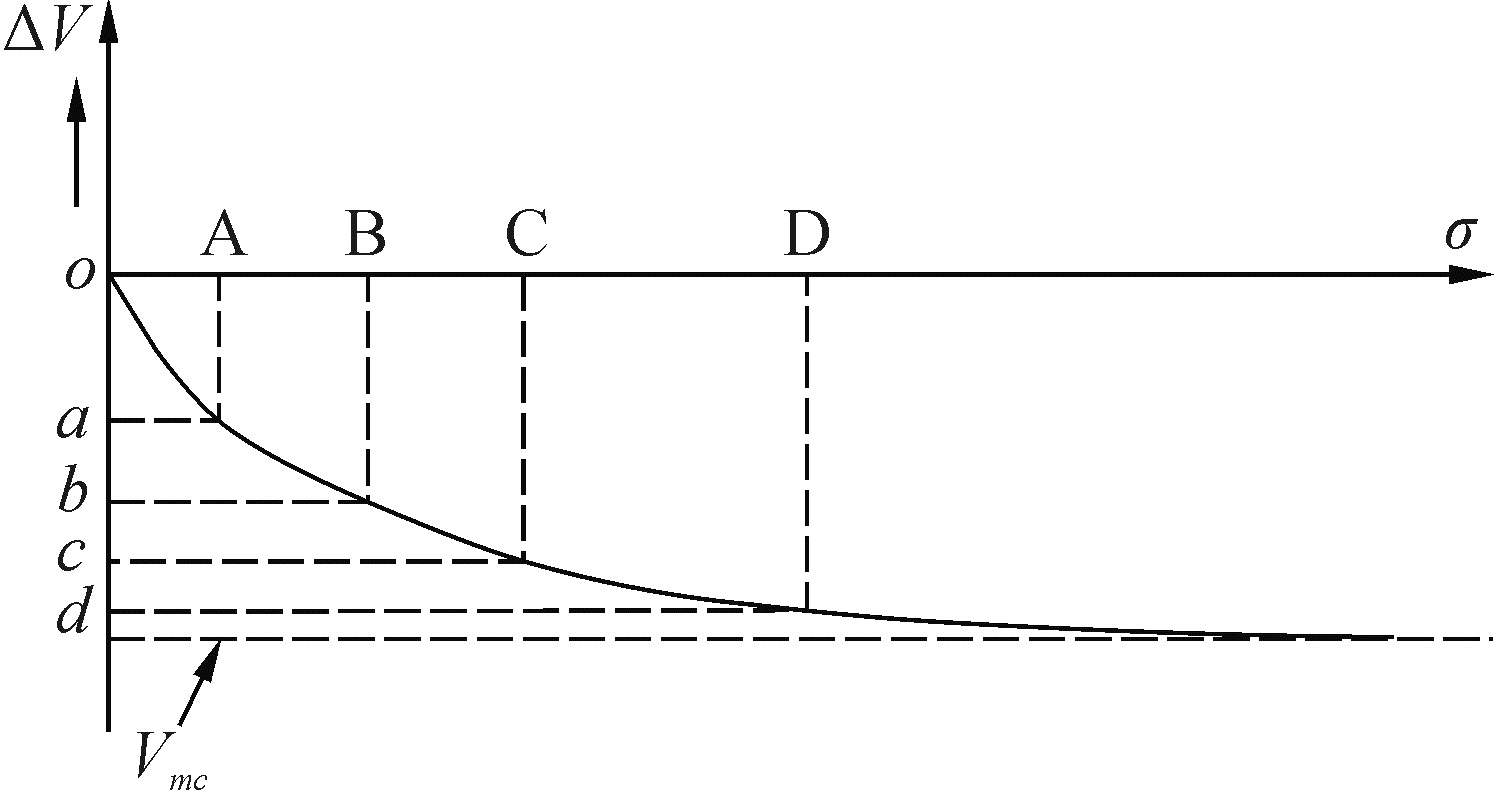
式中:S为接触面到荷载作用面的距离,在基础内压应力核心体计算中可视为基础高度。通过上述论述可知,等效各向同性介质的弹性模量En与剪切模量Gnt小于未考虑接触面影响材料的弹性模量E与剪切模量Gn,因此kn与ks是恒正的。kn可通过统计试验中接触面上的法向应力σ与法向位移Δv得到;ks同理可通过统计试验中接触面上的切向应力τ与位移Δw得到。以kn为例,计算简图如图 7。计算中可根据不同阶段的应力与对应的位移采用式(5)、(6)求得不同阶段的kn和ks。
| $ {k_n} = \frac{\sigma }{{\Delta v}} $ | (5) |
| $ {k_s} = \frac{\tau }{{\Delta \omega }} $ | (6) |
|
Download:
|
| 图 7 试验计算kn数据图 Fig. 7 Test calculation kn used data parameters | |
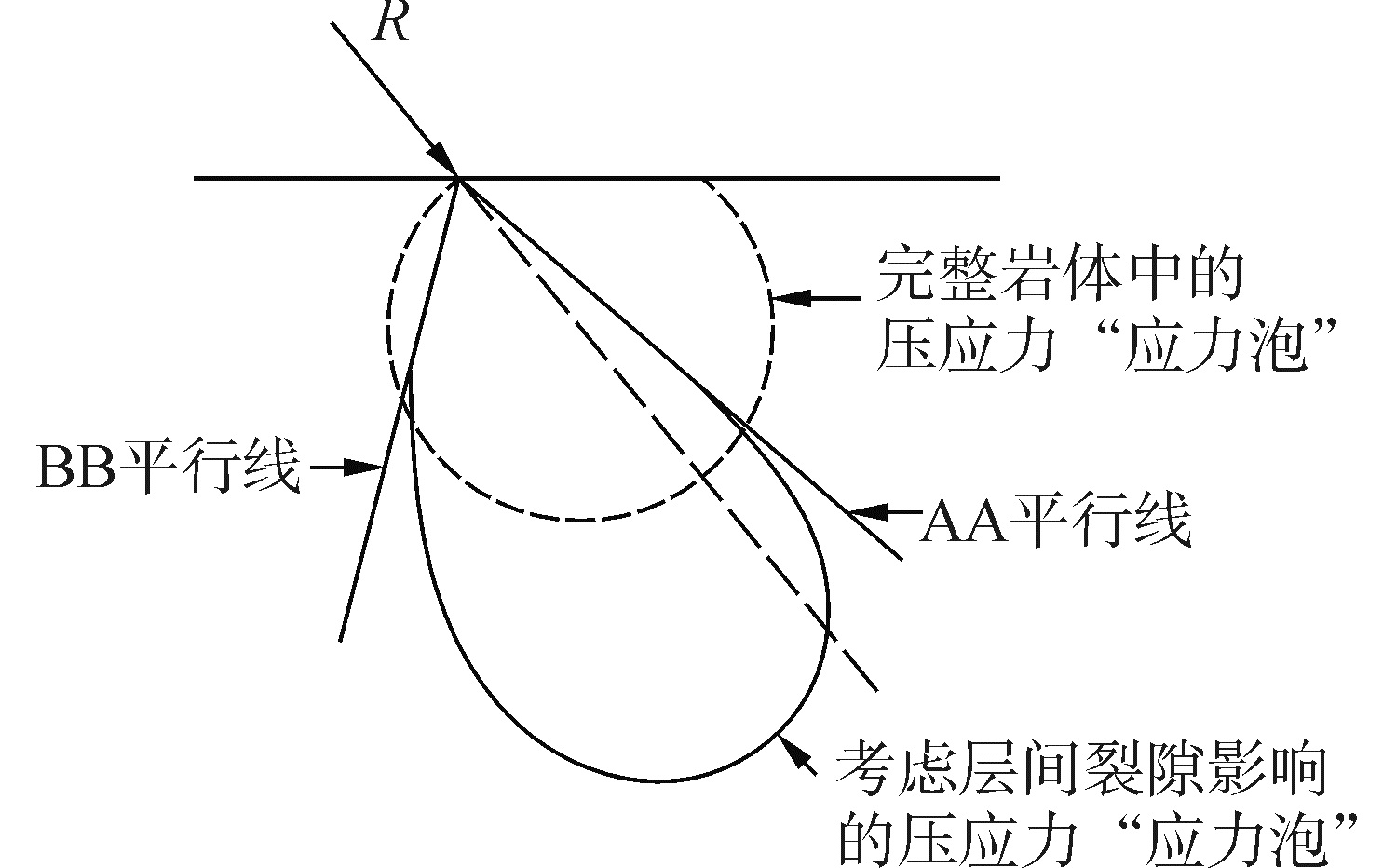
根据“等效各向同性介质”理论,可采用径向应力对压应力核心体边界进行求解,求解示意图如图 8。
|
Download:
|
| 图 8 考虑接触面影响的应力等值线图 Fig. 8 Considering interlayer effect of radial stress contour | |
| $ {\sigma _r} = \frac{{h\left( {X\cos \beta + Yg\sin \beta } \right)}}{{{\rm{ \mathsf{ π} }}r\left( {{{\left( {{{\cos }^2}\beta - g{{\sin }^2}\beta } \right)}^2} + {h^2}{{\sin }^2}\beta {{\cos }^2}\beta } \right)}} $ | (7) |
其中
| $ g = {\left[ {1 + \frac{E}{{\left( {1 - {v^2}} \right){k_n}S}}} \right]^{1/2}} $ | (8) |
| $ h = {\left\{ {\frac{E}{{1 - {\nu ^2}}}\left[ {\frac{{2\left( {1 + \nu } \right)}}{E} + \frac{1}{{{k_s}S}}} \right] + 2\left( {g - \frac{\nu }{{1 - \nu }}} \right)} \right\}^{1/2}} $ | (9) |
在实际应用中对于参数kn和ks存在2个难点:1)采用试验数据进行参数求解受试验结果的影响较大,准确性差;2)计算中主要关注荷载稳定后基底应力与位移所对应的kn和ks,试验中测试结果易受前期测试数据干扰。
针对上述问题,本文提出在Southwell基本方程基础上应用Hankle变换对受均布荷载作用下的基底应力与位移进行求解。
Southwell基本方程:
| $ \left\{ \begin{array}{l} {\sigma _r} + {\sigma _\theta } = \frac{1}{r}\frac{{{\partial ^3}\lambda }}{{\partial r\partial {z^2}}}\\ {\sigma _r} - {\sigma _\theta } = r\frac{\partial }{{\partial r}}\frac{1}{{{r^2}}}\left( {\frac{{{\partial ^2}\lambda }}{{\partial {z^2}}} - 2\mu {\vartheta ^2}\lambda } \right)\\ {\sigma _z} = - \frac{1}{r}\frac{\partial }{{\partial r}}\left[ {\frac{{{\partial ^2}\lambda }}{{\partial {z^2}}} - \left( {1 + \mu } \right){\vartheta ^2}\lambda } \right]\\ {\tau _{\gamma z}} = \frac{1}{r}\frac{\partial }{{\partial z}}\left[ {\frac{{{\partial ^2}\lambda }}{{\partial {z^2}}} - \left( {1 + \mu } \right){\vartheta ^2}\lambda } \right] \end{array} \right. $ | (10) |
应力函数应满足柱座标四阶微分方程:
| $ {\vartheta ^2}\left( {{\vartheta ^2}\lambda } \right) = 0 $ | (11) |
| $ {\vartheta ^2} = \frac{{{\partial ^2}}}{{\partial {r^2}}} + \frac{1}{r}\left( {\frac{\partial }{{\partial r}} + \frac{{{\partial ^2}}}{{\partial {z^2}}}} \right) $ | (12) |
令:
| $ \left\{ \begin{array}{l} \phi \left( {r,z} \right) = {\vartheta ^2}\lambda \\ \psi \left( {r,z} \right) = \frac{{{\partial ^2}\lambda }}{{\partial {z^2}}} - \left( {1 + \mu } \right){\vartheta ^2}\lambda \end{array} \right. $ | (13) |
式(13)中ϕ与ψ应满足下式:
| $ {\vartheta ^2}\phi \left( {r,z} \right) = 0 $ | (14) |
| $ {\vartheta ^2}\psi \left( {r,z} \right) = \frac{{{\partial ^2}\phi }}{{\partial {z^2}}} $ | (15) |
对式(14)进行Hankel变换:
| $ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\rightharpoonup$}} \over \phi } = {H_1}\left[ {\phi \left( {r,z} \right);r \to \xi } \right] = \int_0^\infty {\xi \phi \left( {\xi ,z} \right){J_1}\left( {r\xi } \right){\rm{d}}\xi } $ | (16) |
将式(16)代入Southwell基本方程后进行逆变换整理后可得:
| $ \begin{array}{*{20}{c}} {{\sigma _z} = - \frac{1}{2}\int_0^\infty {\xi {J_0}\left( {\xi r} \right)\left\{ {\exp \left( {\xi z} \right)\left( {2C + \xi zA} \right) + } \right.} }\\ {\left. {\exp \left( { - \xi z} \right)\left[ {2D - \xi zB} \right]} \right\}{\rm{d}}\xi } \end{array} $ | (17) |
| $ \begin{array}{*{20}{c}} {{\tau _z} = \frac{1}{2}\int_0^\infty {\xi {J_1}\left( {\xi r} \right)\left\{ {\exp \left( {\xi z} \right) \cdot \left[ {2C + \left( {1 + \xi z} \right)A} \right] - } \right.} }\\ {\left. {\exp \left( { - \xi z} \right)\left[ {2D + \left( {1 - \xi z} \right)B} \right]} \right\}{\rm{d}}\xi } \end{array} $ | (18) |
| $ \begin{array}{*{20}{c}} {u = \frac{{1 + u}}{{2E}}\int_0^\infty {{J_1}\left( {\xi r} \right)\left\{ {\exp \left( {\xi z} \right)\left[ {2C + \left( {2 - 2u + \xi z} \right)A} \right]} \right. + } }\\ {\left. {\exp \left( { - \xi z} \right)\left[ {2D + \left( {2 - 2u - \xi z} \right)B} \right]} \right\}{\rm{d}}\xi } \end{array} $ | (19) |
| $ \begin{array}{*{20}{c}} {w = - \frac{{1 + u}}{{2E}}\int_0^\infty {{J_0}\left( {\xi r} \right)\left\{ {\exp \left( {\xi z} \right)\left[ {2C - \left( {1 - 2u - \xi z} \right)A} \right]} \right. - } }\\ {\left. {\exp \left( { - \xi z} \right)\left[ {2D - \left( {1 - 2u + \xi z} \right)B} \right]} \right\}{\rm{d}}\xi } \end{array} $ | (20) |
引入边界条件与荷载条件可求得完整表达式为
| $ {\sigma _z} = - \int_0^\infty {\xi {J_0}\left( {\xi r} \right)\left[ {2C{\rm{ch}}\left( {\xi z} \right) + \xi zA{\rm{sh}}\left( {\xi z} \right)} \right]{\rm{d}}\xi } $ | (21) |
| $ \begin{array}{l} {\tau _z} = \int_0^\infty {\xi {J_1}\left( {\xi r} \right)\left\{ {2C{\rm{sh}}\left( {\xi z} \right) + A\left[ {{\rm{sh}}\left( {\xi z} \right) + } \right.} \right.} \\ \;\;\;\;\;\;\left. {\left. {\xi z{\rm{ch}}\left( {\xi z} \right)} \right]} \right\}{\rm{d}}\xi \end{array} $ | (22) |
| $ \begin{array}{l} u = \frac{{1 + u}}{{2E}}\int_0^\infty {{J_1}\left( {\xi r} \right)\left\{ {2C{\rm{ch}}\left( {\xi z} \right) + } \right.} \\ \;\;\;\;\;\;\left. {A\left[ {2\left( {1 - \mu } \right){\rm{ch}}\left( {\xi z} \right) + \xi z{\rm{sh}}\left( {\xi z} \right)} \right]} \right\}{\rm{d}}\xi \end{array} $ | (23) |
| $ \begin{array}{l} w = - \frac{{1 + u}}{E}\int_0^\infty {{J_0}\left( {\xi r} \right)\left\{ {2C{\rm{sh}}\left( {\xi z} \right) + } \right.} \\ \;\;\;\;\;\;\left. {A\left[ {\xi z{\rm{ch}}\left( {\xi z} \right) - \left( {1 - 2\mu } \right){\rm{sh}}\left( {\xi z} \right)} \right]} \right\}{\rm{d}}\xi \end{array} $ | (24) |
式中:F0 A(β)、F0C(β)、F1 A(β)、F1C(β)是不随材料变化的参数,可参照文献[12]取值。
将式(21)~(24)计算结果代入式(5)、(6)可得kn与ks,可求得压应力核心体的边界。对不同高度基础压应力核心区边界计算结果如图 9。

|
Download:
|
| 图 9 时压应力核心区等势线图 Fig. 9 Compressive stress core equipotential figures | |
1) 通过对模型试验与三维有限元结果的分析,得到了斜向荷载作用下岩质地基基础破坏模式是一种压胀-受拉破坏。
2) 本文提出了基础中压应力核心区边界和边界求解中主要参数kn与ks的理论计算方法。将上述两种计算方法对不同高度基础中的压应力核心区边界进行了求解,并对计算结果进行了验证, 为岩质地基基础的内应力后续研究与设计提供了理论依据。
3) 通过对压应力核心区边界理论计算结果与三维有限元分析结论进行对比,发现理论计算与三维有限元分析得到的边界基本一致,从而验证了基于等效各向同性介质理论提出的理论计算方法和参数kn和ks理论计算方法的可行性。
| [1] |
FOX L. Computation of traffic stresses in a simple road structure[C]//Proceedings of 2nd Interntional Conference of Soil Mechanics and Foundation Engineering. 1948, 2: 236-246.
(  0) 0)
|
| [2] |
WHITMAN R V, RICHART F E JR. Design procedures for dynamically loaded foundations[J]. Journa1 of the soil mechanics and foundations division, 1967, 93(6): 169-193. (  0) 0)
|
| [3] |
MUKI T. Asymmetric problems of the theory of elasticity for a semi-infinite solid and a thick plate[M]//SNEDDON I N, HILL R. Progress in Solid Mechanics, Vol. 1. Amsterdam: North-Holland Publishing Co., 1960.
(  0) 0)
|
| [4] |
SCHIFFMAN R L, AGGARWALA D B. Stresses and displacements produced in a semi-infinite elastic solid by a rigid elliptical footing[C]//Proceedings of the 5th International Conference of Soil Mechanics and Foundation Engineering. 1961, 1: 795-801.
(  0) 0)
|
| [5] |
云天铨. 水平刚性岩基上的弹性层表面受垂直集中力问题的积分方程解法[J]. 固体力学学报, 1983(3): 375-383. YUN Tianquan. An integral equation method for problem of load acting perpendicularly on the surface of a half space with rigid horizontal level[J]. Acta mechanica solida sinica, 1983(3): 375-383. (  0) 0)
|
| [6] |
文丕华. 水平刚性基础上弹性层表面受垂直集中力的精确解[J]. 应用数学与力学, 1986, 7(5): 467-475. WEN Pihua. An accurate solution for the surface of elastic layer under normal concentrated load acting on a rigid horizontal base[J]. Applied mathematics and mechanics, 1986, 7(5): 467-475. (  0) 0)
|
| [7] |
阴可, 程毅, 周晓雪, 等. 岩石地基上扩展基础的基底反力实测分析[J]. 重庆建筑大学学报, 2006, 28(6): 72-74. YIN Ke, CHENG Yi, ZHOU Xiaoxue, et al. Experimental study on sub-grade reaction of spreading Foundation on rock sub-grade[J]. Journal of Chongqing Jianzhu University, 2006, 28(6): 72-74. (  0) 0)
|
| [8] |
艾智勇, 吴超. 分层地基上矩形刚性基础的基底反力、沉降和倾斜计算[J]. 力学季刊, 2008, 29(1): 113-119. AI Zhiyong, WU Chao. Calculation of reaction forces of base, settlement and inclinatian of rectangular rigid plate on Multi-Layered soils[J]. Chinese quarterly of mechanics, 2008, 29(1): 113-119. (  0) 0)
|
| [9] |
阴可, 殷杰. 岩石地基上扩展基础的受力特性分析[J]. 重庆建筑大学学报, 2008, 30(2): 27-31. YIN Ke, YIN Jie. Mechanical behavior of spread foundations on rock[J]. Journal of Chongqing Jianzhu University, 2008, 30(2): 27-31. (  0) 0)
|
| [10] |
BATHE K J. Finite element procedures[M]. Cambridge, MA: Klaus-Jürgen Bathe, 2007.
(  0) 0)
|
| [11] |
GOODMAN R E, Van T K, HEUZE F E. The role of structure and solid mechanics in the design of surface and underground excavation[C]//Proceedings, Conference on Structure, Solid Mechanics an Engineering Design, Part2, paper 105, p. 137, Wiley, New York.
(  0) 0)
|
| [12] |
江见鲸, 陆新征, 叶列平. 混凝土结构有限元分析[M]. 北京: 清华大学出版社, 2005. JIANG Jianjing, LU Xinzheng, YE Lieping. Finite element analysis of concrete strucures[M]. Beijing: Tsinghua University Press, 2005. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


