2. 哈尔滨理工大学 计算机科学与技术学院, 黑龙江 哈尔滨 150080
2. School of Computer Science and Technology, Harbin University of Science and Technology, Harbin 150080, China
采用计算机辅助技术实现细胞的自动识别对提高细胞病理诊断效率和准确率具有实际的意义。细胞图像的精确分割是细胞识别的关键技术,国内外研究人员在细胞分割领域进行了大量研究。文献[1]通过k-means聚类标记出每个细胞的细胞核,进行特征分析和提取,并通过完整的图像预处理技术克服了由外界光照引起的背景的不均匀性。文献[2]提出采用k-means分割、特征提取和神经网络分类器实现细胞检测过程,再通过SVM分类器完成血液显微图像细胞的分类。文献[3]提出了将颜色空间调整和k-means聚类相结合的白细胞分割方法,克服了由外界光照、染色时间不一、涂片厚度等引起的颜色影响。文献[4]提出一种基于mean-shift聚类的逐步融合规则和应用梯度向量流(GVF)snake模型的边界去除规则相结合的白细胞自动分割方法。文献[5]采用了一种基于RGB和HSV颜色空间的双阈值分割方法分割白细胞。文献[6]提出一种基于颜色和形状特征相结合的标记分水岭算法,实现外周血和骨髓图像的白细胞分割。文献[7]应用核模糊C均值聚类(kernel fuzzy C-means,KFCM)将原始细胞图像分为前景(有细胞)和背景(无细胞),然后采用基于距离变换和分水岭算法实现图像分割。然而,以上方法对图像中的粘连细胞区域分割误差较大。
基于人工智能的图像理解研究表明,图像是一个有机的整体,图像的元素在空间上具有高度相关性,每一个像素在语义表达上都不是孤立的,像素的空间位置具有统计依赖关系。因此,挖掘细胞图像元素的空间特征,对提高细胞图像分割与识别准确性、增强细胞图像的理解具有重要的意义。本文提出一种细胞图像分割算法,利用HMRF模型构建图像的表达,采用EM概率方法描述图像像素之间的空间约束,在图像的聚类分割过程中有效地利用了空间上下文信息,克服待分割图像背景的复杂性,进而得到比较准确的细胞轮廓和边界。
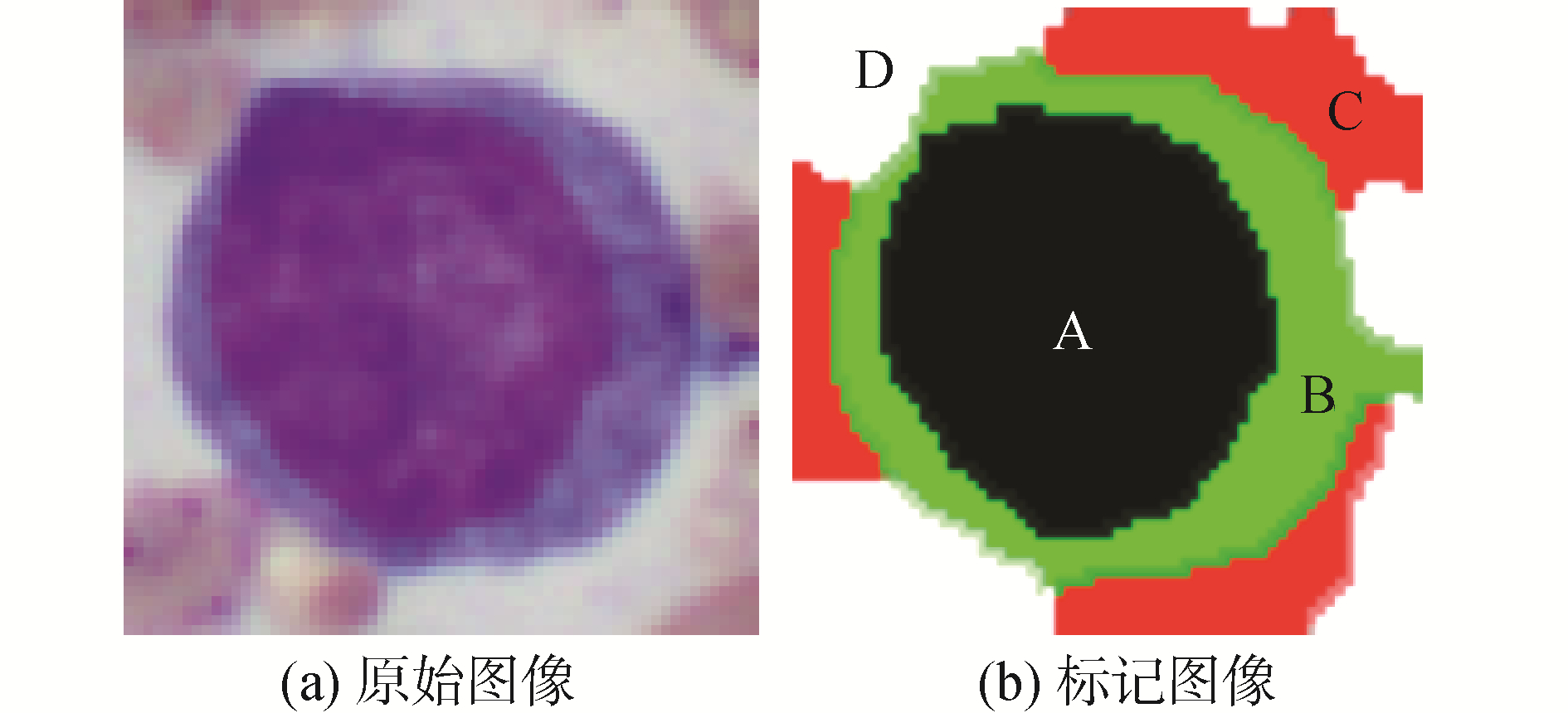
1 细胞图像的HMRF模型将一幅待分割细胞图像看作二维平面栅栏结构S={S(i, j) |1≤i≤W,1≤j≤H},S表示图像像素点的集合,W、H分别为图像的宽和高。S中每个元素的颜色特征及其类别属性定义为随机变量,整幅图像S就是一个标准的随机场[8]。细胞图像分割的过程定义为S到L映射:f:S→L,其中,L为标签集合,L={l1, l2, …, lk},k个为标签集合元素个数。如图 1所示,AML细胞图像标记为4类:A(细胞核)、B(细胞质)、C(背景)、D(其他细胞)。
|
Download:
|
| 图 1 细胞标记结果 Fig. 1 Cell labeling result | |
图像像素存在空间依赖关系,通过二阶邻域系统[9]表示,如图 2所示,像素点的二阶邻域系统及其双点基团(本文采用二阶邻域系统的双点基团形式计算能量)。

|
Download:
|
| 图 2 二阶邻域系统及其双点基团 Fig. 2 Second-order neighborhood system and its two-pixel clique | |
整个空间随机场满足马尔可夫性[10]:
| $ \begin{array}{*{20}{c}} {P\left( x \right) > 0,\forall x \in L;}\\ {P\left( {{x_i}\left| {{x_{S - \left\{ i \right\}}}} \right.} \right) = P\left( {{x_i}\left| {{x_{{N_i}}}} \right.} \right)} \end{array} $ |
二阶邻域系统的HMRF满足局部特性,即:对于任意像素点i,若随机变量值xS-{i}已知,随机场在i处的取值概率只与i的二阶邻域集合相关。仅根据局部性不能统计随机场内所有像素点的联合分布,为了表达全局性,Hammersly-Clifford定理[11]通过势函数Vc(x)求解HMRF的概率分布:
| $ P\left( {{x_i}\left| {{x_{{N_i}}}} \right.} \right) = \frac{1}{Z}\exp \left\{ { - \frac{1}{T}\sum\limits_{c \in C} {{V_c}\left( {{x_i}\left| {{x_{{N_i}}}} \right.} \right)} } \right\} $ | (1) |
| $ Z = \sum\limits_x {\exp \left\{ { - \frac{1}{T}\sum\limits_{c \in C} {{V_c}\left( {{x_i}\left| {{x_{{N_i}}}} \right.} \right)} } \right\}} $ | (2) |
式中:Z是能量归一化常数;T为温度常数(本文取1);Vc(xi|xNi)为基团集合C的能量函数。上述方法将求解概率分布转换为求解能量函数的形式,实现了像素点之间的全局性联系。
2 基于HMRF模型的细胞分割算法 2.1 初始标签集的获取为了避免算法陷入局部最优解,使用k-means++方法[12]计算细胞图像的初始标记。采用欧式距离作为相似性评价度量,根据颜色特征值将像素点集合X={ x(0), x(1), …, x(n) }划分为k个簇。在Lab烟商务空间[12]中的聚类过程:
1) 从X中随机选取1个点作为第一个聚类中心μ1;
2) 计算X中的每一个点x(i)与已确定的最近聚类中心μj(j=1,2,…, k)的距离D(xi);
3) 选择D值较大的点作为新的聚类中心;
4) 重复步骤2)、3)直到选出k个聚类中心;
5) 循环执行以下2个步骤,直到聚类结果收敛或达到最大聚类迭代次数:
① 计算数据集X中的所有对象x(i)与各个聚类中心μj的欧氏距离,按照式(3)将所有对象逐个分配到最近聚类:
| $ {c^{\left( i \right)}}: = \mathop {\arg \min }\limits_j {\left\| {{\mathit{\boldsymbol{x}}_{\left( i \right)}} - {\mu _j}} \right\|^2} $ | (3) |
式中:c(i)表示像素i与k个簇中距离最近的类;μj表示第j个簇质心。
② 按照式(4)更新聚类中心:
| $ {\mu _j}: = \frac{{\sum\limits_{i = 1}^n {l\left\{ {{c^{\left( i \right)}} = j} \right\}{x_{\left( i \right)}}} }}{{\sum\limits_{i = 1}^n {l\left\{ {{c^{\left( i \right)}} = j} \right\}} }} $ | (4) |
式中:n代表数据集中像素点的总个数;l{c(i)=j}为关系权值函数,若像素i属于第j个簇,则l{c(i)=j}=1;否则,l{c(i)=j}=0。
6) 得到以k个聚类结果的图像初始标签x(0)。
2.2 基于MAP的HMRF精细分割设y是观测场Y上的观测数据,x是标号场X上的对应分割结果,鉴于分割算法的迭代过程中观测场数据y的不断变化,无法从y直接得出最终分割标签,应用最大后验概率(maximum a posteriori,MAP)准则[8]给出x的一个最优估计,使得后验概率P(x|y)达到最大,即满足:
| $ \hat x = \arg \mathop {\max }\limits_{x \in \mathit{\Omega }} P\left( {X = x\left| {Y = y} \right.} \right) $ | (5) |
由贝叶斯(Bayesian)公式得
| $ P\left( {X = x\left| {Y = y} \right.} \right) = \frac{{P\left( {Y = y\left| {X = x} \right.} \right)P\left( {X = x} \right)}}{{P\left( {Y = y} \right)}} $ | (6) |
式中:P(Y=y|X=x)是条件概率;P(X=x)是标号场的先验Gibbs分布;P(Y=y)表示的是观测图像的先验分布,当观测数据已知时为定值,不参与计算过程,即:
| $ P\left( {X = x\left| {Y = y} \right.} \right) \propto P\left( {Y = y\left| {X = x} \right.} \right)P\left( {X = x} \right) $ | (7) |
对式(7)取对数得到HMRF分割问题中的最小化能量目标函数:
| $ \begin{array}{*{20}{c}} {\hat x \propto \arg \mathop {\max }\limits_{x \in \mathit{L}} \left\{ {\ln P\left( x \right) + \ln P\left( {y\left| x \right.} \right)} \right\} \propto }\\ {\arg \mathop {\max }\limits_{x \in \mathit{L}} \left\{ {U\left( x \right) + U\left( {y\left| x \right.} \right)} \right\}} \end{array} $ | (8) |
本文采用二阶邻域系统所对应的基团为双点基团,选用Potts模型[13]定义各基团的势能量:
| $ {V_c}\left( {{x_i},{x_j}} \right) = \left\{ \begin{array}{l} 0,\;\;\;\;{x_i} = {x_j}\\ \beta ,\;\;\;{x_i} \ne {x_j} \end{array} \right. $ | (9) |
式中:xi和xj为当前邻域系统c中像素i和j的标记,如果c中两像素点标记为同一类,即xi=xj,则基团势函数值为0;反之,如果xi≠xj; 则基团势函数值为β(本文取0.2)。
利用图像的先验信息将当前邻域系统内的像素点尽量标记为相同,满足能量最小原则,降低了分割过程中孤立点或者噪声点的影响,使分割结果具有较好的区域连续性。
由Hammersly-Clifford定理得知,标记场中x的先验概率为:
| $ \begin{array}{*{20}{c}} {P\left( {{x_i}} \right) = P\left( {{x_i}\left| {{x_{{N_i}}}} \right.} \right) = \frac{{\exp \left\{ { - \sum\limits_{c \in C} {{V_c}\left( {{x_i}\left| {{x_{{N_i}}}} \right.} \right)} } \right\}}}{{\sum\limits_x {\exp \left\{ { - \sum\limits_{c \in C} {{V_c}\left( {{x_i}\left| {{x_{{N_i}}}} \right.} \right)} } \right\}} }} = }\\ {\frac{{\exp \left\{ { - \beta \times n\left( {j\left| {{x_i} \ne {x_j}} \right.} \right)} \right\}}}{{\sum\limits_x {\exp \left\{ { - \beta \times n\left( {j\left| {{x_i} \ne {x_j}} \right.} \right)} \right\}} }}} \end{array} $ | (10) |
故整个二维标记场的先验能量函数:
| $ U\left( {X = x} \right) = \sum\limits_{i \in X} {\sum\limits_{j \in {N_i}} {\beta \times n\left( {j\left| {{x_i} \ne {x_j}} \right.} \right)} } $ | (11) |
根据中心极限定理,相同类别的数据在大样本下总是趋于高斯分布,细胞图像中类别k的均值和样本差表示为μk和
| $ \begin{array}{*{20}{c}} {P\left( {{\mathit{\boldsymbol{y}}_i}\left| {{\mathit{\boldsymbol{x}}_i}} \right.} \right) = }\\ {\frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}\sum\limits_k {} } }}\exp \left( { - \frac{{\left( {{\mathit{\boldsymbol{y}}_i} - {\mathit{\boldsymbol{\mu }}_k}} \right)\sum\limits_k^{ - 1} {{{\left( {{\mathit{\boldsymbol{y}}_i} - {\mathit{\boldsymbol{\mu }}_k}} \right)}^{\rm{T}}}} }}{2}} \right)} \end{array} $ | (12) |
所有像素点相互独立且同分布,依据Gibbs分布
| $ \begin{array}{*{20}{c}} {P\left( {y\left| x \right.} \right) = \prod\limits_{i \in Y} {P\left( {{\mathit{\boldsymbol{y}}_i}\left| {{\mathit{\boldsymbol{x}}_i}} \right.;{\mathit{\boldsymbol{\mu }}_k},\sum\limits_k {} } \right)} = }\\ {\frac{1}{{Z'}}\exp \left( { - \prod\limits_{i \in Y} {\left[ {\frac{{{{\left( {{\mathit{\boldsymbol{y}}_i} - {\mathit{\boldsymbol{\mu }}_k}} \right)}^2}}}{{2\sum\limits_k {} }} + \ln \sqrt {\sum\limits_k {} } } \right]} } \right)} \end{array} $ | (13) |
式中:
| $ U\left( {y\left| x \right.} \right) = \sum\limits_{i \in Y} {\left[ {\frac{{{{\left( {{\mathit{\boldsymbol{y}}_i} - {\mathit{\boldsymbol{\mu }}_k}} \right)}^2}}}{{2\sum\limits_k {} }} + \ln \sqrt {\sum\limits_k {} } } \right]} $ | (14) |
根据先验能量函数和条件能量函数得出能量函数的最小化形式:
| $ \begin{array}{*{20}{c}} {\hat x \propto \arg \mathop {\min }\limits_x \left\{ {U\left( {y\left| x \right.} \right) + U\left( x \right)} \right\} = }\\ {\arg \mathop {\min }\limits_x \left[ {\sum\limits_{i \in Y} {\frac{{{{\left( {{\mathit{\boldsymbol{y}}_i} - {\mathit{\boldsymbol{\mu }}_k}} \right)}^2}}}{{2\sum\limits_k {} }} + \ln \sqrt {\sum\limits_k {} } } } \right] + }\\ {\left. {\sum\limits_{i \in X} {\sum\limits_{j \in {N_i}} {\beta \times n\left( {j\left| {{x_i} \ne {x_j}} \right.} \right)} } } \right\}} \end{array} $ | (15) |
HMRF模型中,参数集θ={θk|k∈L}和
| $ \hat \theta = \arg \mathop {\max }\limits_\theta \ln P\left( {x,y\left| \theta \right.} \right) $ | (16) |
EM算法的每一次迭代包括步骤E和步骤M:
1) E步:计算在给定观测数据y和当前参数估计的情况下,求解完全数据(x, y)对数似然函数的条件期望值,即求:
| $ Q\left( {\theta \left| {{\theta ^{\left( t \right)}}} \right.} \right) = E\left[ {\ln \left( {P\left( {x,y\left| \theta \right.} \right)\left| y \right.,{\theta ^{\left( t \right)}}} \right)} \right] $ | (17) |
式中θ(t)是第t步迭代时M步所获得的θ值。
2) M步:选择θ,使Q(θ|θ(t))最大,即:
| $ {\theta ^{\left( {t + 1} \right)}} = \arg \mathop {\max }\limits_\theta Q\left( {\theta \left| {{\theta ^{\left( t \right)}}} \right.} \right) $ | (18) |
用θ(t+1)代替θ(t),重复步骤E,使得θ(t+1)→θ(t)。
2.4 算法流程输入数据为原始细胞图像、分类数k和最大迭代次数,输出数据为最终标记x={x1, x2, …, xn},算法流程为:
1) 采用k-means++算法对读入图像进行初始化分割得到初始分类标记x(0);
2) 将初始分割结果一一映射到观测场Y中,采用EM算法估计出图像中每一类别的均值和方差
3) 利用高斯分布函数P(y|x)计算出观测场能量Ef:
4) 选择potts模型对标记场建模,定义势函数为
5) 根据目标函数
6) 若达到最大迭代次数或者|Δ(Ef+El)|小于给定阈值,退出循环,得到最终分割结果。否则返回步骤2)。
3 实验测试与结果分析本实验是在Microsoft Windows 7 Professional操作系统、Intel酷睿i5-4460 4核CPU实验环境下验证算法有效性。数据来源于美国H.LEE莫菲特癌症中心(Moffitt Cancer Center)医院提供的61幅1 600×1 200 pixel骨髓细胞图像,细胞图像具有以下特点:1)细胞种类多,主要包括母细胞、红细胞、淋巴细胞、单核细胞、骨髓细胞、中性粒细胞等;2)细胞形态复杂,细胞形状、大小、边缘、位置、色度等差异较大;3)细胞重叠现象严重;4)细胞边缘与背景之间的对比度受到图像捕捉时的光照等环境的影响,存在差异。
实验验证各类细胞的细胞核、细胞质的分割准确率和效率。为了定量分析各算法的分割效果,本文采用经典的图像分割精度的评判方法ZIS[16]:
| $ {Z_{IS}} = 2 \times \frac{{n\left\{ {{A_1} \cap {A_2}} \right\}}}{{n\left\{ {{A_1}} \right\} + n\left\{ {{A_2}} \right\}}} $ | (19) |
式中:A1为真实细胞区域,由专业的医师手动分割细胞图像得到,A2为分割结果得到的细胞区域,n{·}表示取图像区域像素点的数量。ZIS指数反映了算法分割结果与真实细胞的相似度,其值越大(接近1)则表明分割越准确。
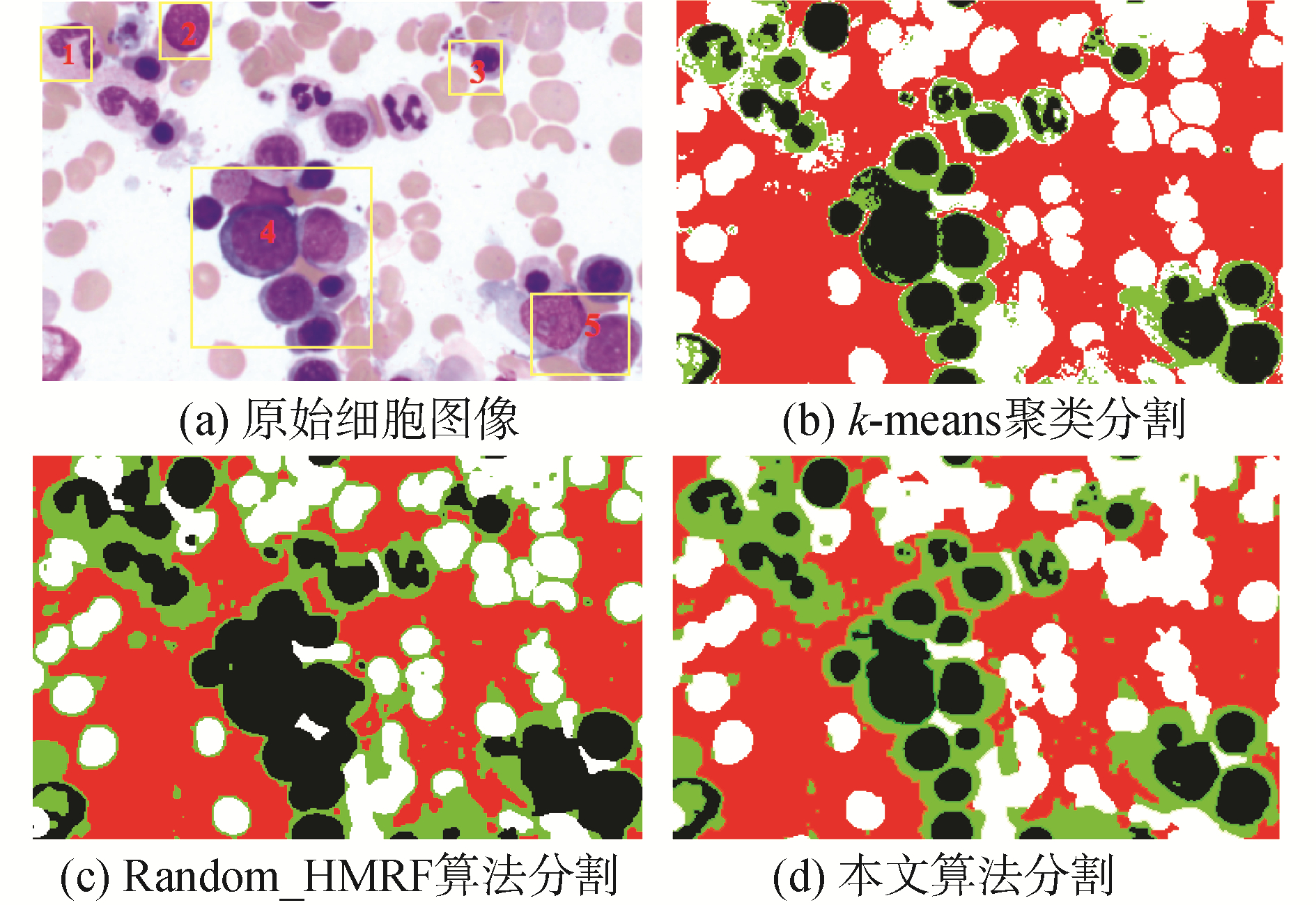
以图 3(a)为待分割图像,截取自原始图像的代表性区域,图 3(b)~(d)分别为k-means聚类算法、Random_HMRF算法、本文k-means_HMRF算法的实验结果。
|
Download:
|
| 图 3 细胞图像分割结果 Fig. 3 Cell image segmentation results | |
图 3(a)标记的1、2和3单细胞区域受算法局限性影响小,3种分割方法均能得到满意的结果。区域4、5由于细胞聚合、粘连,k-means分割结果易受噪声点影响,核、质标签集合相互交叉,标记结果不平滑,不利于后期的特征提取工作;Random_HMRF模型算法由于初始标签随机选取,算法容易陷入局部最优,无法取得令人满意的分割结果;本文算法能有效地分隔出细胞聚合区域。
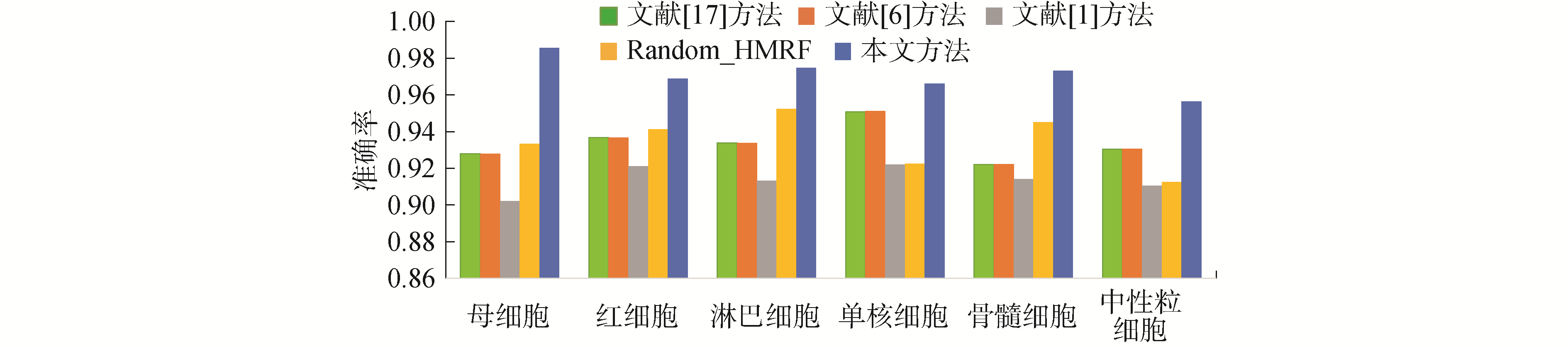
图 4所示为本算法与4种典型分割算法的准确率统计结果。
|
Download:
|
| 图 4 不同分割方法的结果准确率对比 Fig. 4 Comparison of the accuracy of different segmentation methods | |
对母细胞子图像分割,验证本文算法的准确性与效率,如图 5所示。细胞图片大小为65×65 piexl,与病理医生的手工标记比较,算法分割结果基本符合人工标记结果,细胞核与细胞质分割清晰,满足识别要求。利用能量函数U(x)判定算法的收敛性。由于本文算法是基于Bayes决策理论MAP分割过程,算法将图像分割看作是最小化能量函数的过程,当目标能量函数达到收敛时,算法结束。第1次迭代结束时,算法未能准确分割细胞核与细胞质,分割精度仅为0.812 7,能量函数值较大;算法经过6次迭代,母细胞子图的分割精确率为0.964 6,能量函数U(x)开始收敛;当算法经过10次迭代,能量函数基本收敛,此时分割精度为0.968 5,基本符合预期分割,且具有较强的鲁棒性,更适于后期细胞特征提取工作。

|
Download:
|
| 图 5 随迭代次数增加的U(x)及ZIS的变化 Fig. 5 The change of the U(x) and ZIS with the increase of the number of iterations | |
1) 在Lab色彩空间中,利用基于颜色特征的欧氏距离作为样本之间的相似性度量,采用k-means++方法计算出图像初始化标签集;
2) 利用像素点的空间约束关系,定义HMRF分割模型,实现二次精细化分割。算法采用potts模型降低噪声点影响、平滑分割区域,并采用期望最大值(EM)算法优化模型参数以达到精确分割;
3) 应用Hammersly-Clifford定理和Bayesian理论,将细胞分割问题转化为求能量函数的最大后验概率估计问题,定义观测场和标记场的约束,通过迭代算法不断调整标签集合,直至总能量函数值收敛至最小,实现全局最优分割;
4) 对骨髓细胞图像实验结果表明,算法对粘连、重合、形态复杂等细胞区域的分割准确性有所提高,分割结果具有更好的区域连续性。
应用本文算法便于提取细胞形态特征,后续将针对细胞内部结构特征的识别方法展开研究。
| [1] |
AGAIAN S, MADHUKAR M, CHRONOPOULOS A T. Automated screening system for acute myelogenous leukemia detection in blood microscopic images[J]. IEEE systems journal, 2014, 8(3): 995-1004. DOI:10.1109/JSYST.2014.2308452 (  0) 0)
|
| [2] |
GOUTAM D, SAILAJA S. Classification of acute myelogenous leukemia in blood microscopic images using supervised classifier[C]//Proceedings of 2015 IEEE International Conference on Engineering and Technology. Coimbatore, India, 2015: 1-5.
(  0) 0)
|
| [3] |
ZHANG Congcong, XIAO Xiaoyan, LI Xaomei, et al. White blood cell segmentation by color-space-based k-means clustering[J]. Sensors, 2014, 14(9): 16128-16147. DOI:10.3390/s140916128 (  0) 0)
|
| [4] |
KO B C, GIM J W, NAM J Y. Automatic white blood cell segmentation using stepwise merging rules and gradient vector flow snake[J]. Micron, 2011, 42(7): 695-705. DOI:10.1016/j.micron.2011.03.009 (  0) 0)
|
| [5] |
LI Yan, ZHU Rui, MI Lei, et al. Segmentation of white blood cell from acute lymphoblastic leukemia images using dual-threshold method[J]. Computational and mathematical methods in medicine, 2016, 2016: 9514707. (  0) 0)
|
| [6] |
ARSLAN S, OZYUREK E, GUNDUZ-DEMIR C. A color and shape based algorithm for segmentation of white blood cells in peripheral blood and bone marrow images[J]. Cytometry part A, 2014, 85(6): 480-490. DOI:10.1002/cyto.a.v85.6 (  0) 0)
|
| [7] |
HUANG Haiqing, FANG Xiangzhong, SHI Jun, et al. Abnormal localization of immature precursors (ALIP) detection for early prediction of acute myelocytic leukemia (AML) relapse[J]. Medical & biological engineering & computing, 2014, 52(2): 121-129. (  0) 0)
|
| [8] |
孙立晔, 韩军伟, 胡新韬, 等. 基于Markov随机场理论的鼠脑切片显微图像的分割研究[J]. 模式识别与人工智能, 2013, 26(5): 498-503. SUN Liye, HAN Junwei, HU Xintao, et al. Cell segmentation in microscopic images of mice brain based on markov random field theory[J]. PR & AI, 2013, 26(5): 498-503. DOI:10.3969/j.issn.1003-6059.2013.05.013 (  0) 0)
|
| [9] |
叶秀芬, 张元科. 基于马尔可夫随机场的非监督声呐图像分割方法[J]. 哈尔滨工程大学学报, 2015, 36(4): 516-521. YE Xiufen, ZHANG Yuanke. Unsupervised sonar image segmentation method based on Markov random field[J]. Journal of Harbin Engineering University, 2015, 36(4): 516-521. (  0) 0)
|
| [10] |
ZHANG Hui, WEN Tian, ZHENG Yuhui, et al. Two fast and robust modified gaussian mixture models incorporating local spatial information for image segmentation[J]. Journal of signal processing systems, 2015, 81(1): 45-58. (  0) 0)
|
| [11] |
宋艳涛, 纪则轩, 孙权森. 基于图像片马尔可夫随机场的脑MR图像分割算法[J]. 自动化学报, 2014, 40(8): 1754-1763. SONG Yantao, JI Zexuan, SUN Quansen. Brain MR image segmentation algorithm based on markov random field with image patch[J]. Acta automatica sinica, 2014, 40(8): 1754-1763. (  0) 0)
|
| [12] |
MOHAPATRA S, PATRA D, SATPATHY S. Automated leukemia detection in blood microscopic images using statistical texture analysis[C]//Proceedings of the 2011 International Conference on Communication, Computing & Security. Rourkela, Odisha, India, 2011: 184-187.
(  0) 0)
|
| [13] |
姚婷婷, 谢昭. 多层次MRF重标记及映射法则下的图像分割[J]. 自动化学报, 2013, 39(10): 1581-1593. YAO Tingting, XIE Zhao. Top-down inference with relabeling and mapping rules in hierarchical MRF for image segmentation[J]. Acta automatica sinica, 2013, 39(10): 1581-1593. (  0) 0)
|
| [14] |
曹家梓, 宋爱国. 基于马尔可夫随机场的纹理图像分割方法研究[J]. 仪器仪表学报, 2015, 36(4): 776-786. CAO Jiazi, SONG Aiguo. Research on the texture image segmentation method based on Markov random field[J]. Chinese journal of scientific instrument, 2015, 36(4): 776-786. (  0) 0)
|
| [15] |
ZHANG Yongyue, BRADY M, SMITH S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm[J]. IEEE transactions on medical imaging, 2001, 20(1): 45-57. DOI:10.1109/42.906424 (  0) 0)
|
| [16] |
关涛, 周东翔, 樊玮虹, 等. 基于稀疏轮廓点模型的彩色重叠细胞图像分割[J]. 计算机研究与发展, 2015, 52(7): 1682-1691. GUAN Tao, ZHOU Dongxiang, FAN Weihong, et al. Segmentation of color overlapping cells image based on sparse contour point model[J]. Journal of computer research and development, 2015, 52(7): 1682-1691. (  0) 0)
|
| [17] |
HOU Jiali, LI Baokui. An improved algorithm for horizon detection based on OSTU[C]//Proceedings of the 2015 7th International Conference on Intelligent Human-Machine Systems and Cybernetics. Hangzhou, China, 2015: 414-417.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


