2. 哈尔滨工程大学 航天与建筑工程学院, 黑龙江 哈尔滨 150001;
3. 上海市空间智能控制技术重点实验室, 上海 201109
2. College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin 150001, China;
3. Shanghai Key Laboratory of Aerospace Intelligence Control Technology, Shanghai 201109, China
失效航天器在空间摄动力矩作用下会逐渐进入翻滚状态[1],因此捕获、维修和接管此类目标的前提是对空间翻滚目标的姿轨同步逼近和稳定跟踪。空间翻滚目标逼近与跟踪控制的主要困难是存在不确定性,如:相对状态测量的不确定性、逼近路径的动态时变性、多源干扰力和力矩的耦合影响等。因此有众多学者关注空间翻滚目标在不确定性和干扰下的逼近与跟踪控制。
Xu等[2]采用滑模控制方法对近距离自主交会的六自由度控制问题进行了研究;Ma等[3]通过最小化时间/燃料消耗设计了一个接近翻滚卫星的前馈最优控制策略,但仅考虑了受限平面刚体运动。LI Peng等[4]提出积分退步控制器实现翻滚非合作目标的最终逼近控制。耿云海等[5]研究了在轨服务航天器逼近与捕获失控目标过程中的姿态同步控制问题。这些研究重点解决了翻滚目标逼近跟踪的姿轨耦合动力学与控制算法,但是对于测量不确定性、控制干扰等问题考虑不多。
为提高控制算法的鲁棒性,Subbarao等[6]提出了一种基于自适应反馈线性化的方法来解决姿态同步和相对位置跟踪问题,以保证航天器可以对接和抓捕可用的翻滚目标。通过使用这种方法,可以解决由于重力梯度产生的干扰和一些未知但是有界的翻滚目标。Hyeongjun Park等[7]采用模型预测控制方法实现了旋转/翻滚目标的交会对接控制,同时考虑了逼近过程的障碍规避机动问题,提出的方法对推力器、接近速度、视线角等约束进行了系统考虑。Yan等[8-9]利用安全正不变集(safe positively in-variant sets)和模型预测控制方法研究了自主障碍规避下的翻滚目标交会对接控制问题。
一些学者将滑模控制算法应用到了翻滚目标的逼近与跟踪的姿轨耦合控制中。Li等[10]通过结合递推回归技术和滑模控制提出了一种应用于自适应飞行控制的独特观点,其使用一个二阶滑膜积分滤波器消除虚拟输入的分析计算。这种自适应控制器能够使得参数不确定、输入不确定以及功能不确定的系统渐进稳定。李九人[11]针对无控旋转目标的逼近问题,将滑模控制与自适应控制相结合,获得了一种六自由度逼近的自适应滑模控制器,克服了传统滑模控制器存在抖振的缺陷。本文作者在文献[12]中构建了期望坐标系下的参考轨迹与姿态模型,提出了姿轨耦合滑模控制算法。陈炳龙[13]提出了二阶滑模平面设计改进的Twisting控制器,并研究了Super Twisting(ST)和自适应ST等控制算法。
上述滑模控制方法均设计了单一滑模面,尽管通过滑模面参数的自适应调整,具备了一定的针对不确定性影响的补偿作用,但对于更为严重的测量不确定性,补偿作用仍然有限。为此,有学者提出了双滑模面控制算法,通过设置第二滑模面,专门实现对不确定性和干扰影响的抑制,显著增强了控制算法的鲁棒性。
卢伟研究了滑模控制在翻滚目标逼近与跟踪任务中的应用[12],对比分析了传统滑模控制、带滑模估计器的滑模控制、双滑模面控制、最优滑模控制等算法,但卢伟在文中提出的双滑模控制律存在计算复杂、稳定条件苛刻等缺陷。同时,现有的研究成果未深入分析实际空间任务中的测量不确定性、干扰力和力矩、控制约束等因素,设计的双滑模控制律未综合考虑测量不确定性与干扰补偿、滑模控制抖振抑制、控制执行约束等需求,导致控制律在真实空间任务的适应性与可行性存在疑问。
针对上述问题,本文设计了综合测量不确定性与干扰补偿、抖振抑制能力的双滑模面控制算法(dual slide-mode surface controller, DSMSC),分析并建立了空间实际任务中的测量不确定影响因素及其传播模型,在充分考虑测量不确定性、控制执行约束等因素的条件下,对文献[12]提出的单滑模面控制算法(single slide-mode surface controller, SSMSC)和本文提出的双滑模面控制算法进行了数学仿真对比分析。
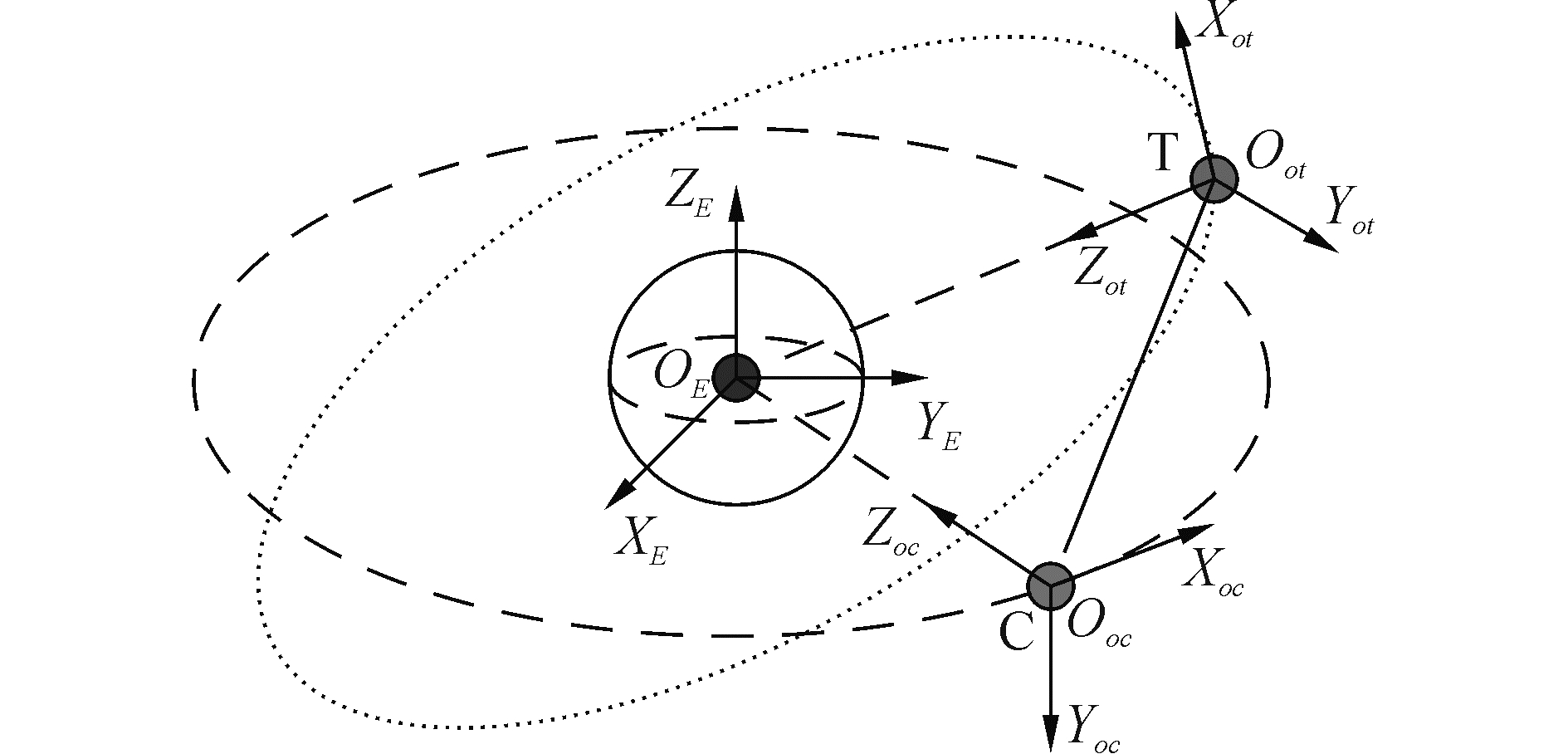
1 姿轨耦合动力学建模 1.1 相对轨道动力学参考坐标系如图 1所示。图中C表示追踪器,T表示目标器。OE-XEYEZE、Ooc-XocYocZoc、Oot-XotYotZot分别表示地心惯性系、追踪星轨道系和目标星轨道系。
|
图 1 相对运动坐标系与地心惯性坐标系 Fig.1 Orbital coordinate systems of the target satellite |
以目标星轨道系为参考坐标系,追踪星相对于目标星的非线性相对轨道动力学模型可表示为[11]
| $ \mathit{\boldsymbol{\ddot r = }}{O_1}\mathit{\boldsymbol{r}} + {O_2}\mathit{\boldsymbol{\dot r}} + \mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{r}} \right) + {\mathit{\boldsymbol{f}}_d} + {\mathit{\boldsymbol{a}}_c} $ | (1) |
式中:r=[x y z]T、
| $ {\mathit{\boldsymbol{O}}_1} = \left[ {\begin{array}{*{20}{c}} {{{\dot \theta }^2}}&0&{\ddot \theta }\\ 0&0&0\\ { - \ddot \theta }&0&{{{\dot \theta }^2}} \end{array}} \right],{\mathit{\boldsymbol{O}}_2} = \left[ {\begin{array}{*{20}{c}} 0&0&{2\dot \theta }\\ 0&0&0\\ { - 2\dot \theta }&0&0 \end{array}} \right], $ |
| $ \mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{r}} \right) = \left[ {\begin{array}{*{20}{c}} { - \frac{{\mu x}}{{r_c^3}}}\\ { - \frac{{\mu y}}{{r_c^3}}}\\ { - \frac{\mu }{{r_t^2}} - \frac{{\mu \left( {z - {r_t}} \right)}}{{r_c^3}}} \end{array}} \right] $ |
式中:rc和rt分别表示地心到追踪器质心和目标器质心的距离,μ为地球引力常数,θ、
考虑到逼近与跟踪翻滚目标的不同部位时,追踪星本体系Cbc相对目标星本体系Cbt的期望姿态不同。因此,引入期望坐标系Cd作为追踪星姿态跟踪的对象,期望坐标系姿态即为期望姿态。期望坐标系固连在目标星本体系上,原点重合。在跟踪部位位于目标星本体的六个不同平面上时,对应的目标本体系到期望系的转换矩阵Adbt取值分别如下
| $ + X\;面:{\mathit{\boldsymbol{A}}_{{\rm{dbt}}}} = \left[ {\begin{array}{*{20}{c}} { - 1}&0&0\\ 0&{ - 1}&0\\ 0&0&1 \end{array}} \right], $ |
| $ - X\;面:{\mathit{\boldsymbol{A}}_{{\rm{dbt}}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&1&0\\ 0&0&1 \end{array}} \right], $ |
| $ + Y\;面:{\mathit{\boldsymbol{A}}_{{\rm{dbt}}}} = \left[ {\begin{array}{*{20}{c}} 0&{ - 1}&0\\ 1&0&0\\ 0&0&1 \end{array}} \right], $ |
| $ - Y\;面:{\mathit{\boldsymbol{A}}_{{\rm{dbt}}}} = \left[ {\begin{array}{*{20}{c}} 0&1&0\\ { - 1}&0&0\\ 0&0&1 \end{array}} \right], $ |
| $ + Z\;面:{\mathit{\boldsymbol{A}}_{{\rm{dbt}}}} = \left[ {\begin{array}{*{20}{c}} 0&0&{ - 1}\\ 1&0&0\\ 0&{ - 1}&0 \end{array}} \right], $ |
| $ - Z\;面:{\mathit{\boldsymbol{A}}_{{\rm{dbt}}}} = \left[ {\begin{array}{*{20}{c}} 0&0&1\\ { - 1}&0&0\\ 0&{ - 1}&0 \end{array}} \right]. $ |
设追踪星本体系相对于期望坐标系的姿态四元数为
| $ {{\mathit{\boldsymbol{\dot q}}}_e} = \frac{1}{2}{\mathit{\boldsymbol{q}}_e} \otimes \left[ {\begin{array}{*{20}{c}} 0\\ {{\mathit{\boldsymbol{\omega }}_e}} \end{array}} \right] = \frac{1}{2}{\mathit{\boldsymbol{Q}}_e}\left[ {\begin{array}{*{20}{c}} 0\\ {{\mathit{\boldsymbol{\omega }}_e}} \end{array}} \right] $ | (2) |
姿态动力学方程为
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot q}}}_e} = - \frac{1}{4}{{\left\| {{\mathit{\boldsymbol{\omega }}_e}} \right\|}^2}{\mathit{\boldsymbol{q}}_e} + }\\ {\frac{1}{2}{\mathit{\boldsymbol{Q}}_e}\left[ {\begin{array}{*{20}{c}} 0\\ {\mathit{\boldsymbol{f}}\left( {{\mathit{\boldsymbol{\omega }}_e},{\mathit{\boldsymbol{\omega }}_c},{\mathit{\boldsymbol{\omega }}_d},{{\mathit{\boldsymbol{\dot \omega }}}_d}} \right) + \mathit{\boldsymbol{J}}_c^{ - 1}\left( {{\mathit{\boldsymbol{M}}_c} + {\mathit{\boldsymbol{M}}_{dc}}} \right)} \end{array}} \right]} \end{array} $ | (3) |
式中:Jc为追踪星的转动惯量;ωc为追踪星惯性姿态角速度;ωd和
| $ {\mathit{\boldsymbol{Q}}_\mathit{\boldsymbol{e}}} = \left[ {\begin{array}{*{20}{c}} {{q_{e0}}}&{ - {q_{e1}}}&{ - {q_{e2}}}&{ - {q_{e3}}}\\ {{q_{e1}}}&{{q_{e0}}}&{ - {q_{e3}}}&{{q_{e2}}}\\ {{q_{e2}}}&{{q_{e3}}}&{{q_{e0}}}&{ - {q_{e1}}}\\ {{q_{e3}}}&{ - {q_{e2}}}&{{q_{e1}}}&{{q_{e0}}} \end{array}} \right], $ |
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{f}}\left( {{\mathit{\boldsymbol{\omega }}_e},{\mathit{\boldsymbol{\omega }}_c},{\mathit{\boldsymbol{\omega }}_d},{{\mathit{\boldsymbol{\dot \omega }}}_d}} \right) = - \mathit{\boldsymbol{J}}_c^{ - 1}{\mathit{\boldsymbol{\omega }}_c} \times {\mathit{\boldsymbol{J}}_c}{\mathit{\boldsymbol{\omega }}_c} - }\\ {{\mathit{\boldsymbol{A}}_e}{{\mathit{\boldsymbol{\dot \omega }}}_d} + {\mathit{\boldsymbol{\omega }}_e} \times {\mathit{\boldsymbol{A}}_e}{\mathit{\boldsymbol{\omega }}_d}} \end{array} $ |
追踪星在控制作用下需要跟随的期望轨迹是安全路径规划算法的输出,但本文研究集中在控制算法上,故将安全路径简化考虑为目标星本体坐标系下沿跟踪部位矢量反方向的指数逼近路径,则目标星本体坐标系下期望位置矢量函数为
| $ \mathit{\boldsymbol{r}}_d^{bt}\left( t \right) = \left[ {{r_D} - \left( {{r_D} - {r_0}} \right){{\rm{e}}^{ - \beta t}}} \right]\mathit{\boldsymbol{p}}_D^{bt} $ | (4) |
式中:r0和rD分别表示初始和终端两星相对距离,β为指数减速系数,pDbt表示目标星本体坐标系下跟踪部位的单位方向矢量。
目标星轨道系下的期望位置rd、期望速度
| $ {\mathit{\boldsymbol{r}}_d} = {\mathit{\boldsymbol{A}}_{otbt}}\mathit{\boldsymbol{r}}_d^{bt} $ | (5) |
| $ {{\mathit{\boldsymbol{\dot r}}}_d} = {\mathit{\boldsymbol{A}}_{otbt}}\mathit{\boldsymbol{\dot r}}_d^{bt} - \mathit{\boldsymbol{\omega }}_{otbt}^{ot} \times {\mathit{\boldsymbol{r}}_d} $ | (6) |
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\ddot r}}}_d} = {\mathit{\boldsymbol{A}}_{otbt}}\mathit{\boldsymbol{\dot r}}_d^{bt} - \mathit{\boldsymbol{\dot \omega }}_{otbt}^{ot} \times {\mathit{\boldsymbol{r}}_d} - \mathit{\boldsymbol{\omega }}_{otbt}^{ot} \times }\\ {\left( {\mathit{\boldsymbol{\omega }}_{otbt}^{ot} \times {\mathit{\boldsymbol{r}}_d}} \right) - 2\mathit{\boldsymbol{\omega }}_{otbt}^{ot} \times {{\mathit{\boldsymbol{\dot r}}}_d}} \end{array} $ | (7) |
式中:Aotbt为目标星本体系到目标星轨道系转换矩阵,ωotbtot、
定义翻滚目标逼近与跟踪控制的误差矢量为
| $ \mathit{\boldsymbol{e}} = {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{r}}^{\rm{T}}} - \mathit{\boldsymbol{r}}_d^{\rm{T}}}&{\mathit{\boldsymbol{q}}_{ev}^{\rm{T}}} \end{array}} \right]^{\rm{T}}} $ | (8) |
式中:r和rd分别为目标星轨道系下的相对位置矢量和期望的相对位置矢量, qev为追踪星当前姿态与期望姿态之间偏差四元数的矢量部分。
对式(8)两边进行求导,可得误差矢量的导数为
| $ \mathit{\boldsymbol{\dot e}} = {\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}} - \mathit{\boldsymbol{\dot r}}_d^{\rm{T}}}&{\mathit{\boldsymbol{\dot q}}_{ev}^{\rm{T}}} \end{array}} \right]^{\rm{T}}} $ | (9) |
| $ \mathit{\boldsymbol{\ddot e}} = {\left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\ddot r}}}^{\rm{T}}} - \mathit{\boldsymbol{\ddot r}}_d^{\rm{T}}}&{\mathit{\boldsymbol{\ddot q}}_{ev}^{\rm{T}}} \end{array}} \right]^{\rm{T}}} $ | (10) |
将相对位置和姿态动力学模型代入式(10),可得控制误差的姿轨耦合动力学方程:
| $ \mathit{\boldsymbol{\ddot e}} = \mathit{\boldsymbol{f}} + \mathit{\boldsymbol{Bu}} $ | (11) |
式中
| $ \mathit{\boldsymbol{f}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{O}}_1}\mathit{\boldsymbol{r + }}{\mathit{\boldsymbol{O}}_2}\mathit{\boldsymbol{\dot r}} + \mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{r}} \right) + {\mathit{\boldsymbol{f}}_d} - {{\mathit{\boldsymbol{\ddot r}}}_d}}\\ {{\mathit{\boldsymbol{f}}_{ev}} + \frac{1}{2}{\mathit{\boldsymbol{Q}}_{ev}}\mathit{\boldsymbol{J}}_c^{ - 1}{\mathit{\boldsymbol{M}}_{cd}}} \end{array}} \right], $ |
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}\\ {{{\bf{0}}_{3 \times 3}}}&{\frac{1}{2}{\mathit{\boldsymbol{Q}}_{ev}}\mathit{\boldsymbol{J}}_c^{ - 1}} \end{array}} \right],\mathit{\boldsymbol{u}} = {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{a}}_c^{\rm{T}}}&{\mathit{\boldsymbol{M}}_c^{\rm{T}}} \end{array}} \right]^{\rm{T}}} $ |
| $ {\mathit{\boldsymbol{f}}_{ev}} = - \frac{1}{4}{\left\| {{\omega _e}} \right\|^2}{\mathit{\boldsymbol{q}}_{ev}} + \frac{1}{2}{\mathit{\boldsymbol{Q}}_{ev}}\mathit{\boldsymbol{f}}\left( {{\mathit{\boldsymbol{\omega }}_e},{\mathit{\boldsymbol{\omega }}_c},{\mathit{\boldsymbol{\omega }}_d},{{\mathit{\boldsymbol{\dot \omega }}}_d}} \right)。$ |
传统滑模控制器以大增益来抵消未建模测量不确定性和控制干扰的影响,要求控制系统提供较大的控制力和力矩,但在实际任务中,执行机构输出能力一般受限,无法完全实现控制指令,影响控制性能。
双滑模面控制方法是解决上述问题的有效途径,由第二滑模面自动补偿测量不确定性和干扰对系统的影响,第一滑模面保证系统误差收敛特性。文献[12]尽管对双滑模面控制律进行了研究,但并未深入分析和构建测量不确定性的传播模型,且本文采用指数趋近律描述滑模面趋近运动,采用双曲正切函数抑制滑模抖振,以提升控制过程的稳定性。
定义滑模控制器的第一滑模面为
| $ \mathit{\boldsymbol{s}} = \mathit{\boldsymbol{\dot e}} + \mathit{\boldsymbol{\lambda e}} $ | (12) |
式中λ为六阶正定对角矩阵:
| $ \mathit{\boldsymbol{\lambda}} = {\rm{diag}}\left( {{\lambda _1},{\lambda _2}, \cdots ,{\lambda _6}} \right),{\lambda _i} > 0,i = 1,2, \cdots ,6 $ |
定义滑模控制器的第二滑模面为
| $ \mathit{\boldsymbol{\eta }} = \mathit{\boldsymbol{s}} + {\mathit{\boldsymbol{k}}_0}\int_0^t {{\rm{sign}}\left( \mathit{\boldsymbol{s}} \right){\rm{d}}\tau } $ | (13) |
式中k0为六阶正定对角矩阵。第二滑模面是通过对第一滑模面的符号函数进行积分而得到,主要功能便是自动补偿未知有界干扰与系统不确定性对系统的影响。
对式(13)求导,可得
| $ \mathit{\boldsymbol{\dot \eta }} = \mathit{\boldsymbol{\dot s}} + {\mathit{\boldsymbol{k}}_0}{\rm{sign}}\left( \mathit{\boldsymbol{s}} \right) $ | (14) |
本文采用趋近率描述趋近运动,且采用如下指数趋近率
| $ \mathit{\boldsymbol{\dot \eta }} = - \mathit{\boldsymbol{k\eta }} - \mathit{\boldsymbol{\varepsilon }}{\rm{sign}}\left( \mathit{\boldsymbol{\eta }} \right) $ | (15) |
式中:k和ε为六阶正定对称阵,具体表达式分别为
| $ \mathit{\boldsymbol{k}} = {\rm{diag}}\left( {{k_1},{k_2}, \cdots ,{k_6}} \right),{k_i} > 0,i = 1,2, \cdots ,6 $ |
| $ \mathit{\boldsymbol{\varepsilon }} = {\rm{diag}}\left( {{\varepsilon _1},{\varepsilon _2}, \cdots ,{\varepsilon _6}} \right),{\varepsilon _i} > 0,i = 1,2, \cdots ,6 $ |
对式(12)求导,并代入式(14),结合式(15),经过整理可得
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\ddot e}} = - \left( {\mathit{\boldsymbol{k}} + \lambda } \right)\dot e - \mathit{\boldsymbol{k\lambda e}} - }\\ {\mathit{\boldsymbol{k}}{\mathit{\boldsymbol{k}}_0}\int_0^t {{\rm{sign}}\left( \mathit{\boldsymbol{s}} \right){\rm{d}}\tau - \mathit{\boldsymbol{\varepsilon }}{\rm{sign}}\left( \mathit{\boldsymbol{\eta }} \right) - {\mathit{\boldsymbol{k}}_0}{\mathop{\rm sign}\nolimits} \left( \mathit{\boldsymbol{s}} \right)} } \end{array} $ | (16) |
将式(11)代入式(16),可得
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{B}}^{ - 1}}\left( { - \mathit{\boldsymbol{f}} - \left( {\mathit{\boldsymbol{k}} + \lambda } \right)\mathit{\boldsymbol{\dot e}} - \mathit{\boldsymbol{k\lambda e}} - } \right.}\\ {\left. {\mathit{\boldsymbol{k}}{\mathit{\boldsymbol{k}}_0}\int_0^t {{\rm{sign}}\left( \mathit{\boldsymbol{s}} \right){\rm{d}}\tau - \mathit{\boldsymbol{\varepsilon }}{\rm{sign}}\left( \mathit{\boldsymbol{\eta }} \right) - {k_0}{\mathop{\rm sign}\nolimits} \left( \mathit{\boldsymbol{s}} \right)} } \right)} \end{array} $ | (17) |
式(17)中采用了符号函数,符号函数的存在使得ac和Mc不连续,在稳态时会有抖振存在。为了减小稳态时的抖振,用双曲正切函数tanh(s/p12)和tanh(η/p22)来代替符号函数sign(s)和sign(η),即用平滑函数代替不连续函数,其中p1、p2为转移因子。则控制律变为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{B}}^{ - 1}}\left( { - \mathit{\boldsymbol{f}} - \left( {\mathit{\boldsymbol{k}} + \lambda } \right)\mathit{\boldsymbol{\dot e}} - \mathit{\boldsymbol{k\lambda e}} - } \right.}\\ {\mathit{\boldsymbol{k}}{\mathit{\boldsymbol{k}}_0}\int_0^t {{\rm{tanh}}\left( {\mathit{\boldsymbol{s}}/p_1^2} \right){\rm{d}}\tau - \mathit{\boldsymbol{\varepsilon }}{\rm{tanh}}\left( {\mathit{\boldsymbol{\eta }}/p_2^2} \right) - } }\\ {\left. {{\mathit{\boldsymbol{k}}_0}{\rm{tanh}}\left( {\mathit{\boldsymbol{s}}/p_1^2} \right)} \right)} \end{array} $ | (18) |
为了保证函数tanh(s/p12)和tanh(η/p22)接近sign(s)和sign(η)有较高的动态性能,p1、p2应取较小值;为了有效消除抖振,p1、p2应取较大值。因此应综合考虑来确定p1、p2值。
为获得控制量u,需要代入目标星和追踪星的绝对姿态、相对姿态、绝对轨道和相对轨道信息。实际在轨任务中,追踪星可借助星敏感器、陀螺、GPS等获得自身绝对姿态和轨道估计信息,借助相对测量敏感器获得目标星相对追踪星的姿态、位置等估计信息,目标星的绝对姿态和轨道估计信息需要借助上述信息解算获得。各项估计误差将引入系统,从而导致测量不确定性。本文将推导分析估计误差在系统中的传播特性,作为仿真验证的依据。
追踪星轨道估计值
追踪星惯性姿态估计值
定义追踪星通过相对导航得到期望坐标系相对追踪星本体系的相对位置
目标星轨道估计值
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat R}}_t^i = \mathit{\boldsymbol{\hat R}}_c^i + {{\mathit{\boldsymbol{\hat A}}}_{ibc}}\mathit{\boldsymbol{\hat r}}_{dbc}^{bc}}\\ {\mathit{\boldsymbol{\hat V}}_t^i = \mathit{\boldsymbol{\hat V}}_c^i + {{\mathit{\boldsymbol{\hat A}}}_{ibc}}\mathit{\boldsymbol{\dot {\hat r}}}_{dbc}^{bc} + \left( {{{\mathit{\boldsymbol{\hat A}}}_{ibc}}\mathit{\boldsymbol{\hat \omega }}_{dci}^{bc}} \right) \times \left( {{{\mathit{\boldsymbol{\hat A}}}_{ibc}}\mathit{\boldsymbol{\hat r}}_{dbc}^{bc}} \right)} \end{array} $ | (19) |
其中,追踪星本体系到惯性系转换矩阵
目标星姿态估计值
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat q}}}_{bti}} = {{\left( {{\mathit{\boldsymbol{q}}_{dbt}} \otimes {{\mathit{\boldsymbol{\hat q}}}_{bcd}} \otimes {{\mathit{\boldsymbol{\hat q}}}_{ibc}}} \right)}^{ - 1}},}\\ {{{\mathit{\boldsymbol{\hat \omega }}}_{bti}} = {\mathit{\boldsymbol{A}}_{btd}}{{\mathit{\boldsymbol{\hat A}}}_{dbc}}\left( {\mathit{\boldsymbol{\hat \omega }}_{bci}^{bc} + \mathit{\boldsymbol{\hat \omega }}_{dbc}^{bc}} \right)} \end{array} $ | (20) |
式中追踪星本体系到期望坐标系转换矩阵
追踪星在目标星轨道系下的相对位置和速度估计值
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat r}} = {{\mathit{\boldsymbol{\hat A}}}_{otbt}}{\mathit{\boldsymbol{A}}_{btd}}{{\mathit{\boldsymbol{\hat A}}}_{dbc}}\left( { - \mathit{\boldsymbol{\hat r}}_{dbc}^{bc}} \right)\mathit{\boldsymbol{\hat r}} \cdot = {{\mathit{\boldsymbol{\hat A}}}_{otbt}}{\mathit{\boldsymbol{A}}_{btd}}{{\mathit{\boldsymbol{\hat A}}}_{dbc}}\left( { - \mathit{\boldsymbol{\hat r}}_{dbc}^{bc}} \right) - }\\ {\left( {\mathit{\boldsymbol{\hat \omega }}_{oti}^{ot} - {{\mathit{\boldsymbol{\hat A}}}_{oti}}{{\mathit{\boldsymbol{\hat A}}}_{ibc}}\mathit{\boldsymbol{\hat \omega }}_{bci}^{bc}} \right) \times \left( {{{\mathit{\boldsymbol{\hat A}}}_{otbt}}{\mathit{\boldsymbol{A}}_{btd}}{{\mathit{\boldsymbol{\hat A}}}_{dbc}}\left( { - \mathit{\boldsymbol{\hat r}}_{dbc}^{bc}} \right)} \right)} \end{array} $ | (21) |
式中,目标星本体系到目标星轨道系转换矩阵
通过上述解算,即可由追踪星的绝对导航、姿态确定和相对导航估计值计算得到控制量
| $ \begin{array}{*{20}{c}} {\hat u = {{\hat B}^{ - 1}}\left( { - \hat f - \left( {k + \lambda } \right)\hat e \cdot - k\lambda \hat e - } \right.}\\ {k{k_0}\int_0^t {\tanh \left( {\hat s/p_1^2} \right){\rm{d}}\tau } + \varepsilon \tanh \left( {\hat \eta /p_2^2} \right) - }\\ {\left. {{k_0}\tanh \left( {\hat s/p_1^2} \right)} \right)} \end{array} $ | (22) |
易知,控制量
考虑到控制受限的因素,为了使控制输出不超出实际可用的执行机构的最大和最小输出,并保证控制系统的跟踪特性,分别对控制量u中的位置控制量ac和姿态控制量Mc进行向量限幅,定义sat(ac)和sat(Mc)分别为
| $ {\rm{sat}}\left( {{\mathit{\boldsymbol{a}}_c}} \right) = \left\{ \begin{array}{l} 0,{\underline a _{c\max }} < {\underline A _{\min }}\\ {\mathit{\boldsymbol{a}}_c},{\underline A _{\min }} \le {\underline a _{c\max }} < {\underline A _{\max }}\\ {\mathit{\boldsymbol{a}}_c}{\mathit{\boldsymbol{A}}_{\max }}/{a_{c\max }},{\underline a _{c\max }} \ge {\underline A _{\max }} \end{array} \right. $ | (23) |
| $ {\rm{sat}}\left( {{\mathit{\boldsymbol{M}}_c}} \right) = \left\{ \begin{array}{l} 0,{M_{c\max }} < {T_{\min }}\\ {\mathit{\boldsymbol{M}}_c},{T_{\min }} \le {M_{c\max }} < {T_{\max }}\\ {\mathit{\boldsymbol{M}}_c}{T_{\max }}/{M_{c\max }},{M_{c\max }} \ge {T_{\max }} \end{array} \right. $ | (24) |
式中:ac max=
为对比分析,本文同样给出只有式(12)表示的第一滑模面的单滑模面控制律[14]。同样采用趋近率描述趋近运动,且采用如下指数趋近率:
| $ \mathit{\boldsymbol{\dot s}} = - \mathit{\boldsymbol{ks}} - \mathit{\boldsymbol{\varepsilon }}{\rm{sgn}}\left( \mathit{\boldsymbol{s}} \right) $ | (25) |
与上述推导过程类似,可以获得单滑模面控制律的表达式:
| $ \mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{B}}^{ - 1}}\left( { - \mathit{\boldsymbol{f}} - \left( {\mathit{\boldsymbol{k}} + \mathit{\boldsymbol{\lambda }}} \right)\mathit{\boldsymbol{\dot e}} - \mathit{\boldsymbol{k\lambda e}} - \mathit{\boldsymbol{\varepsilon }}\tanh \left( {\mathit{\boldsymbol{s}}/p_1^2} \right)} \right) $ | (26) |
由追踪星的轨道、姿态、相对状态估计值计算得到的控制量
| $ \mathit{\boldsymbol{\hat u}} = {{\mathit{\boldsymbol{\hat B}}}^{ - 1}}\left( { - \mathit{\boldsymbol{\hat f}} - \left( {\mathit{\boldsymbol{k}} + \mathit{\boldsymbol{\lambda }}} \right)\mathit{\boldsymbol{\dot {\hat e}}} - \mathit{\boldsymbol{k\lambda \hat e}} - \mathit{\boldsymbol{\varepsilon }}\tanh \left( {\mathit{\boldsymbol{\hat s}}/p_1^2} \right)} \right) $ | (27) |
本文将在相同的仿真条件下,对式(22)表示的双滑模面控制律、式(27)表示的单滑模面控制律进行数学仿真和对比分析,以准确评价双滑模面控制律的控制性能。
3.1 仿真条件目标星初始轨道参数见表 1。
| 表 1 目标卫星初始轨道根数 Tab.1 Original orbit element of target |
追踪星初始轨道位于目标星同轨道后方20 m。
目标星质量mt=400 kg,追踪星质量mc=450 kg,两星的转动惯量分别为
| $ {\mathit{\boldsymbol{J}}_{\rm{t}}} = {\rm{diag}}\left( {150,180,210} \right){\rm{kg}} \cdot {{\rm{m}}^2} $ |
| $ {\mathit{\boldsymbol{J}}_{\rm{c}}} = {\rm{diag}}\left( {160,190,200} \right){\rm{kg}} \cdot {{\rm{m}}^2} $ |
假定目标星初始时刻旋转轴在目标星本体系下的高低角和方位角均为30°,旋转角速度为1.5(°)/s,则初始时刻目标星旋转角速度:
| $ {\mathit{\boldsymbol{\omega }}_{{\rm{bit}}}}\left| {_{t = 0}} \right. = {\left[ {\begin{array}{*{20}{c}} {1.125}&{0.650}&{ - 0.750} \end{array}} \right]^{\rm{T}}}\left( \circ \right)/s $ |
目标星初始姿态设定为:在3-1-2转序下,三轴姿态初值均为10°,则转换为惯性四元数初值为
| $ {\mathit{\boldsymbol{q}}_{{\rm{bti}}}}\left| {_{t = 0}} \right. = {\left[ {\begin{array}{*{20}{c}} { - 0.1752}&{0.7188}&{ - 0.6380}&{0.2135} \end{array}} \right]^{\rm{T}}} $ |
追踪星处于三轴稳定状态,初始姿态设定为:在3-1-2转序下,三轴姿态初值均为1°,则转换为惯性四元数初值为
| $ {\mathit{\boldsymbol{q}}_{{\rm{bci}}}}\left| {_{t = 0}} \right. = {\left[ {\begin{array}{*{20}{c}} { - 0.1592}&{0.7967}&{ - 0.5705}&{0.1200} \end{array}} \right]^{\rm{T}}} $ |
追踪星和目标星的干扰力矩均由下式表示:
| $ {\mathit{\boldsymbol{M}}_{\rm{d}}}\left( t \right) = \left\{ \begin{array}{l} {M_0}\left( {3\cos \left( {{\omega _o}t} \right) + 1} \right)\\ {M_0}\left( {1.5\sin \left( {{\omega _o}t} \right) + 3\cos \left( {{\omega _o}t} \right)} \right)\\ {M_0}\left( {3\cos \left( {{\omega _o}t} \right) + 1} \right) \end{array} \right. $ |
其中M0为常值系数。
追踪星在惯性系下受到的干扰力设为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{a}}_{\rm{d}}}\left( t \right) = {{\left[ {\begin{array}{*{20}{c}} {\sin \left( {{\omega _o}t} \right)}&{ - 2\sin \left( {{\omega _o}t} \right)}&{ - 1\sin \left( {{\omega _o}t} \right)} \end{array}} \right]}^{\rm{T}}} \times }\\ {{{10}^{ - 3}}{\rm{m/}}{{\rm{s}}^2}} \end{array} $ |
追踪星采用GPS加INS实现绝对导航,对应轨道估计精度:三轴位置精度(3σ)分别为15、15、30 m,三轴速度精度(3σ)分别为0.15、0.15、0.15 m/s;采用星敏加陀螺联合滤波实现惯性姿态确定,对应三轴姿态角估计精度(3σ)分别为0.03°、0.01°、0.01°,三轴姿态角速度估计精度(3σ)均为0.01(°)/s。
追踪星采用视觉导航敏感器实现目标星相对测量和导航,对应相对导航精度:Y、Z轴相对位置精度(3σ)均为0.02+0.01(R-2) m,相对速度精度(3σ)均为0.005 +0.001(R-2) m/s;X轴相对位置精度(3σ)为0.02+0.001R2 m,相对速度精度(3σ)为0.005 +0.000 3R2 m/s;Y、Z轴相对姿态角精度(3σ)均为0.05+0.01(R-2)°,相对角速度精度(3σ)均为0.01+0.001(R-2)(°)/s;Z轴相对姿态角精度(3σ)为0.05+0.001R2(°),相对姿态角速度精度(3σ)为0.01+0.000 2×R2(°)/s。
追踪星采用推力器作为轨道和姿态控制执行机构,对应三轴控制加速度限幅范围Amax=0.1 m/s2、Amin=0.01m/s2,三轴控制力矩限幅范围Tmax= 0.1 N·m、Tmin=0.01 N·m。
设目标星本体系下的抓捕位置坐标为pDbt=[-1 0 0]T,此时期望坐标系与目标星本体系重合。要求控制算法在1 200 s内使得追踪星到达目标星本体系下坐标[-5 0 0]T,并形成稳定的姿轨跟踪状态。
设追踪星控制步长为0.2 s,优化调整后滑模控制参数分别为
| $ \mathit{\boldsymbol{\lambda }} = {\rm{diag}}\left( {1,1,1,0.02,0.02,0.02} \right) $ |
| $ \mathit{\boldsymbol{k}} = {\rm{diag}}\left( {0.1,0.1,0.1,0.01,0.01,0.01} \right) $ |
| $ {\mathit{\boldsymbol{k}}_0} = {\rm{diag}}\left( {0.01,0.01,0.01,0.001,0.001,0.001} \right) $ |
| $ \mathit{\boldsymbol{\varepsilon }} = {\rm{diag}}\left( {2,2,2,0.02,0.02,0.02} \right) \times {10^{ - 2}} $ |
| $ {P_1} = 0.01,{P_2} = 0.1 $ |
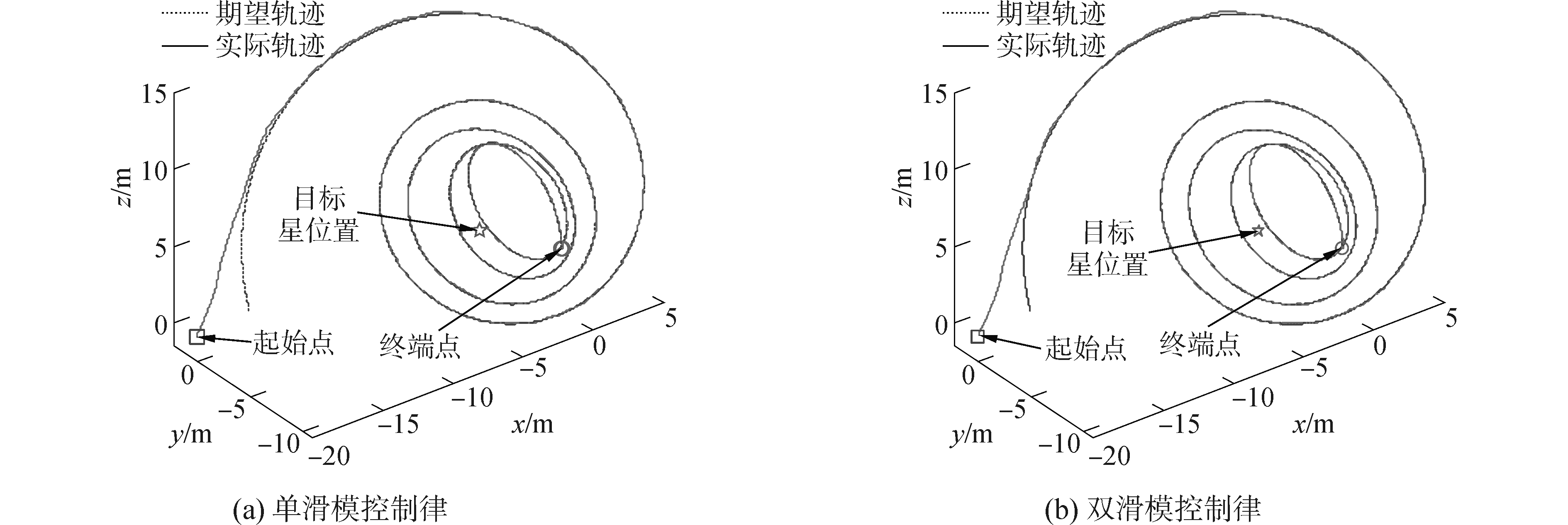
基于上述仿真条件,分别对单滑模面控制律和双滑模面控制律进行数学仿真分析,得到结果如图 2~8所示。分别计算两种控制律对应的稳定之后的位置、速度、姿态角、姿态角速度控制误差的均值和标准差,汇总如表 2。
|
图 2 追踪星在目标星轨道系下的运动轨迹 Fig.2 Chaser trajectory in target orbit coordinate system |
|
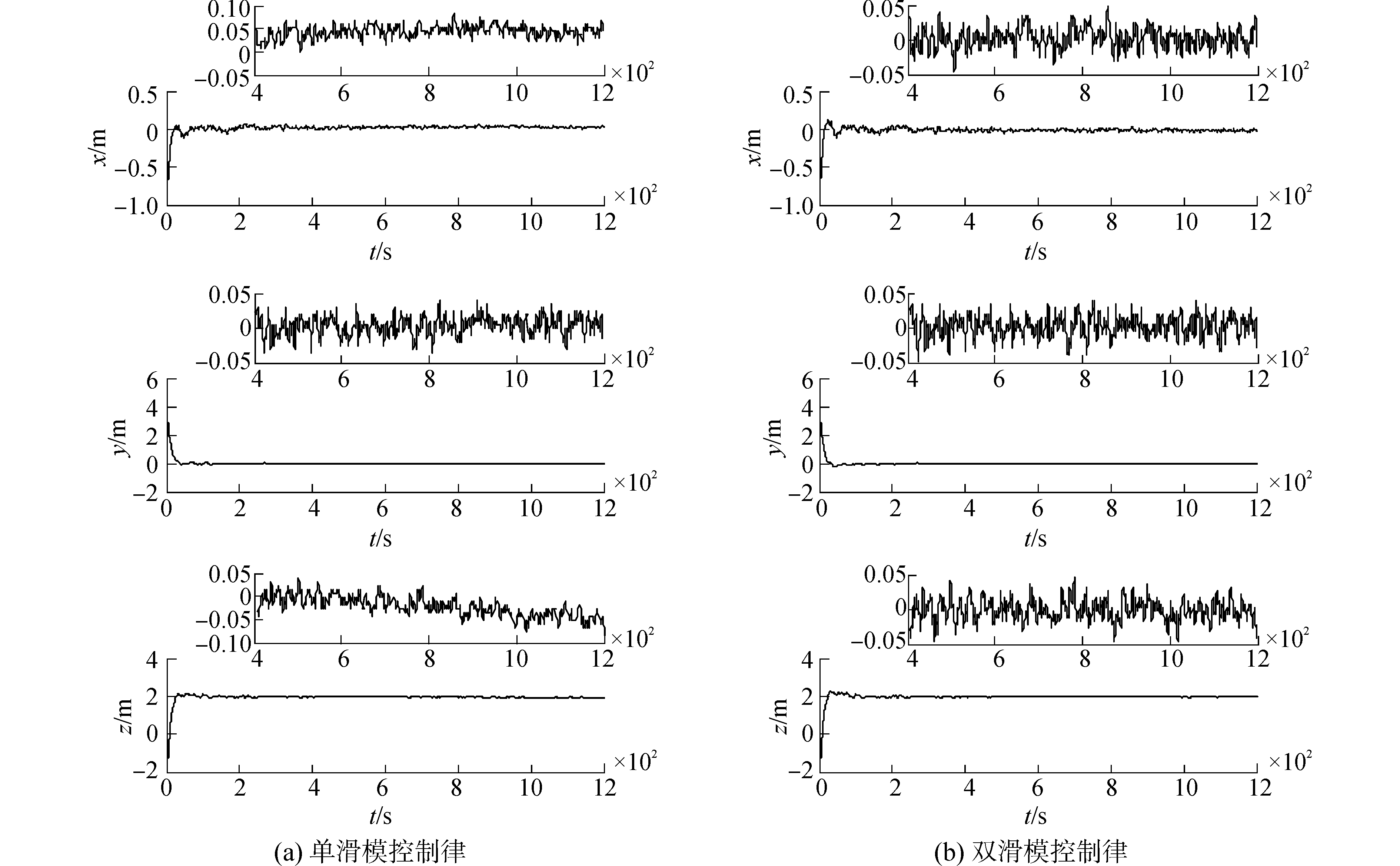
图 3 追踪星位置控制误差曲线 Fig.3 Chaser position control errors curves |

|
图 4 追踪星速度控制误差曲线 Fig.4 Chaser velocity control errors curves |
|
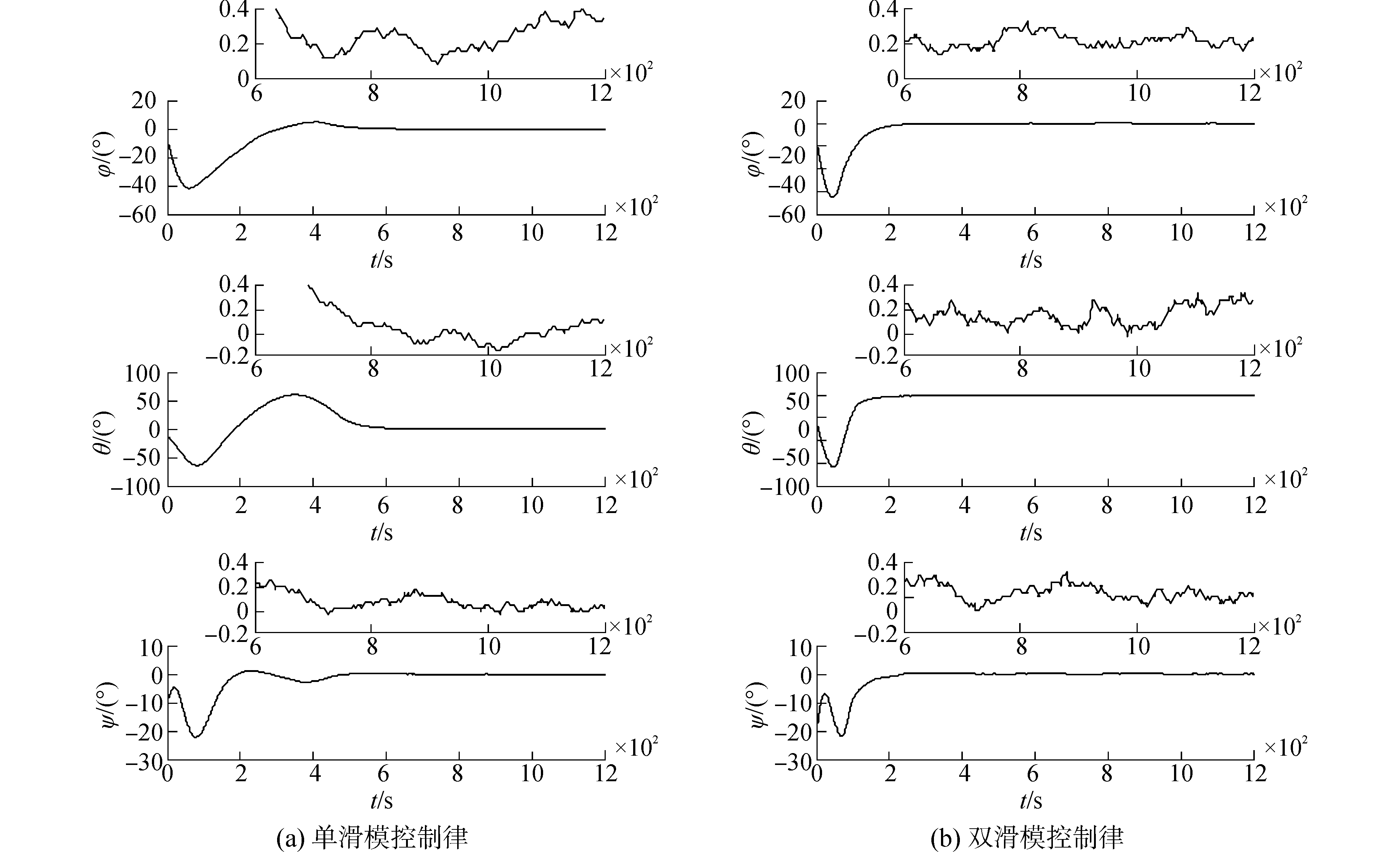
图 5 追踪星姿态角控制误差曲线 Fig.5 Chaser attitude angle control errors curves |

|
图 6 追踪星姿态角速度控制误差曲线 Fig.6 Chaser attitude angle velocity control errors curves |
|
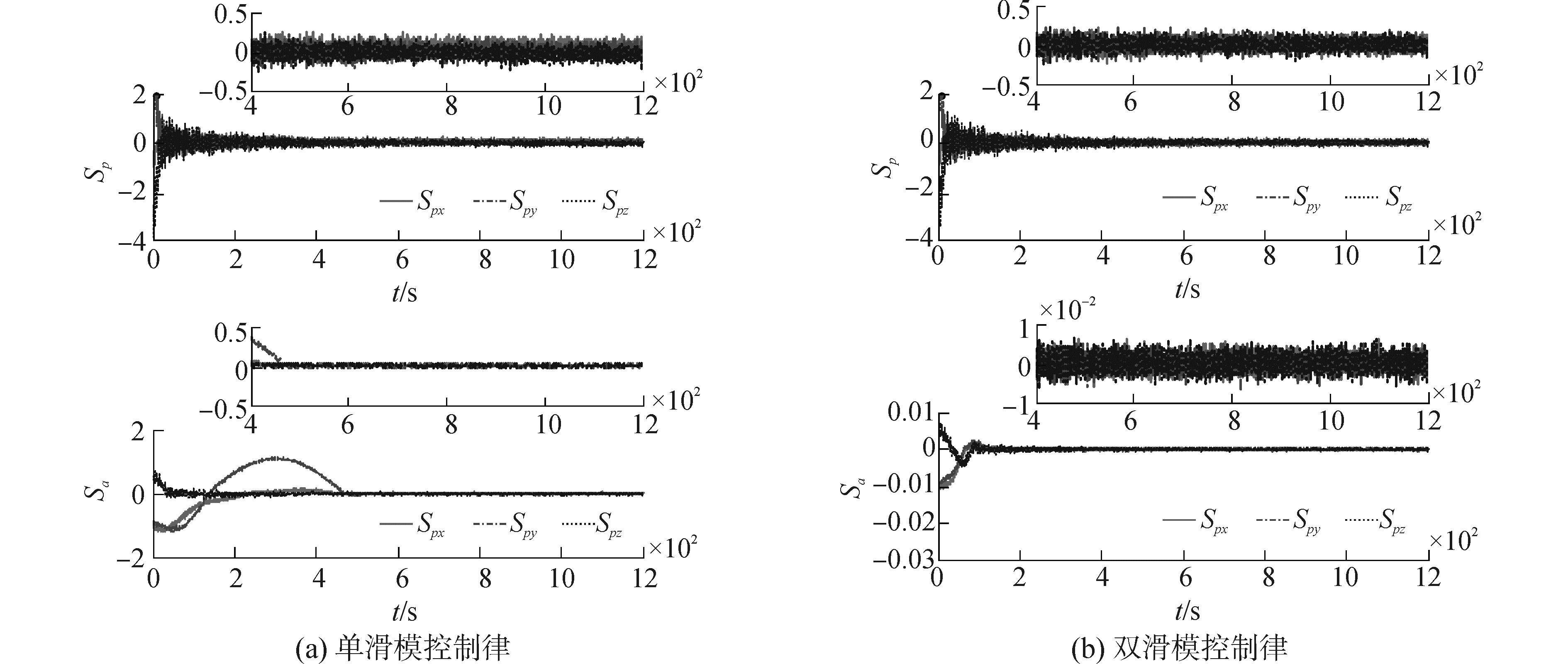
图 7 滑模面s数值变化曲线 Fig.7 Solid-mode surface s value curves |
|
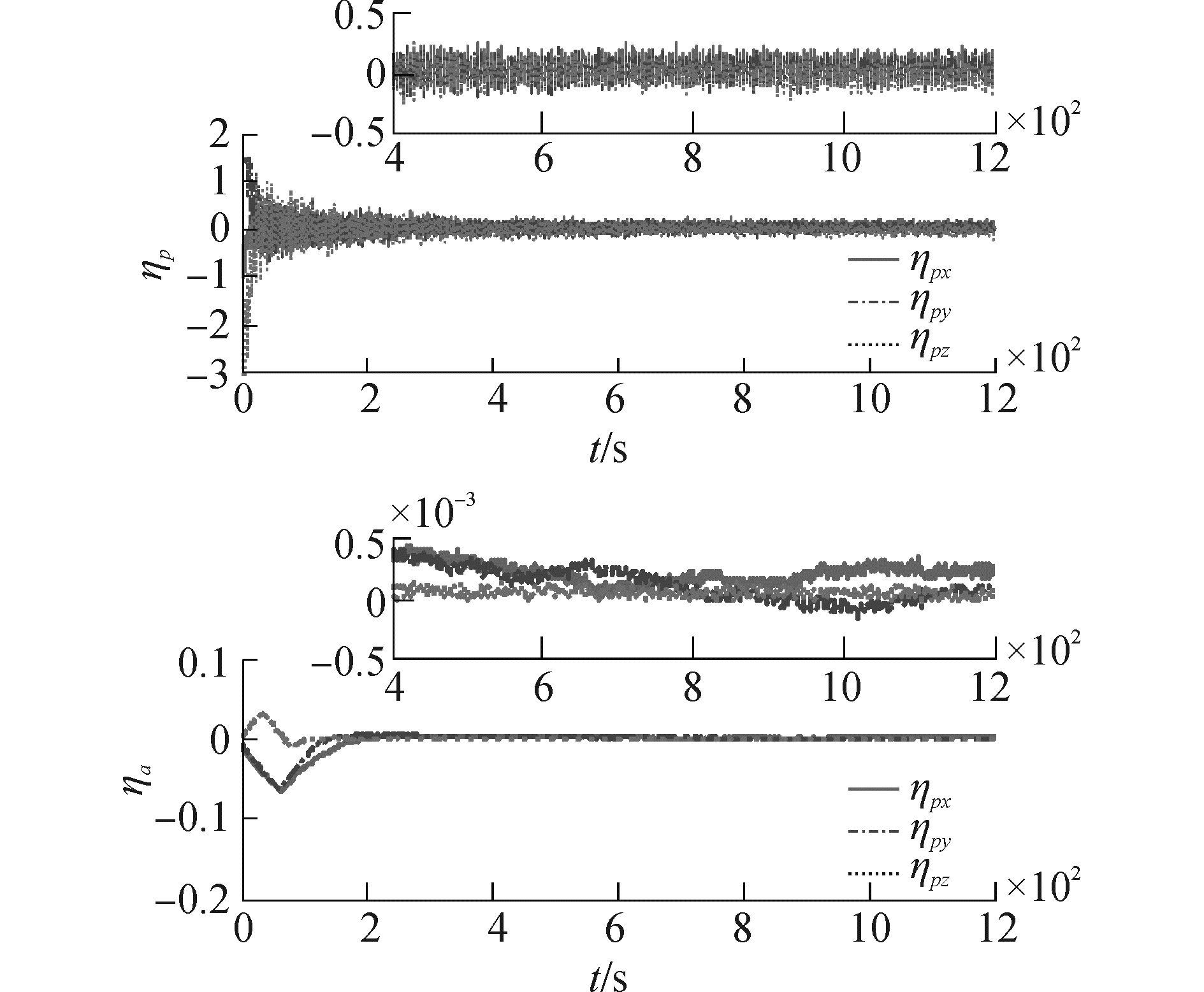
图 8 第二滑模面η数值变化曲线 Fig.8 The second solid-mode surface η value curves |
| 表 2 控制误差的均值和标准差汇总 Tab.2 Mean value and standard deviation of control error |
由图 2中追踪星在目标星轨道系下的运动轨迹可知,经过一段调整后,单滑模控制律和双滑模控制律均能使得追踪星的位置实时跟随期望轨迹,最终形成对旋转目标的同步运动状态。
由图 3和表 2可知,单滑模面控制律使得位置误差在100 s后进入稳定,但X轴和Z轴位置误差存在分别存在约0.047、-0.037 m的常值偏差,无法收敛到0附近。双滑模面控制律同样使得位置误差在100 s后进入稳定,且三轴误差平均值均收敛到了0附近,表现出了更优的控制效果。
由图 4和表 2可知,两种控制律均使得速度误差较快地收敛到0附近,双滑模面控制律对应更低的误差标准差,速度控制精度相对更高。
由图 5和表 2可知,单滑模面控制律使得姿态角误差在600 s之后才逐渐进入稳定,稳定后的三轴姿态角误差并没有较好地收敛到0,偏差均值分别为0.237°、0.169°、0.065°;双滑模面控制律使得姿态角在200 s之后逐渐进入稳定,且稳定后的三轴姿态角误差均收敛到了0附近,明显优于单滑模面控制律。
由图 6和表 2可知,两种控制律均使角速度误差最终收敛到0附近,但是双滑模面控制律明显比单滑模面控制律更快收敛。
两种控制律对应滑模面数值的均值和标准差汇总如表 3。图 7中sp和sa分别对应相对轨道和相对姿态偏差对应的第一滑模面数值;图 8中ηp和ηa分别对应相对轨道和相对姿态偏差对应的第二滑模面数值。
| 表 3 滑模面数值的均值和标准差 Tab.3 Mean value and standard deviation of solid-mode surface values |
由图 7、8和表 3可知,两种控制律的滑模面s最终均收敛到0附近,但双滑模面控制律的稳态偏差更接近于0,且收敛时间更短。双滑模面控制律第二滑模面η数值的相对轨道部分最终均收敛到0附近,相对姿态部分在一定范围内震荡,说明主要由第二滑模面承受有界干扰、测量误差等因素的影响,有效保证了第一滑模面的稳定。
综合上述分析结果,对于翻滚目标的逼近与跟踪控制过程,双滑模面控制律相对于单滑模面控制律表现出了更好的控制性能,收敛时间更短,控制精度更高,说明第二滑模面明显地补偿和抑制了绝对和相对测量不确定性、大幅度干扰力和力矩对系统的影响。因此,本文提出的双滑模面控制律对于于真实的空间翻滚目标捕获等任务场景能够获得更优的控制性能。
4 结论1) 针对空间翻滚目标逼近与跟踪控制问题,设计了双滑模面控制律,能够按照指数趋近率在有限时间到达两个滑模面,保证系统稳定性。
2) 分析建立了测量误差向控制指令的传播模型,可为后续控制量偏差的估计提供依据。
3) 设计了充分考虑测量不确定性、控制受限、干扰力和力矩等因素的数学仿真条件,对提出的双滑模面控制律进行了仿真验证,并与单滑模面控制律对比,结果表明:双滑模面控制律收敛时间更短,稳态常值偏差更小,第二滑模面有效抑制了测量误差、有界干扰、系统参数不确定等因素的影响。
4) 对于存在有界干扰、测量误差、参数不确定等因素的真实空间翻滚目标捕获等任务场景,本文提出的双滑模面控制律能够获得更优的控制性能。
| [1] |
LIU Houde, WANG Xueqian, LIANG Bin, et al. Motion characteristics analysis and ground simulation method of spin target in autonomous capture[J]. Robot, 2013, 35(1): 1-8. DOI:10.3724/SP.J.1218.2013.00001 (  0) 0)
|
| [2] |
XU Y, TATSCH A, FITZCOY N G.Chattering free sliding mode control for a 6 DOF formation flying mission[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit San Francisco, California, 2005:235-242.
(  0) 0)
|
| [3] |
MA Z, MA O, SHASHIKANTH B N. Optimal approach to and alignment with a rotating rigid body for capture[J]. Journal of the astronautical sciences, 2007, 55(4): 407-419. DOI:10.1007/BF03256532 (  0) 0)
|
| [4] |
LI Peng, YUE Xiaokui, YUAN Jianping. Coupled back-stepping control for spacecraft to approach with a tumbling non-cooperative object during the final phase[J]. Journal of Harbin Institute of Technology, 2013, 45(1): 94-100. (  0) 0)
|
| [5] |
耿云海, 卢伟, 陈雪芹. 在轨服务航天器对失控目标的姿态同步控制[J]. 哈尔滨工业大学学报, 2012, 44(1): 1-6. GENG Yunhai, LU Wei, CHEN Xueqin. Attitude synchronization control of on-orbit servicing spacecraft with respect to out-of-control target[J]. Journal of Harbin Institute of Technology, 2012, 44(1): 1-6. DOI:10.11918/j.issn.0367-6234.2012.01.001 (  0) 0)
|
| [6] |
SUBBARAO K, WELSH S. Nonlinear control of motion synchronization for satellite proximity operations[J]. Journal of guidance, control and dynamics, 2008, 31(5): 1284-1294. DOI:10.2514/1.34248 (  0) 0)
|
| [7] |
HYEONGJUN P, STEFANO D C, ILYA K. Model predictive control for spacecraft rendezvous and docking with a rotating/tumbling platform and for debris avoidance[C]//American Control Conference, San Francisco, USA, 2011:125-132.
(  0) 0)
|
| [8] |
YAN Z, LE X, WANG J. Tube-based robust model predictive control of nonlinear systems via collective neurodynamic optimization[J]. IEEE transactions on industrial electronics, 2016, 63(7): 4377-4386. DOI:10.1109/TIE.2016.2544718 (  0) 0)
|
| [9] |
LEE S, HAO L, HWANG I. Analytical uncertainty propagation for satellite relative motion along elliptic orbits[J]. Journal of guidance control & dynamics, 2017: 1593-1601. (  0) 0)
|
| [10] |
LI C, JING W, GAO C. Adaptive back-stepping-based flight control system using integral filters[J]. Aerospace science and technology, 2009, 13: 105-113. DOI:10.1016/j.ast.2008.05.002 (  0) 0)
|
| [11] |
李九人, 李海阳, 唐国金. 对无控旋转目标逼近的自适应滑模控制[J]. 宇航学报, 2011, 32(4): 815-822. LI Jiuren, LI Haiyang, TANG Guojin. Adaptive sliding mode control for approach to uncontrolled rotating satellite[J]. Journal of astronautics, 2011, 32(4): 815-822. (  0) 0)
|
| [12] |
卢伟. 在轨服务航天器与失控目标交会对接的相对位姿耦合控制[D]. 哈尔滨: 哈尔滨工业大学, 2012: 66-89. LU Wei. Relative position and attitude coupled control for on-orbit servicing spacecraft rendezvous and docking to an out-of-control target[D]. Harbin:Harbin Institute of Technology, 2012:66-89. http: //cdmd. cnki. com. cn/Article/CDMD-10213-1013035461. htm (  0) 0)
|
| [13] |
陈炳龙. 基于二阶滑模算法的航天器相对位姿耦合控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2015: 45-67. CHEN Binglong. Research on spacecraft relative position and attitude coupled control on the base of second-order sliding mode algorithm[D]. Harbin:Harbin Institute of Technology, 2015:45-67. http: //cdmd. cnki. com. cn/Article/CDMD-10213-1015957650. htm (  0) 0)
|
| [14] |
HAN Fei, WU Hailei, HOU Jianwen, et al. The 6-DOF synchronized sliding-mode control for approaching to the slowly rotating satellite[C]//Proceedings of the 34th Chinese Control Conference. Hangzhou, China, 2015:3269-3274.
(  0) 0)
|
| [15] |
张志刚, 张锦绣. 基于高斯伪谱法的系绳式InSAR系统展开滑模控制[J]. 哈尔滨工程大学学报, 2017, 38(2): 293-299. ZHANG Jinxiu, ZHANG Zhigang. Sliding mode control of a tethered InSAR system deployment on the basis of the Gauss pseudospectral method[J]. Journal of Harbin Engineering University, 2017, 38(2): 293-299. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


