随机噪声与单频波在非线性介质中传播时,两者的相互作用会导致各自能量在频域上的重新分配,对该问题的研究具有重要的实际应用价值,如利用强单频波控制随机噪声能量在某一频段增加或者减小以及控制噪声能量由某一频段转移到另一频段[1]。文献[2]在空气声管中试验观察了弱噪声与强单频的非线性传播畸变,并从Earnshaw解出发仿真了不同距离的功率谱变化,其理论和实验结果吻合较好,但未给出解析结果。Rudenko等利用简单波解和相关函数法推导了随机噪声和单频波相互作用过程中不同距离功率谱的解析表达式,包括随机噪声和单频波相互作用过程中噪声受到单频波影响后的能量变化、单频波在加入随机噪声后的能量变化、相互作用后产生的新频谱能量的变化[3-8]。但该推导过程相对复杂,其结果仍需借助计算机进行数值计算,且得到的功率谱只是在高频频率附近能量变化,而对于高频及其倍频的情况没有考虑[9]。杜功焕等提出了一种有限振幅无规声波相互作用的理论,即将Fenlon理论由单频波的相互作用理论推广到窄带随机噪声的情况,但该理论只适用于窄带情况[10-12]。
本文以Burgers方程为模型,推导了任意发射波形即任意随机噪声与单频波相互作用的功率谱随距离的演化规律,以高斯分布噪声为例分析加入强高频波后其能量的变换规律,并利用有限差分法数值计算不同距离处声信号的功率谱[13]。结果表明,强高频波对随机噪声具有频率展宽、高频能量增强的效果,能量被分配至高频及其倍频的两侧。
1 噪声与单频波的非线性互作用理论分析分析声波非线性互作用,并以描述非线性声波的Burgers方程为模型,在不考虑频散情况下其一维形式为
| $ \frac{{\partial u}}{{\partial x}} - \beta 'u\frac{{\partial u}}{{\partial \tau }} = - \delta \frac{{{\partial ^2}u}}{{\partial {\tau ^2}}} $ | (1) |
式中:u表示声场的质点声速,x表示沿声传播方向的位置坐标,τ=t-x/c0表示时间变量,β′=β/c02是衡量介质非线性大小的系数。δ表示声波的衰减。假设不考虑吸收效应即δ=0,在x=0有边界条件u=u0(t),则由简单波解,上述方程的解析解可写为
| $ u\left( {\tau ,x} \right) = {u_0}\left( \eta \right) = {u_0}\left( {\tau + \beta 'ux} \right) $ | (2) |
由傅里叶变换和傅里叶反变换得
| $ u\left( {\tau ,x} \right) = \frac{1}{{2{\rm{\pi }}}}\int\limits_{ - \infty }^{ + \infty } {\int\limits_{ - \infty }^{ + \infty } {{u_0}\left( {\tau ',x} \right){{\rm{e}}^{i\omega \left( {\tau - \tau '} \right)}}{\rm{d}}\tau '{\rm{d}}\omega } } $ | (3) |
将上述两式合并,令τ′=η-β′ux得
| $ \begin{gathered} u\left( {\tau ,x} \right) = - \frac{{\text{i}}}{{2{\text{π }}}}\iint\limits_{ - \infty } {{\omega ^{ - 1}}{{\dot u}_0}\left( \eta \right)\exp } \cdot \hfill \\ \left( { - {\text{i}}\omega \left( {\eta - \beta '{u_0}\left( \eta \right)x - \tau } \right)} \right){\text{d}}\omega {\text{d}}\eta \hfill \\ \end{gathered} $ | (4) |
如果考虑吸收效应,则
| $ \begin{gathered} u\left( {\tau ,x} \right) = u{{\text{e}}^{\delta z}} = - \frac{{\text{i}}}{{2{\text{π }}}}\iint\limits_{ - \infty } {{\omega ^{ - 1}}{{\dot u}_0}\left( \eta \right)\exp } \cdot \hfill \\ \left( { - {\text{i}}\omega \left( {\eta - \beta '{u_0}\left( \eta \right)x - \tau } \right)} \right){\text{d}}\omega {\text{d}}\theta \hfill \\ \end{gathered} $ | (5) |
其中
| $ x = \frac{{1 - {{\rm{e}}^{ - {\rm{\delta }}z}}}}{\delta } $ | (6) |
当令u0(η)为随机函数,所对应的问题即是要讨论的与噪声相关的问题。不同边界条件对应相关函数为
| $ B\left( {{\tau _1},{\tau _2};x} \right) = \left\langle {u\left( {{\tau _1},x} \right){u^ * }\left( {{\tau _2},x} \right)} \right\rangle $ | (7) |
将u(τ, x)的表达式代入式(7) 得
| $ \begin{array}{*{20}{c}} {B\left( {{\tau _1},{\tau _2};x} \right) = \frac{1}{{4{{\text{π }}^2}{\beta ^2}{x^2}}}\iint\limits_{ - \infty } {\frac{{\exp \left( {{\text{i}}{\omega _1}{\tau _1} - {\text{i}}{\omega _2}{\tau _2}} \right)}}{{\omega _1^2\omega _2^2}} \cdot }} \\ {{\text{d}}{\omega _1}{\text{d}}{\omega _2} \times \iint\limits_{ - \infty } {L\left( {{\omega _1},{\eta _1};{\omega _2},{\eta _2}} \right)\exp \left( {{\text{i}}{\omega _1}{\eta _1} - {\omega _2}{\eta _2}} \right)} \cdot } \\ {\left\langle {\exp \left( {{\text{i}}\beta x\left( {{\omega _1}{u_0}\left( {{\eta _1}} \right) - {\omega _2}{u_0}\left( {{\eta _2}} \right)} \right)} \right)} \right\rangle {\text{d}}{\eta _1}{\text{d}}{\eta _2}} \end{array} $ | (8) |
其中
| $ \begin{array}{*{20}{c}} {L\left( {{\omega _1},{\eta _1};{\omega _2},{\eta _2}} \right) = \frac{{{{\rm{d}}^2}}}{{{\rm{d}}{\eta _1}{\rm{d}}{\eta _2}}} + }\\ {{\rm{i}}{\omega _1}\frac{{\rm{d}}}{{{\rm{d}}{\eta _2}}} - {\rm{i}}{\omega _2}\frac{{\rm{d}}}{{{\rm{d}}{\eta _1}}} + {\omega _1}{\omega _2}} \end{array} $ |
假设边界条件是确定信号和随机信号的叠加,即
| $ {u_0}\left( \eta \right) = f\left( \eta \right) + \xi \left( \eta \right) $ | (9) |
式中:f(η)是确定的函数,ξ(η)是服从正态分布的随机过程,且均值为零,自相关系数为
| $ R\left( \tau \right) = \frac{{\left\langle {\xi \left( \theta \right)\xi \left( {\theta + \tau } \right)} \right\rangle }}{{{\sigma ^2}}} $ | (10) |
式中:σ2=〈ξ(θ)2〉是随机过程自相关函数在零点的取值即此随机过程的强度,式(8) 中的统计平均可以化为
| $ \begin{array}{*{20}{c}} {\left\langle {\exp \left( {{\rm{i}}\beta x\left( {{\omega _1}{u_0}\left( {{\eta _1}} \right) - {\omega _2}{u_0}\left( {{\eta _2}} \right)} \right)} \right)} \right\rangle = \exp \cdot }\\ {\left( { - \frac{1}{2}{{\left( {\beta '\sigma x} \right)}^2}\left( {\omega _1^2 + \omega _2^2 - 2{\omega _1}{\omega _2}R\left( {{\eta _1} - {\eta _2}} \right)} \right)} \right)} \end{array} $ | (11) |
则相关函数可以表示为
| $ \begin{array}{*{20}{c}} {B\left( {\tau ,x} \right) = \int\limits_{ - \infty }^\infty {\frac{{{{\text{e}}^{ - {\text{i}}\omega \tau }}}}{{2{\text{π }}{\omega ^2}}}{{\text{e}}^{ - {{\left( {\sigma \beta '\omega x} \right)}^2}}}{\text{d}}\omega } \cdot } \\ {\iint\limits_{ - \infty } {\left( {{\psi _1} + {\psi _2} + {\psi _3}} \right){{\text{e}}^{ - {\text{i}}\omega \left( {{\eta _1} - {\eta _2}} \right) + {\text{i}}\beta '\omega x\left[ {f\left( {{\eta _1}} \right) - f\left( {{\eta _2}} \right)} \right]}}} \cdot } \\ {{{\text{e}}^{{{\left( {\sigma \beta '\omega x} \right)}^2}R\left( {{\eta _1} - {\eta _2}} \right)}}{\text{d}}{\eta _1}{\text{d}}{\eta _2}} \end{array} $ | (12) |
其中
| $ \left\{ \begin{array}{l} {\ell _1} = - {\sigma ^2}\left[ {\frac{{{\partial ^2}R}}{{\partial \eta _1^2}} + {{\left( {\sigma \beta '\omega x} \right)}^2}{{\left( {\frac{{\partial R}}{{\partial {\eta _1}}}} \right)}^2}} \right]\\ {\ell _2} = - {\rm{i}}{\sigma ^2}\beta '\omega x\left[ {\frac{{\partial R}}{{\partial {\eta _1}}}\frac{{\partial f}}{{\partial {\eta _2}}} - \frac{{\partial R}}{{\partial {\eta _2}}}\frac{{\partial f}}{{\partial {\eta _1}}}} \right]\\ {\ell _3} = \frac{{\partial f}}{{\partial {\eta _1}}}\frac{{\partial f}}{{\partial {\eta _2}}} \end{array} \right. $ | (13) |
针对单频声波和噪声相互作用的情况,令f(θ)=Asin(ω0θ),即声波是频率为ω0的正弦信号。此时可以化简得到其相互作用过程中的功率谱密度随距离的变化关系,表示如下
| $ S\left( {\omega ,x} \right) = {S_1}\left( {\omega ,x} \right) + {S_2}\left( {\omega ,x} \right) + {S_3}\left( {\omega ,x} \right) $ | (14) |
其中
| $ \left\{ \begin{array}{l} {S_1}\left( {\omega ,x} \right) = - \frac{{{\sigma ^2}}}{{2{\rm{\pi }}}}\int\limits_{ - \infty }^{ + \infty } {\left[ {\frac{{{\partial ^2}R}}{{\partial {\eta ^2}}} + {{\left( {\sigma \beta '\omega x} \right)}^2}{{\left( {\frac{{\partial R}}{{\partial \eta }}} \right)}^2}} \right] \cdot } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\rm{e}}^{\chi \left( \eta \right)}}{{\rm{J}}_0}\left[ {\varphi \left( \eta \right)} \right]{\rm{d}}\eta \\ {S_2}\left( {\omega ,x} \right) = \frac{{\sigma A}}{{\omega {\rm{\pi }}}}\int\limits_{ - \infty }^{ + \infty } {\frac{{\partial R}}{{\partial \eta }}\cos \left( {\frac{{{\omega _0}\eta }}{2}} \right){{\rm{e}}^{\chi \left( \eta \right)}}{{\rm{J}}_1}\left[ {\varphi \left( \eta \right)} \right]{\rm{d}}\eta } \\ {S_3}\left( {\omega ,x} \right) = \frac{{\omega _0^2{A^2}}}{{4{\omega ^2}{\rm{\pi }}}}\int\limits_{ - \infty }^{ + \infty } {\left\{ {{{\rm{J}}_0}\left[ {\varphi \left( \eta \right)} \right]\cos \left( {{\omega _0}\eta } \right) - } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{{\rm{J}}_2}\left[ {\varphi \left( \eta \right)} \right]} \right\}{{\rm{e}}^{\chi \left( \eta \right)}}{\rm{d}}\eta \end{array} \right. $ |
| $ \varphi \left( \eta \right) = 2\beta 'A\omega \sin \left( {{\omega _0}\eta /2} \right) $ |
| $ \chi \left( \eta \right) = - {\rm{i}}\omega \eta - \sigma \beta '\omega x\left[ {1 - R\left( \eta \right)} \right] $ |
式中:S1为噪声成分ξ(η)在传播过程中考虑单频波影响时的非线性畸变;J0[φ(η)]为考虑该影响的修正;当单频波幅值A为零, S1为随机声波在非线性介质中的传播规律;S2为声传播过程中由于两者相互作用产生的新的频率成分;S3为单频波在考虑了噪声的影响后的传播规律,当令噪声的强度σ2为零后,所得到的结果就成了Bessel-Fubini解。进一步将上式转化可得如下公式:
| $ \left\{ \begin{array}{l} {S_\xi }\left( {\omega ,x} \right) = - \frac{{{\sigma ^2}}}{{\rm{\pi }}}{\rm{J}}_0^2\left( {A\beta '\omega x} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\int\limits_0^{ + \infty } {\frac{{{\rm{d}}R}}{{{\rm{d}}\eta }}\frac{{\sin \left( {\omega \eta } \right)}}{\omega }{{\rm{e}}^{{{\left( {\sigma \beta '\omega x} \right)}^2}\left[ {R\left( \eta \right) - 1} \right]}}{\rm{d}}\eta } \\ {S_{f,\xi }}\left( {\omega ,x} \right) = - \frac{{{\sigma ^2}}}{{\rm{\pi }}}{\rm{J}}_1^2\left( {A\beta '\omega x} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\int\limits_0^{ + \infty } {\frac{{{\rm{d}}R}}{{{\rm{d}}\eta }}\frac{{\sin \left( {\omega - {\omega _0}} \right)\eta }}{{\omega - {\omega _0}}}{{\rm{e}}^{{{\left( {\sigma \beta '\omega x} \right)}^2}\left[ {R\left( \eta \right) - 1} \right]}}{\rm{d}}\eta } \\ {S_{f,n}}\left( {\omega ,x} \right) = {A^2}{{\rm{e}}^{ - {{\left( {\sigma \beta '\omega x} \right)}^2}}}{\left[ {\frac{{{\rm{J}}_n^2\left( {nA\beta '\omega x} \right)}}{{nA\beta '\omega x}}} \right]^2} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\delta \left( {\omega - n{\omega _0}} \right) \end{array} \right. $ | (15) |
令噪声的相关系数为
| $ R\left( \eta \right) = \left( {1 - 2{\gamma ^2}{\eta ^2}} \right){{\rm{e}}^{ - {\gamma ^2}{\eta ^2}}} $ | (16) |
得
| $ \left\{ \begin{array}{l} {S_\xi }\left( {\omega ,x} \right) = - \frac{{{\sigma ^2}}}{{\rm{\pi }}}{\rm{J}}_0^2\left( {\frac{{A\beta \omega x}}{{c_0^2}}} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\int\limits_0^{ + \infty } {2{\gamma ^2}\eta \left( { - 3 + 2{\gamma ^2}{\eta ^2}} \right){{\rm{e}}^{ - {\gamma ^2}{\eta ^2}}}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\sin \left( {\omega \eta } \right)}}{\omega }{{\rm{e}}^{{{\left( {\sigma \beta \omega x/c_0^2} \right)}^2}\left[ {\left( {1 - 2{\gamma ^2}{\eta ^2}} \right){{\rm{e}}^{ - {\gamma ^2}{\eta ^2}}} - 1} \right]}}{\rm{d}}\eta \\ {S_{f,\xi }}\left( {\omega ,x} \right) = - \frac{{{\sigma ^2}}}{{\rm{\pi }}}{\rm{J}}_1^2\left( {\frac{{A\beta \omega x}}{{c_0^2}}} \right) \times \int\limits_0^{ + \infty } {2{\gamma ^2}\eta \left( { - 3 + } \right.} \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {2{\gamma ^2}{\eta ^2}} \right){{\rm{e}}^{ - {\gamma ^2}{\eta ^2}}} \times \frac{{\sin \left( {\left( {\omega - {\omega _0}} \right)\eta } \right)}}{{\omega - {\omega _0}}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{{\rm{e}}^{{{\left( {\sigma \beta \omega x/c_0^2} \right)}^2}\left[ {\left( {1 - 2{\gamma ^2}{\eta ^2}} \right){{\rm{e}}^{ - {\gamma ^2}{\eta ^2}}} - 1} \right]}}{\rm{d}}\eta \\ {S_{f,n}}\left( {\omega ,x} \right) = {A^2}{{\rm{e}}^{ - {{\left( {n\sigma \beta \omega x/c_0^2} \right)}^2}}}{\left[ {\frac{{{\rm{J}}_n^2\left( {n\sigma \beta \omega x/c_0^2} \right)}}{{n\sigma \beta \omega x/c_0^2}}} \right]^2} \cdot \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\delta \left( {\omega - n{\omega _0}} \right) \end{array} \right. $ | (17) |
假设单频波质点振速幅值A=0.2,频率f0=10 kHz,噪声的均方差σ=0.1,γ=1 000,如图 1所示相互作用过程中产生的新的频谱成分Sf, ξ(ω, x)。从图 1(a)可知在边界位置即距离声源0 m处,在10 kHz两侧声能量为0,随着距离的增加,在高频波两侧将出现两个边带,且边带能量随距离逐渐增大,如图中0.8 m和1.2 m,开始右侧峰大于左侧峰,随后幅度开始减小,左侧峰值大于右侧峰值。图中1.6 m处,传播距离不断增大,两峰逐渐趋向重合成为一个峰,且峰值在高频的左侧位置。图 1(b)表示噪声与单频波在非线性介质中传播时不同距离的能量变化的灰度图,从该图可以更容易得到上述结论。

|
图 1 不同距离噪声与单频波相互用产生的新频谱成分 Fig.1 The power spectrum of noise with monochromatic wave depending on distance |
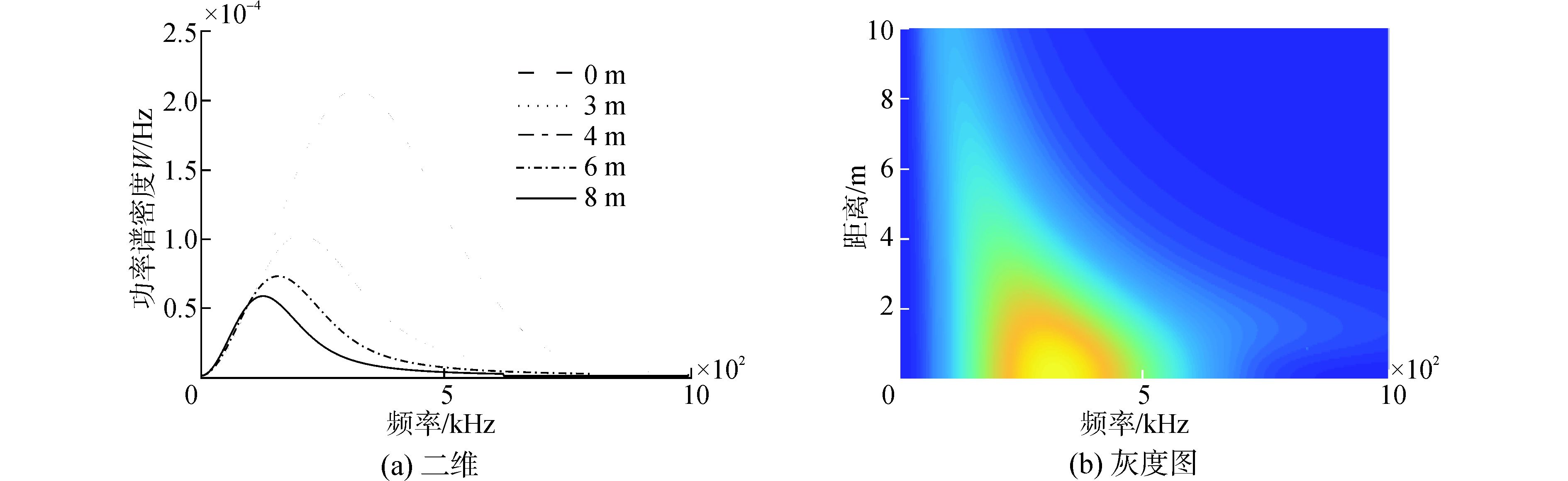
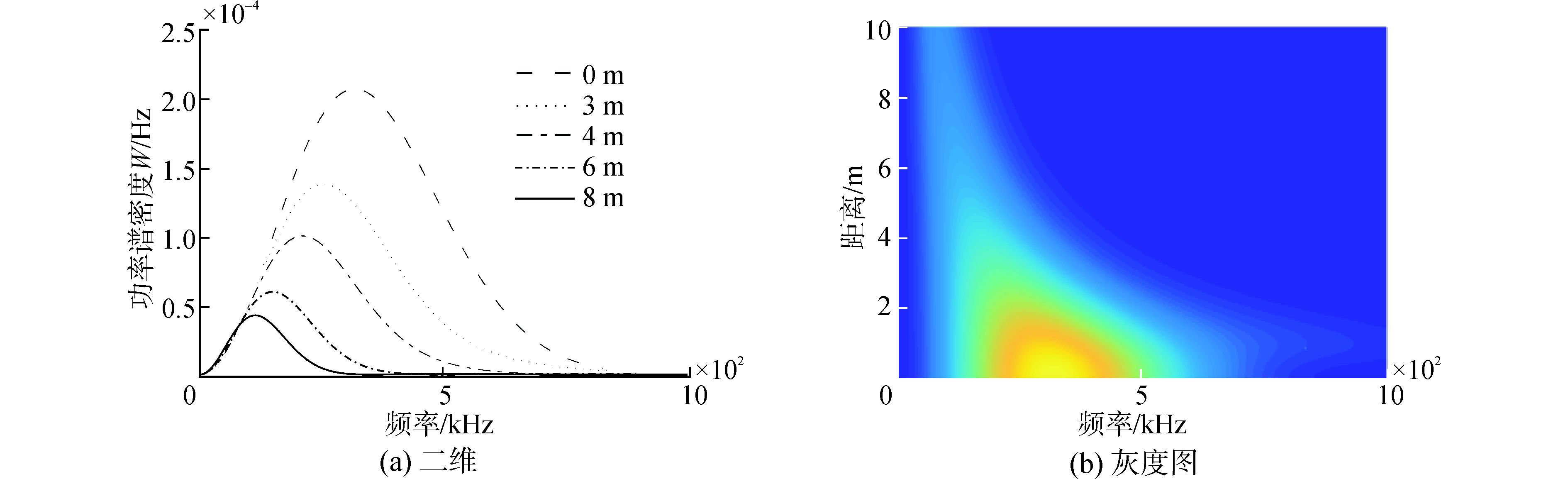
如果没有单频波,则令单频波质点振速幅值A=0,假设噪声的均方差σ=1,γ=1 000,仿真距离是0~10 m。其能量转移规律如图 2所示,有限振幅噪声在非线性介质中传播时能量一部分向高频转移,另有一部分向低频转移,对应于功率谱峰向低频移动,该现象是由于冲击波形成距离处传播速度不一致,导致间断面的重合造成的。图 3是有强高频波存在时噪声能量转移规律,当有强单频波存在时,噪声的能量转移效率被增强,相同距离能量向其他频率转换更多。
|
图 2 噪声与单频波相互作用的功率谱随距离变化(A=0) Fig.2 The power spectrum of noise with monochromatic wave depending on distance |
|
图 3 噪声与单频波相互作用产生新频谱成分(A=1) Fig.3 The power spectrum of noise with monochromatic wave depending on distance |
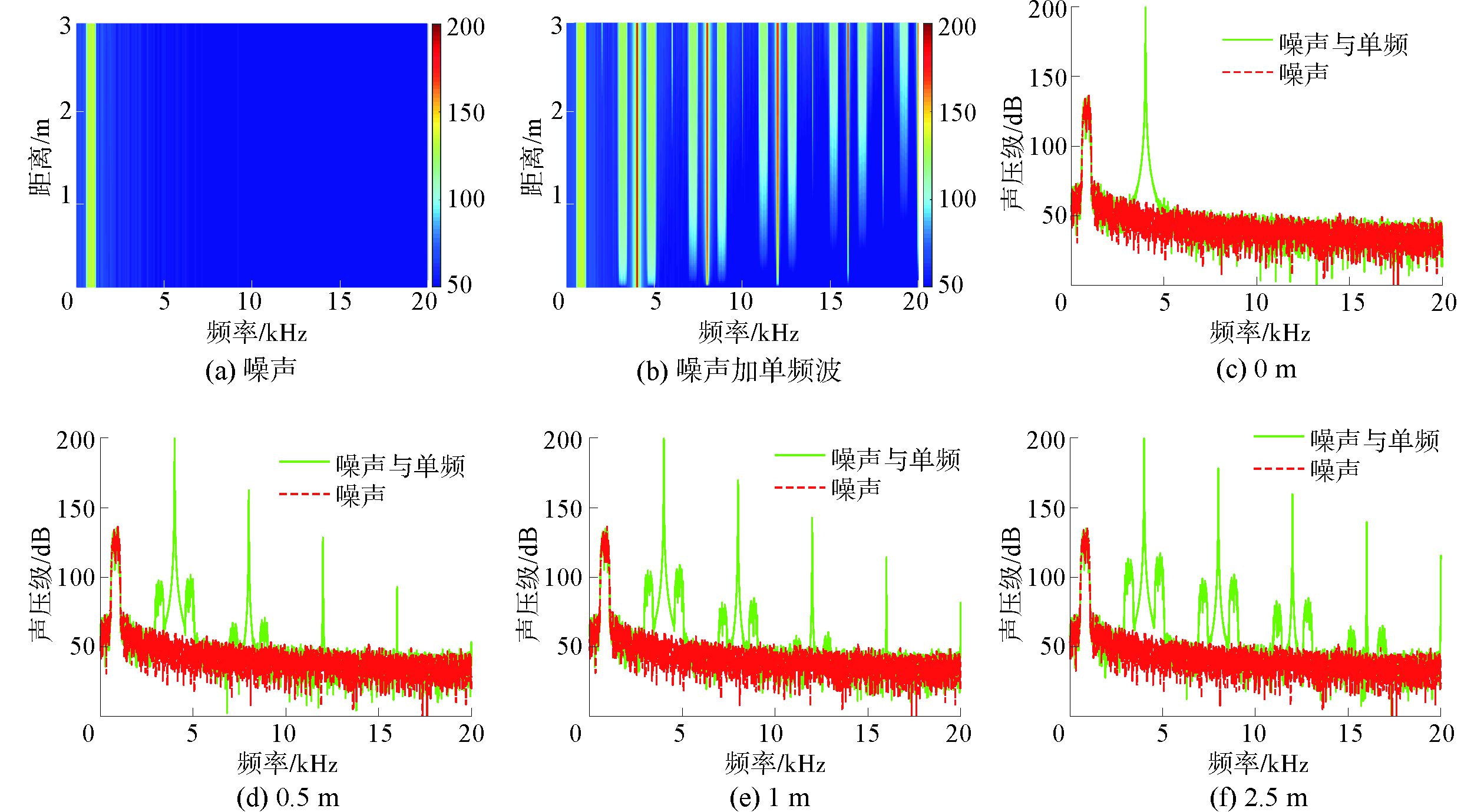
利用有限差分方法计算,边界条件的设置分别按照只有噪声及噪声叠加单频波两种情况,仿真时单频波是4 kHz,声源级200 dB,噪声是中心频率800 Hz带宽1/3倍频程的信号,噪声方差为单频波的1/100,此时高频频率相对于噪声频率高很多,仿真结果如图 4所示。图 4(a)是只有噪声情况下不同距离的功率谱,这种情况下的噪声能量不随距离改变,因为噪声幅度较小,非线性畸变较小。图 4(b)是加入强单频后的功率谱随距离的变化,结果表明噪声在加入强单频波后,在单频波频率及其倍频两侧出现了两谱峰,且随着距离的增大两谱峰也随之增大,这与上述理论推导结果一致。图 4(c)~(f)分别对应0、0.5、1和2.5 m的声信号功率谱,其中黑色表示只有噪声情况,灰色表示噪声和单频互作用的情况,这说明随距离的增长,强单频对噪声在频率上进行了调制。
|
图 4 单频波频率高于噪声频率情况下功率谱随距离变化 Fig.4 The power spectrum of noise with monochromatic wave depending on distance |
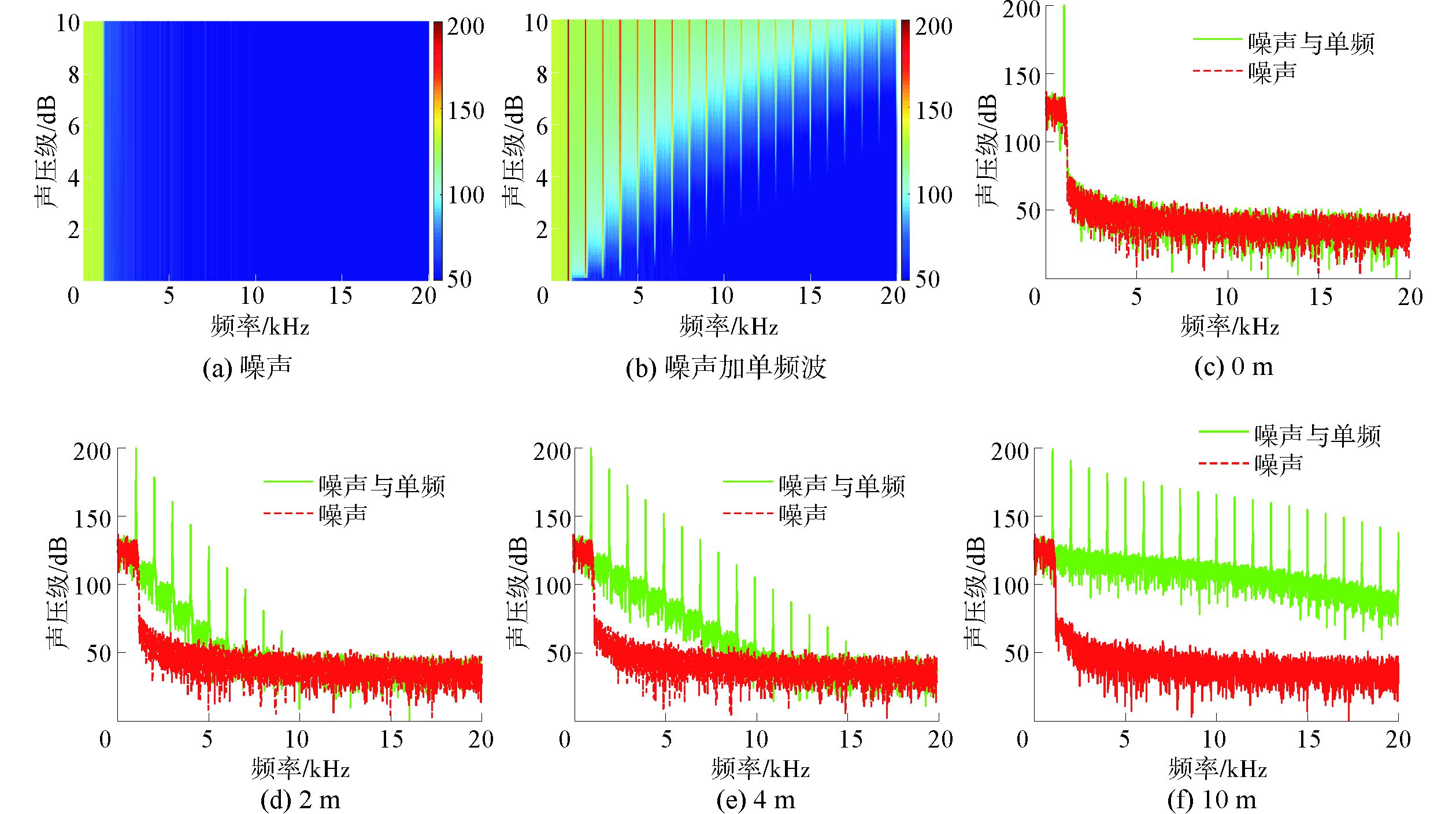
仿真时强单频波是1 kHz,声源级200 dB,噪声是0~1.1 kHz带宽信号,噪声方差为单频波幅度的1/100。此时强单频波频率在噪声频带内,如图 5所示。噪声在该介质中传播仍然没有非线性畸变,其功率谱不随距离变化;当加入单频波后,在高频部分同样出现较强的噪声,且随距离不断增大,噪声带宽不断增大,高频噪声级也随之增大,受高频及其倍频对噪声频谱的调制,原噪声演变为带宽更宽的连续噪声。
|
图 5 单频波频率在噪声频带内时功率谱随距离变化 Fig.5 The power spectrum of noise with monochromatic wave depending on distance |
上述仿真结果对应于噪声幅度较小的情况,噪声在传播过程中波形没有非线性畸变,当噪声幅度较大,其传播过程本身由于各阶频率之间的相互作用而发生能量转移。此时如果有强噪声存在,对原始噪声功率谱有何影响有待分析讨论,仿真时单频波是1 kHz,声源级200 dB,噪声是中心频率800 Hz带宽1/3倍频程的信号,噪声方差与单频波的幅度相等。如图 6(a)所示,无单频波存在时噪声本身在介质中传播会就有谐波产生。如图 6(b)所示,当有单频波存在时,在相同距离处噪声频带更宽,谐波位置处噪声级更大。说明强单频波的存在使得能量往高频噪声转移的效率更高,图 6(c)~(f)表明除了能量往高频成分转移外,由于噪声各频率成分之间的相互作用,产生了差频,能量有一部分转移到低频部分。

|
图 6 有限振幅噪声与单频波非线性互作用能量转移随距离变化 Fig.6 The power spectrum of finite-amplitude noise with monochromatic wave depending on distance |
1) 强高频波对弱低频随机噪声具有频率展宽和高频能量增强的效果,能量被分配至高频及其倍频的两侧;
2) 高频频率在噪声带宽内时其噪声能量被拓展至更高频率,形成带宽更宽的连续谱;
3) 如果噪声能量较强,则除噪声本身的非线性畸变引起的能量转移外,单频波也会使高频能量增加更快,说明该情况下噪声的能量转移效率更高。
| [1] |
HAMILTON M F, BLACKSTOCK D T. Nonlinear acoustics[M]. Pittsburge: Academic Press, 1998.
( 0) 0)
|
| [2] |
WEBSTER D A, BLACKSTOCK D T. Collinear interaction of noise with a finite-amplitude tone[J]. The journal of the acoustical society of america, 1978, 63(3): 687. DOI:10.1121/1.381795 ( 0) 0)
|
| [3] |
RUDENKO O V, CHIRKIN A S. Theory of nonlinear interaction between monochromatic and noise waves in weakly dispersive media[J]. Journal of experimental & theoretical physics, 1975, 40(5): 945. ( 0) 0)
|
| [4] |
RUDENKO O V. Interactions of intense noise waves[J]. Soviet physics uspekhi, 1986, 29(7): 620-641. DOI:10.1070/PU1986v029n07ABEH003460 ( 0) 0)
|
| [5] |
RUDENKO O V, SOLUYAN S I. Theoretical foundations of nonlinear acoustics[M]. Pittsburge: Springer-verlag Newyork Inc, 1977.
( 0) 0)
|
| [6] |
RUDENKO O V, GURBATOV S N, DEMIN I Y. Absorption of intense regular and noise waves in relaxing media[J]. Acoustical physics, 2014, 60(5): 499-505. DOI:10.1134/S106377101405011X ( 0) 0)
|
| [7] |
RUDENKO O V. Nonlinear interactions of regular and noise spectra in intense radiation from a piston in a linear medium[J]. Acoustical physics, 1998, 44(6): 717-721. ( 0) 0)
|
| [8] |
GURBATOV S N, RUDENKO O V, DEMIN I Y. Nonlinear propagation and decay of intense regular and random waves in relaxing media[J]. Recent developments in nonlinear acoustics, 2015, 10: 1685. ( 0) 0)
|
| [9] |
RUDENKO O V. Nonlinear integro-differential models for intense waves in media like biological tissues and geostruc-tures with complex internal relaxation-type dynamics[J]. Acoustical physics, 2014, 60(4): 398-404. DOI:10.1134/S1063771014040162 ( 0) 0)
|
| [10] |
杜功焕, 龚秀芬, 朱哲民. 有限振幅无规声波(噪声)非线性相互作用理论[J]. 声学学报, 1982(1): 3-9. DU Gonghuan, GONG Xiufen, ZHU Zhemin. The nonlinear interaction theory of finite amplitude random sound waves (noise)[J]. Acta acustica, 1982(1): 3-9. (  0) 0)
|
| [11] |
FENLON F H. An extension of the bessel-fubini series for a multiple frequency source of finite amplitude[J]. Journal of the acoustical society of America, 1972, 51(1A): 83. ( 0) 0)
|
| [12] |
FENLON F H. Derivation of the multiple frequency Bessel-Fubini series via Fourier analysis of the preshock time waveform[J]. The journal of the acoustical society of America, 2005, 53(6): 1752-1754. ( 0) 0)
|
| [13] |
杨森. 广义组合KdV-Burgers方程的差分格式[D]. 西安: 西安建筑科技大学, 2008. YANG Sen.The difference scheme of generalized combined KdV-burgers equation[D]. Xi'an:Xi'an University of Architecture and Technology, 2008. (  0) 0)
|
 2017, Vol. 38
2017, Vol. 38


