数据流上的频繁项集挖掘是数据挖掘中一个重要的研究问题,研究人员提出了大量的方法,例如Moment[1]等,可是数据流上的频繁项集挖掘存在两个限制:1)项在数据流中的权重没有被考虑;2)项在每条事务中的数量没有被考虑。因此,研究人员提出了“数据流上的高效用项集挖掘”。在数据流上的高效用项集挖掘中,数据流中的项与一外部效用(权重)关联,例如商品的单位利润;在数据流每条事务中项与一内部效用关联,例如商品的购买数量。如果项集在数据流中的效用不小于用户指定的阈值,则称为高效用项集。数据流上的高效用项集挖掘是指在数据流中寻找效用值不小于用户指定最小效用阈值的所有项集。数据流上的高效用项集挖掘在现实生活中应用广泛,例如消费者购物行为分析、web点击流分析和股票市场价格预测等。
在数据流的挖掘中,因数据流存在事务尺寸未知的特性,研究人员通常采用滑动窗口模型, 即指定窗口尺寸,限定窗口中事务的数量,在新数据到达时,移除窗口中时间上最早的数据。现有的基于滑动窗口挖掘数据流上高效用项集的方法通常包含两类:第一类采用与Apriori[2]相似的候选项集生成和测试框架,典型算法包括THUI-Mine[3]、MHUI-max[4]和MHUI-TID[5];第二类采用与FP-Growth[6]相似的模式增长方法,典型算法包括HUPMS[7]和SHU-Growth[8]。这些方法均采用两个阶段计算滑动窗口中的高效用项集,第一阶段生成候选项集,第二阶段校验生成候选项集。可是这些方法存在两个问题:1)第一阶段生成的候选项集数量巨大,消耗了大量的内存空间;2)计算第一阶段生成候选项集的真实效用耗时巨大。针对以上问题,本文提出一种新的数据结构HUIL-Tree (High Utility Itemset Tree which arranges items according to Lexicographic order)存储滑动窗口中的项集;并提出一种基于滑动窗口挖掘数据流高效用项集的有效算法HUISW;最后在真实和合成数据集模拟的数据流中进行了HUISW的实验评估。
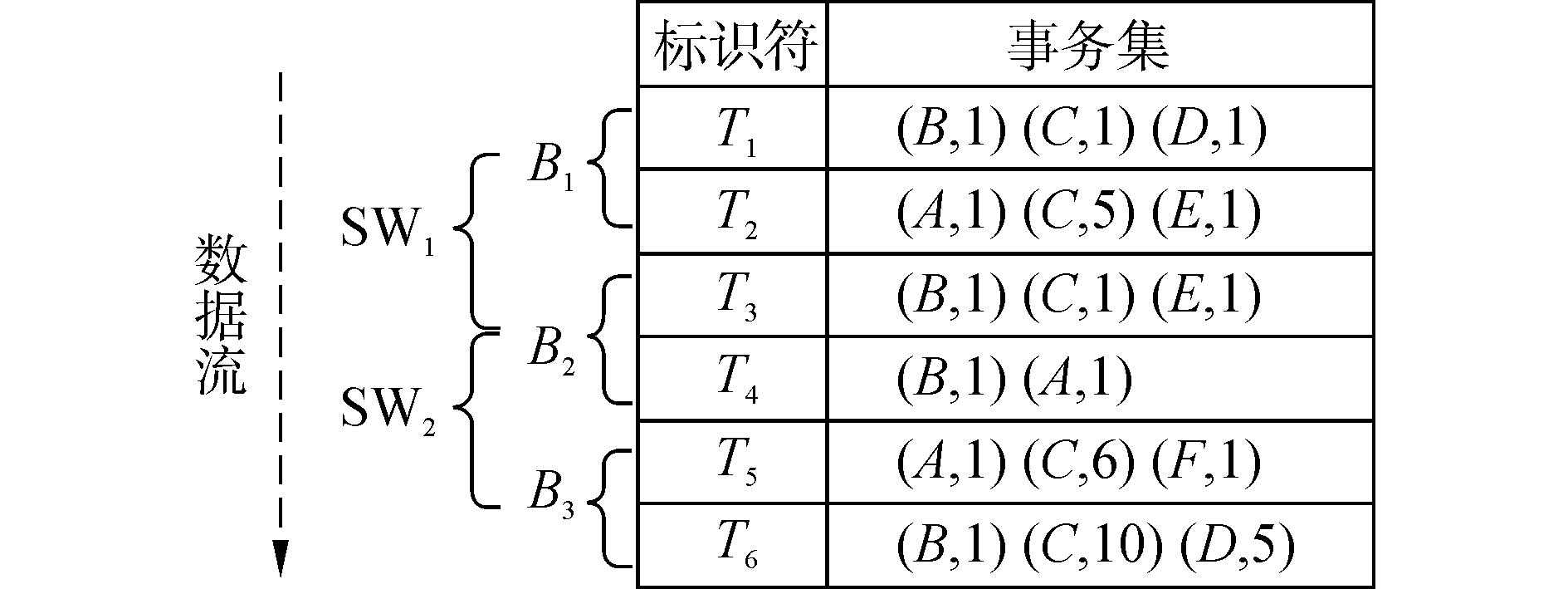
1 高效用项集相关定义及问题描述假定I={i1, i2, …, in}为包含n个不同项的集合,每个项ip (1≤p≤n)关联一个单位收益p(ip),这里称之为外部效用。若项集X={i1, i2, …, ik}由k个不同的项组成,其中ij ∈ I(1≤j≤k),则称k为项集X的长度。长度为k的项集称为k-项集。不失一般性,假定项集中的项按字母序排列,一个数据流DS ={T1, T2, …, T+∞}为一组事务的集合,DS中每条事务Td(1 ≤d<+∞)有唯一标识符d,称之为TID。事务Td中的任意项ip关联一数值q(ip, Td),例如ip在Td中的购买数量,称之为内部效用。假定数据流中的事务以批为单位到达,每个批数据Bk={T(k-1)n+1, T(k-1)n+2, …, Tkn} (1≤k<+∞)由时间上连续的n个事务组成。一个滑动窗口由m个时间上最近的批数据组成,m称为窗口尺寸,由winSize代表。如果滑动窗口中的第一个批数据为Bi (1≤i<+∞),则该滑动窗口为SWi={Bi, Bi+1, …, Bi+winSize-1}。例如,在图 1的数据流中存在3个批数据,每个批数据包含两条事务,即B1={T1, T2}、B2={T3, T4}和B3={T5, T6}。假定winSize =2,前两个批数据形成第一个滑动窗口SW1={B1, B2}。当第三个批数据到达时,时间上最早的批数据B1从滑动窗口移除,将B3添加到滑动窗口,新滑动窗口为SW2={B2, B3}。
|
Download:
|
| 图 1 在线销售数据流 Fig. 1 Online sale data stream | |
定义1(项在事务中的效用) 项ip在事务Td中的效用是指ip在Td中的内部效用与ip外部效用的乘积,形式化为u(ip, Td)=p(ip) × q(ip, Td)。
定义2(项集在事务中的效用) 项集X在事务Td中的效用是指X中每项在Td中的效用和,形式化为u(X, Td)=∑ip∈X∧X⊆Tdu(ip, Td)。
定义3(项集在滑动窗口中的效用) 项集X在滑动窗口SW中的效用是指X在SW所有包含X的事务中的效用和,u(X)=
例如,在图 1中项的单位利润为{(A, 5) (B, 2) (C, 1) (D, 4), (E, 3) (F, 1)},项B在T1中的效用u(B, T1)=2×1=2,项集{BC}在T1中的效用u({BC}, T1)=u(B, T1)+u(C, T1)=2+1=3。项集{BC}在SW1中的效用u({BC})=u({BC}, T1)+u({BC}, T3)=3+3=6。
定义4(高效用项集) 如果项集X在滑动窗口SW中的效用不小于用户指定的阈值,则称X为SW的高效用项集。
定义5(事务效用) 事务效用是指事务所包含的项在事务中的效用和,形式化为TU(Td)=
定义6(滑动窗口的效用) 滑动窗口SW的效用是指窗口中所包含事务的事务效用和,即为
例如,在图 1的数据流中T1的事务效用TU(T1) =u(B, T1) + u(C, T1) + u(D, T1) =7,滑动窗口SW1的效用为TU(T1) + TU(T2) + TU(T3) + TU(T4)=45。
AHMED等[9]提出,基于树结构的高效用项集挖掘算法采用分治法将搜索空间划分为若干子空间。假定(a1, a2, …, an)为树结构头表中的项,搜索空间可划分为如下子空间:
{an}的条件模式树;
{an-1}的条件模式树,树结构中不包含an;
…
{aj}的条件模式树,树结构中不包含集合{aj+1, aj+2, …, an}中任何一项(1≤j<n)。
从{aj}的条件模式树可以看出,树中所有的路径不包含集合{aj+1, aj+2, …, an}中任意一项。因此,ZIHAYAT等[10]提出“前缀效用”的概念,为项集在滑动窗口中的效用提供了一个上界。
定义7(项在事务中的前缀集) 假定事务中的项依据字母序排列,项ip在事务Td中的前缀集PrefixSet(ip, Td)由Td中ip及排在ip前面的项组成。
定义8(项在事务中的前缀效用) 项ip在事务Td中的前缀效用是指ip在Td前缀集中的所有项在Td中的效用和,形式化为PrefixUtil(ip, Td)=
定义9(项在滑动窗口中的前缀效用) 项ip在滑动窗口SW中的前缀效用是指ip在SW所有包含ip的事务中的前缀效用和,即为PrefixUtil(ip, SW)=
例如,在图 1的数据流中项C在T1中的前缀集为prefixSet(C, T1)={BC},前缀效用为PrefixUtil(C, T1)=u(B, T1)+u(C, T1)=2+1=3,在滑动窗口SW1中的前缀效用为PrefixUtil(C, SW1)=PrefixUtil(C, T1) + PrefixUtil(C, T2)+PrefixUtil(C, T3)=26。
问题描述:给定一个数据流DS,最小效用阈值min_util和滑动窗口尺寸winSize,基于滑动窗口的高效用项集挖掘是指在由DS连续不断生成的滑动窗口中寻找效用值不小于min_util的所有项集。不失一般性,对min_util使用效用数值描述算法,在实验中使用滑动窗口效用百分比进行算法评估。
2 在滑动窗口上挖掘高效用项集提出的HUISW由三个步骤组成:1)扫描滑动窗口中的事务,构建一棵HUIL-Tree和一个效用数据库,由滑动窗口中事务构建的HUIL-Tree和效用数据库称为全局HUIL-Tree和全局效用数据库;2)基于全局HUIL-Tree和全局效用数据库采用模式增长的方法计算滑动窗口中的高效用项集;3)当滑动窗口发生滑动时,在全局HUIL-Tree和全局效用数据库中将时间上最早的批数据移除,同时添加最新到达的批数据。其中第2、3步重复执行,直到没有新的批数据到达。
2.1 HUIL-Tree和效用数据库采用一个新的树结构HUIL-Tree和一个效用数据库存储滑动窗口中的项集及其效用信息。效用数据库是一个二维数组,长度为滑动窗口中所有项的最大尺寸,宽度为滑动窗口的尺寸。
定义10(HUIL-Tree) HUIL-Tree是满足下列条件的一个树结构。
1) 由一个根结点(标记为null)、项前缀子树集(作为根结点的子女)和一个头表组成。
2) 项前缀子树中的每个结点包括三个域:项标记、结点链接和事务指针数组。其中,结点链接是指连接树中具有相同项标记的下一个树结点,事务指针是指对效用数据库中事务的链接。
3) 头表中的每条记录包含三个域:项标记、项在滑动窗口中的前缀效用及指向树中第一个具有相同项标记的树结点的指针。
HUISW使用如下算法构建全局HUIL-Tree和全局效用数据库,整个过程仅需扫描滑动窗口一次。
输入:数据流第一个滑动窗口SW1
输出:全局HUIL-Tree Tree和全局效用数据库UDB
创建Tree的根结点R, 标记为null
初始化Tree的头表Header←ϕ
对SW1中的每条事务
依据字母序对项进行排序, 新事务为Trans
在UDB中为Trans分配一条记录Record
调用Insert_trans(Trans, R, Record, Header, Tree)
Insert_trans(Trans, R, Record, Header, Tree)
将Trans代表为[p|P], 其中p为第一项,P为剩余项组成的列表
如果树结点R不存在孩子结点N,使得N的项标记与p相同,则
创建一个新结点作为R的孩子结点
将p作为新结点的项标记
如果Header中不存在项标记为p的记录E,则
在Header中创建一个项标记为p的新记录E
将E依据字母序插入到Header中
初始化E中p在滑动窗口中的前缀效用
E.prefix_utility为0
将创建的新结点链接到由E出发的结点链接中
计算p在Trans中的效用p.utility
将p.utility存储在Record中
计算p在Trans中的前缀效用p.prefix_utility
将p.prefix_utility累积到E.prefix_utility
如果P为空
将Trans的事务标识符TID插入到N的事务指针数组中
否则
调用Insert_trans(P, N, Record, Header, Tree)
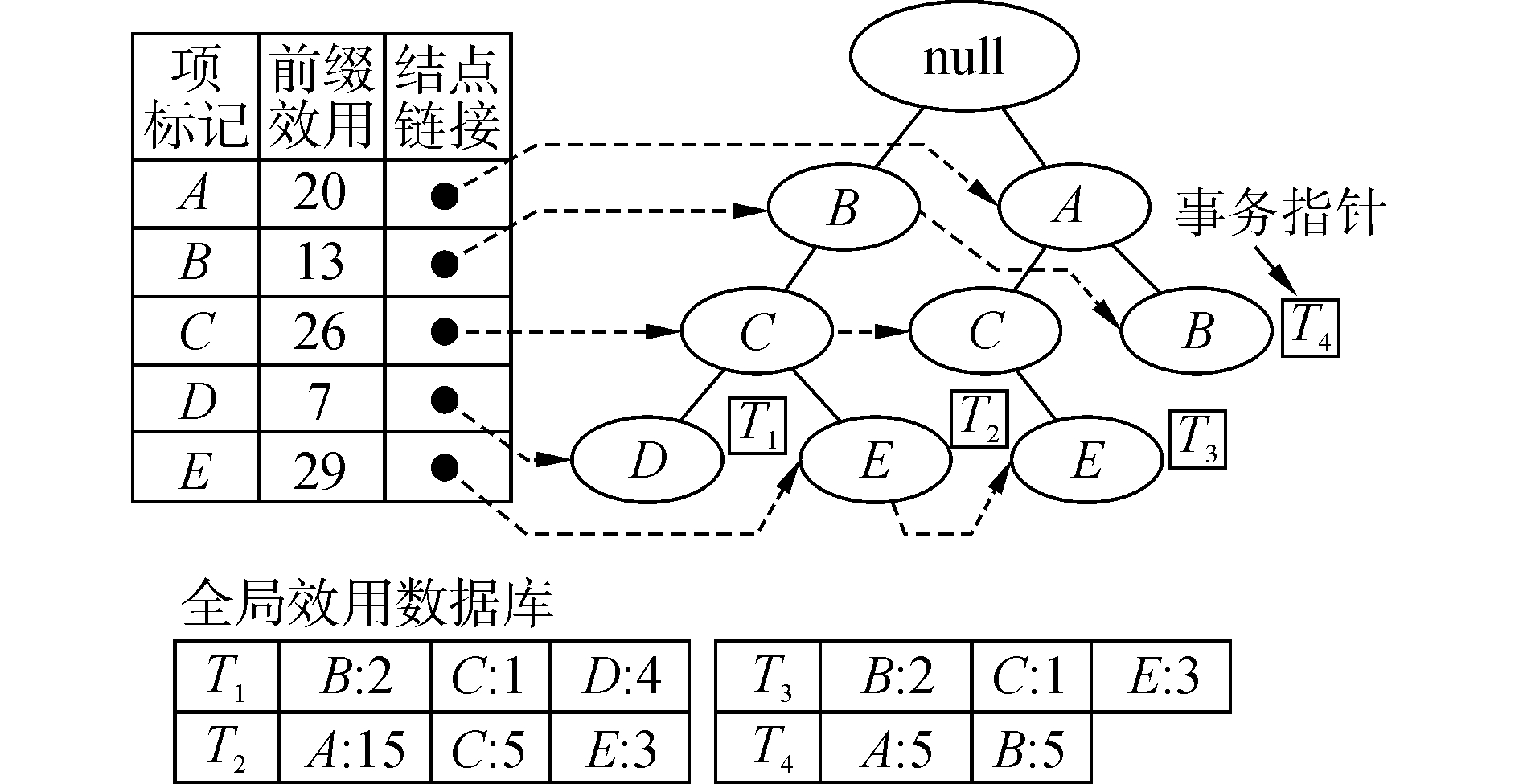
例如在图 1的滑动窗口SW1中,每条事务依据字母序排列。将第一条事务T1 ={(B, 1) (C, 1) (D, 1)}插入全局HUIL-Tree时,结点NB被首先创建(结点NB的项标记为B),计算项B在T1中的效用2×1=2,存储在全局效用数据库UDB的第一条记录中。在头表中添加项标记为B的记录,计算项B在T1中的前缀效用2,累计进入头表中项B在滑动窗口SW1中的前缀效用。对项C、项D执行相同操作,因项D为事务的最后一项,将事务标识符T1添加到ND结点的事务指针数组中。将SW1中所有事务插入到全局HUIL-Tree后,全局HUIL-Tree和全局效用数据库如图 2所示。
|
Download:
|
| 图 2 全局HUIL-Tree和全局效用数据库 Fig. 2 Global HUIL-Tree and global utility database | |
注意在全局效用数据库中为了表明项标记与项在事务中效用的对应关系,本文将项标记列示在全局效用数据库中。而在算法的实现中,为了减少内存消耗,在全局效用数据库和挖掘过程中创建的条件效用数据库中仅保存项在事务中效用,故在图 2的全局效用数据库中,项标记以50%透明度表示。
与CanTree[12]类似,HUIL-Tree采用字母序排列树结点,是因为在采用字母序排列的树结构中,项序不会受到滑动窗口发生滑动的影响。
2.2 挖掘方法HUISW在全局HUIL-Tree和全局效用数据库构建完成后,HUISW采用模式增长的方式挖掘滑动窗口中的高效用项集,全局HUIL-Tree头表采用自底向上的遍历顺序。ZIHAYAT等指出,项在滑动窗口中的前缀效用具有向下闭合属性,并提出了引理1[10]。
引理1 假定在滑动窗口SW的每条事务中,项依据字母序排列,X为一非空项集,ip为X的最后一项,则ip在SW中的前缀效用不小于X在SW中的效用,即PrefixUtil(ip, SW) ≥ u(X)。(证明过程参见文献[10])
引理1表明在HUIL-Tree头表的遍历过程中,如果头表中项ip在滑动窗口中的前缀效用小于min_util,则以ip为最后一项的所有项集均不可能为高效用项集。即无需构建{ip}的条件模式树。因此,HUIL-Tree头表中项在滑动窗口中的前缀效用可用于修剪搜索空间。
如果头表中项ip在滑动窗口中的前缀效用不小于min_util,则HUISW包含四个步骤计算以ip为最后一项项集的效用。1)通过遍历全局HUIL-Tree中与ip相关的路径,生成{ip}的条件模式库;2)基于{ip}条件模式库中的信息构建{ip}的条件模式树及{ip}的条件效用数据库;3)在{ip}的条件模式树和条件效用数据库中,递归地挖掘以ip为最后一项的高效用项集;4)更新全局HUIL-Tree和全局效用数据库中与项ip相关的信息。
1) 生成条件模式库。如果全局HUIL-Tree头表中的项ip (1≤p≤n)在滑动窗口中的前缀效用不小于min_util,则首先计算1-项集{ip}的效用,然后按如下方式构建{ip}的条件模式库:①遍历头表中由项标记为ip的记录出发的结点链接,收集结点链接上的树结点;②由①中的树结点到全局HUIL-Tree根结点形成路径所代表的项集,形成{ip}的条件模式库;③依据①中树结点的事务指针数组,从全局效用数据库收集②中路径所有项在事务中的效用,载入{ip}的条件模式库。
例如,在图 2的全局HUIL-Tree和全局效用数据库中,因项E在滑动窗口中的前缀效用29不小于min_util=18,计算1-项集{E}的效用3 + 3=6,可知{E}为低效用项集。遍历头表中由项标记E出发的结点链接队列,获得两条路径A→C→E和B→C→E。同时依据项标记为E的树结点的事务指针数组,即T2和T3,获得路径中的项在事务中的效用,进而形成{E}的条件模式库如表 1第二列所示。注意在{E}的条件模式库中采用一种新的形式“[项,项在事务中的效用]”替代原数据库中的“(项,项在事务中的内部效用)”。
| 表 1 数据流中商品的单位利润 Tab.1 Unit price of items in data stream |
2) 构建一棵条件HUIL-Tree。{ip}的条件HUIL-Tree的构建需要二次扫描{ip}的条件模式库,在条件模式树的构建中HUISW采用“项集的事务权重值”高估项集在滑动窗口中的效用。
定义11(项集的事务权重值) 项集X的事务权重值是指滑动窗口SW中所有包含X的事务的事务效用和,即TWU(X)=
很明显,在滑动窗口中TWU(X) ≥ u(X)。同时TWU(X)满足向下闭合属性,即如果项集Y是X的子集,则在滑动窗口中TWU(Y) ≥ TWU(X)。因此,项集的事务权重值可用于修剪搜索空间。
在对{ip}条件模式库的第一次扫描中,累积{ip}条件模式库中单项的事务权重值。第一次扫描结束后,事务权重值小于min_util的项组成的集合由S代表。由于S中的项及其超集均不可能为高效用项集,所以在第二次扫描中对每条事务移除S中的项。对移除所有S中的项的事务,称之为修订事务。HUISW对{ip}条件模式库中的修订事务采用与全局树相似的方式构建{ip}的条件模式树和{ip}的条件效用数据库,{ip}的条件模式树与全局HUIL-Tree存在两点不同:1){ip}条件模式树的根结点标记为{ip},即条件项集;2)对{ip}条件模式树头表中的项iq,条件项集{ip}在包含iq的所有事务中的效用需要累积进入头表iq在滑动窗口中的前缀效用。与全局效用数据库相比,条件效用数据库需要在每条事务中保留条件项集的效用。
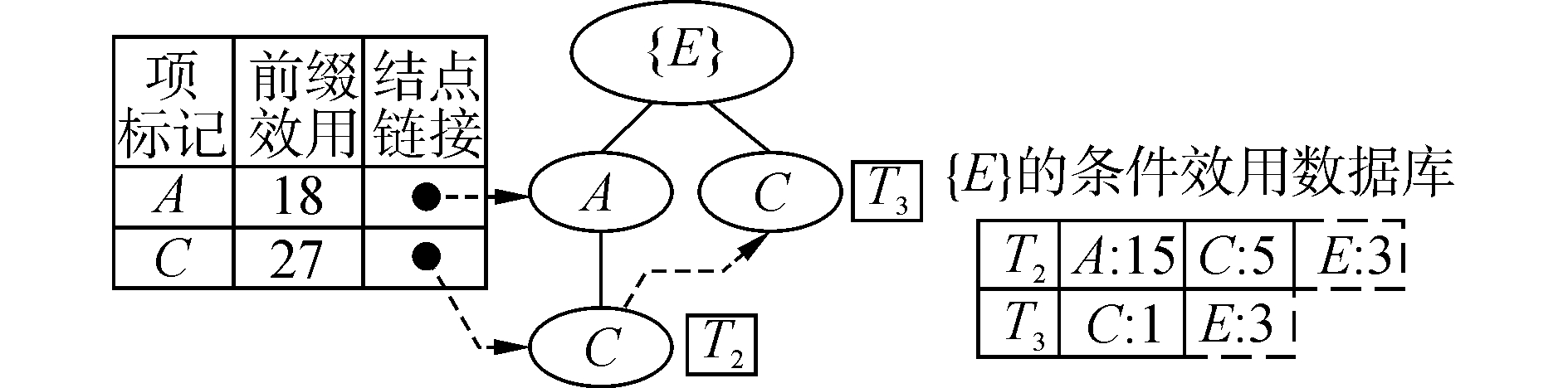
例如,在{E}的条件模式库中(表 1),单项的事务权重值为{(A: 23), (B: 6), (C: 29)},其中“:”后面的数字代表单项的事务权重值。项B的事务权重值小于min_util=18,因此项B需要从{E}条件模式库的每条事务中移除。完成修订后,{E}的条件模式库如表 1第三列所示。创建{E}条件模式树的根结点,标记为{E}。依据字母序对第一次扫描中事务权重值不小于min_util的项排序(A, C),然后插入到{E}的条件模式树的头表中。在对{E}条件模式库的第二次扫描中,第一条修订事务T2={(A, 1) (C, 1)}形成第一条分支,附着在{E}条件模式树的根结点,树结点NC的事务指针设置为T2。项A和项C在事务T2中的效用存储在{E}的条件效用数据库的第一条记录中。项A在T2中的前缀效用与条件项集{E}在T2中的效用和为15+3=18,累积进入项A在{E}条件模式树头表中的前缀效用,对项C在头表中的前缀效用以相同的方式计算。在插入第二条修订事务之后,{E}的条件模式树及{E}的条件效用数据库如图 3所示。
|
Download:
|
| 图 3 {E}的条件模式树和条件效用数据库 Fig. 3 {E}s conditional pattern tree and conditional utility database | |
3) 挖掘条件模式树和条件效用数据库的高效用项集。从条件模式树和条件效用数据库中挖掘高效用项集与从全局树和全局效用数据库中挖掘高效用项集包含相同的步骤,即如果头表中iq的前缀效用不小于min_util,则首先计算由条件项集联接iq组成的新项集X在滑动窗口中的效用,然后生成X的条件模式库,构建X的条件模式树和X的条件效用数据库,最后迭代地挖掘X的条件模式树和条件效用数据库。
例如,在{E}的条件模式树中(图 3),项C在头表中的效用27不小于min_util=18,计算项集{CE}的效用为(5+3)+(1 + 3)=12,可以得出{CE}为低效用项集。然后构建{CE}的条件模式树及{CE}的条件效用数据库,如图 4所示。在{CE}的条件模式树中,项A在头表中的效用23不小于min_util=18,计算项集{ACE}的效用为23,可以得出{ACE}为高效用项集。在{E}的条件模式树中,当完成所有包含项C项集的效用计算后,需要对{E}的条件模式树和条件效用数据库进行更新。继续遍历{E}条件模式树的头表,项A在头表中的效用18不小于min_util,计算项集{AE}的效用为15+3=18,可知{AE}为高效用项集。

|
Download:
|
| 图 4 {CE}的条件模式树和条件效用数据库 Fig. 4 {CE}s conditional pattern tree and conditional utility database | |
4) 更新全局HUIL-Tree。当完成包含ip所有项集的效用计算后,HUISW需要更新全局HUIL-Tree,实现以头表中后续遍历项为最后一项项集效用的计算。全局HUIL-Tree的更新方式如下:在全局HUIL-Tree中所有项标记为ip的树结点将其事务指针数组中的事务标识符传递给其在全局HUIL-Tree中的父结点。如果其父结点的事务指针数组不空,则将事务指针数组中的事务标识符合并到其父结点的事务指针数组中。例如,在图 2的全局HUIL-Tree中,当完成对包含项E项集的效用计算时,对全局HUIL-Tree的更新如图 5所示。

|
Download:
|
| 图 5 全局HUIL-Tree中项E的更新过程 Fig. 5 Updating process of item E in global HUIL-Tree | |
基于以上的分析,HUISW采用如下算法挖掘滑动窗口中的高效用项集。该算法为一个迭代程序,首次调用的输入参数为全局HUIL-Tree和全局效用数据库,项集X为空集。
输入:一棵HUIL-Tree Tree、效用数据库UDB、最小效用阈值min_util和条件项集X
输出:滑动窗口中的高效用项集
对Tree头表中的项ip,执行
如果ip在头表中的前缀效用不小于min_util
计算项集Y=X ∪{ip}在滑动窗口中的效用u(Y)
如果u(Y)≥min_util,则
输出高效用项集Y
生成Y的条件模式库
修剪Y的条件模式库中事务权重值小于min_util的项
构建Y的条件模式树Tree′及条件效用数据库UDB′
如果Tree′不为空,则
调用HUISW(Tree′, UDB′, min_util, Y)
更新Tree及UDB中与ip相关的信息
2.3 窗口发生滑动对数据结构的更新当完成对滑动窗口中高效用项集的挖掘后,滑动窗口发生滑动。在滑动窗口中移除时间上最早的批数据,同时添加新到达的批数据。HUISW在全局HUIL-Tree中维护一个指针数组,指向滑动窗口中每条事务最后一项在全局HUIL-Tree中对应的树结点,HUISW采用如下算法完成全局HUIL-Tree和全局效用数据库的更新。
输入:全局HUIL-Tree Tree、全局效用数据库UDB、一个批数据Bi
输出:全局HUIL-Tree Tree′、全局效用数据库UDB′
如果批数据的标识符i>winSize,则
对Bi-winSize中的每条事务Trans,执行
找到Trans最后一项在树中对应的结点
在树结点的事务指针数组中移除Trans的标识符
如果树结点的事务指针数组为空,同时为叶子,则
删除该树结点
递归删除满足line 05中条件的父结点
在头表中移除Trans中各项在Trans中的前缀效用
在UDB中移除存储Trans中各项效用的记录
对Bi中的每条事务,执行
插入事务的子程序
返回全局HUIL-Tree和全局效用数据库
例如,在图 1中当滑动窗口SW1发生滑动时,B1需要从滑动窗口中移除,B3需要添加到滑动窗口中。对B1中的事务如T1,找到T1最后一项D在全局HUIL-Tree中对应的结点ND,在其事务指针数组中移除事务标识符T1。因ND的事务指针数组为空,同时ND为叶子结点,删除ND然后校验父结点NC是否满足上述条件。NC为非叶子结点,故停止删除树结点,在头表中移除项B、C和D在T1中的前缀效用2、3和7,最后移除UDB中第一条记录。当滑动窗口完成由SW1到SW2的更新后,全局HUIL-Tree和全局效用数据库如图 6所示。

|
Download:
|
| 图 6 由SW2生成的全局HUIL-Tree Fig. 6 Global HUIL-Tree generated from SW2 | |
对提出的HUISW算法进行性能评估,从文献[8]的实验中可以看出,基于模式增长的滑动窗口高效用项集挖掘算法性能优于基于Apriori的算法,SHU-Growth为当前最好的基于模式增长的算法。因此,本文选择将HUISW与SHU-Growth进行比较,以运行时间和内存使用峰值作为评估标准。两个算法均由C++语言实现,采用g++编译,执行环境为基于2.93 GHz Intel双核处理器和4G内存的戴尔台式机,操作系统ubuntu 12.04。
实验选取了3个数据集(网站http:///fimi.ua.ac.be/)(Mushroom、Retail和T10I4D100K)模拟流数据,因数据集中未包含项的外部效用及项在事务中的内部效用,采用文献[12-13]中的性能评估方法:1)将数据集中所有项的外部效用按对数正态分布生成0.01~10的随机数,2)项的内部效用按1~10的均匀分布随机生成,选用的数据集特性如表 2所示。
| 表 2 数据集特性 Tab.2 Characteristics of datasets |
在mushroom模拟的数据流中,每个批数据的事务数量设置为400,窗口尺寸设置为10,则整个数据流产生11个窗口。图 7展示了HUISW和SHU-Growth的运行时间及内存使用峰值,从图 7(a)中可以看出,HUISW的运行时间比SHU-Growth提升两个数量级。例如在min_util=16%时,HUISW和SHU-Growth的运行时间分别为0.4 s和448 s。从图 7(b)中可以看出,HUISW的内存使用峰值远小于SHU-Growth。例如在min_util=20%时,HUISW和SHU-Growth的内存使用峰值分别为3.1 MB和11.9 MB。

|
Download:
|
| 图 7 Mushroom数据流上的实验结果 Fig. 7 Experimental results on mushroom data stream | |
在retail模拟的数据流中,每个批数据的事务数量设置为5 000,窗口尺寸设置为8,则整个数据流产生11个窗口。图 8展示了两个算法的运行时间及内存使用峰值,从图 8(a)中可以看出,HUISW的运行时间比SHU-Growth提升一个数量级。例如在min_util=0.08%时,SHU-Growth的运行时间是HUISW的31.3倍。从图 8(b)中可以看出,HUISW和SHU-Growth的内存使用峰值均比较稳定,HUISW的内存使用峰值远小于SHU-Growth。例如在min_util=0.08%时,SHU-Growth的内存使用峰值为HUISW的4.4倍。

|
Download:
|
| 图 8 Retail数据流上的实验结果 Fig. 8 Experimental results on retail data stream | |
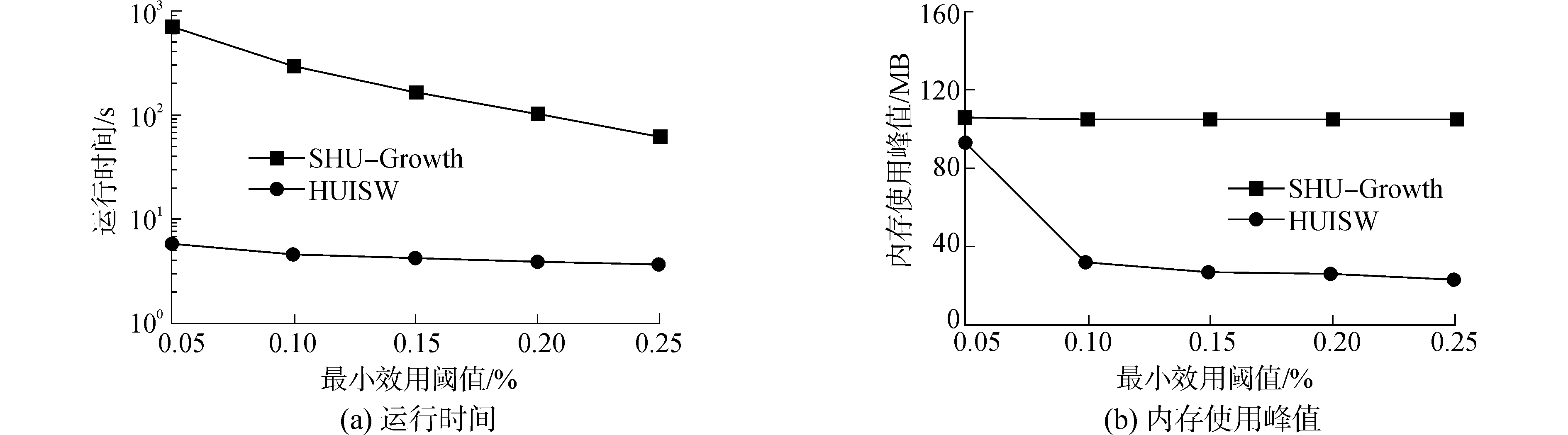
在T10I4D100K模拟的数据流中,每个批数据的事务数量设置为5 000,窗口尺寸设置为8,则整个数据流产生13个窗口。图 9展示了两个算法的运行时间及内存使用峰值,从图 9(a)中可以看出,随着min_util的减少,两个算法的运行时间逐渐增加,同时两个算法的运行时间差距逐渐增大。例如在min_util=0.25%时,HUISW的运行时间为SHU-Growth的1/20,当min_util减少至0.05%时,HUISW的运行时间仅为SHU-Growth的1/100。从图 9(b)中可以看出,SHU-Growth的内存使用峰值比较稳定,而HUISW的内存使用峰值随着min_util的减少快速增长。例如当min_util由0.1%减少至0.05%时,HUISW的内存使用峰值增加了近2倍。这是由于随着min_util的减少,HUISW需要构建更多的条件模式树及条件效用数据库,而在稀疏数据流T10I4D100K中,由于事务在HUIL-Tree中的压缩率低,事务的同一项及其在事务中的效用需要在多个条件模式树及条件效用数据库中重复存储,导致内存使用峰值的快速增长。
|
Download:
|
| 图 9 T10I4D100K数据流上的实验结果 Fig. 9 Experimental results on T10I4D100K data stream | |
从以上实验可以看出,HUISW显著优于SHU-Growth。这是由于SHU-Growth首先计算高效用项集候选项集,然后计算候选项集的真实效用。表 3~5展示了在三个数据流所有滑动窗口中候选项集及高效用项集的数量。从图 7~9和表 3~5可以看出,随着候选项集的增加,算法的运行时间和内存消耗成比例增长。从表 3~5可以看出,在多数情况下候选项集的数量远超于高效用项集。而在HUISW中,项集在窗口中的效用可通过HUIL-Tree和效用数据库直接计算,避免了候选项集的生成及对候选项集真实效用的计算。与稀疏数据流相比,稠密数据流中的事务能够有效压缩进入HUIL-Tree,同时条件数据库中的事务可进一步压缩进入条件HUIL-Tree,因此在挖掘过程中HUISW的性能提升明显,与SHU-Growth相比在稠密数据流中HUISW最快可提升两个数量级。
| 表 3 Mushroom数据流上候选项集及高效用项集数量 Tab.3 Number of candidates and high utility itemsets over Mushroom |
| 表 4 Retail数据流上候选项集及高效用项集数量 Tab.4 Number of candidates and high utility itemsets over Retail |
| 表 5 T10I4D100K数据流上候选项集及高效用项集数量 Tab.5 Number of candidates and high utility itemsets over T10I4D100K |
1) 提出一个新的树结构HUIL-Tree和一个在滑动窗口中挖掘高效用项集的有效算法HUISW,HUISW采用HUIL-Tree和效用数据库,维护滑动窗口中的项集及其效用信息,在搜索空间的遍历中,对每个项集直接计算其在滑动窗口中的效用,避免了同类算法候选项集的生成。
2) 对HUISW和同类算法SHU-Growth进行了实验评估,在真实和合成数据集模拟的数据流上进行了实验,实验结果表明HUISW的性能显著优于SHU-Growth,在稠密数据流中HUISW的运行时间最快比SHU-Growth提升两个数量级,同时使用更少的内存。
| [1] |
CHI Yun, WANG Haixun, YU P S, et al. Moment: maintaining closed frequent itemsets over a stream sliding Window[C]//Proceedings of the 4th IEEE International Conference on Data Mining. Brighton, UK: IEEE, 2004: 59-66. http://doi.ieeecomputersociety.org/10.1109/ICDM.2004.10084
(  0) 0)
|
| [2] |
AGRAWAL R, SRIKANT R. Fast algorithms for mining association rules in large databases[C]//Proceedings of the 20th International Conference on Very Large Data Bases. San Francisco, CA: Morgan Kaufmann Press, 1994: 487-499. http://dl.acm.org/citation.cfm?id=672836
(  0) 0)
|
| [3] |
CHU C J, TSENG V S, LIANG T. An efficient algorithm for mining temporal high utility itemsets from data streams[J]. Journal of systems and software, 2008, 81(7): 1105-1117. DOI:10.1016/j.jss.2007.07.026 (  0) 0)
|
| [4] |
LI Huafu. MHUI-max:an efficient algorithm for discovering high-utility itemsets from data streams[J]. Journal of information science, 2011, 37(5): 532-545. DOI:10.1177/0165551511416436 (  0) 0)
|
| [5] |
LI Huafu, HUANG H Y, CHEN Yicheng, et al. Fast and memory efficient mining of high utility itemsets in data streams[C]//Proceedings of the 8th IEEE International Conference on Data Mining. Pisa, Italy: IEEE, 2008: 881-886. http://dl.acm.org/citation.cfm?id=1511323
(  0) 0)
|
| [6] |
HAN Jiawei, PEI Jian, YIN Yiwen. Mining frequent patterns without candidate generation[C]//Proceedings of 2000 ACM SIGMOD International Conference on Management of Data. Dallas, Texas, USA: ACM, 2000: 1-12. http://dl.acm.org/citation.cfm?id=335372
(  0) 0)
|
| [7] |
AHMED C F, TANBEER S K, JEONG B S, et al. Interactive mining of high utility patterns over data streams[J]. Expert systems with applications, 2012, 39(15): 11979-11991. DOI:10.1016/j.eswa.2012.03.062 (  0) 0)
|
| [8] |
RYANG H, YUN U. High utility pattern mining over data streams with sliding window technique[J]. Expert systems with applications, 2016, 57: 214-231. DOI:10.1016/j.eswa.2016.03.001 (  0) 0)
|
| [9] |
AHMED C F, TANBEER S K, JEONG B S, et al. Efficient tree structures for high utility pattern mining in incremental databases[J]. IEEE transactions on knowledge and data engineering, 2009, 21(12): 1708-1721. DOI:10.1109/TKDE.2009.46 (  0) 0)
|
| [10] |
ZIHAYAT M, AN Aijun. Mining top-k high utility patterns over data streams[J]. Information sciences, 2014, 285: 138-161. DOI:10.1016/j.ins.2014.01.045 (  0) 0)
|
| [11] |
LEUNG C K S, KHAN Q I, LI Zhan, et al. CanTree:a canonical-order tree for incremental frequent-pattern mining[J]. Knowledge and information systems, 2007, 11(3): 287-311. DOI:10.1007/s10115-006-0032-8 (  0) 0)
|
| [12] |
LIU Ying, LIAO Weikeng, CHOUDHARY A. A two-phase algorithm for fast discovery of high utility itemsets[C]//Proceedings of the 9th Pacific-Asia Conference on Advances in Knowledge Discovery and Data Mining. Hanoi, Vietnam: Springer, 2005: 689-695. http://www.springerlink.com/content/l9dk2l8d0y388ad0/
(  0) 0)
|
| [13] |
LIU Mengchi, QU Junfeng. Mining high utility itemsets without candidate generation[C]//Proceedings of the 21st ACM International Conference on Information and Knowledge Management. Maui, Hawaii, USA: ACM, 2012: 55-64. http://www.researchgate.net/publication/262369808_Mining_high_utility_itemsets_without_candidate_generation?ev=auth_pub
(  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


