2. 河南工业大学 电气工程学院, 河南 郑州 450001;
3. 哈尔滨工程大学 自动化学院, 黑龙江 哈尔滨 150001
2. College of Electrical Engineering, Henan University of Technology, Zhengzhou 450001, China;
3. College of Automation, Harbin Engineering University, Harbin 150001, China
柔性关节机械臂的轨迹跟踪控制问题在过去几年中得到了高度重视[1-9]。工业机器人的谐波传动系统都不可避免的存在柔性环节,当系统需要快速响应时,就会造成明显的扭转震颤。同时,弹性环节存在于机械臂系统的减速箱、传送带、连接腱等诸多构件当中,适用于刚性机械臂的成熟控制算法应用于含有弹性环节的动态系统中时,其响应速度和动态精度都会受到很大限制。因此,机械臂关节系统中弹性环节的动态特性在机械臂的建模与控制问题中都是不可或缺的[1-6]。柔性关节的引入增加了机械臂动力学系统的复杂性,系统阶次变成了相同连杆数量机械臂系统的两倍,系统输出自由度的数量超过了控制输入的数量,给控制系统的设计带来了新的挑战[7-10]。
鉴于此,国内外学者提出了各种控制策略来解决柔性关节为机械臂控制带来的问题。例如反馈线性化[3, 11-12]、基于无源性理论的控制方法[13-14]、奇异扰动控制策略[15]、反步法[15-17]、自适应控制[18-20]等。以上文献中提出的方法存在如下几个方面的问题。首先,系统对于广义干扰的鲁棒性是以干扰上界已知为前提,控制策略具有较高的保守性。其次,控制策略要求柔性关节机械臂系统的全部状态已知。众所周知,工业机械臂传动系统机构设计非常紧凑,在狭小的空间内为伺服电机传动轴和关节末端同时安装角度传感器和速度传感器,不仅提高了设计成本,而且增加了工程设计难度[1-2, 6, 10]。同时,一些速度传感器由于本身设计机理的原因,其抗噪性不能满足复杂工业现场的要求[11, 20-21]。因此,从经济适用性和物理约束两个方面综合考虑,无速度传感器的柔性关节机械臂控制系统具有更高的研究价值。
近年来,一些学者研究了基于观测器的输出跟踪控制问题[3, 12, 22-25]。文献[17]针对一类非线性动态系统,结合反步法与小增益定理,提出了一种自适应鲁棒模糊输出跟踪控制策略;Lightcap等[26]设计了扩展卡尔曼滤波器对柔性关节机械臂进行状态估计;文献[27]设计了柔性关节系统的反步控制器,利用自适应神经网络对柔性关节机械臂进行状态估计;文献[28]针对含有参数不确定性和外界干扰的柔性关节机械臂系统设计了滑模鲁棒观测器,并且可以扩展到一般形式的系统状态方程中去。上述文献所提出的方法虽解决了部分状态可测条件下的柔性关节系统的输出跟踪问题,但在控制器设计方面大多仅设计了基于反馈回路的鲁棒控制策略来解决模型不确定性抑或外界干扰对柔性关节机械臂轨迹跟踪问题带来的影响。
此外,对于机械臂系统的跟踪控制而言,伺服电机的减速器以及机械臂的外部传动系统等部件会不可避免地将非线性摩擦环节引入控制系统当中[29-32],为柔性关节机械臂的高精度控制带来更大的挑战。在控制器策略的设计中,如果不能精确地、恰当地对系统的非线性摩擦进行补偿,那么在系统控制中,尤其对机械臂的低速控制问题,将不可避免的出现较大的跟踪误差和粘滑运动[29-30]。因此,为了对潜在的非线性摩擦进行补偿,学者们建立了多种摩擦环节的数学模型[31-32]。其中,LuGre模型由于其结构简易同时能对多种摩擦特性进行模拟而被广泛使用。但是,LuGre摩擦模型在工程实践当中也存在着诸多不足。首先,在控制器设计当中使用LuGre模型,要单独设计估计器对鬃毛形变状态变量进行估计。当同时考虑模型不确定性时,控制器的一体化设计目的很难达到。其次,在高速情况下,LuGre模型急剧增加的摩擦刚性会为控制器的数字实现产生不利影响,因而不得不对控制器进行进一步改进。再次,基于LuGre模型的摩擦补偿器设计会不可避免地为系统引入符号函数, 导致控制输出存在高频抖振,降低了控制器对高频噪声的鲁棒性。实验表明,优良的静态摩擦模型能够对实际系统存在的非线性摩擦进行高于90%的补偿[29-30]。同时文献[31]表明,与动态摩擦模型相比,静态摩擦模型可以对包含极限环在内的摩擦现象进行几乎同等程度的估计。综上考虑,为了便于工程实现,基于静态摩擦模型的补偿器在柔性关节机械臂的跟踪控制中具有更强的现实意义[33]。
综上所述,本文针对柔性关节机械臂的输出跟踪问题,提出了基于迭代学习观测器(iterative learning observer,ILO)的滤波反步控制策略,解决柔性关节系统状态估计问题的同时兼顾了控制系统的干扰抑制性能。针对柔性关节的动态特性,分析了系统不可测状态和模型不确定性对跟踪控制精度带来的影响。ILO作为系统内环,对系统的内部状态和由模型不确定性引起的复合扰动进行在线估计;利用指令滤波器解决了传统反步法控制器中存在的微分膨胀问题;同时,基于一种新型连续静态摩擦模型,设计了非线性摩擦补偿器,进一步提高了柔性关节机械臂输出跟踪的精度。通过Lyapunov稳定性理论分析了闭环控制系统的全局稳定性。
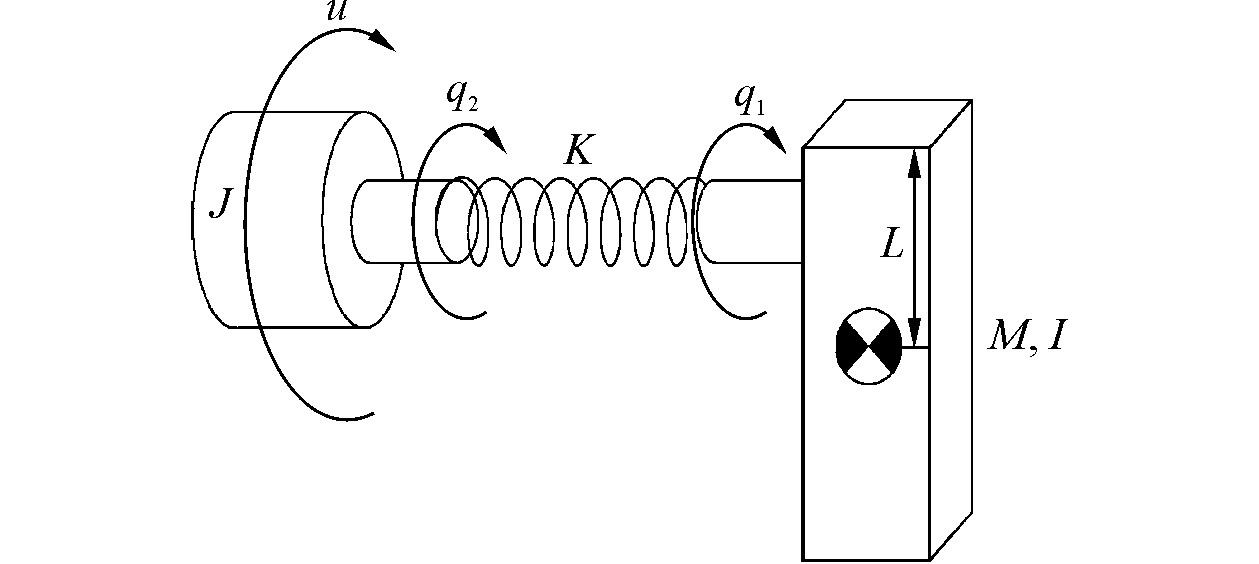
1 柔性关节机械臂控制系统设计 1.1 柔性关节机械臂模型建立本文将单臂柔性关节机械臂作为研究对象,转动副由直流电机直接驱动,将关节视为一个具有线性弹性系数的扭转弹簧系统,如图 1所示。
|
图 1 单臂柔性关节机械臂 Fig.1 Single link flexible joint manipulator |
| $ \left\{ \begin{array}{l} I{{\ddot q}_1} + MgL\sin \left( {{q_1}} \right) + K\left( {{q_1} - {q_2}} \right) = 0\\ J{{\ddot q}_2} - K\left( {{q_1} - {q_2}} \right) = {\tau _u} + {\tau _d} + f\left( {{{\dot q}_2}} \right) \end{array} \right. $ | (1) |
式中:q1为机械臂转角,q2为电机转角,I为转动臂的转动惯量,J为电机的惯性矩,K为关节的弹性刚度系数,τu是输入转矩,τd是外加干扰,
根据文献[30-33],本文建立如下连续可微的静态非线性摩擦模型,为后续的补偿器设计打下基础:
| $ \begin{array}{l} f\left( {{{\dot q}_2}} \right) = - {a_1}\tanh \left( {{c_1}{{\dot q}_2}} \right) - \\ {a_2}\left[ {\tanh \left( {{c_2}{{\dot q}_2}} \right) - \tanh \left( {{c_3}{{\dot q}_2}} \right)} \right] \end{array} $ | (2) |
式中:a1与a2代表不同等级的摩擦系数,c1、c2和c3为拟合不同摩擦效应所需的成型参数。
为了便于后续的控制系统设计,定义如下状态变量:x1=q1,
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2}\\ {{\dot x}_2} = {a_{21}}{x_1} + {a_{22}}\sin {x_1} + {a_{23}}{x_3}\\ {{\dot x}_3} = {x_4}\\ {{\dot x}_4} = {a_{41}}{x_1} + {a_{42}}{x_3} + {b_{41}}\left( {{\tau _u} + {\tau _d} + f\left( {{x_4}} \right)} \right) \end{array} \right. $ | (3) |
式中:a21=-K/I,a22=-MgL/I,a23=K/I,a41=K/J,a42=-K/J,b41=1/J。
考虑系统模型存在的参数不确定性,则有
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2}\\ {{\dot x}_2} = \left( {{a_{21}} + \Delta {a_{21}}} \right){x_1} + \\ \;\;\;\left( {{a_{22}} + \Delta {a_{22}}} \right)\sin {x_1} + \left( {{a_{23}} + \Delta {a_{23}}} \right){x_3}\\ {{\dot x}_3} = {x_4}\\ {{\dot x}_4} = \left( {{a_{41}} + \Delta {a_{41}}} \right){x_1} + \left( {{a_{42}} + \Delta {a_{42}}} \right){x_3} + \\ \left( {{b_{41}} + \Delta {b_{41}}} \right){\tau _u} + {b_{41}}{\tau _d} + {b_{41}}f\left( {{x_4}} \right) \end{array} \right. $ | (4) |
式中Δ(·)表示参数的摄动值。
将(4)整理成一般形式,则有:
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2}\\ {{\dot x}_2} = {a_{21}}{x_1} + {a_{22}}\sin {x_1} + {a_{23}}{x_3} + {d_1}\\ {{\dot x}_3} = {x_4}\\ {{\dot x}_4} = {a_{41}}{x_1} + {a_{42}}{x_3} + {b_{41}}\left( {{\tau _u}} \right) + {F_f}\left( {{x_4}} \right) + {d_2} \end{array} \right. $ | (5) |
式中:Ff(x4)=b41f(x4);d1、d2为由模型不确定性和外加干扰造成的复合干扰,假设复合扰动为有界变量,定义为
| $ {d_1} = \Delta {a_{21}}{x_1} + \Delta {a_{22}}\sin {x_1} + \Delta {a_{23}}{x_3} $ |
| $ {d_2} = \Delta {a_{41}}{x_1} + \Delta {a_{42}}{x_3} + \Delta {b_{41}}{\tau _u} + {b_{41}}{\tau _d} $ |
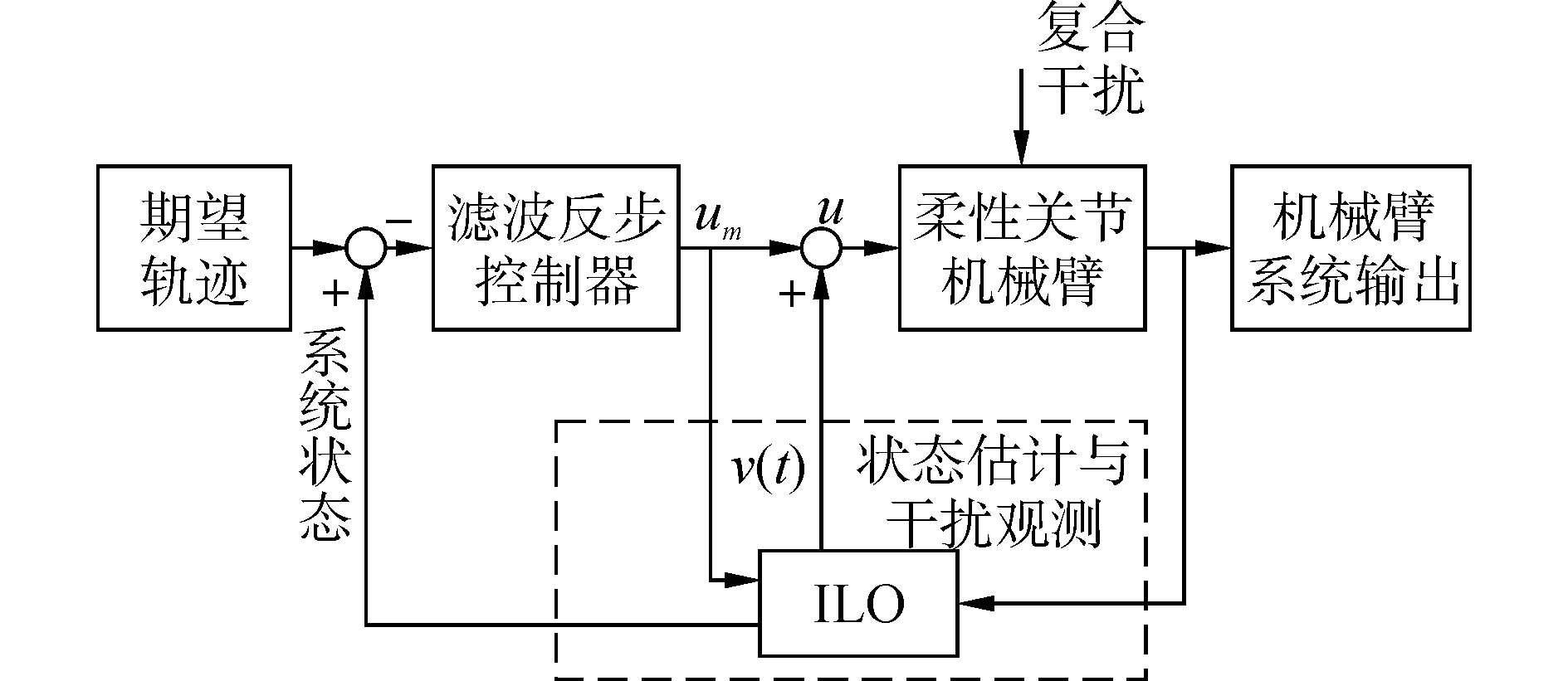
对于跟踪控制任务而言,输出反馈控制结构通常无法获得理想的跟踪性能,且非线性系统存在的模型不确定性及外界扰动会对控制性能产生较大影响。因此,本文将整个控制系统分为内环观测器和外环控制器分别进行设计。对于内环系统,考虑到系统模型不确定性和外界扰动的影响,设计一个ILO对未知状态和系统不确定性进行在线估计,并在控制系统中对复合扰动进行补偿,将系统转化为标称形式。进而利用系统状态估计值将外环控制器设计为状态反馈形式,从而获得理想的跟踪性能。控制系统结构如图 2所示。
|
图 2 控制系统框图 Fig.2 Framework of the control structure |
本节首先根据非线性系统(5)设计ILO,实现对于系统内部状态和复合扰动的在线估计。
由于系统状态x1可测,可以将式(5)所示的非线性系统转化为如下标准形式:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{A}}x + \mathit{\boldsymbol{\xi }}\left( \mathit{\boldsymbol{x}} \right) + \mathit{\boldsymbol{Bu}} + {\mathit{\boldsymbol{d}}_t}\\ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{C}}x \end{array} \right. $ | (6) |
其中:
此时,根据式(6)所述系统模型,可以设计如下ILO:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\hat {\dot x}}} = \mathit{\boldsymbol{A}}\hat x + \mathit{\boldsymbol{\xi }}\left( {\mathit{\boldsymbol{\hat x}}} \right) + \mathit{\boldsymbol{Bu}} + \mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{\hat y}}} \right) + \mathit{\boldsymbol{\gamma }}\left( t \right)\\ \mathit{\boldsymbol{\gamma }}\left( t \right) = {\mathit{\boldsymbol{\mu }}_1}\mathit{\boldsymbol{\gamma }}\left( {t - \tau } \right) + {\mathit{\boldsymbol{\mu }}_2}\left[ {\mathit{\boldsymbol{y}}\left( t \right) - \mathit{\boldsymbol{\hat y}}\left( t \right)} \right]\\ \mathit{\boldsymbol{\hat y}} = \mathit{\boldsymbol{C\hat x}} \end{array} \right. $ | (7) |
式中:
由(6)、(7)可得ILO观测误差动态方程:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\dot {\tilde x} = }}\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{LC}}} \right)\mathit{\boldsymbol{\tilde x}} + \left[ {\mathit{\boldsymbol{\xi }}\left( \mathit{\boldsymbol{x}} \right) - \mathit{\boldsymbol{\xi }}\left( {\mathit{\boldsymbol{\hat x}}} \right)} \right] + {\mathit{\boldsymbol{d}}_t} - \mathit{\boldsymbol{\gamma }}\left( t \right)\\ \mathit{\boldsymbol{\tilde y}} = \mathit{\boldsymbol{C\tilde x}} \end{array} \right. $ | (8) |
式中
设
| $ \mathit{\boldsymbol{\tilde d}}\left( t \right) = {\mathit{\boldsymbol{\mu }}_1}\mathit{\boldsymbol{\tilde d}}\left( {t - \tau } \right) - {\mathit{\boldsymbol{\mu }}_2}\mathit{\boldsymbol{C\tilde x}}\left( t \right) + {\mathit{\boldsymbol{d}}_\tau } $ | (9) |
此时,观测误差动态方程可改写为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot {\tilde x} = }}\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{LC}}} \right)\mathit{\boldsymbol{\tilde x + }}{\mathit{\boldsymbol{\mu }}_1}\mathit{\boldsymbol{\tilde d}}\left( {t - \tau } \right) - }\\ {{\mathit{\boldsymbol{\mu }}_2}\mathit{\boldsymbol{C\tilde x}}\left( t \right){\mathit{\boldsymbol{d}}_\tau } + \left[ {\mathit{\boldsymbol{\xi }}\left( \mathit{\boldsymbol{x}} \right) - \mathit{\boldsymbol{\xi }}\left( {\mathit{\boldsymbol{\hat x}}} \right)} \right]} \end{array} $ | (10) |
定理1 考虑式(4)所描述的柔性关节机械臂动力学系统和式(7)所述ILO,若以下条件成立,则最终观测误差是有界收敛的。
| $ {\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{LC}}} \right)^{\rm{T}}}\mathit{\boldsymbol{P}} + \mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{LC}}} \right) + \mathit{\boldsymbol{R}} + {\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{P}} = - \mathit{\boldsymbol{Q}} $ | (11) |
| $ \mathit{\boldsymbol{P}} = \mathit{\boldsymbol{\rho }}{\left( {{\mathit{\boldsymbol{\mu }}_2}\mathit{\boldsymbol{C}}} \right)^{\rm{T}}} $ | (12) |
| $ 0 < \left( {\rho + {m^2}} \right)\mathit{\boldsymbol{\mu }}_1^{\rm{T}}{\mathit{\boldsymbol{\mu }}_1} \le \mathit{\boldsymbol{I}} $ | (13) |
证明 定义如下Lyapunov函数,其中P、R为正定对称阵。
| $ {\mathit{\boldsymbol{V}}_1} = {{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}\mathit{\boldsymbol{P\tilde x}} + \int_{t - \to \tau }^t {{{\mathit{\boldsymbol{\tilde d}}}^{\rm{T}}}\left( \alpha \right)\mathit{\boldsymbol{\tilde d}}\left( \alpha \right){\rm{d}}\alpha } $ | (14) |
将V对时间求导,并结合ILO的观测误差动态方程(10)可得
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot V}}}_1} = {{\mathit{\boldsymbol{\dot {\tilde x}}}}^{\rm{T}}}\mathit{\boldsymbol{P}}{{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{P\dot {\tilde x}}}\left( t \right) + 2{{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{\mu }}_1}\mathit{\boldsymbol{\tilde d}}\left( {t - \tau } \right) - }\\ {2\mathit{\boldsymbol{\tilde x}}\left( t \right)\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{\mu }}_2}\mathit{\boldsymbol{C}}{{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{d}}_\tau }\left( t \right) - \varepsilon {{\mathit{\boldsymbol{\tilde d}}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{\tilde d}}\left( t \right) + }\\ {\rho {{\mathit{\boldsymbol{\tilde d}}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{\tilde d}}\left( t \right) - {{\mathit{\boldsymbol{\tilde d}}}^{\rm{T}}}\left( {t - \tau } \right)\mathit{\boldsymbol{\tilde d}}\left( {t - \tau } \right) + }\\ {2{{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{P}}\left[ {\mathit{\boldsymbol{\xi }}\left( \mathit{{x}} \right) - \mathit{\boldsymbol{\xi }}\left( {\mathit{{\hat x}}} \right)} \right]} \end{array} $ | (15) |
式中ρ-ε=1。
结合式(9),可进一步得出
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot V}}}_1} = {{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}\left[ {{{\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{LC}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{P}} + \mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{LC}}} \right)} \right]\mathit{\boldsymbol{\tilde x + }}}\\ {2{{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{\mu }}_1}\mathit{\boldsymbol{\tilde d}}\left( {t - \tau } \right) + 2{{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}\left( t \right)\left[ {\mathit{\boldsymbol{\xi }}\left( \mathit{\boldsymbol{x}} \right) - \mathit{\boldsymbol{\xi }}\left( {\mathit{\boldsymbol{\hat x}}} \right)} \right] - }\\ {2\mathit{\boldsymbol{\tilde x}}\left( t \right)\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{\mu }}_2}\mathit{\boldsymbol{C\tilde x}}\left( t \right) + 2{{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{d}}_\tau }\left( t \right) - \varepsilon {{\mathit{\boldsymbol{\tilde d}}}^{\rm{T}}}\left( t \right)\mathit{\boldsymbol{\tilde d}}\left( t \right) + }\\ {\rho \mathit{\boldsymbol{\tilde d}}\left( {t - \tau } \right)\mu _1^{\rm{T}}{\mu _1}{{\tilde d}_\tau }\left( {t - \tau } \right) + \rho \mathit{\boldsymbol{d}}_\tau ^{\rm{T}}{\mathit{\boldsymbol{d}}_\tau } + }\\ {2\mathit{\boldsymbol{p\tilde d}}\left( {t - \tau } \right)\mathit{\boldsymbol{\mu }}_1^{\rm{T}}{\mathit{\boldsymbol{d}}_\tau }\left( t \right) - 2\rho {{\mathit{\boldsymbol{\tilde x}}}^{\rm{T}}}{{\left( {{\mathit{\boldsymbol{\mu }}_2}\mathit{\boldsymbol{C}}} \right)}^{\rm{T}}}{\mathit{\boldsymbol{d}}_\tau }\left( t \right) - }\\ {{{\mathit{\boldsymbol{\tilde d}}}^{\rm{T}}}\left( {t - \tau } \right)\mathit{\boldsymbol{\tilde d}}\left( {t - \tau } \right)} \end{array} $ | (16) |
由于d(t)有界,则辅助变量dτ也为有界变量,即‖dτ‖≤dτ。
由式(11)、(12)有
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot V}}}_1} \le - {\lambda _{\min }}\left( \mathit{\boldsymbol{Q}} \right){{\left\| {\mathit{\boldsymbol{\tilde x}}} \right\|}^2} - \varepsilon {{\left\| {\mathit{\boldsymbol{\tilde d}}\left( t \right)} \right\|}^2} - }\\ {{{\mathit{\boldsymbol{\tilde d}}}^{\rm{T}}}\left( {t - \tau } \right)\mathit{\boldsymbol{\tilde d}}\left( {t - \tau } \right) + - \rho \mathit{\boldsymbol{\tilde d}}\left( {t - \tau } \right)\mathit{\boldsymbol{\mu }}_1^{\rm{T}}{\mathit{\boldsymbol{\mu }}_1}\mathit{\boldsymbol{\tilde d}}\left( {t - \tau } \right) + }\\ {2\rho \mathit{\boldsymbol{\tilde d}}\left( {t - \tau } \right)\mathit{\boldsymbol{\mu }}_1^{\rm{T}}{\mathit{\boldsymbol{d}}_\tau }\left( t \right) + \rho \mathit{\boldsymbol{\tilde d}}_\tau ^2 + 2\eta \left\| \mathit{\boldsymbol{P}} \right\|{{\left\| {\mathit{\boldsymbol{\tilde x}}} \right\|}^2}} \end{array} $ | (17) |
由三角不等式可得
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot V}} \le - \left( {{\lambda _{\min }}\left( \mathit{\boldsymbol{Q}} \right) - 2\eta {\lambda _{\max }}\left( \mathit{\boldsymbol{P}} \right)} \right){{\left\| {\mathit{\boldsymbol{\tilde x}}} \right\|}^2} - }\\ {\varepsilon {{\left\| {\mathit{\boldsymbol{\tilde d}}\left( t \right)} \right\|}^2} + {{\mathit{\boldsymbol{\tilde d}}}^{\rm{T}}}\left( {t - \tau } \right)\left[ {{{\left( {\rho + m} \right)}^2}\mathit{\boldsymbol{\mu }}_1^{\rm{T}}{\mathit{\boldsymbol{\mu }}_1} - } \right.}\\ {\left. \mathit{\boldsymbol{I}} \right]\mathit{\boldsymbol{\tilde d}}\left( {t - \tau } \right) + \left( {\rho + \frac{{{\rho ^2}}}{{{m^2}}}} \right)\mathit{\boldsymbol{\tilde d}}_\tau ^2} \end{array} $ | (18) |
式中m为正实数。此时,由式(13)可得
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot V}} \le - \left( {{\lambda _{\min }}\left( \mathit{\boldsymbol{Q}} \right) - 2\eta {\lambda _{\max }}\left( \mathit{\boldsymbol{P}} \right)} \right){{\left\| {\mathit{\boldsymbol{\tilde x}}} \right\|}^2} - }\\ {\varepsilon {{\left\| {\mathit{\boldsymbol{\tilde d}}\left( t \right)} \right\|}^2} + \left( {\rho + \frac{{{\rho ^2}}}{{{m^2}}}} \right)\mathit{\boldsymbol{\tilde d}}_\tau ^2} \end{array} $ | (19) |
由于dτ是有界的,因此观测器对系统状态和等效扰动的估计误差是一致最终有界的。
1.4 控制器设计为了获得期望的跟踪性能,利用ILO估计得到的系统内部状态,设计滤波反步控制器,使系统状态实现对于期望轨迹的跟踪。控制器设计包括以下几个步骤:
1) 定义闭环系统的跟踪误差为: e1=x1-x1d。此时,设计虚拟控制量为
| $ {\beta _1} = - {k_1}{e_1} + {{\dot x}_{1{\rm{d}}}} $ | (20) |
式中k1为正实数。
为了避免下一步中对虚拟控制量进行求导运算,引入如下的滤波器:
| $ \left\{ \begin{array}{l} \dot \beta _{1,1}^c = {\omega _1}\beta _{1,2}^c\\ \dot \beta _{1,2}^c = - 2{\zeta _1}{\omega _1}\beta _{1,2}^c - \omega _1^2\left( {\beta _{1,1}^c - {\beta _1}} \right) \end{array} \right. $ | (21) |
式中:滤波器的初值设置为β1, 1c(t0)=β1(t0),β1, 2c(t0)=0, t0为系统初始时刻。此时,β1, 1c和β1, 2c分别为对于β1及其一阶导数的估计值。
定义一个补偿跟踪误差系统:
| $ \left\{ \begin{array}{l} {v_1} = {e_1} - {\xi _1}\\ {{\dot \xi }_1} = - {k_1}{\xi _1} + \left( {\beta _{1,1}^c - {\beta _1}} \right) + {\xi _2} \end{array} \right. $ | (22) |
初值选取为ξ(t0)=0,ξ2的定义将在步骤2给出。
2) 定义系统的跟踪误差为: e2=x2-β1, 1c。此时,设计虚拟控制量为
| $ {\beta _2} = \frac{1}{{{a_{23}}}}\left[ { - {k_2}{{\hat e}_2} + \beta _{1,2}^c - {a_{21}}{{\hat x}_1} - {a_{22}}\sin \left( {{{\hat x}_1}} \right) - {v_1} - {{\hat d}_1}} \right] $ | (23) |
式中: k2为正实数,
为了避免下一步中对虚拟控制量进行求导运算,同样引入如下滤波器:
| $ \left\{ \begin{array}{l} \dot \beta _{2,1}^c = {\omega _2}\beta _{2,2}^c\\ \dot \beta _{2,2}^c = - 2{\zeta _2}{\omega _2}\beta _{2,2}^c - \omega _2^2\left( {\beta _{2,1}^c - {\beta _2}} \right) \end{array} \right. $ | (24) |
并引入一个跟踪误差补偿系统:
| $ \left\{ \begin{array}{l} {v_2} = {e_2} - {\xi _2}\\ {{\dot \xi }_2} = - {k_2}{\xi _2} + {a_{23}}\left( {\beta _{2,1}^c - {\beta _2}} \right) + {a_{23}}{\xi _3} \end{array} \right. $ | (25) |
其中,滤波器和跟踪误差补偿系统的初值设置与1)相同,ξ3的定义将在步骤3给出。
3) 定义系统的跟踪误差为: e3=x3-β2, 1c。此时,设计虚拟控制量为
| $ {\beta _3} = - {k_3}{{\hat e}_3} + \beta _{2,2}^c - {a_{23}}{v_2} $ | (26) |
式中:k3为正实数,
为了避免步骤3中对虚拟控制量进行求导运算,同样引入如下的滤波器:
| $ \left\{ \begin{array}{l} \dot \beta _{3,1}^c = {\omega _3}\beta _{3,2}^c\\ \dot \beta _{3,2}^c = - 2{\zeta _3}{\omega _3}\beta _{3,2}^c - \omega _3^2\left( {\beta _{3,1}^c - {\beta _3}} \right) \end{array} \right. $ | (27) |
并引入一个跟踪误差补偿系统:
| $ \left\{ \begin{array}{l} {v_3} = {e_3} - {\xi _3}\\ {{\dot \xi }_3} = - {k_3}{\xi _3} + \left( {\beta _{3,1}^c - {\beta _3}} \right) \end{array} \right. $ | (28) |
滤波器和跟踪误差补偿系统的初值设置与步骤1)相同。
4) 定义系统的跟踪误差为:e4=x4-β3, 1c。此时,设计得到最终的控制量为
| $ \begin{array}{*{20}{c}} {{\beta _4} = \frac{1}{{{b_{41}}}}\left[ { - {k_4}{{\hat e}_4} + \beta _{3,2}^c - {a_{41}}{{\mathit{\boldsymbol{\hat x}}}_1} - } \right.}\\ {\left. {{a_{42}}{{\mathit{\boldsymbol{\hat x}}}_3} - {\mathit{\boldsymbol{v}}_3} - {F_f}\left( {{{\mathit{\boldsymbol{\hat x}}}_4}} \right) - {{\mathit{\boldsymbol{\hat d}}}_2}} \right]} \end{array} $ | (29) |
式中:k4为正实数,
此时,取v4=e4,得到补偿跟踪误差系统的动态方程为
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\dot v}}}_1} = - {k_1}{\mathit{\boldsymbol{v}}_1} + {\mathit{\boldsymbol{v}}_2}\\ {{\mathit{\boldsymbol{\dot v}}}_2} = - {k_2}{\mathit{\boldsymbol{v}}_2} - {\mathit{\boldsymbol{v}}_1} + {a_{23}}{\mathit{\boldsymbol{v}}_3} + {k_2}{{\mathit{\boldsymbol{\tilde x}}}_2} + {a_{21}}{{\mathit{\boldsymbol{\tilde x}}}_1} + \\ \;\;\;\;\left. {{a_{22}}\left( {\sin {\mathit{\boldsymbol{x}}_1} - \sin {{\mathit{\boldsymbol{\hat x}}}_1}} \right)} \right) + \left( {{\mathit{\boldsymbol{d}}_1} - {{\mathit{\boldsymbol{\hat d}}}_1}} \right)\\ {{\mathit{\boldsymbol{\dot v}}}_3} = - {k_3}{v_3} + {v_3} - {a_{23}}{v_2} + {k_3}{{\tilde x}_3}\\ {{\mathit{\boldsymbol{\dot v}}}_4} = - {k_4}{\mathit{\boldsymbol{v}}_4} - {\mathit{\boldsymbol{v}}_3} + {k_4}{{\mathit{\boldsymbol{\tilde x}}}_4} + {a_{41}}{{\mathit{\boldsymbol{\tilde x}}}_1} + \\ \;\;\;\;{a_{42}}{{\mathit{\boldsymbol{\tilde x}}}_3} + \left( {{F_f}\left( {{\mathit{\boldsymbol{x}}_4}} \right) - {f_f}\left( {{{\mathit{\boldsymbol{\hat x}}}_4}} \right)} \right) + \left( {{\mathit{\boldsymbol{d}}_2} - {{\mathit{\boldsymbol{\hat d}}}_2}} \right) \end{array} \right. $ | (30) |
可以看出,vi是跟踪误差ei的微分同胚,镇定ei等价于镇定虚拟跟踪误差vi,进而,由于在定义vi的过程中引入了指令滤波跟踪误差ξi,因此,针对vi进行稳定性分析能够在镇定跟踪误差ei的同时,镇定指令滤波器跟踪误差ξi。
1.5 稳定性分析定理2 考虑式(4)所述的柔性关节机械臂模型,考虑系统的外部扰动和内部不确定性,设计式(6)所述的ILO和式(28)所述的滤波反步控制器,则系统的跟踪误差、状态估计误差和扰动估计误差是一致最终有界的。
证明 根据ILO和滤波反步法设计步骤,定义如下的Lyapunov函数:
| $ \mathit{\boldsymbol{V}} = \sum\limits_{i = 1}^4 {v_i^2 + {\mathit{\boldsymbol{V}}_1}} $ | (31) |
考虑式(29)所述的跟踪误差补偿的动态方程,及式(18)所述的观测器稳定性结论,得到上述Lyapunov函数对时间的导数为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot V}} \le - \sum\limits_{i = 1}^4 {{k_1}\mathit{\boldsymbol{v}}_i^2} + {{\mathit{\boldsymbol{\dot V}}}_1} + {k_2}{\mathit{\boldsymbol{v}}_2}{{\mathit{\boldsymbol{\tilde x}}}_2} + {k_3}{\mathit{\boldsymbol{v}}_3}{{\mathit{\boldsymbol{\tilde x}}}_3} + {k_4}{\mathit{\boldsymbol{v}}_4}{{\mathit{\boldsymbol{\tilde x}}}_4} + }\\ {\left( {{a_{21}} + {a_{22}}} \right){\mathit{\boldsymbol{v}}_2}{{\mathit{\boldsymbol{\tilde x}}}_1} + {a_{41}}{\mathit{\boldsymbol{v}}_4}{{\mathit{\boldsymbol{\tilde x}}}_1} + {a_{42}}{\mathit{\boldsymbol{v}}_4}{{\mathit{\boldsymbol{\tilde x}}}_3} + }\\ {{\mathit{\boldsymbol{v}}_2}\left( {{\mathit{\boldsymbol{d}}_1} - {{\mathit{\boldsymbol{\hat d}}}_1}} \right) + {v_4}\left( {{\mathit{\boldsymbol{F}}_f}\left( {{\mathit{\boldsymbol{x}}_4}} \right) - {\mathit{\boldsymbol{F}}_f}\left( {{{\mathit{\boldsymbol{\hat x}}}_4}} \right)} \right) + {\mathit{\boldsymbol{v}}_4}\left( {{\mathit{\boldsymbol{d}}_2} - {{\mathit{\boldsymbol{\hat d}}}_2}} \right)} \end{array} $ | (32) |
由于Ff(x4)满足Lipschitz条件,即
| $ \left\| {{\mathit{\boldsymbol{F}}_f}\left( {{\mathit{\boldsymbol{x}}_4}} \right) - {\mathit{\boldsymbol{F}}_f}\left( {{{\mathit{\boldsymbol{\hat x}}}_4}} \right)} \right\| \le \xi \left\| {{\mathit{\boldsymbol{x}}_4} - {{\mathit{\boldsymbol{\hat x}}}_4}} \right\|,\xi > 0 $ | (33) |
因此,将式(32)展开,利用式(33)与柯西不等式可得
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot V}} \le - {k_1}{{\left\| {{\mathit{\boldsymbol{v}}_1}} \right\|}^2} - \frac{{\left( {{k_2} - {a_{21}} - {a_{22}} - 1} \right)}}{2}{{\left\| {{\mathit{\boldsymbol{v}}_2}} \right\|}^2} - }\\ {{k_3}{{\left\| {{\mathit{\boldsymbol{v}}_3}} \right\|}^2} - \left( {{k_4} - {a_{41}} - {a_{42}} - 1} \right){{\left\| {{\mathit{\boldsymbol{v}}_4}} \right\|}^2} - }\\ {\left( {{\lambda _m} - \frac{{{a_{21}} + {a_{22}} + {a_{41}}}}{2}} \right){{\left\| {{{\mathit{\boldsymbol{\tilde x}}}_1}} \right\|}^2} - }\\ {\left( {{\lambda _m} - \frac{{{k_2}}}{2}} \right){{\left\| {{{\mathit{\boldsymbol{\tilde x}}}_2}} \right\|}^2} - \left( {{\lambda _m} - \frac{{{k_3} + {a_{23}}}}{2}} \right){{\left\| {{{\mathit{\boldsymbol{\tilde x}}}_3}} \right\|}^3} - }\\ {\left( {{\lambda _m} - \frac{{{k_4} + {\xi ^2}}}{2}} \right){{\left\| {{{\mathit{\boldsymbol{\tilde x}}}_4}} \right\|}^2} - \left( {\varepsilon - 1} \right){{\left\| {\mathit{\boldsymbol{\tilde d}}\left( t \right)} \right\|}^2} + }\\ {\left( {\rho + \frac{{{\rho ^2}}}{{{m^2}}}} \right)\mathit{\boldsymbol{\tilde d}}_\tau ^2} \end{array} $ | (34) |
式中λm=-(λmin(Q)-2ηλmax(P))。
此时,通过选取合适的控制参数,闭环系统的补偿跟踪误差和观测器误差是一致最终有界的。进而,根据滤波反步法中补偿跟踪误差的定义可知,系统的跟踪误差和指令滤波器跟踪误差是一致最终有界的。
2 仿真分析为了评价本文提出的柔性关节机械臂输出跟踪控制方法的有效性,本节针对柔性关节机械臂的输出跟踪问题进行了数值仿真。
根据文献[18-19]所描述的单臂柔性关节机械臂的数学模型,选取系统参数如下:I=1.35×10-4 kg·m2,J=2.16×10-3 kg·m2,K=7.47 N·m/rad,M=0.2 kg,L=0.02 m,g=9.8 m/s2。系统摩擦模型参数为a1=0.016 3,a2=0.008 11,c1=15,c3=1.5[30]。在仿真中,选取系统的参考输入信号为:xd=2πsin t。系统状态初值选取为:x1=0,x2=0,x3=0,x4=0。系统的参数摄动量为15%,取外界干扰τd=10sin t。设置滤波器参数为: ωn=600 rad/s,ζ=0.9。选取的系统控制器参数为
| $ {\mathit{\boldsymbol{\mu }}_1} = {\rm{diag}}\left( {0.45,0.42,0.38,0.39} \right), $ |
| $ {\mathit{\boldsymbol{\mu }}_2} = {\left[ {0.12\;41\;0.39\;293} \right]^{\rm{T}}}, $ |
| $ \mathit{\boldsymbol{L}} = {\left[ {0.81\;983\;12.36\;1079} \right]^{\rm{T}}}, $ |
| $ {k_1} = 53.1,{k_2} = 42.4,{k_3} = 51.7,{k_4} = 67.7。$ |
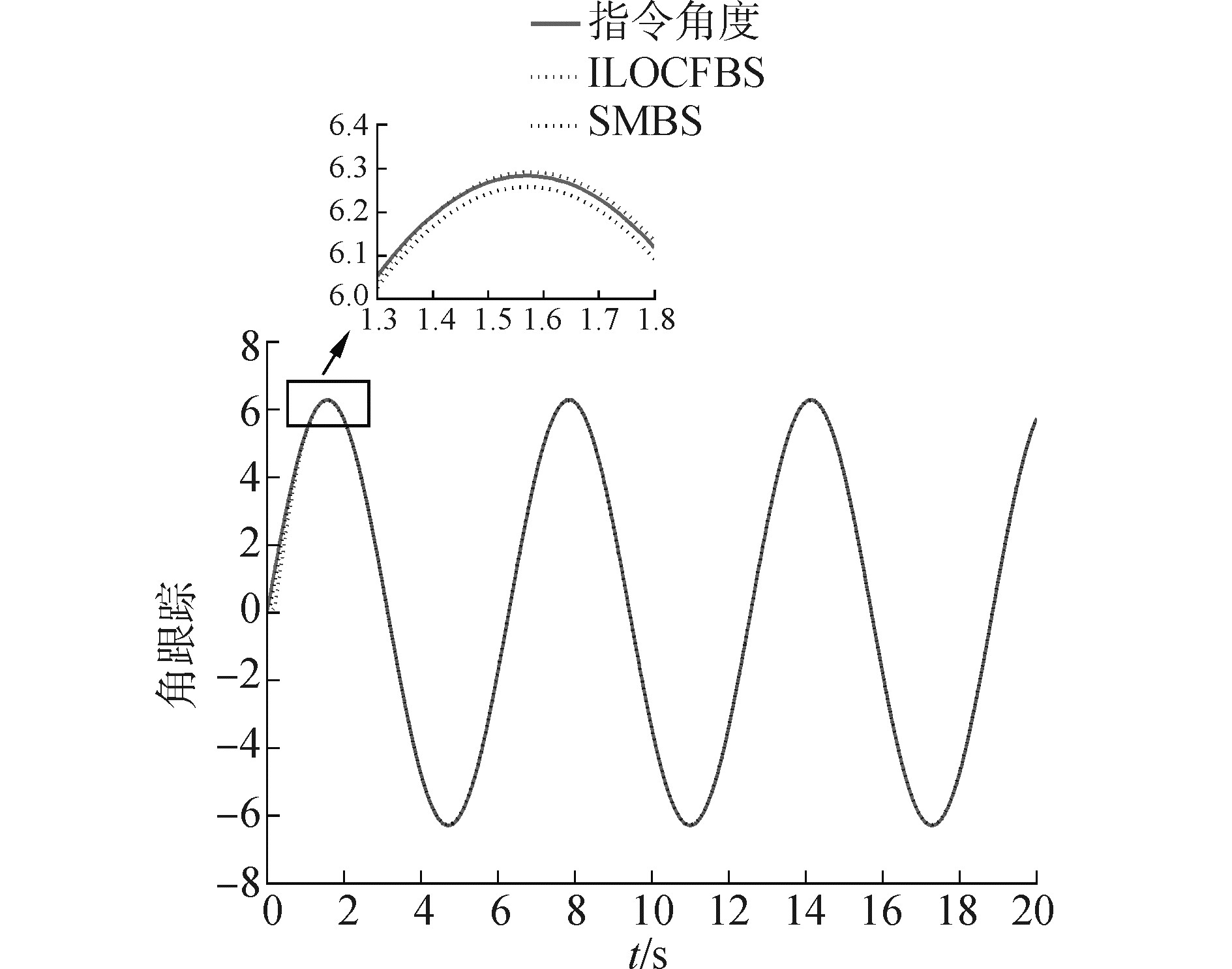
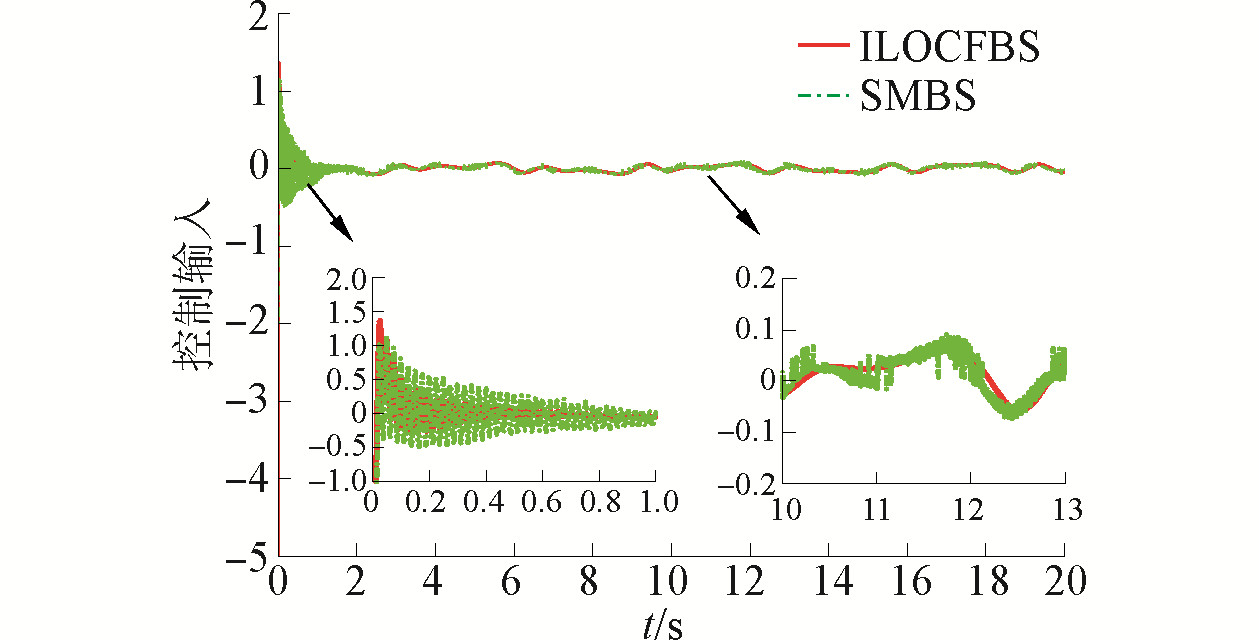
分别使用本文所述控制策略与传统滑模反步控制器对柔性关节机械臂的跟踪控制效果进行对比仿真。图 3为使用两种控制策略得到的输出跟踪响应曲线,图 4为上述两种控制方法的控制输入曲线对比。由图 3可以看出,基于ILO的指令滤波反步控制器对柔性关节机械臂动力学中的匹配与非匹配干扰进行了良好的估计,并且对系统存在的摩擦进行了精确补偿,因此能够获得比常规滑模反步法更高的跟踪精度。就控制器输出特性而言,从图 4可以看出,使用滑模反步控制器得到的系统控制输入具有明显的抖振现象,而本文提出的控制策略能够得到平滑的响应曲线,且具有相对较低的功耗。
|
图 3 柔性关节机械臂的系统输出 Fig.3 Output of the flexible manipulator |
|
图 4 系统的控制输入 Fig.4 Control system input |
图 5列出了迭代学习观测器的状态估计曲线。由状态估计曲线可以看出,本文所述的迭代学习观测器能够对柔性关节机械臂两个惯性装置的转角与角速度进行较好的在线估计,且观测误差能够在极短的时间内收敛。柔性关节机械臂是一个典型的非线性四阶系统,ILO对其状态的估计效能表明其对一些具有较高相对阶的非线性系统具有更良好的观测精度。ILO中包含的观测更新律能够同时对系统的复合干扰进行估计,图 6(a)为ILO对非匹配干扰项d1的估计,图 6(b)为对匹配干扰项d2的估计。由此可以看出,无论是匹配干扰还是非匹配干扰,ILO都能够对其进行快速跟踪。且对于一个四阶系统,观测器对于扰动和状态估计的超调量较小,使得该方法具有较高的实用价值。
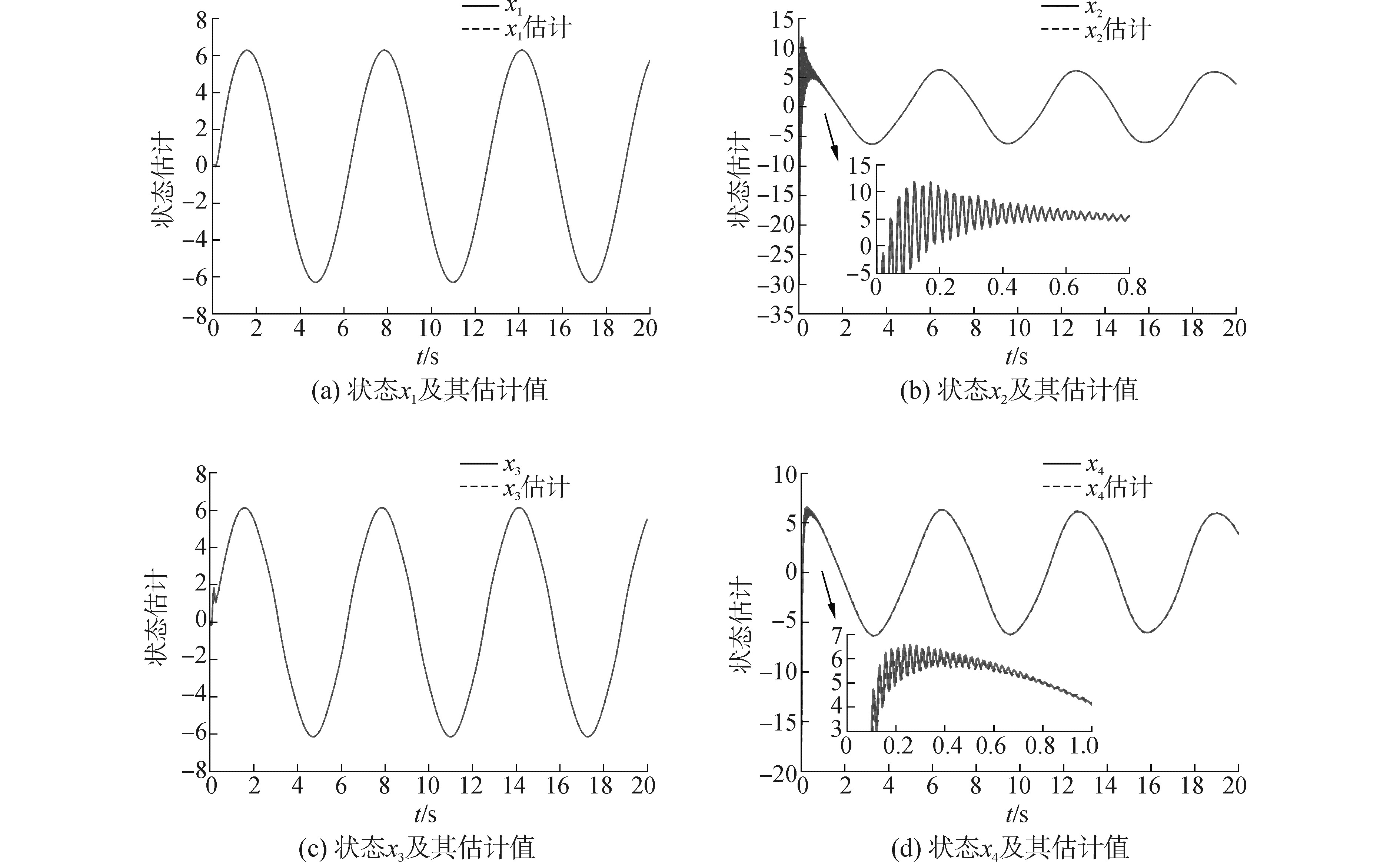
|
图 5 系统状态及其估计值 Fig.5 System state and its estimation |
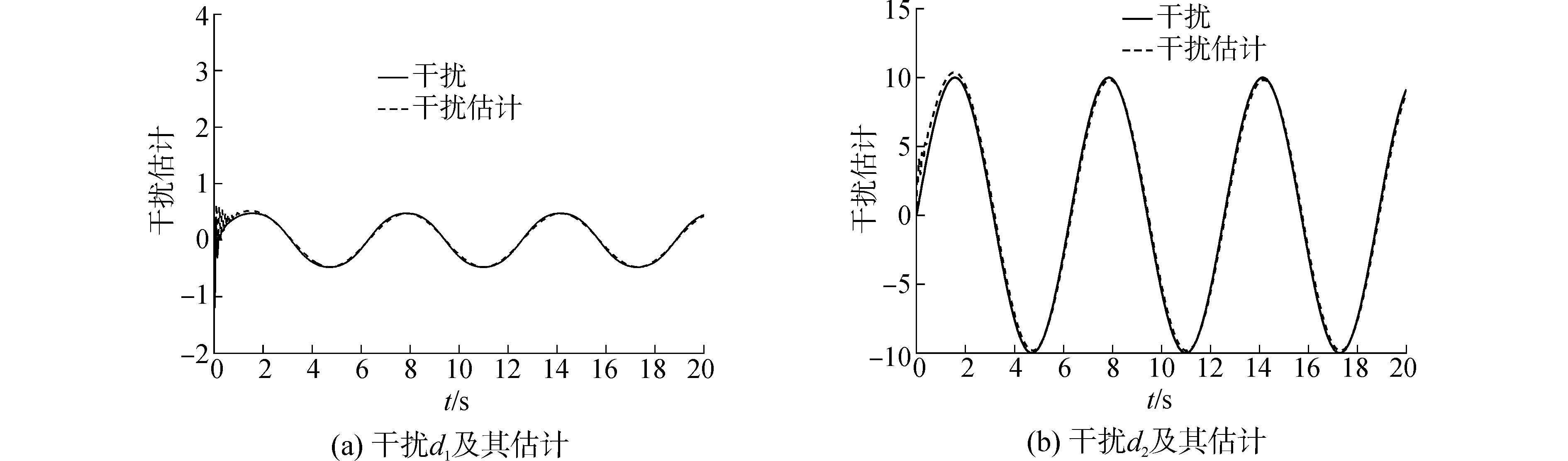
|
图 6 系统干扰干扰及其估计 Fig.6 System disturbance and its estimation |
1) ILO能够同时对柔性关节机械臂的关节角速度和集总干扰进行高精度估计。
2) 基于ILO的干扰估计功能设计的带有前馈补偿的指令滤波反步控制器解决了反步迭代过程中的项数膨胀问题,实现了对指令角度的跟踪。通过Lyapunov稳定性分析可以得出,闭环系统的状态是一致最终有界的。
本文所述控制策略能够有效实现柔性关节机械臂的鲁棒输出反馈跟踪控制。与传统控制方法相比,本文提出的控制策略具有更高的控制精度和较低的能量损耗。
| [1] |
LUCA A D, WAYNE J. Robots with flexible elements[M]. .
(  0) 0)
|
| [2] |
王树新, 贠今天, 石菊荣, 等. 柔性机械臂建模理论与控制方法研究综述[J]. 机器人, 2002, 24(1): 86-85. WANG Shuxin, YUN Jintian, SHI Jurong, et al. Roadmap of research on modeling and control strategy for flexible manipulators[J]. Robot, 2002, 24(1): 86-85. (  0) 0)
|
| [3] |
OZGOLI S, TAGHIRAD H D. A survey on the control of flexible joint robots[J]. Asian journal of control, 2006, 8(4): 332-344. (  0) 0)
|
| [4] |
SPONG M W. Modeling and control of elastic joint robots[J]. Journal of dynamic systems, measurement, and control, 1987, 109(4): 310-318. DOI:10.1115/1.3143860 (  0) 0)
|
| [5] |
CHANG Y Z, DANIEL R W. On the adaptive control of flexible joint robots[J]. Automatica, 1992, 28(5): 969-974. DOI:10.1016/0005-1098(92)90149-A (  0) 0)
|
| [6] |
孙敬颋, 史士财, 王学飞, 等. 大型空间机械臂柔性关节的微分几何算法控制器设计[J]. 哈尔滨工程大学学报, 2012, 33(11): 1371-1376. SUN Jingting, SHI Shicai, WANG Xuefei, et al. Controller design of large space manipulator flexible joint using differential geometry algorithm[J]. Journal of Harbin Engineering University, 2012, 33(11): 1371-1376. (  0) 0)
|
| [7] |
XU B, YUAN Y. Two performance enhanced control of flexible-link manipulator with system uncertainty and disturbances[J]. Science China information sciences, 2017, 60(5): 050202. DOI:10.1007/s11432-016-0604-6 (  0) 0)
|
| [8] |
LOZANO R, BROGLIATO B. Adaptive control of robot manipulators with flexible joints[J]. IEEE transactions on automatic control, 1992, 37(2): 174-181. DOI:10.1109/9.121619 (  0) 0)
|
| [9] |
JIN M, LEE J, TSAGARAKIS N G. Model-free robust adaptive control of humanoid robots with flexible joints[J]. IEEE transactions on industrial electronics, 2017(99): 1-7. (  0) 0)
|
| [10] |
戴学丰, 孙立宁, 刘品宽, 等. 柔性臂机器人控制算法综述[J]. 电机与控制学报, 2002, 6(2): 158-161. DAI Xuefeng, SUN Lining, LIU Pinkuan, et al. A survey of control algorithms for flexible link manipulators[J]. Electric machines & control, 2002, 6(2): 158-161. (  0) 0)
|
| [11] |
CAMBERA J C, FELIU-BATLLE V. Input-state feedback linearization control of a single-link flexible robot arm moving under gravity and joint friction[J]. Robotics & autonomous systems, 2017, 88: 24-36. (  0) 0)
|
| [12] |
TALOLE S E, KOLHE J P, PHADKE S B. Extended state observer based control of flexible-joint system with experimental validation[J]. IEEE transactions on industrial electronics, 2010, 57(4): 1411-1419. DOI:10.1109/TIE.2009.2029528 (  0) 0)
|
| [13] |
FELIU V, PEREIRA E, DIAZ I M. Passivity-based control of single-link flexible manipulators using a linear strain feedback[J]. Mechanism & machine theory, 2014, 71(1): 191-208. (  0) 0)
|
| [14] |
KUGI A, OTT C, ALBU-SCHAFFER A, et al. On the passivity based impedance control of flexible joint robots[J]. IEEE transactions on robotics, 2008, 24(2): 416-429. DOI:10.1109/TRO.2008.915438 (  0) 0)
|
| [15] |
YUAN J, STEPANENKO Y. Composite adaptive control of flexible joint robots[J]. Automatica, 1993, 29(3): 609-619. DOI:10.1016/0005-1098(93)90058-2 (  0) 0)
|
| [16] |
熊根良, 刘伊威, 黄剑斌, 等. 基于DSP/FPGA的反步法阻抗控制柔性关节机械臂[J]. 控制与决策, 2009, 24(8): 1137-1142. XIONG Genliang, LIU Yiwei, HUANG Jianbin, et al. Backstepping impedance control flexible joint manipulators using DSP/FPGA structure[J]. Control & decision, 2009, 24(8): 1137-1142. (  0) 0)
|
| [17] |
TONG S C, HE X L, ZHANG H G. A combined backstepping and small-gain approach to robust adaptive fuzzy output feedback control[J]. IEEE transactions on fuzzy systems, 2009, 17(5): 1059-1069. DOI:10.1109/TFUZZ.2009.2021648 (  0) 0)
|
| [18] |
LI Y, LI T. Fuzzy adaptive dynamic surface control for a single-link flexible-joint robot[J]. Nonlinear dynamics, 2012, 70(3): 2035-2048. DOI:10.1007/s11071-012-0596-7 (  0) 0)
|
| [19] |
HUANG A C, CHEN Y C. Adaptive sliding control for single-link flexible-joint robot with mismatched uncertainties[J]. IEEE transactions on control systems technology, 2004, 12(5): 770-775. DOI:10.1109/TCST.2004.826968 (  0) 0)
|
| [20] |
CHAO Liu, CHIEN C C, SLOTINE J J. Adaptive task-space regulation of rigid-link flexible-joint robots with uncertain kinematics[J]. Automatica, 2008, 44(7): 1806-1814. DOI:10.1016/j.automatica.2007.10.039 (  0) 0)
|
| [21] |
陈明金, 李树荣, 曹乾磊. 时滞柔性关节机械臂自适应位置/力控制[J]. 控制理论与应用, 2015, 32(2): 217-223. CHEN Mingjing, LI Shurong, CAO Qianlei. Adaptive motion/force control for rigid-link flexible-joint manipulators with time delay[J]. Control theory and applications, 2015, 32(2): 217-223. (  0) 0)
|
| [22] |
ZHANG L, LIU J. Observer-based partial differential equation boundary control for a flexible two-link manipulator in task space[J]. IET control theory and applications, 2012, 6(13): 2120-2133. DOI:10.1049/iet-cta.2011.0545 (  0) 0)
|
| [23] |
NICOSIA S, TOMEI P. Robot control by using only joint position measurements[J]. IEEE transactions on automatic control, 1990, 35(9): 1058-1061. DOI:10.1109/9.58537 (  0) 0)
|
| [24] |
谢立敏, 陈力. 具有柔性关节的漂浮基空间机械臂基于状态观测器的轨迹跟踪鲁棒反步控制及弹性振动抑制[J]. 机器人, 2012, 34(6): 722-729. XIE Limin, CHEN Li. Robust backstepping control based on state observer and elastic vibration suppressing of free-floating space manipulator with flexible joints[J]. Robot, 2012, 34(6): 722-729. (  0) 0)
|
| [25] |
CHANG Y C, YEN H M. Robust tracking control for a class of electrically driven flexible-joint robots without velocity measurements[J]. International journal of control, 2012, 85(2): 194-212. DOI:10.1080/00207179.2011.643241 (  0) 0)
|
| [26] |
LIGHTCAP C A, BANKS S A. An extended Kalman filter for real-time estimation and control of a rigidlink flexible-joint manipulator[J]. IEEE transactions on control systems technology, 2010, 18(1): 91-103. DOI:10.1109/TCST.2009.2014959 (  0) 0)
|
| [27] |
CHATLATANAGULCHAI W, NHO H C, MECKL P H. Robust observer backstepping neural network control of flexible-joint manipulator[C]//Proceedings of the American Control Conference. 2004: 5250-5255.
(  0) 0)
|
| [28] |
CHALHOUB N, KFOURY G. Development of a robust nonlinear observer for a single link flexible manipulator[J]. Nonlinear dynamics, 2005, 3(39): 217-233. (  0) 0)
|
| [29] |
YAO J, YANG G, JIAO Z, et al. Adaptive robust motion control of direct-drive dc motors with continuous friction compensation[J]. Abstract & applied analysis, 2013, 2013(6): 1-14. (  0) 0)
|
| [30] |
YAO J, JIAO Z, YAO B. Robust control for static loading of electro-hydraulic load simulator with friction compensation[J]. Chinese journal of aeronautics, 2012, 25(6): 954-962. DOI:10.1016/S1000-9361(11)60467-6 (  0) 0)
|
| [31] |
HENSEN A R H, MOLENGRAFT V D. Friction induced hunting limit cycles:a comparison between the LuGre and switch friction model[J]. Automatica, 2003, 39(12): 2131-2137. DOI:10.1016/S0005-1098(03)00234-6 (  0) 0)
|
| [32] |
YAO J, JIAO Z, MA D. RISE-based precision motion control of dc motors with continuous friction compensation[J]. IEEE transactions on industrial electronics, 2014, 61(12): 7067-7075. DOI:10.1109/TIE.2014.2321344 (  0) 0)
|
| [33] |
MAKKAR C, DIXON W E, SAWYER W G, et al. A new continuously differentiable friction model for control systems design[C]//IEEE/ASME International Conference on Advanced Intelligent Mechatronics. 2005: 600-605. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1511048
(  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


