2. 山东大学(威海)基建处, 山东 威海 264209
2. Infrastructure Department, Shandong University, Weihai 264209, China
足式(步行)机器人相比轮式机器人, 具有更高的机动能力和越障能力, 更适合在复杂地形中执行作业任务, 尤其是在突发灾难的区域, 如:地震、火灾、沉船等场合[1]。四足步行机器人由于运动灵活, 稳定性好, 在整个步行机器人中占有很大的比重, 是目前机器人研究领域的热点之一[2-3]。
现有的四足机器人腿部结构大多采用串联机构, 如美国波士顿动力公司研制的BigDog[4]和LittleDog[5]、意大利理工学院研制的HyQ[6]、日本千叶技术学院研制的Hyperion 4机器人和山东大学研制的液压驱动四足仿生机器人[7]等。串联腿机器人由于腿部安装了驱动器和相应的传感器, 增加了腿部较低位置的质量及机器人的腿部转动惯量, 降低了腿部的机动性。而并联腿机构主要应用在单足或双足机器人中, 在四足机器人领域的应用还较少, 王洪波[8]、Gao F等[9]分别提出了四足并联腿机器人, 并对其进行了腿部机构的力学性能分析。并联腿机构具有较大的刚度, 可提高机器人的载重自重比, 同时使机身运动更加平稳;但通常形式复杂、构件数目较多、驱动器布置容易干涉、工作空间小, 阻碍了高速高承载能力的发挥。
为克服上述不足, 田兴华[10]、高建设[11]等将串并混联机构引入四足仿生机器人中, 提出了几种不同的混联腿机构, 并对其进行了比较及运动分析与仿真。混联腿机构结合了并联机构和串联机构的优点, 可在提高机器人载重/自重比的同时, 满足快速稳定响应的需求, 从而实现高速、低能耗、高承载的运动。但由于结构本身原因, 在性能分析方面相对并联机构要复杂一些。
本文针对水陆两栖机器人的工作特点, 提出了一种同时拥有直线驱动和转动驱动的四足步行串并混联机器人, 该机器人的串并混联腿机构为具有两移动两转动(2T2R)的空间四自由度机构。2T2R机构把空间的移动和转动有机结合起来, 在工业中有着广泛的应用。国内外学者对2T2R机构已开展了一定的研究, 如Fan等[12-16]对2T2R并联机构的构型综合方法进行了研究。Ye等[17-18]对不同的2T2R并联机构进行了运动学分析和性能分析, 为2T2R并联机构的应用提供了较好的技术支持。为了方便对串并混联2T2R机构进行运动学分析和性能分析, 本文将其等效为2UPU-UPR并联机构, 然后基于螺旋理论对其自由度进行分析, 推导其动平台姿态约束方程及机构的位置反解方程, 利用速度雅克比矩阵分析了机构的奇异特性。
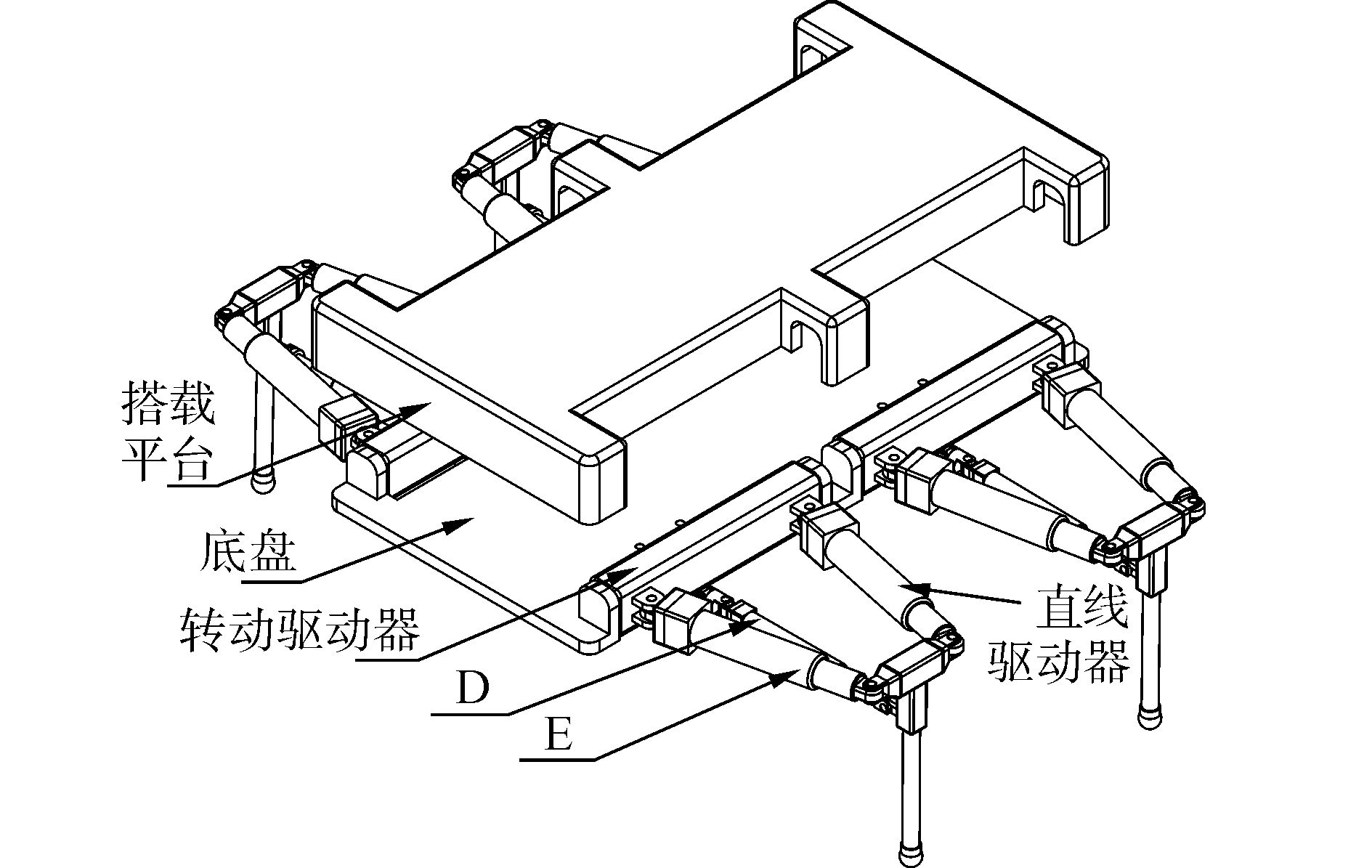
1 串并混联步行机器人及其腿部结构图 1为设计的四足串并混联步行机器人, 搭载平台A固定在底盘B上, 既可以保护步行机器人的控制系统设备又可以为步行机器人提供外部拓展功能的搭载平台, 如各项侦测、维修、抢险等具备复杂功能的拓展操作设备, 实现水下、陆地各种复杂环境下的操作任务。
|
注:A.搭载平台, B.底盘, C.转动驱动器, D、E、F.直线驱动器。 图 1 四足串并混联步行机器人 Fig.1 Quadruped serial-parallel walking manipulator |
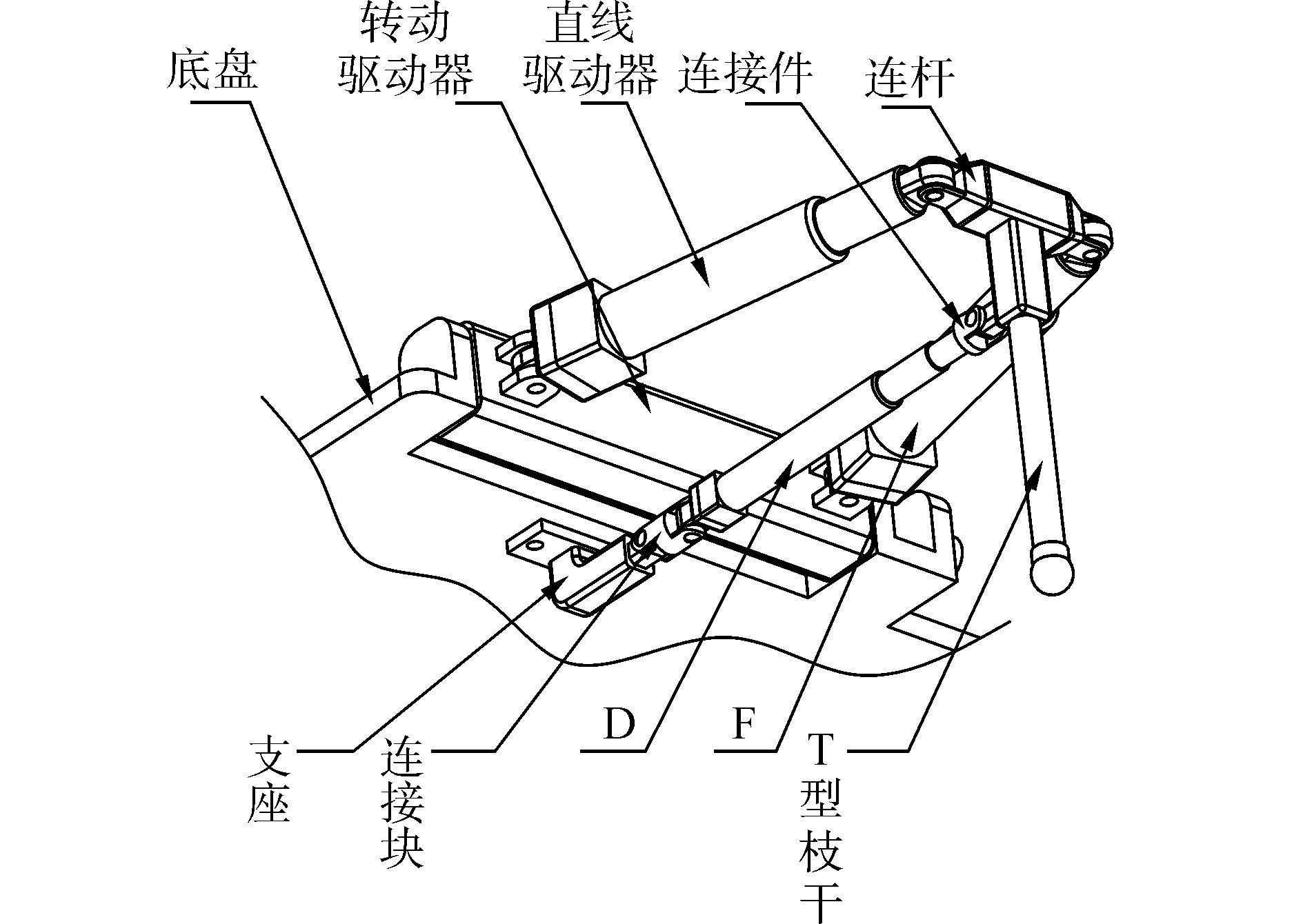
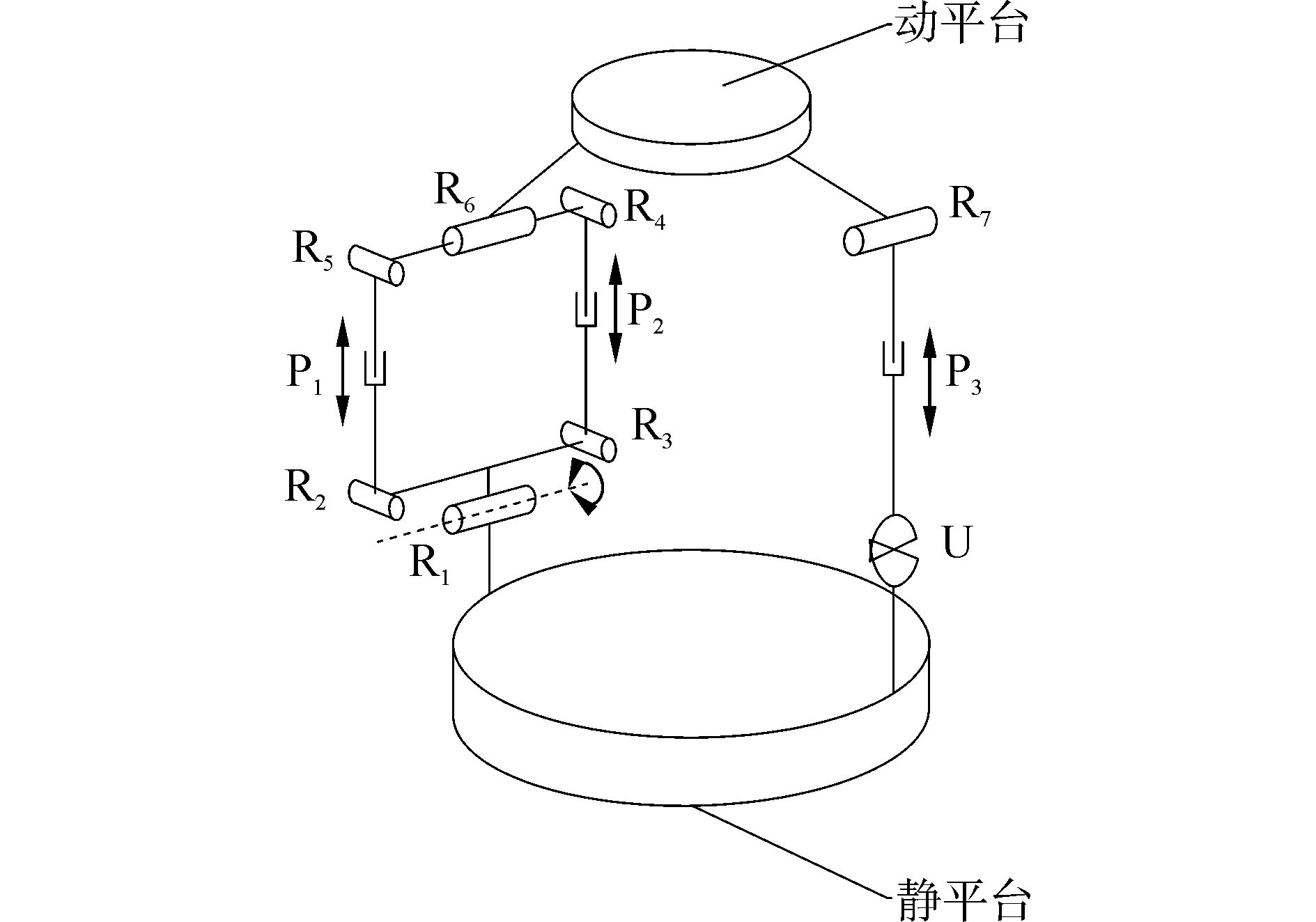
图 2为串并混联步行机器人的腿部构型。转动驱动器C、直线驱动器E、F和连杆4构成主驱动支链;直线驱动器D、U副连接块2和R副连接件5构成副驱动支链。其中主驱动支链的转动驱动器C分别与底盘B的对应位置连接形成转动副, 副驱动支链的U副连接块2分别与四个支座1连接形成转动副, 四个支座1分别固定在底盘B下方的对应位置。T型腿部3上端杆件中空并与主驱动支链的连杆4连接形成转动副, T型腿部3下端杆件与副驱动支链连接形成转动副, 每条支路的移动副由液压缸驱动, 转动副由伺服电机驱动, 将T型腿安装在动平台上, 便可作为水陆两栖机器人的末端执行机构。其腿部构型简图如图 3所示。
|
注:1.支座, 2.连接块, 3.T型腿部, 4.连杆, 5.连接件, B.底盘, C.转动驱动器, D、F.直线驱动器。 图 2 机器人腿部结构 Fig.2 The leg structure of the manipulator |
|
图 3 串并混联腿部结构构型简图 Fig.3 The serial-parallel leg configuration diagram |
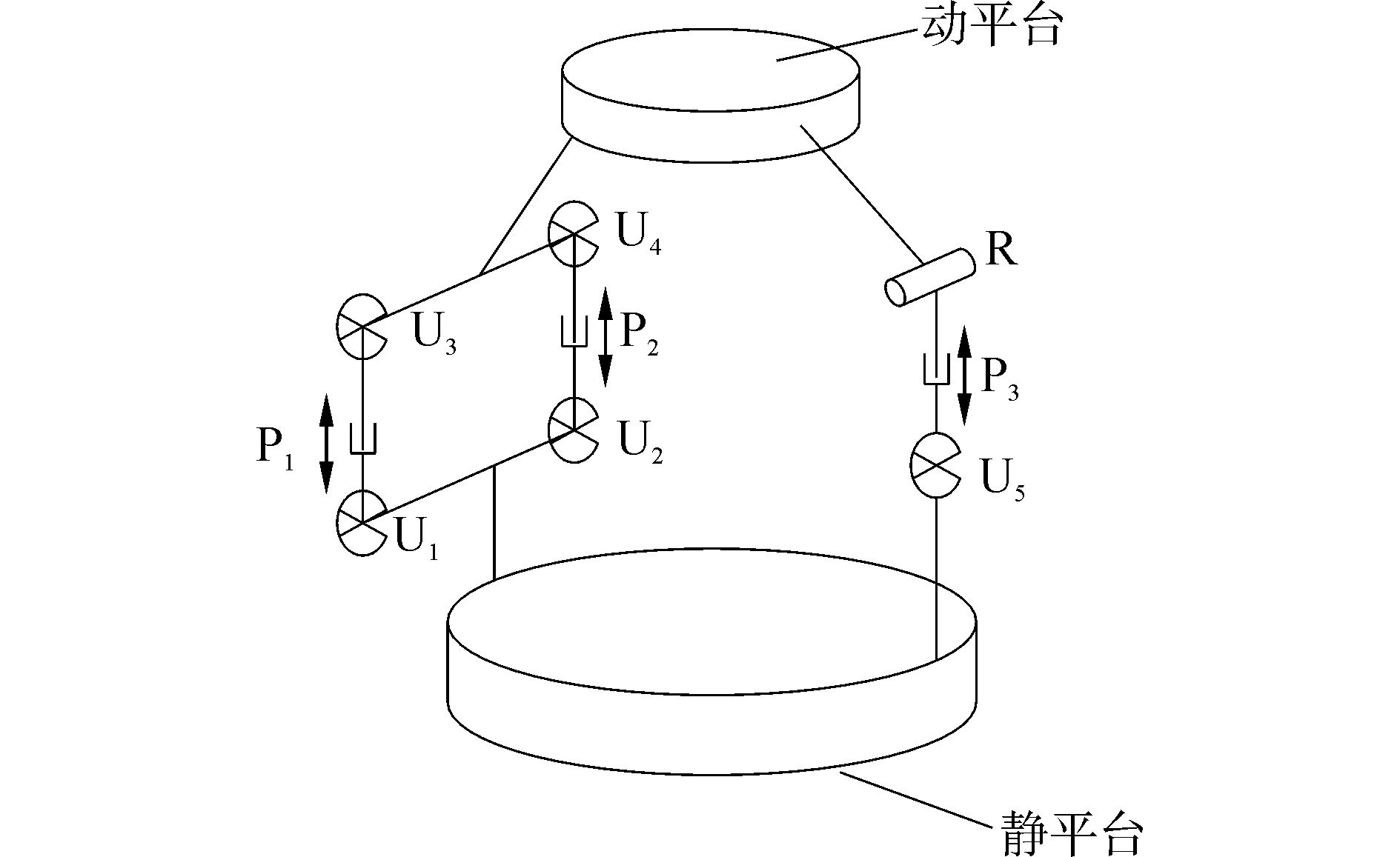
考虑到图 3中串并混联结构构型的复杂性, 在不影响其运动状态的情况下, 将上述结构简化为图 4。图 4主要对主驱动支链做了下面两部分改变:第一, 将转动副R1去掉, 把两个支链的转动副R2、R3用两个U副(U1、U2)代替;第二, 将转动副R6去掉, 将两端的转动副R4、R5变成两个U副(U3, U4)。这样整个腿部结构的运动状态没有改变, 而原来的串并混联机构变成了2UPU-UPR并联机构, 可以利用并联机构分析方法对其进行运动分析和奇异分析。
|
图 4 2UPU-UPR并联机构构型简图 Fig.4 2UPU-UPR parallel mechanism configuration diagram |
目前, 并联机构自由度的计算常采用修正的Kutzbach-Grübler公式[19]:
| $ F = d\left( {n - g - 1} \right) + \sum\limits_{i = 1}^g {{f_i} + \upsilon - \zeta } $ | (1) |
式中:F是机构的自由度数, d表示机构的阶数, d=6-λ, λ表示公共约束数, n表示机构的所有构件数目, g为机构运动副数目, fi表示第i个运动副的自由度数, υ表示机构去除公共约束后的冗余约束数目, ζ为局部自由度数。
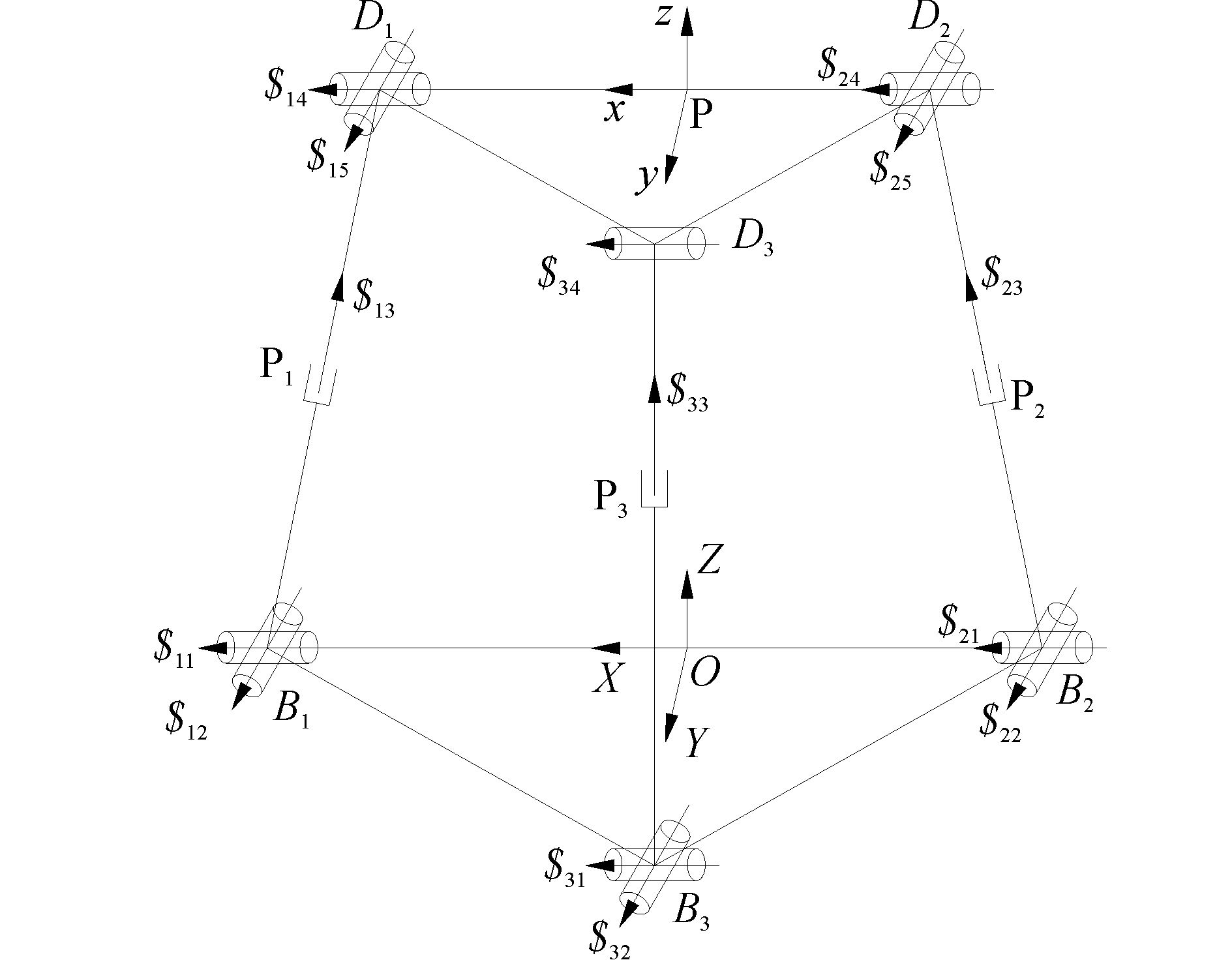
如图 5所示, 2UPU-UPR并联机构的定平台通过两个UPU(1, 2) 分支和一个UPR(3) 分支与动平台相连, 与静平台相连的分支1、2、3中的三个U副中心分别记为B1、B2、B3点;与动平台相连的两个U副与一个R副中心分别记为D1、D2、D3点;与静平台相连的三个U副的固定轴线相互平行, 都沿B1B2方向;三个U副的可动轴线与分支1, 2的R副轴线平行;分支3中的R副轴线与D1D2方向平行。建立如图 5所示的定坐标系O-XYZ与动坐标系P-xyz。O、P分别为B1B2、D1D2的中点, X和x轴正向分别指向B1和D1点, Y和y轴正向分别指向B3和D3点, Z和z轴按右手定则确定。静平台各点到定坐标系原点O的距离分别为:lOB1= lOB2=b, lOB3=c, 动平台各点到动坐标系原点P的距离分别为:lPD1= lPD2=d, lOD3=e。则在定坐标系中, 定平台中三个万向铰链中心点的坐标为:B1=(b 0 0) T, B2=(-b 0 0) T, B3=(0 c 0) T;动平台中各点的坐标分别为:D1=(XD1 YD1 ZD1)T, D2=(XD2 YD2 ZD2)T, D3=(XD3 YD3 ZD3)T;动坐标系中心点P的坐标为:P=(XP YP ZP)T。在动系中, 动平台各点的坐标为:d1=(d 0 0) T, d2=(-d 0 0) T, d3=(0 e 0) T。
|
图 5 2UPU-UPR并联机构简图 Fig.5 2UPU-UPR parallel mechanism diagram |
假定在初始位形时, 动平台与静平台平行, 两坐标系的各坐标轴相互平行。此时, 动平台各点在定系下的坐标分别为:D1=(XD1 0 ZD1)T, D2=(XD2 0 ZD2)T, D3=(0 YD3 ZD3)T。分支1的运动螺旋系为:$11=(1 0 0; 0 0 0), $12=(0 1 0; 0 0 b), $13=(0 0 0; l13 0 n13), $14=(1 0 0; 0 ZD1 0), $15=(0 1 0; -ZD1 0 XD1), 其中lij, nij表示第i分支第j个运动副轴线的方向余弦。可以看出, 上述螺旋系的反螺旋为:$11r=(0 0 0; 0 0 1)。分支1与分支2相同, 因此可得分支2的反螺旋为:$21r=(0 0 0; 0 0 1)。
分支3的运动螺旋系为:$31=(1 0 0; 0 0-c), $32=(0 1 0; 0 0 0), $33=(0 0 0; 0 m33 n33), $34=(1 0 0; 0 ZD3 -YD3), 式中, mij和nij表示第i分支第j个运动副轴线的方向余弦, 其反螺旋为:$31r=(1 0 0; 0 0 0), $32r= (0 0 0; 0 0 1)。可以看出三个分支反螺旋中, $11r、$21r、$32r相同, 都表示沿Z轴方向的约束力偶, 所以构成1个公共约束, 即各分支都不能绕垂直与静平台的轴线转动, 所以λ=1, d=5。剩余1个反螺旋$31r表示一过原点沿X轴方向的约束力, 秩为1, 所以没有冗余约束, 即υ=1-1=0, 局部自由度ζ为0。
2UPU-UPR并联机构构件数为8, 机构的运动副总数为9, 代入式(1) 可得2UPU-UPR并联机构的自由度F=4。经过公式计算验证该机构确实具有4个自由度, 且由约束螺旋系可知其分别为沿y轴z轴的移动自由度和围绕x轴、y轴的转动自由度。
2.2 2UPU-UPR并联腿机构的位置建模设动坐标系P-xyz到定坐标系O-XYZ的变换矩阵:
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {{n_i}}&{{o_i}}&{{a_i}}&{{X_P}}\\ {{n_j}}&{{o_j}}&{{a_j}}&{{Y_P}}\\ {{n_k}}&{{o_k}}&{{a_k}}&{{Z_P}}\\ 0&0&0&1 \end{array}} \right] $ |
在定坐标系O-XYZ下, Di点的坐标可以表示为
| $ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{D}}_i}}\\ 1 \end{array}} \right]_{XYZ}} = \mathit{\boldsymbol{T}}{\left[ {\begin{array}{*{20}{c}} {{d_i}}\\ 1 \end{array}} \right]_{xyz}} $ |
式中:Di和di分别表示动平台D1D2D3上铰链中心处点Di(i=1, 2, 3) 在定坐标系O-XYZ和动坐标系P-xyz中的位置矢量。取Z-Y-X型欧拉角(α, β, γ)表示动平台D1D2D3的姿态, 则
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {\cos \alpha \cos \beta }&{\cos \alpha \sin \beta \sin \gamma - \sin \alpha \cos \gamma }&{\cos \alpha \sin \beta \cos \gamma + \sin \alpha \sin \gamma }&{{X_P}}\\ {\sin \alpha \cos \beta }&{\sin \alpha \sin \beta \sin \gamma + \cos \alpha \cos \gamma }&{\sin \alpha \sin \beta \cos \gamma - \cos \alpha \sin \gamma }&{{Y_P}}\\ { - \sin \beta }&{\cos \beta \sin \gamma }&{\cos \beta \cos \gamma }&{{Z_P}}\\ 0&0&0&1 \end{array}} \right] $ |
由机构运动特性可知, B1D1, B2D2始终在一个平面内运动, 所以有:YD1=YD2, 即njd+YP=-njd+YP, 得nj=0(d≠0)。结合式(2) 可得sin α cos β=0, 存在以下三种情况:① sin α=0, α=0°;② cos β=0, β=90°;③ sin α=cos β=0, α=0°, β=90°。根据机构自由度分析可知, 机构不能绕Z轴转动, 因此第一种情况成立, 即α=0°。
另外, 从机构结构组成可知, 矢量B3D3与D2D1始终垂直, 即
| $ {\mathit{\boldsymbol{B}}_3}\mathit{\boldsymbol{D}}_3^{\rm{T}} \cdot {\mathit{\boldsymbol{D}}_2}{\mathit{\boldsymbol{D}}_1} = 0 $ | (3) |
将B3D3=[oie+XP oje+YP-c oke+ZP]T, D2D1=[2nid 2njd 2nkd]T代入式(3), 得:
| $ \begin{array}{*{20}{c}} {2{n_i}d\left( {{o_i}e + {X_P}} \right) + 2{n_j}d\left( {{o_j}e + {Y_P} - c} \right) + }\\ {2{n_k}d\left( {{o_k}e + {Z_P}} \right) = 0} \end{array} $ | (4) |
由α=0及式(2) 可知, ni=cos β, nj=0, nk=-sin β, oi=sin β sin γ, oj=cosγ, ok=cos β sin γ, 代入式(4), 得cos β XP-sin β ZP=0, 所以得
| $ {X_P} = {Z_P}\tan \beta $ | (5) |
所以, 得到2UPU-UPR并联机构的两个约束条件为
由式(6) 可以看出:
| $ \alpha = {0^ \circ },{X_P}\tan \beta $ | (6) |
1) α只能为0°、YP, γ是完全独立的两个变量, 可以任意选择, 与其他四个参量XP、ZP、α、β无关。
2) XP、ZP、β三个参数线性相关, 只有两个可以任意选择。
3) 当β为0时, XP也为0。
2.2.2 并联腿机构的位置反解模型运动学的位置反解即给定动平台的姿态计算相关关节变量。在本例中, 求运动学的位置反解即是给定位置YP、ZP和动平台的姿态β、γ, 求三个分支移动副的位移|BiDi|和四边形B1D1D2B2与静平台的夹角φ(初始位置时φ=90°)。由Bi、Di在定坐标系下的坐标向量及式(2), 可以得到矢量:B1D1=[ZPtan β+dcos β-b YP ZP-dsinβ]T, B2D2=[ZPtan β-dcos β+b YP ZP+dsinβ]T, B3D3=[ZPtan β+esin β sinγ YP+ecos γ-c ZP+ecos β·sinγ]T。由机构图形可得四边形B1D1D2B2与静平台的夹角φ=arctan(ZP/YP)=arccot(YP/ZP)。
因此, 对矢量BiDi求模, 并结合φ角的表达式即可以得到2UPU-UPR并联机构的运动学位置反解为
| $ \left\{ \begin{array}{l} \left| {{\mathit{\boldsymbol{B}}_1}{\mathit{\boldsymbol{D}}_1}} \right| = \sqrt {{{\left( {{Z_P}\tan \beta + d\cos \beta - b} \right)}^2} + {{\left( {{Y_P}} \right)}^2} + {{\left( {{Z_P} - d\sin \beta } \right)}^2}} \\ \left| {{\mathit{\boldsymbol{B}}_2}{\mathit{\boldsymbol{D}}_2}} \right| = \sqrt {{{\left( {{Z_P}\tan \beta - d\cos \beta + b} \right)}^2} + {{\left( {{Y_P}} \right)}^2} + {{\left( {{Z_P} + d\sin \beta } \right)}^2}} \\ \left| {{\mathit{\boldsymbol{B}}_3}{\mathit{\boldsymbol{D}}_3}} \right| = \sqrt {{{\left( {{Z_P}\tan \beta + e\sin \beta \sin \gamma } \right)}^2} + {{\left( {{Y_P} + e\cos \gamma - c} \right)}^2} + {{\left( {{Z_P} + e\cos \beta \sin \gamma } \right)}^2}} \\ \varphi = \arctan \frac{{{Z_P}}}{{{Y_P}}} = {\rm{arccot}}\frac{{{Y_P}}}{{{Z_P}}} \end{array} \right. $ | (7) |
令qi=BiDi(i=1, 2, 3), 对式(7) 等号两边同时对t求导可得
| $ {\mathit{\boldsymbol{J}}_q}{\left[ {\begin{array}{*{20}{c}} {{{\dot q}_1}}&{{{\dot q}_2}}&{{{\dot q}_3}}&{\dot \varphi } \end{array}} \right]^{\rm{T}}} - \mathit{\boldsymbol{G}}{\left[ {\begin{array}{*{20}{c}} {\dot \beta }&{\dot \gamma }&{{{\dot Y}_P}}&{{{\dot Z}_P}} \end{array}} \right]^{\rm{T}}} = 0 $ | (8) |
其中矩阵Jq与G分别为
| $ {\mathit{\boldsymbol{J}}_q} = \left[ {\begin{array}{*{20}{c}} {{J_{q11}}}&0&0&0\\ 0&{{J_{q22}}}&0&0\\ 0&0&{{J_{q33}}}&0\\ 0&0&0&{{J_{q44}}} \end{array}} \right] $ | (9) |
| $ \mathit{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} {{G_{11}}}&{{G_{12}}}&{{G_{13}}}&{{G_{14}}}\\ {{G_{21}}}&{{G_{22}}}&{{G_{23}}}&{{G_{24}}}\\ {{G_{31}}}&{{G_{32}}}&{{G_{33}}}&{{G_{34}}}\\ {{G_{41}}}&{{G_{42}}}&{{G_{43}}}&{{G_{44}}} \end{array}} \right] $ | (10) |
其中:Jq11、Jq22、Jq33、Jq44分别为:
当矩阵G不为奇异矩阵时可得
| $ {\left[ {\begin{array}{*{20}{c}} {\dot \beta }&{\dot \gamma }&{{{\dot Y}_P}}&{{{\dot Z}_P}} \end{array}} \right]^{\rm{T}}} = {\mathit{\boldsymbol{G}}^{ - 1}}{\mathit{\boldsymbol{J}}_q}{\left[ {\begin{array}{*{20}{c}} {{{\dot q}_1}}&{{{\dot q}_2}}&{{{\dot q}_3}}&{\dot \varphi } \end{array}} \right]^{\rm{T}}} $ | (11) |
式中J=G-1Jq为并联机构的速度雅克比矩阵。
2.4 2UPU-UPR并联腿机构的奇异性分析根据Jq和G的欠秩形式, 可以将奇异分为三类:运动学反解奇异、运动学正解奇异、混合奇异。
2.4.1 运动学反解奇异第一类奇异为运动学反解奇异, 发生在|Jq|=0、|G|≠0时。在发生反解奇异位形时, 可以认为动平台失去一个或者多个自由度。这意味着在该位形下, 当驱动副上没有任何力矩和力的情况下, 动平台可以承受一个或多个力或力偶。反解奇异通常发生在工作空间的边界处。当|Jq|=0时, 有以下三种可能性。
1) 当Jq11=0, 有B1=0、C1=0、YP=0。即B1=ZPtan β+dcos β-b=0, C1=ZP-dsin β=0。解得:
| $ \left\{ \begin{array}{l} \beta = \arccos \left( {d/b} \right)\\ {Z_P} = \frac{{d\sqrt {{b^2} - {d^2}} }}{b} \end{array} \right.或\left\{ \begin{array}{l} \beta = - \arccos \left( {d/b} \right)\\ {Z_P} = - \frac{{d\sqrt {{b^2} - {d^2}} }}{b} \end{array} \right. $ | (12) |
2) 当Jq22=0, 有B2=0、C2=0、YP=0, 即B2=ZPtan β-dcos β+b=0, C2= ZP+dsin β=0。解得
| $ \left\{ \begin{array}{l} \beta = \arccos \left( {d/b} \right)\\ {Z_P} = - \frac{{d\sqrt {{b^2} - {d^2}} }}{b} \end{array} \right.或\left\{ \begin{array}{l} \beta = - \arccos \left( {d/b} \right)\\ {Z_P} = \frac{{d\sqrt {{b^2} - {d^2}} }}{b} \end{array} \right. $ | (13) |
3) 当Jq33=0, 有B3=0、C3=0、D=0, 即B3=ZP tan β+e sin β sin γ=0, C3=YP+e cos γ-c=0, D=ZP+e cos β sin γ=0。解得
| $ \left\{ \begin{array}{l} {Y_P} = c - e\cos \gamma \\ {Z_P} = - e\cos \beta \sin \gamma \end{array} \right. $ | (14) |
4) 由Jq44=1+F2可知, Jq44≠0。
根据Jq和G的欠秩形式, 可以将奇异分为三类:运动学反解奇异、运动学正解奇异、混合奇异。
但是, 当Jq11=0时, 可得G11=G12=G13=G14=0, 可以推出|G|=0, 与假设条件矛盾。同样, 当Jq22=0时, 可得G21=G22=G23=G24=0。当Jq33=0时, 可得G31=G32=G33=G34=0, 都可以推出|G|=0。因此该机构不存在运动学反解奇异。
2.4.2 运动学正解奇异第二类奇异为运动学正解奇异, 发生在|Jq|≠0、|G|=0时。在发生正解奇异位形时, 可以认为动平台得到一个或者多个自由度。这意味着在此种情况下, 动平台可以在所有驱动都锁住的情况下在某些方向发生运动。在正解奇异位形下, 当所有驱动都锁住时, 机构动平台不能承受一个或多个力或力偶。当|G|=0时, 有以下四种可能性。
1) G14=0, 即tan β(ZP tan β+d cos β-b)+ZP-d sin β=0, 化简得
| $ {Z_P} = b\sin \beta \cos \beta $ | (15) |
2) G21=0, 即[ZP(1+tan β)+d sin β](ZP tan β-d cos β+b)+d cos β(ZP+d sin β)=0, 化简得:
| $ {Z_P} = \left( {1 + {{\tan }^2}\beta } \right)\left( {{Z_P}\tan \beta + b} \right) + bd\sin \beta = 0 $ | (16) |
3) G32=0, 即e sin β cos γ(ZP tan β+e sin β·sin γ)-e sin γ(YP+e cos γ-c)+ e cos β cos· γ(ZP+e cos β sin γ)=0, 化简得
| $ \cos \gamma {Z_P}\left( {\sin \beta \tan \beta + \cos \beta } \right) + c\sin \gamma - \sin \gamma {Y_P} = 0 $ | (17) |
4) G43=0, 即-F/YP=0, F= ZP/YP=0, 化简得
| $ {Z_P} = 0 $ | (18) |
当ZP=0时, 有以下两种情况:① 动平台与静平台重叠, 即三个支链长度都为0, 实际情况不可能出现, 舍去;② 支链1、2与静平台在一个平面内, 此时可以通过限制转动驱动器的转角φ的范围规避。经验证, 当满足式(15) ~(18) 时, |Jq|≠0, 因此该机构存在四种运动学正解奇异, 其中第四种可以通过限制转动驱动器的转角φ进行规避。
2.4.3 混合奇异第三类奇异为混合奇异, 发生在|Jq|=0、|G|=0时。该奇异位形发生在所有驱动都锁住的情况下分支可以承受一个有限运动, 或者当驱动副发生一个有限运动时而动平台不产生运动。
根据前文分析内容, 当|Jq|=|G|=0, 即Jq11=0, 或Jq22=0, 或Jq33=0时, 该机构有三种可能的混合奇异位形。第一种混合奇异发生在第一分支上的两个U副中心重叠到一点(即B1D1杆长为0), 且γ=0时;第二种混合奇异发生在第二分支上的两个U副中心重叠到一点(即B2D2杆长为0), 且γ=0时;第三种混合奇异发生在第三分支上的U副中心与R副中心重叠到一点(即B3D3杆长为0), 且ZP < 0时, 考虑到实际结构此位形不可能出现, 故舍去。因此, 该机构存在两种混合奇异, 且两种混合奇异发生的位型都较为特殊, 可以在设计阶段通过限制支链1、2的杆件尺寸进行规避。
3 机器人步态规划为了保证四足步行机器人行走时机体的静态稳定性, 机器人需保证至少三个腿以上与地面相互接触处于着地状态, 并且四个腿按一定顺序轮换运动, 使其重心能够位于支撑足所构成的支撑三角形内, 即稳定裕度必须大于零。本研究选择“2-1-3-4”的抬腿顺序, 在相同占空比条件下, 该抬腿顺序稳定性最好[20]。
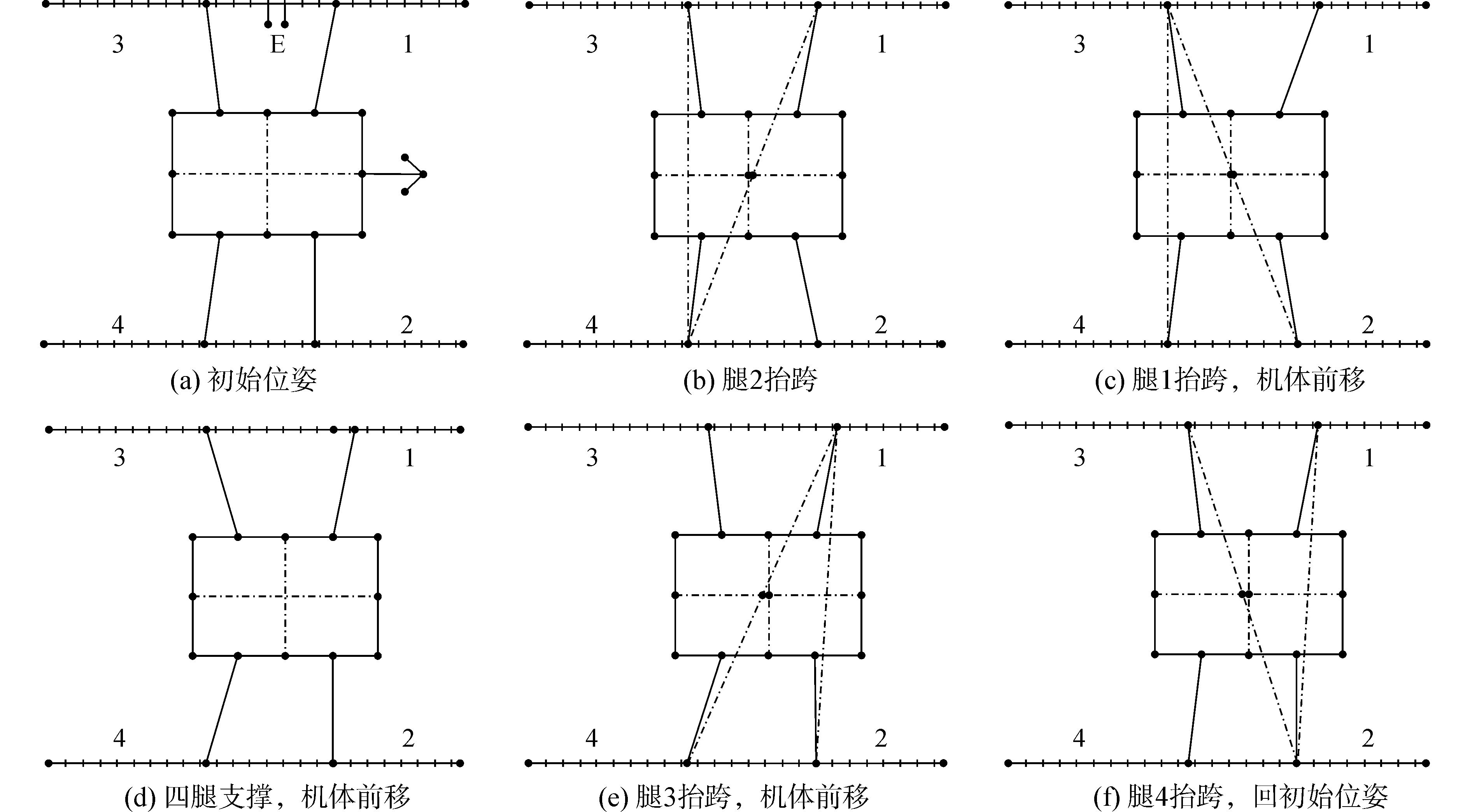
机器人一个周期内的步态如图 4所示, 整个步态分为6步, 初始稳定裕量S=20 mm, 步距λ=120 mm, 箭头所指方向为前进方向。如图 6所示, 机器人具体步态依次如下:1) 初始位姿, 四条腿着地;2) 腿2抬跨, 初始稳定裕量为20 mm, 机体相对于地面无移动, 足尖相对于机体移动120 mm;3) 腿1抬跨, 三条腿支撑地面, 同时机体前移10 mm, 足尖相对于机体移动110 mm;4) 四条腿支撑地面, 同时机体前移100 mm, 保证下一次抬跨腿时机器人的重心位于稳定三角形区域内;5) 腿3抬跨, 三条腿支撑地面, 同时机体前移10 mm, 足尖相对于机体移动110 mm;6) 腿4抬跨, 机体相对于地面无移动, 足尖相对于机体移动120 mm, 回到初始位姿。
|
图 6 机器人直行步态规划 Fig.6 The straight gait planning of the manipulator |
在上述动作过程中, 机体共完成了3次重心调整, 足端相对于地面前移120 mm, 与步距相等。机器人每条腿抬跨时间和四足支撑机体重心调整时间均为2 s, 机器人直行步态行走周期为10 s, 占空比为0.8, 机器人行走平均速度为12 mm/s。
4 算例分析系统参数:构件长度lOB1= lOB2=b=0.5 m, lOB3=c=0.4 m, 动平台各点到动坐标系原点P的距离分别为:lPD1= lPD2=d=0.25 m, lOD3=e=0.2 m。t0=0 s, tf =10 s。系统动平台的运动规律为
α=0;β=10πs(t)/180;γ=20πs(t)/180;Yp=0.50 s3(t)+0.10 s2(t);Zp=0.60 s3(t)+0.2 s2(t)+0.40。其中, s(t)=t/10-sin(2πt/10) /2π (t0≤t≤tf)。
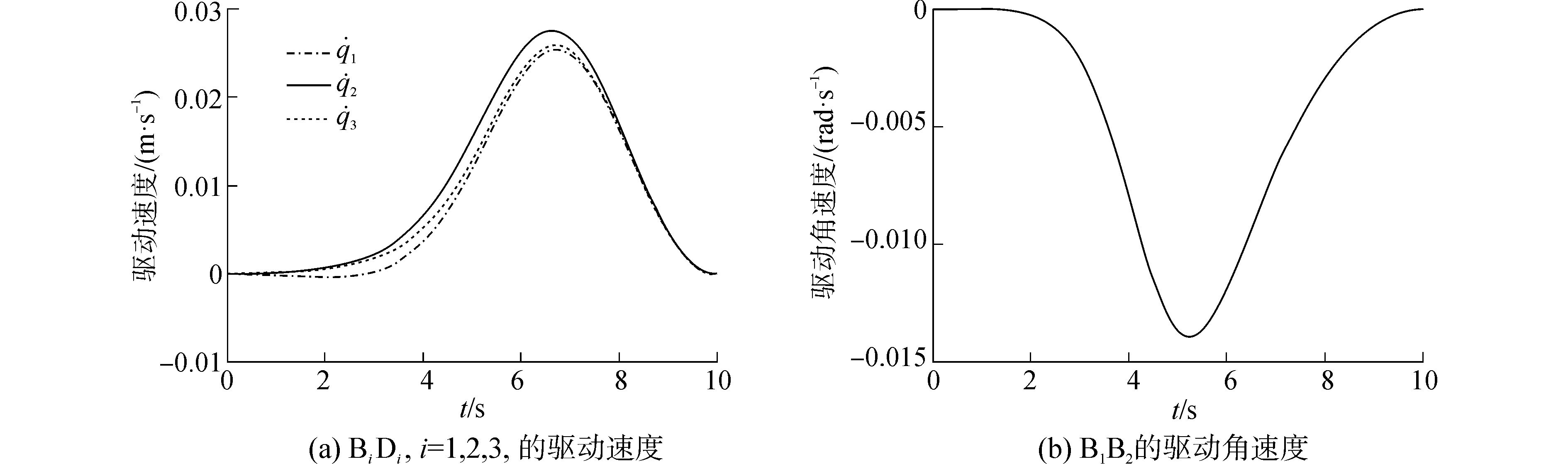
根据上述动平台运动规律, 可以得到动平台的姿态变化曲线, 如图 7所示。其中, 图 7(a)为动平台姿态的速度变化曲线, 图 7(b)为动平台姿态的角速度变化曲线。对于系统给定的动平台运动规律, 通过2UPU-UPR并联机构的运动学反解, 可以求出此并联机构中各驱动构件的运动规律, 如图 8所示。图 8(a)为驱动构件BiDi的线速度变化曲线, 图 8(b)为驱动构件B1B2的角速度变化曲线。

|
图 7 动平台姿态变化曲线 Fig.7 The change curves of the moving platform attitude |
|
图 8 驱动构件运动曲线 Fig.8 The motion curves of the driving components |
从图中可以看出, 在动平台, 静平台均为等腰三角形时, 在给定上述动平台运动规律的情况下, 所有构件的运动为单向运转, 三个移动驱动构件BiDi的线速度运动规律基本相同, 速度大小接近, 在t=7 s左右出现极值, 与动平台姿态速度极值出现位置基本一致;转动驱动构件B1B2的运动方向为反向运转, 在t=5 s左右出现极值, 与动平台姿态角速度极值位置基本一致。
5 结论1) α只能为0°;YP, γ是完全独立的两个变量, 可以任意选择;XP、ZP、β三个参数线性相关, 只有两个可以任意选择;当β为0时, XP也为0。
2) 2UPU-UPR并联机构具有两个转动、两个移动共四个自由度。
3) 2UPU-UPR并联机构不存在运动学反解奇异。
4) 2UPU-UPR并联机构有四种正解奇异和两种混合奇异, 其中第四种正解奇异和两种混合奇异可以通过限制驱动器的转角以及支链的杆长规避。
5) 通过合理的设计, 可以使2UPU-UPR并联机构奇异位形尽可能减少, 满足机构性能要求, 提高其应用潜力。
6) 由2UPU-UPR并联机构组成的四足机器人, 其直行步态规划可以达到较好的运动稳定性和稳定裕度, 适于步行机器人的腿部机构。
| [1] |
谭民, 王硕. 机器人技术研究进展[J]. 自动化学报, 2013, 39(7): 964-972. TAN Min, WANG Shuo. Research progress on robotics[J]. Acta automatica sinica, 2013, 39(7): 964-972. (  0) 0)
|
| [2] |
HIROSHI K, YASUHIRO F, AVIS H C, et al. Adaptive dynamic walking of a quadruped robot on natural ground based on biological concepts[J]. International journal of robotics research, 2007, 26(5): 475-490. DOI:10.1177/0278364907078089 (  0) 0)
|
| [3] |
李满天, 蒋振宇, 郭伟, 等. 四足仿生机器人单腿系统[J]. 机器人, 2014, 36(1): 21-28. LI Mantian, JIANG Zhenyu, GUO Wei, et al. Leg pro-totype of a bio-inspired quadruped robot[J]. Robot, 2014, 36(1): 21-28. (  0) 0)
|
| [4] |
RAIBERT M, BLANKSPOOR K, NELSON G, et al.Bigdog, the rough-terrain quadruped robot[C]//Proceedings of 17th World Congress.The International Federation of Automatic Control. Seoul, Korea, 2008:6-9.
(  0) 0)
|
| [5] |
KALAKRISHNAN M, BUCHLI J, PASTOR P, et al. Learning, planning, and control for quadruped locomotion over challenging terrain[J]. International journal of robotics research, 2011, 30: 236-258. DOI:10.1177/0278364910388677 (  0) 0)
|
| [6] |
SEMINI C, TSAFARAKIS N G, GUGLIELMINO E, et al. Design of HyQ-a hydraulically and electrically actuated quadruped robot[J]. Journal of systems and control engineering, 2011, 225(6): 831-849. (  0) 0)
|
| [7] |
李贻斌, 李彬, 荣学文, 等. 液压驱动四足仿生机器人的结构设计和步态规划[J]. 山东大学学报, 2011, 41(5): 32-36. LI Yibin, LI Bin, RONG Xuewen, et al. Mechanical design and gait planning of a hydraulically actuated quadruped bionic robot[J]. Journal of Shandong University, 2011, 41(5): 32-36. (  0) 0)
|
| [8] |
王洪波, 徐桂玲, 胡星, 等. 四足并联腿步行机器人动力学[J]. 机械工程学报, 2012, 48(23): 76-82. WANG Hongbo, XU Guiling, HU Xing, et al. Dynamics of quadruped walking robot with parallel leg mechanism[J]. Journal of mechanical engineering, 2012, 48(23): 76-82. (  0) 0)
|
| [9] |
GAO F, QI C K, SUN Q, et al. A quadruped robot with parallel mechanism legs[C]//IEEE International Conference on Robotics and Automation. Hong Kong, China, 2014:2566-2566.
(  0) 0)
|
| [10] |
田兴华, 高峰, 陈先宝, 等. 四足仿生机器人混联腿构型设计及比较[J]. 机械工程学报, 2013, 49(6): 81-88. TIAN Xinghua, GAO Feng, CHEN Xianbao, et al. Mechanism design and comparison for quadruped robot with parallel-serial leg[J]. Journal of mechanical engineering, 2013, 49(6): 81-88. (  0) 0)
|
| [11] |
高建设, 李明祥, 侯伯杰, 等. 新型四足步行机器人串并混联腿的运动学分析[J]. 光学精密工程, 2015, 23(11): 3147-3160. GAO Jianshe, LI Mingxiang, HOU Bojie, et al. Kinematics analysis on the serial-parallel leg of a novel quadruped walking robot[J]. Optics and precision engineering, 2015, 23(11): 3147-3160. (  0) 0)
|
| [12] |
FAN C, LIN H, ZHANG Y. Type synthesis of 2T2R, 1T2R and 2R parallel mechanisms[J]. Mechanism and machine theory, 2012, 61: 184-190. (  0) 0)
|
| [13] |
KUMAR N, PICCIN O, BAYLE B. A task-based type synthesis of novel 2T2R parallel mechanisms[J]. Mechanism and machine theory, 2014, 77: 59-72. DOI:10.1016/j.mechmachtheory.2014.02.007 (  0) 0)
|
| [14] |
YE W, FANG Y F, GUO S, et al. Type synthesis of 2T2R parallel mechanisms based on motion equivalent chain method[C]//Proceedings of the Institution of Mechanical Engineers, Part C:Journal of Mechanical Engineering Science, 2014:3209-3217.
(  0) 0)
|
| [15] |
张彦斌, 吴鑫. 完全解耦二移动二转动并联机构结构综合[J]. 农业机械学报, 2013, 44(8): 250-256. ZHANG Yanbin, WU Xin. Structural synthesis of fully-decoupled two-translational and two-rotational parallel Mechanisms[J]. Transactions of the Chinese society of agricultural Machinery, 2013, 44(8): 250-256. DOI:10.6041/j.issn.1000-1298.2013.08.043 (  0) 0)
|
| [16] |
曹毅, 秦友蕾, 陈海, 等. 完全各向同性解耦2T2R型并联机器人构型综合[J]. 哈尔滨工业大学学报, 2016, 48(7): 94-100. CAO Yi, QIN Youlei, CHEN Hai, et al. Structural synthesis of fully isotropic and decoupled 2T2R parallel robot[J]. Journal of Harbin Institute of Technology, 2016, 48(7): 94-100. DOI:10.11918/j.issn.0367-6234.2016.07.015 (  0) 0)
|
| [17] |
YE W, FANG Y F, GUO S, et al. Kinematics and singularity analysis of a 2R2T parallel mechanisms[C]//Proceedings of the ASME International Design Engineering Technical Conferences and Computers and Information in Engineering Conference.[S.l.], 2015:9-14.
(  0) 0)
|
| [18] |
温如凤, 方跃法, 陈亚琼. 一种2R2T并联机构的运动学及性能分析[J]. 北京交通大学学报, 2016, 40(1): 72-79. WEN Rufeng, FANG Yuefa, CHEN Yaqiong. Kinematics and performance analysis of a 2R2T parallel mechanism[J]. Journal of Beijing Jiaotong University, 2016, 40(1): 72-79. (  0) 0)
|
| [19] |
黄真, 赵永生, 赵铁石. 高等空间机构学[M]. 北京: 北京高等教育出版社, 2006. HUANG Zhen, ZHAO Yongsheng, ZHAO Tieshi. Advanced spatial mechanism[M]. Beijing: Higher Education Press, 2006. (  0) 0)
|
| [20] |
蒋新松. 机器人学导论[M]. 沈阳: 辽宁科学技术出版社, 1994. JIANG Xinsong. Introduction to robotics[M]. Shenyang: Liaoning Science and Technology Press, 1994. (  0) 0)
|
 2018, Vol. 39
2018, Vol. 39


