穿孔消声器被广泛应用于机械设备的噪声控制。SELAMET等使用准一维方法对三通穿孔管消声器进行了研究并分析了结构参数变化对传递损失的影响[1]。SELAMET等应用解析方法预测了直通穿孔管阻性消声器的声学性能[2]。JI使用子结构多域边界元方法对直通穿孔管消声器及具有共振腔的穿孔管消声器进行了研究[3],此后,多域边界元方法被用于阻性消声器的声学性能预测[4]。JI等使用同样的方法对三通穿孔管消声器进行了计算,研究了穿孔率、穿孔部分长度等对消声性能的影响[5]。FANG等[6]使用有限元方法对穿孔管消声器进行了模态分析。解析方法适用于规则结构消声器的声学性能预测,对实际应用中具有复杂内部结构的消声器无法应用,有限元方法和多域边界元方法在理论上适用于任意结构。但也存在一些缺点,在应用多域边界元方法时,必须按照边界条件将内部结构划分为许多子结构,再根据声学变量的连续性条件在边界上建立各子结构之间的联系,对于复杂的内部结构,前处理过程势必过于繁琐,进而限制了其应用范围。应用有限元方法进行穿孔消声器的计算已经十分成熟,相应的商业软件已经被广泛应用,但是对于穿孔面,由于有限元方法一般采用传递阻抗建立穿孔面内外两侧的关系,所以一般要求两个面的网格一一对应,对于具有多个穿孔面的消声器,前处理也会较为繁琐。WU等提出了一种混体边界元方法[7-8],此方法适合具有复杂内部结构消声器的声学性能计算,不需要人为划分子结构,对于穿孔面,只需要建立一层面网格,因此非常适合具有较多穿孔结构消声器的传递损失计算。
然而,由于传统边界元方法自身的局限性,在处理大尺度和高频问题时对计算机内存的要求较高并会消耗较多的计算时间,近年来,快速多极算法的出现有效地克服了传统边界元方法的局限,应用快速多极边界元方法计算大尺度声学问题也取得了较大的进展[9-13]。
本文将混体边界元方法与快速多极算法结合用于穿孔消声器传递损失的计算,考察快速多极混体边界元方法的计算精度和计算效率,研究穿孔管位置对两通穿孔管消声器传递损失的影响,分析穿孔挡板对三通穿孔消声器声学性能的影响。
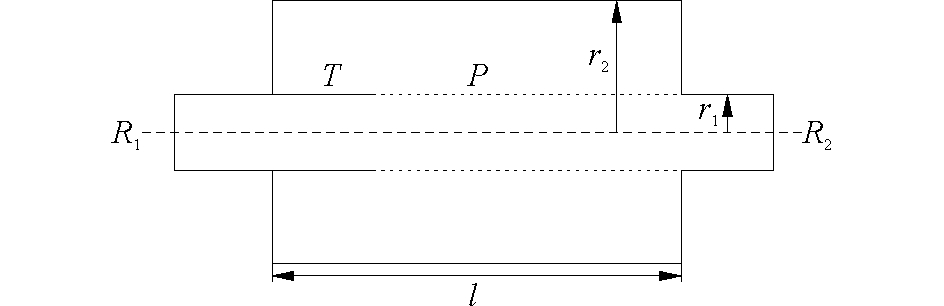
1 计算方法 1.1 混体边界元方法直接混体边界元方法源于传统的子结构边界元方法,将具有复杂内部结构的消声器分成若干具有明确边界的几个部分,对每一部分使用边界积分方程描述,然后,根据各部分的交界面的声学参数连续条件,得到整体控制方程,交界面有两个未知量时,超奇异积分方程被用来提供额外的方程。对于如图 1所示的直通穿孔管消声器,混体边界元方法可以表示为[7]
| $ \begin{array}{*{20}{c}} {\int_R {\left( {p\left( {{r_Q}} \right)\frac{{\partial G\left( {{r_p},{r_Q}} \right)}}{{\partial {n_Q}}} + {\rm{j}}kz{v_n}\left( {{r_Q}} \right)G\left( {{r_p},{r_Q}} \right)} \right){\rm{d}}S} + }\\ {\int_{T + P} {\frac{{\partial G\left( {{r_p},{r_Q}} \right)}}{{\partial {n_Q}}}\left( {{p^ + } - {p^ - }} \right){\rm{d}}S} = } \end{array} $ | (1) |
| $ \left\{ \begin{array}{l} 0.5p\left( {{r_p}} \right),p \in R\\ 0.5\left[ {{p^ + }\left( {{r_p}} \right) + {p^ - }\left( {{r_p}} \right)} \right],p \in T + P \end{array} \right. $ | (2) |
| $ \begin{array}{*{20}{c}} {\int_R {\left( {p\left( {{r_Q}} \right)\frac{{{\partial ^2}G\left( {{r_p},{r_Q}} \right)}}{{\partial {n_Q}\partial {n_p}}} + jkz{v_n}\left( {{r_Q}} \right)\frac{{\partial G\left( {{r_p},{r_Q}} \right)}}{{\partial {n_p}}}} \right){\rm{d}}S} + }\\ {\int_{T + P} {\frac{{{\partial ^2}G\left( {{r_p},{r_Q}} \right)}}{{\partial {n_Q}\partial {n_p}}}\left( {{p^ + } - {p^ - }} \right){\rm{d}}S} = } \end{array} $ | (3) |
| $ \left\{ \begin{array}{l} 0,p \in T\\ \frac{{{\rm{j}}{k_0}}}{\zeta }\left[ {{p^ + }\left( {{r_p}} \right) - {p^ - }\left( {{r_p}} \right)} \right],p \in P \end{array} \right. $ | (4) |
式中:P和Q分别为源点和场点;G=e-jk0r/4πrPQ,为格林函数;k为波数;z为空气中的特性阻抗;ζ为穿孔阻抗。边界条件R为常规边界条件,包括进口边界R1,出口边界R2以及刚性壁,T为内部薄壁边界,P为穿孔边界。这里只列出了本文涉及到的边界的直接混体边界元的数学表达式,完整的控制方程可以从文献[7]获得,此处不再赘述。进口给定振速v=1,出口给定阻抗边界条件,式(1)~(3) 组成方程组:
| $ \left[ {\begin{array}{*{20}{c}} {E + B + C}&I\\ {E' + B' + C'}&{I'} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} p\\ {\Delta {p_{T + P}}} \end{array}} \right] = {\rm{j}}\rho \omega \left[ {\begin{array}{*{20}{c}} {{v_n}}&0\\ 0&{{v_n}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} A\\ {A'} \end{array}} \right] $ | (5) |
其中
| $ {E_{ij}} = \frac{1}{2}{\delta _{ij}},\;\;\;{{E'}_{ij}} = \frac{{ik}}{\zeta }{\delta _{ij}}, $ |
| $ {B_{ij}} = \int\limits_R {\frac{{\partial G}}{{\partial n}}{\rm{d}}{S_Q}} ,\;\;\;{{B'}_{ij}} = \int\limits_R {\frac{{{\partial ^2}G}}{{\partial n\partial {n_P}}}{\rm{d}}{S_Q}} , $ |
| $ {C_{ij}} = \frac{{ik}}{z}\int\limits_{{R_2}} {G{\rm{d}}{S_Q}} ,\;\;\;{{C'}_{ij}} = \frac{{ik}}{z}\int\limits_{{R_2}} {\frac{{\partial G}}{{\partial {n_P}}}{\rm{d}}{S_Q}} , $ |
| $ {A_{ij}} = - \int\limits_{{R_1}} {G{\rm{d}}{S_Q}} ,\;\;\;{{A'}_{ij}} = - \int\limits_{{R_1}} {\frac{{\partial G}}{{\partial {n_P}}}{\rm{d}}{S_Q}} , $ |
| $ {I_{ij}} = \int\limits_P {\frac{{\partial G}}{{\partial n}}{\rm{d}}{S_Q}} ,\;\;\;{{I'}_{ij}} = \int\limits_p {\frac{{{\partial ^2}G}}{{\partial n\partial {n_P}}}{\rm{d}}{S_Q}} $ |
式中:E′只有源点P在穿孔边界时存在,对刚性壁边界其值为0,δ为Kronecker′s delta函数。求解式(5),即可得到消声器进出口节点的声压值用于传递损失的计算,本文中,使用的单元类型为常单元。
|
图 1 直通穿孔管消声器 Fig.1 Straight-through perforated tube silencer |
快速多极边界元中格林函数可以表示为[9]
| $ G = \frac{{{\rm{j}}k}}{{16{{\rm{ \mathsf{ π} }}^2}}}\oint {{E_{PL}}\left( {\mathit{\boldsymbol{\hat s}}} \right){T_{LM}}\left( {\mathit{\boldsymbol{\hat s}}} \right){E_{MQ}}\left( {\mathit{\boldsymbol{\hat s}}} \right){\rm{d}}\mathit{\boldsymbol{\hat s}}} $ | (6) |
其中,
| $ {E_{PL}}\left( {\hat s} \right) = \exp \left( {{\rm{j}}k\mathit{\boldsymbol{\hat s}} \cdot {\mathit{\boldsymbol{r}}_{PL}}} \right) $ | (7) |
| $ {T_{LM}}\left( {\hat s} \right) = \sum\limits_{l = 0}^\infty {{{\rm{j}}^l}\left( {2l + 1} \right)h_l^{\left( 1 \right)}\left( {k{r_{LM}}} \right){P_l}\left( {\mathit{\boldsymbol{\hat s}} \cdot {{\mathit{\boldsymbol{\hat r}}}_{LM}}} \right)} $ | (8) |
式中:L为本地展开点,M为多极展开点,
| $ \frac{{\partial G}}{{\partial n}} = \frac{{{{\left( {{\rm{j}}k} \right)}^2}}}{{16{{\rm{ \mathsf{ π} }}^2}}}\oint {{E_{PL}}\left( {\mathit{\boldsymbol{\hat s}}} \right){T_{LM}}\left( {\hat s} \right){E_{MQ}}\left( {\mathit{\boldsymbol{\hat s}}} \right)\left( {\mathit{\boldsymbol{n}} \cdot \mathit{\boldsymbol{\hat s}}} \right){\rm{d}}\mathit{\boldsymbol{\hat s}}} $ | (9) |
将式(9) 对P求偏导,得到
| $ \begin{array}{*{20}{c}} {\frac{{{\partial ^2}G}}{{\partial n\partial {n_P}}} = \frac{{{{\left( {{\rm{j}}k} \right)}^3}}}{{16{{\rm{ \mathsf{ π} }}^2}}}\oint {\left( {{\mathit{\boldsymbol{n}}_P} \cdot \mathit{\boldsymbol{\hat s}}} \right){E_{PL}}\left( {\mathit{\boldsymbol{\hat s}}} \right){T_{LM}}\left( {\mathit{\boldsymbol{\hat s}}} \right) \cdot } }\\ {{E_{MQ}}\left( {\mathit{\boldsymbol{\hat s}}} \right)\left( {\mathit{\boldsymbol{n}} \cdot \mathit{\boldsymbol{\hat s}}} \right){\rm{d}}\hat s} \end{array} $ | (10) |
在远场计算中,源点与场点之间的影响系数存在多级传递关系,格林函数及其导数的多极子展开式可写成:
| $ G = \frac{{{\rm{j}}k}}{{16{{\rm{ \mathsf{ π} }}^2}}}\oint {{E_{P{\lambda _{mL}}}}\left( {\mathit{\boldsymbol{\hat s}}} \right)Z_{{\lambda _{mL}}{\lambda _{m'L}}}^I\left( {\mathit{\boldsymbol{\hat s}}} \right){E_{{\lambda _{m'L}}Q}}\left( {\mathit{\boldsymbol{\hat s}}} \right){\rm{d}}\mathit{\boldsymbol{\hat s}}} $ | (11) |
| $ \frac{{\partial G}}{{\partial n}} = \frac{{{{\left( {jk} \right)}^2}}}{{16{{\rm{ \mathsf{ π} }}^2}}}\oint {{E_{P{\lambda _{mL}}}}\left( {\mathit{\boldsymbol{\hat s}}} \right)Z_{{\lambda _{mL}}{\lambda _{m'L}}}^I\left( {\mathit{\boldsymbol{\hat s}}} \right){E_{{\lambda _{m'L}}Q}}\left( {\mathit{\boldsymbol{\hat s}}} \right)\left( {\mathit{\boldsymbol{n}} \cdot \mathit{\boldsymbol{\hat s}}} \right){\rm{d}}\mathit{\boldsymbol{\hat s}}} $ | (12) |
同理,将式(12) 对P求偏导,得到
| $ \begin{array}{*{20}{c}} {\frac{{{\partial ^2}G}}{{\partial n\partial {n_P}}} = \frac{{{{\left( {{\rm{j}}k} \right)}^3}}}{{16{{\rm{ \mathsf{ π} }}^2}}}\oint {\left( {{\mathit{\boldsymbol{n}}_P} \cdot \mathit{\boldsymbol{\hat s}}} \right){E_{P{\lambda _{{m_L}}}}}\left( {\mathit{\boldsymbol{\hat s}}} \right)Z_{{\lambda _{{m_L}}}{\lambda _{{{m'}_L}}}}^I\left( {\mathit{\boldsymbol{\hat s}}} \right) \cdot } }\\ {{E_{{\lambda _{{{m'}_L}}}Q}}\left( {\mathit{\boldsymbol{\hat s}}} \right)\left( {\mathit{\boldsymbol{n}} \cdot \mathit{\boldsymbol{\hat s}}} \right){\rm{d}}\hat s} \end{array} $ | (13) |
其中,
| $ Z_{{\lambda _{{m_L}}}{\lambda _{{{m'}_L}}}}^I\left( {\mathit{\boldsymbol{\hat s}}} \right) = \prod\limits_{l = I}^{L - 1} {{E_{{\lambda _{{m_{l + 1}}}}}}\left( {\mathit{\boldsymbol{\hat s}}} \right){T_{{\lambda _{{m_I}}}{\lambda _{{{m'}_I}}}}}\left( {\mathit{\boldsymbol{\hat s}}} \right)} \prod\limits_{l = 1}^{L - 1} {{E_{{\lambda _{{{m'}_l}}}{\lambda _{{{m'}_{l + 1}}}}}}} $ | (14) |
式中: λx指格栅组x的中心点;组m′l表示在l级中组ml的交互组;L为对边界节点分级时的最低级数;I为所计算交互组所在的级数,在2级之前不存在交互组,近场组、交互组的定义和划分如图 2所示。图 2将式(11)~(13) 代入式(5) 中的系数表达式,得到
| $ \left[ {\begin{array}{*{20}{c}} {{A_{ij}}}\\ {{B_{ij}}}\\ {{C_{ij}}}\\ {{I_{ij}}} \end{array}} \right] = \frac{{{\rm{j}}k}}{{16{{\rm{ \mathsf{ π} }}^2}}}\oint {{E_{i{\lambda _{{m_L}}}}}\left( {\mathit{\boldsymbol{\hat s}}} \right)Z_{{\lambda _{{m_L}}}{\lambda _{{{m'}_L}}}}^I\left( {\mathit{\boldsymbol{\hat s}}} \right)} \left[ {\begin{array}{*{20}{c}} {{\alpha _{{\lambda _{m_L^{'j}}}}}}\\ {{\beta _{{\lambda _{m_L^{'j}}}}}}\\ {{\gamma _{{\lambda _{m_L^{'j}}}}}}\\ {{\eta _{{\lambda _{m_L^{'j}}}}}} \end{array}} \right]{\rm{d}}\mathit{\boldsymbol{\hat s}} $ | (15) |
| $ \left[ {\begin{array}{*{20}{c}} {{{A'}_{ij}}}\\ {{{B'}_{ij}}}\\ {{{C'}_{ij}}}\\ {{{I'}_{ij}}} \end{array}} \right] = \frac{{ - {k^2}}}{{16{{\rm{ \mathsf{ π} }}^2}}}\oint {{{\left( {{\mathit{\boldsymbol{n}}_P} \cdot \mathit{\boldsymbol{\hat s}}} \right)}_{i{\lambda _{{m_L}}}}}\left( {\mathit{\boldsymbol{\hat s}}} \right)Z_{{\lambda _{{m_L}}}{\lambda _{{{m'}_L}}}}^I\left( {\mathit{\boldsymbol{\hat s}}} \right)} \left[ {\begin{array}{*{20}{c}} {{\alpha _{{\lambda _{m_L^{'j}}}}}}\\ {{\beta _{{\lambda _{m_L^{'j}}}}}}\\ {{\gamma _{{\lambda _{m_L^{'j}}}}}}\\ {{\eta _{{\lambda _{m_L^{'j}}}}}} \end{array}} \right]{\rm{d}}\mathit{\boldsymbol{\hat s}} $ | (16) |
其中
| $ {\alpha _{{\lambda _{m_L^{'j}}}}}\left( {\mathit{\boldsymbol{\hat s}}} \right) = \int_{{R_1}} {{E_{{\lambda _{m_L^{'Q}}}}}\left( {\mathit{\boldsymbol{\hat s}}} \right){\rm{d}}{S_Q}} $ | (17) |
| $ {\beta _{{\lambda _{m_L^{'j}}}}}\left( {\mathit{\boldsymbol{\hat s}}} \right) = {\rm{i}}k\int_{{R_1}} {{E_{{\lambda _{m_L^{'Q}}}}}\left( {\mathit{\boldsymbol{\hat s}}} \right)\left( {{\mathit{\boldsymbol{n}}_Q} \cdot \mathit{\boldsymbol{\hat s}}} \right){\rm{d}}{S_Q}} $ | (18) |
| $ {\gamma _{{\lambda _{m_L^{'j}}}}}\left( {\mathit{\boldsymbol{\hat s}}} \right) = \frac{{{\rm{j}}k}}{z}\int_{{R_2}} {{E_{{\lambda _{m_L^{'Q}}}}}\left( {\mathit{\boldsymbol{\hat s}}} \right){\rm{d}}{S_Q}} $ | (19) |
| $ {\eta _{{\lambda _{m_L^{'j}}}}}\left( {\mathit{\boldsymbol{\hat s}}} \right) = {\rm{i}}k\int_P {{E_{{\lambda _{m_L^{'Q}}}}}\left( {\mathit{\boldsymbol{\hat s}}} \right)\left( {{\mathit{\boldsymbol{n}}_Q} \cdot \mathit{\boldsymbol{\hat s}}} \right){\rm{d}}{S_Q}} $ | (20) |

|
图 2 分级结构及通用交互组 Fig.2 Hierarchical cell structure and common interaction cell |
快速多极混体边界元方法的计算过程如下:
1) 远场区域矩阵矢量积计算过程。
① 在最低级L,计算所有组mL在每个球面积分插值点
| $ \begin{array}{l} {\xi _{{m_L}}} = \left( {\hat s_n^L} \right) = \sum\limits_{j \in {B_{{m_L}}}} {} \\ \left[ {\begin{array}{*{20}{c}} {\left( {{\beta _{{\lambda _{mL}}j}}\left( {\mathit{\boldsymbol{\hat s}}_n^L} \right) + {\gamma _{{\lambda _{mL}}j}}\left( {\mathit{\boldsymbol{\hat s}}_n^L} \right) + {\eta _{{\lambda _{mL}}j}}\left( {\mathit{\boldsymbol{\hat s}}_n^L} \right)} \right){p_j}}\\ {{\alpha _{{\lambda _{mL}}j}}\left( {\mathit{\boldsymbol{\hat s}}_n^L} \right){v_j}} \end{array}} \right] \end{array} $ | (21) |
式中:n∈[0, 2(NcL)2],代表单位球面的离散点;BmL为组mL所包含的单元集合。
② 在接下来的较高级l(l=L-1,L-2,…,2) 中,继续计算所有组在积分插值点
| $ {\xi _{{m_l}}}\left( {\mathit{\boldsymbol{\hat s}}_{n'}^l} \right) = \sum\limits_{{m_{l + 1}} \in {C_{{m_l}}}} {{E_{{\lambda _{{m_l}}}{\lambda _{{m_{l + 1}}}}}}\left( {\mathit{\boldsymbol{\hat s}}_{n'}^l} \right)} \cdot \sum\limits_{n = 1}^{2{{\left( {N_c^{l + 1}} \right)}^2}} {{W_{n'n}}{\xi _{{m_{l + 1}}}}\left( {\mathit{\boldsymbol{\hat s}}_n^{l + 1}} \right)} $ | (22) |
式中:Wn′n为插值方法(如拉格朗日法)的插值系数,Cml为组ml+1的父辈组所包含的子组集,此步计算将在向上传递的每一级中进行,直到级数为2。
③ 在每一级l(l=2,3,…,L),计算该级所有组在积分插值点
| $ {\tau _{{m_l}}}\left( {\mathit{\boldsymbol{\hat s}}_n^l} \right) = \sum\limits_{{{m'}_l} \in {F_{{m_l}}}} {{T_{{\lambda _{{m_l}}}{\lambda _{{{m'}_l}}}}}\left( {\mathit{\boldsymbol{\hat s}}_{n'}^l} \right){\xi _{{{m'}_l}}}\left( {\mathit{\boldsymbol{\hat s}}_{n'}^l} \right)} $ | (23) |
式中:Fml为组ml的交互组集。需要注意的是,为了简便,在Tλmlλm′l的计算中,使用了通用交互组,其定义划分见图 2,在迭代计算之前,根据格栅的位置关系,Tλmlλm′l已经计算完毕,迭代过程中只需根据距离关系调用。
④ 在接下来的较高级l(l=2,3,…,L-1),计算所有组在积分插值点
| $ \begin{array}{l} {\zeta _{{m_{l + 1}}}}\left( {\mathit{\boldsymbol{\hat s}}_n^{l + 1}} \right) = \sum\limits_{n' = 1}^{2{{\left( {N_c^l} \right)}^2}} {\frac{{\omega _{n'}^l}}{{\omega _n^{l + 1}}}{W_{n'n}}{E_{{\lambda _{{m_l} + 1}}{\lambda _{{m_l}}}}}\left( {\mathit{\boldsymbol{\hat s}}_{n'}^l} \right) \cdot } \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {{\zeta _{{m_l}}}\left( {\mathit{\boldsymbol{\hat s}}_{n'}^l} \right) + {\tau _{{m_l}}}\left( {\mathit{\boldsymbol{\hat s}}_{n'}^l} \right)} \right) \end{array} $ | (24) |
可见,式(24) 为递推公式,由于在1级与2级之间不存在向下传递关系,因而有
| $ {\zeta _{{m_2}}}\left( {\mathit{\boldsymbol{\hat s}}_{n'}^2} \right) = 0 $ | (25) |
此步计算将在向下传递的每一级中进行,直到级数为L-1。
⑤ 在最低级L,计算每个节点i的远场影响系数ϕF, i,对应式(15),计算公式为
| $ {\phi _{F,i}} = \frac{{{\rm{j}}k}}{{16{{\rm{ \mathsf{ π} }}^2}}}\sum\limits_{n = 1}^{2{{\left( {N_c^L} \right)}^2}} {\omega _n^L{E_{i{\lambda _{{m_L}}}}}\left( {\mathit{\boldsymbol{\hat s}}_n^L} \right) \cdot \left( {{\zeta _{{m_L}}}\left( {\mathit{\boldsymbol{\hat s}}_n^L} \right) + {\tau _{{m_l}}}\left( {\mathit{\boldsymbol{\hat s}}_n^L} \right)} \right)} $ | (26) |
对应式(16),计算公式为
| $ \begin{array}{l} {\psi _{F,i}} = \frac{{ - {k^2}}}{{16{{\rm{ \mathsf{ π} }}^2}}}\sum\limits_{n = 1}^{2{{\left( {N_c^L} \right)}^2}} {\omega _n^L\left( {{\mathit{\boldsymbol{n}}_i} \cdot \mathit{\boldsymbol{\hat s}}_n^L} \right){E_{i{\lambda _{{m_L}}}}}\left( {\mathit{\boldsymbol{\hat s}}_n^L} \right) \cdot } \\ \;\;\;\;\;\;\;\;\;\left( {{\zeta _{{m_L}}}\left( {\mathit{\boldsymbol{\hat s}}_n^L} \right) + {\tau _{{m_l}}}\left( {\mathit{\boldsymbol{\hat s}}_n^L} \right)} \right) \end{array} $ | (27) |
2) 近场区域矩阵矢量积计算过程。
在最低级,若节点i所在组为mL,其近场组集为NmL,则近场矩阵矢量积即为计算节点i与所含节点间的影响系数,对奇异积分方程,计算公式为
| $ {\phi _{N,i}} = \sum\limits_{{{m'}_L} \in {N_{{m_L}}}} {\sum\limits_{j \in {B_{{{m'}_L}}}} {\left[ {\begin{array}{*{20}{c}} {\left( {{E_{ij}} + {B_{ij}} + {C_{ij}}} \right){p_j} + {I_{ij}}\Delta {p_j}}\\ {{A_{ij}}{v_j}} \end{array}} \right]} } $ | (28) |
对超奇异积分方程,计算公式为
| $ {\psi _{N,i}} = \sum\limits_{{{m'}_L} \in {N_{{m_L}}}} {\sum\limits_{j \in {B_{{{m'}_L}}}} {\left[ {\begin{array}{*{20}{c}} {\left( {{{E'}_{ij}} + {{B'}_{ij}} + {{C'}_{ij}}} \right){p_j} + {{I'}_{ij}}\Delta {p_j}}\\ {{{A''}_{ij}}{v_j}} \end{array}} \right]} } $ | (29) |
最后,将近场影响系数与远场影响系数相加得到每个节点的影响系数,经过迭代计算即可得到消声器进出口节点的声压值。
2 算例验证及计算效率分析考虑一个直通穿孔管消声器,对应图 1中尺寸为:r1=0.024 5 m,r2=0.082 2 m,l=0.257 2 m,穿孔率Ф==0.08,孔径dh0.002 49 m,壁厚tw=0.000 9 m。
穿孔阻抗表示为[14]
| $ \zeta = \left[ {R + {\rm{j}}X} \right]/\phi $ | (30) |
R和X的计算表达式:
| $ R = \left( {1 + {t_w}/{d_h}} \right)\sqrt {8k\mu /{z_0}} $ | (31) |
| $ X = k\left( {{t_w} + \alpha {d_h}} \right) $ | (32) |
式中:μ为空气动力粘性系数,α为单一孔模型的端部修正系数,基于活塞驱动模型
| $ \alpha =\frac{4}{{{\text{ }\!\!\pi\!\!\text{ }}^{2}}}\frac{1}{{{\left( \xi \eta \right)}^{0.5}}}\sum\limits_{m=0}^{\infty }{\sum\limits_{n=0}^{\infty }{{}^{'}{{\varepsilon }_{mn}}\frac{\text{J}_{1}^{2}\left( \text{ }\!\!\pi\!\!\text{ }\sqrt{{{\left( m\xi \right)}^{2}}+{{\left( n\eta \right)}^{2}}} \right)}{{{\left( {{m}^{2}}\left( h/b \right)+{{n}^{2}}\left( b/h \right) \right)}^{1.5}}}}} $ | (33) |
式中:b和h为相邻两孔在两个方向上的距离;ξ=dh/b,η=dh/h;式中第二个求和符号的上标“′”表示m和n不能同时为零,当m≠0且n≠0时,εmn=1,否则εmn=0.5;J1为第一类一阶贝塞尔函数。
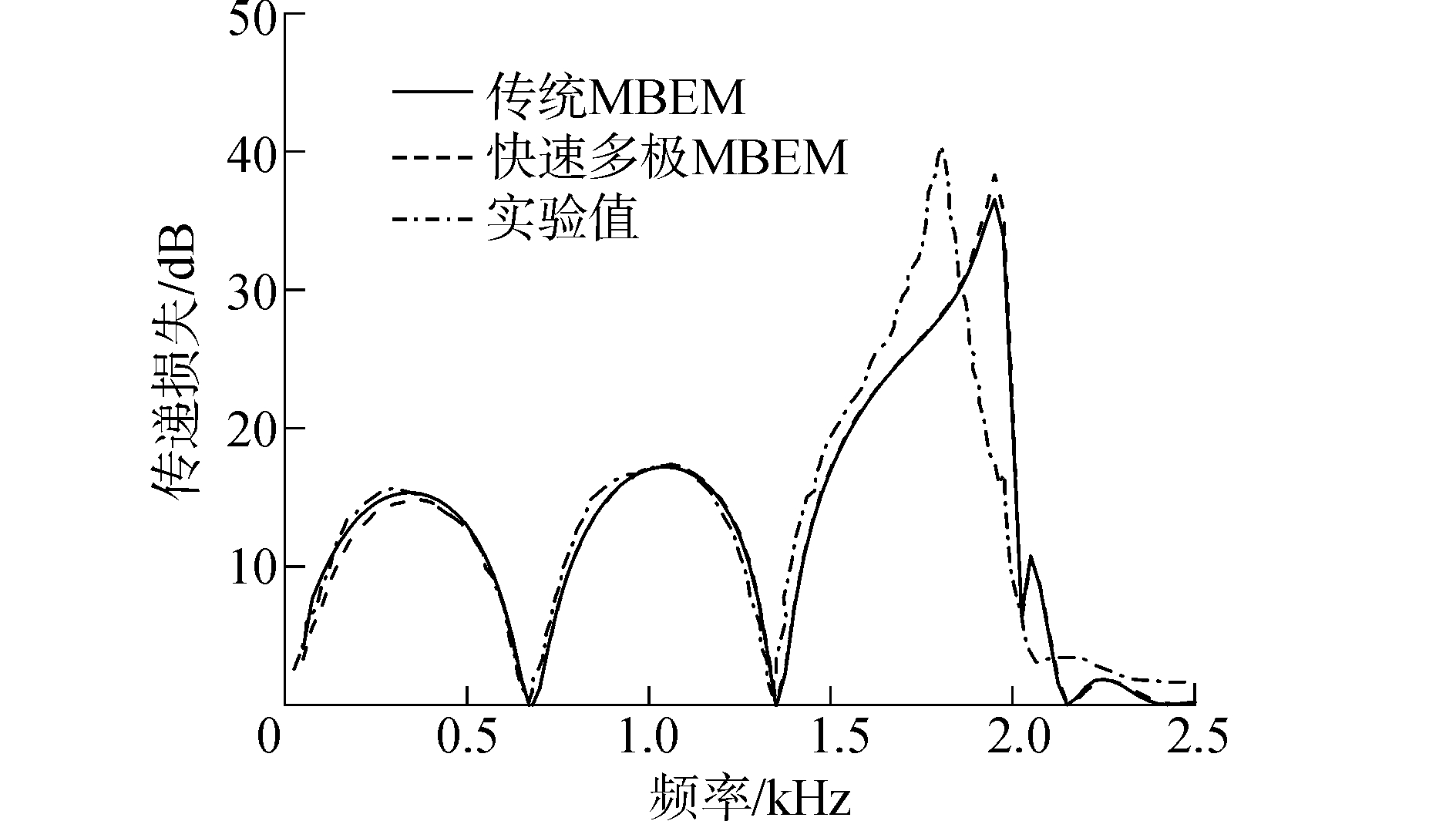
使用传统混体边界元方法与快速多极混体边界元方法分别计算传递损失并与实验值比较得到结果如图 3所示。可以看出,两种方法的计算结果与实验值吻合良好,验证了快速多极混体边界元方法的正确性。
|
图 3 直通穿孔管消声器计算结果比较 Fig.3 Transmission loss prediction of straight-through perforated silencer |
下面从计算效率方面比较两种方法,选定频率为350 Hz,在不同的网格数量的情况下比较计算时间,结果列于表 1。所有计算均在Intel i7 3632QM, 2.2 GHz的计算机上进行,从表中可以看出,在给定频率下,随着网格数量的增加,相比于传统混体边界元方法,快速多极混体边界元方法的优势越来越明显,所以,在实际应用中,可以根据研究问题的尺度大小选择适当的方法。
| 表 1 直通穿孔管消声器计算时间比较 Tab.1 Computation time comparison of straight through perforated tube silencer |
本节应用快速多极混体边界元方法研究穿孔管位置及穿孔挡板对消声器传递损失的影响。
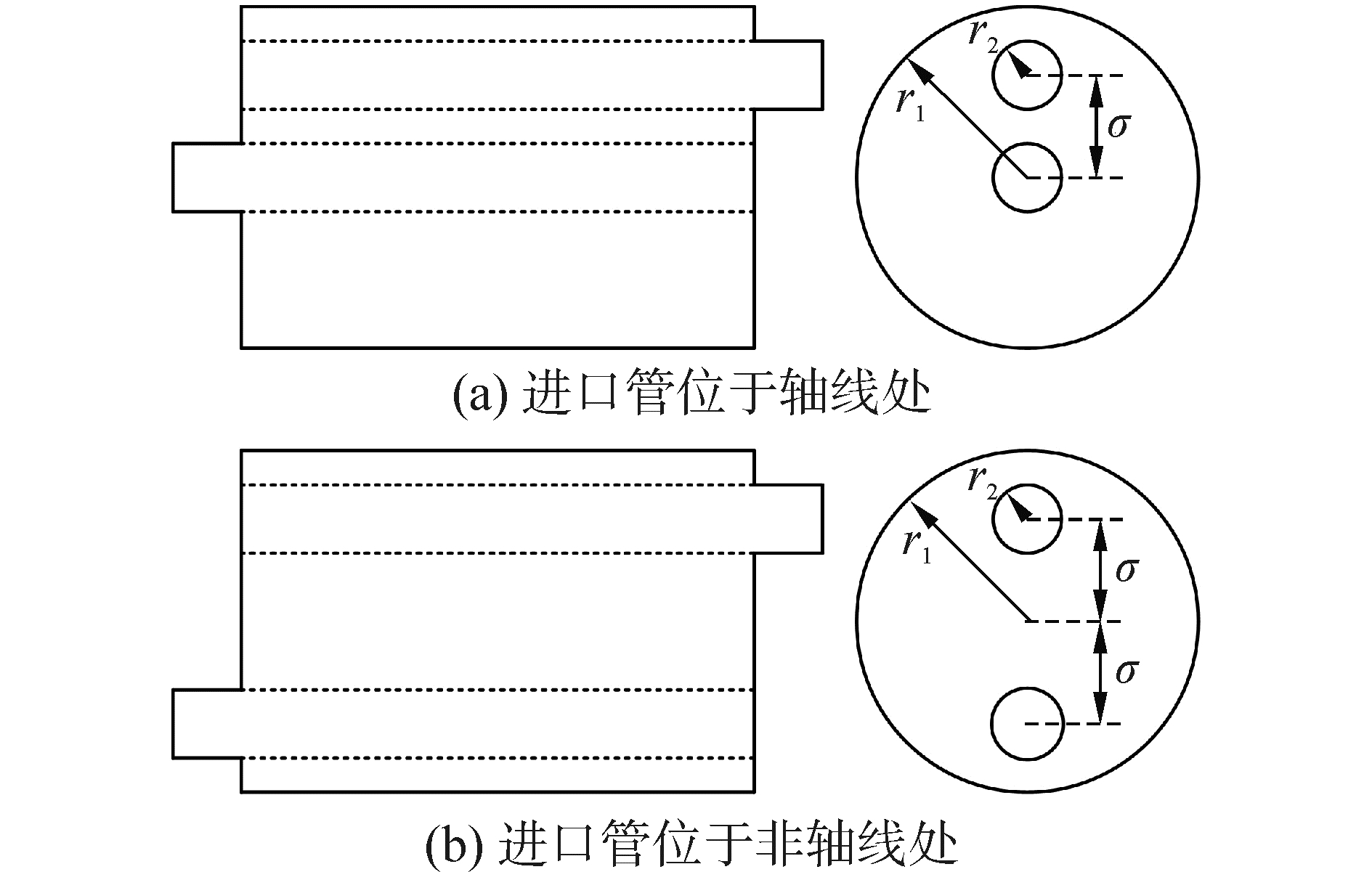
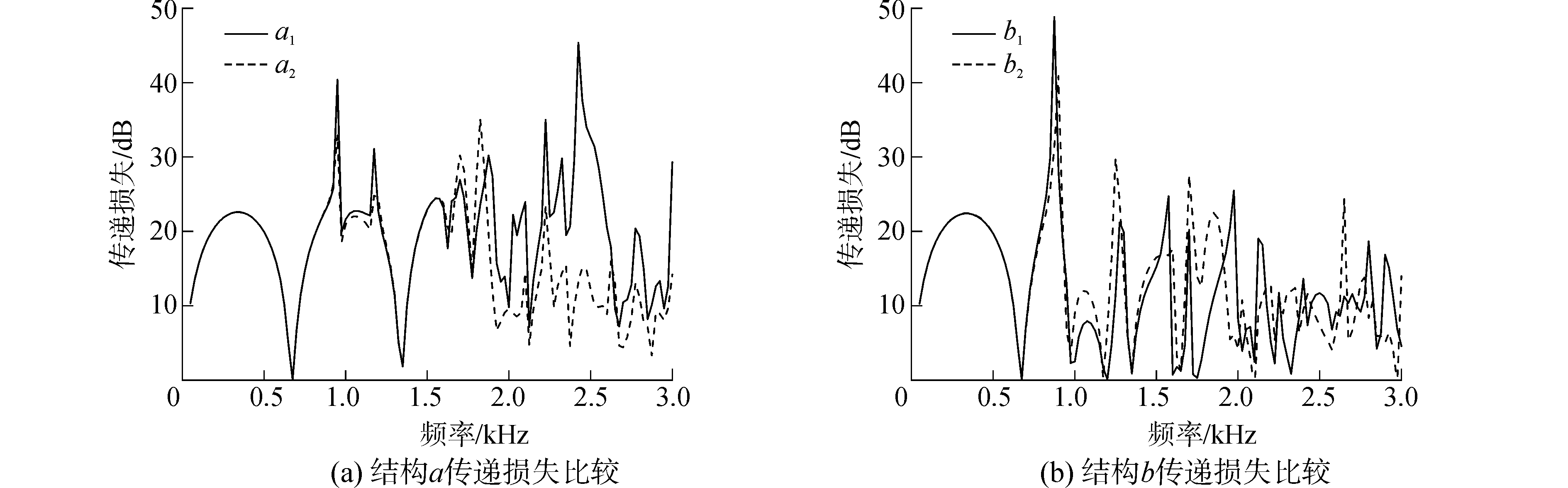
首先,考虑如图 4所示的两通穿孔管消声器,膨胀腔长度均为l=0.257 2 m,穿孔壁厚tw=0.000 9 m,穿孔率Ф=0.08,孔径dh=0.002 49 m,穿孔管半径r1=0.02 m,膨胀腔半径r2=0.1 m。对结构a,消声器进口管处于轴线处,考虑两种情况:a1出口管与进口管之间距离σ=0.06 m,a2出口管与进口管之间距离σ=0.05 m。对结构b,进出口穿孔管位于轴线两侧,考虑两种情况:b1两穿孔管距离轴线距离均为σ=0.06 m,b2两穿孔管距离轴线距离均为σ=0.04 m。比较穿孔管位置的变化对两种结构声学性能的影响,结果如图 5所示。
|
图 4 两通穿孔管消声器 Fig.4 Two-pass perforated tube silencer |
|
图 5 两通穿孔管消声器传递损失计算结果 Fig.5 TL comparison of two-pass perforated tube silencer |
可见,当进(出)口穿孔管处于轴线处时,传递损失曲线更接近轴对称的直通穿孔管消声器,消声效果也更好。穿孔管位置的改变对a、b两种结构的影响是不同的,对结构a,保持进口穿孔管处于轴线位置,改变处于非轴线位置的出口穿孔管的位置对传递损失有较大影响,在高频处更加明显。而对结构b,改变两个处于非轴线位置的穿孔管的位置对传递损失结果影响很小。
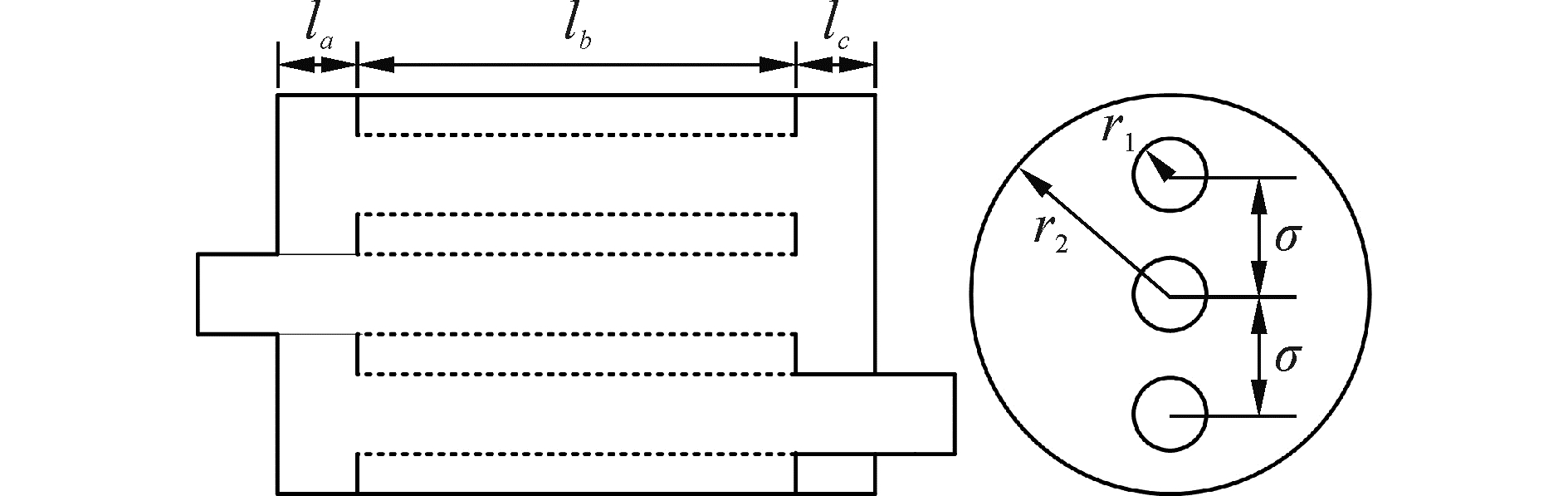
在实际应用中,常采用在消声器进出口添加刚性挡板构成三通穿孔管消声器的形式,如图 6所示,穿孔管半径r1=0.02 m,膨胀腔半径r2=0.1 m,穿孔孔径dh=0.002 49 m,穿孔壁及挡板壁厚tw=0.000 9 m,穿孔率Ф=0.08,la=0.1 m,lp=0.3 m,lb=0.15 m,σ=0.06 m。分别使用混体边界元方法和快速多极混体边界元方法计算传递损失,结果如图 7所示。同样选定频率为350 Hz,比较两种方法的计算时间列于表 2。
|
图 6 三通穿孔管消声器 Fig.6 Three-pass perforated tube silencer |

|
图 7 三通穿孔管消声器计算结果比较 Fig.7 Transmission loss prediction results of three-pass perforated tube silencer |
| 表 2 三通穿孔管消声器计算时间比较 Tab.2 Computation time comparison of three-pass perforated tube silencers |
一般三通穿孔管消声器中的挡板是刚性薄壁,现在考虑将刚性薄壁结构替换为穿孔板,研究其对消声器声学性能的影响。在挡板分别为刚性壁面和穿孔板的情况下计算传递损失如图 8所示。在中低频处,穿孔挡板三通穿孔消声器的有效消声频率更宽,性能更好,应用穿孔挡板代替刚性壁挡板是有意义的。

|
图 8 穿孔挡板对消声器传递损失的影响 Fig.8 Effect of perforated baffle on silencer TL |
现在考虑穿孔挡板的物理参数变化对传递损失计算结果的影响,在穿孔率分别为0.03、0.08以及0.16的情况下计算传递损失,结果如图 9所示。

|
图 9 挡板穿孔率对三通穿孔消声器传递损失的影响 Fig.9 Effect of baffle porosity on TL of three-pass perforated tube silencer |
挡板穿孔率的变化对消声器的传递损失有一定程度的影响,随着穿孔率的增大,传递损失曲线向高频方向移动,与此同时,在200~800 Hz的中频范围内,穿孔率的增大会改善消声器的声学性能。
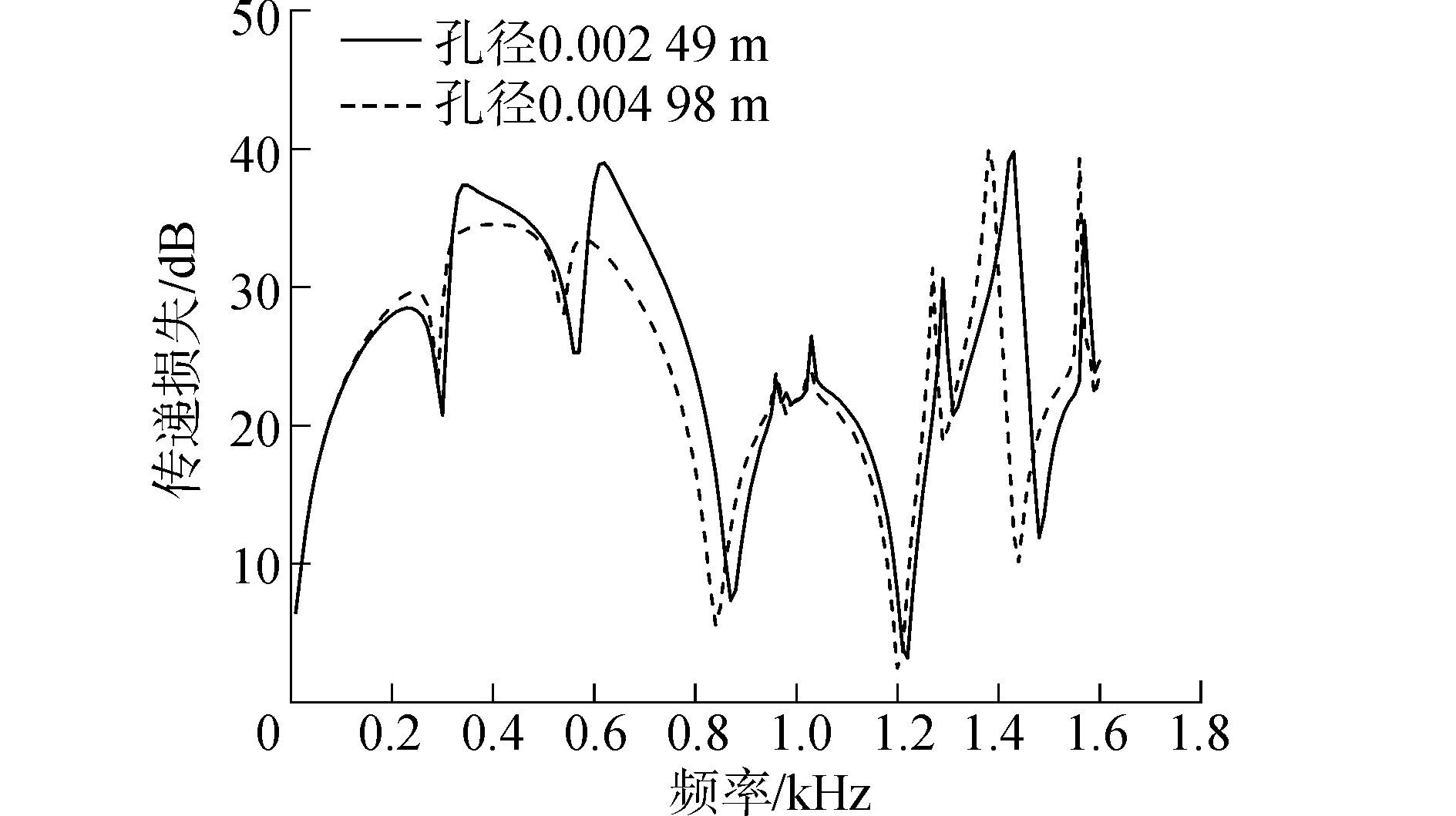
下面考虑穿孔孔径大小对传递损失的影响,在孔径分别为0.002 49 m和0.004 98 m的情况下计算传递损失,结果如图 10所示。增大穿孔孔径,会使传递损失曲线向低频方向移动。
|
图 10 挡板孔径对三通穿孔消声器传递损失的影响 Fig.10 Effect of baffle hole diameter on TL of three-pass perforated tube silencer |
在穿孔挡板的情况下,考虑三通穿孔管消声器左右两端膨胀腔长度对声学性能的影响,改变膨胀腔长度,计算结果如图 11所示。由图可知,增大左右膨胀腔的长度会使传递损失曲线向低频方向移动。

|
图 11 膨胀腔长度对三通穿孔消声器传递损失的影响 Fig.11 Effect of inlet/outlet expansion chamber length on TL of three-pass perforated tube silencer |
1) 快速多极混体边界元方法在能够保证计算精度的情况下,对大尺度高频问题能够有效地减少计算时间,在实际应用中,可以根据研究问题的情况选择适当的方法进行计算。
2) 当进口位于轴线处时,消声器的声学性能更好,出口穿孔管的位置变化对计算结果的影响应该给予考虑,而当进口位于非轴线处时,进出口穿孔管距离的变化对传递损失影响很小,基本可以忽略不计。
3) 使用穿孔板代替三通穿孔消声器中的刚性隔板能改善其中低频的声学性能,减小穿孔板穿孔孔径、增大穿孔率以及进出口膨胀腔的长度会使传递损失曲线向高频方向移动。
| [1] |
SELAMET A, EASWARAN V, FALKOWSKI A G. Three-pass mufflers with uniform perforations[J]. The journal of the acoustical society of America, 1999, 105(3): 1548-1562. DOI:10.1121/1.426694 ( 0) 0)
|
| [2] |
SELAMET A, XU M B, LEE I J, et al. Analytical approach for sound attenuation in perforated dissipative silencers with inlet/outlet extensions[J]. The journal of the acoustical society of America, 2005, 117(4): 2078-2089. DOI:10.1121/1.1867884 ( 0) 0)
|
| [3] |
JI Z L. Acoustic attenuation characteristics of straight-through perforated tube silencers and resonators[J]. Journal of computational acoustics, 2008, 16(03): 361-379. DOI:10.1142/S0218396X08003622 ( 0) 0)
|
| [4] |
JI Z L. Boundary element acoustic analysis of hybrid expansion chamber silencers with perforated facing[J]. Engineering analysis with boundary elements, 2010, 34(7): 690-696. DOI:10.1016/j.enganabound.2010.02.006 ( 0) 0)
|
| [5] |
JI Z L, SELAMET A. Boundary element analysis of three-pass perforated duct mufflers[J]. Noise control engineering journal, 2000, 48(5): 151-156. DOI:10.3397/1.2827962 ( 0) 0)
|
| [6] |
FANG Z, JI Z L. Finite element analysis of transversal modes and acoustic attenuation characteristics of perforated tube silencers[J]. Noise control engineering journal, 2012, 60(3): 340-349. DOI:10.3397/1.3701000 ( 0) 0)
|
| [7] |
WU T W, CHENG C Y R, ZHANG P. A direct mixed-body boundary element method for packed silencers[J]. The Journal of the acoustical society of America, 2002, 111(6): 2566-2572. DOI:10.1121/1.1476920 ( 0) 0)
|
| [8] |
WU T W, WAN G C. Muffler performance studies using a direct mixed-body boundary element method and a three-point method for evaluating transmission loss[J]. Journal of vibration and acoustics, 1996, 118(3): 479-484. DOI:10.1115/1.2888209 ( 0) 0)
|
| [9] |
SAKUMA T, YASUDA Y. Fast multipole boundary element method for large-scale steady-state sound field analysis. Part Ⅰ:setup and validation[J]. Acta acustica united with acustica, 2002, 88(4): 513-525. ( 0) 0)
|
| [10] |
WU H, LIU Y, JIANG W. A low-frequency fast multipole boundary element method based on analytical integration of the hypersingular integral for 3D acoustic problems[J]. Engineering analysis with boundary elements, 2013, 37(2): 309-318. DOI:10.1016/j.enganabound.2012.09.011 ( 0) 0)
|
| [11] |
LI S, HUANG Q. A fast multipole boundary element method based on the improved Burton-Miller formulation for three-dimensional acoustic problems[J]. Engineering analysis with boundary elements, 2011, 35(5): 719-728. DOI:10.1016/j.enganabound.2010.12.004 ( 0) 0)
|
| [12] |
王雪仁, 季振林. 快速多极子声学边界元法及其应用研究[J]. 哈尔滨工程大学学报, 2007, 28(7): 752-757. WANG Xueren, JI Zhenlin. Fast multipole acoustic BEM and its application[J]. Journal of Harbin Engineering University, 2007, 28(7): 752-757. (  0) 0)
|
| [13] |
吴海军, 蒋伟康, 鲁文波. 三维声学多层快速多极子边界元及其应用[J]. 物理学报, 2012, 61(5): 54301-054301. WU Haijun, JIANG Weikang, LU Wenbo. Multilevel fast multipole boundary element method for 3D acoustic problems and its applications[J]. Acta physica sinica, 2012, 61(5): 54301-054301. DOI:10.7498/aps.61.054301 (  0) 0)
|
| [14] |
JI Z L, FANG Z. On the acoustic impedance of perforates and its application to acoustic attenuation predictions for perforated tube silencers[C]//Proceedings of INTER-NOISE. Osaka, 2011(5):2803-2813.
( 0) 0)
|
 2017, Vol. 38
2017, Vol. 38


