近年来,自主水面船(autonomous surface vehicle,ASV)协调控制问题成为船舶运动控制领域的研究热点之一。相较于单个ASV,多ASV协调作业有活动范围大、鲁棒性与容错性强等优点[1],因而广泛应用于海底绘图、资源勘探、环境监控以及其他军事邻域等[2]。ASV根据控制输入数量分为全驱动ASV与欠驱动ASV。全驱动ASV协调控制相对简单,其研究成果已相对成熟[2-4]。由于欠驱动ASV在侧向缺少控制输入,属于含二阶非完整约束的欠驱动系统[5],所以全驱动ASV[2-4]与非完整移动机器人[6]的协调控制研究成果无法直接应用。此外,ASV易受到复杂海洋环境的干扰,且船之间通信伴随着延时,这都为多欠驱动ASV协调控制带来了困难。
欠驱动ASV协调控制按照研究方法可分为领航者-跟随者法[7]、基于行为法[8]、虚拟结构法[9]以及基于图论法[10-12]。基于图论法的协调控制是指各个船之间通过无线网络交换信息,进而实现协调控制。目前,基于图论的欠驱动ASV协调控制问题研究较少。Dong[10]利用图论和Lyapunov理论实现了多欠驱动ASV以一定期望队形跟踪期望轨迹,但需要假设其艏向角速度持续激励,即期望轨迹不可以是直线;Børhaug[11]将控制分为基于视线导航原理的实现跟踪和非线性协同律两部分,并用非线性级联理论证明了系统的稳定性,但该方法仅限于直线跟踪;上述两种策略共同缺点是期望轨迹无法同时跟踪直线和曲线,且依赖于精确的ASV数学模型;针对ASV模型不确定问题,Peng[12]基于动态面神经网络法提出了一种鲁棒轨迹协同策略,但其在线运算量较大,不易于工程实际,且仅实现了半全局闭环系统稳定。
基于图论法的协调控制的核心问题是如何设置协议使得各个ASV特定状态在时间上是趋于一致的,即一致性问题。近十年来,一致性理论广泛应用于一阶系统[13]、二阶系统[14]、拉格朗日系统[15]以及其他复杂非线性系统[16]。一阶或二阶系统的一致性算法是完美的,但如何将其与欠驱动ASV这类特殊模型相结合,并考虑通信延时是充满挑战的。此外,上述一致性算法并未考虑实际物理约束。
针对上述问题,本文借鉴文献[17]点对点引导原理,利用反演技术和上下界快端滑模法,结合图论、Lyapunov稳定性理论以及约束函数特性等相关知识,提出了一种基于通信延时下的多欠驱动ASV鲁棒协调编队控制策略,实现了在外界环境干扰、水动力参数摄动以及通信延时情况下的轨迹协同。在运动学回路中,结合图论相关知识、Lyapunov稳定性理论以及饱和函数特性设计一种基于饱和延时特性的一致性虚拟控制律来实现协同控制目标;在动力学回路中,利用上下界终端滑模法实现对虚拟控制的跟踪,且能够较好抑制水动力参数变化以及外界海洋环境干扰对协同控制的影响;最终证明了多ASV闭环系统的全局稳定性;此外,本文进一步考虑了通信延时下的鲁棒协调控制。
1 图论与稳定性理论首先给出图论相关知识:
考虑N个ASV组成的协调系统,ASV之间的通信拓扑结构可由无向连通图G=G(V, ε)表示。G包含节点集合V={v1, v2, …, vN}和边集ε={(ni, nj)∈V×V},其中εij=(ni, nj)表示信息从节点ni传递至节点nj,同时εij∈ε意味着εji∈ε。如果ASVi可以获得ASVj的相关信息,一定存在边εji∈ε,即G是无向的,此时称ASVj是ASVi的一个邻居。对于ASVi,其所有邻居的集合可用表示Ni。图G的一个路径是指一组有向边构成的连通边集合。如果无向图G中的任意两个节点都存在一个路径,则称G是连通的。定义无向图G的邻接矩阵A=[aij]∈RN×N,如果εji∈ε,则aij=aji=1;反之aij=aji=0。定义图G的入度矩阵D=[dij]∈RN×N,若i≠j,dij=0;若i≠j,
| $ {d_{ii}} = \sum\limits_{j \in {N_i}} {{a_{ij}}} $ |
进一步,定义无向图的Laplacian矩阵L,其满足L=D-A。若无向图G是连通的,则0是L特征值且L的其他非零特征值为正数,即L半正定。
给出级联系统稳定性引理。
引理1[5] 针对以下两个子系统构成的非线性时变级联系统:
| $ {{\mathit{\boldsymbol{\dot x}}}_1} = {f_1}\left( {t, {\mathit{\boldsymbol{x}}_1}} \right) + g\left( {t, {x_1}, {\mathit{\boldsymbol{x}}_2}} \right){\mathit{\boldsymbol{x}}_2} $ | (1) |
| $ {{\mathit{\boldsymbol{\dot x}}}_2} = {f_2}\left( {t, {\mathit{\boldsymbol{x}}_2}, \mathit{\boldsymbol{u}}} \right) $ | (2) |
式中:x1∈Rn1, x2∈Rn2, u∈Rn3。函数f1(t, x1)在(t, x1)上连续可微,f2(t, x2, u)和g(t, x1, x2)是局部Lipschitz且连续。若上述级联系统满足以下条件,则该系统是全局一致渐进稳定(globally uniformly asymptotically stable, GUAS):
1) 系统
2) 级联项函数g(t, x1, x2)满足对任意时刻t有
| $ \begin{array}{*{20}{c}} {{{\left\| {g\left( {t, {\mathit{\boldsymbol{x}}_1}, {\mathit{\boldsymbol{x}}_2}} \right)} \right\|}_2} \le {\theta _1}\left( {{{\left\| {{\mathit{\boldsymbol{x}}_2}} \right\|}_2}} \right) + }\\ {{\theta _2}\left( {{{\left\| {{\mathit{\boldsymbol{x}}_2}} \right\|}_2}} \right){{\left\| {{\mathit{\boldsymbol{x}}_1}} \right\|}_2}} \end{array} $ | (3) |
式中θ1、θ2:R≥0→R≥0为连续函数;
3) 存在控制律u使得子系统(2)全局渐进稳定(globally asymptotically stable, GAS)。
进一步给出有限时间稳定性引理:
引理2[18] 考虑自治系统:
| $ \mathit{\boldsymbol{\dot X}} = f\left( \mathit{\boldsymbol{X}} \right) $ | (4) |
其中X∈Rn,函数f:D→Rn是包含原点的定义域D到n维空间Rn的连续映射。针对式(4),若存在一个连续可微正定函数V(X):D→R满足:
| $ \dot V\left( \mathit{\boldsymbol{X}} \right) + {c_1}{V^{{\alpha _1}}}\left( \mathit{\boldsymbol{X}} \right) + lV\left( \mathit{\boldsymbol{X}} \right) \le 0, \mathit{\boldsymbol{X}} \in {D_0}\backslash \left\{ 0 \right\} $ | (5) |
式中:常数c1, l>0且α1∈(0, 1), 原点开邻域D0∈D,则系统(4)局部有限时间稳定(locally finite time stable, LFTS),即在时间T(X0)内系统稳定,且抵达时间T(X0)满足:
| $ T\left( {{\mathit{\boldsymbol{X}}_0}} \right) \le \frac{{\ln \left( {1 + \frac{l}{{{c_1}}}V{{\left( {{\mathit{\boldsymbol{X}}_0}} \right)}^{1 - {\alpha _1}}}} \right)}}{{l\left( {1 - {\alpha _1}} \right)}}, {\mathit{\boldsymbol{X}}_0} \in {D_0} $ | (6) |
若D=Rn,且式(5)在Rn/{0}上均成立,则系统(4)全局有限时间稳定(global finite time stable, GFTS)。
引理3[19] 考虑自治系统:
针对系统(4),若存在一个连续可微正定函数V(X):D→R满足:
| $ \dot V\left( \mathit{\boldsymbol{X}} \right) + {c_2}{V^{{\alpha _2}}}\left( \mathit{\boldsymbol{X}} \right) \le 0, \mathit{\boldsymbol{X}} \in {D_0}\backslash \left\{ 0 \right\} $ | (7) |
式中:常数c2>0且α2∈(0, 1), 原点开邻域D0∈D,则系统(4)局部有限时间稳定LFTS,即在时间T(X0)内系统稳定,且抵达时间T(X0)满足:
| $ T\left( {{\mathit{\boldsymbol{X}}_0}} \right) \le \frac{{{V^{1 - {\alpha _2}}}\left( {{\mathit{\boldsymbol{X}}_0}} \right)}}{{{c_2}\left( {1 - {\alpha _2}} \right)}}, {\mathit{\boldsymbol{X}}_0} \in {D_0} $ | (8) |
若D=Rn,不等式(7)在Rn/{0}上均成立,则系统(4)全局有限时间稳定(GFTS)。
2 控制问题描述 2.1 单个ASV数学建模ASVi水平面运动学与动力学方程表示为[20]
| $ \left\{ \begin{array}{l} {{\dot x}_i} = {u_i}\cos {\psi _i} - {v_i}\sin {\psi _i}\\ {{\dot y}_i} = {u_i}\sin {\psi _i} + {v_i}\cos {\psi _i}\\ {{\dot \psi }_i} = {r_i} \end{array} \right. $ | (9) |
| $ \left\{ \begin{array}{l} {{\dot u}_i} = \frac{{{m_{22}}}}{{{m_{11}}}}{v_i}{r_i} - \frac{{{d_u}}}{{{m_{11}}}}{u_i} - \frac{{{d_{u2}}}}{{{m_{11}}}}\left| {{u_i}} \right|{u_i} + \\ \;\;\;\;\;\;\;\frac{1}{{{m_{11}}}}{\tau _{ui}} + \frac{1}{{{m_{11}}}}{\tau _{wui}}\\ {{\dot V}_i} = - \frac{{{m_{11}}}}{{{m_{22}}}}{u_i}{r_i} - \frac{{{d_v}}}{{{m_{22}}}}{v_i} - \frac{{{d_{v2}}}}{{{m_{22}}}}\left| {{v_i}} \right|{v_i} - \\ \;\;\;\;\;\;\;\frac{{{d_{vr}}}}{{{m_{22}}}}{r_i} + \frac{1}{{{m_{22}}}}{\tau _{wvi}}\\ {{\dot r}_i} = \frac{{{m_{11}} - {m_{22}}}}{{{m_{33}}}}{u_i}{v_i} - \frac{{{d_r}}}{{{m_{33}}}}{r_i} - \frac{{{d_{r2}}}}{{{m_{33}}}}\left| {{r_i}} \right|{r_i} - \\ \;\;\;\;\;\;\frac{{{d_{rv}}}}{{{m_{33}}}}{v_i} + \frac{1}{{{m_{33}}}}{\tau _{ri}} + \frac{1}{{{m_{33}}}}{\tau _{wri}} \end{array} \right. $ | (10) |
式中:(xi, yi)表示ASVi在大地坐标系下的位置信息,ψi表示ASVi艏向角信息;ui、vi以及ri分别表示ASVi的体坐标系下的前进速度、横移速度以及艏向角速度;m11、m22以及m33表示ASVi包含其附加质量的惯性参数且均为正数;du、du2、dv、dv2、dvr、dr、dr2、drv表示ASVi的水动力阻尼项参数且均为正;τwui、τwvi以及τwri表示ASVi收到的外界海洋环境干扰。τui与τri分别表示船的纵向控制输入与艏向控制输入。由于ASV在侧向没有控制力矩,即本文研究的是欠驱动ASV控制问题。
假设1 外界干扰τwui(t)、τwvi(t)、τwri(t)满足|τwui(t)|≤τwui, |τwvi(t)|≤τwvi, |τwri(t)|≤τwri, 其中τwui, τwvi, τwri表示干扰上界。
假设2 ASV之间的通信拓扑是无向连通的。
2.2 问题描述设N个ASV的参考轨迹的位置信息为pd(t)= [xd(t) yd(t)]T∈R2, 期望几何队形定义为Δ={Δi}, 其中Δi=[Δxi(t), Δyi(t)]T∈R2, i=1, 2, …, N。
注意1 为便于分析,期望队形认为是静态的,即满足
进一步,定义ASVi位置跟踪误差为
| $ {x_{ei}} = {x_d} + {\mathit{\Delta} _{xi}} - {x_i}, {y_{ei}} = {y_d} = {\mathit{\Delta} _{yi}} - {y_i} $ | (11) |
借鉴文献[17]点对点引导原理,定义ASVi距离跟踪误差与艏向角跟踪误差为
| $ {d_{ei}} = \sqrt {x_{ei}^2 + y_{ei}^2}, {\psi _{ei}} = {\psi _{di}} - {\psi _i} $ | (12) |
式中:ψdi=arctan 2(yei, xei)∈(-π, π]表示ASVi相对于期望轨迹的期望艏向角,即轨迹协同问题可以转化为对跟踪误差dei, ψei的镇定与协同一致。
注意2 从ψdi的定义可以看出,当xei收敛于0时期望角ψdi将产生奇异现象。为此,引入了正常数偏置量δ,将控制问题转化为镇定zei=dei-δ。
假设3 针对ASV的物理约束,假设ψdi个ASV的虚拟领导者ψdi的一阶二阶导数有界。
协同编队控制目标归纳为:在假设1~3的情况下,针对欠驱动ASVi式(9)和(10),利用自身状态信息与其邻居跟踪偏差信息ψdi设计鲁棒协同控制律ψdi使得ASV的ψdi渐近跟踪其期望轨迹并与编队系统其他邻居保持协同一致,即满足:
| $ \mathop {\lim }\limits_{t \to \infty } {z_{ei}} = 0, \mathop {\lim }\limits_{t \to \infty } {z_{ei}} = {z_{ej}} $ | (13) |
| $ \mathop {\lim }\limits_{t \to \infty } {\psi _{ei}} = 0, \mathop {\lim }\limits_{t \to \infty } {\psi _{ei}} = {\psi _{ej}} $ | (14) |
针对控制目标(13)和(14),考虑ASV之间无通信延时下的协同编队控制问题。整个设计过程分为三个步骤:1)在运动学回路设计一种基于饱和约束函数的协同虚拟控制律αui与αri;2)设计一种基于上下界滑模的鲁棒控制器设计鲁棒控制律τui与τir使得ASVi纵向速度与艏向转速快速收敛于其对应虚拟控制律;3)利用级联稳定性理论证明了N艘欠驱动ASV的闭环系统稳定性。
3.1 运动学回路设计对式(12)求导,经整理可得
| $ \begin{array}{*{20}{c}} {{{\dot z}_{ei}} = {{\dot x}_d}\cos {\psi _{di}} + {{\dot y}_d}\sin {\psi _{di}} - {v_i}\sin {\psi _{ei}} + }\\ {2{u_i}{{\sin }^2}\left( {0.5{\psi _{ei}}} \right) - {u_i}} \end{array} $ | (15) |
| $ {{\dot \psi }_{ei}} = {{\dot \psi }_{di}} - {r_i} $ | (16) |
为实现控制目标(13)和(14),提出一种ui与ri的虚拟控制律αui与αri:
| $ \begin{array}{*{20}{c}} {{\alpha _{ui}} = {k_{ui}}\tanh {z_{ei}} + {p_{ui}}\sum\limits_{j \in {N_i}} {{a_{ij}}\left( {\tanh {z_{ei}} - } \right.} }\\ {\left. {\tanh {z_{ej}}} \right) - {f_i}} \end{array} $ | (17) |
| $ \begin{array}{*{20}{c}} {{\alpha _{ri}} = {k_{ri}}\tanh {\psi _{ei}} + {p_{ri}}\sum\limits_{j \in {N_i}} {{a_{ij}}\left( {\tanh {\psi _{ei}} - } \right.} }\\ {\left. {\tanh {\psi _{ej}}} \right) - {{\dot \psi }_{di}}} \end{array} $ | (18) |
式中:
进一步,给出定理1。
定理1 针对偏差微分方程(15)和(16),当纵向速度与艏向速度满足ui=αui, ri=αri, 且其中控制参数kui, kri, pui, pri, 满足:
| $ \begin{array}{*{20}{c}} {{k_{ui}} \ge 0, {k_{ri}} \ge 0, \sum\limits_{i = 1}^N {{k_{ui}} > 0}, }\\ {\sum\limits_{i = 1}^N {{k_{ri}} > 0}, {p_{ui}} > 0, {p_{ri}} > 0} \end{array} $ | (19) |
则控制目标(13)和(14)成立。
证明 选择如下Lyapunov能量函数:
| $ {V_0} = \sum\limits_{i = 1}^N {\int_0^{{z_{ei}}} {\tanh {\delta _i}{\rm{d}}{\delta _i}} } + \sum\limits_{i = 1}^N {\int_0^{{\psi _{ei}}} {\tanh {\sigma _i}{\rm{d}}{\sigma _i}} } $ | (20) |
显然有V0≥0,并当且仅当zei=ψei=0时有V0i为零。对V0i关于时间t求导得
| $ \begin{array}{*{20}{c}} {{{\dot V}_0} = \sum\limits_{i = 1}^N {{{\dot z}_{ei}}\tanh {z_{ei}}} + \sum\limits_{i = 1}^N {{{\dot \psi }_{ei}}\tanh {\psi _{ei}}} = }\\ { - \sum\limits_{i = 1}^N {{k_{ui}}{{\tanh }^2}{z_{ei}}} - \sum\limits_{i = 1}^N {{p_{ui}}\sum\limits_{j \in {N_i}} {{a_{ij}}\left( {\tanh {z_{ei}} - } \right.} } }\\ {\left. {\tanh {z_{ej}}} \right)\tanh {z_{ei}} - \sum\limits_{i = 1}^N {{k_{ri}}{{\tanh }^2}{p_{ei}}} - }\\ {\sum\limits_{i = 1}^N {{p_{ri}}\sum\limits_{j \in {N_i}} {{a_{ij}}\left( {\tanh {\psi _{ei}} - \tanh {\psi _{ej}}} \right)\tanh {\psi _{ei}}} } = }\\ { - \sum\limits_{i = 1}^N {{k_{ui}}{{\tanh }^2}{z_{ei}} - {P_u}\left( {\tanh {z_{ei}}} \right)TL\tanh {z_{ei}}} - }\\ {\sum\limits_{i = 1}^N {{k_{ri}}{{\tanh }^2}{z_{ei}} - {P_r}\left( {\tanh {z_{ei}}} \right)TL\tanh {z_{ei}}} } \end{array} $ | (21) |
式中:Pu=diag(pu1, pu2, …, puN), Pr=diag(pr1, pr2, …, prN), pui, pri>0, (i=1, 2, …, N)。
由图G是无向连通可知L≥0,故
| $ \mathop {\lim }\limits_{t \to \infty } \sum\limits_{i = 1}^N {{k_{ui}}{{\tanh }^2}{z_{ei}}} = \mathop {\lim }\limits_{t \to \infty } \sum\limits_{i = 1}^N {{k_{ri}}{{\tanh }^2}{z_{ei}}} = 0 $ | (22) |
| $ \mathop {\lim }\limits_{t \to \infty } {\left( {\tanh {z_{ei}}} \right)^{\rm{T}}}L\tanh {z_{ei}} = 0 $ | (23) |
| $ \mathop {\lim }\limits_{t \to \infty } {\left( {\tanh {\psi _{ei}}} \right)^{\rm{T}}}L\tanh {\psi _{ei}} = 0 $ | (24) |
此时一定存在正整数c1, c2满足kuc>0, krc>0使得
由式(23)和(24)可知
注意3 为实现协同控制目标,虚拟控制律αui与αri也可设计为
| $ {\alpha _{ui}} = - {k_{ui}}{z_{ei}} - {p_{ui}}\sum\limits_{j \in {N_i}} {{a_{ij}}\left( {{z_{ei}} - {z_{ej}}} \right) + {f_i}} $ | (25) |
| $ {\alpha _{ri}} = - {k_{ri}}{\psi _{ei}} - {p_{ri}}\sum\limits_{j \in {N_i}} {{a_{ij}}\left( {{\psi _{ei}} - {\psi _{ej}}} \right) + {{\dot \psi }_{di}}} $ | (26) |
然而,系统在初始状态下|zei|、|zej|、|ψei|、|ψej|,往往使得虚拟控制律αui与αri超过各个ASV的纵向速度与艏向速度的物理极限值,造成控制失效。针对此问题,本文在虚拟控制律设计中引入了连续可微的饱和函数,防止初始偏差量过大对系统的影响。
注意4 为了便于后续设计,对
| $ \begin{array}{*{20}{c}} {{{\dot \alpha }_{ui}} = - \left( {{k_{ui}} + \sum\limits_{j \in {N_i}} {{p_{ui}}{a_{ij}}} } \right)\left( {1 - {{\tanh }^2}{z_{ei}}} \right){{\dot z}_{ei}} + {{\dot f}_i} + }\\ {\sum\limits_{j \in {N_i}} {{p_{ui}}{a_{ij}}\left( {1 - {{\tanh }^2}{z_{ej}}} \right){{\dot z}_{ej}}} } \end{array} $ | (27) |
| $ \begin{array}{*{20}{c}} {{{\dot \alpha }_{ri}} = - \left( {{k_{ri}} + \sum\limits_{j \in {N_i}} {{p_{ri}}{a_{ij}}} } \right)\left( {1 - {{\tanh }^2}{\psi _{ei}}} \right){{\dot \psi }_{ei}} + {{ \psi }_{di}} + }\\ {\sum\limits_{j \in {N_i}} {{p_{ri}}{a_{ij}}\left( {1 - {{\tanh }^2}{\psi _{ej}}} \right){{\dot \psi }_{ej}}} } \end{array} $ | (28) |
式中:
定义ASVi的纵向速度跟踪误差为
| $ {u_{ei}} = {u_i} - {\alpha _{ui}} $ | (29) |
定义关于uei的一阶终端滑模面:
| $ \begin{array}{*{20}{c}} {{S_{1i}} = {u_{ei}} + {\lambda _{1i}}\int_0^t {{u_{ei}}\left( \tau \right)\tau } + }\\ {{\lambda _{2i}}\int_0^t {{{\left| {{u_{ei}}\left( \tau \right)} \right|}^p}{\rm{sign}}\left( {{u_{ei}}\left( \tau \right)} \right){\rm{d}}\tau } } \end{array} $ | (30) |
式中:常数λ1i, λ2i>0,0 < p < 1。
对式(30)求导得
| $ \begin{array}{*{20}{c}} {{{\dot S}_{1i}} = {{\dot u}_i} - {{\dot \alpha }_{ui}} + {\lambda _{1i}}{u_{ei}} + {\lambda _{2i}}{{\left| {{u_{ei}}} \right|}^p}{\rm{sign}}\left( {{u_{ei}}} \right) = }\\ {\frac{1}{{{m_{11}}}}\left( {{m_{22}}{v_i}{r_i} - {d_u}{u_i} - {d_{u2}}\left| {{u_i}} \right|{u_i} + {\tau _{ui}} + } \right.}\\ {{\tau _{wui}}\left( t \right) - {m_{11}}{{\dot \alpha }_{ui}} + {\lambda _{2i}}{m_{11}}{{\left| {{u_{ei}}} \right|}^p}{\rm{sign}}\left( {{u_{ei}}} \right) + }\\ {\left. {{\lambda _{1i}}{m_{11}}{u_{ei}}} \right)} \end{array} $ | (31) |
当系统状态处于滑模面时,有
| $ \begin{array}{*{20}{c}} {{\tau _{u1i}} = - {{\hat m}_{22}}{v_i}{r_i} + {{\hat d}_u}{u_i} + {{\hat d}_{u2}}\left| {{u_i}} \right|{u_i} + {{\hat m}_{11}}{{\dot \alpha }_{ui}} - }\\ {{\lambda _{1i}}{{\hat m}_{11}}{u_{ei}} - {\lambda _{2i}}{{\hat m}_{11}}{{\left| {{u_{ei}}} \right|}^p}{\rm{sign}}\left( {{u_{ei}}} \right)} \end{array} $ | (32) |
式中:
同时考虑海洋外界干扰以及水动力参数不确定性,设计纵向控制律τui
| $ \begin{array}{*{20}{c}} {{\tau _{ui}} = {\tau _{u1i}} - {K_{ui}}{\rm{sign}}\left( {{S_{1i}}} \right) = }\\ { - {K_{ui}}{\rm{sign}}\left( {{S_{1i}}} \right) - {{\hat m}_{22}}{v_i}{r_i} + {{\hat d}_u}{u_i} + {{\hat d}_{u2}}\left| {{u_i}} \right|{u_i} + }\\ {{{\dot \alpha }_{ui}} - {\lambda _{1i}}{u_{ei}} - {\lambda _{2i}}{{\left| {{u_{ei}}} \right|}^p}{\rm{sign}}\left( {{u_{ei}}} \right)} \end{array} $ | (33) |
式中:Kui=ηui+τwui+M22|viri|+Du|ui|+Du2ui2+M11|
进一步,选择纵向Lyapunov能量函数:
| $ {V_{1i}} = \frac{1}{2}{m_{1i}}S_{1i}^2 $ | (34) |
对式(34)两边求导,并代入控制律式(33)可得
| $ \begin{array}{*{20}{c}} {{{\dot V}_{2i}} = {S_{1i}}\left( {\left( {{m_{22}} - {{\hat m}_{22}}} \right){v_i}{r_i} + \left( {{{\hat d}_u} - {d_u}} \right){u_i} + } \right.}\\ {\left( {{{\hat d}_{u2}} - {d_{u2}}} \right)\left| {{u_i}} \right|{u_i} + \left( {{m_{11}} - {{\hat m}_{11}}} \right){{\dot \alpha }_{ui}} + }\\ {{\lambda _{1i}}\left( {{m_{11}} - {{\hat m}_{11}}} \right){u_{ei}} + {\lambda _{2i}}\left( {{m_{11}} - } \right.}\\ {\left. {{{\hat m}_{11}}} \right){{\left| {{u_{ei}}} \right|}^p}\left| {{\rm{sign}}\left( {{u_{ei}}} \right)} \right| + {\tau _{wui}} - }\\ {\left. {{K_{ui}}{\rm{sign}}\left( {{S_{1i}}} \right)} \right) \le - {\eta _{2i}}\left| {{S_{2i}}} \right| = - \sqrt 2 {\eta _{2i}}V_{2i}^{0.5}} \end{array} $ | (35) |
由引理3可知S1i在有限时间趋近于0,且抵达时间Tu1i满足:
| $ {T_{u1i}} \le \frac{{V_{1i}^{0.5}\left( {{V_{1i}}\left( 0 \right)} \right)}}{{0.5\sqrt 2 {\eta _{1i}}}} $ | (36) |
当系统状态位于滑模面时有
| $ {{\dot S}_{1i}} = {{\dot u}_{ei}} + {\lambda _{1i}}{u_{ei}} + {\lambda _{2i}}{\left| {{u_{ei}}} \right|^p}{\rm{sign}}\left( {{u_{ei}}} \right) = 0 $ | (37) |
由引理2可知uei在有限时间内趋于0,且抵达时间uei满足:
| $ {T_{u2i}} \le \frac{{\ln \left( {1 + \frac{{{\lambda _{1i}}}}{{{\lambda _{2i}}}}u_{ei}^{1 - p}\left( 0 \right)} \right)}}{{{\lambda _{1i}}\left( {1 - p} \right)}} $ | (38) |
综上论述,给出定理2。
定理2 假设1~3成立,针对纵向速度跟踪误差uei,在采用控制律(33)的情况下,在任何初始状态下跟踪误差uei都能在有限时间内趋于零附近邻域,且收敛时间Tui满足Tui≤Tu1i+Tu2i。
注意5 与文献[22]采用的一阶指数型滑模不同,本文在滑模面设计过程的中引入了一种非线性项
定义ASVi的艏向速度跟踪误差:
| $ {r_{ei}} = {r_i} - {\alpha _{ri}} $ | (39) |
定义关于rei的滑模面
| $ \begin{array}{*{20}{c}} {{S_{2i}} = {r_{ei}} + {\gamma _{1i}}\int_0^t {{r_{ei}}\left( \tau \right)\tau } + }\\ {{\gamma _{2i}}\int_0^t {{{\left| {{r_{ei}}\left( \tau \right)} \right|}^\sigma }{\rm{sign}}\left( {{r_{ei}}\left( \tau \right)} \right){\rm{d}}\tau } } \end{array} $ | (40) |
式中:常数γ1i, γ2i>0,0 < σ < 1。
对式(40)求导得
| $ \begin{array}{*{20}{c}} {{{\dot S}_{2i}} = {{\dot r}_i} - {{\dot \alpha }_{ri}} + {\gamma _{1i}}{r_{ei}} + {\gamma _{2i}}{{\left| {{r_{ei}}} \right|}^p}{\rm{sign}}\left( {{r_{ei}}} \right) = }\\ {\frac{1}{{{m_{33}}}}\left( {\left( {{m_{11}} - {m_{22}}} \right){u_i}{v_i} - {d_r}{r_i} - {d_{r2}}\left| {{r_i}} \right|{r_i} - } \right.}\\ {\left. {{d_{rv}}{v_i} + {\tau _{ri}} + {\tau _{wri}} - {m_{33}}{{\dot \alpha }_{ri}}} \right)} \end{array} $ | (41) |
当系统状态处于滑模面时,有
| $ \begin{array}{*{20}{c}} {{\tau _{r1i}} = - {{\hat m}_{11}}{u_i}{v_i} + {{\hat m}_{22}}{u_i}{v_i} + {{\hat d}_r}{r_i} + {d_{r2}}\left| {{r_i}} \right|{r_i} + }\\ {{d_{rv}}{v_i} + {{\hat m}_{33}}{{\dot \alpha }_{ri}} - {\gamma _{1i}}{{\hat m}_{33}}{r_{ei}} - {\lambda _{2i}}{{\hat m}_{33}}{{\left| {{r_{ei}}} \right|}^\sigma }{\rm{sign}}\left( {{r_{ei}}} \right)} \end{array} $ | (42) |
式中:
同时考虑海洋外界干扰以及水动力参数不确定性,设计艏向控制律τri:
| $ \begin{array}{*{20}{c}} {{\tau _{ri}} = {\tau _{r1i}} - {K_{ri}}{\rm{sign}}\left( {{S_{2i}}} \right) = }\\ { - {K_{ri}}{\rm{sign}}\left( {{S_{2i}}} \right) - {{\hat m}_{11}}{u_i}{v_i} + {{\hat m}_{22}}{u_i}{v_i} + {{\hat d}_r}{r_i} + }\\ {{{\hat d}_{r2}}\left| {{r_i}} \right|{r_i} + {d_{rv}}{v_i} + {{\hat m}_{33}}{{\dot \alpha }_{ri}} - {\gamma _{1i}}{{\hat m}_{33}}{r_{ei}} - }\\ {{\gamma _{2i}}{{\hat m}_{33}}{{\left| {{r_{ei}}} \right|}^\sigma }{\rm{sign}}\left( {{r_{ei}}} \right)} \end{array} $ | (43) |
其中,Kri=ηri+τwri+M11|uivi|+M22|uivi|+Dr|ri|+Dr2ri2 +Drv|vi|+M33|
选取艏向Lyapunov能量函数:
| $ {V_{2i}} = \frac{1}{2}{m_{33}}S_{2i}^2 $ | (44) |
对式(44)两边求导,并代入式(43)得
| $ \begin{array}{*{20}{c}} {{{\dot V}_{2i}} = {S_{2i}}\left( {\left( {{m_{11}} - {{\hat m}_{11}}} \right){u_i}{v_i} + \left( {{m_{22}} - {{\hat m}_{22}}} \right){u_i}{v_i} + } \right.}\\ {\left( {{{\hat d}_r} - {d_r}} \right){r_i} + \left( {{{\hat d}_{r2}} - {d_{r2}}} \right)\left| {{r_i}} \right|{r_i} + \left( {{{\hat d}_{rv}} - {d_{rv}}} \right){v_i} + }\\ {\left( {{{\hat m}_{33}} - {m_{33}}} \right){{\dot \alpha }_{ri}} + {\gamma _{1i}}\left( {{m_{33}} - {{\hat m}_{33}}} \right){r_{ei}} + }\\ {{\gamma _{2i}}\left( {{m_{33}} - {{\hat m}_{33}}} \right){{\left| {{r_{ei}}} \right|}^\sigma }{\rm{sign}}\left( {{r_{ei}}} \right) - {K_{2i}}{\rm{sign}}\left( {{S_{2i}}} \right) + }\\ {{\tau _{wri}} \le - {\eta _{2i}}\left| {{S_{2i}}} \right| = - \sqrt 2 {\eta _{2i}}V_{2i}^{0.5}} \end{array} $ | (45) |
与定理2分析类似,这里不再展开,直接给出定理3。
定理3 假设1~3成立,针对艏向速度跟踪误差rei,在控制律(43)作用下,在任何初始状态下rei都能在有限时间内趋于零附近邻域,且收敛时间满足Tri≤Tr1i+Tr2i, 其中Tr1i, Tr2i满足:
| $ {T_{r1i}} \le \frac{{V_{2i}^{0.5}\left( {{V_{2i}}\left( 0 \right)} \right)}}{{0.5\sqrt 2 {\eta _{2i}}}}, {T_{r2i}} \le \frac{{\ln \left( {1 + \frac{{{\gamma _{1i}}}}{{{\gamma _{2i}}}}r_{ei}^{1 - \sigma }\left( 0 \right)} \right)}}{{{\lambda _{1i}}\left( {1 - \sigma } \right)}} $ | (46) |
注意6 结合式(10)、(29)、(33)、(39)和(43)可将ASVi动力学闭环系统化为
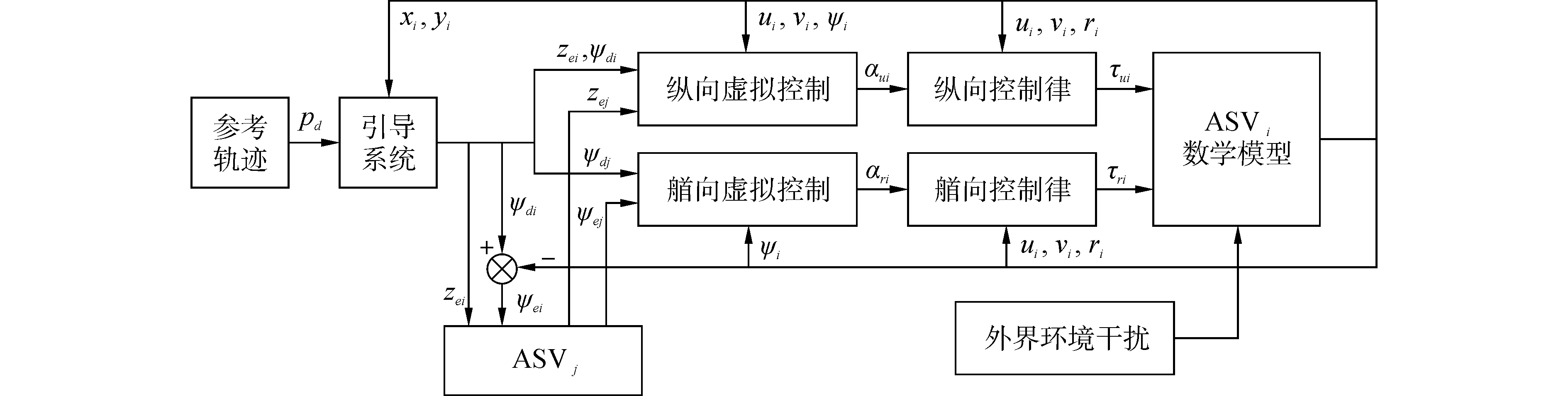
整个ASVi控制结构如图 1所示,共包括三部分:引导系统、运动学回路以及动力学回路。首先,引导系统通过ASV自身位置信息以及参考轨迹产生期望航向角ψdi以及距离跟踪误差zei,并将信息传递给ASVi的邻居以及运动学回路;进一步,运动学回路通过zej、ψdj,ASVi邻居信息zej、ψdj和自身状态信息产生纵向和艏向的虚拟控制律αui、αri来实现编队协同一致的目标;最后,在运动学回路设计中考虑模型不确定以及外界环境扰动因素,设计鲁棒控制律,实现纵向速度ui和艏向转速ri对虚拟控制律αui、αri的复现。
|
图 1 协调控制策略的结构图 Fig.1 Architecture of the coordination control design |
在控制律(34)和(43)作用下,闭环系统(15)、(16)与(10)可分解为以下级联结构:
| $ {{\mathit{\boldsymbol{\dot x}}}_1} = {\mathit{\boldsymbol{f}}_1}\left( {t, {\mathit{\boldsymbol{x}}_1}} \right) + \mathit{\boldsymbol{g}}\left( {t, {\mathit{\boldsymbol{x}}_1}, {\mathit{\boldsymbol{x}}_2}} \right){\mathit{\boldsymbol{x}}_2} $ | (47) |
| $ {{\mathit{\boldsymbol{\dot x}}}_2} = {\mathit{\boldsymbol{f}}_2}\left( {t, {\mathit{\boldsymbol{x}}_2}, \mathit{\boldsymbol{u}}} \right) $ | (48) |
其中x1=(ze1, ψe1, ze2, ψe2, …, zeN, ψeN)T, x2=(uei, re1, ue2, re2, …, ueN, reN)T, u=(τu1, τr1, τu2, τr2, …, τuN, τrN)T, f1(t, x1)=-K2Ntanh x1-LP2Ntanh x2, g(t, x1, x2)=-I2N, f2(t, x2, u)= [f21T, f22T, …, f2NT]T,
定理4与注6表明闭环级联系统(47)、(48)的子系统
| $ \begin{array}{*{20}{c}} {{{\left\| {\mathit{\boldsymbol{g}}\left( {t, {\mathit{\boldsymbol{x}}_1}, {\mathit{\boldsymbol{x}}_2}} \right)} \right\|}_2} = 1 \le 1 + \sqrt {\sum\limits_{i = 1}^N {\left( {u_{ei}^2 + r_{ei}^2} \right)} } = }\\ {1 + {{\left\| {{\mathit{\boldsymbol{x}}_2}} \right\|}_2} + 0 \cdot {{\left\| {{\mathit{\boldsymbol{x}}_1}} \right\|}_2}} \end{array} $ | (49) |
此时定义连续函数ρ1(‖x2‖2)=1+‖x2‖2以及ρ2(‖x2‖2)=0满足引理1的条件2。综上所述,在假设1~3满足条件下,N个ASV组成的闭环系统(47)与(48)是GUAS,即满足(zei, ψei, uei, rei)T渐进趋近于(0, 0, 0, 0)T。
3.3.2 横移速度vi有界性选取横向Lyapunov能量函数:
| $ {V_{vi}} = \frac{1}{2}{m_{22}}v_i^2 $ | (50) |
对式(50)求导可得
| $ \begin{array}{*{20}{c}} {{{\dot V}_{vi}} = - \left( {{d_v} + {d_{v2}}\left| {{v_i}} \right|} \right)v_i^2 + \left( { - {m_{11}}{u_i}{r_i} - } \right.}\\ {\left. {{d_{vr}}{r_i} + {\tau _{wvi}}\left( t \right)} \right){v_i} \le - {d_v}v_i^2 + \varphi \left| {{v_i}} \right|} \end{array} $ | (51) |
其中φ=max(m11|uiri|+dvr|ri|)+τwvi。若dv|vi|>φ, 则
实际海洋环境比较复杂,ASV之间的相互信息交互往往伴随着通信延时,这里假设信息从ASVj发送至ASVi的延迟时间为常数εij。针对式(15)与(16),提出一种基于通信延时和状态约束的ui和ri的虚拟协同控制律
| $ \begin{array}{*{20}{c}} {{\alpha _{ui}} = {k_{ui}}\tanh {z_{ei}} + {p_{ui}}\sum\limits_{j \in {N_i}} {{a_{ij}}\left( {\tanh {z_{ei}}\left( t \right) - } \right.} }\\ {\left. {\tanh \left( {{z_{ej}}\left( {t - {\varepsilon _{ij}}} \right)} \right)} \right) - {f_i}} \end{array} $ | (52) |
| $ \begin{array}{*{20}{c}} {{\alpha _{ri}} = {k_{ri}}\tanh {\psi _{ei}} + {p_{ui}}\sum\limits_{j \in {N_i}} {{a_{ij}}\left( {\tanh {\psi _{ei}}\left( t \right) - } \right.} }\\ {\left. {\tanh \left( {{\psi _{ej}}\left( {t - {\varepsilon _{ij}}} \right)} \right)} \right) - {{\dot \psi }_{di}}} \end{array} $ | (53) |
定理4 针对运动学方程(15)和(16),当纵向速度与艏向速度满足ui=αui, ri=αri且控制参数kui、kri、pui、pri满足式(19),则
| $ \mathop {\lim }\limits_{t \to \infty } {z_{ei}} = 0, \mathop {\lim }\limits_{t \to \infty } {z_{ei}} = {z_{ej}}\left( {t - {\varepsilon _{ij}}} \right) $ | (54) |
| $ \mathop {\lim }\limits_{t \to \infty } {\psi _{ei}} = 0, \mathop {\lim }\limits_{t \to \infty } {\psi _{ei}} = {\psi _{ej}}\left( {t - {\varepsilon _{ij}}} \right) $ | (55) |
证明 选择如下Lyapunov能量函数
| $ \begin{array}{*{20}{c}} {{V_4} = \sum\limits_{i = 1}^N {\int_0^{{z_{ei}}} {\tanh {s_i}{\rm{d}}{s_i}} } + }\\ {\frac{1}{2}\sum\limits_{i = 1}^N {{p_{ui}}} \sum\limits_{j \in {N_i}} {{a_{ij}}\int_{t - {\varepsilon _{ij}}}^t {{{\tanh }^2}{z_{ej}}\left( {{s_j}} \right){\rm{d}}{s_j}} } + }\\ {\sum\limits_{i = 1}^N {\int_0^{{\psi _{ei}}} {\tanh {s_i}{\rm{d}}{s_i}} } + }\\ {\frac{1}{2}\sum\limits_{i = 1}^N {{p_{ri}}} \sum\limits_{j \in {N_i}} {{a_{ij}}\int_{t - {\varepsilon _{ij}}}^t {{{\tanh }^2}{\psi_{ej}}\left( {{s_j}} \right){\rm{d}}{s_j}} } } \end{array} $ | (56) |
对式(56)求导,并代入(52)和(53)得
| $ \begin{array}{*{20}{c}} {{{\dot V}_4} = - \sum\limits_{i = 1}^N {{k_{ui}}{{\tanh }^2}{z_{ei}}} - }\\ {\frac{1}{2}\sum\limits_{i = 1}^N {\sum\limits_{j \in {N_i}} {{p_{ui}}{a_{ij}}\left( {\tanh {z_{ei}}\left( t \right) - } \right.} } }\\ {{{\left. {\tanh {z_{ej}}\left( {t - {\varepsilon _{ij}}} \right)} \right)}^2} - }\\ {\frac{1}{2}\sum\limits_{i = 1}^N {\sum\limits_{j \in {N_i}} {{p_{ui}}{a_{ij}}\left( {\tanh {\psi _{ei}}\left( t \right) - } \right.} } }\\ {{{\left. {\tanh {\psi _{ej}}\left( {t - {\varepsilon _{ij}}} \right)} \right)}^2} - \sum\limits_{i = 1}^N {{k_{ri}}{{\tanh }^2}{\psi _{ei}}} } \end{array} $ | (57) |
显然
| $ \mathop {\lim }\limits_{t \to \infty } \sum\limits_{i = 1}^N {{k_{ui}}{{\tanh }^2}{z_{ei}}} = \mathop {\lim }\limits_{t \to \infty } \sum\limits_{i = 1}^N {{k_{ri}}{{\tanh }^2}{\psi _{ei}}} = 0 $ | (58) |
| $ \mathop {\lim }\limits_{t \to \infty } \sum\limits_{i = 1}^N {\sum\limits_{j \in {N_i}} {{a_{ij}}{{\left( {\tanh {z_{ei}}\left( t \right) - \tanh {z_{ej}}\left( {t - {\varepsilon _{ij}}} \right)} \right)}^2}} } = 0 $ | (59) |
| $ \mathop {\lim }\limits_{t \to \infty } \sum\limits_{i = 1}^N {\sum\limits_{j \in {N_i}} {{a_{ij}}{{\left( {\tanh {\psi _{ei}}\left( t \right) - \tanh \left( {{\psi _{ej}}\left( {t - {\varepsilon _{ij}}} \right)} \right)} \right)}^2}} } = 0 $ | (60) |
显然存在正整数b1, b2满足kub1>0, krb2>0使得
进一步得
| $ \mathop {\lim }\limits_{t \to \infty } \left( {{z_{ei}}\left( t \right) - {z_{ej}}\left( {t - {\varepsilon _{ij}}} \right)} \right) = 0, $ |
| $ \mathop {\lim }\limits_{t \to \infty } \left( {{\psi _{ei}}\left( t \right) - {\psi _{ej}}\left( {t - {\varepsilon _{ij}}} \right)} \right) = 0 $ |
证毕。
基于通信延时下的动力学回路设计及其稳定性分析与第3节一致,这里不在展开讨论。
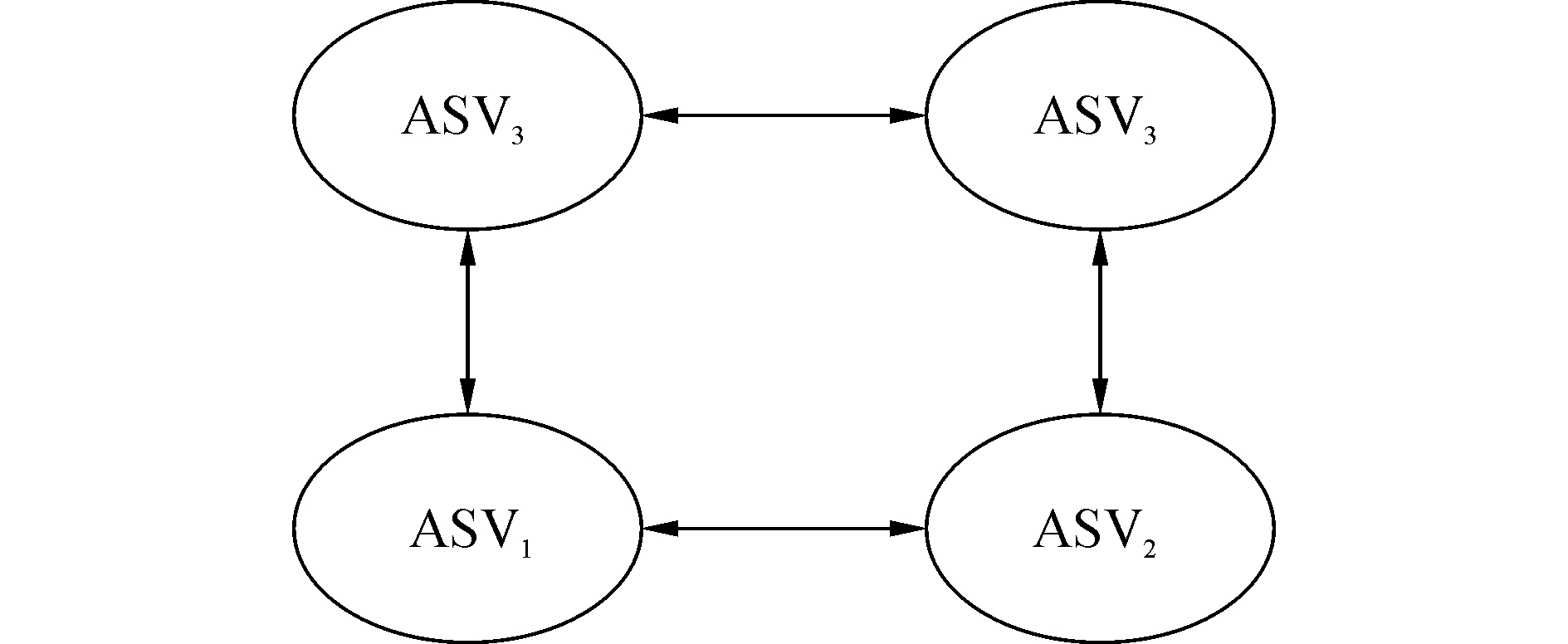
5 仿真实验为验证鲁棒协同控制律的有效性,采用四艘相同欠驱动ASV船模,其模型参数如表 1所示[20]。假设欠驱动ASV之间的通信拓扑结构如图 2所示。
| 表 1 ASV参数 Tab.1 Parameters of ASVs |
|
图 2 通信拓扑图 Fig.2 Communication topology |
通信拓扑结构对应Laplacian阵设为
| $ \mathit{\boldsymbol{L}} = \left[{\begin{array}{*{20}{c}} 2&{-1}&0&{-1}\\ {-1}&2&{ - 1}&0\\ 0&{ - 1}&2&{ - 1}\\ { - 1}&0&{ - 1}&2 \end{array}} \right] $ |
设定参考轨迹为pd(t)=(0.05 t,0.015 t)及各个ASV对应的期望队形向量分别为
Δ1=(-4;0), Δ2=(0;-4), Δ3=(4;0), Δ4=(0;4);4个ASV的初始速度为ui(0)=vi(0)=0 m/s; ri(0)=0 rad/s; (i=1, 2, …, N)。
初始位置向量为
η1(0)=(-5,-1.8,-π/4), η2(0)=(1.5,-5.2,-π/6), η3(0)=(5,-1.4,π/3), η4(0)=(-1.25,4.3,π/3)。
设定偏置量为δ=0.3, 控制参数为
kui=0.015, kri=0.3, pui=pri=0.02, λ1i=0.5, λ2i=0.1, γ1i=0.5, γ2i=0.1, p=σ=0.75。
水动力参数估计误差取:
M11=0.02m11, M22=0.02m22, Du=0.02du, Du2=0.02du2, Dv=0.02dv, Dv2=0.02dv2, Dvr=0.02dvr, Dr=0.02dr, Dr2=0.02dr2, Drv=0.02drv。
下面分析三种不同情况下的协同控制效果。
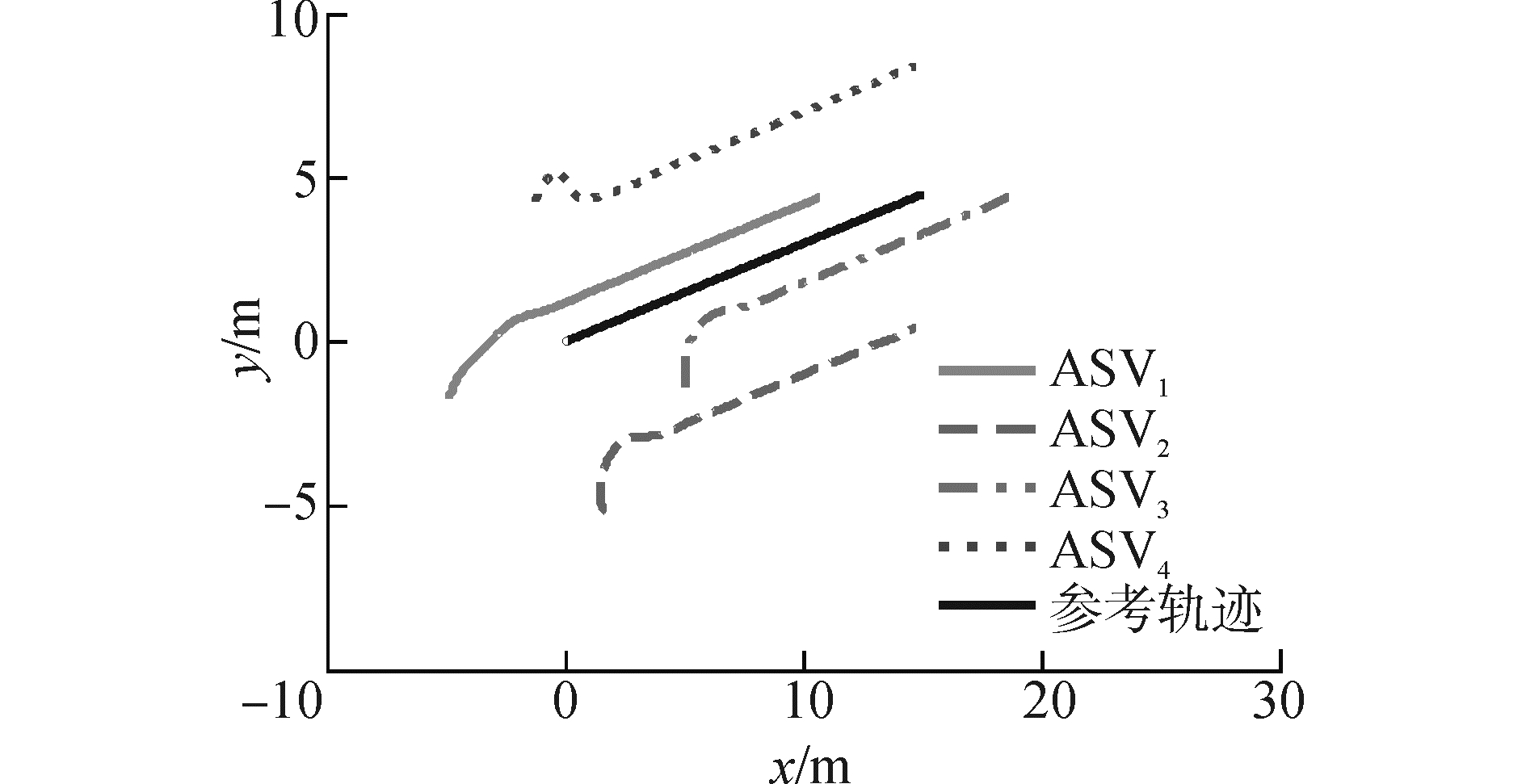
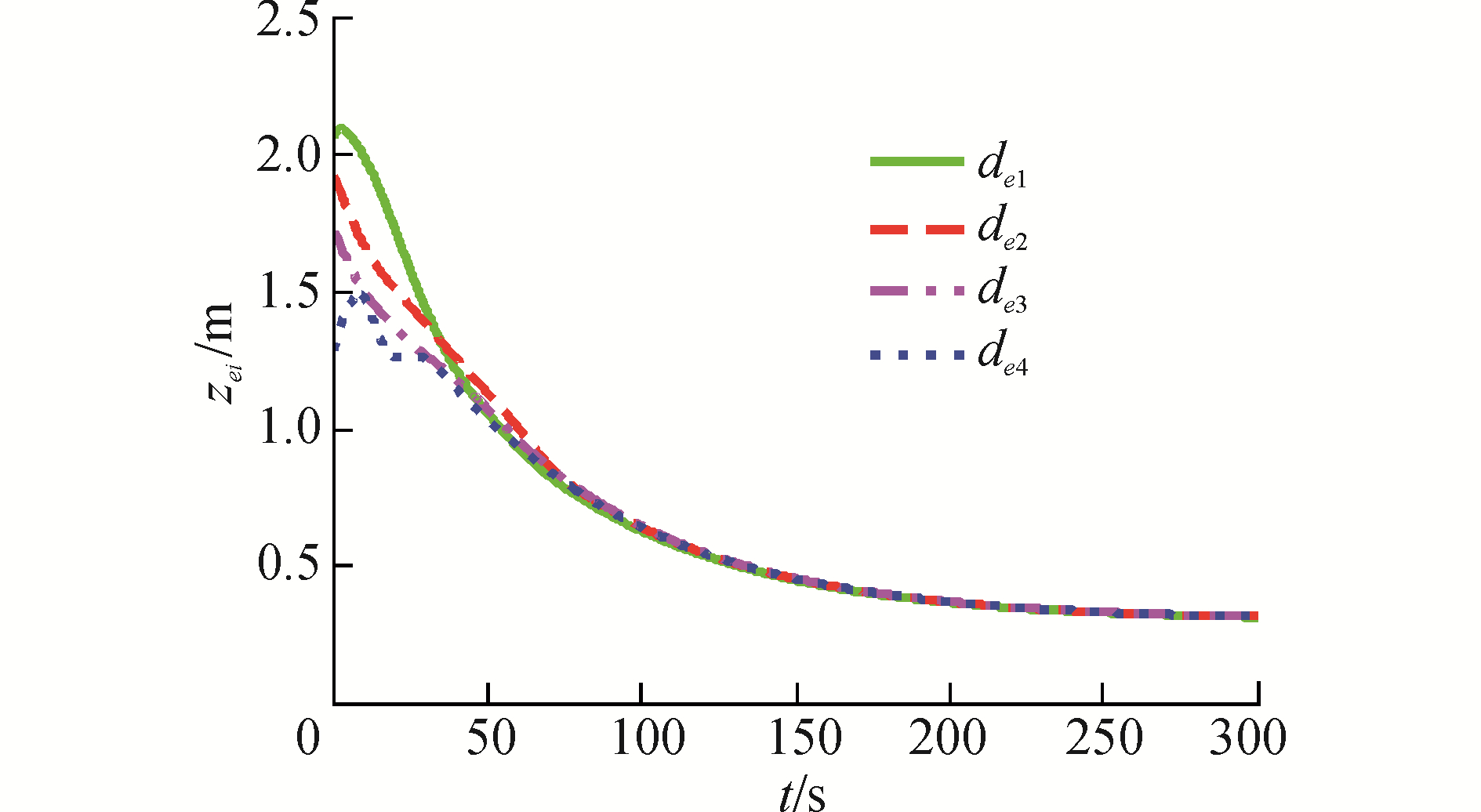
5.1 实时通信与无干扰情况图 3~5给出的是多ASV协同控制系统在实时通信与无外界环境干扰下的控制效果。4艘ASV运动轨迹曲线如图 3,可以看出各个ASV能够以期望队形运行;各个ASV的距离跟踪误差和艏向角跟踪误差分别如图 4与5所示。从图中可以发现dei、ψei在100 s时候趋于一致,dei最终收敛于0.3左右(即zei收敛于零附近邻域),ψei收敛于零附近,即实现了协同控制目标(15)和(16)。
|
图 3 实时通信与无干扰下各个ASV的运动轨迹 Fig.3 Trajectory of each ASV without considering the communication delay and the external disturbance |
|
图 4 实时通信与无干扰下位置跟踪误差 Fig.4 Time evolution of position errors without considering the communication delay and the external disturbance |
|
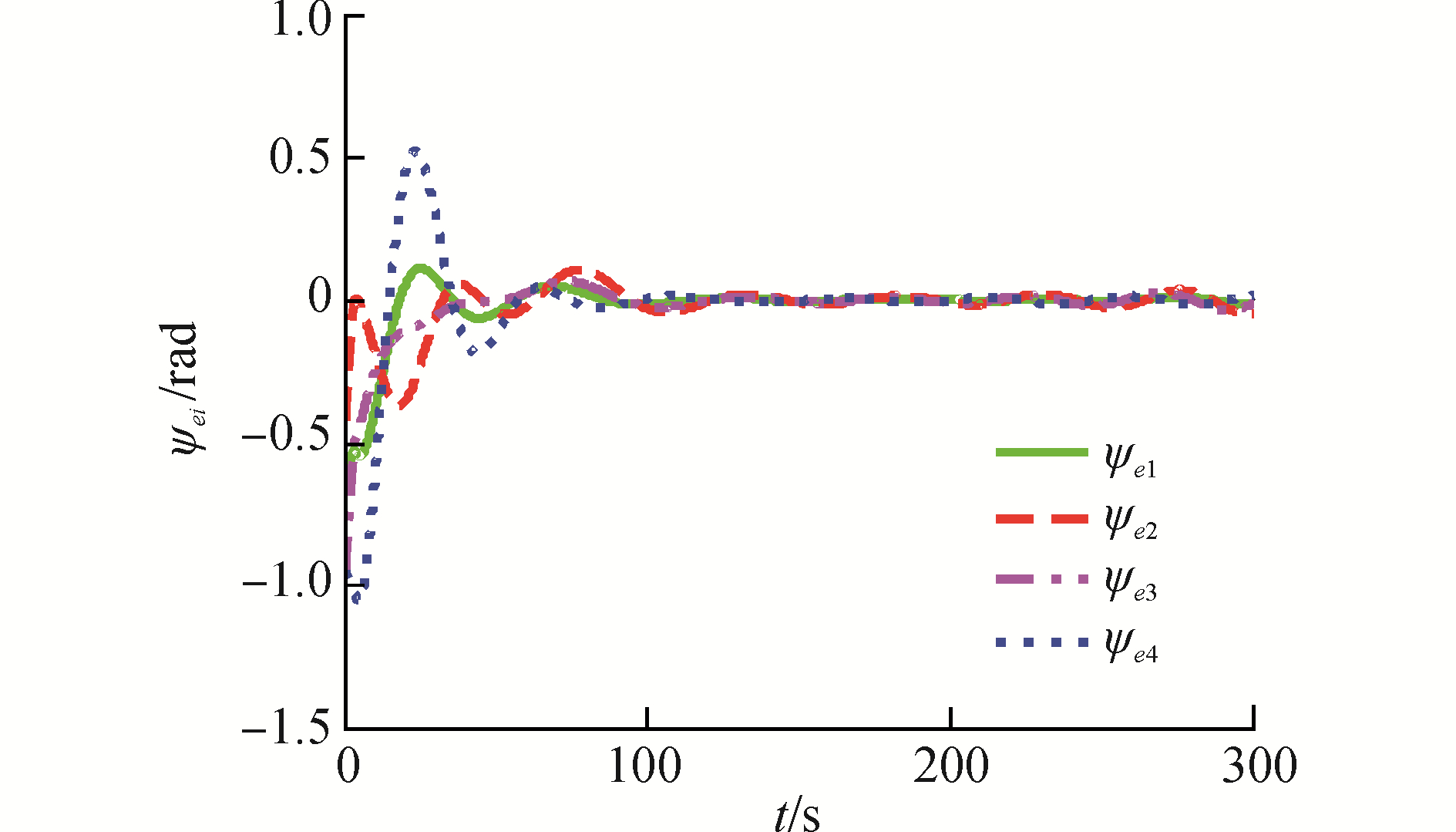
图 5 实时通信与无干扰下艏向角跟踪偏差 Fig.5 Time evolution of heading errors without considering the communication delay and the external disturbance |
图 6~8为同时考虑通信延时、参数摄动以及外界环境干扰作用下的协同控制效果。假设ASV受到的环境扰动为
|
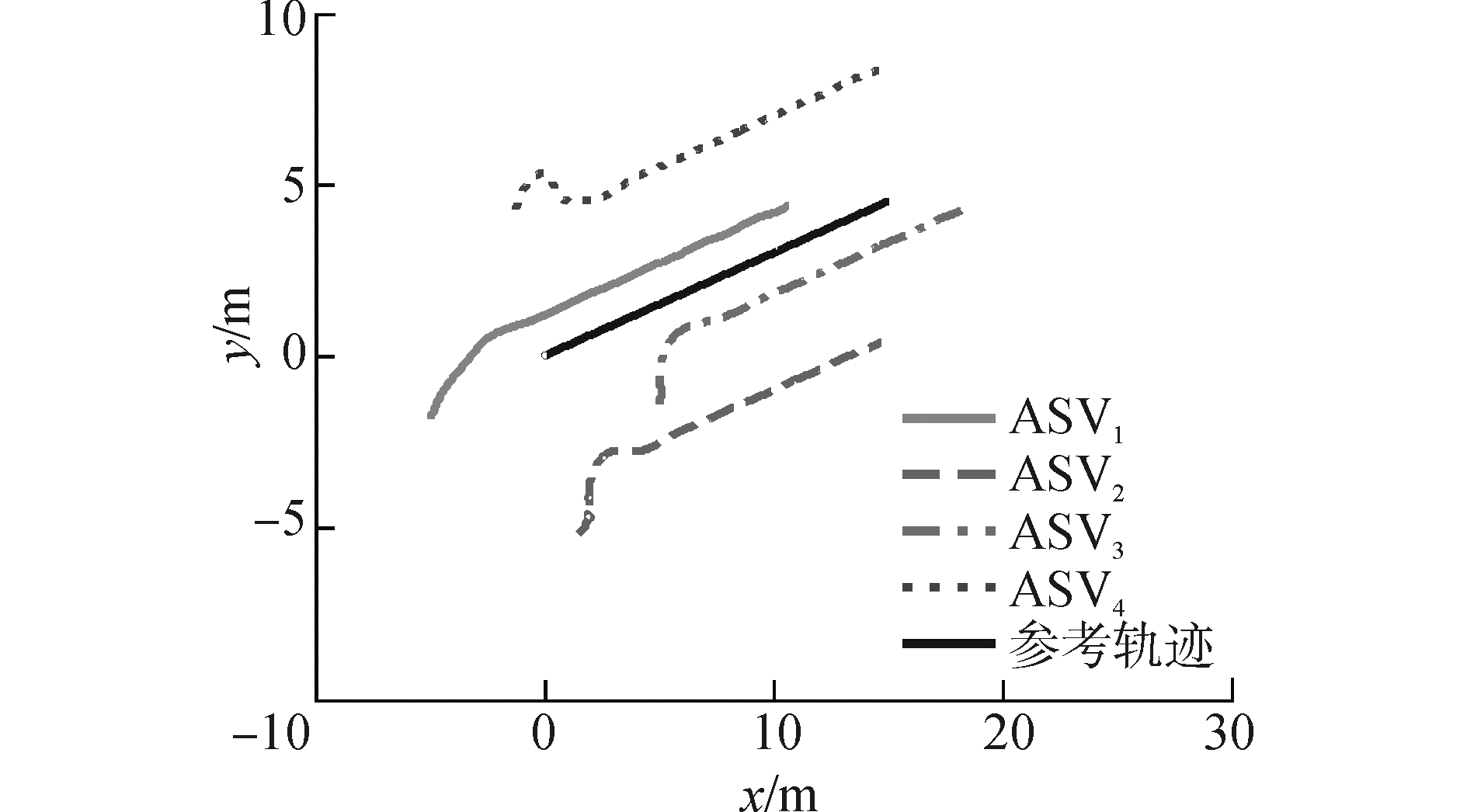
图 6 在通信延时1 s和外界干扰下各个ASV的运动轨迹 Fig.6 Trajectory of each ASV with considering the communication delay 1 s and the external disturbances |

|
图 7 在通信延时1 s和外界干扰下位置跟踪误差 Fig.7 Time evolution of position errors with considering the communication delay 1 s and the external disturbances |

|
图 8 在通信延时1 s和外界干扰下艏向角跟踪偏差 Fig.8 Time evolution of heading errors with considering the communication delay 1 s and the external disturbances |
| $ {\tau _{wui}}\left( t \right) = 0.35\sin \left( {0.012t + {\rm{ \mathit{ π} }}/6} \right) + 0.05 $ |
| $ {\tau _{wvi}}\left( t \right) = 0.018\cos \left( {0.01t + {\rm{ \mathit{ π} /4}}} \right) + 0.002 $ |
| $ {\tau _{wri}}\left( t \right) = 0.042\sin \left( {0.008t + {\rm{ \mathit{ π} /4}}} \right) + 0.008 $ |
从图 6可以看出在外界干扰下各个ASV仍能够按照其期望队形运行;从图 7和8可以看出曲线在瞬态和稳态都出现了波动增大的现象,但最终曲线均收敛于平衡状态附近,即实现了控制目标。
6 结论1) 与文献[13]相比,本文提出一种基于饱和约束的一致性算法,防止变量较大时控制输入超过模型的物理约束;
2) 本文克服了文献[10]需要假设艏向转速持续激励的问题,即可以同时实现对直线与曲线轨迹的协同跟踪;
3) 与文献[10-12]不同,本文借鉴文献[17]的引导部分,将系统分为运动环和动力环,并将闭环编队控制系统构建成级联系统形式,证明了系统的全局稳定性;
4) 区别于文献[9, 12],本文无需在线估计不确定项,克服神经网络设置参数过多的难题,仅需设定干扰与参数摄动的上界,设计参数少,具有结构简单、鲁棒性强等优点。
| [1] |
BELLETER D J W, PETTERSEN K Y. Path following for formations of underactuated marine vessels under influence of constant ocean currents[C]//2014 IEEE 53rd Annual Conference on Decision and Control (CDC). 2014: 4521-4528.
(  0) 0)
|
| [2] |
ALMEIDA J, SILVESTRE C, PASCOAL A M. Cooperative control of multiple surface vessels with discrete time periodic communications[J]. International journal of robust and nonlinear control, 2012, 22(4): 398-419. DOI:10.1002/rnc.v22.4 (  0) 0)
|
| [3] |
KYRKJEBØ E, PETTERSEN K Y, WONDERGEM M, et al. Output synchronization control of ship replenishment operations:theory and experiments[J]. Control engineering practice, 2007, 15(6): 741-755. DOI:10.1016/j.conengprac.2006.07.001 (  0) 0)
|
| [4] |
LIU L, WANG D, PENG Z H. Direct and composite iterative neural control for cooperative dynamic positioning of marine surface vessels[J]. Nonlinear dynamics, 2015, 81(3): 1315-1328. DOI:10.1007/s11071-015-2071-8 (  0) 0)
|
| [5] |
GHOMMAM J, MNIF F, BENALI A, et al. Asymptotic backstepping stabilization of an underactuated surface vessel[J]. IEEE transactions on control systems technology, 2006, 14(6): 1150-1157. DOI:10.1109/TCST.2006.880220 (  0) 0)
|
| [6] |
XIE W, MA B. Position centroid rendezvous and centroid formation of multiple unicycle agents[J]. IET control theory and applications, 2014, 8(17): 2055-2061. DOI:10.1049/iet-cta.2013.0940 (  0) 0)
|
| [7] |
SHOJAEI K. Leader-follower formation control of under-actuated autonomous marine surface vehicles with limited torque[J]. Ocean engineering, 2015, 105: 196-205. DOI:10.1016/j.oceaneng.2015.06.026 (  0) 0)
|
| [8] |
ARRICHIELLO F, CHIAVERINI S, FOSSEN T. Formati-on control of underactuated surface vessel using the null-space-based behavioral control[C]//2006 IEEE/RSJ International Conference on Intelligent Robots and Systems. 2006: 5942-5947. http://www.springerlink.com/content/2r562rm338118405
(  0) 0)
|
| [9] |
PENG Z H, WANG D, HU X J. Robust adaptive formation control of underaetuated autonomous surface vehicles with uncertain dynamics[J]. IET Control theory and applications, 2011, 5(12): 1378-1387. DOI:10.1049/iet-cta.2010.0429 (  0) 0)
|
| [10] |
DONG W. Cooperative control of underactuated surface vessels[J]. IET control theory and applications, 2010, 4(9): 1569-1580. DOI:10.1049/iet-cta.2009.0362 (  0) 0)
|
| [11] |
BØRHAUG E, PAVLOV A, PANTELEY E, et al. Straight line path following for formations of underactuated marine surface vessels[J]. IEEE transactions on control systems technology, 2011, 19(3): 493-506. DOI:10.1109/TCST.2010.2050889 (  0) 0)
|
| [12] |
PENG Z, WANG D, LAN W, et al. Decentralized cooperative control of autonomous surface vehicles with uncertain dynamics: a dynamic surface approach[C]//Am-erican Control Conference (ACC), 2011: 2174-2179. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=5990621
(  0) 0)
|
| [13] |
DE La TORRE G, YUCELEN T. Consensus with reduced communication links via relative neighboring velocity information[C]//American Control Conference (ACC). 2015: 3410-3415. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=7171859
(  0) 0)
|
| [14] |
ZUO Z. Nonsingular fixed-time consensus tracking for second-order multi-agent networks[J]. Automatica, 2015, 54: 305-309. DOI:10.1016/j.automatica.2015.01.021 (  0) 0)
|
| [15] |
YANG Q, FANG H, CHEN J, et al. Distributed observer-1 based coordination for multiple Lagrangian systems using 2 only position measurements[J]. Control theory and applilations, 2014, 8(17): 2102-2114. DOI:10.1049/iet-cta.2014.0392 (  0) 0)
|
| [16] |
DONG W. Flocking of multiple mobile robots based on backstepping[J]. IEEE Transactions on systems, man, and cybernetics, Part B:cybernetics, 2011, 41(2): 414-424. DOI:10.1109/TSMCB.2010.2056917 (  0) 0)
|
| [17] |
LI J H, LEE P M, JUN B H, et al. Point-to-point navigation of underactuated ships[J]. Automatica, 2008, 44(12): 3201-3205. DOI:10.1016/j.automatica.2008.08.003 (  0) 0)
|
| [18] |
沈艳军, 刘万海, 张勇. 一类非线性系统全局有限时间观测器设计[J]. 控制理论与应用, 2010, 27(5): 668-674. SHEN Y J, LIU W H, ZHANG Y. Global finite-time observers for a class of nonlinear systems[J]. Control theory & applications, 2010, 27(5): 668-674. (  0) 0)
|
| [19] |
BHAT S P, BERNSTEIN D S. Finite-time stability of homogeneous systems[C]//Proc of the American Control Conference, 1997: 2513-2514. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=609245
(  0) 0)
|
| [20] |
LIU L, WANG D, PENG Z. Path following of marine surface vehicles with dynamical uncertainty and time-varying ocean disturbances[J]. Neurocomputing, 2016, 173: 799-808. DOI:10.1016/j.neucom.2015.08.033 (  0) 0)
|
| [21] |
FOSSEN T I. Handbook of Marine Craft Hydrodynamics and Motion Control[M]. West Sussex: John Wiley & Sons Ltd, 2011: 45-58.
(  0) 0)
|
 2017, Vol. 38
2017, Vol. 38


