电力推进船舶采用电动机取代传统的推进柴油机直接驱动螺旋桨,具有节约空间、节能环保及易于控制等优点[1]。由于推进电机是电力推进船舶的主要动力源,其电气特性、机械特性与节能特性会直接影响船舶推进性能[2]。因此,推进电机的运行性能需要与螺旋桨特性相匹配,且需要满足功率和转速变化范围均很宽的多工况运行条件[3]。
目前,船舶电力推进系统所采用的推进电机主要包括三类(异步、同步、永磁)四种电机(异步、同步、方波电动机、正弦波电动机)。其中,永磁同步电机具有效率高、体积小、功率密度大等优点,开关磁阻电机具有结构简单、容错性能好等优点,因此永磁电机中的永磁同步电机[4]、开关磁阻电机[5]等已经成功应用到船舶推进系统中。而永磁容错电机FTPMM是在综合考虑永磁同步电机和开关磁阻电机优缺点的基础上设计而成的,具有良好的容错性、动静态控制性能及可靠性,可以很好地满足船舶电力推进系统的要求[6]。
船舶推进器的控制性能与控制策略也需要与推进电动机配套,交流变频技术的发展使得电机的矢量控制、直接转矩控制、V/F变频变压控制等策略可以适应不同船舶推进要求[7]。其中,电压空间矢量脉宽调制SVPWM和电流滞环跟踪脉宽调制CHBPW是两种常用的PWM矢量控制策略,在基于全桥逆变电路的电机控制中已得到成熟应用[8-9]。近些年,越来越多的文献开始研究基于H桥逆变电路的SVPWM和CHBPWM两种控制策略,但很少有文献分析两种控制策略的优缺点及适用范围[10-11]。因此,为了更好地研究基于H桥逆变器的永磁容错电机在船舶电力推进控制系统中的应用,本文首先分析三相永磁容错电机和H桥逆变电路基本结构,根据永磁容错电机矢量控制系统的基本原理,搭建仿真模型和实验平台,通过对公式、仿真和实验结果的分析,归纳对比了SVPWM和CHBPWM控制技术的优缺点、相互关系及适用范围。
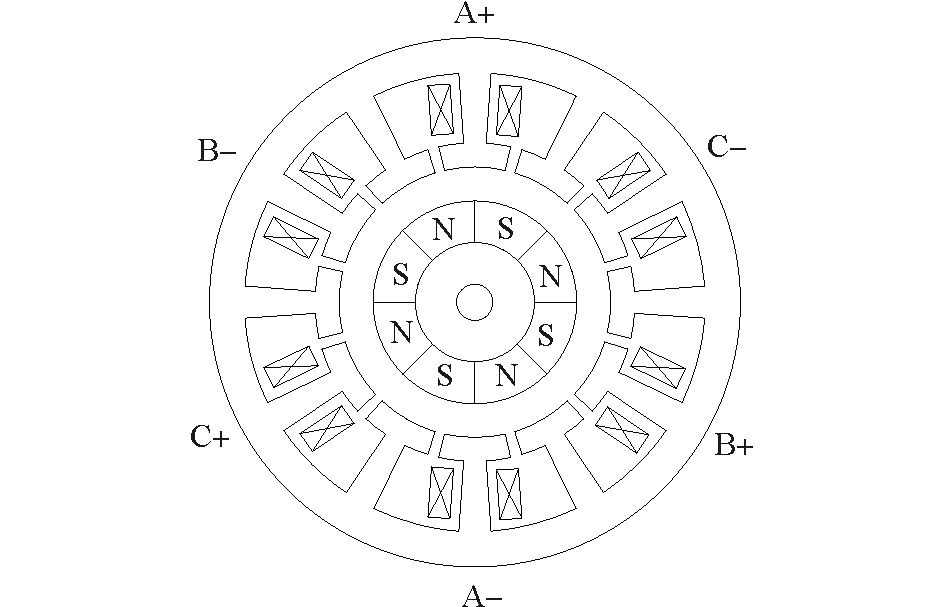
1 永磁容错电机结构及H桥逆变电路图 1为三相永磁容错电机结构,每个槽内只有一相绕组,绕组间电枢齿隔开,实现了物理隔离、热隔离、磁隔离,各绕组间采用H桥逆变电路,实现了电气隔离,通过开槽深度和绕组匝数设计提高电抗,减小了短路电流,具有故障容错能力[12]。
|
图 1 12槽3相8极永磁容错电机结构图 Fig.1 Structure diagram of 3-phase 8-pole 12-slot FTPMM |
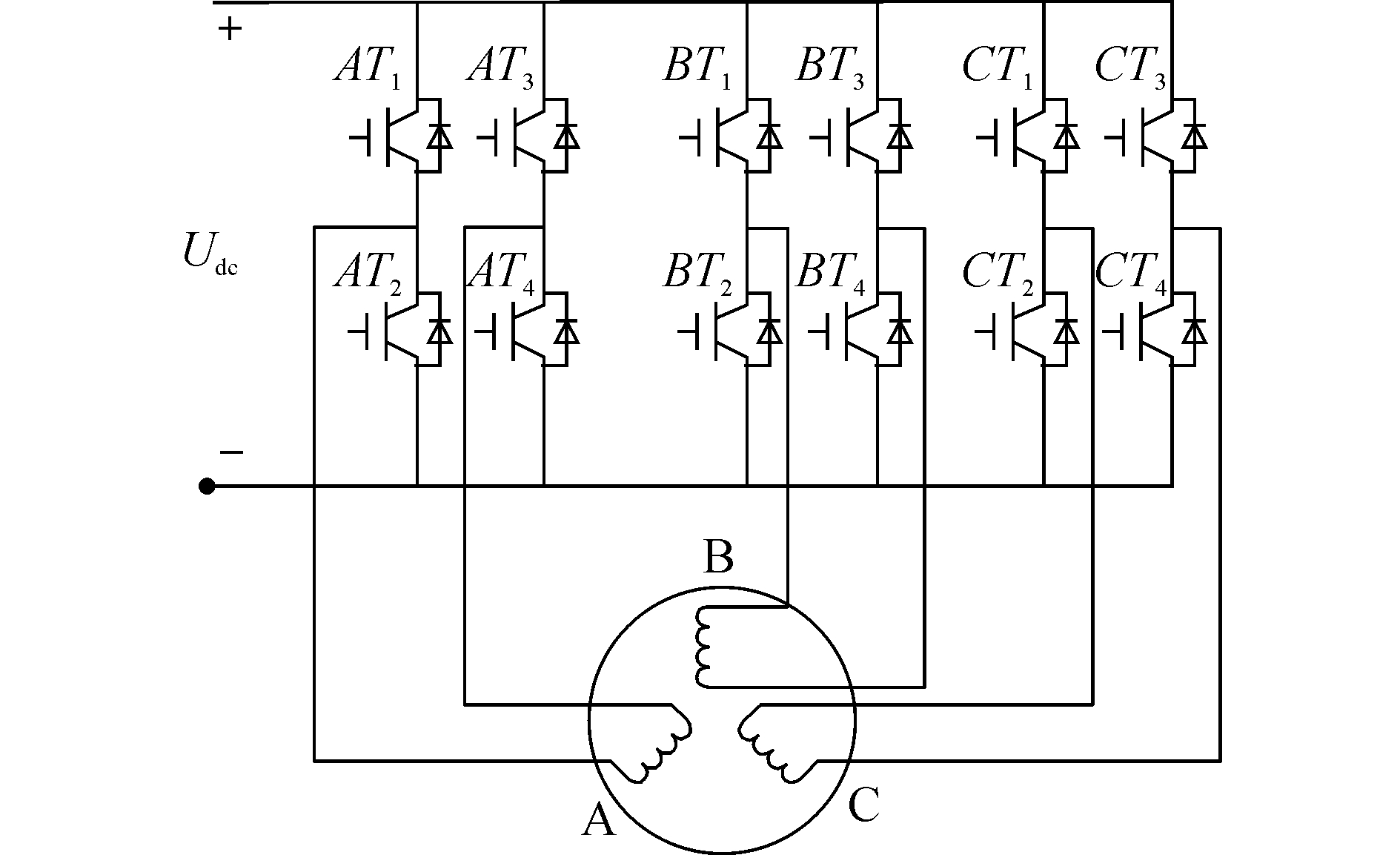
永磁容错电机的H桥逆变电路如图 2所示。同普通的三相全桥逆变电路相比,H桥逆变电路的电压基波幅值更大,直流电源的利用率更高。电机各个绕组间无中性点,增加了器件的可靠性,提供了丰富的电压空间矢量,为提高电机的容错控制能力提供了条件[13]。
|
图 2 三相永磁容错电机H桥逆变电路 Fig.2 H-bridge inverters of the FTPMM |
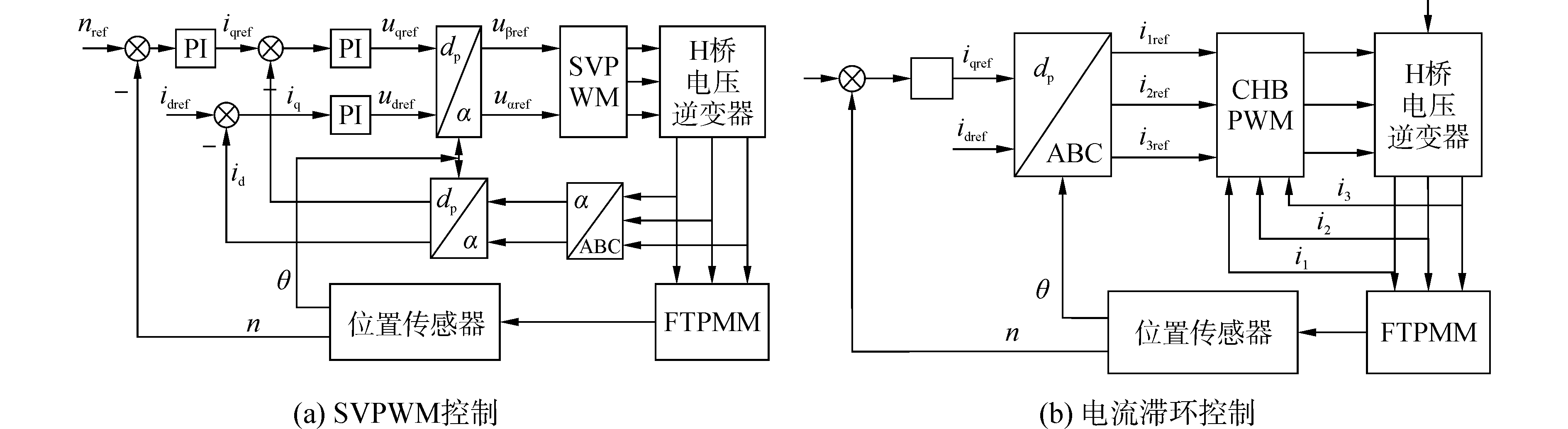
永磁容错电机的矢量控制系统由永磁容错电机、H桥逆变器、转子位置与转速传感器和电流控制环节等多个部分组成。电机转速闭环通常采用比例积分(proportional integral,PI)控制,定子电流闭环分别采用SVPWM控制和CHBPWM控制。两种矢量控制系统结构框图如图 3所示。
|
图 3 矢量控制系统结构框图 Fig.3 Vector control system of the FTPMM |
SVPWM控制算法是将逆变器与电机视为一体,根据逆变器在不同工作模式下所产生的实际磁链矢量来追踪基准磁链圆,由逆变器功率器件的开关模式和脉宽宽度产生调制波,产生互差120°电角度且失真尽可能小的三相正弦电流波形[16]。
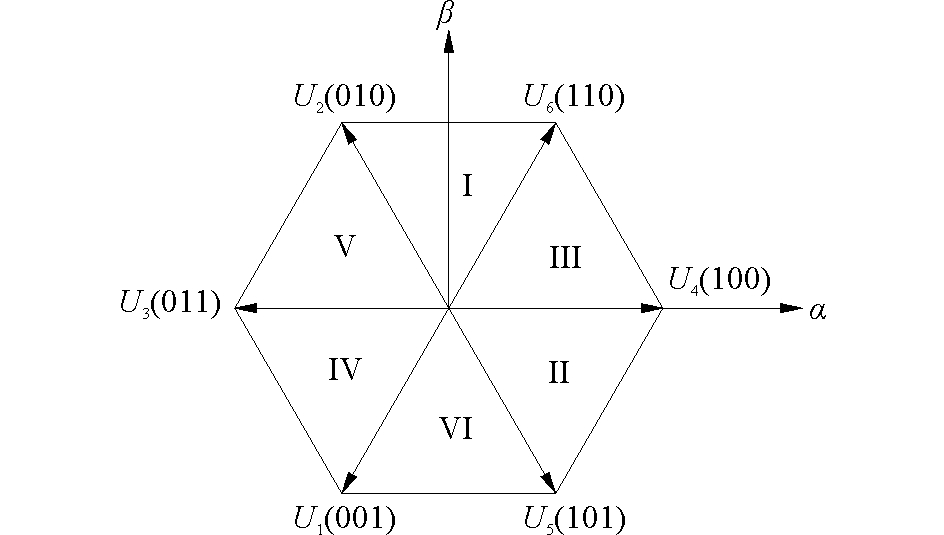
H桥逆变电路为180°导通型功率开关管,上下桥臂不能同时导通,则可得到23=8个合成电压矢量,如图 4所示。
|
图 4 电压空间矢量图 Fig.4 Sector distribution of voltage space vector |
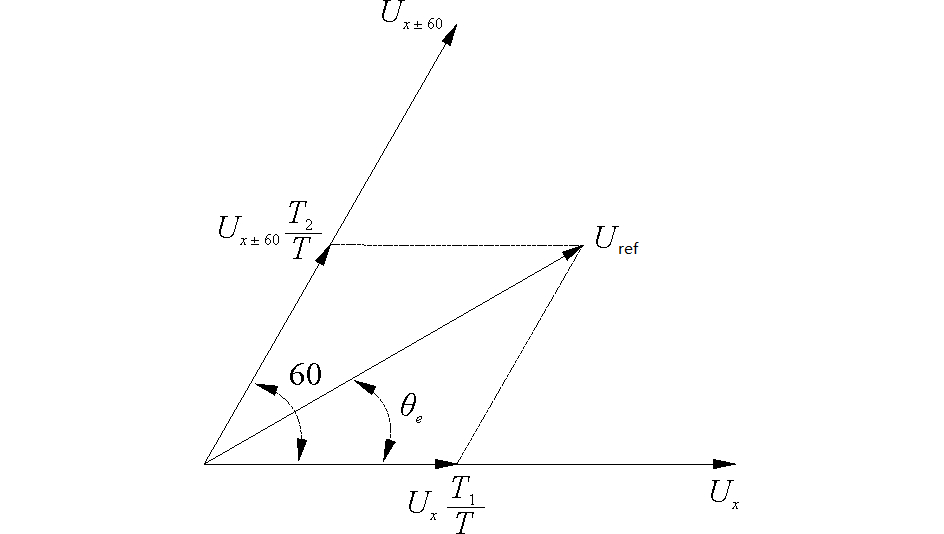
在一个控制周期T内,SVPWM参考与电压矢量最接近的两个开关矢量,通过控制每个开关矢量工作时间,使各开关矢量在平均伏秒意义上与参考电压矢量的控制效果等效,如图 5所示,可表示为
|
图 5 电压合成矢量图 Fig.5 Voltage space vector diagram |
| $ {U_x} \cdot {T_1} + {U_{x \pm 60^\circ }} \cdot {T_2} + {U_{0,7}} \cdot {T_0} = {U_{{\rm{ref}}}}\cdot T $ | (1) |
式中:T1、T2表示所选的相邻两电压矢量的作用时间,T0表示零矢量的作用时间,T满足关系T=T1+T2+T0,Uref为期望电压矢量。
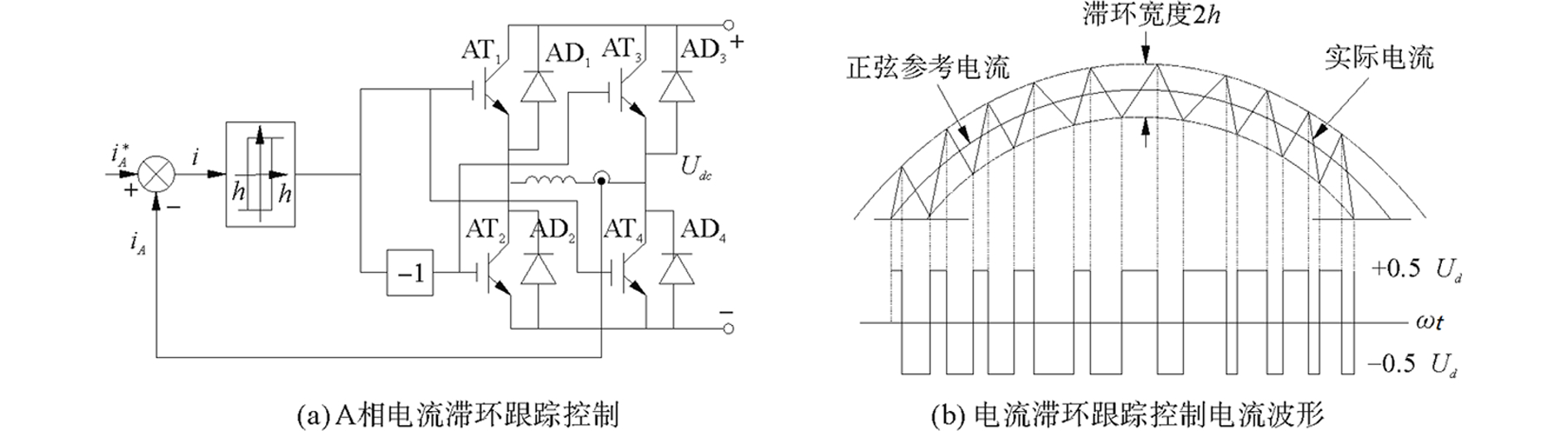
2.3 CHBPWM控制CHBPWM技术的基本思想是根据给定的三相定子电流信号与检测到的实际定子电流信号的误差关系确定H桥逆变电路中各开关的状态,保证在实际电流大于给定值时,通过逆变器使之减小,反之增大[14]。最终,实际的电流波形围绕给定的电流在一定误差范围内作锯齿状变化,图 6为控制原理图。
|
图 6 电流滞环跟踪控制原理图 Fig.6 CHBPWM control principle of the FTPMM |
图 6(b)为正弦参考电流在滞环控制下相电流的产生过程,频率足够高时,开关管的开关频率为[15]
| $ f = \frac{1}{T} = \frac{{{U_{\rm{d}}}}}{{2hL}} $ | (2) |
式中:Ud为逆变器输出的直流母线电压,2h为滞环比较器的环宽,L为滤波电感。式(2) 可以看出,滞环比较器的环宽2h直接影响电流的跟踪性能:h过大时,开关频率低,跟踪误差大;h过小时,跟踪误差小,但开关频率过高,开关损耗增大。
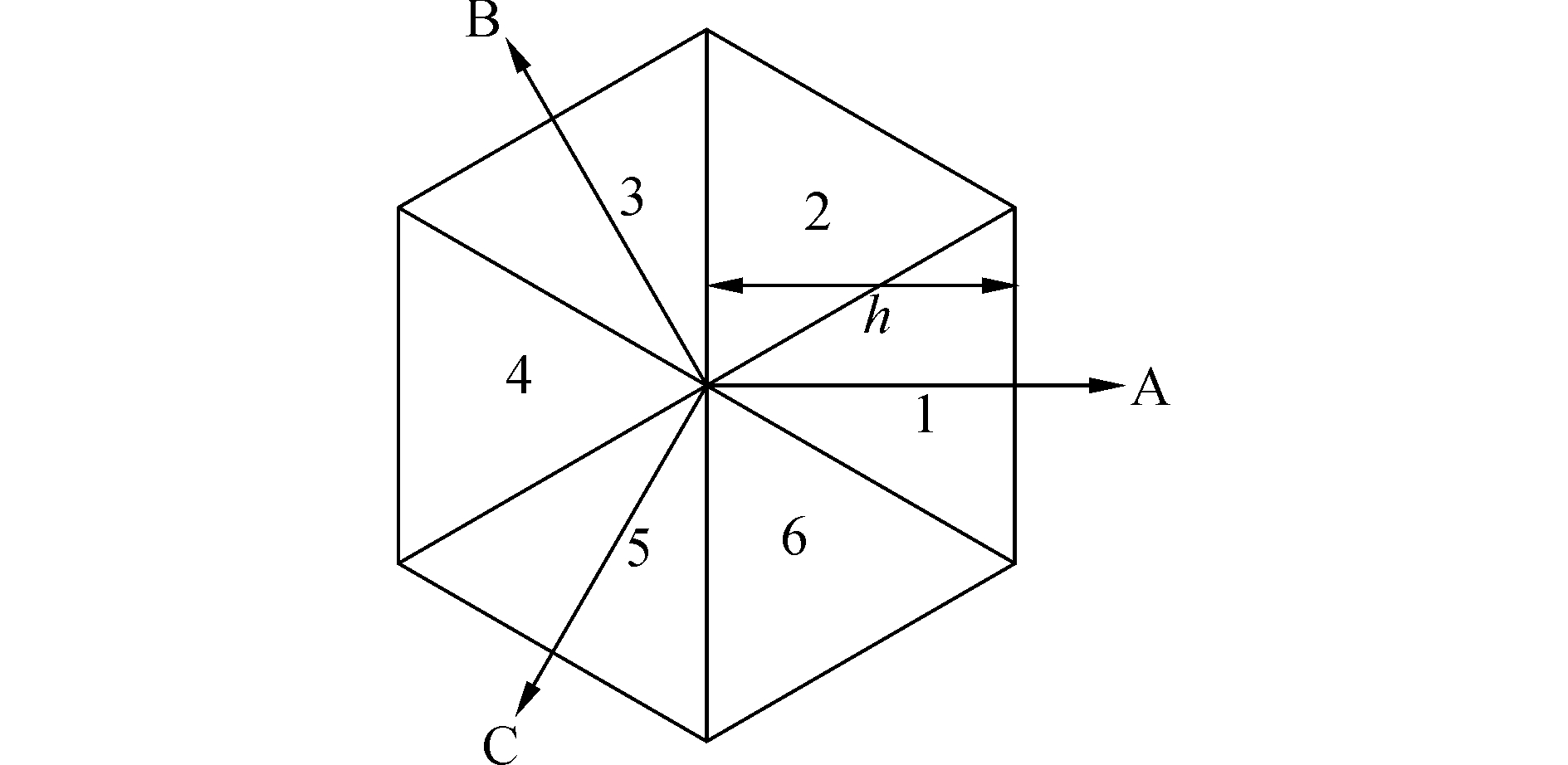
在滞环比较器作用下,实际电流矢量I在跟踪参考电流矢量I*的过程中,其偏差会被限定在由三相开关线构成的内六边形内,如图 7所示。
|
图 7 电流矢量偏差区域分配 Fig.7 Sector distribution of current vector deviation |
电流滞环控制的电路结构简单易于实现,但开关频率不固定,而SVPWM控制属于电压调制方式,系统开关频率恒定,但由于死区时间的存在,系统的动态响应和开关频率特性有一定的局限性,但两种矢量控制均属于电流控制。
3.1 两种控制方式的谐波分析三相永磁容错电机输出的周期为T=2π/ω的非正弦电压UA(ωt)满足Dirichlet收敛条件,可分解为如下形式的傅里叶级数[17]:
| $ {U_{\rm{A}}}\left( {\omega t} \right) = {a_0} + \sum\limits_{n = 1}^\infty {\left[ {{a_n}\cos \left( {n\omega t} \right) + {b_n}\sin \left( {n\omega t} \right)} \right]} {\rm{ }} $ | (3) |
其中
| $ \begin{array}{l} {a_0} = \frac{1}{{2\pi }}\int_0^{2\pi } {U\left( {\omega t} \right){\rm{d}}\left( {\omega t} \right)} \\ {a_n} = \frac{1}{\pi }\int_0^{2\pi } {U\left( {\omega t} \right)\cos \left( {n\omega t} \right){\rm{d}}\left( {\omega t} \right)} \\ {b_n} = \frac{1}{\pi }\int_0^{2\pi } {U\left( {\omega t} \right)\sin \left( {n\omega t} \right){\rm{d}}\left( {\omega t} \right)} \end{array} $ |
由Dirichlet收敛定理可知,其傅里叶级数收敛。由SVPWM控制的工作原理展开为
| $ \begin{array}{l} {U_{{\rm{A}}n}}\left( {\omega t} \right) = \frac{2}{{\sqrt 3 }}\cos \left( {\omega t} \right) - \frac{3}{{4\pi }}\cos 3\left( {\omega t} \right) - {\rm{ }}\frac{3}{{40\pi }}\cos \left( {9\omega t} \right) - \\ \;\;\;\;\;\;\;\frac{3}{{112\pi }}\cos \left( {15\omega t} \right) - \frac{3}{{220\pi }}\cos\left( {21\omega t} \right) - \ldots \end{array} $ | (4) |
式中:UAn(ωt)是对UA(ωt)的逼近。由式(4) 可看出SVPWM控制的电压主要由基波和三次谐波构成。由于H桥逆变电路各相绕组相互独立,不能像普通同步电机那样通过星形连接滤除三次谐波,所以该逆变电路输出的电压和电流会受到三次谐波影响。
由于CHBPWM控制过程中无需载波,所以输出电压中不含特定频率的谐波分量。
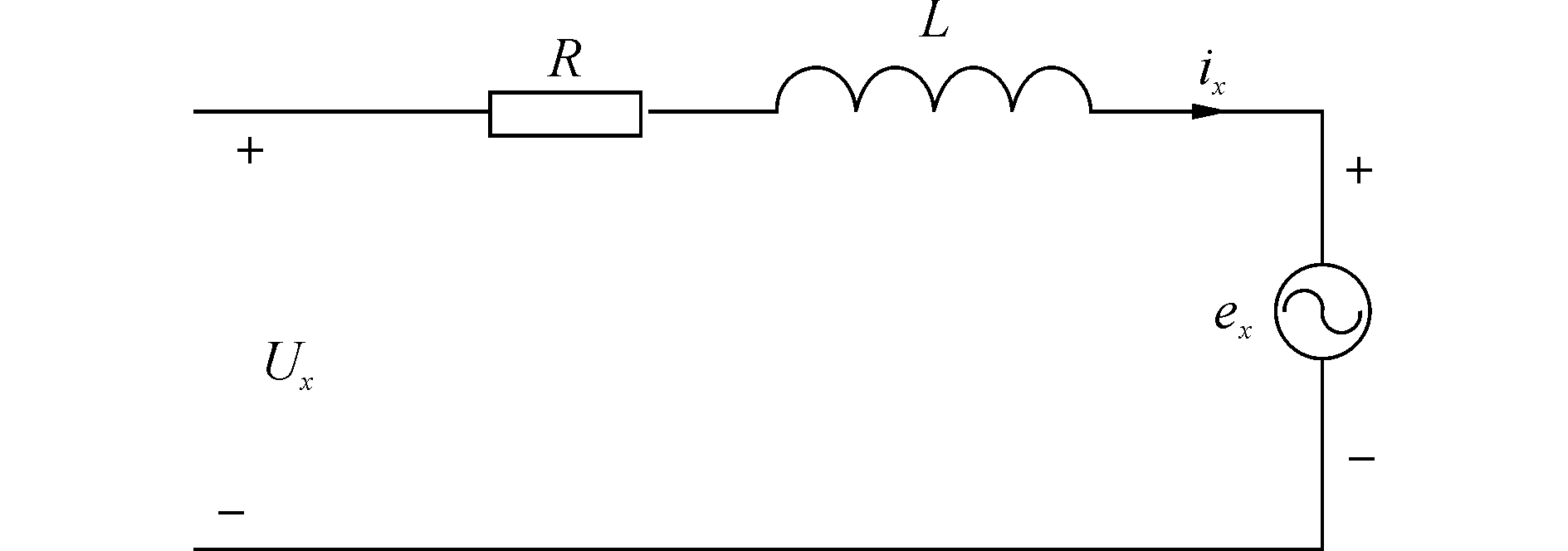
3.2 两种控制方式的控制效果关系永磁容错电机的互感可以忽略不计,则绕组的等效电路如图 8所示。其中,L、R分别为电机该相绕组的电感和定子电阻,ex(x表示a、b、c)为该相绕组产生的反电动势,ux为该相绕组两端电压。
|
图 8 x相绕组电路模型 Fig.8 The circuit model of x-phase winding |
由图 8可得,电机每相绕组电压方程如下:
| $ \left[ {\begin{array}{*{20}{c}} {{u_a}}\\ {{u_b}}\\ {{u_c}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} R&0&0\\ 0&R&0\\ 0&0&R \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{i_a}}\\ {{i_b}}\\ {{i_c}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} L&0&0\\ 0&L&0\\ 0&0&L \end{array}} \right]\frac{{\rm{d}}}{{{\rm{d}}t}}\left[ {\begin{array}{*{20}{c}} {{i_a}}\\ {{i_b}}\\ {{i_c}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{e_a}}\\ {{e_b}}\\ {{e_c}} \end{array}} \right] $ | (5) |
忽略绕组电阻,式(5) 可近似表示为
| $ \boldsymbol{U} = \boldsymbol{E} + \boldsymbol{L}\frac{{{\rm{d}}I}}{{{\rm{d}}t}} $ | (6) |
假设给定电流矢量为I*,则误差电流为
| $ \Delta \boldsymbol{I} = {\boldsymbol{I}^*} - \boldsymbol{I} $ | (7) |
将式(7) 代入式(6) 中得,
| $ \boldsymbol{L}\frac{{{\rm{d}}\Delta I}}{{{\rm{d}}t}} = \boldsymbol{E} + \boldsymbol{L}\frac{{{\rm{d}}{\boldsymbol{I}^*}}}{{{\rm{d}}t}} - \boldsymbol{U} $ | (8) |
由式(8) 可看出,误差电流矢量跟反电动势、给定电流矢量变化率及电压有关系。当ΔI=0时,交流侧电压给定值满足:
| $ {\boldsymbol{U}_{{\rm{ref}}}} = \boldsymbol{E} + \boldsymbol{L}\frac{{{\rm{d}}{\boldsymbol{I}^*}}}{{{\rm{d}}t}} $ | (9) |
由于三相H桥逆变电路有23=8种电压输出uk(k=0,1,……,7) 状态,则式(8) 可改为
| $ \boldsymbol{L}\frac{{{\rm{d}}\Delta \boldsymbol{I}}}{{{\rm{d}}t}} = \boldsymbol{E} + \boldsymbol{L}\frac{{{\rm{d}}{\boldsymbol{I}^*}}}{{{\rm{d}}t}} - {\boldsymbol{u}_{\rm{k}}} $ | (10) |
代入式(9) 中得:
| $ \boldsymbol{L}\frac{{{\rm{d}}\Delta \boldsymbol{I}}}{{{\rm{d}}t}} = {\boldsymbol{U}_{{\rm{ref}}}} - {\boldsymbol{u}_{\rm{k}}} $ | (11) |
由于CHBPWM控制是由电流矢量偏差ΔI区域检测判断开关顺序的,SVPWM根据参考电压选择合适的电压矢量来判断开关顺序的,则由(11) 可知,通过给定电压矢量Uref和选择的空间电压矢量uk,可以控制误差电流矢量的变化率
为了验证上述两种矢量控制策略的正确性,在Matlab/Simulink R2012a中搭建三相永磁容错电机矢量控制系统仿真模型,对基于CHBPWM和SVPWM的两种控制策略的性能进行比较,两种方法均采用id=0的控制策略。表 1为仿真时所需的电机参数,仿真时间设置为0.3 s。
| 表 1 仿真所需的电机参数 Tab.1 Simulation parameters of the FTPMM |
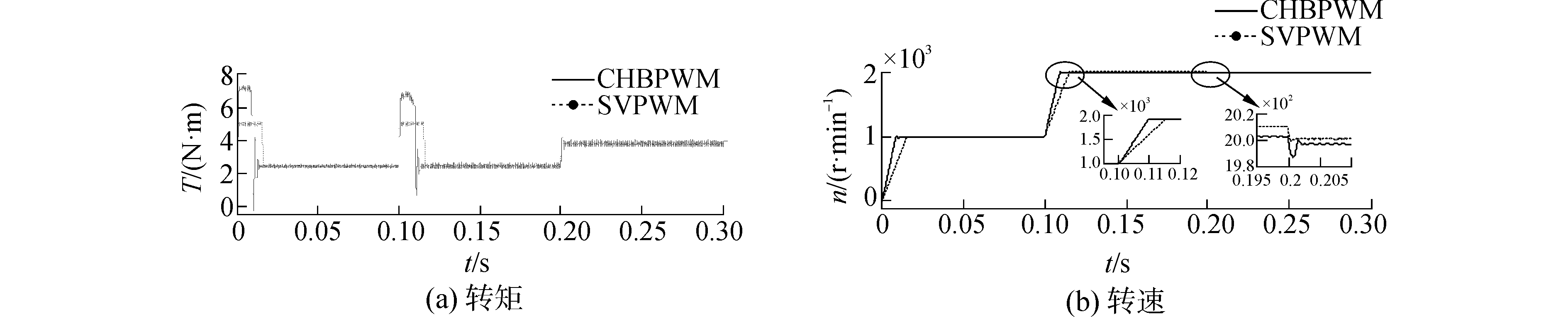
为便于比较,两者的速度环均采用PI控制且取相同的PI系数,仿真时间均设置为0.3 s,电流滞环控制的环宽h=0.01。启动时给定转速n=1 000 r/min,转矩T=2.3 N·m,在t=0.1 s突加转速到n=2 000 r/min,在t=0.2 s时突加负载到额定转矩T=3.75 N·m,所得转速和转矩的仿真波形如图 9所示。在SVPWM控制中,起动过程中最大转矩相对较小,约为5.1 N·m,大约经过0.015 s达到稳定运行状态,此时转矩最大值约为2.38 N·m,最小转矩值约为2.22 N·m,转矩脉动约为6.96%;转速最大值约为1 010 r/min,最小转速值约为990 r/min,转速脉动约为2.0%;转速突变至2 000 r/min时,经过大约0.05 s即达到稳定。在CHBPWM控制中,起动过程中最大转矩达到7.2 N·m,大约经过0.01 s达到稳定运行状态,此时转矩最大值约为2.42 N·m,最小转矩值约为2.20 N·m,转矩脉动约为9.52%;转速最大值约为1 015 r/min,最小转速值约为980 r/min,转速脉动约为3.51%;转速突变至2 000 r/min时,经过大约0.01 s即达到稳定;转矩突变时,达到稳定所需时间更短,约为0.002 s。
|
图 9 转速、负载突变时的波形变化图 Fig.9 The changing waveforms of torque and speed |
由图 9可看出,CHBPWM控制的响应速度比SVPWM控制稍快;但是在负载和速度突变时,由于CHBPWM控制的开关频率不固定,所以其转矩脉动和速度脉动比SVPWM要大的多。
0.211~0.3 s时间内,两种控制方式均为稳定运行,对该时间段内的电压进行谐波分析,可得图 10。由图 10可以看出,在参数相同的情况下,SVPWM在基波频率附近的谐波畸变率(total harmonic distortion,THD)值较大,而CHBPWM没有特定频率的谐波含量。

|
图 10 电压谐波分析 Fig.10 Voltage harmonic analysis |
仿真结果表明:基于SVPWM控制策略的转矩和转速脉动小、谐波含量少,而CHBPWM控制方法相对简单,响应速度较快,当功率器件的开关频率足够高时,不依赖于电机参数,鲁棒性好。因此在对响应速度要求较高的场合应该优先考虑CHBPWM控制,而对于转矩和转速精度要求较高的场合则需要考虑采用SVPWM控制。
船舶根据用途差别有不同的要求,如小型轮渡船舶对调速精确度要求相对较低,但要求具有良好的启动性能和响应速度;而科学测量船舶则需要精确的速度、定位和较小的脉动,但对响应速度的要求相对不高。此时就可以选择SVPWM控制策略或SVPWM控制策略使得船舶推进电机发挥最优功能。
5 实验验证及分析为了进一步分析基于H桥逆变电路的永磁容错电机的性能,对基于CHBPWM和SVPWM的两种控制方式进行闭环实验研究,实验用三相四极永磁容错电机控制系统, 如图 11所示。其中功率器件选用FGA25N120ANTD IGBT,控制器采用TMS320F28335 DSP芯片。永磁容错电机同轴安装一台永磁同步发电机作为负载,其三相输出经整流后连接可调变阻器,通过调节变阻器改变系统负载的大小。其中,实验电机的参数同表 1中的仿真参数相同。

|
图 11 永磁容错电机控制系统实验平台 Fig.11 Experiment platform of FTPMM control system |
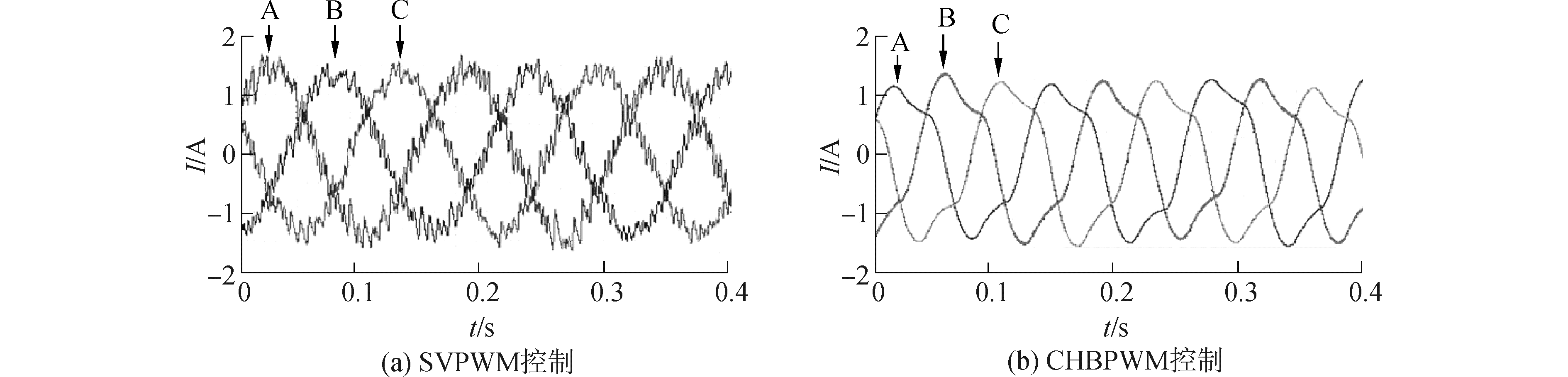
实验时,给定转速为1 000 r/min。两种控制策略下电机输出到示波器中的三相电流波形分别如图 12所示。由图 12可知,两种控制策略下三相电流波形均为近似正弦波,验证了H桥逆变电路驱动的两种控制方式的正确性。经过滤波后,SVPWM后基本没有毛刺,但由于含有三次谐波,其正弦度有一定的影响,CHBPWM在环宽范围内作锯齿状波动,均与理论分析一致。
|
图 12 电流波形图 Fig.12 Current waveforms |
同样工作条件下,测得两种控制方式的转速波形如图 13所示。由图 13(a)可知,最大转速约为1 007 r/min,最小转速约为985 r/min,转速脉动约为2.21%。由图 13(b)可知,最大转速约为1 016 r/min,最小转速约为977 r/min,转速脉动约为3.91%。

|
图 13 转速波形图 Fig.13 Speed waveforms |
由图 13可知,两种控制策略下转速均可以正确跟踪给定转速,而且SVPWM控制的转速脉动约为2.21%,CHBPWM控制的转速脉动约为3.91%,与仿真结果相同。
同样工作条件下,测得两种控制方式的转矩波形如图 14所示。由图 14(a)可知,最大输出转矩约为2.42 N·m,最小输出转矩约为2.15 N·m,转矩脉动约为11.82%。由图 14(b)可知,最大输出转矩约为2.43 N·m,最小输出转矩约为2.12 N·m,转矩脉动约为13.62%。

|
图 14 转矩波形图 Fig.14 Torque waveforms |
由图 14可知,两种控制策略均可输出给定的转矩,SVPWM控制的转矩脉动(约为11.82%)比CHBPWM控制的转矩脉动(约为13.62%)稍小。
实验过程中,由于变量离散化, 设备精度不够等因素转速和转矩脉动均比仿真波形要大,但均能控制在要求的范围内。
6 结论1) 通过调整SVPWM控制中给定电压矢量和选择的空间电压矢量,或调整CHBPWM控制中误差电流矢量的变化率,可使两种控制方式在一定情况下实现同样的控制效果。
2) SVPWM控制策略转矩和转速脉动小、谐波含量少,而CHBPWM控制方法相对简单,响应速度较快,鲁棒性好。因此在对响应速度要求较高的场合应优先考虑CHBPWM控制,而对转矩和转速精度要求较高的场合则优先采用SVPWM控制。
3) 对于以永磁容错电机为推进电机的电推船,可以进一步研究在电机发生故障时,采用容错控制策略后对整个船舶系统性能的影响,分析船舶系统的容错性能,进一步提高整个船舶系统的可靠性和稳定性。
| [1] |
白洪芬, 朱景伟, 秦俊峰. 改进滑模观测器在船舶电力推进PMSM无位置控制中的应用[J]. 中国航海, 2015, 38(4): 22-25. BAI Hongfen, ZHU Jingwei, QIN Junfeng. Improved SMO based sensorless PMSM vector control in ship electric propulsion system[J]. Navigation of China, 2015, 38(4): 22-25. (  0) 0)
|
| [2] |
华斌, 周艳红, 谢冰若, 等. 电机技术在舰船电力推进系统中的应用研究[J]. 微电机, 2015, 48(5): 101-105. HUA Bin, ZHOU Yanhong, XIE Bingruo, et al. Motor technology applied in naval ship electric drive propulsion[J]. Micormotors, 2015, 48(5): 101-105. (  0) 0)
|
| [3] |
汤天浩, 韩朝珍. 船舶电力推进系统[M]. 北京: 机械工业出版社, 2015.
( 0) 0)
|
| [4] |
REN J, LIU Y, WANG N, et al. Sensorless control of ship propulsion interior permanent magnet synchronous motor based on a new sliding mode observer[J]. ISA transactions, 2015, 54(1): 15-26. ( 0) 0)
|
| [5] |
MITRA A, EMADI A. On the suitability of large switched reluctance machines for propulsion applications[C]//2012 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, 2012:1-5. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6243423
( 0) 0)
|
| [6] |
MECROW B C, JACK A G, ATKINSON D J, et al. Design and testing of a four-phase fault-tolerant permanent-magnet machine for an engine fuel pump[J]. IEEE transaction on energy conversion, 2004, 19(2): 132-137. ( 0) 0)
|
| [7] |
乔鸣忠, 曾海燕, 夏益辉, 等. 船舶电力推进系统稳定性分析[J]. 哈尔滨工程大学学报, 2015, 36(5): 611-615. QIAO Mingzhong, ZENG Haiyan, XIA Yihui, et al. The stability analysis of an electric propulsion system for ships[J]. Journal of Harbin Engineering University, 2015, 36(5): 611-615. (  0) 0)
|
| [8] |
付胜杰, 彭侠夫. 六相逆变器空间矢量脉宽调制策略的分析与优化[J]. 哈尔滨工程大学学报, 2012, 33(4): 512-516. FU Shengjie, PENG Xiafu. Analysis and optimization of SVPWM strategy for a six-phase inverter[J]. Journal of Harbin Engineering University, 2012, 33(4): 512-516. (  0) 0)
|
| [9] |
廖金国, 花为, 程明, 等. 一种永磁同步电机变占空比电流滞环控制策略[J]. 中国电机工程学报, 2015, 35(18): 4762-4770. LIAO Jinguo, HUA Wei, CHENG Ming, et al. A variable-duty-cycle current-hysteresis control strategy for permanent magnet synchronous motors[J]. Proceedings of the CSEE, 2015, 35(18): 4762-4770. (  0) 0)
|
| [10] |
BAI H, ZHU J, QIN J. Fault-tolerant control for a dual-winding fault-tolerant permanent magnet motor drive based on SVPWM[J]. IET power electronics, 2017, 10(5): 509-516. DOI:10.1049/iet-pel.2015.1033 ( 0) 0)
|
| [11] |
蔡巍, 乔鸣忠, 张晓锋. H桥型五相感应电机SVPWM控制技术[J]. 电力系统及其自动化学报, 2008, 20(4): 33-38. CAI Wei, QIAO Mingzhong, ZHANG Xiaofeng. SVPWM control technique for five-phase H-bridge induction motor[J]. Proceedings of the CSU-EPSA, 2008, 20(4): 33-38. (  0) 0)
|
| [12] |
白洪芬, 朱景伟, 孙军浩, 等. 双绕组永磁容错电机不同故障容错控制策略的比较研究[J]. 电工技术学报, 2016, 31(13): 189-199. BAI Hongfen, ZHU Jingwei, SUN Junhao, et al. Comparative study of different fault-tolerant control strategies for dual-winding fault tolerant permanent magnet motor[J]. Transactions of China electrotechnical society, 2016, 31(13): 189-199. DOI:10.3969/j.issn.1000-6753.2016.13.022 (  0) 0)
|
| [13] |
朱景伟, 刁亮, 任宝珠. 具有冗余特性的永磁容错电机短路故障分析与控制[J]. 电工技术学报, 2013, 28(3): 80-86. ZHU Jingwei, DIAO Liang, REN Baozhu. Analysis and control of short-circuit fault in a fault-tolerant permanent magnet motor drive with redundancy[J]. Transactions of China electrotechnical society, 2013, 28(3): 80-86. (  0) 0)
|
| [14] |
王成元, 夏加宽, 孙宜标. 现代电机控制技术[M]. 北京: 机械工业出版社, 2014.
( 0) 0)
|
| [15] |
洪峰, 单任仲, 王慧贞, 等. 一种变环宽准恒频电流滞环控制方法[J]. 电工技术学报, 2009, 24(1): 115-119. HONG Feng, SHAN Renzhong, WANG Huizhen, et al. A varied hysteresis-band current controller with fixed switching frequency[J]. Transactions of China electrotechnical society, 2009, 24(1): 115-119. (  0) 0)
|
| [16] |
司宾强, 朱纪洪, 吉敬华. 四相永磁容错电机短路故障容错策略[J]. 控制与决策, 2014, 29(8): 1489-1494. SI Binqiang, ZHU Jihong, JI Jinghua. Two short-circuit fault tolerant strategies for four-phase permanent-magnet fault-tolerant machine[J]. Control and decision, 2014, 29(8): 1489-1494. (  0) 0)
|
| [17] |
GUO Hong, XU Jinquan, HUANG Xiaolin. A novel fault tolerant permanent magnet synchronous motor with improved optimal torque control for aerospace application[J]. Chinese journal of aeronautics, 2015, 28(2): 535-544. DOI:10.1016/j.cja.2015.01.008 ( 0) 0)
|
 2017, Vol. 38
2017, Vol. 38


